POLITECHNIKA WARSZAWSKA

Instytut Podstaw Budowy Maszyn

PRACOWNIA WIBROAKUSTYKI

02-524 Warszawa, ul. Narbutta 84

02-524 Warszawa, ul. Narbutta 84, tel. [phone]

Laboratorium Eksploatacji

Autorzy opracowania:

Jacek Dybała, Adam Gałęzia, Marcin Jasiński

Jędrzej Mączak, Stanisław Radkowski

Pakiet Matlab

Wprowadzenie w środowisko

(do użytku wewnętrznego)

Warszawa 2005

1

Wstęp

Pakiet MATLAB (od ang. MATrix LABoratory) w chwili obecnej jest faktycznym

standardem w obliczeniach naukowo technicznych. Zbudowany jest jako aplikacja mogąca
pracować w środowisku MS Windows oraz Unix. Jego jądro stanowi interpreter języka
programowania umożliwiający wykonywanie obliczeń numerycznych na macierzach (w
ogólności zespolonych) zgodnie z zaprogramowanymi algorytmami obliczeniowymi. Wokół
jądra jest zbudowane interaktywne środowisko (ekran poleceń do komunikacji z systemem i
ekrany graficzne) przeznaczone do tworzenia algorytmów obliczeniowych, wizualizacji
graficznej wyników, analizy danych i obliczeń numerycznych.

Podstawowym typem danych Matlaba jest macierz liczb zespolonych. Macierz liczb

rzeczywistych jest traktowana jako szczególny przypadek liczby zespolonej zgodnie z
regułami algebry. Liczba całkowita jest szczególnym przypadkiem macierzy mającej jeden
wiersz i jedną kolumnę (macierz jednoelementowa). Na macierzach można wykonywać
wszystkie typowe operacje arytmetyczne (suma, iloczyn iloraz, obliczanie wyznaczników,
odwracanie macierzy itd.) zgodnie z regułami rachunku macierzowego. Operacje te są
zazwyczaj wykonywane w jednej instrukcji programowej co pozwala na uzyskanie
olbrzymiej szybkości i sprawności działania a dodatkowo upraszcza zapis operacji. Dla
użytkownika dostępne są wszystkie podstawowe funkcje matematyczne, statystyczne i
inżynierskie, w tym analiza widmowa (szybka transformata Fouriera - FFT, filtry cyfrowe
itd.). Cechy te stanowią o niezwykłej wartości Matlaba wszędzie tam, gdzie niezbędne jest
wykonywanie obliczeń na bardzo dużych zbiorach danych.

Język Matlaba jest językiem wysokiego poziomu jak Basic, Fortran czy Pascal i

pozwala na pisanie programów realizujących określone algorytmy. Cechą Matlaba są tzw.
toolboxy, tekstowe biblioteki funkcji i procedur, przeznaczone do realizacji konkretnych
zadań w różnych dziedzinach. Wraz z Matlabem można zakupić kilkadziesiąt różnych
bibliotek procedur pokrywających zakres zastosowań od analizy sygnałów, teorii sterowania
(automatyka) i metody elementów skończonych, poprzez rachunek statystyczny, analizę
obrazów aż do biotechnologii i genetyki. Matlab umożliwia również w ograniczonym
zakresie na sterowanie aparaturą pomiarową i pozwala na opracowywanie układów
sterowania automatyką przemysłową (opracowywanie algorytmów sterowania kart
procesorów sygnałowych).

Matlab pozwala na wizualizację graficzną wyników obliczeń. Zawiera wszelkie

procedury graficzne niezbędne do wizualizacji danych Matlaba. Dotyczy to zarówno
wykresów dwu- jak i trójwymiarowych oraz wizualizacji objętości. Wszystkie obiekty na
wykresach mogą być interaktywnie edytowane (zmiana kształtu linii, koloru, opisów, skali
itd.) i eksportowane do typowych formatów graficznych. Tworzenie wykresów jest bardzo
proste i intuicyjne.

Udostępnienie w środowisku Matlaba niezawodnych implementacji algorytmów

matematyki stosowanej, bogatych funkcji graficznych i licznych modułów rozszerzeń
zorientowanych na określone dziedziny zastosowań oraz otwarta architektura środowiska
(rozszerzalność - możliwość budowania własnych funkcji użytkownika, przenośność -
jednakowy m-kod Matlaba dla różnych platform sprzętowych) sprawiły, że obecnie
MATLAB w znacznym stopniu wyparł z obliczeń naukowo-technicznych języki uniwersalne
(Fortran, C, C++) ograniczając ich zasadniczą rolę do funkcji oprogramowania
narzędziowego.

2

Wprowadzenie do pracy w środowisku Matlaba

Poniższy opis został potraktowany bardzo skrótowo  przedstawia środowisko Matlaba

tylko w takim zakresie w jakim jest to niezbędne dla wykonania ćwiczeń laboratoryjnych.
Osoby zainteresowane szerszym poznaniem możliwości Matlaba odsyła się do pomocy
dostępnych w internecie pod adresem producenta (firmy The Mathworks Inc.) np.

http://www.mathworks.com/access/helpdesk/help/pdf_doc/matlab/learnmatlab.pdf

(w języku

angielskim) a także licznych książek (dostępnych również w języku polskim) oraz
samouczków, które można w dużej liczbie znaleźć w internecie pod hasłem „matlab”.

Po uruchomieniu Matlaba na ekranie widoczne jest okno z migającym kursorem po

znakach >> pozwalającym na wpisanie polecenia. Wykonanie tego polecenia (jego
interpretacja) odbywa się po naciśnięciu klawisza <Enter>.

Z Matlaba można korzystać w dwojaki sposób:

1. Można traktować Matlaba jak zaawansowany kalkulator wykonujący operacje podane

w linii poleceń.

2. Można tworzyć programy (ciągi kolejnych poleceń) i nowe funkcje, które następnie

będą uruchamiane przez interpreter języka Matlab. Programy (nazywane skryptami) i
funkcje umieszcza się w plikach tekstowych (ASCII) z rozszerzeniami „.m”.
Programy i funkcje uruchamia się pisząc ich nazwy w linii poleceń.

Dla potrzeb Laboratorium Eksploatacji wystarczające jest korzystanie z Matlaba w pierwszy
z podanych sposobów, tj. korzystanie jedynie z linii poleceń. Aby wykonać działanie
matematyczne na liczbach wystarczy napisać to działanie tak jak na zwykłym kalkulatorze i
nacisnąć klawisz <Enter>. Poprzednie linie poleceń można wywołać naciskając ↑ i ↓.

Matlab wyświetli wynik umieszczając go w standardowej zmiennej ans (answer -
odpowiedź).

Operatory używane w Matlabie

Poniżej przedstawiono listę ważniejszych operatorów używanych w Matlabie (A i B
oznaczają zmienne zawierające macierze):

+

dodawanie macierzy.

A+B (A i B muszą mieć te same rozmiary)

-

odejmowanie macierzy. A-B

(A i B muszą mieć te same rozmiary)

*

mnożenie macierzy.

A*B (liczba kolumn A musi być równa liczbie wierszy B)

/

dzielenie macierzy.

X=A/B rozwiązuje liniowe działanie A*X=B

.* mnożenie odpowiadających sobie elementów macierzy przez siebie. A.*B (rozmiary A i B

muszą być takie same)

./

dzielenie odpowiadających sobie elementów macierzy przez siebie. A./B (rozmiary A i B

muszą być takie same)

^

podnoszenie macierzy do potęgi. A^P (P jest skalarem, A musi być macierzą kwadratową)

.^ podnoszenie elementów macierzy do potęgi
’

(znak apostrofu) transpozycja macierzy. A’ zamienia kolumny wierszami

>>2+2
ans=

4

3

Zmienne

Podstawienie

powoduje utworzenie w pamięci zmiennej a o wartości równej 5. Zmienna ta istnieje aż do
momentu celowego jej usunięcia poleceniem clear a lub poleceniem usunięcia wszystkich
zmiennych clear. Po zamknięciu Matlaba zmienne są usuwane z pamięci.

Zakończenie linii znakiem średnika powoduje niewyświetlenie wyniku na ekranie;

Zdefiniowane dotychczas zmienne można wyświetlić na ekranie korzystając z polecenia whos

Macierze

Macierze można wprowadzać do Matlaba na kilka różnych sposobów

1. poprzez podanie listy elementów;

2. poprzez wczytanie macierzy z pliku dyskowego (np. dane pomiarowe);

3. poprzez wygenerowanie macierzy za pomocą wbudowanych funkcji;

4. poprzez ich utworzenie za pomocą procedur (m-plików) napisanych przez

użytkownika.

Ad 1)

Wprowadzając macierz z klawiatury należy

• oddzielać kolejne elementy wiersza spacjami lub przecinkami,
• koniec wiersza oznaczać średnikiem;
• całą lista elementów umieścić w nawiasach klamrowych.

>>a=5
a=

5

>> whos
Name

Size Bytes

Class

a

1x1 8

double array

Grand total is 1 element using 8 bytes

>> A=[1 2 3; 4 5 6;7 8 9]
A =
1 2 3
4 5 6
7 8 9
>> whos
Name Size Bytes Class

A 3x3 72 double array
a 1x1 8 double array

Grand total is 10 elements using 80 bytes

4

UWAGA: Matlab rozróżnia duże i małe litery.

Ad 2)

Macierz może być wczytana do środowiska Matlaba z pliku dyskowego. Jeżeli w pliku tym
została zapisana w formacie znakowym (ASCII) wówczas wczytanie jej odbywa się poprzez
napisanie polecenia load nazwa_pliku –ASCII

W wyniku takiego polecenia utworzona zostanie zmienna o nazwie takiej jak nazwa

wczytanego pliku zawierającego macierz (rozszerzenie jest pomijane).

Macierze zdefiniowane w Matlabie można zapisać na dysku w postaci binarnej (rozszerzenie
„.mat” poleceniem save nazwa_pliku nazwy_macierzy lub w postaci tekstowej poleceniem
save nazwa_pliku nazwa_macierzy -ASCII

Ad 3)

Macierz może też być utworzona poprzez podanie pierwszego elementu, kroku zwiększania
wartości kolejnych elementów oraz ostatniego elementu oddzielonych dwukropkami. Jeżeli
parametr kroku jest pominięty, wówczas domyślnie przyjmowany jest za 1.

Takie rozwiązanie jest szczególnie często wykorzystywane w tych przypadkach, gdy
potrzebujemy macierzy opisującej ze stałym krokiem zmienną niezależną jakiejś funkcji
(czas, częstotliwość, kąt itp.) np.

Powyższe polecenia pozwalają na obliczenie funkcji sinus dla kątów od 0 do 2π z krokiem

π/2 i umieszczenie macierzy wynikowej w zmiennej s.

>> C=1:2:10
C =
1 3 5 7 9
>> D=1:5
D =
1 2 3 4 5
>> E=[1:2:12; 1:6]
E =
1 3 5 7 9 11
1 2 3 4 5 6

>> alfa=0:pi/2:2*pi
alfa =
0 1.5708 3.1416 4.7124 6.2832
>> s= sin(alfa)
s =
0 1.0000 0.0000 -1.0000 0.0000

>> load matrixA -ASCII
>> matrixA
matrixA =
1 2 3 4
5 6 7 8
9 10 11 12

>> save plikA matrixA
>>

5

Macierze można też tworzyć z uprzednio utworzonych macierzy pamiętając o zgodności
wymiarów.

Na macierzach można wykonywać różne operacje matematyczne, np.

oblicza sumę wartości elementów macierzy w poszczególnych kolumnach.

Inne przydatne operatory macierzowe to:

max(X)

- maksimum elementów z każdej z kolumn

min(X)

- minimum elementów z każdej z kolumn

mean(X)

- wartość średnia elementów z każdej z kolumn

std(X)

- odchylenie standardowe elementów z każdej z kolumn

sqrt(X)

- pierwiastki z elementów macierzy

Operatorem transpozycji macierzy (zamiany miejscami wierszy i kolumn) jest apostrof (').

Rozmiar macierzy można sprawdzić korzystając z polecenia size, zaś większy wymiar
macierzy poleceniem length.

Dostęp do elementów macierzy można uzyskać poprzez podanie adresu elementu

(wiersz,kolumna) w macierzy:

>> F=[C;D]
F =
1 3 5 7 9
1 2 3 4 5

>> sum(F)
ans =
2 5 8 11 14

>> F = [1 3 5 7; 1 2 3 4]
F =
1 3 5 7
1 2 3 4
>> F'
ans =
1 1
3 2
5 3
7 4

>> size(F)
ans =

2

4

>>length(F)
ans=
4

>> F(2,3)
ans =
3

6

lub zakresu adresów elementów (zakres wierszy, zakres kolumn) w macierzy:

Elementy grafiki 2D

Funkcję jednej zmiennej

)

( x

f

y

=

można przedstawić na wykresie w postaci graficznej

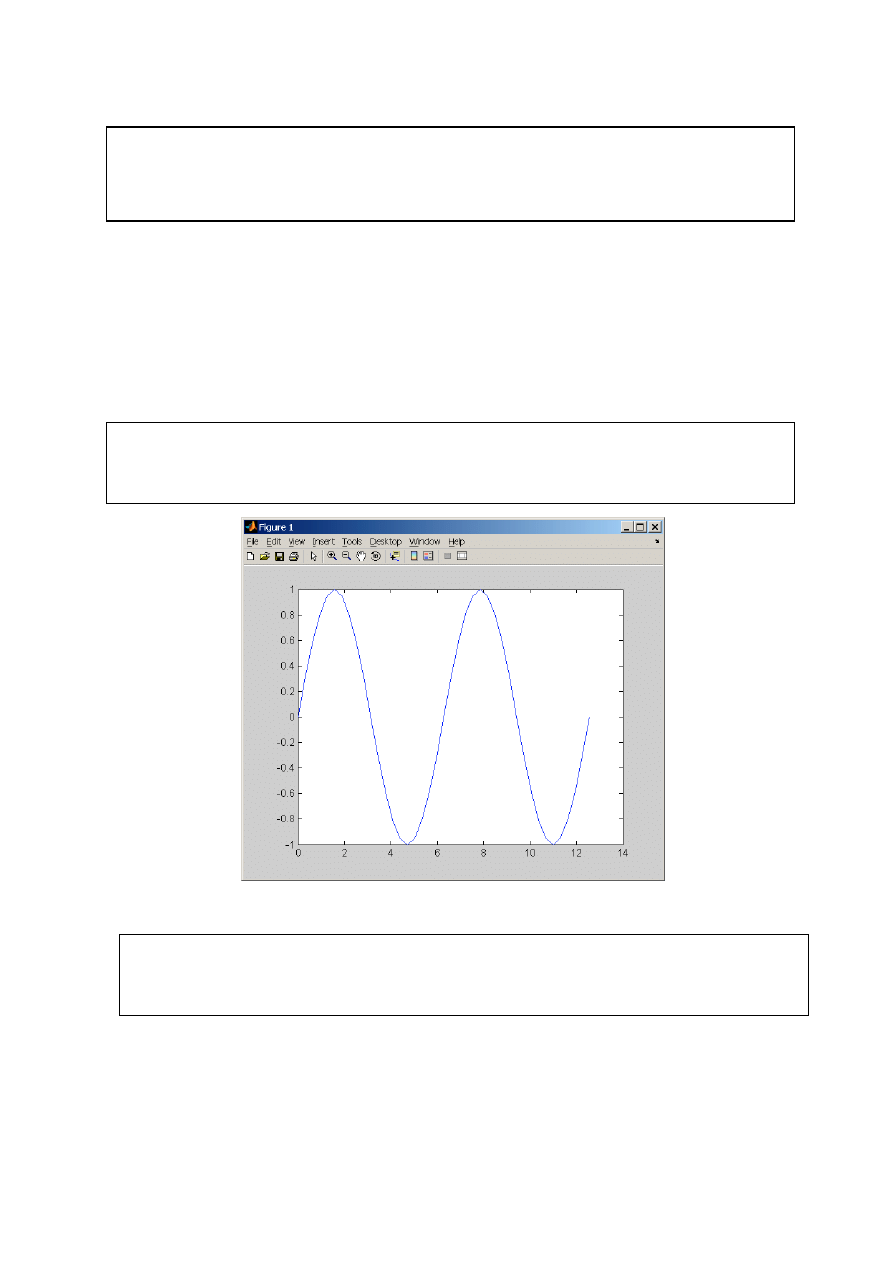
korzystając z polecenia plot(X,Y) gdzie X i Y są macierzami. Na wykresie, pojawiającym się
w osobnym oknie, rysowane są linie odpowiadające połączonym punktom X i Y. Jeżeli X jest
macierzą jednowymiarową, zaś Y dwuwymiarową, osobna linia jest tworzona dla każdego
wiersza lub kolumny Y zależnie od tego, który wymiar macierzy Y odpowiada długości
macierzy X.

>> F(1:2,2:3)
ans =
3 5
2 3

>> alpha=0:pi/10:4*pi;
>> s=sin(alpha);
>> plot(alpha,s)

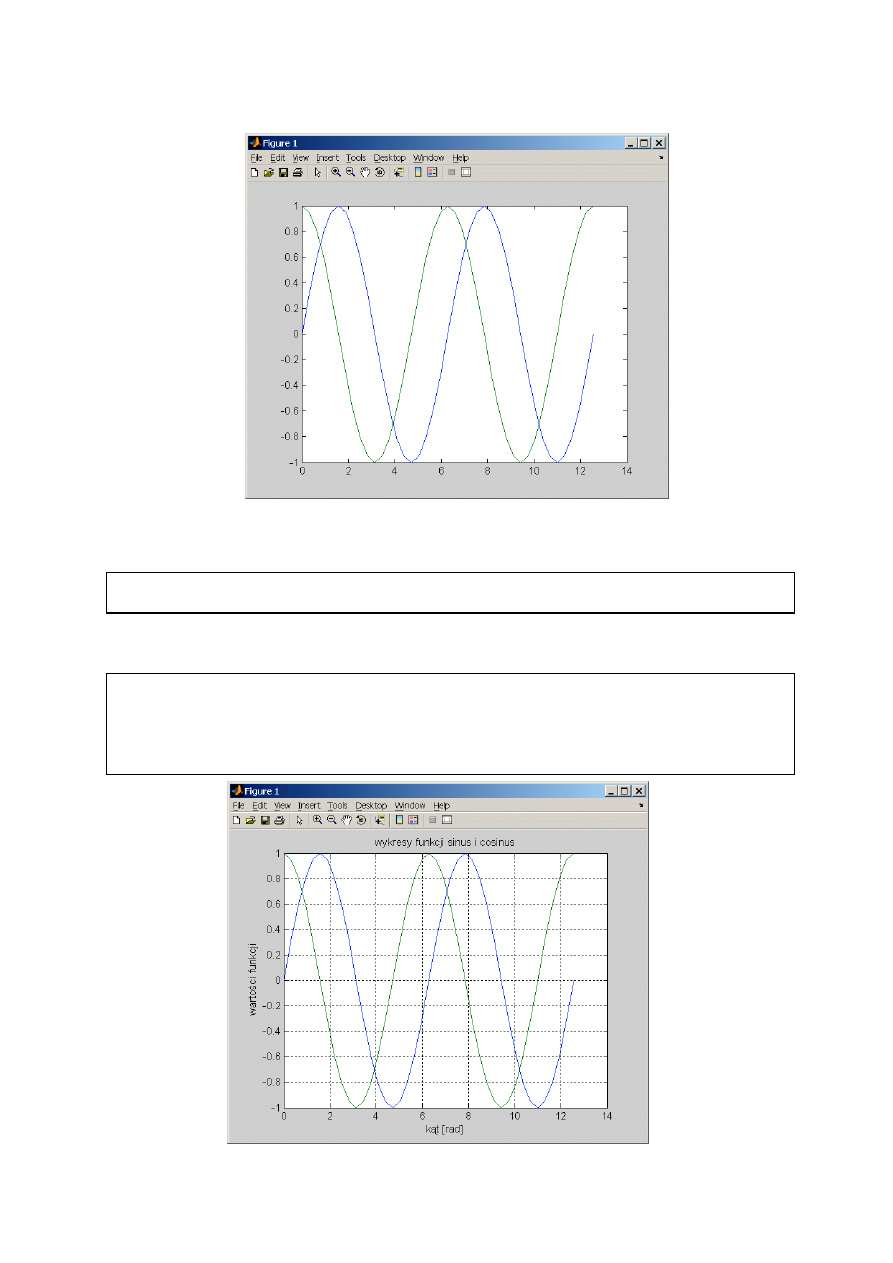
>> c=cos(alpha);
>> sc=[s;c];
>> plot(alpha,sc)

Rys. 1. Okno z wykresem funkcji sinus w zakresie <

π

2

,

0

>.

7

Ten sam efekt można uzyskać za pomocą rozszerzonej składni polecenia plot(X1,Y1,X2,Y2,...)

Rysunkowi można nadać tytuł poleceniem title('opis'), a także dodać opisy osi poziomej i
pionowej poleceniami xlabel('opis') i ylabel('opis') oraz siatkę poleceniem grid.

>> plot(alpha,s, alpha,c)

>> title('wykresy funkcji sinus i cosinus')
>> xlabel('kąt [rad]')
>> ylabel('wartości funkcji')
>> grid

Rys.2. Okno z wykresami funkcji sinus i cosinus

Rys. 3. Wykresy funkcji wraz z opiami osi i siatką

8

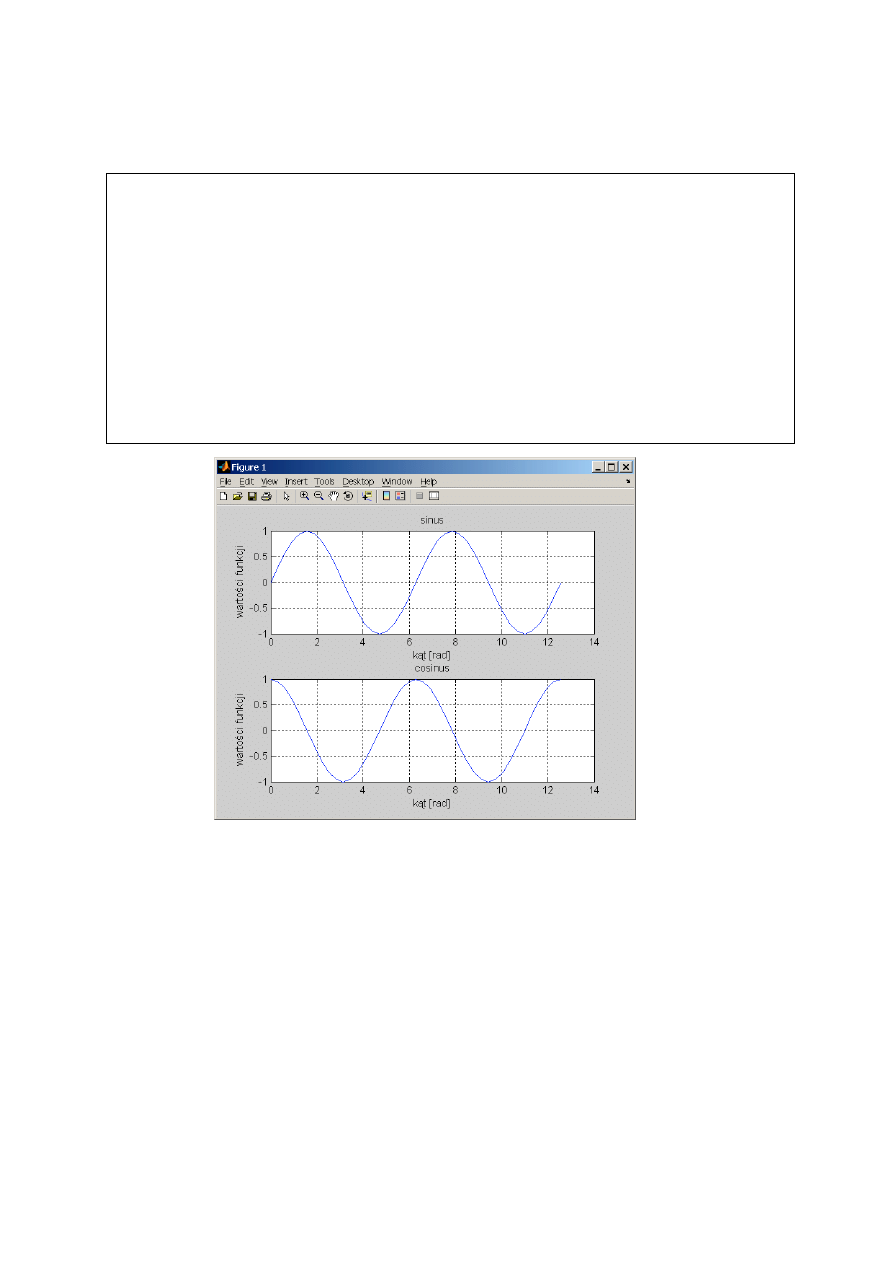
Ekran graficzny można podzielić na osobne wykresy za pomocą polecenia subplot(m,n,p),
gdzie m jest liczbą wykresów w pionie, n – liczbą wykresów w poziomie, zaś p – kolejnym
numerem wykresu licząc od lewego górnego.

Skrypty

Ciągi wielu instrukcji takie jak w przykładzie do rys. 4 wygodnie jest umieszczać w osobnych
plikach tekstowych z rozszerzeniem „.m”. Pozwala to na ich łatwą edycję bez konieczności
przepisywania instrukcji w razie potrzeby ich kilkakrotnego wykorzystania. Takie pliki,
nazywane skryptami, są odpowiednikiem programów w innych językach programowania. W
skrypcie możemy wywołać inne, uprzednio zdefiniowane skrypty. Skrypt uruchamiany jest
poprzez wpisanie w linii poleceń jego nazwy (bez rozszerzenia).

>> subplot(2,1,1)
>> plot(alpha,s)
>> grid
>> title('sinus')
>> ylabel('wartości funkcji')
>> xlabel('kąt [rad]')
>> subplot(2,1,2)
>> plot(alpha,c)
>> title('cosinus')
>> ylabel('wartości funkcji')
>> xlabel('kąt [rad]')
>> grid

Rys. 4. Wykorzystanie polecenia subplot do podziału ekranu

graficznego

9

Funkcje matematyczne (przykłady)

Funkcje matematyczne (jeżeli zostaną wywołane z argumentem macierzowym, z
założenia operują „na elementach”):

sin(x)

sinus

cos(x)

cosinus

tan(x)

tangens

asin(x)

arcus sinus

acos(x)

arcus cosinus

atan(x)

arcus tangens

sinh(x)

sinus hiperboliczny

cosh(x)

cosinus hiperboliczny

tanh(x)

tangens hiperboliczny

asinh(x)

arcus sinus hiperboliczny

acosh(x)

arcus cosinus hiperboliczny

atanh(x)

arcus tangens hiperboliczny

sqrt(x)

pierwiastek kwadratowy

exp(x)

e

x

log(x)

logarytm naturalny

log2(x)

logarytm przy podstawie 2

log10(x)

logarytm przy podstawie 10

Funkcje związane z obliczeniami w dziedzinie liczb zespolonych:

abs(x)

macierz modułów elementów macierzy x (także macierz wartości
bezwzględnych elementów macierzy rzeczywistej x)

angle(x)

macierz argumentów elementów macierzy x

real(x)

macierz części rzeczywistych elementów macierzy x

imag(x)

macierz części urojonych elementów macierzy x

conj(x)

macierz o elementach sprzężonych z elementami macierzy x

Funkcje dodatkowe:

round(x)

zaokrągla elementy macierzy x

do najbliższej liczby całkowitej

rem(x,y)

oblicza resztę z dzielenia odpowiadających sobie elementów macierzy x

i y

gcd(a,b)

oblicza największy wspólny dzielnik liczb a i b

lcm(a,b)

oblicza najmniejszą wspólną wielokrotną liczb a i b

Korzystanie z pomocy

Matlab posiada bardzo rozbudowany system pomocy. W każdej chwili można z linii poleceń
podać help nazwa_polecenia aby przeczytać skrócony opis działania danej komendy.
Dodatkowo w menu znajduje się przycisk Help uruchamiający dostęp do pełnej dokumentacji
HTML Matlaba.

Bibliografia

[1]

Szymkat M.: Komputerowe wspomaganie w projektowaniu układów regulacji.

Wydawnictwa Naukowo-Techniczne, Warszawa, 1993

10

[2]

Brzózka J., Dorobczyński L.: Programowanie w Matlab. Zakład Nauczania

Informatyki „MIKOM”, Warszawa, 1998

[3]

Kamińska A., Pańczyk B.: Ćwiczenia z Matlab. Przykłady i zadania. Wydawnictwo

„MIKOM”, Warszawa, 2002

[4]

Regel W.: Statystyka matematyczna w programie Matlab. Wydawnictwo „MIKOM”,

Warszawa, 2003

[5]

Mrozek B., Mrozek Z.: MATLAB i Simulink : poradnik użytkownika. Helion, Gliwice,

2004

[6]

http://www.mathworks.com/access/helpdesk/help/pdf_doc/matlab/learnmatlab.pdf

[7]

http://www.pg.gda.pl/~kmb/polish/skrypt.pdf