WM

12. PRZEMIESZCZENIA W BELKACH

1

12. PRZEMIESZCZENIA W BELKACH

12.1. Wiadomości podstawowe

Jak wiadomo siły przekrojowe wyznacza się wykorzystując  zasadę zesztywnienia  czyli obliczamy 

wszystkie siły zakładając, że belka jest nieodkształcalną tarczą sztywną. Jednak w tym rozdziale będziemy 
przyjmować, że belka może się odkształcać jednak siły przekrojowe w dalszym ciągu będziemy wyznaczać 
z zastosowaniem  zasady  zesztywnienia.   Przemieszczenie   belki   będziemy  opisywali   za   pomocą  wektora 
przemieszczenia, który w układzie współrzędnych XYZ będzie miał postać

f =u⋅iv⋅jw⋅k

.

(12.1)

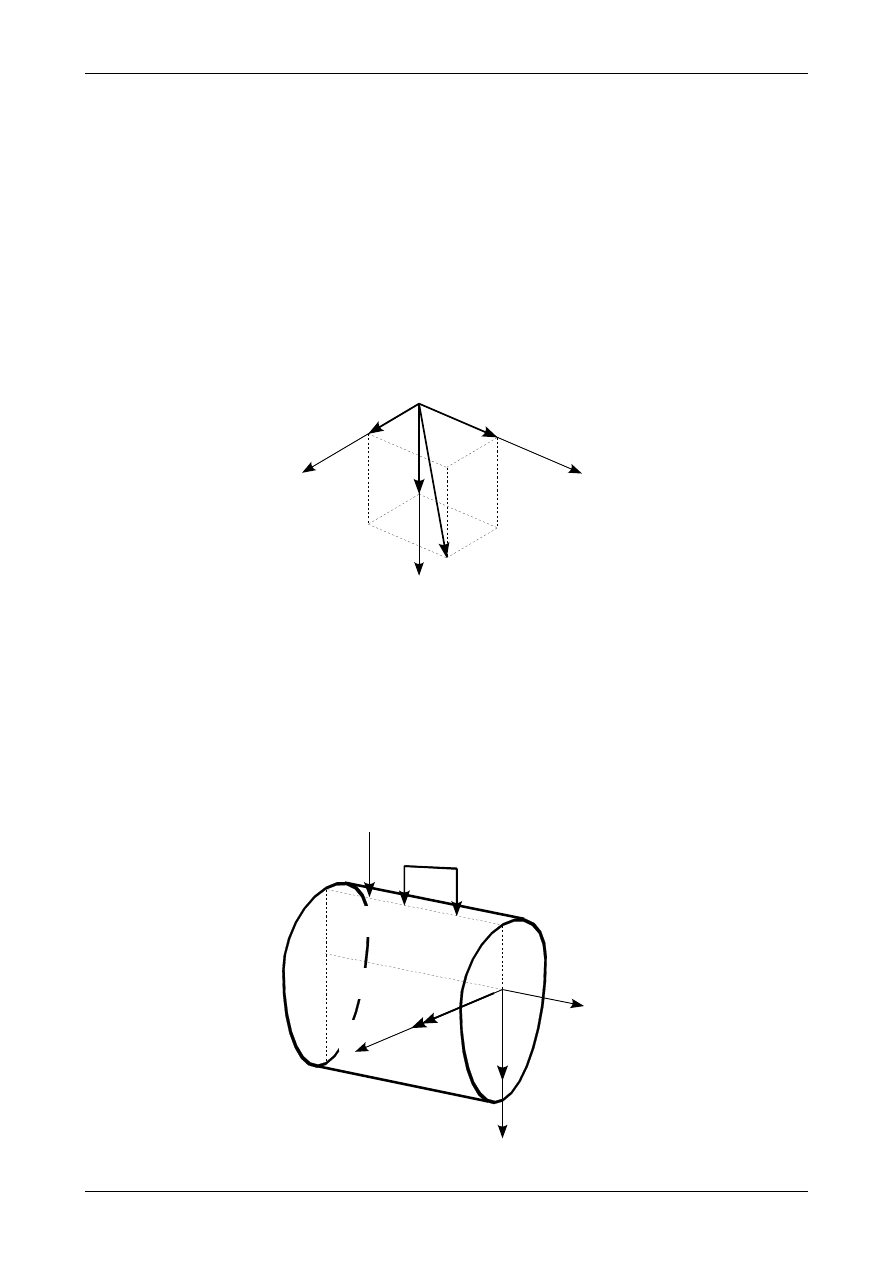
Składowe wektora (12.1) w układzie XYZ przedstawia rysunek 12.1.

X

Y

Z

u

v

w

f

Rys. 12.1. Wektor przemieszczenia

W niniejszym rozdziale ograniczymy się do przypadku, w którym płaszczyzna obciążenia pokrywa się 

z osią główną bezwładności Z=Z

gl

. Przypadek taki nazywamy  zginaniem prostym.  Rysunki 12.2, 12.3 i 

12.4 przedstawiają obciążenie pręta oraz siły przekrojowe czyli siłę poprzeczną i moment zginający.  W 
belce jak wiadomo siła normalna jest w większości przypadków równa zero. We wszystkich rozpatrywanych 
przez  nas   przypadkach   będzie  się   ona   równała   zero.   Na   rysunkach   12.2,   12.3  i   12.4 przedstawione  są 
dodatnie siły przekrojowe. W dalszej części pominiemy wpływ siły poprzecznej T=T

Z

 na przemieszczenia 

belki. Przemieszczenia będą zależeć więc tylko od momentu zginającego M=M

Y

. 

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

X

P

q(x)

M=M

Y

T

=

T

Z

Rys. 12.2. Obciążenie i siły przekrojowe w belce

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

2

Y=Y

0

=Y

gl

Z=Z

0

=Z

gl

X

P

q(x)

M

=M

Y

T

=

T

Z

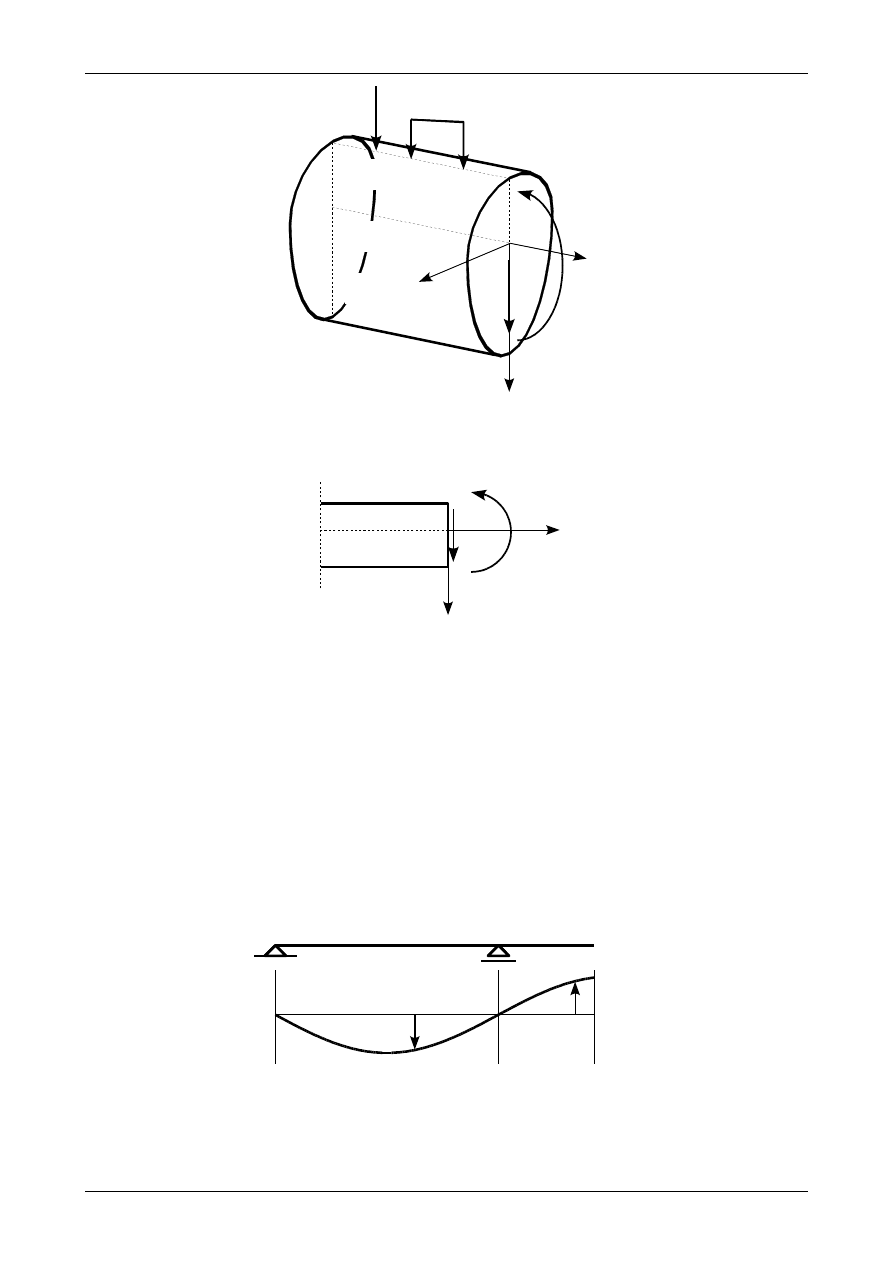
Rys. 12.3. Statycznie równoważne obciążenie i siły przekrojowe

X

T

=

T

Z

M=M

Y

Z=Z

0

=Z

gl

Rys. 12.4. Widok z boku pręta na dodatnie siły przekrojowe

Jeżeli   obciążenie   działa   w   płaszczyźnie   ZX   to   belka   będzie   doznawać   tylko   przemieszczeń   po 

kierunku głównej osi bezwładności Z=Z

gl

. Wektor przemieszczenia będzie miał tylko jedną składową czyli

f =w⋅k

.

(12.2)

Jednostką przemieszczenia (nazywanego dalej ugięciem) jest metr.  Zamiast zapisywać ugięcie w jako 
wektor będziemy używać  funkcji  linii ugięcia  w(x), której  znak będzie zależał od tego, w którą stronę 
przemieści się belka.  Jeżeli ugięcie nastąpi w dół (zgodnie ze zwrotem osi Z) to będzie ono dodatnie, 
jeżeli do góry (przeciwnie do zwrotu osi Z) to będzie ono ujemne. Przedstawia to rysunek 12.5.

w(x)

w>0

w<0

Rys. 12.5. Przykładowa linia ugięcia

Oprócz linii ugięcia będzie ważny także wykres funkcji kąta obrotu przekroju pręta. Jak wiadomo 

przekrój   pręta   jest   zawsze   prostopadły   do   osi   pręta   zarówno   przed   przyłożeniem   obciążenia   jak   i   po. 
Rysunek 12.6 przedstawia fragment pręta przed przyłożeniem i po przyłożeniu obciążenia. Oba przekroje, 

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

3

które przed przyłożeniem obciążenia były pionowe obróciły się. Jeden z przekrojów obrócił się o kąt  

φ

1 

a drugi o kąt 

φ

2

. Na rysunku 12.6 zaznaczony jest układ współrzędnych ZX. Jeżeli obrót przekroju pręta 

nastąpi od osi X do osi Z to taki kąt obrotu jest dodatni natomiast jeżeli obrót przekroju pręta nastąpi 
od osi Z do osi X to taki kąt obrotu jest kątem ujemnym. Jak widać na rysunku 12.6 kąt 

φ

1

 jest dodatni 

(obrót od osi X do osi Z) natomiast kąt 

φ

2

 jest ujemny (obrót od osi Z do osi X). Jednostką kąta obrotu jest 

radian.

X

Z

φ

2

φ

2

<0

φ

1

>0

φ

1

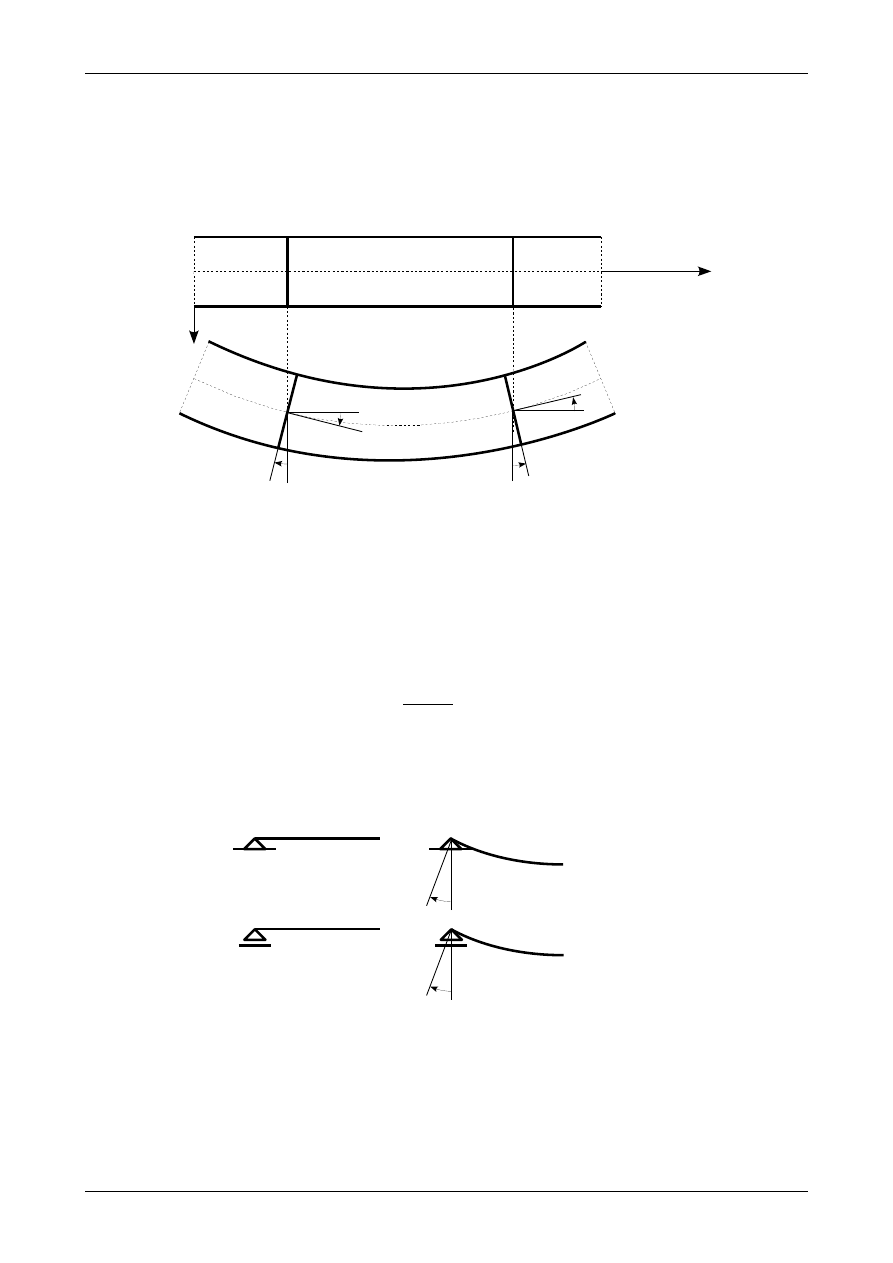
Rys. 12.6. Interpretacja kąta obrotu przekroju pręta

Na rysunku 12.6 pokazane jest, że kąt obrotu przekroju jest także kątem nachylenia stycznej do linii 

ugięcia.   Jak   wiadomo   z  rachunku   różniczkowego   tangens   kąta   nachylenia   stycznej   do  wykresu   funkcji 
w punkcie równa się wartości pochodnej funkcji w tym punkcie. Ponieważ kąty obrotu przekroju pręta są 
wielkością bardzo małą możemy przyjąć, że tangens kąta obrotu przekroju pręta równa się samemu kątowi 
obrotu wyrażonemu w radianach. Możemy więc ogólnie zapisać, że

 

x=

d w x

d x

.

(12.3)

Przy rozwiązywaniu zadań z wyznaczania ugięć bardzo potrzebne będą informacje o ugięciach i ką-

tach obrotów na różnego rodzaju więzach. Informacje te nazywają się warunkami brzegowymi.

w = 0

φ

 ≠ 0

w = 0

φ

 ≠ 0

φ

φ

Rys. 12.7. Warunki brzegowe dla podpór przegubowo- przesuwnej i przegubowo-nieprzesuwnej na końcu belki

Na rysunku 12.7 przedstawione są warunki brzegowe dla podpór przegubowo-przesuwnej i przegu-

bowo-nieprzesuwnej na końcu belki. Jak widać dla tych podpór ugięcie w wynosi zawsze zero natomiast kąt 
obrotu jest w ogólnym przypadku różny od zera.

Na rysunku 12.8 przedstawione są warunki brzegowe dla podpór przegubowo-przesuwnej i przegu-

bowo-nieprzesuwnej na długości belki. Jak widać dla tych podpór ugięcie w wynosi zawsze zero natomiast 
kąt obrotu jest w ogólnym przypadku różny od zera.

Dr inż. Janusz Dębiński

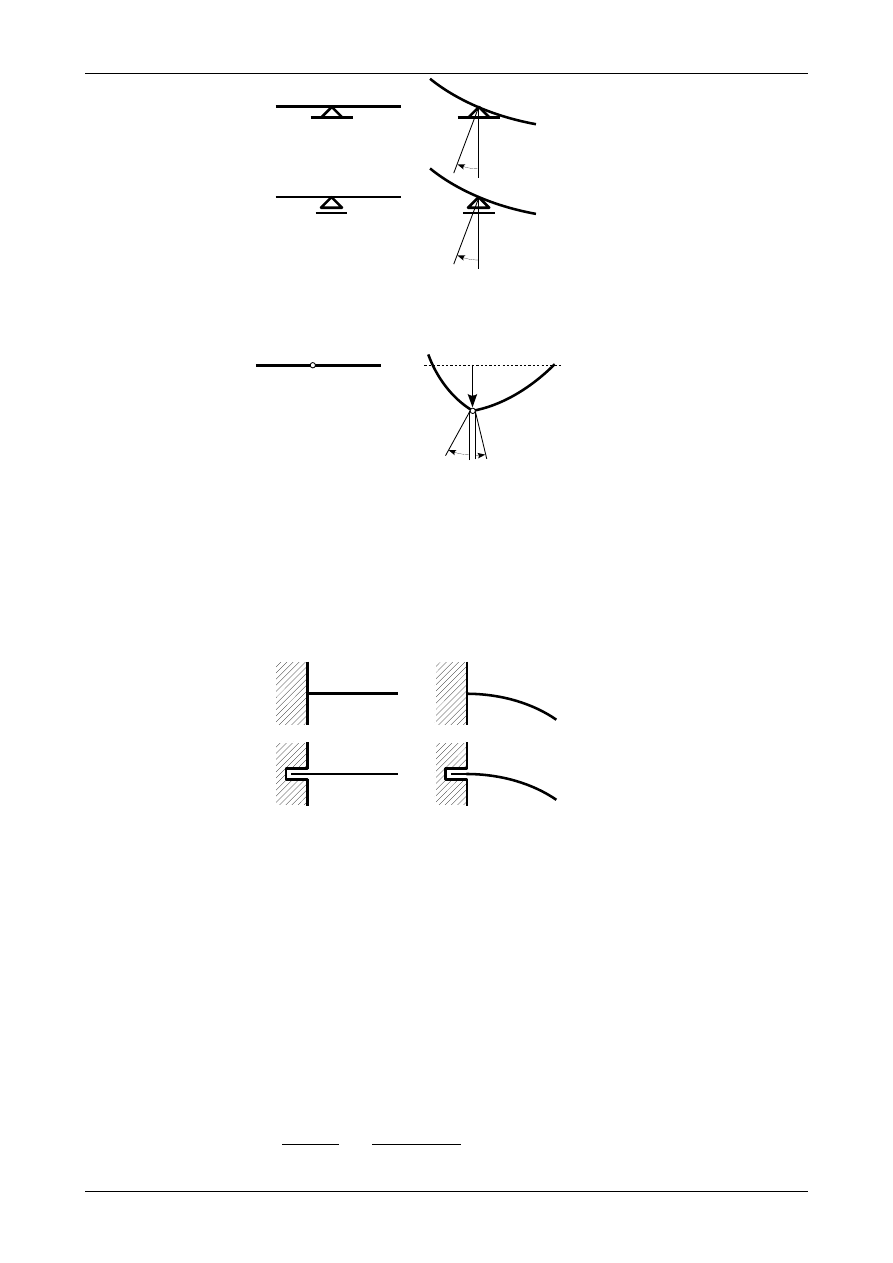
WM

12. PRZEMIESZCZENIA W BELKACH

4

w = 0

φ

 ≠ 0

w = 0

φ

 ≠ 0

φ

φ

Rys. 12.8. Warunki brzegowe dla podpór przegubowo- przesuwnej i przegubowo-nieprzesuwnej na długości belki

v

w ≠ 0

φ

L

 ≠ 0

φ

P

 ≠ 0

φ

L

 ≠ 

φ

P

φ

L

φ

P

Rys. 12.9. Warunki brzegowe dla przegubu łączącego dwie belki proste

Rysunek 12.9 przedstawia warunki brzegowe dla przegubu łączącego dwie belki proste. Jak widać 

ugięcie w przegubie jest w ogólnym przypadku różne od zera. W przegubie będziemy mieli dwa kąty obrotu: 
z lewej strony 

φ

L

 oraz z prawej strony 

φ

P

. Jak widać oba kąty są w ogólnym przypadku różne od zera oraz 

oba są od siebie różne.

w = 0

φ

 = 0

w = 0

φ

 = 0

Rys. 12.10. Warunki brzegowe dla podpory teleskopowej i utwierdzenia

Ostatnimi podporami, dla których określimy warunki brzegowe są podpora teleskopowa oraz utwier-

dzenie. Dla tych podpór ugięcie oraz kąt obrotu są zawsze równe zero. Podpory te oraz warunki brzegowe na 
nich przedstawia rysunek 12.10.

12.2. Równanie różniczkowe linii ugięcia

Na ugięcia w belkach wpływ  mają  siła poprzeczna i moment  zginający.  Jednak wpływ  siły pop-

rzecznej  wynosi  tylko kilka procent  i w niniejszym kursie  pominiemy go. Zależność pomiędzy funkcją 
ugięcia w(x) a funkcją  momentu zginającego M(x)=M

Y

(x) nazywa  się  równaniem różniczkowym linii 

ugięcia i ma postać

d

2

w  x

d x

2

=−

M  x

E  x ⋅J

Y



x 

=−

x 

,

(12.4)

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

5

w którym E(x) jest funkcją wartości modułu Younga od położenia, J

Y

(x) jest funkcją momentu bezwładności 

względem osi Y=Y

gl

 od położenia natomiast 

κ

 oznacza krzywiznę osi belki. Ze względu na to, że będziemy 

rozpatrywać belki wykonane z materiału izotropowego mającego w każdym punkcie te same właściwości 
więc moduł Younga będzie miał wartość stałą a równanie różniczkowe równowagi będzie miało postać

d

2

w  x

d x

2

=−

M  x 

E⋅J

Y



x

=−

x

.

(12.5)

Jeżeli pewien odcinek belki będzie prętem pryzmatycznym czyli moment bezwładności będzie stały rów-
nanie różniczkowe równowagi będzie miało postać

d

2

w  x

d x

2

=−

M  x 

E⋅J

Y

=−

x 

.

(12.6)

Iloczyn   modułu   Younga   oraz   momentu   bezwładności   nazywamy  sztywnością   przekroju   na   zginanie. 
Jednostką sztywności jest

[

kPa⋅m

4

]

=

[

kN

m

2

⋅

m

4

]

=

[

kN⋅m

2

]

.

(12.7)

Chcąc wyznaczyć postać linii ugięcia w(x) i funkcję kąta obrotu przekroju pręta 

φ

(x) należy równanie (12.4) 

lub (12.5), lub (12.6) dwukrotnie scałkować. Przy całkowaniu potrzebne będą warunki brzegowe zaprezen-
towane wcześniej oraz pojawią się dwie stałe całkowania.

12.3. Wyznaczenie ugięć metodą bezpośredniego całkowania

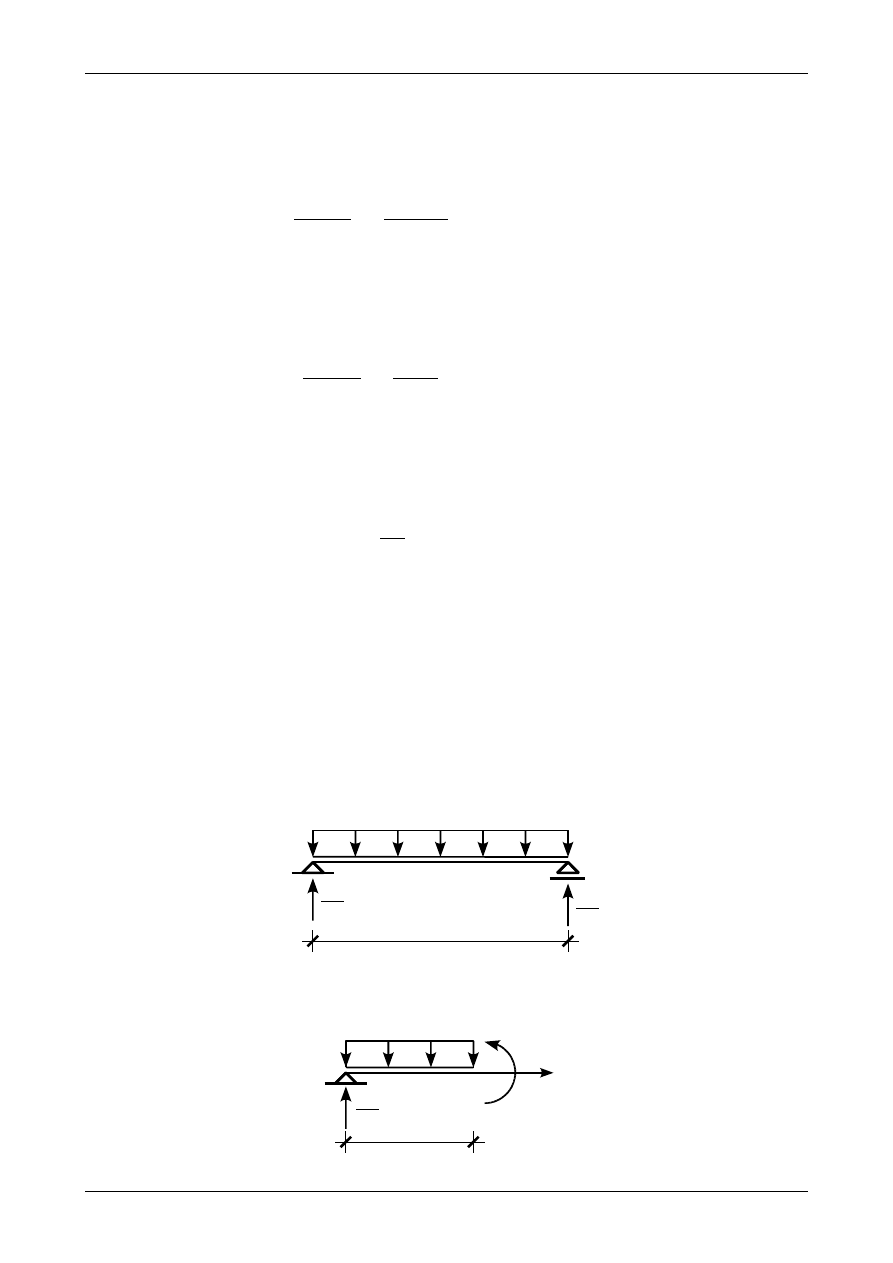
Jako przykład wyznaczenia ugięć obliczmy linię ugięcia i funkcję kąta obrotu dla belki swobodnie 

podpartej przedstawionej na rysunku 12.11. Na rysunku tym zaznaczone są także reakcje w belce.

q

L

q⋅L

2

q⋅L

2

Rys. 12.11. Belka swobodnie podparta

q

x

M(x)

q⋅L

2

X

Rys. 12.12. Równowaga odciętej części belki swobodnie podpartej z obciążeniem ciągłym równomiernie rozłożonym

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

6

Rysunek 12.12 przedstawia równowagę odciętej części belki, z której to wyznaczymy postać funkcji 

momentu zginającego. Dodatni moment zginający będzie rozciągał dolną część przekroju pręta. Moment 
zginający wynosi więc

M  x =

q⋅L

2

⋅

x−q⋅x⋅

x

2

=

q⋅L

2

⋅

x −

q⋅x

2

2

.

(12.8)

Belka jest prętem pryzmatycznym więc równanie różniczkowe równowagi będzie miało postać

E⋅J

Y

⋅

d

2

w  x 

d x

2

=

q⋅x

2

2

−

q⋅L

2

⋅

x

.

(12.9)

Po pierwszym całkowaniu otrzymamy funkcję kąta obrotu, która będzie miała następującą postać

E⋅J

Y

⋅

d w  x 

d x

=

E⋅J

Y

⋅

x=

q⋅x

3

6

−

q⋅L

4

⋅

x

2



C

.

(12.10)

We wzorze (12.10) C oznacza pierwszą stałą całkowania. Po drugim całkowaniu otrzymamy funkcję linii 
ugięcia w postaci

E⋅J

Y

⋅

w  x=

q⋅x

4

24

−

q⋅L

12

⋅

x

3



C⋅xD

,

(12.11)

w którym D oznacza drugą stałą całkowania. Chcąc wyznaczyć wartości stałych całkowania należy wstawić 
do równań (12.10) lub (12.11) dwa warunki brzegowe. Patrząc na rysunek 12.11 widać, że ugięcia nad 
podporami wynoszą zero czyli otrzymamy

w0=0
w L=0

.

(12.12)

Podstawiając warunek pierwszy do równania (12.11) otrzymamy

q⋅0

4

24

−

q⋅L

12

⋅

0

3



C⋅0D=0

,

(12.13)

czyli stała D wynosi jak widać zero. Zajmijmy się jeszcze jednostką tej stałej. Patrząc na równanie (12.11) 
widać, że stała D musi mieć ten sam wymiar co iloczyn sztywności przekroju i ugięcia czyli

[

kN⋅m

2

⋅

m

]

=

[

kN⋅m

3

]

.

(12.14)

Podstawiając warunek drugi do równania (12.11) otrzymamy

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

7

q⋅L

4

24

−

q⋅L

12

⋅

L

3



C⋅L=0

.

(12.15)

W równaniu (12.15) zostało już uwzględnione, że stała D wynosi zero. Z równania (12.15) stała C wynosi

C=

q⋅L

3

24

.

(12.16)

Zajmijmy się jeszcze jednostką tej stałej. Patrząc na równanie (12.10) widać, że stała C musi mieć ten sam 
wymiar co iloczyn sztywności przekroju i kąta obrotu przekroju. Kąt obrotu jak wiadomo jest wyrażony 
w radianach,  które  tutaj  możemy  traktować   jako  jednostkę  bezwymiarową  czyli   stała  C ma   ostatecznie 
jednostkę

[

kN⋅m

2

]

.

(12.17)

Po uwzględnieniu stałych całkowania funkcje kąta obrotu i linii ugięcia mają postacie



x=

1

E⋅J

Y

⋅



q⋅x

3

6

−

q⋅L

4

⋅

x

2



q⋅L

3

24



,

(12.18)

w  x =

1

E⋅J

Y

⋅



q⋅x

4

24

−

q⋅L

12

⋅

x

3



q⋅L

3

24

⋅

x



.

(12.19)

Kąty obrotu przekrojów pręta na obu końcach belki wynoszą



0=

1

E⋅J

Y

⋅



q⋅0

3

6

−

q⋅L

4

⋅

0

2



q⋅L

3

24



=

q⋅L

3

24⋅E⋅J

Y

,

(12.20)



L=

1

E⋅J

Y

⋅



q⋅L

3

6

−

q⋅L

4

⋅

L

2



q⋅L

3

24



=−

q⋅L

3

24⋅E⋅J

Y

.

(12.21)

Miejsce zerowe funkcji kąta obrotu przekroju pręta znajduje się w miejscu

x

0

=

L

2

.

(12.22)

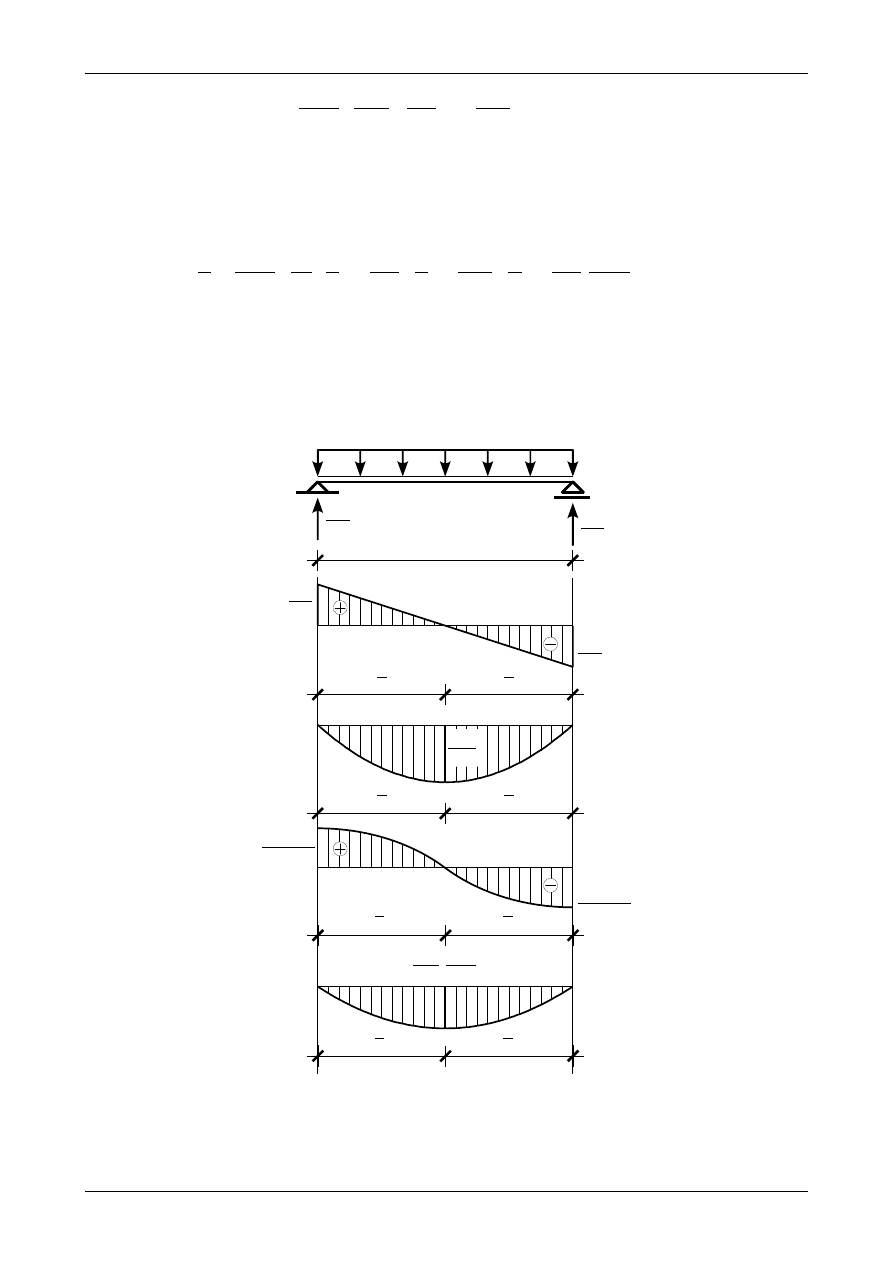
Rysunek 12.13 przedstawia wykres funkcji kąta obrotu przekroju na długości belki. Ugięcia belki na obu 
końcach wynoszą

w0=0

,

(12.23)

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

8

w  L=

1

E⋅J

Y

⋅



q⋅L

4

24

−

q⋅L

12

⋅

L

3



q⋅L

3

24

⋅

L



=

0

.

(12.24)

Czyli jest to zgodne z warunkami brzegowymi (12.12). Ugięcie w środku belki czyli w miejscu zerowym 
funkcji kąta obrotu przekroju wynosi

w



L
2



=

1

E⋅J

Y

⋅

[

q

24

⋅



L

2



4

−

q⋅L

12

⋅



L
2



3



q⋅L

3

24

⋅



L
2



]

=

5

384

⋅

q⋅L

4

E⋅J

Y

.

(12.25)

Rysunek 12.13 przedstawia wykres linii ugięcia. Funkcja kąta obrotu posiada ekstremum w miejscu zero-
wym funkcji momentu zginającego M(x) natomiast linia ugięcia posiada ekstremum w miejscu zerowym 
funkcji kąta obrotu przekroju pręta. 

q

L

T(x)

M(x)

0,0

0,0

L

2

L

2

L

2

L

2

q⋅L

2

q⋅L

2

q⋅L

2

q⋅L

2

q⋅L

2

8

φ

(x)

w(x)

0,0

0,0

L

2

L

2

L

2

L

2

q⋅L

3

24⋅E⋅J

Y

q⋅L

3

24⋅E⋅J

Y

5

384

⋅

q⋅L

4

E⋅J

Y

Rys. 12.13. Wykresy funkcji kąta obrotu przekroju pręta oraz linii ugięcia

Belka przedstawiona powyżej składała się z jednego przedziału. W przypadku belek składających się 

z wielu przedziałów należy obliczenia przeprowadzić we wszystkich przedziałach osobno zapisując odpo-

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

9

wiednie   funkcje   momentu   zginającego   M(x)   i   całkując   każde   z   osobna   otrzymać   funkcję   kąta   obrotu 
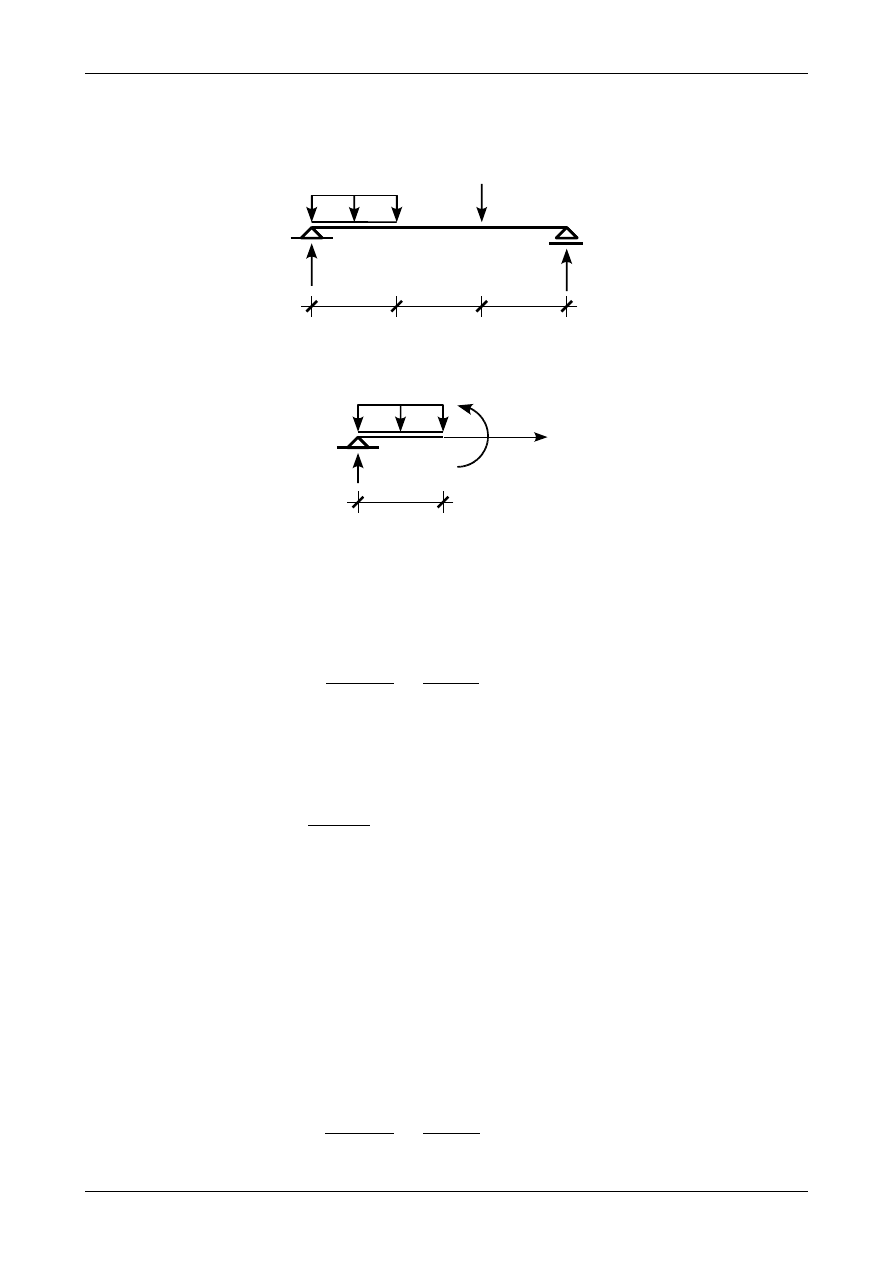
przekroju   pręta   oraz   linię   ugięcia.   Na   rysunku   12.14   przedstawiona   jest   belka   składająca   się   z   trzech 
przedziałów. 

q

A

B

C

D

P

V

A

V

D

b

a

c

Rys. 12.14. Belka swobodnie podparta składająca się z trzech przedziałów

q

A

V

A

x

1

X

1

M

1

(x

1

)

Rys. 12.15. Równowaga w przedziale AB

W przedziale AB jako zmienną będziemy mieli x

1

. Równowagę odciętej części belki w przedziale AB 

przedstawia rysunek 12.15. Równanie różniczkowe linii ugięcia w przedziale AB będzie miało postać

d

2

w

1



x

1



d x

1

2

=−

M

1



x

1



E⋅J

Y



1

.

(12.26)

Po pierwszym całkowaniu otrzymamy funkcję kąta obrotu przekroju w postaci

E⋅J

Y



1

⋅

d w

1



x

1



d x

1

=

E⋅J

Y



1

⋅

1



x

1

=

...C

1

.

(12.27)

Po drugim całkowaniu otrzymamy linię ugięcia w postaci

E⋅J

Y



1

⋅

w

1



x

1

=

...C

1

⋅

x

1



D

1

.

(12.28)

W równaniach (12.27) i (12.28) występują dwie stałe całkowania C

1

 oraz D

1

.

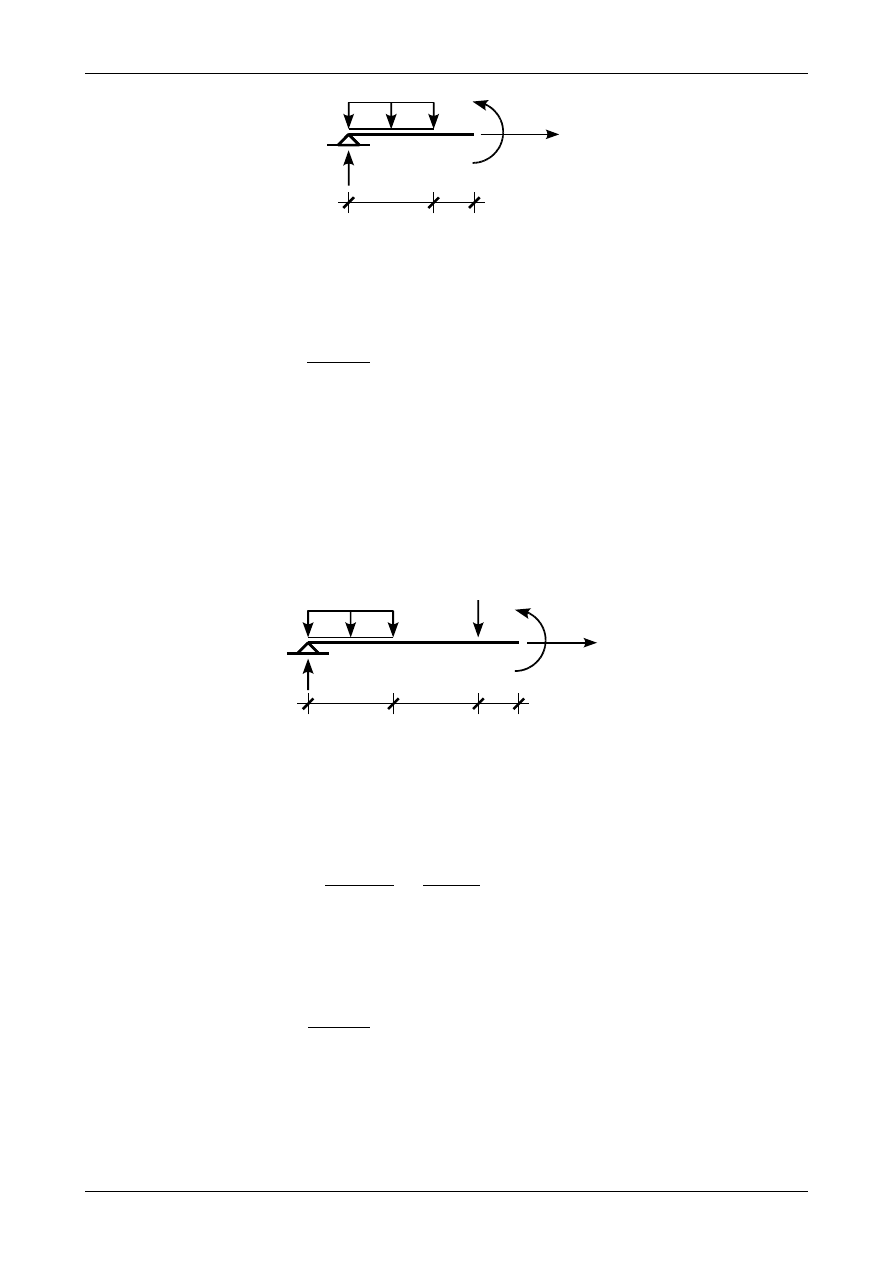
W przedziale BC jako zmienną będziemy mieli x

2

. Równowagę odciętej części belki w przedziale BC 

przedstawia rysunek 12.16. Równanie różniczkowe linii ugięcia w przedziale BC będzie miało postać

d

2

w

2



x

2



d x

2

2

=−

M

2



x

2



E⋅J

Y



2 

.

(12.29)

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

10

q

a

A

B

V

A

M

2

(x

2

)

x

2

X

2

Rys. 12.16. Równowaga w przedziale BC

Po pierwszym całkowaniu otrzymamy funkcję kąta obrotu przekroju w postaci

E⋅J

Y



2 

⋅

d w

2



x

2



d x

2

=

E⋅J

Y



2

⋅

2



x

2

=

...C

2

.

(12.30)

Po drugim całkowaniu otrzymamy linię ugięcia w postaci

E⋅J

Y



2 

⋅

w

2



x

2

=

...C

2

⋅

x

2



D

2

.

(12.31)

W równaniach (12.30) i (12.31) występują dwie stałe całkowania C

2

 oraz D

2

.

q

a

A

B

C

P

V

A

b

x

3

M

3

(x

3

)

X

3

Rys. 12.17. Równowaga w przedziale CD

W przedziale CD jako zmienną będziemy mieli x

3

. Równowagę odciętej części belki w przedziale CD 

przedstawia rysunek 12.17. Równanie różniczkowe linii ugięcia w przedziale CD będzie miało postać

d

2

w

3



x

3



d x

3

2

=−

M

3



x

3



E⋅J

Y



3 

.

(12.32)

Po pierwszym całkowaniu otrzymamy funkcję kąta obrotu przekroju w postaci

E⋅J

Y



3 

⋅

d w

3



x

3



d x

3

=

E⋅J

Y



3 

⋅

3



x

3

=

...C

3

.

(12.33)

Po drugim całkowaniu otrzymamy linię ugięcia w postaci

E⋅J

Y



3 

⋅

w

3



x

3

=

...C

3

⋅

x

3



D

3

.

(12.34)

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

11

W równaniach (12.33) i (12.34) występują dwie stałe całkowania C

3

 oraz D

3

. Ogółem mamy sześć stałych 

całkowania.  Potrzebujemy więc  sześciu warunków brzegowych.  Pierwsze  dwa  to warunki  brzegowe  na 
podporach czyli

w

1



x

1

=

0=0

,

(12.35)

w

3



x

3

=

c=0

.

(12.36)

Następne dwa warunki wiążą się z ciągłością funkcji kąta obrotu przekroju pręta. Kąty obrotów w punktach 
B i C z lewej i prawej strony są sobie równe. Otrzymamy warunki brzegowe w postaci



1



x

1

=

a =

2



x

2

=

0

,

(12.37)



2



x

2

=

b=

3



x

3

=

0

.

(12.38)

Ostatnie dwa warunki brzegowe są związane z ciągłością linii ugięcia (belka oczywiście nie może ulec 
przerwaniu). Otrzymamy warunki brzegowe w postaci

w

1



x

1

=

a=w

2



x

2

=

0

,

(12.39)

w

2



x

2

=

b=w

3



x

3

=

0

.

(12.40)

Podstawiając warunki brzegowe (12.35) do (12.40) do równań (12.27), (12.28), (12.30), (12.31), (12.33) 
oraz (12.34) otrzymamy układ sześciu równań, w którym niewiadomymi są stałe C

1

, D

1

, C

2

, D

2

, C

3

  i D

3

. 

Rozwiązując go otrzymamy wszystkie sześć stałych. Jak widać jest to sposób bardzo uciążliwy.  Liczbę 
stałych możemy zredukować do dwóch lecz musimy w specyficzny sposób zapisać wyrażenie na moment 
zginający M(x). Sposób ten został zaproponowany przez Alfreda Clebscha.

12.4. Wyznaczanie ugięć metodą Clebscha

Na  początek  przyjmiemy,  że  że  belka  jest   wykonana  z pręta   pryzmatycznego  czyli   posiada  stały 

moment   bezwładności   J

Y

.   Dodatkowo   obciążenie   ciągłe   ograniczymy   tylko   do   przypadku   obciążenia 

ciągłego równomiernie rozłożonego. Metoda Clebscha pozwala na zredukowanie liczby stałych całkowania 
do dwóch bez względu na liczbę przedziałów z obciążeniem na belce. Konieczne jest jednak przestrzeganie 
kilku zasad przy zapisie równania momentu zginającego i jego całkowaniu. 

Na   początek   należy  przyjąć   początek   układu   ZX   w   lewym   końcu   belki.   Wyrażenie   na   moment 

zginający w dowolnym przedziale musi być wyrażone zawsze przez siły działające na lewą odciętą część 
belki.

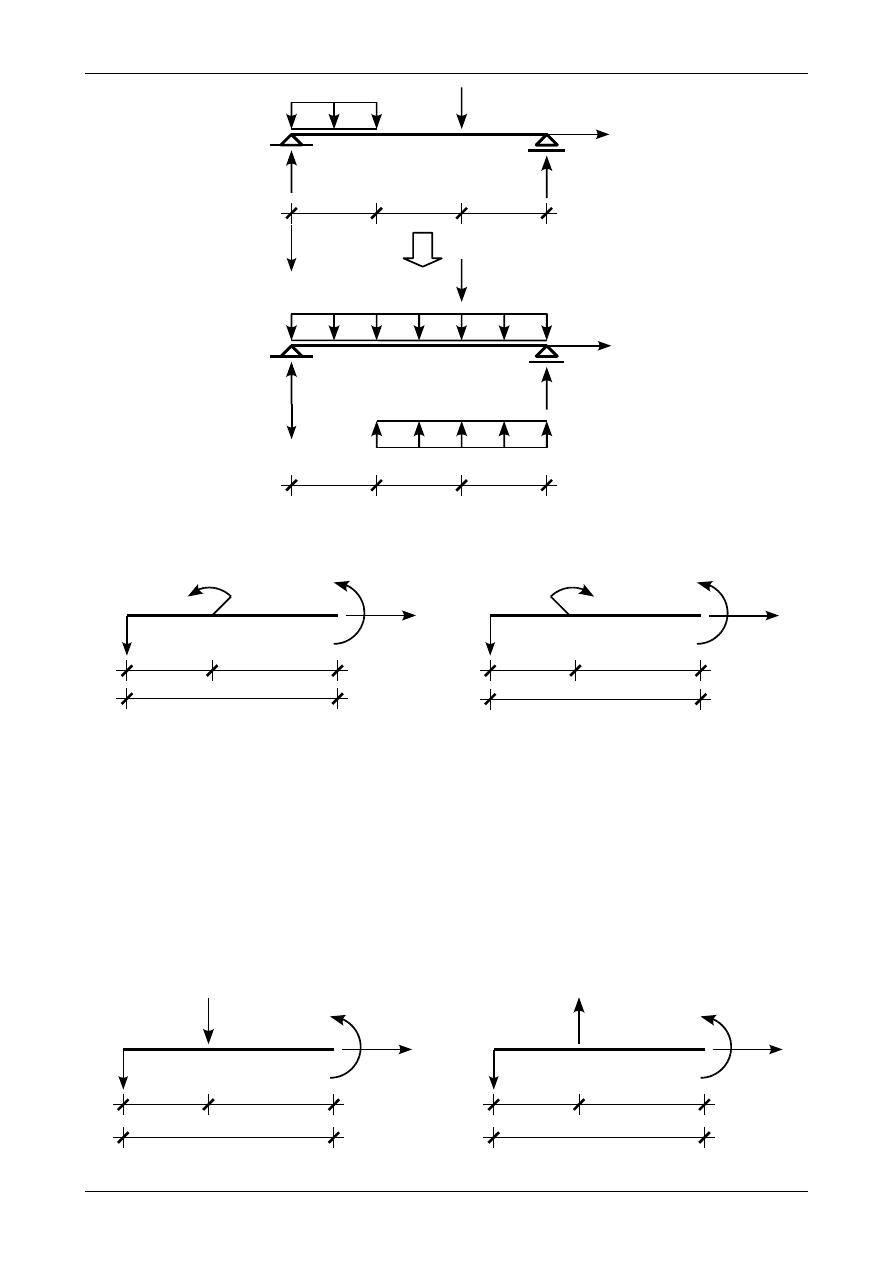
Zapisując wyrażenie na moment zginający w dowolnym przedziale musimy uwzględnić w postaci nie-

zmienionej wszystkie człony wyrażenia na moment zginający w przedziałach poprzednich. Jeżeli obciążenie 
ciągłe równomiernie rozłożone kończy się przed końcem belki to musimy je przedłużyć do samego końca 
belki a w przedziałach, w których to obciążenie nie działa należy dodać obciążenie o tej samej wartości lecz 
przeciwnie skierowane. Przedstawia to rysunek 12.18.

Rysunek 12.19 a) przedstawia moment skupiony M

0

  mający zwrot przeciwny do ruchu wskazówek 

zegara działający w punkcie o współrzędnej  x równej  a.  Wyrażenie  na moment zginający będzie miało 
postać

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

12

q

A

B

C

D

P

V

A

V

D

b

a

c

q

A

B

C

D

P

V

A

b

a

c

q

V

D

X

Z=w

X

Z=w

Rys. 12.18. Statycznie równoważne obciążenie ciągłe równomiernie rozłożone w metodzie Clebscha

a

M(x)

X

x-a

x

M

0

a

M(x)

X

x-a

x

M

0

Z

Z

a)

b)

Rys. 12.19. Moment zginający od momentu skupionego na belce

M  x =−M

0

⋅



x−a



0

.

(12.41)

Rysunek 12.19 b) przedstawia moment skupiony M

0

  mający zwrot zgodny z ruchem wskazówek zegara 

działający w punkcie o współrzędnej x równej a. Wyrażenie na moment zginający będzie miało postać

M  x=M

0

⋅



x−a



0

.

(12.42)

a

M(x)

X

x-a

x

P

a

M(x)

X

x-a

x

P

Z

Z

a)

b)

Rys. 12.20. Moment zginający od siły skupionej

Dr inż. Janusz Dębiński

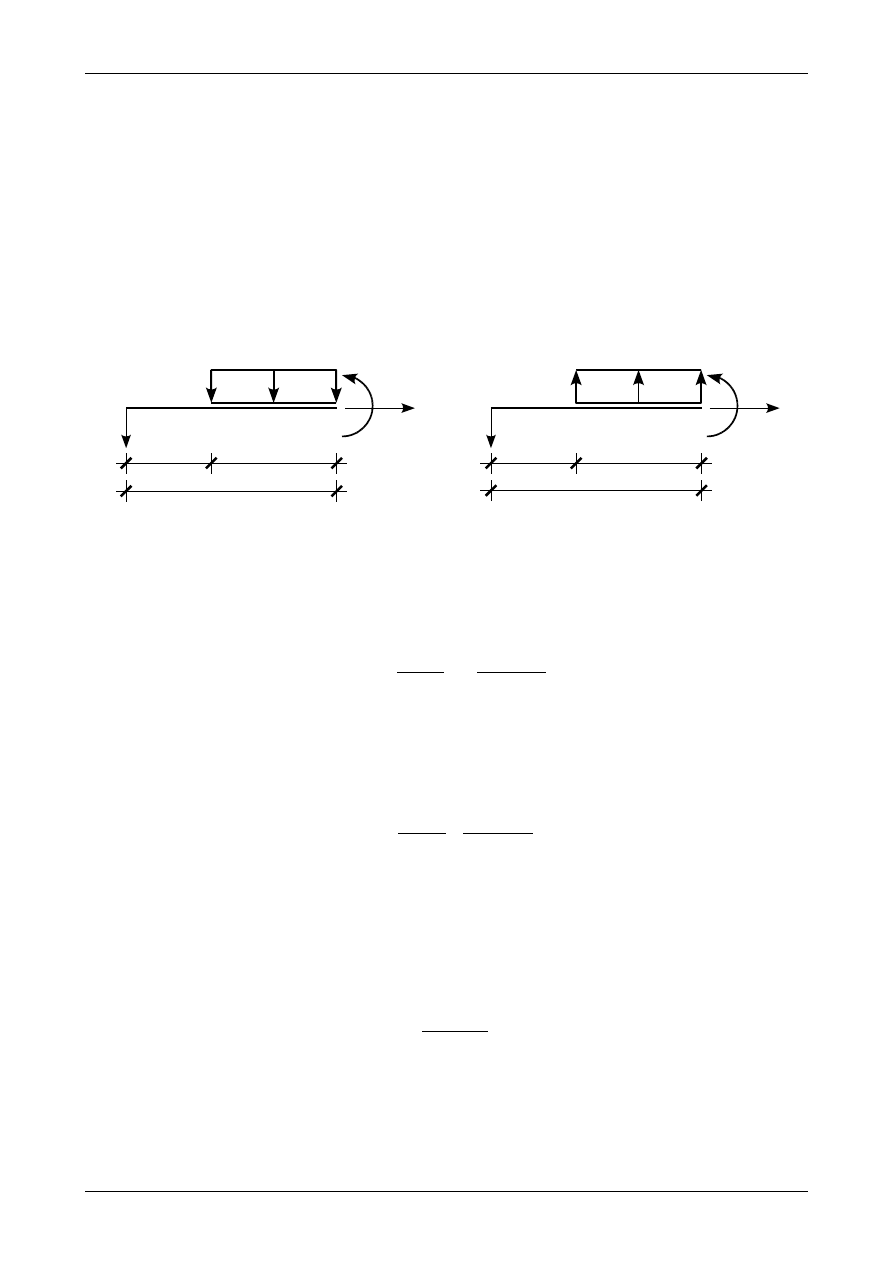
WM

12. PRZEMIESZCZENIA W BELKACH

13

Rysunek 12.20 a) przedstawia siłę skupioną P działającą w dół w punkcie o współrzędnej x równej a. 

Wyrażenie na moment zginający będzie miało postać

M  x =−P⋅



x−a



1

.

(12.43)

Rysunek 12.20 b) przedstawia siłę skupioną P działającą do góry w punkcie o współrzędnej x równej a. 
Wyrażenie na moment zginający będzie miało postać

M  x=P⋅



x−a



1

.

(12.44)

a

M(x)

X

x-a

x

q

a

M(x)

X

x-a

x

q

Z

Z

a)

b)

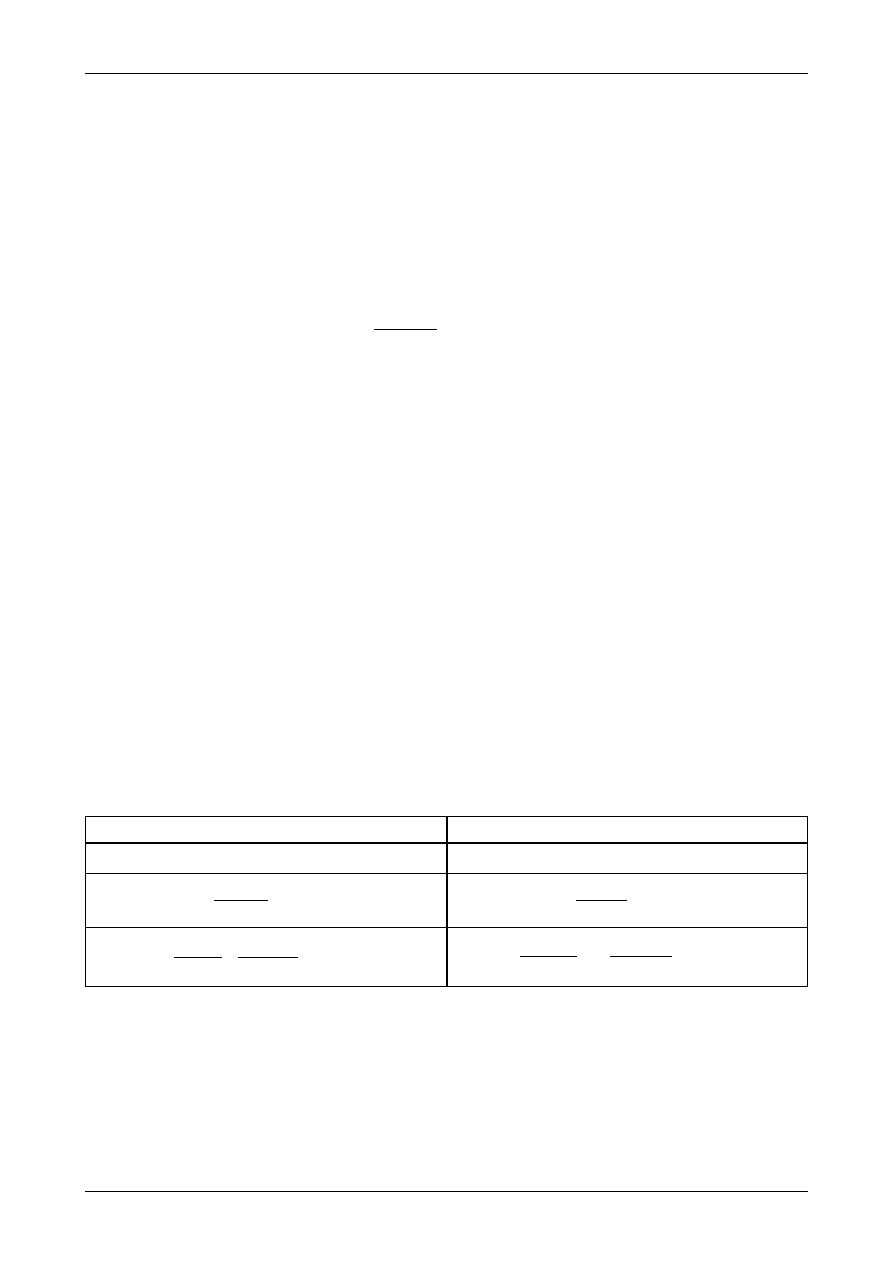
Rys. 12.21. Moment zginający od obciążenia ciągłego równomiernie rozłożonego

Rysunek 12.21 a) przedstawia obciążenie ciągłe równomiernie rozłożone  działające w dół i zaczy-

nające się w punkcie o współrzędnej x równej a. Wyrażenie na moment zginający będzie miało postać

M  x =−q⋅



x−a



⋅



x−a



2

=−

q⋅



x−a



2

2

.

(12.45)

Rysunek 12.21 b) przedstawia obciążenie ciągłe równomiernie rozłożone działające do góry i zaczynające 
się w punkcie o współrzędnej x równej a. Wyrażenie na moment zginający będzie miało postać

M  x=q⋅



x−a



⋅



x−a



2

=

q⋅



x−a



2

2

.

(12.46)

Mając już zapisaną postać momentu zginającego możemy zacząć całkować. Należy pamiętać o tym, 

że  stałe   C   i   D   zapisujemy   zawsze   na   początku   wyrażenia   czyli   stałe   te   obowiązują   w   każdym 
przedziale. Ponadto w trakcie całkowania nie wolno rozwijać wyrażeń w nawiasach czyli całkujemy według 
wzoru

∫



x−a



n

⋅

dx=



x−a



n1

n1

.

(12.47)

Wyrażenia na moment zginający, funkcję kąta obrotu przekroju oraz linię ugięcia będziemy zapisywali od 
razu dla całej belki. Kreskami będziemy zaznaczać, gdzie kończy się odpowiednie wyrażenie. Jeżeli jakiś 
punkt będzie się znajdował w odpowiednim przedziale to wyrażenie na moment zginający, funkcję 
kąta obrotu i linię  ugięcia będzie obowiązywało tylko do kreski  kończącej  dany przedział. Innymi 
słowy w równaniach tych odrzucamy człony,  w których wyrażenia  x-a w nawiasach przyjmują  wartość 

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

14

ujemną lub zero. Przykłady zastosowania tej metody znajdują się w zadaniach załączonych do niniejszego 
rozdziału.

12.5. Wyznaczanie ugięć metodą obciążenia krzywiznami

Metodą obciążeń krzywiznami będziemy wyznaczać ugięcia w określonych punktach. Opiera się ona 

na podobieństwie różniczkowych równań równowagi oraz równań wynikających z równania różniczkowego 
linii ugięcia. Tabela 12.1 przedstawia powyższe wzory. Z porównania wzorów w czwartym wierszu Tabeli 
12.1 wynika, że jeżeli jako obciążenie przyjmiemy krzywiznę 

κ

(x)

q

*



x =

M  x

E⋅I

Y



x

=

x 

(12.48)

to siła poprzeczna będzie równa kątowi obrotu przekroju pręta (trzeci wiersz Tabeli 12.1) natomiast moment 
zginający   będzie   równy   ugięciu   (drugi   wiersz   Tabeli   12.1).   Obciążenie   q

*

(x)   będziemy   nazywali 

obciążeniem wtórnym. Siłę poprzeczną równą kątowi obrotu przekroju pręta będziemy nazywali  wtórną 
siłą poprzeczną. Moment zginający równy ugięciu będziemy nazywali wtórnym momentem zginającym. 
Kąt obrotu będzie więc wynosił



x =T

*



x 

.

(12.49)

We wzorze (12.49) T

*

 oznacza właśnie wtórną siłę poprzeczną. Ugięcie będzie więc wynosiło

w x=M

*



x

.

(12.50)

We wzorze (12.50) M

*

 oznacza właśnie wtórny moment zginający. Analizując wzór (12.49) dochodzimy do 

wniosku,   że  jednostką   wtórnej   siły   poprzecznej   będzie   wielkość   bezwymiarowa.   Analizując   wzór 
(12.50) dochodzimy do wniosku, że jednostką wtórnego momentu zginającego jest metr.

Tabela. 12.1. Różniczkowe równania równowagi i różniczkowe równanie linii ugięcia

Różniczkowe równania równowagi

Różniczkowe równanie linii ugięcia

M  x 

w x

d M x 

d x

=

T x 

d w x

d dx

=

x 

dT  x 

d x

=

d

2

M  x

d x

2

=−

q x

d

2

w  x

d x

2

=−

M  x

E⋅I

Y



x

=−

x 

Obciążeniem wtórnym q

*

(x) nie możemy obciążać belki rzeczywistej, ponieważ nie byłyby spełnione 

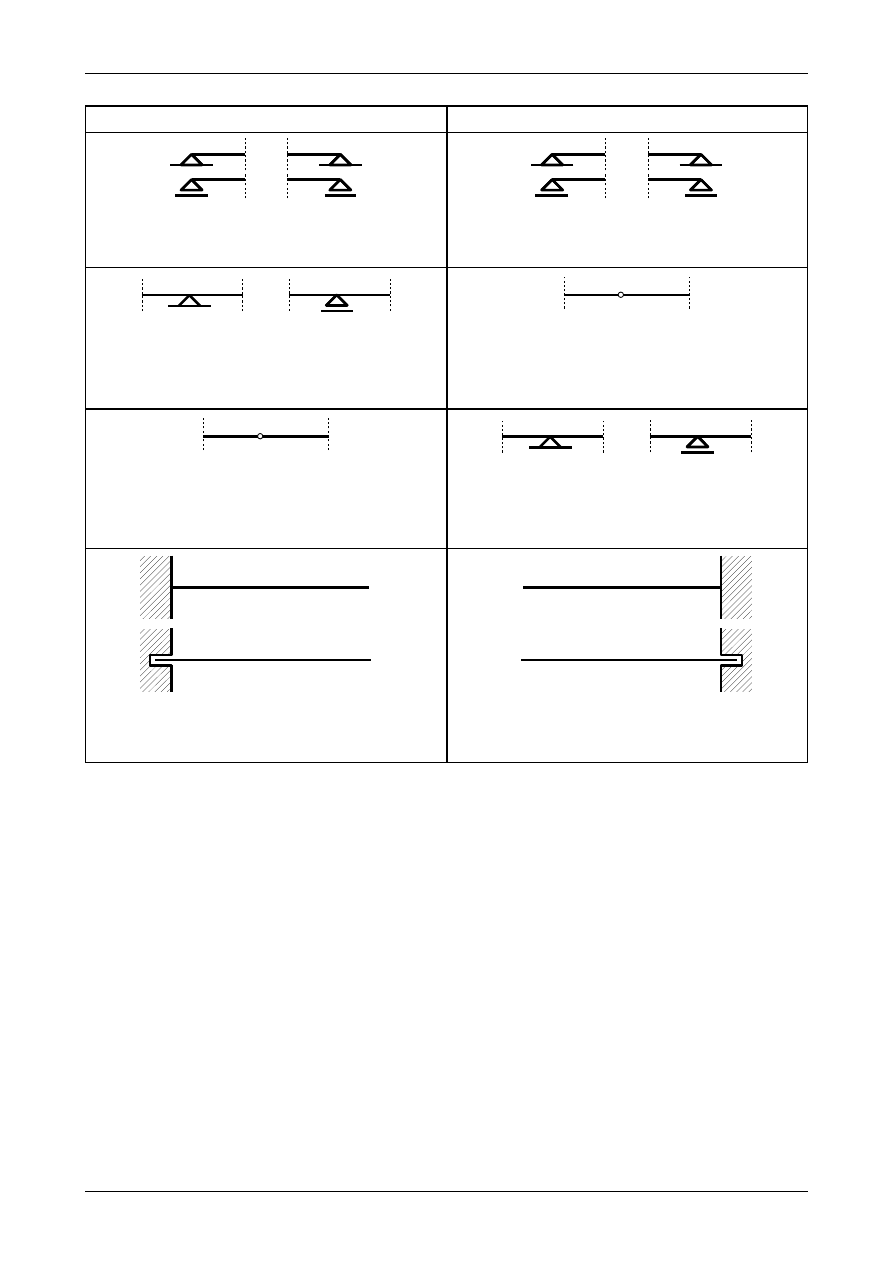
warunki brzegowe. Musimy obciążać belkę nazywaną  belką fikcyjną. Tabela 12.2 przedstawia podpory 
w belce rzeczywistej i odpowiadające im podpory w belce fikcyjnej.  Jak widać podpora przegubowa na 
końcu   belki   przechodzi   w   podporę   przegubową.   Podpora   przegubowa   na   długości   belki   przechodzi 
w przegub rzeczywisty. Przegub rzeczywisty na długości belki przechodzi w podporę przegubową. Pełne 
utwierdzenie i podpora teleskopowa przechodzi w wolny koniec natomiast wolny koniec przechodzi albo 
w utwierdzenie   albo   w   podporę   teleskopową.   Podpory   w   belce   fikcyjnej   muszą   być   tak   dobrane   aby 
spełniony był warunki konieczny i dostateczne geometrycznej niezmienności.

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

15

Tabela 12.2. Podpory w belce rzeczywistej i fikcyjnej.

Belka rzeczywista

Belka fikcyjna

A

A

A

A

A

A

A

A

w

A

=

0



A

≠

0

M

A

*

=

0

T

A

*

≠

0

B

B

B

w

B

=

0



B



L

=

B



P 



B



L

≠

0 ,

B



P 

≠

0

M

B

*

=

0

T

B

*(L)

=

T

B

*(P)

T

B

*(L)

≠

0 , T

B

*(P)

≠

0

B

B

B

w

B

≠

0



B



L

≠

B



P 



B



L

≠

0 ,

B



P 

≠

0

M

B

*

≠

0

T

B

*(L)

≠

T

B

*(P)

T

B

*(L)

≠

0, T

B

*(P)

≠

0

A

B

A

B

A

B

A

B

w

A

=

0



A

=

0

w

B

≠

0



B

≠

0

M

A

*

=

0

T

A

*

=

0

M

B

*

≠

0

T

B

*

≠

0

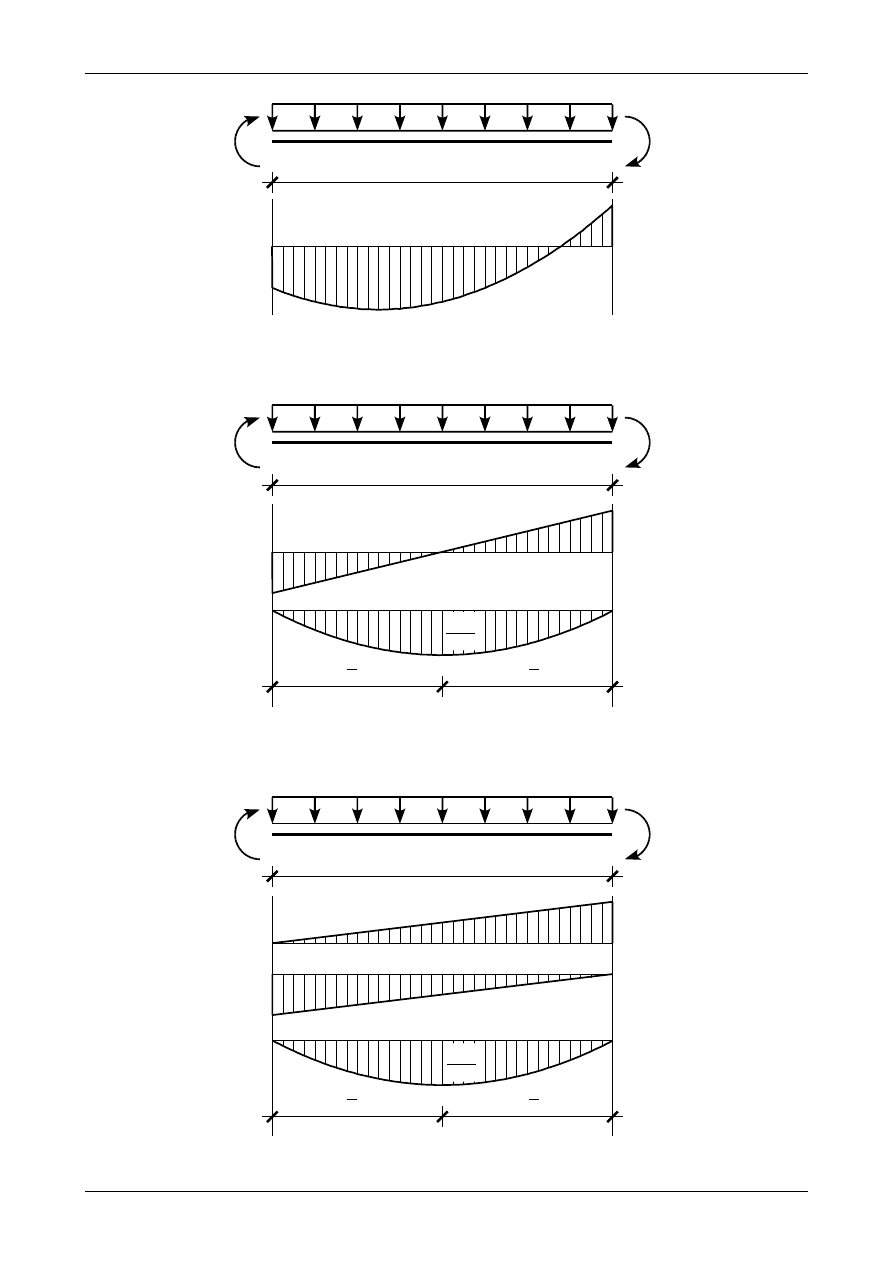
Pewnym problemem jest moment zginający w przedziale, w którym działa obciążenie ciągłe równo-

miernie rozłożone. Jak wiadomo wykres momentu zginającego jest w takim przypadku parabolą, dla której 
należałoby za pomocą całek znaleźć wartość i położenie wypadkowej. Można jednak tego uniknąć. Rysunek 
12.22   przedstawia   wykres   momentu   zginającego   w   przedziale,   w   którym   działa   obciążenie   ciągłe 
równomiernie rozłożone. Na końcach tego przedziału momenty zginające wynoszą M

1

  i M

2

. Jeden z nich 

rozciąga dolną a drugi górną część belki. Łączymy te dwa punkty linią prostą i dodajemy wykres momentu 
zginającego   jak   dla   belki   swobodnie   popartej   (rysunek   5.99).   Otrzymamy   wykresy   przedstawione   na 
rysunku   12.23.   Ostatnim   etapem   będzie   przerobienie   przewiniętego   wykresu   liniowego.   W   tym   celu 
łączymy punkt M

1

 na lewym końcu z zerem na prawym końcu, a punkt M

2

 na prawym końcu z zerem na 

lewym   końcu.   W   wyniku   tego   otrzymamy   ostatecznie   przerobiony   wykres   momentu   zginającego 
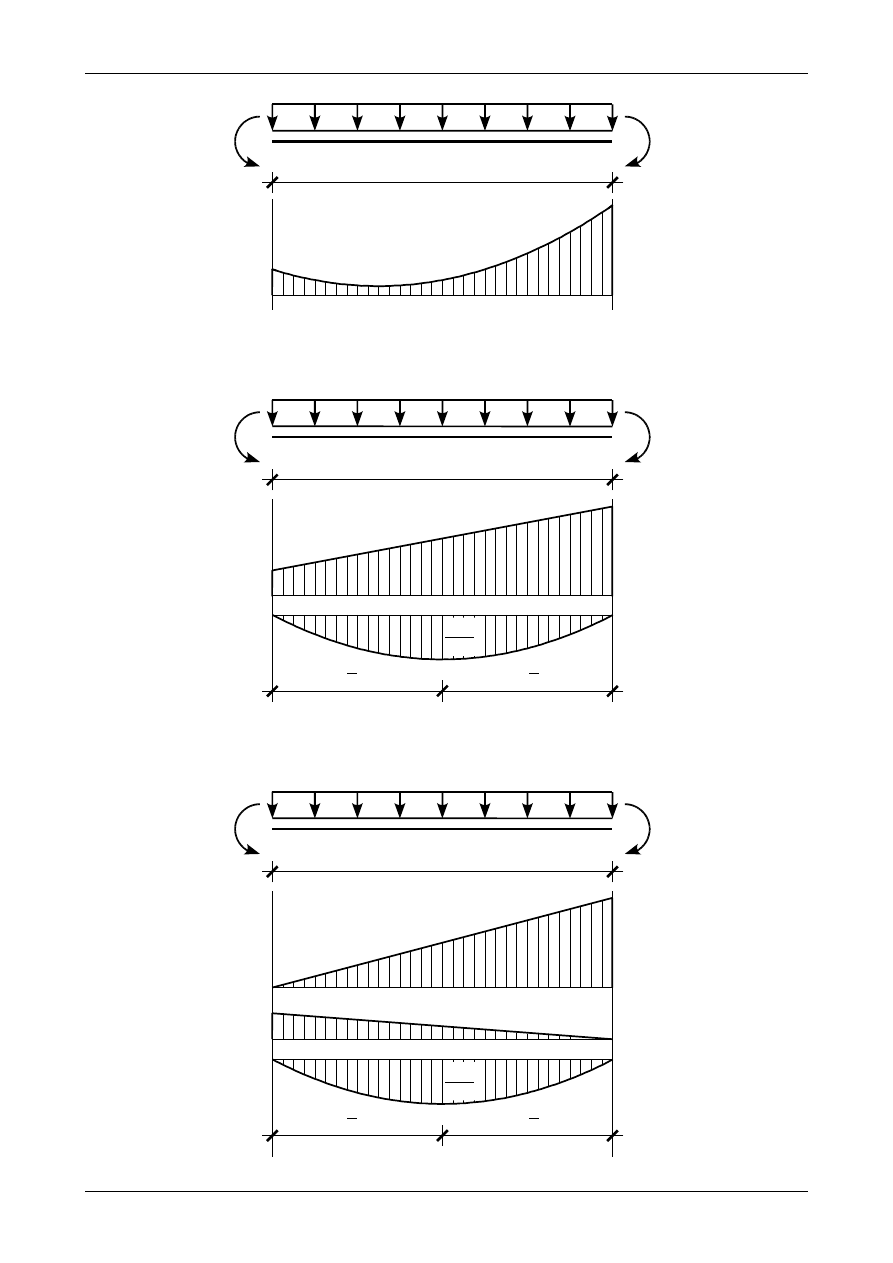
przedstawiony na rysunku 12.24. Rysunek 12.25 przedstawia wykres momentu zginającego w przedziale, w 
którym   także   działa   obciążenie   ciągłe   równomiernie   rozłożone.   Na   końcach   tego   przedziału   momenty 
zginające   wynoszą   M

1

  i   M

2

.   Oba   rozciągają   górną   część   belki.   Łączymy   te   dwa   punkty  linią   prostą   i 

dodajemy   wykres   momentu   zginającego   jak   dla   belki   swobodnie   popartej   (rysunek   5.99).   Otrzymamy 
wykresy   przedstawione   na   rysunku   12.26.   Ostatnim   etapem   będzie   przerobienie   trapezowego   wykresu 
liniowego. W tym celu łączymy punkt M

1

  na lewym końcu z zerem na prawym końcu, a punkt M

2

  na 

prawym   końcu   z   zerem  na   lewym   końcu.   W   wyniku   tego   otrzymamy   ostatecznie   przerobiony   wykres 
momentu zginającego przedstawiony na rysunku 12.27. Jeżeli obciążenie ciągłe równomiernie rozłożone 
q w belce rzeczywistej działa w dół to parabola ma „brzuszek” skierowany w dół, jeżeli odciążenie to 
działa do góry to parabola jest także skierowana do góry.

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

16

q

L

M

1

M

2

M

1

M

2

Rys. 12.22. Wykres momentu zginającego w przedziale z obciążeniem ciągłym równomiernie rozłożonym

q

L

M

1

M

2

M

1

M

2

L

2

L

2

+

q⋅L

2

8

Rys. 12.23. Wykres liniowy i paraboliczny

q

L

M

1

M

2

M

1

M

2

L

2

L

2

+

+

0

0

q⋅L

2

8

Rys. 12.24. Ostatecznie przerobiony wykres momentu zginającego

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

17

q

L

M

1

M

2

M

1

M

2

Rys. 12.25. Wykres momentu zginającego w przedziale z obciążeniem ciągłym równomiernie rozłożonym

q

L

M

1

M

2

M

1

M

2

L

2

L

2

+

q⋅L

2

8

Rys. 12.26. Wykres liniowy i paraboliczny

q

L

M

1

M

2

M

1

M

2

L

2

L

2

+

+

0

0

q⋅L

2

8

Rys. 12.27. Ostatecznie przerobiony wykres momentu zginającego

Dr inż. Janusz Dębiński

WM

12. PRZEMIESZCZENIA W BELKACH

18

W wyniku przerobienia wykresu momentu zginającego otrzymamy wykres składający się z trójkątów 

prostokątnych   i   parabol.   Dzieląc   odpowiedni   rzędne   wykresu   przez   sztywność   na   zginanie   otrzymamy 
wartości obciążenia wtórnego q

*

. Jego znak jest taki sam jak znak momentu zginającego. Wynika to ze 

wzoru (12.48). Jeżeli moment zginający w belce rzeczywistej rozciąga dolną część belki to obciążenie 
wtórne q

*

 działa w dół, jeżeli moment ten rozciąga górną część belki to obciążenie wtórne działa do 

góry. 

L

0

L

0

L

3

2
3

⋅

L

L

3

2
3

⋅

L

q*

q*

W

*

W

*

Rys. 12.28. Siła wypadkowa z obciążenia trójkątnego w dół

L

0

L

0

L

3

2
3

⋅

L

L

3

2
3

⋅

L

q*

q*

W

*

W

*

Rys. 12.29. Siła wypadkowa z obciążenia trójkątnego do góry

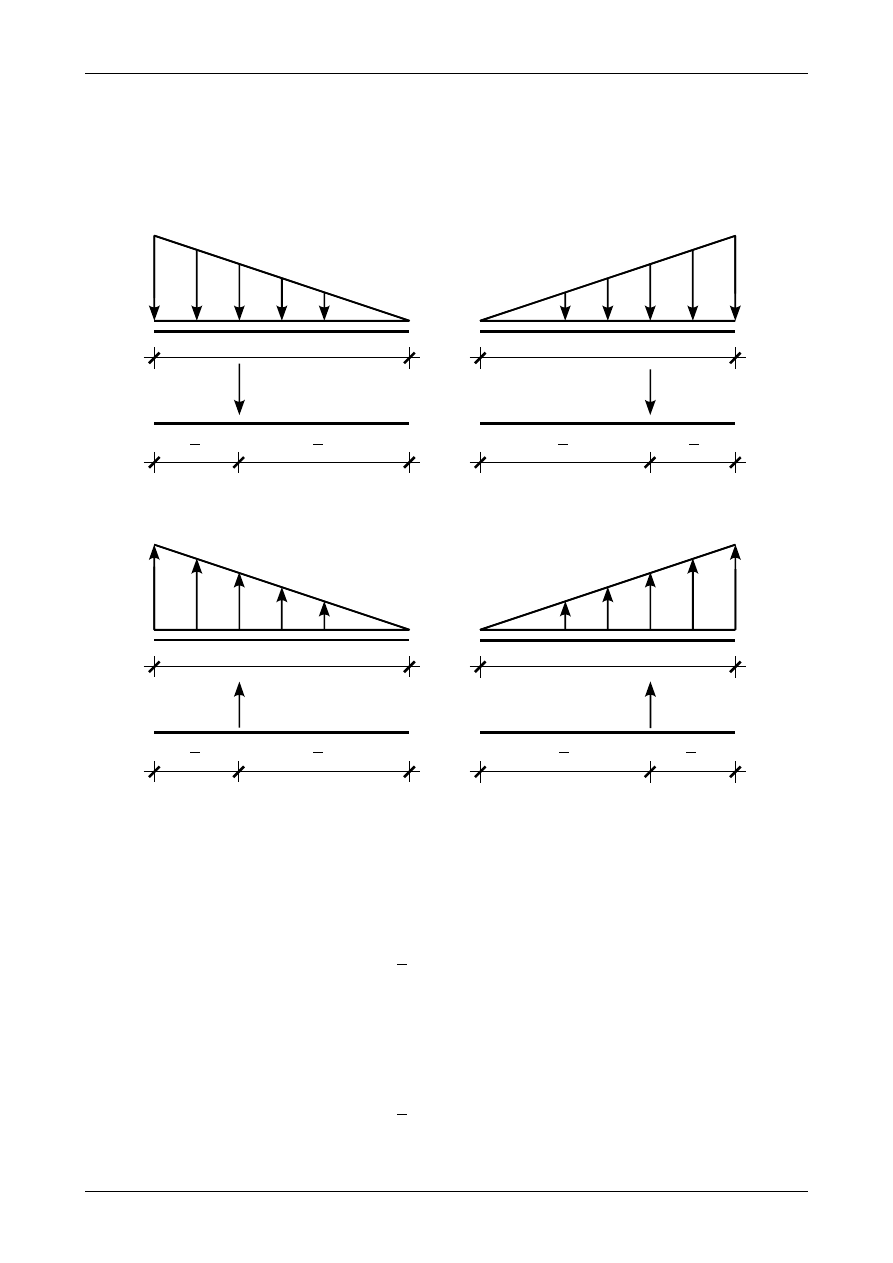
Obciążenie wtórne jest obciążeniem ciągłym. Musimy wyznaczyć wartości i położenie wtórnych sił 

wypadkowych  z tego obciążenia. Wtórną  siłę wypadkową  W

*

  z obciążenia trójkątnego wyznaczymy ze 

wzoru 

W

*

=

1
2

⋅

q

*

⋅

L

.

(12.51)

Położenie jej przedstawiają rysunki 12.28 i 12.29. Wtórną siłę wypadkową W

* 

z obciążenia parabolicznego 

wyznaczymy ze wzoru 

W

*

=

2
3

⋅

q

*

⋅

L

.

(12.52)

Położenie jej przedstawia rysunek 12.30. 

Dr inż. Janusz Dębiński

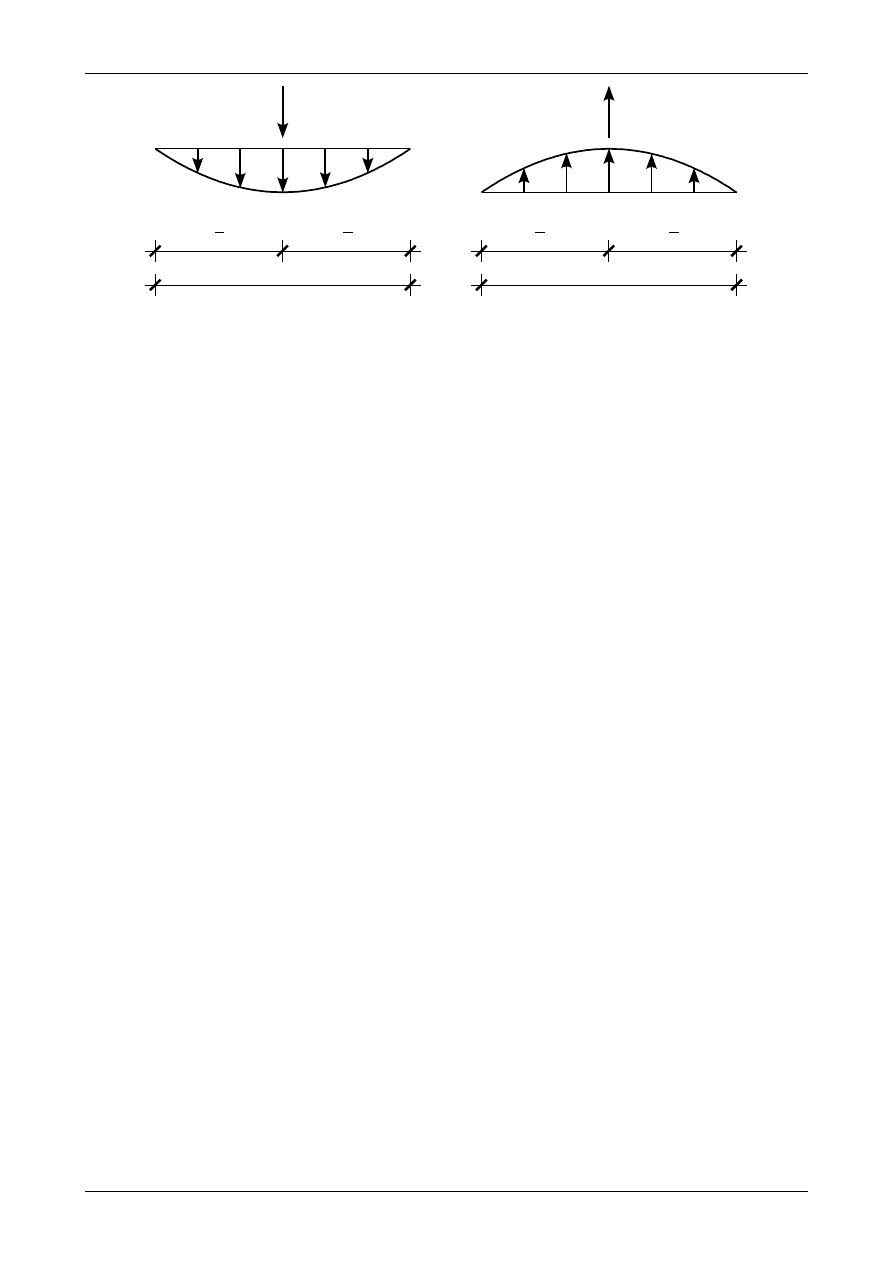
WM

12. PRZEMIESZCZENIA W BELKACH

19

L

L

L

2

L

2

L

2

L

2

q*

q*

W

*

W

*

Rys. 12.30. Siła wypadkowa z obciążenia parabolicznego

Mając   wyznaczone   wtórne   siły   wypadkowe   z   obciążenia   wtórnego   możemy   wyznaczyć   wtórne 

reakcje oraz siły poprzeczne i momenty zginające w interesujących nas punktach belki fikcyjnej. Otrzy-
mamy w ten sposób kąty obrotu i ugięcia w belce rzeczywistej.

Dr inż. Janusz Dębiński