SYNTEZA UKŁADÓW KOMBINACYJNYCH
1.
Układy kombinacyjne - wiadomości ogólne
Logiczne układy kombinacyjne są to układy, w których sygnały wyj. w danej chwili czasu zależne są
tylko od aktualnych sygnałów wejściowych i nie zależą od sygnałów wejściowych w przeszłości. Są to
układy bez pamięci (ich analogowym odpowiednikiem są układy bezinercyjne np. sieci R).
Zależność między sygnałami WE i WY można dla nich określić podając funkcję Y=f(X).
Podstawowym sposobem przedstawiania funkcji logicznych (przełączających) jest opis słowny.
Musi on jednoznacznie określać przypadki, w których sygnały wyjściowe mają wartość 0 lub 1.
Układy cyfrowe przetwarzają informacje binarne i dla ich opisu konieczny jest aparat
matematyczny operujący dwoma symbolami.
Okazało się że algebra sformułowana w połowie XIX wieku przez angielskiego logika G. Boole’a
jest dobrym narzędziem opisu tych układów (postać algebraiczna).
Również wykres czasowy jest dobrym sposobem na przedstawienie zapisu funkcji.
Inna formą zapisu funkcji logicznej jest tablica, w której wszystkim możliwym wartościom
argumentów przyporządkowuje się odpowiednie wartości funkcji.
Tablica wartości jest bardziej konkretną i pełną postacią zapisu funkcji niż opis słowny i dlatego często z
opisu słownego przechodzi się do tablicy, sprawdzając przy tym, czy posiadane informacje o funkcji są
pełne i wystarczają do wypełnienia wszystkich pozycji.
Niekiedy zdarza się, że wartość funkcji przy pewnych kombinacjach sygnałów wejściowych jest
dowolna lub nieokreślona np. gdy taka kombinacja wejściowa nigdy w rzeczywistości nie występuje.
Funkcja nosi wówczas nazwę funkcji niepełnej (niezupełnej, nie w pełni określonej), a w jej tablicy, w
odpowiednich pozycjach kolumny y
, wstawia się kreskę.
W praktyce wygodniej posługiwać się innymi postaciami tabeli wartości. Najbardziej użyteczna
jest tablica Karnaugha.
2. Synteza układów kombinacyjnych
W celu dokonania syntezy układu kombinacyjnego należy:
1.
Na podstawie zadanego opisu słownego określić funkcję logiczną rozpatrywanego problemu, np. za
pomocą zespołu funkcji lub tabelą wiążącą każde wyjście układu z wejściami.
2.
Dokonać minimalizacji funkcji logicznej wykorzystując metody algebraiczne lub tablice Karnaugha.
3.
Sporządzić schemat układu logicznego, realizującego zminimalizowaną funkcję logiczną.
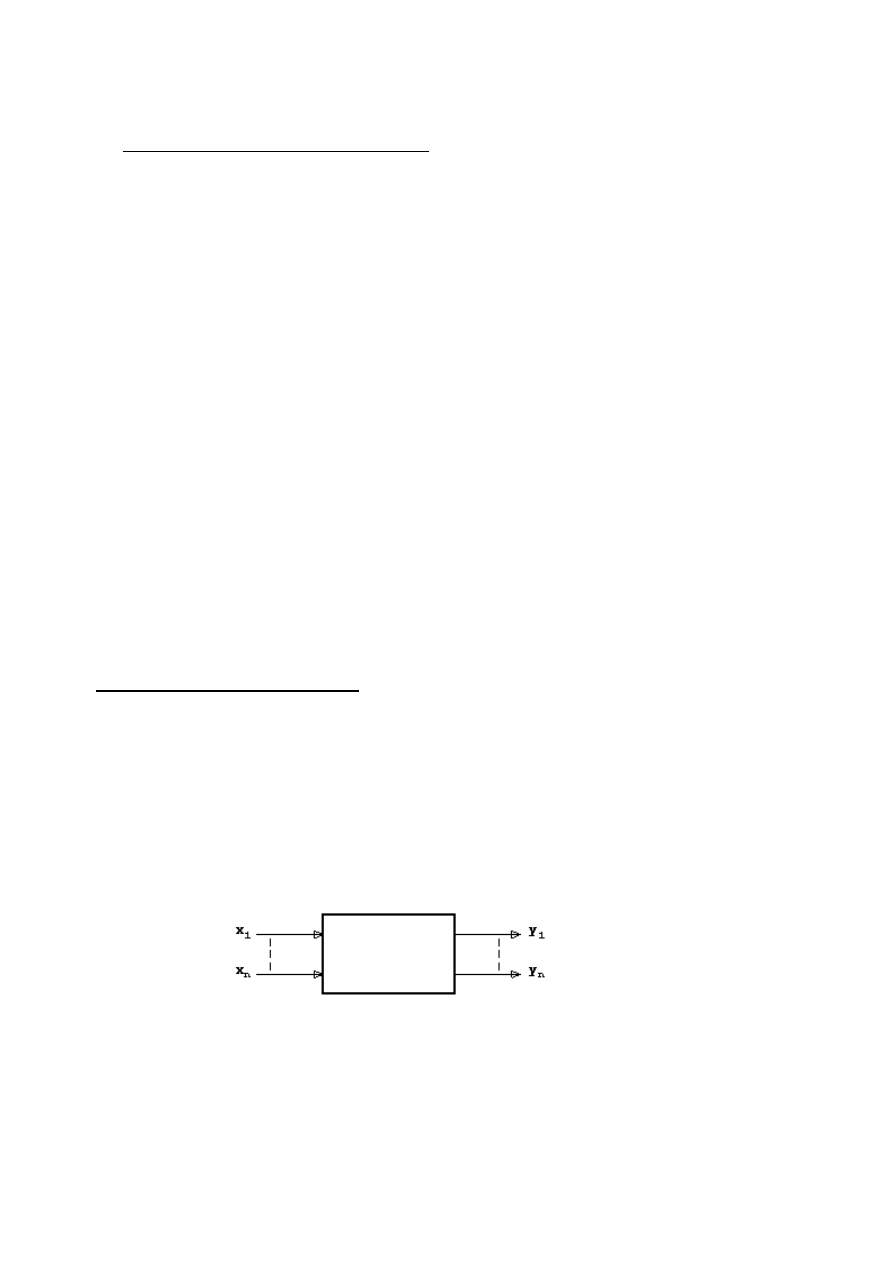
Logiczny u
kład kombinacyjny UK o m wejściach i n wyjściach nazywamy układ, w którym każdej z
możliwych kombinacji sygnałów wejściowych przyporządkowana jest jedna i tylko jedna kombinacja
sygnałów wyjściowych.
Rys. 1. Schemat blokowy układu kombinacyjnego
Jeżeli sygnały wejściowe potraktujemy jako zmienne binarne x
1
,...,x
m
, tj. dowolne elementy zbioru {0,1} ,
a sygnały wyjściowe y
1
,...,y
n
jako wartości binarne funkcji zmiennych binarnych x
1
,...,x
m
, to możemy
powiedzieć, że układ kombinacyjny jest opisany przez n funkcji boolowskich określonych na zbiorze m
zmiennych wejściowych.
Układ funkcji boolowskich można zapisać w postaci tablicy o (m+n) kolumnach i 2
m
wierszach.
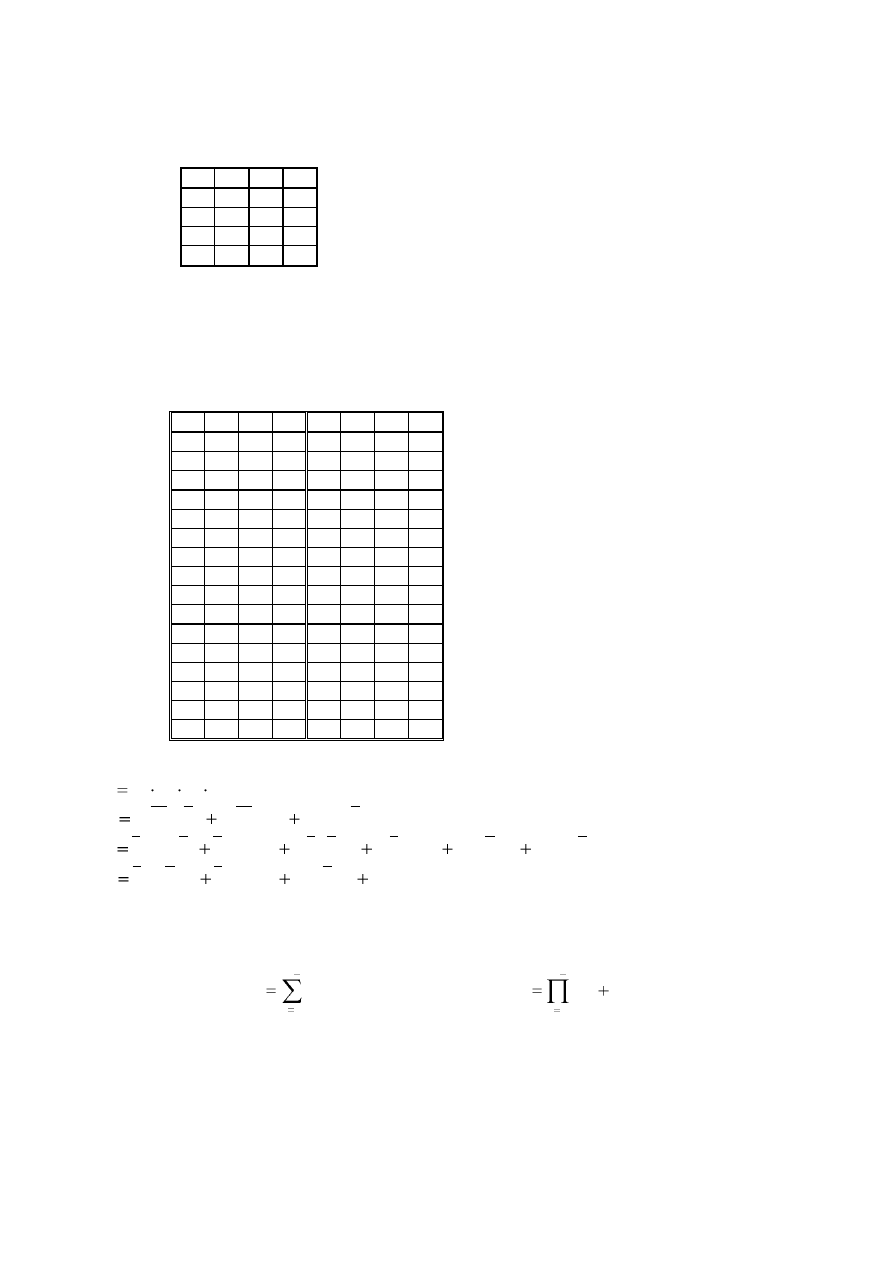
W wierszach kolumn od 1 do m
będą zapisane wszystkie kombinacje wartości binarnych zmiennych
x
1
,...,x
m
, a w kolumnach od m+1 do m+n
– odpowiadające tym kombinacjom wartości binarne funkcji
wyjściowych.
x
1
x
2
y
1
y
2
0
0
1
0
0
1
-
1
1
0
1
-
1
1
0
0
Przykład
Podać opis układu kombinacyjnego mnożącego dwie dwubitowe liczby binarne.
Układ posiada 4 we i 4 wy bo (11)
2
x (11)
2
= (1001)
2
= 9
10
Oznaczając wejścia przez x
1
, x
2
i y
1
, y
2
oraz wyjścia z
1
, z
2
, z
3
i z
4
otrzymujemy tabelę:
x
1
x
2
y
1
y
2
z
1
z
2
z
3
z
4
0
0
0
0
0
0
0
0
0
0
0
1
0
0
0
0
0
0
1
0
0
0
0
0
0
0
1
1
0
0
0
0
0
1
0
0
0
0
0
0
0
1
0
1
0
0
0
1
0
1
1
0
0
0
1
0
0
1
1
1
0
0
1
1
1
0
0
0
0
0
0
0
1
0
0
1
0
0
1
0
1
0
1
0
0
1
0
0
1
0
1
1
0
1
1
0
1
1
0
0
0
0
0
0
1
1
0
1
0
0
1
1
1
1
1
0
0
1
1
0
1
1
1
1
1
0
0
1
2
1
2
1
1
y
y
x
x
z
2
1
2
1
2
1
2
1
2
1
2
1
2
y
y
x
x
y
y
x
x
y
y
x
x
z
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
3
y
y
x
x
y
y
x
x
y
y
x
x
y
y
x
x
y
y
x
x
y
y
x
x
z
2
1
2
1
2
1
2
1
2
1
2
1
2
1
2
1
4
y
y
x
x
y
y
x
x
y
y
x
x
y
y
x
x
z
Funkcja
boolowska może być przedstawiona w postaci sumy pełnych iloczynów zmiennych x
1
,...,x
m
lub
w postaci
iloczynu pełnych sum tych zmiennych w sposób następujący:
i
m
i
i
m
a
K
x
x
x
f
1
2
0
2
1
)
,....,
,
(
lub
)
(
)
,....,
,
(
1
2
0
2
1
i
m
i
i
m
a
D
x
x
x
f
gdzie:
K -
iloczyn pełny, D - suma pełna, a – wartość funkcji dla konkretnych argumentów
Powyższe zależności umożliwiają łatwe przejście od tablicy wartości funkcji (lub równoważnego zapisu)
do wyrażenia logicznego.
Tablica wartości przedstawia kolejne wartości a
i
.
Ponieważ 0 x K
i
= 0 oraz 1 x K
i
= K
i
, dla przedstawienia funkcji wg zależności z wykorzystaniem
iloczynów pełnych należy wybrać sumę tych K
i
, dla których a
i
= 1
Przykładowa tablica wartości
i
x
1
x
2
x
3
y
1
0
0
0
0
2
0
0
1
1
3
0
1
0
0
4
0
1
1
1
5
1
0
0
0
6
1
0
1
1
7
1
1
0
1
8
1
1
1
1
Dla podanej tablicy wyrażenie logiczne ma następującą postać:
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
7
6
5
3
1
3
2
1
)
,
,
(
K
K
K
K
K
x
x
x
y
Formułę taką można uzyskać bezpośrednio z tablicy, biorąc pod uwagę jedynie te wiersze, dla których
y = 1
i przypisując wartościom x
i
= 1
zmienną x
i
a wartościom x
i
= 0
zmienną
i
x
.
Tak utworzone iloczyny pełne należy dodać. Uzyskana postać funkcji jest jedną z postaci kanonicznych
funkcji logicznej i nosi nazwę zupełnej normalnej postaci sumacyjnej (ZNPS).
Z za
sad jej tworzenia wynika, że każda funkcja może mieć tylko jedną taką postać.
Wykorzystując wzory na zapis funkcji, wzory wykorzystujące sumy pełne należy zauważyć, że
0 + D
i
= D
i
, 1 + D
i
= 1
więc w odpowiednich wyrażeniach należy wypisać iloczyn tych D
i
, dla których a
i
= 0.
Wyrażenie dla powyższej tabeli:
)
)(
)(
(
)
,
,
(
3
2
1
3
2
1
3
2
1
4
2
0
3
2
1
x
x
x
x
x
x
x
x
x
y
czyli
D
D
D
x
x
x
y
Formułę tę można otrzymać bezpośrednio z tablicy, biorąc pod uwagę jedynie te wiersze, dla których
y = 0
i przypisując wartościom x
i
= 0
zmienną x
i
a wartościom x
i
= 1 zmie
nną
i
x
.
Tak utworzone sumy pełne należy pomnożyć.
Uzyskana postać funkcji nosi nazwę zupełnej normalnej postaci iloczynu (ZNPI) i również jest jedna
dla każdej funkcji.
Postać kanoniczną często zapisuje się w skrócie, w postaci zbioru indeksów (bez symbolów K i
D), z odpowiednim symbolem operacji np.
y(x
1
, x
2
, x
3
) = (1, 3, 5, 6, 7)
oraz
y(x
1
, x
2
, x
3
) = (0, 2, 4)
Dla funkcji bez wartości nieokreślonych, występujące w tych dwóch postaciach liczby indeksowe muszą
wyczerpywać wszystkie możliwe wartości od 0 do 2
m
-
1, co umożliwia łatwe wyznaczenie jednej postaci
na podstawie znajomości drugiej (przez uzupełnienie liczb).
Np.
jeśli
y
1
(x
1
, x
2
) = (0, 1) ,
to
y
1
(x
1
, x
2
) = (2, 3)
jeśli
y
2
(x
1
, x
2
, x
3
) = (4, 5, 7)
to
y
2
(x
1
, x
2
, x
3
) = (0, 1, 2, 3, 6)
Gdy funkcja jest niepełna, indeks odpowiadający kombinacji nieokreślonej może wystąpić zarówno w
jednej postaci jak i w drugiej, gdyż y może być zarówno 0 jak i 1.
Oznacza się to przez wzięcie odpowiedniego składnika w nawias np.
y (x
1
, x
2
) = [2, (1)] czyli
)
(
)
(
2
1
2
1
2
,
1
x
x
x
x
x
x
y
oraz
y (x
1
, x
2
) = [ 0, 3, (1)] czyli
)]
)[(
)(
(
)
(
2
1
2
1
2
1
2
,
1
x
x
x
x
x
x
x
x
y
Minimalizacja funkcji
Zakładając, że do realizacji schematu logicznego postaci kanonicznych sumy i iloczynu dla
p
rzykładu z tablicą wartości użyjemy elementów NOT, AND i OR, łatwo policzyć że realizacja postaci
kanonicznej sumy wymaga 3 elementów NOT, 5 elementów AND i jeden element OR.
Odpowiednia postać kanoniczna iloczynu może być zrealizowana za pomocą
2 x NOT, 3 x OR i 1 x AND.
Można przypuszczać, że druga wersja będzie tańsza i prostsza, a więc lepsza.
Na ogół, układ o mniejszej liczbie elementów logicznych jest tańszy i bardziej niezawodny, a
spośród dwóch układów o tej samej liczbie elementów lepszy jest ten, który operuje mniejszą liczbą
sygnałów (mniej wejść mają wszystkie jego elementy).
Niezależnie od zastosowanych dalej elementów schematu logicznego, bardzo ważnym etapem
syntezy jest poszukiwanie takiej postaci funkcji przełączającej, w której występuje minimalna liczba liter
(tzn. zmiennych lub ich negacji).
Realizacja funkcji logicznej przedstawionej w postaci kanonicznej nie jest zazwyczaj
realizacją najprostszą.
Oczywiście jest możliwe minimalizowanie funkcji logicznych dokonując przekształceń algebraicznych.
Postacie kanoniczne tych funkcji przekształca się zgodnie z prawami oraz twierdzeniami algebry Boole’a
tak, aby uzyskać wyrażenie równoważne, ale tańsze wg przyjętych kryteriów kosztów. Otrzymane
wyrażenia zależą w dużej mierze od umiejętności projektanta.
Inny sposób poszukiwania postaci minimalnej funkcji opiera się na tzw. regułach
sklejania:
A
x
A
Ax
B
x
B
x
B
)
)(
(
gdzie A i B zmienne lub funkcje przełączające.
Reguły te można wyrazić następująco:
Suma lub iloc
zyn dwóch wyrażeń różniących się między sobą tylko na jednej pozycji –
znakiem negacji, mogą być zastąpione jednym wyrażeniem, bez litery stanowiącej różnicę.
Np.
3
2
3
2
1
3
2
1
2
1
3
2
1
3
2
1
1
1
2
2
1
2
1
2
1
)
)(
(
1
)
(
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
Wyrażenia podlegające sklejaniu nazywane są wyrażeniami sąsiednimi.
Jeśli w otrzymanych postaciach kanonicznych funkcji takie wyrażenia sąsiednie występują, to postać
kanoniczną można uprościć, z wyraźną korzyścią dla realizacji technicznej.
x
1
x
y
2
1
1
0
0
Postać kanoniczną sumy z omawianego przykładu można zminimalizować w następujący
sposób:
2
1
3
2
1
3
2
3
2
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
3
2
1
)
(
)
(
)
(
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
x
y
Wpisano dwukrotnie iloczyn
3
2
1
x
x
x
, ponieważ A = A + A tzn. każdy składnik może się powtarzać bez
zmiany wartości funkcji.
Przeprowadzając sklejanie w postaci kanonicznej iloczynu (dla tego samego przykładu) otrzymuje się:
)
)(
(
)
)(
)(
(
3
2
3
1
3
2
1
3
2
1
3
2
1
x
x
x
x
x
x
x
x
x
x
x
x
x
y
Z zasady rozdzielności a+bc = (a + b)(a + c) wynika, że obydwa wyniki są sobie równe.
Prostsza jest realizacja
2
1
3
x
x
x
w której potrzebujemy 1 x OR i 1 x AND.
Różnica między realizacją zupełnej postaci kanonicznej i postaci minimalnej jest więc duża.
W wyniku sklejania
uzyskuje się wyrażenia, które już nie są postaciami kanonicznymi, ale zachowują
postać sumy iloczynów oraz iloczynu sum.
Wyrażenia tego typu przyjęto nazywać normalną postacią sumy NPS (normalną postacią alternatywy) i
normalną postacią iloczynu NPI (normalną postacią koniunkcyjną).
W przypadku złożonych funkcji wielu zmiennych wyszukiwanie wyrażeń sąsiednich i sklejanie w podany
sposób staje się bardzo uciążliwe, zwłaszcza że do otrzymania postaci minimalnej trzeba dokonać
wszystkich możliwych sklejeń.
Istnieją inżynierskie metody upraszczające procedurę minimalizacji gdy liczba zmiennych nie
przekracza 6, lub gdy liczba wyrazów zadanej postaci kanonicznej nie jest zbyt duża.
W
innych przypadkach rozwiązań minimalnych trzeba szukać za pomocą cyfrowych maszyn
matematycznych.
Metoda Karnaugha
Jest to graficzna metoda minimalizacji, powszechnie nazywana metodą tablic Karnaugha.
Metoda ta ułatwia sklejanie przez takie usytuowanie na płaszczyźnie wyrażeń postaci kanonicznej, aby
wyrażenia sąsiednie podlegające sklejeniu były umieszczone blisko siebie, a więc były sąsiednimi
również w sensie geograficznym.
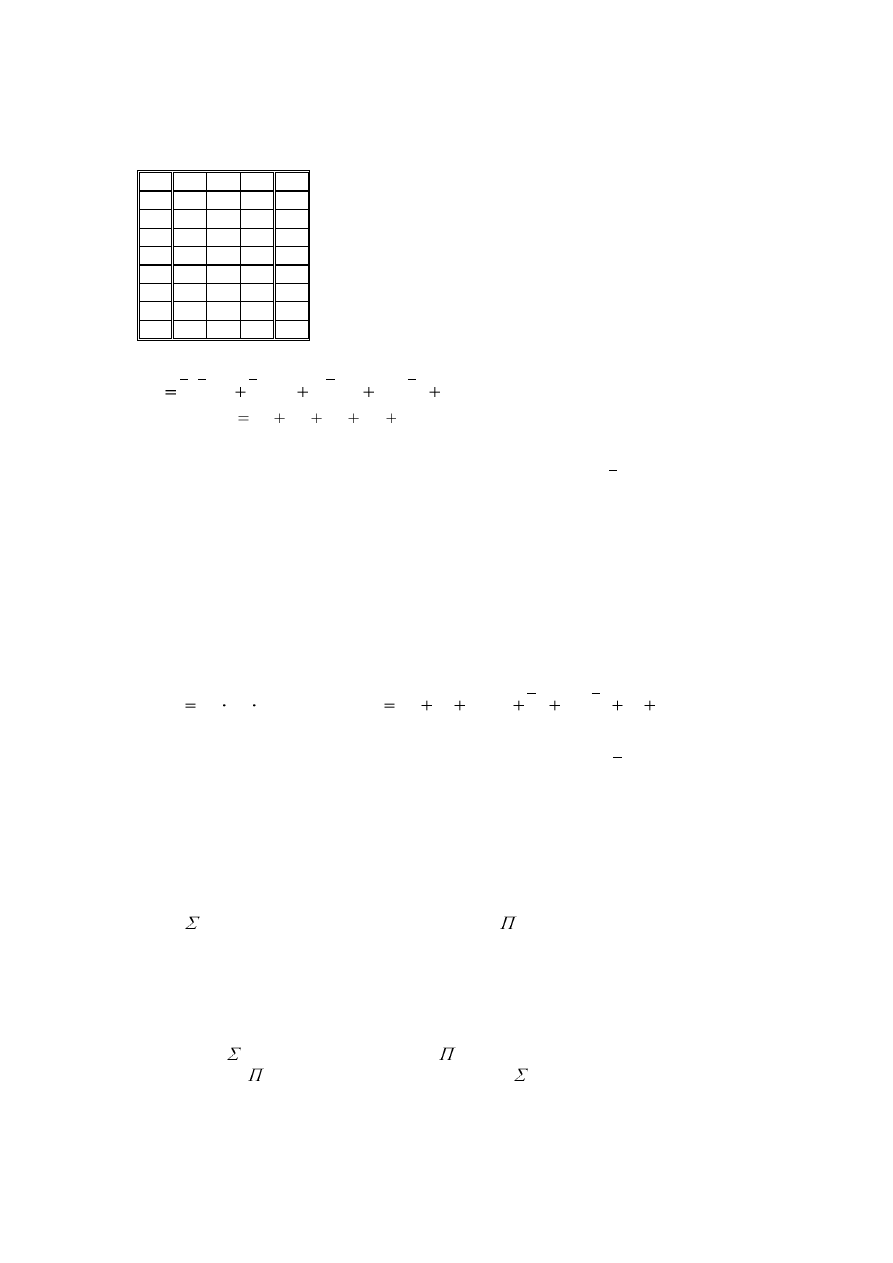
Jeżeli rozpatrywany układ ma n elementów dwustanowych, to liczba możliwych stanów tego
układu wynosi 2
n
.
W tablicy prawdy stany te przedstawiamy w 2
n
wierszach, w tablicy Karnaugha w 2
n
kratkach.
W przypadku n
parzystego, tablica Karnaugha będzie miała kształt kwadratu zawierającego 2
0,5n
x 2
0,5n
kratek, a w przypadku nieparzystych n
kształt prostokąta zawierającego 2
0,5(n+1)
x 2
0,5(n-1)
kratek.
Każda kratka tablicy Karnaugha odpowiada jednej kombinacji wartości zmiennych wejściowych,
czyli każdej kratce odpowiada jeden wiersz tablicy prawdy.
Jeśli np. układ zawiera dwie zmienne x
1
i x
2
(dwa elementy wejściowe) to liczba
możliwych kombinacji stanów tych zmiennych wynosi 2
2
= 4. Tablica prawdy
miałaby 4 wiersze
x
x
1
2
00 01
10 11
0
1
0
1
0
1
0
00
x
4
1
1
x
01
2
5
3
x
6
11 10
3
7
2
0
1
00
00
4
1
01
x
01
3
5
4
x
6
11 10
3
7
2
9
15
8
10
13
14
11
12
10
11
x
2
x
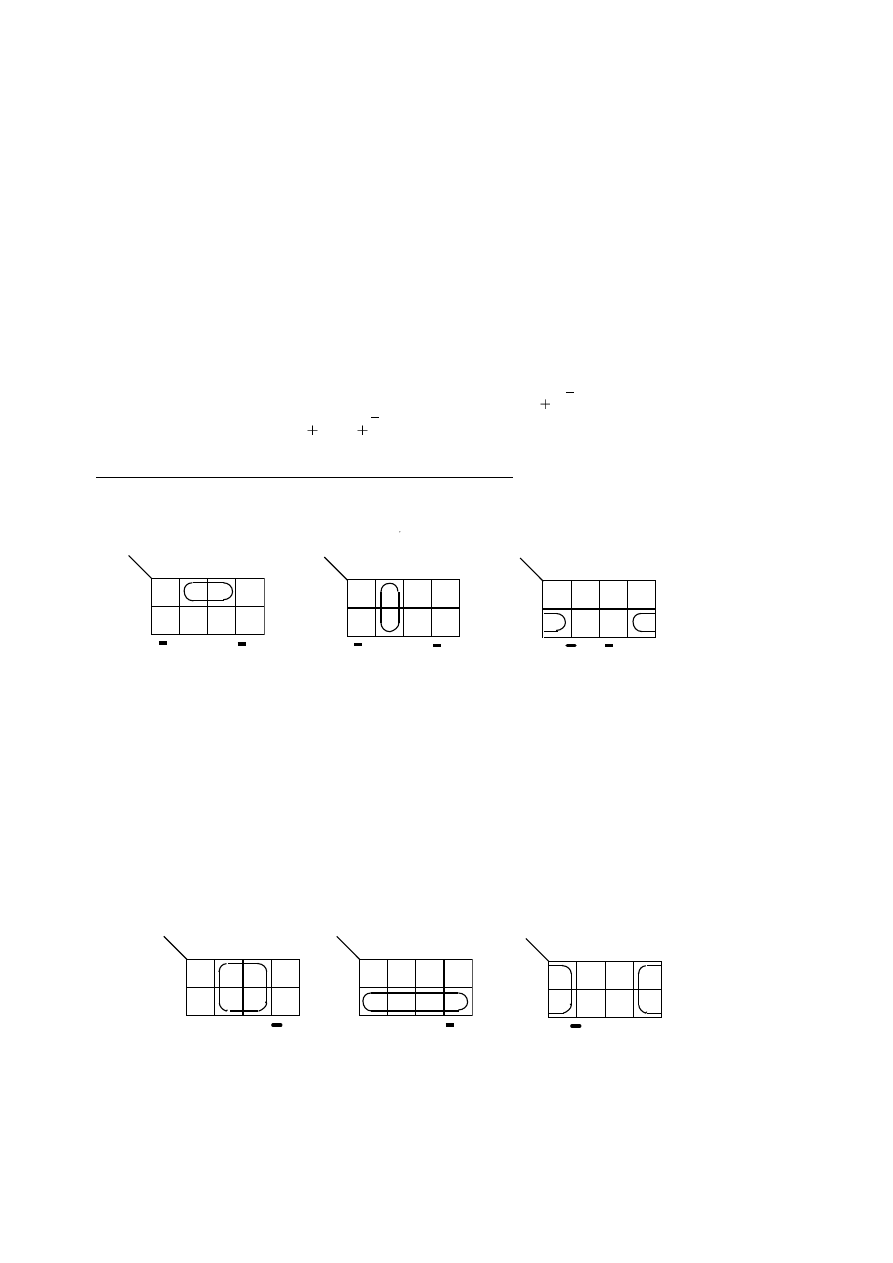
Tablice Karnaugha dla 3 i 4 zmiennych.
Aby ułatwić wpisywanie w przypadku, gdy funkcja jest zadana w postaci
liczb dziesiętnych, w tablicach wpisano odpowiednie liczby
Cechą charakterystyczną tablicy Karnaugha jest sposób ustawienia jej wierszy i kolumn. Użyty do
tego celu kod Graya
sprawia, że sąsiednie kratki tablicy odpowiadają ciągom zero-jedynkowym
różniącym się tylko jednym elementem (za kratki sąsiednie uważa się również te, które leżą na
przeciwnych końcach jednego wiersza lub kolumny).
Jeżeli w dwóch sąsiednich kratkach wypełnionej tablicy Karnaugha znajdują się jednakowe
symbole (0 lub 1), to odp
owiadające tym kratkom wyrażenia można skleić, co odpowiada usunięciu litery,
która w ramach sklejanej grupy zmienia wartość.
Takie sąsiednie kratki tablicy tworzące pary, łączy się linią dla zaznaczenia możliwości sklejania.
Gdy wyróżnione kratki
-
zawie
rają jedynki, zamiast odpowiadającego im wyrażenia
x
A
Ax
można przyjąć A
-
zawierają zera, zamiast
)
)(
(
x
B
x
B
można przyjąć B.
Wersje usytuowania takich par dla trzech i czterech zmiennych.
Na rysunkach podane są wyniki sklejenia, przy czym na pierwszym miejscu umieszczono wyrażenia
opisujące grupę jedynek, a na drugim grupę zer.
Dwie kratki tworzące parę o jednakowych symbolach można skleić z inną parą o takich samych
symbolach, jeśli obie pary tworzą kwadrat lub prostokąt
Jednakowe symbole objęte prostokątem można więc opisać iloczynem (jedynki) lub sumą (zera) w które
wchodzą tylko litery o wartościach nie zmieniających się w ramach tej grupy.
Minimalizację funkcji przełączających niewielkiej liczby zmiennych (do 6 zmiennych) najwygodniej jest
przeprowadzić na tablicy Karnaugha. Dzięki temu, że opis wartości zmiennych w tablicy Karnaugha
dokonany jest w kodzie Graya, ciągi wartości zmiennych opisujących kratki tablicy leżące obok siebie,
różnią się tylko na jednej pozycji, czyli odpowiednie pełne iloczyny (sumy) są sąsiednie.
Proste iloczyny (sumy
) na tablicy Karnaugha wyznacza się łącząc ze sobą sąsiednie jedynki (zera)
w grupy składające się z 2
n
(2, 4, 8,16, ...) kr
atek. Należy przy tym pamiętać, że brzegi tablicy również
sąsiadują ze sobą.
x
3
0
1
11
1
01
10
x
x
00
2
3
1
x
; x
+
x
3
x
1
3
10
x
;
2
00
x
x
x
01
x
0
x
2
1
11
3
x
1
+
3
2
3
x
1
0
1
;
01
3
+
x
x
10
x
x
1
00
11
2
1
x
3
x
10
1
0
;
2
00
x
x
01
1
3
3
x
3
11
x
x
x
x
10
1
00
11
0
x
01
2
;
x
3
x
1
1
1
x
11
3
x
3
10
x
2
0
1
3
00
1
x
x ;
01
Rys. ..
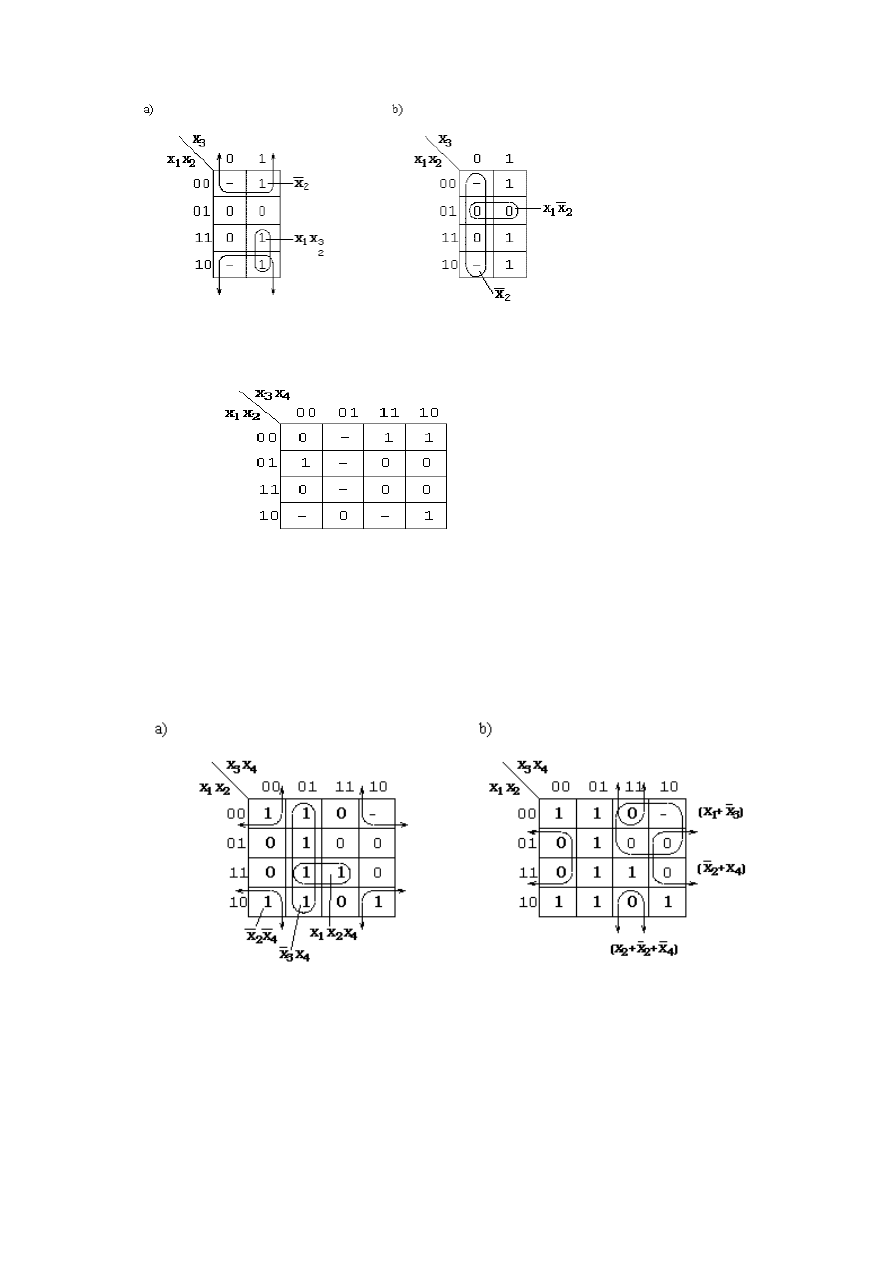
Przykłady sklejania funkcji trzech zmiennych
Na rys.
następnym przedstawiono tablicę Karnaugha funkcji nie w pełni określonej.
Rys. 3.
Tablica Karnaugha funkcji nie w pełni określonej
Kr
atki zawierające kreski mogą być łączone zarówno z jedynkami jak i zerami funkcji. Dla tablicy
4 i 6 zmiennych sąsiednimi są brzegi tablicy - dolny i górny oraz prawy i lewy, rys. 4 i rys. 6. Dla tablicy 5
zmiennych pojęcie sąsiedztwa jest bardziej skomplikowane. Oprócz zwykłego sąsiedztwa, sąsiednie są
również klatki symetryczne względem pionowej i poziomej osi tablicy, zaznaczonej na rys. 5 i 6 grubą
kreską. Na rysunkach tych zaznaczono niektóre sąsiednie kratki.
Rys. 4
. Przykłady sklejania funkcji czterech zmiennych
Rys. 5
. Przykładowa tablica Karnaugha dla funkcji pięciu zmiennych
Rys. 6
. Przykładowa tablica Karnaugha dla funkcji sześciu zmiennych
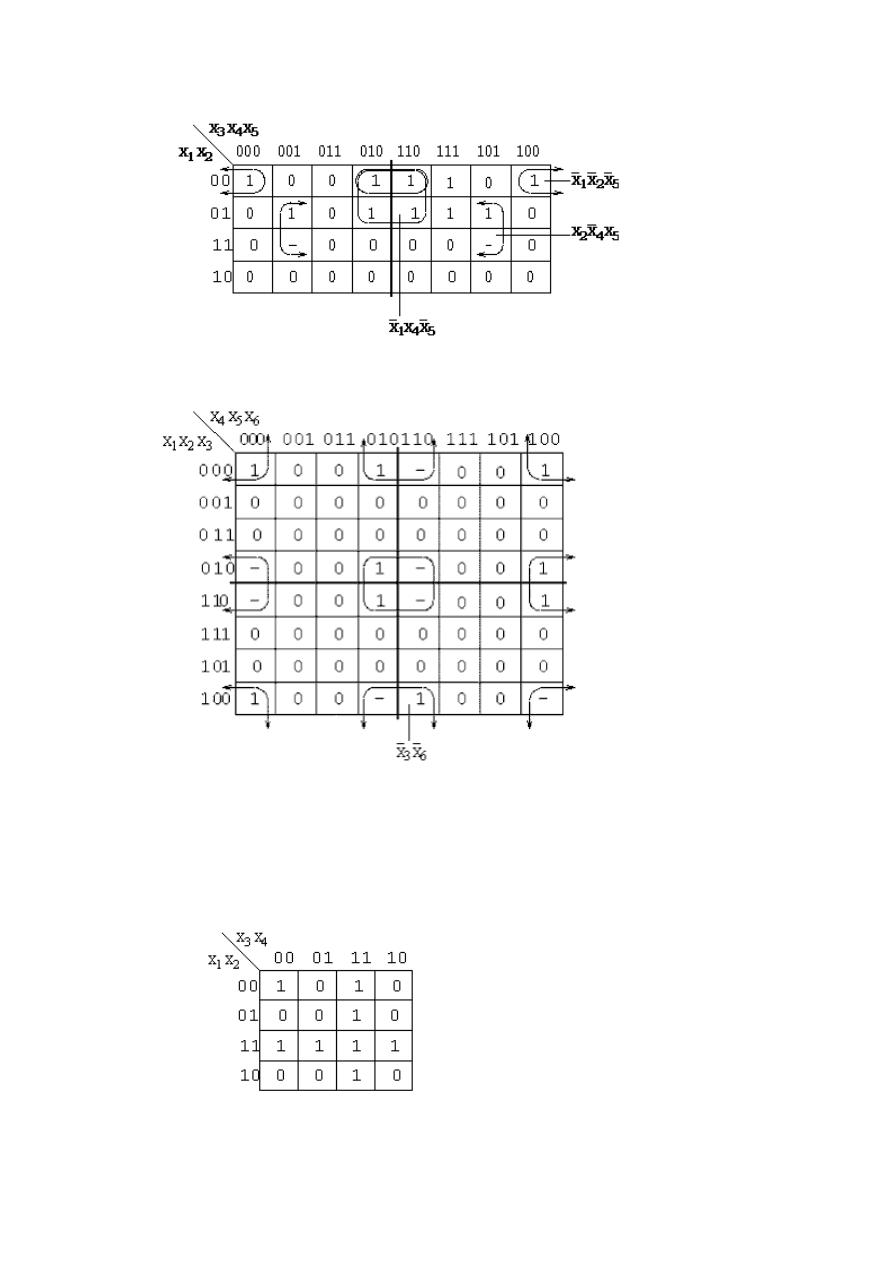
2.
Realizacja układów kombinacyjnych
Przykład
Na rys. 7
przedstawiono tablicę Karnaugha funkcji czterech zmiennych.
Rys. 7. Tablica Karnaugha funkcji czterech zmiennych
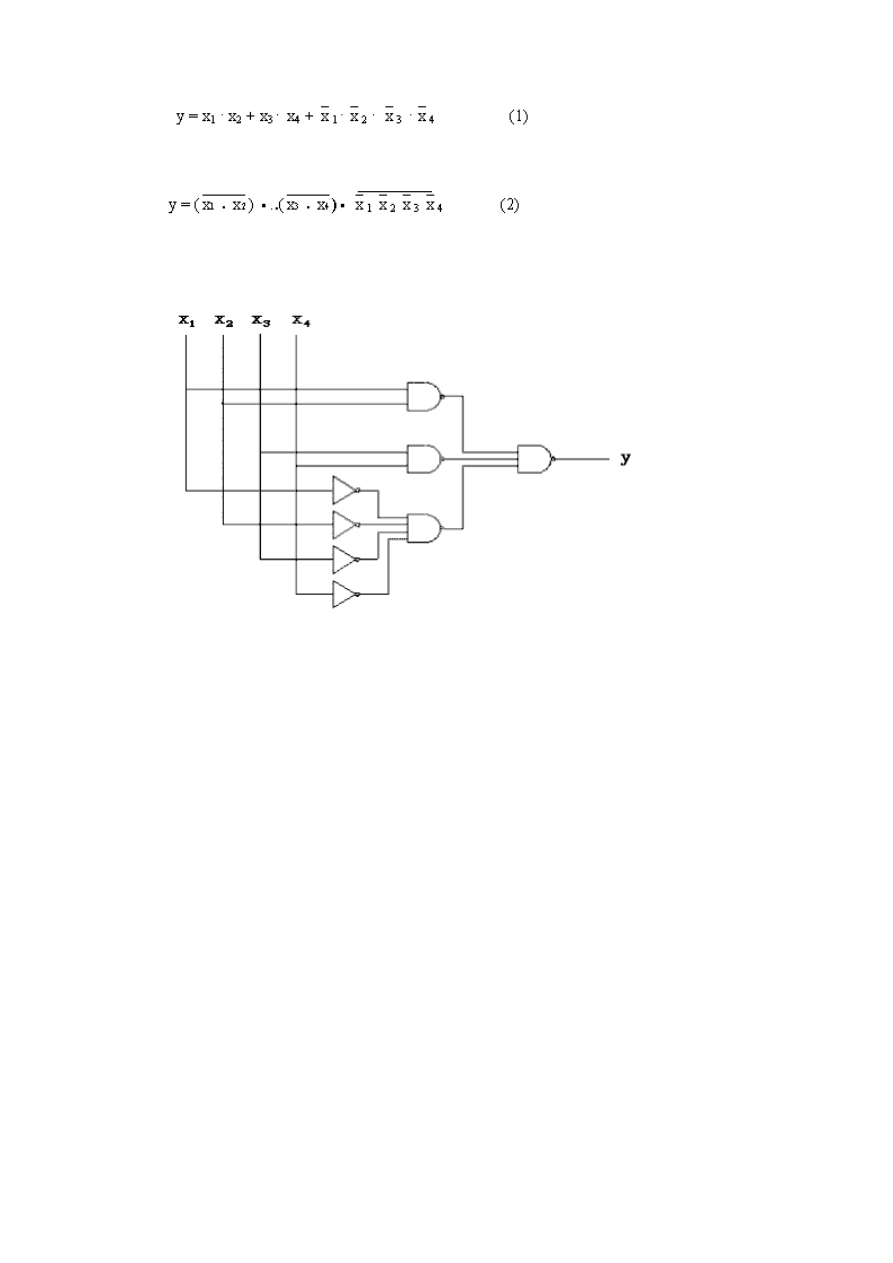
Funkcję przełączającą zapisaną w tablicy Karnaugha można przedstawić w postaci boolowskiej
Chcąc powyższą funkcję zrealizować używając elementów NAND należy dokonać jej przekształcenia.
Korzystając z praw de Morgana przekształca się funkcję przełączającą do postaci
Na rys. 8
przedstawiono schemat układu realizującego funkcję przełączającą y przy użyciu bramek
NAND.
Rys. 8
. Schemat układu zrealizowanego przy użyciu bramek NAND
Literatura:
1. Majewski W., Albicki A. „Projektowanie cyfrowych układów telekomunikacyjnych”.
WKŁ, Warszawa 1977.
2. Pieńkoś J.,Turczyński J. „Układy scalone TTL w systemach cyfrowych” .
WKŁ, Warszawa 1980.