Pierwsza część zajęć będzie dotyczyć opływu ciała płynem lepkim. Załóżmy, że ruch
odbywa się w płaszczyźnie. Sytuacja będzie zachodzić, w przybliżeniu, przy opływie
skrzydła samolotu albo przy opływie łopatki maszyny wirnikowej. Jeśli rozpiętość
skrzydła (albo łopatki) istotnie przekracza pozostałe wymiary, to dokonując przekroju
płaszczyzną prostopadłą do kierunku wyznaczonego przez tą rozpiętość otrzymujemy,
poza otoczeniem końca bryły, ruch niemal płaski. Napływający strumień ma daleko
przed opływaną figurą jednorodną, stałą w czasie prędkość i jednorodne, stałe ciśnienie.

Przy minimalnych prędkościach ściśliwość gazu (powietrze, jeśli i o zapalenie lotnicze)
można pominąć. Uprości to dalsze rozważania: unikniemy skomplikowanego opisu
termodynamicznego. Nie ma bowiem powodu, by uwzględniać temperaturę (jest stała) i
zależności lepkości od zmiennych warunków termodynamicznych.

Wymiary ciał są rzędu metrów, lub gdy rozważamy opływ łopatki, rzędu centymetrów.
Prędkość napływającego strumienia wynosi kilkadziesiąt – sto kilkadziesiąt metrów na
sekundę. Ponieważ lepkość kinematyczna jest rzędu 10

-5

(m

2

/sek) to liczba Reynolda

wynosi 10

5

-10

7

. To oznacza, iż siły bezwładności (ich skala jest U

2

/L) wielokrotnie

przekraczają siły lepkości (skala tych sił jest νU

2

/L) *. Można więc powiedzieć, że

lepkość nie odgrywa ważnej roli. Chyba, że prędkość zmienia się istotnie przy
niewielkiej zmianie położenia. Pamiętamy, iż na brzegu opływającej bryły płyn

*UZASADNIJ (przypomnij sobie bezwymiarowe równanie Naviera-Stokes’a. Aby
otrzymać liczbę Reynoldsa dzieliliśmy równanie przez U

2

/L.

„przylepia” się do powierzchni ciała stałego. Blisko tej powierzchni następuje istotna
zmiana prędkości na małym odcinku w kierunku prostopadłym do brzegu. Długość
opływanej linii jest wielokrotnie większa niż grubość warstwy w której zachodzi istotna
zmiana prędkości. Oznaczmy grubość warstwy leżącej przy brzegu w której zachodzi
znaczna zmiana ruchu (od zerowej prędkości do prędkości porównywalnej z prędkością
napływającego strumienia) symbolem δ. Jest: δ << L.

Promień krzywizny linii brzegowej jest wielkością rzędu L. A więc, skoro grubość
naszej warstwy jest również wielkością mniejszą od tego promienia, to można po prostu,
rozwinąć opływaną linią. Współrzędna X jest długością brzegu opływanego konturu, a Y
– prostopadła do brzegu. Pamiętamy: prędkość zmienia się znacząco w kierunku
prostopadłym do brzegu, a wzdłuż brzegu zmiany są niewielkie. Dalej: ruch odbywa się
– głównie – wzdłuż linii brzegowej. Składowa poprzeczna prędkości – zerowa na
konturze – nie powinna być znacząca. A więc:
Maksymalna wartość składowej wzdłużnej jest rzędu U

∞

, a maksymalna wartość

składowej poprzecznej jest istotnie mniejsze od U

∞

.

Napiszmy równania Naviera-Stokesa i ciągłości:

2

2

2

2

2

2

2

2

0

1

1

u

u

x

y

u

u

p

u

u

u

v

x

y

x

x

u

u

p

v

v

u

v

y

x

y

y

x

y

υ

ρ

υ

ρ

∂

∂

+

=

∂

∂

⎛

⎞

∂

∂

∂

∂

∂

+

= −

+

+

⎜

⎟

∂

∂

∂

∂

∂

⎝

⎠

⎛

⎞

∂

∂

∂

∂

∂

+

= −

+

+

⎜

⎟

∂

∂

∂

∂

∂

⎝

⎠

Pochodna względem X powinna być wielokrotnie mniejsza od pochodnej względem Y,
bo X jest rzędu L a Y – rzędu δ. Można więc napisać:

2

2

2

2

u

u

x

y

∂

∂

<<

∂

∂

Dalej: iloczyn

u

u

x

∂

∂

zawiera wprawdzie „małą” wielkość

u

x

∂

∂

, ale mnożną przez

znaczącą wielkość u Nie można go więc zaniedbać. Podobnie:

u

y

∂

∂

jest znaczne, ale , po

pomnożeniu przez ν nie musi być jedyną znaczną wielkością w równaniu ruchu dla

składowej x-owej prędkości: Po uproszczeniu

2

2

u

y

∂
∂

otrzymamy:

2

2

1

u

u

p

u

v

v

x

y

x

υ

ρ

∂

∂

∂

∂

+

=

+

∂

∂

∂

∂y

. Składowa poprzeczna prędkości, czyli ν może być

oznaczona na postaci równania ciągłości:

max

y

o

u

u

v

dy

v

x

x

δ

∂

∂

⎛

⎞

=

→ <

⎜

⎟

∂

∂

⎝

⎠

∫

•

Jest to wielkość rzędu δ. Gdy grubość δ jest znikoma, to z drugiego równania ruchu

pozostaje tylko:

( )

1

0

p

.

p

p x

y

ρ

∂

= −

→ =

∂

Napiszmy uproszczone równania. Są

następujące:

2

2

0

1

u

u

x

y

u

u

p

u

v

u

x

y

x

υ

ρ

∂

∂

+

=

∂

∂

∂

∂

∂

∂

+

= −

+

∂

∂

∂

∂y

Nazywamy je równaniami PRANTLA. Obowiązują w sąsiedztwie powierzchni
opływanego skrzydła lub łopatki. Ogólniej: w pobliżu opływanej powierzchni ciała
stycznego.

Warstwa, w której obowiązują nazywa się WARSTWA PRZYŚCIENNA. Warstwa ta
jest tym cieńsza, im większa jest liczba Reynoldsa. Dokładne oszacowanie prowadzi do

wyniku:

1
Re

L

δ

≈

. Jeśli Re->∞, to grubość warstwy przyściennej znika...

Na zewnątrz warstwy przyściennej lepkość nie jest istotna. Ludwieg PRANDTL
zaproponował następujące postępowanie: gdy Re jest wielka (->∞ - w granicy) to:

1. Wyznaczamy opływ konturu płynem nielepkim. Otrzymujemy p=p(x), czyli

rozkład ciśnienia na konturze.

2. Rozwiązujemy równania Prandtla ze znaną już wielkością

( )

p x

x

∂

∂

. Wyznaczone

pole prędkości pozwala określić składową styczną siły powierzchniowej, i w
rezultacie, opór.

Rozumowanie to pozwala zastąpić zadanie trudne, jakim jest rozwiązanie równań
Naviera-Stokesa, dwoma zadaniami prostymi.
Popełniony błąd związany z przeniesieniem obliczonego na konturze ciśnienia p(x) na
zewnętrzną granice warstwy jest tym mniejszy, im warstwa przyścienna ma mniejszą
grubość. W granicy, gdy Re->∞ błąd znika.* Teoria oparta o podane rozumowanie
nazywa się „Opływem z Warstwą Przyścienną.” Powróćmy do równań Prandtla.
Niewiadomymi są u(x,y) i v(x,y). Aby je wyznaczyć trzeba, oprócz znanych (sw. 3)
równań sformułować warunki brzegowe i warunki początkowe.

* Rozumowanie Prandtla pochodzi z początku WB. Wieku. Dowód znikania błędu
podała O.Olejnik (Rosjanka) w połowie stulecia.

Warstwa przyścienna rozpływa się w przednim punkcie spiętrzania. To taki punkt, w
którym

. Oczywiście, grubość warstwy w punkcie tym jest zerowa. Dalej: na

brzegu opływanego konturu mamy warunek przylepienia:

0

v

≡

r

0

( , )

0

y

u x y

=

=

, a na

zewnętrznej granicy prędkość w warstwie jest taka, jaka by zaistniała na konturze
opływanym płynem nielepkim:

( , )

( )

y

u x y

U x

δ

=

=

.

Rekapitulujemy: równania Prandtla, warunki brzegowe i warunek początkowy to:

0

u

u

x

y

∂

∂

+

=

∂

∂

,

2

2

1

u

u

p

u

u

v

x

y

x

υ

ρ

∂

∂

∂

∂

+

= −

+

∂

∂

∂

∂

0

v

y

,

≡

r

,

0

( , )

0

y

u x y

=

=

,

( , )

( )

y

u x y

U x

δ

=

=

.

Termin „warunek początkowy” nie odnosi się do czasu (ruch jest od czasu niezależny),
ale do początku warstwy przyściennej. Czytelnik zauważył, że symbol U(x) oznacza
prędkość na konturze opływanym płynem nielepkim. Płyn taki jest, oczywiście, tworem
naszej wyobraźni... Podlega równaniom Eulera. Wyznaczenie pola prędkości w takim
płynie jest względnie proste. Zauważymy, że na mocy równania Brenoulliego

obowiązującego przy braku lepkości możemy napisać:

2

.

2

l pradu

V

P

const

ρ

+

=

. Ponieważ

opływany kontur jest linią prądu (prędkość jest styczna do linii konturu) to:

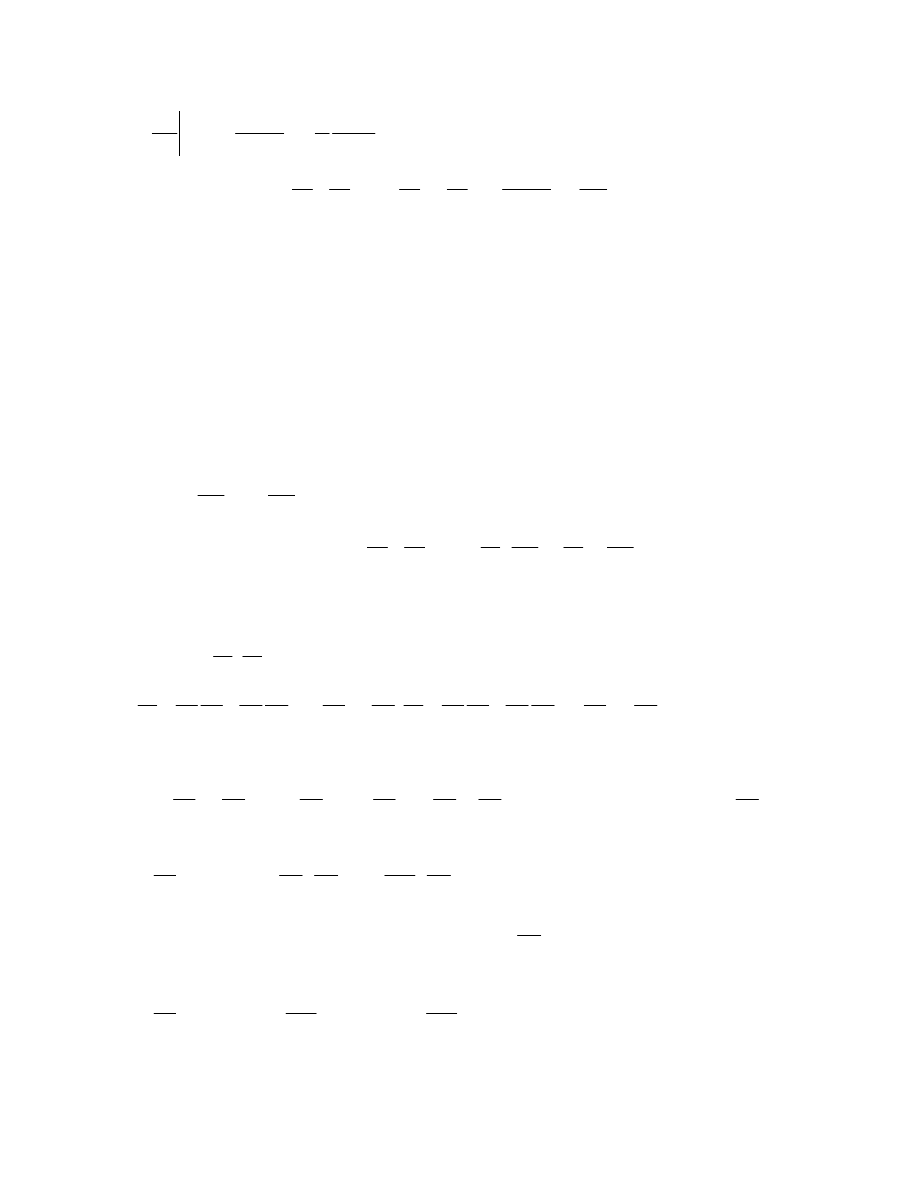
0

( )

1

( )

y

dV

dU x

dp x

V

U

dx

dx

dx

ρ

=

=

= −

. Używając tego zapisu, przepisujemy równania

Prandtla następująco:

0

u

u

x

y

∂

∂

+

=

∂

∂

,

2

2

( )

u

u

dU x

u

v

U

u

x

y

dx

υ

y

∂

∂

∂

+

=

+

∂

∂

∂

.

Warunki brzegowe i warunek początkowy pozostają niezmienione.

Równanie Prandtla rozwiązujemy numerycznie. Nie można bowiem, przy dowolnej
wielkości U(x) znaleźć rozwiązania „na papierze.” Można to zrobić dla pewnych
przypadków: gdy

, lub gdy

( )

m

U x

cx

=

1

2

3

1

2

3

( )

...

m

m

m

U x

c x

c x

c x

=

+

+

+

i jeszcze dla

kilku innych.
Metody numeryczne są – na ogół – metodami różnicowymi. Wygodne jest wcześniej
przekształcić równania. Najlepiej jest zamienić zmienne niezależne tak, by
wyeliminować jedną z niewiadomych. Zabieg ten, powoduje, że otrzymamy tylko jedno
równanie (i jedną niewiadomą).

Podajemy (dla zainteresowanych) odpowiednie rachunki. Otóż, określamy funkcje ψ

taką że:

,

v

x

y

.

u

ψ

ψ

∂

∂

= −

=

∂

∂

(ψ nazywamy funkcją prądu). Funkcja ta redukuje do

tożsamości równanie ciągłości:

0

u

u

x

y

∂

∂

+

=

∂

∂

→

0

x

y

y

x

ψ

ψ

⎛

⎞

∂ ∂

∂

∂

⎛

⎞

+

−

=

⎜

⎟

⎜

⎟

∂

∂

∂

∂

⎝

⎠

⎝

⎠

(tantologia!)

I wprowadzamy nowe zmienne niezależne:

.

0

( )

( ),

( , )

( , )

x

U x dx

x Z

x y

Z x y

ξ

ξ

ψ

=

=

=

=

∫

Pochodne

i

x

y

∂ ∂

∂ ∂

trzeba wyznaczyć przez nowe zmienne:

,

0

Z

Z

U

v

u

x

x

x Z

Z

y

y

y Z

Z

ξ

ξ

ξ

ξ

ξ

ξ

∂

∂ ∂

∂

∂

∂

∂ ∂

∂ ∂

∂

∂

∂

∂

=

+

=

−

=

+

=

+

∂

∂ ∂

∂ ∂

∂

∂

∂

∂ ∂

∂ ∂

∂

∂

.

Wstawiamy te operatory różniczkowania do równania Prandtla. Ponieważ U(x) wyraża
się tylko przez zmienną ξ (x=x(ξ)) to:

2

u

u

u

u

u

u U

v

v u

U

u

u

Z

Z

Z

υ

ξ

ξ

⎡

⎤

∂

∂

∂

∂

∂

∂

⎡

⎤

⎡

−

+

=

+

⎢

⎥

⎢

⎥

⎢

∂

∂

∂

∂

∂

∂

⎣

⎦

⎣

⎦

⎣

⎦

Z

⎤

⎥ . Upraszczamy wyrażenie

u

u

Z

υ

∂

∂

.

Pozostałość przepisujemy tak:

2

2

2

2

2

(

)

2

2

d

U

U

U

u

U

U

u

d

Z

υ

ξ

ξ

⎛

⎞

⎛

⎞

∂

∂

−

=

+

⎜

⎟

⎜

⎟

∂

∂

⎝

⎠

⎝

⎠

2

I wprowadzamy nową funkcję niewiadomą

2

2

2

1

u

W

U

⎛

⎞

= − ⎜

⎟

⎝

⎠

. Przy jej użyciu otrzymamy

(po następujących przekształceniach) proste równanie:

(

)

(

)

2

2

2

2

2

2

U

u

U

u

u

U

Z

υ

ξ

∂

∂

−

=

−

∂

∂

( )

2

2

2

0!

bo

U

Z

ξ

⎛

⎞

∂

=

⎜

⎟

∂

⎝

⎠

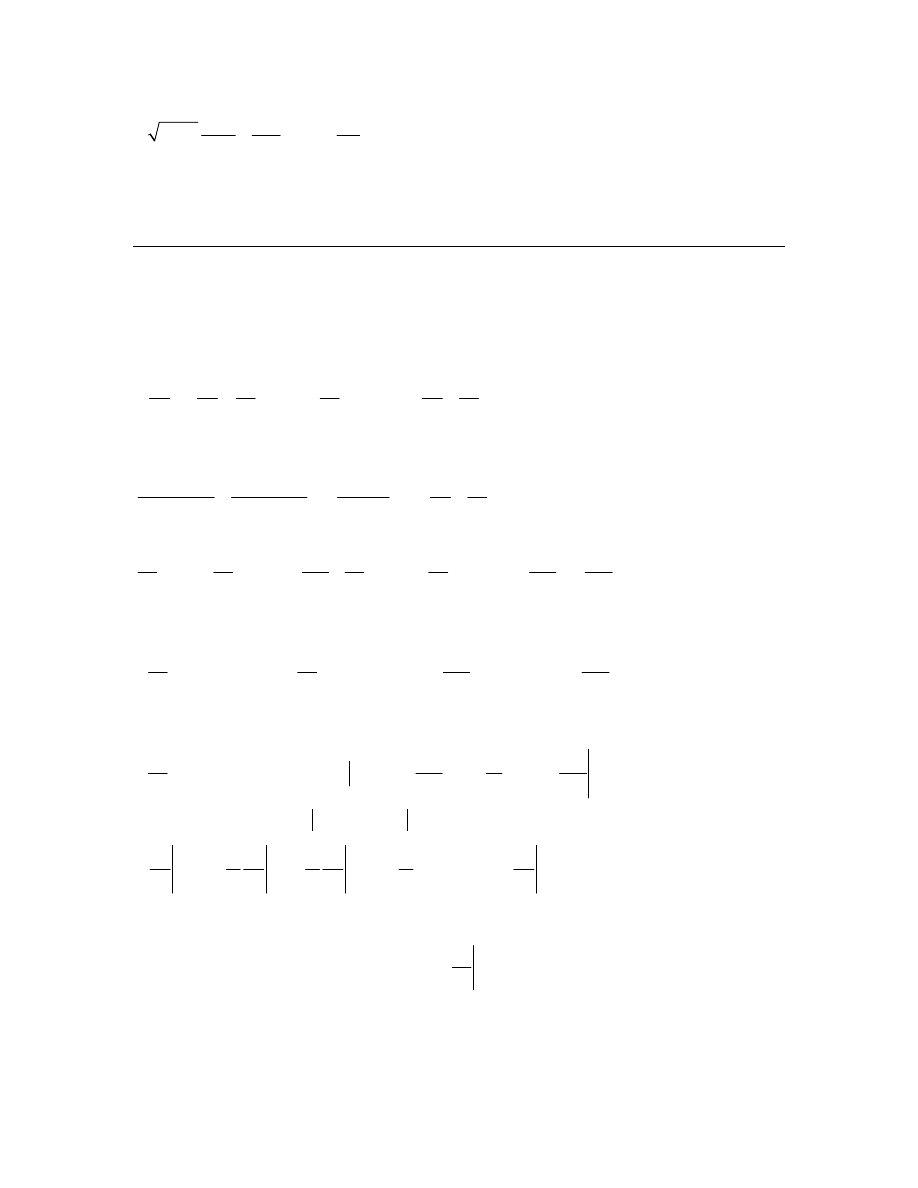
2

2

2

1

l

W

W

d

W

W

Z

d

υ

ξ

ξ

⎛

⎞

∂

∂

−

−

= − ⎜

⎟

∂

∂

⎝

⎠

nU

Dla y=0, co odpowiada z=0, jest W=1m a gdy z jest znaczne, to W=0. Otrzymane
równanie jest podobne do znanego równania przewodnictwa i bez trudu można je
rozwiązać zwykła metoda różnicowa.


Równania Prandtla można przedstawić i otrzymać użyteczny Wzór Całkowy Karmana.
Okaże się użyteczny przy pomiarach i dla przybliżonego wyznaczenia ruchu w warstwie
przyściennej. Oto odpowiednie rachunki:

Przekształcamy pochodną konwekcyjną:

(

)

(

)

u

u

u

v

u

v

u u

u v

u

x

y

x

y

x

y

⎡

⎤

∂

∂

∂

∂

∂

∂

+

=

• +

• −

+

⎢

⎥

∂

∂

∂

∂

∂

∂

⎣

⎦

Wyrażenie w nawiasie kwadratowym jest zerem (patrz: równanie ciągłości). Podobnie
obliczymy wyrażenie:

( )

(

)

( )

(

)

( )

uU x

vU x

dU x

u

v

u

U

x

y

dx

x

∂

∂

y

⎡

⎤

∂

∂

+

=

+

+

⎢

⎥

∂

∂

∂

∂

⎣

⎦

Łącznie, układ równań jest więc następujący:

( )

( )

dU

uU

vU

u

x

y

dx

∂

∂

+

=

∂

∂

,

(

)

(

)

2

2

dU

u

u u

v u

U

x

y

dx

y

υ

∂

∂

∂

• +

•

=

+

∂

∂

∂

Odejmujemy drugie z nich od pierwszego i całkujemy względem y w granicach 0-δ:

(

)

(

)

(

)

2

2

o

o

o

dU

u

u U

u

dy

v U

v dy

u U dy

dy

x

y

dx

δ

δ

δ

υ

∂

∂

⎡

⎤

⎡

⎤

−

+

−

=

−

−

⎣

⎦

⎣

⎦

∂

∂

∫

∫

∫

o

y

δ

∂
∂

∫

Całki z pochodnych względem y są banalne. Funkcje U nie zależą od y. Wobec tego,
otrzymujemy:

(

)

(

)

2

2

0

0

1

y

y

y

o

o

y

dU

u

u

u U

u

dy

v U

v

U

dy

x

dx

U

y

δ

δ

δ

δ

υ

=

=

=

=

∂

∂

⎛

⎞

⎡

⎤

−

+

−

+ •

−

−

⎜

⎟

⎣

⎦

∂

∂

⎝

⎠

∫

∫

Drugi wyraz znika, bo

0

0 _ _

y

y

v

i u

δ

=

=

=

U

=

. Ostatni człon (po prawej stronie) to

0

y

y

y

y

u

u

u

y

y

y

δ

δ

δ

μ

μ

τ

υ

ρ

ρ

ρ

=

=

=

=

∂

∂

∂

= −

+

= −

∂

∂

∂

, gdzie

0

y

u

y

τ μ

=

∂

=

∂

jest Naprężeniem Stycznym.

(Czyli składową styczną jednostkowej siły powierzchniowej na opływanej powierzchni.
(udowodnij to stwierdzenie... *)

* Pomoc: na brzegu y=0 v=0 i, wobec tego

0

0

y

v

x

=

∂

≡

∂

. Napisz iloczyn 2μ

Dυn i

otrzymasz wynik.

Pierwszy wyraz jest kłopotliwy. Gdyby udało się wyprowadzić operacje różniczkowania
przed całką – to by mógł zostać napisany w prostej formie... Przekształcamy go

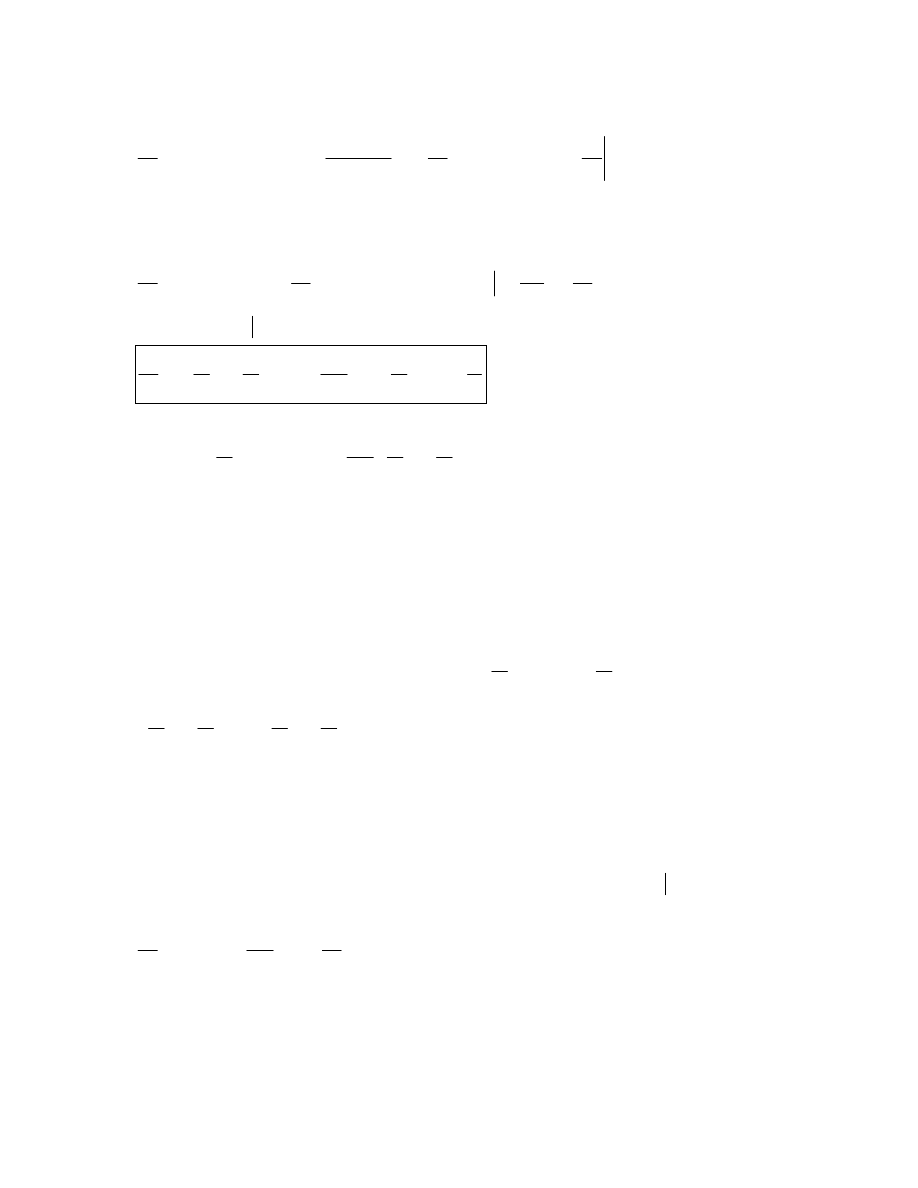
wykorzystując formułę różniczkowania całki:

( )

( )

( )

( )

( )

( )

( )

0

0

0

,

,

,

y f x

y f x

y f x

y f x

F x y

d

d

F x y dy

dy

F x y dy

dx

x

y

dx

=

=

=

=

⎡

⎤

∂

∂

=

+

⎢

⎥

∂

∂ ⎢

⎥

⎣

⎦

∫

∫

∫

y

W naszym przypadku F=u(U-u). Wiemy, że pochodne całki względem górnej granicy to
funkcje podcałkowe, czyli F. Ale – trzeba napisać jej wartości dla y=f, co w naszym
przypadku oznacza y=δ. Piszemy:

(

)

(

)

(

)

(

)

0

0

0

y

y

d

d

u U

u dy

u U

u

dy u U

u

u U

u

dy

dx

x

dx

x

δ

δ

δ

δ

δ

=

=

∂

∂

⎡

⎤

⎡

⎤

−

=

−

+

−

=

−

⎣

⎦

⎣

⎦

∂

∂

∫

∫

∫

Jest to tak, bo

y

u

δ

=

= U

i w rezultacie otrzymujemy

2

0

0

1

1

d

u

u

dU

u

U

dy U

dy

dx

U

U

dx

U

δ

δ

τ

ρ

⎛

⎞

⎛

⎞

−

+

−

= +

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∫

∫

To wzór całkowy Karmana.

Wielkości określone całkami oznaczamy symbolami δ

**

i δ

*

:

**

*

0

0

1

_ _

1

u

dU

u

dy i

U

dy

U

dx

U

δ

δ

δ

δ

⎛

⎞

⎛

⎞

=

−

=

−

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∫

∫

u

U

δ

)

. Nazywamy je „grubością (straty)

wydatku” i „grubością (straty) pędu.” Interpretujemy te nazwy tak:

*

0

0

0

U

Udy

udy

U

udy

δ

δ

δ

δ

• =

−

=

−

∫

∫

∫

. Całka jest rzeczywistym wydatkiem płynącym w

warstwie. Jest on mniejszy, niż wydatek który by płynął przy prędkości U(x). Ubytek

określa wielkości δ

*

.

*

0

(

udy

U

δ

δ δ

=

−

∫

. Ponieważ wydatek jest dodatni, to δ

*

<δ.*

Zauważamy, że dla y>δ u=U i wobec tego

0

0

1

1

u

dy

dy

U

U

δ

∞

⎛

⎞

⎛

⎞

−

=

−

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∫

∫

u

, i podobnie

0

0

1

1

u

u

u

u

dy

dy

U

U

U

U

δ

∞

⎛

⎞

⎛

⎞

−

=

−

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∫

∫

. Fakt ten wykorzystamy w zaprojektowaniu pomiaru

siły stycznej (jednostkowej) określającej na opływaną powierzchnią. (Bezpośredni
pomiar nie jest łatwy!)
* dokonaj podobnych przekształceń dla wielkości δ

*

i δ

**.

W różnych punktach konturu odległych o ∆x od siebie nazywamy prędkość wzdłuż
normalnej. Wynikiem jest u(x,y) i u(x+∆x,y). Daleko od konturu

( , )

( )

y

u x y

U x

δ

≥

=

.

Obliczamy całki δ

*

i δ

**

. Różniczkując numerycznie znajdujemy

(

)

2

**

*

d

dU

U

U

dx

dx

δ

δ

fx

ρ

+

= +

. Przez fx=-τ oznaczyliśmy jednostkową siłę styczną na

konturze. Zauważymy na koniec, że zarówno δ

*

jak δ

**

są wielkościami dobrze

zdefiniowanymi. Można zawsze je poprawnie obliczyć: Wynika to z faktu znikania
wyrażeń podcałkowych poza warstwą przyścienną. Suma wielkości δ jest źle
zdefiniowana: Wiadomo, że istnieje – lecz z góry nie wiadomo, ile wynosi. Niekiedy

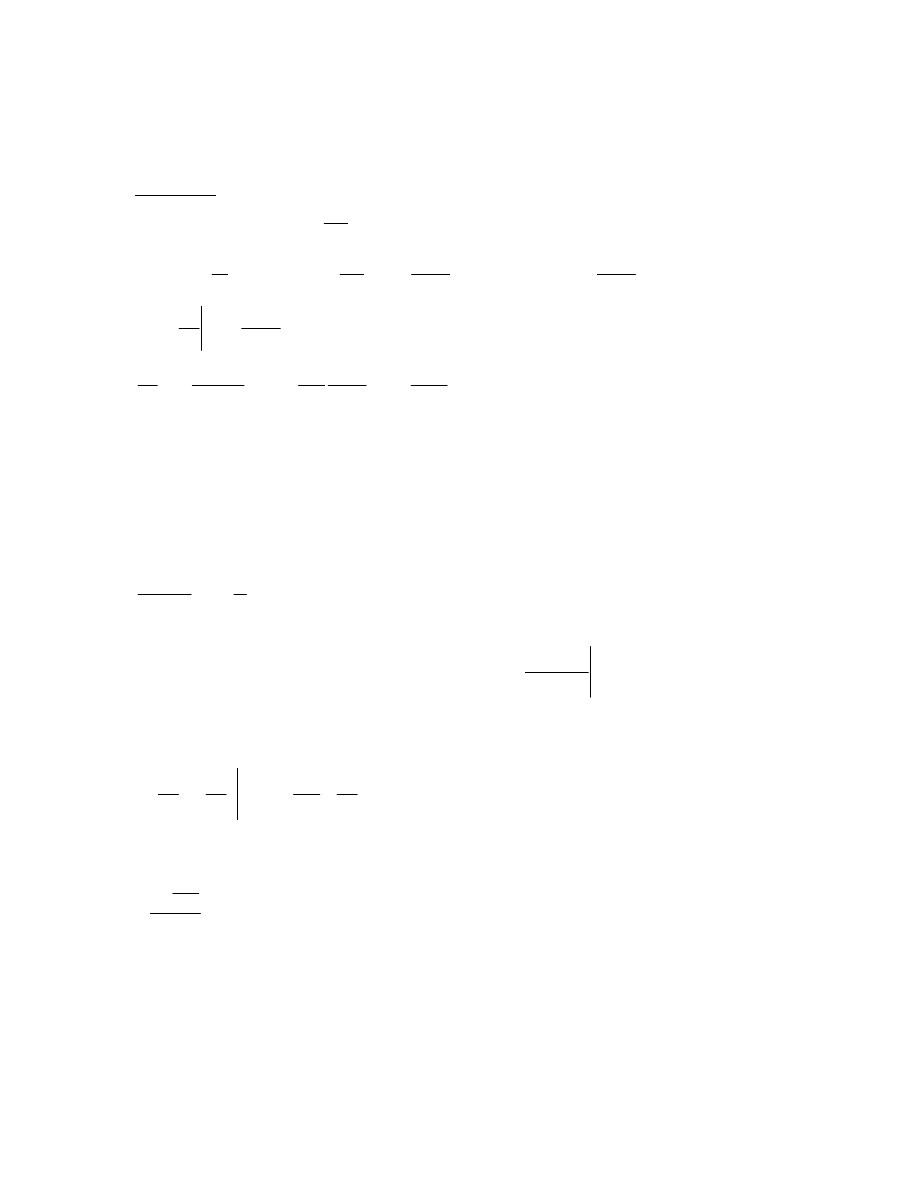
definiuje się ją umownie: δ to taka odległość od brzegu, w której u=0,99U. Jasne, że jest
to niezbyt dobra definicja...

Ćwiczenie: Zadano U(x). Wyprowadzić równanie określające δ(x).

Przyjąć

( , )

( )sin

2

y

y

U x

π

u x

δ

=

. Wiadomo że δ(0)=0. Obliczamy δ

*

i δ

**:

*

0

0

2

1

1 sin

2

u

y

dy

dy

U

δ

δ

π

π

δ

δ

δ

π

−

⎛

⎞

⎛

⎞

=

−

=

−

=

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

∫

∫

, i podobnie

**

4

2

π

δ

δ

π

−

=

. Dalej:

0

2

y

u

U

x

μ π

τ μ

δ

=

∂

=

=

∂

. Otrzymujemy równanie:

(

)

2

4

2

2

2

d

dU

U

U

dx

dx

π

U

π

υ π

δ

δ

π

π

δ

⎡

⎤

−

−

+

= +

⎢

⎥

⎣

⎦

Trzeba to równanie scałkować z podanym warunkiem początkowym wyrażającym
znikanie δ w x=0. Spróbuj to zrobić! Po znalezieniu δ(x) mamy jasną zależność
określającą u(x,y). Tym samym wyznaczamy ruch w warstwie przyściennej.. Dla
płaskiej płyty U(x)=U

∞

=const. Policz δ.

Uogólnijmy doświadczenie płynące z ćwiczenia. Otóż, wybraliśmy funkcję opisującą
u(x,y). Była bardzo prosta. Trochę ogólniej jest, gdy przyjąć:

( )

( )

(

,

,

u x y

y

f

f

U x

)

,

λ

ξ λ

δ

⎛

⎞

=

=

⎜

⎟

⎝

⎠

. Z pewnym parametrem λ=λ(x). Oczywiście jest też

δ=δ(x). Wybrane funkcje muszą spełniać następujące warunki:

f(0,λ) = 0 – bo y=0 u=0, f(1,λ) = 1 – bo u=U dla y=δ,

(

)

1

,

0

f

ξ

ξ λ

ξ

=

∂

=

∂

- bo „dopasowanie’

na zewnętrznej granicy warstwy musi być dobre.

Kolejny związek otrzymamy pisząc równanie Prandtla dla y=0:

( )

2

0

0,

y

u

u

dU

u

v

U

f

x

y

dx

ξξ

υ

λ

δ

=

⎛

⎞

∂

∂

+

=

+

⎜

⎟

∂

∂

⎝

⎠

U

•

Lewa strona znika z powodu znikania prędkości na brzegu opływającego ciała. Jest
więc:

(

2

0,

dU

dx

f

ξξ

δ

)

λ

υ

−

=

-> to związek pomiędzy δ i λ.

Mamy więc tylko jedną wielkość niewiadomą. Jest nią parametr λ.
Teraz obliczamy δ

*

i δ

*

(λ) i δ

**

i δ

**

(λ). Używamy definicji (całek) określających te

wielkości: Można też obliczyć τ:

( )

0,

/

Uf

ξ

τ ρυ

λ δ

=

.

W równaniu Karmana jest więc tylko jedna niewiadoma. Jest nią λ=λ(x).Całkujemy to
równanie (pojawiają się pewne trudności: dla punktu spiętrzenia U(0)=0 i pochodna

/

d

dx

λ

jest określona wyrażeniem ułamkowym w którym mianownik znika dla punktu

x=0, czyli punktu początkowego. Wobec tego początkowa wartość λ (w x=0) musi być
taka, by otrzymać ułamek typu %. Granice takiego ułamka określa pochodna w punkcie
osobliwym...
Istnieje wiele warunków opisanej metody. W niektórych wprowadza się elementy
empiryczne. Szczegóły można znaleźć w specjalistycznych podręcznikach np.
„Grenzschichttheoria” autorstwa Schlichtinga lub „Laminarnyj pogranicznyj słoj”
Łojcjanskiego.
(str. 11)
Rezultat obliczeń zależy od funkcji U(x). (zakładamy niezmienność lepkości i masy
właściwej. Oznacza to niezmienność płynu opływającego nasze kontury...) Funkcja ta –
prędkość na brzegu przy opływie fikcyjnym płynem nielepkim – jest zadana...
Dla x=0 U znika. Następnie na krótkim odcinku (w rozwinięciu) szybko wzrasta.
Odcinek ten – w przybliżeniu – odpowiada silnemu zaokrągleniu profilu. Dalej prędkość
U(x) jest niemal stała by w otoczeniu spływu (krawędzi spływu) zmniejszyć się do
niewielkiej lub wręcz zerowej.
Zerowa prędkość na krawędzi spływu jest wtedy, gdy kąt ostrza jest niezerowy. Jest tak
bo wektor v końcowym punkcie konturu musi być jednoznacznie określony i ciągły.
Innymi słowami:

_

l

lim

lim

splywu

n _

gorna czesc

do

a czesc

v

v

v

=

=

v v

v

Ale: Kierunki wektorów na górnej i dolnej części są różne.
Wektory o niezerowym module są równe, gdy:
1) Kierunki są jednakowe,
2) zwroty sa jednakowe,
3)moduły są jednakowe.

W naszym przypadku kierunki są różne. Równość wektorów wymaga, by

_

( )

0

krawedz spywu

gora

dol

v

v

U x

=

=

=

v

v

. Dla konturu o innym kształcie zmieni się kształt

funkcji

( )

U x

U

∞

. To samo ma miejsce dla innego ustawienia profilu względem

napływającego strumienia. Ustawienie określa kąt

∝

(szkic obok) nazywamy kątem

natarcia. Na ogół kąt ten określają linie: kierunku U

∞

uv

i najdłuższego odcinka łączącego

dwa punkty konturu. Ten ostatni nazywamy cięciwą. Jeśli przyjąć inne definicje kąta
natarcia – to zależnie od definicji – zmieniamy jego wartość o pewną stałą.

Niekiedy określa się kąt tak, by dla

∝

=0 nie wystąpiła składowa siły prostopadła do

prędkości U

∞

. Wtedy:

∝

określa się względem zerowej siły nośnej.

Warstwa przyścienna ma w punkcie spiętrzenia (x=0) zerową grubość. Dalej, przy
wzroście x, grubość warstwy rośnie. Biorąc L=x, w oszacowaniu grubości δ (str. 4)

otrzymujemy:

x

x

x

U

U

x

υ

δ

υ

∞

∞

≈

=

⋅

≈ . Warstwa grubieje. Rozkłady prędkości stają

się „mniej zmieniające się” wraz z odległością od brzegu. Maleje wielkość

0

y

u

y

=

∂

∂

.

Przeanalizujemy tą cechę pola prędkości. Napiszmy równanie Prandla dla y=0. Jest tam

u=v=0 i wobec tego:

2

2

0

0

0

y

y

u

u

dU

u

u

v

U

x

y

dx

y

υ

=

=

⎛

⎞

∂

∂

∂

+

= =

+

⎜

⎟

∂

∂

∂

⎝

⎠

. Druga pochodna u na

opływanym brzegu zależy tylko od U:

2

2

0

1

y

u

d

U

y

d

υ

=

∂

= −

∂

U

x

Jeśli U rośnie wraz z x-em, to

0

0

y

u

y

=

∂

<

∂

i rozkład prędkości jest wypukły. Gdy

0

dU

dx

<

- prędkość U maleje wzdłuż brzegu – to rozkład prędkości jest wklęsły.

Ponieważ dla małych x jest zawsze dU/dx>0, to ewentualnie wklęsłość pojawia się w
pewnej odległości od punktu spiętrzenia. Szkic przedstawiający wypukłe i wklęsłe
rozkłady prędkości pozwala stwierdzić, że pojawia się obszar ruchu o odwróconym
kierunku przepływu. Warstwa przyścienna gwałtownie zmienia swą grubość... Założenia
o znikomej grubości warstwy przestają być sensowne. Mamy dwie warstwy leżące na
sobie... Punkt w którym rozpoczyna się ruch odwrócony określa równanie:

( )

0

,

0

y

u x y

y

=

∂

=

∂

Punkt ten nazywamy punktem oderwania. Za tym punktem jest

ruch oderwany. Po prostu w punkcie oderwania płynący w sąsiedztwie brzegu płyn
„odpływa” od niego (odrywa się) powodując znaczące zwiększenie obszaru w którym
lepkość jest istotna.
Zachodzące w znacznej części profilu oderwanie zwiększa opór i, zarazem, zmniejsza
siłę nośną.
Polega ono na pojawieniu się turbulencji. Jest tak: grubość warstwy rośnie wraz z x-em.
Do jej wnętrza zawsze docierają zaburzenia generowane w ruchu zewnętrznym.
Zaburzenia te są tłumione przez intensywne tarcie w cienkiej warstwie. Gdy grubość
warstwy jest duża – to zaburzenia przestają być tłumione, a nawet zwiększają się wzdłuż
warstwy.
Mówimy: Warstwa laminarna staje się niestateczna. Po utracie stateczności, pojawia
się turbulencja. Grubość warstwy rośnie, ale – nie zachodzi oderwanie. Odcinek, na
którym warstwa staje się turbulentna (mamy tu silny wzrost amplitudy wszystkich
zewnętrznych zaburzeń i generacje zaburzeń samowzbudnych) jest stosunkowo krótki
(kilkanaście grubości warstwy). Wyznaczenie miejsca przejścia dokonuje się przez
badanie narastania amplitudy dowolnego zaburzenia. (Jest to teoria stabilności
hydrodynamicznej). Podstawowy wynik używany dla teorii warstwy jest przedstawiony
na następującym diagramie: LINIA „” dzieli pole diagramu na część statecznej warstwy
przyściennej i warstwy niestatecznej. Obliczając warstwę przyścienną – począwszy od
punktu spiętrzenia – sprawdzamy w której części diagramu lokują się kolejne (obliczone)
parametry. Jeśli w obszarze statecznym, to warstwa powstaje laminarna. Jeśli w
obszarze niestateczności, to zaszło przejście do ruchu turbulentnego.
Wzór całkowy Karmana obowiązuje również tam gdzie pojawiła się turbulencja.
Zamiast prędkości trzeba tylko użyć prędkości uśrednionych w czasie. Piszemy:

(

)

2

**

*

d

dU

U

dx

dx

τ

δ

δ

ρ

+

=

Prędkość U jest ciągła przy przejściu: laminarna – turbulentna (nie jest związana z
warstwą przyścienną!). Również u(x,y) jest ciągła... wobec tego, δ

*

i δ

**

są ciągłymi

funkcjami x.
Aby użyć równanie Karmana trzeba:

1. Znaleźć związek pomiędzy δ

*

i δ

**

2. Znaleźć związek pomiędzy δ

*,

δ

**

, i τ.

Można wykorzystać wyniki doświadczeń... Istnieje wiele rozmaitych „teorii” (raczej:
przepisów.. ) wiążących te wielkości. Odpowiednie wzory można znaleźć w (wielu!)
specjalistycznych książkach o warstwie przyściennej.

Można zapytać jaką wartość mają metody oparte o wzór całkowy?

Otóż, jeśli opływany kontur ma „typowy” kształt profilu płata nośnego albo łopatki i nie
jest ustawiony pod zbyt wielkim kątem natarcia – to obliczony opór jest wysoce zgodny z
wynikiem badania laboratoryjnego. Wystarczą do dobrej analizy (poniżej 5% błędu)
projektowanego profilu...
Dodamy, że warstwa przyścienna na bryle obrotowej może być opisana w podobny
sposób. Dokonując odpowiednich przekształceń można sprowadzić „osiowoy
metryczne” równanie Prandtla do równań takich, jak w przypadku płaskim.
Dalej: dla ruchów szybkich, gdy nie można zaniedbać ściśliwości problem również
sprowadza się do omówionego. Trzeba tylko założyć, że brzeg opływanego ciała nie
odbiera (nie wydziela) ciepła. (Gdy nie można takiego założenia uczynić – to trzeba
równocześnie z rozwiązywaniem problemu dla warstwy rozwiązać problem rozkładu
temperatury w opływanym ciele).
Jeśli opływana bryła nie ma kształtu łopatki albo płata nośnego (nie jest wydłużona) – to
trzeba stosować teorie niepłaskiej warstwy przyściennej. Taka teoria jest już bardziej
złożona..

Na zewnątrz warstwy przyściennej płyn porusza się tak, jak gdyby był pozbawiony
lepkości.

Ponieważ warstwa przyścienna ma (największą) grubość

Re

L

≈

to, przy Re rzędu

milionów (setek tysięcy) wyznaczanie ruchu na zewnątrz warstwy jest prawie tym
samym, co wyznaczanie opływu naszego konturu fikcyjnym płynem nielepkim.
Wynikiem jest – między innymi – prędkość na brzegu (ponieważ płyn jest nielepki – to

0

breg

v

≠

uv

). Prędkość tą przenosimy następnie na zewnętrzną granice warstwy po to, by

rozwiązać równanie Prandtla.

Otóż, napływa jednorodny strumień płynu nielepkiego. Na każdej linii prądu – a
wszystkie linie łączą punkty wielce oddalone, leżące „przed” i „za” konturem – mamy tą

samą wartość stałej Bernoulliego:

2

2

U

p

C

ρ

∞

∞

=

+

wszędzie taka sama!

Pamiętamy, że gdy stała Bernoulliego jest wszędzie jednakowa, to (tam gdzie jest
wszędzie jednakowa) ruch jest bezwirowy. Znikanie wirowości jest równoznaczne
istnieniu potencjału prędkości. Zapisujemy to tak:

Znikanie wirowości ↔potencjalność;

Czyli:

0

,

v

u

u

v

x

y

x

y

ϕ

ϕ

∂

∂

∂

∂

−

= ↔ =

=

∂

∂

∂

∂

*

Ponieważ spełnione jest równanie ciągłości, to podstawiając składowe prędkości
wyrażone przez pochodne potencjału otrzymamy:

2

2

2

2

_

'

0

rownanie Lapalce a

u

v

divV

x

y

x

y

ϕ

ϕ

∂

∂

∂

∂

=

+

=

+

=

∂

∂

∂

∂

uv

144244

3

Ponieważ prędkości φ jest więc funkcja spełniająca równanie Laplace’a. Funkcja
spełniająca takie równanie to Funkcja Harmoniczna. Jeśli wyznaczymy odpowiednią
funkcję harmoniczną – właściwą dla naszego zadania – to z równania Bernoulliego
otrzymamy ciśnienie:

2

2

2

2

2

2

1
2

p

C

x

y

ϕ

ϕ

ρ

⎡

⎤

⎛

⎞

⎛

⎞

∂

∂

⎢

⎥

+

+

⎜

⎟

⎜

⎟

∂

∂

⎢

⎥

⎝

⎠

⎝

⎠

⎣

⎦

=

)

* Są tylko dwie składowe prędkości: u(x,y) = v

x

= v

1

, u(x,y) = v

y

= v

2

wobec tego pojawia

się jedyna niezerowa składowa wirowości (ω

3

= ω

2

(x,y)) Jeśli znika wirowość

to istnieje potencjał prędkości φ taki, ze

V

g

(

0

rotV

co

=

≡

uv uuv

rad

ϕ

=

uv

.

Ostatnie równanie to zwykle r. Bernoulliego zapisane z użyciem wzorów określających
składowe prędkości. (Patrz równanie *) z poprzedniej strony.) Jeśli uda się wyznaczyć φ
tylko jedna niewiadoma – to problem opływu jest rozwiązany..
Funkcji spełniających równanie Laplace’a jest bardzo dużo...
Równanie to spełnia stała, wielomian o odpowiednio dobranych współczynnikach, ...
część rzeczywista i część urojona różniczkowalnej funkcji zmiennej zespolonej. Funkcja
odpowiadająca naszym potrzebom musi:

1. Spełniać równanie Laplace’a

2

2

2

2

0

x

y

ϕ

ϕ

∂

∂

+

=

∂

∂

2. Określać ruch ze stała prędkością daleko od konturu
3. Określać zerową składową normalną prędkości na konturze

Innymi słowy trzeba wybrać funkcje spełniającą równanie różniczkowe i warunki
brzegowe. Warunki brzegowe to:

V

grad

U

ϕ

∞

∞

∞

=

=

uuv

uv

daleko od konturu,

0

x

y

brzeg

brzeg

brzeg

V

n V

n grad

n

n

x

y

ϕ

ϕ

ϕ

⎛

⎞

∂

∂

= •

= •

=

+

=

⎜

∂

∂

⎝

⎠

uuv

uuv

v

v

⎟

na konturze.

Ponieważ

_ _

x

y

n

i n

n

n

ϕ

ϕ

∂

=

∂

∂

∂

=

to ostatnie równanie można zapisać tak:

...

0

brzeg

n V

n

ϕ

∂

• = =

=

∂

v uv

.

Zanim omówimy szczegóły naszego problemu zbadamy dwa istotne przykłady funkcji
spełniających równań Laplace’a. Pierwszy przykład to:

.,

,

x

y

x

y

U r

U

x U

y U

const U

const

ϕ

= • =

• +

•

=

=

uv v

Drugie pochodne tej funkcji są zerami... A więc jest to funkcja spełniająca r. Laplace’a
(harmoniczna). Prędkość

jest stała...

x

y

V

grad

i U

j U

U

ϕ

=

= •

+ •

=

uv

v

v

uv

* Niech f(x,y)=F(x+iy)=f(z), z=x+iy.

2

2

2

2

2

2

2

2

2

,

...

,

2

f

f

z

f

f

f

f

f

z

f

f

f

i

i i

f

x

z

x

z

x

z

y

z

y

z

y

z

z

∂

∂

∂

∂ ∂

∂

∂

∂

∂

∂ ∂

∂

∂

=

•

=

=

=

•

= •

= • •

= −

∂

∂

∂

∂ ∂

∂

∂

∂

∂

∂ ∂

∂

∂

Wynika więc taki związek:

2

2

2

2

f

f

x

z

∂

∂

= −

∂

∂

lub

2

2

2

2

0

f

f

x

z

∂

∂

+

=

∂

∂

.

Drugi przykład:

(

arctan

)

y

x

ϕ θ

= =

(patrz na rysunek obok)

Obliczamy pochodne:

(

)

(

)

2

2

2

2

2

2

2

2

2

2

2

2

2

2

,

,

,

2

2

y

y

xy

x

x

y

y

x

y

x

y

xy

x

y

x

ϕ

ϕ

ϕ

ϕ

∂

−

∂

∂

+

∂

−

=

=

=

=

∂

+

∂

+

∂

∂

+

+ y

, harmoniczna, bo

2

2

2

2

0

f

f

x

z

∂

∂

+

=

∂

∂

. A więc pochodne φ przedstawiają składowe prędkości:

2

2

2

2

sin

cos

,

y

u

v

y

x

x

y

r

y

x

y

r

ϕ

θ

ϕ

∂

−

∂

=

=

= −

=

=

=

∂

+

∂

+

θ

. Dla r->0 prędkość jest

nieokreślona.

Zauważamy, że na dowolnym okręgu (normalna do okręgu:

r

n

r

=

v

v

, a więc

cos ,

sin

x

y

x

y

n

n

r

r

θ

θ

= =

= =

) składowa V

n

jest taka:

sin

cos

cos

sin

0

n

x

y

V

n V

n

u

n

v

r

r

θ

θ

θ

= • =

• +

• = −

+

=

v uv

θ

. Linia r=const jest więc linia

prądu... mówimy φ=θ opisuje wir. W wirze takim prędkość maleje wraz z oddaleniem

od początku układu:

2

2

1

V

V

u

v

r

= =

+

=

uuv

. Obliczymy jeszcze wielkość zdefiniowaną

następująco:

V ds

udx

vdy

dx

dy

d

x

y

ϕ

ϕ

ϕ

∂

∂

Γ =

•

=

+

=

+

=

∂

∂

∫

∫

∫

∫

uv uuv

. Jeśli linia po której obliczamy

całkę obejmuje początek układu współrzędnych, to

2

0

2

d

d

π

ϕ

θ

π

Γ =

=

=

∫

∫

Jeśli jednak sytuacja jest podobna do pokazanej na dolnym szkicu, to

!

Linia całkowania nie otacza początku.

0

d

d

ϕ

θ

=

=

∫

∫

Czytelnik zauważy, że kilkukrotne okrążenie początku układu powoduje przyrost
wartości całki o 2πn. Funkcja o takiej własności jest wieloznaczna... (Rzeczywiście:
θ+2πn określa tą samą półprostą co θ...)

Wracamy do wyznaczanie funkcji Harmonicznej opisującej opływ zadanego konturu.
Przedstawiamy ją za pomocą trzech składników (każdy z trzech składników jest

harmoniczny):

2

U x

ϕ

θ ϕ

π

∞

Γ

=

+

+

Pierwszy składnik, U

gwarantuje spełnienia warunku w nieskończoności. Drugi i

trzeci składniki określają prędkości znikające daleko od konturu.

x

∞

Aby

0

brzeg

n

ϕ

∂

=

∂

trzeba by

2

brzeg

x

U

n

n

n

ϕ

θ

π

∞

∂

∂

= −

−

∂

∂

Γ ∂

∂

.

A więc funkcja harmoniczna

ϕ

ma zadaną (niezerową!) pochodną normalną na brzegu.

Dla dużych

2

r

x

y

=

+

2

(daleko od konturu) znika wraz z pochodnymi szybciej niż

const/r. (Bo tak szybko znikają pochodne funkcji θ.. ). Taką funkcje harmoniczną
wyznacza się metodami numerycznymi... *)
Pozostaje określić stałą Γ. Problem ten trudno rozwiązać dla konturu z ostrzem (patrz
szkic). W ostrzu, prędkość V

uv

musi znikać. (Gdyby nie znikała – to wektor gradφ musiał

by mieć dwa różne kierunki.. ) Wymóg ten realizujemy dobierając Γ:

:

0

ostrze

V

Γ

=

uuv

.

Warunek ten nazywa się „warunkiem Kutty-Żukowskiego” albo „spływem w ostrzu.”
Jeśli kontur nie ma ostrza – to postulujemy znikanie prędkości w punkcie największej
krzywizny. (Punkt ten jest odpowiednikiem ostrza, w którym krzywizna jest
nieskończona).
* Dziś, używa się metod panelowych. Wynikają z przedstawienia funkcji harmonicznej
całką konturową. W całce tej pojawia się (znana) pochodna normalna i (nieznane)
brzegowe wartości potencjału. Można otrzymać równanie (brzegowe równanie całkowe)
określające brzegowe wartości potencjału.

Znajdujemy jeszcze siłę działającą na opływany kontur. Zastosujemy znaną metodę
bilansu pędu. Napiszmy równanie ruchu (Eulera, bo nie ma lepkości) w takiej formie:

( )

( )

uV

vV

gradp

x

y

ρ

⎡

⎤

∂

∂

+

= −

⎢

⎥

∂

∂

⎣

⎦

uv

uv

i scałkujemy w obszarze pomiędzy konturem C i linią

C

∞

położoną daleko od konturu. Po scałkowaniu stosujemy twierdzenie GGO i piszemy:

(

)

(

)

x

y

x

y

C

C

C

n u

n v V dS

n u

n v V dS

n pdS

n pdS

ρ

ρ

ρ

ρ

∞

∞

+

+

+

= −

⋅

−

⋅

∫

∫

∫

uv

uv

v

v

C

∫

Na linii C

x

y

n V

n u

n v

⋅ =

+

v uv

jest zerem. Pierwsza z całek ≡ 0. Dalej:

- jest

siłą działającą na kontur. A więc:

C

n pdS

R

⋅

=

∫

v

uv

( )

C

C

R

n V VdS

n pdS

ρ

∞

=

⋅

+

⋅

∫

∫

uv

v uv uv

v

.

Trzeba obliczyć całki... Niech C

∞

będzie okręgiem o wielkim promieniu R

∞

. Długość

łuku dS

R d

θ

∞

=

. Funkcja podcałkowa zmienia się, gdy zmienia się kat θ (promień jest

stały). Można napisać:

( )

2

0

...

m

F

dS

R d

R

π

θ

θ

∞

∞

=

∫

∫

Jeśli m>1, to całka znika, gdy

.

R

∞

→ ∞

Jeśli m<1 – to

, bo inaczej całka nie ma sensu. A więc interesują nas tylko

te całki, w których m=1. Dla dużych odległości od początku układu jest:

( )

2

0

0

f

d

π

θ θ

=

∫

2

2

sin

1

sin

1

0

0

2

2

V

i U

j U

r

r

r

r

θ

θ

π

π

∞

∞

⎛

⎞

⎛

⎞

Γ

Γ

⎛

⎞

⎛

⎞

=

−

+

+

−

+

⎜

⎟

⎜

⎟

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

⎝

⎠

⎝

⎠

uv v

v

Obliczamy pierwszą całkę (pamietamy, że n

x

=cosθ, n

y

=sinθ):

( )

2

0

sin cos

sin cos

sin

sin

...

2

2

2

2

c

nV V dS

U

i U

j U

R d

R

R

R

R

π

θ

θ

θ

θ

θ

θ

ρ

ρ

θ

π

π

π

π

∞

∞

∞

∞

∞

∞

∞

⎧

⎫

⎧

⎫ ⎛

⎞

⎛

⎞

Γ

Γ

Γ

Γ

⎪

⎪

=

−

+

+

−

+

−

⎨

⎬⎨ ⎜

⎟

⎜

⎟

⎪

⎪

⎩

⎭ ⎝

⎠

⎝

⎠

⎩

⎭

∫

∫

vuv uv

v

v

∞

∞

⎬

=

( )

2

2

0

cos

2

c

U

nV V dS

j

d

π

ρ

ρ

θ θ

π

∞

∞

Γ

=

∫

∫

vuv uv

v

Druga całka (zawierająca ciśnienie) może być obliczona równie łatwo. Wcześniej –
wyznaczamy ciśnienie:

2

2

2

sin

2

...

2

2

2

p

const

u

v

const

U

U

R

ρ

ρ

π

∞

∞

∞

⎛

⎞

Γ

⎡

⎤

=

−

+

=

−

−

+

⎜

⎟

⎣

⎦

⎝

⎠

θ

Piszemy:

2

2

2

2

0

0

sin

cos

sin

...

sin

2

2

C

U

U

n pdS

i

j

const

U

R d

j

d

R

π

π

ρ

θ

ρ

θ

θ

θ

ρ

θ

π

π

∞

∞

∞

∞

⎡

⎤

Γ

Γ

⎛

⎞

⎡

⎤

⋅

=

+

−

−

∞

=

⎜

⎟

⎢

⎥

⎣

⎦

∞

⎝

⎠

⎣

⎦

∫

∫

∫

v

v

v

v

θ

Dodajemy obydwie całki. Wynik jest prosty: R

j

U

ρ

∞

− =

Γ

uv v

. – Twierdzenie „Kutty-

Żukowskiego.”

Reakcja jest prostopadła do kierunku prędkości niezaburzonego strumienia (V

i U

∞

= ⋅

uv v

).

Jeśli Γ<0 to

R

uv

„ma charakter siły nośnej.”

Zinterpretujemy wielkość Γ. Jak pamiętamy (str. 17) jest to wielkość związana z

intensywnością wiru. W naszym przypadku potencjał skojarzony z Γ to

2

θ

π

Γ

. A więc

im większe jest Γ – to większe jest intensywność wiru... Całkowity potencjał jest sumą

trzech składników:

2

U

ϕ

θ ϕ

π

∞

Γ

=

+

+ .

Scałkujemy prędkość wzdłuż podawanej linii:

_

cala linia

V ds

udx

vdy

=

+

∫

∫

uvuuv

=

stosujemy „płaskie GGO”

0

Obszar

Wewnatrz

v

u

dxdy

x

y

⎛

⎞

∂

∂

=

+

=

⎜

⎟

∂

∂

⎝

⎠

∫∫

Bo pod całką podwójną jest zerowa wirowość.
Całki wzdłuż łączników kasują się. Ponieważ zwroty w całkowaniu wzdłuż C i C

∞

są

przeciwne, to ostatecznie

C

C

V d s

V d s

∞

=

∫

∫

uv v

uv v

Ale, dla wielkiego koła C

∞

(przecież można dowolnie wybrać kształt tej linii)

łatwo obliczyć:

Vd s

∫

uv v

(

)

2

0

2

C

C

C

V d s

d U x

d

d

π

θ

ϕ

π

∞

∞

∞

∞

Γ

=

+

+

∫

∫

∫

∫

uv v

= Γ

Wielkość

nazywamy cyrkulacją. ← Γ

Vd s

Γ =

∫

uv v

Zauważamy, że na górnej części konturu zwroty V

uv

i d s

v

są przeciwne. Wobec tego,

przyczynek do cyrkulacji wytworzony „na grzbiecie” jest ujemny a na spodzie – dodatni.
Konur taki jak na szkicu – nawet niepodzielony – daje ujemną cyrkulację.

Tu – przy symetrii konturu – ale utworzonego pod dodatnim kątem natarcia – cyrkulacja
jest ujemna. Dla niewielkich kątów natarcia Γ ~ - α . Dokładniej: jeśli profil nie jest
bardzo gruby (grubość względna < ~ 20%) to

(

)

sin

LU

π

α ε

∞

Γ ≈ −

+

. Z reguły,

stosowane w lotnictwie (albo maszynach wirnikowych) profile nie mają grubości
wykraczających poza podane ograniczenie...
Kąt α=-є odpowiada zerowej sile nośnej, a L jest cięciwą profilu.

Współczynnik siły nośnej

(

2

2 sin

2

lift

R

C

U

L

)

π

α ε

ρ

∞

=

≈

+

. Co jest ≈ zgodne z

doświadczeniem dla niezbyt wielkich kątów natarcia. (Takich, przy których brak dużych
obszarów oderwania.. )

Przykłady

1. Potencjał

2

2

x

x

x

y

ϕ

= =

+

opisuje opływ kola jednostkowego. Sprawdź. Czy

jest to funkcja harmoniczna? Otóż:

1

Re z

z

ϕ

⎧

⎫

=

+

⎨

⎬

⎩

⎭

- jest częścią rzeczywistą

funkcji zmiennej zespolonej

( )

1

f z

z

z

= +

. Funkcja ta jest różniczkowalna dla

|z|>0. Ale z=0 należy do wnętrza kola... (przypominamy przypis na str. 18).

Prędkość

(

)

(

)

2

2

2

2

2

2

2

2

2

2

1

2

2

1

,

x

x

u

v

x

x

y

y

x

y

x

ϕ

ϕ

∂

∂

=

= +

−

=

= −

∂

+

∂

+

+ y

To

samo:

2

2

2

2

1

cos

sin cos

1

2

,

2

u

v

r

r

y

r

θ

ϕ

θ

∂

= +

−

=

= −

∂

θ

. Jeśli r→∞ to u=1, v=0.

Mamy jednorodne prędkości. Na kole:

cos

sin

n

i

j

θ

θ

=

+

v v

v

. Jeśli r=1, to

2

2sin

,

2sin cos

u

v

θ

θ

=

= −

θ

. Rzut prędkości na

normalną

. Moduł

prędkości

2

2sin

cos

2sin cos sin

0

n V

θ

θ

θ

θ

θ

⋅ =

−

≡

v uv

2

2

4

2

2

2 sin

sin

cos

2 sin

V

V

u

v

θ

θ

θ

=

=

+

=

−

=

uv

θ . Prędkości

styczna – zdefiniowana jako Vθ to:

2sin

V

θ

θ

= −

(dla małych θ wzrosty wersora

e

θ

v

i prędkości są przeciwne).

2. Niech

2

2

x

x

x

y

ϕ

γθ

= +

+

+

. Wyznaczyć prędkość styczna. Wykorzystamy

wynik poprzedni. Zauważymy też, że operacje obliczenia prędkości jest liniową
operacją dokonywaną na potencjale. Wobec tego prędkość styczna jest suma
poprzednio obliczonej i wynikającej ze składnika γθ. Ten drugi składnik to (patrz

str. 17) jest

(

,

1

V

r

r

θ

)

γ

γ

=

= . Mamy więc 2sin .

V

θ

γ

θ

= −

Prędkość znika dla

arcsin

,

arcsin

2

2

γ

γ

θ

θ π

=

= −

. Oczywiście, gdy |γ|<2. A co będzie dla |γ|>2?

Powrocy do obliczonej (na str. 20) reakcji działającej na opływany kontur.
Zauważamy – po pierwsze, że:

1. Reakcja jest prostopadła do prędkości
2. Reakcja=0 dla Γ=0.

Prostopadłość reakcji i prędkości oznacza brak oporu. Nie ma w tym nic dziwnego:
brak przecież dyssypacji energii mechanicznej w wyniku tarcia albo w wyniku procesów
termodynamicznych.
Opór można wyliczyć (niezerowy!) korzystając z teorii warstwy przyciennej. Teorie
opływu bez lepkości warstwy przyściennej uzupełniają się wzajemnie... Takie
połączenie (tylko w tym sensie są poprawne) daje rozsądnie dobry wynik gdy opływany
kontur jest „dobry” aerodynamicznie.
„Dobry” kształt oznacza figurę typu profilu lotniczego / łopatkowego ustawioną pod
umiarkowanym albo małym kątem natarcia... Błąd (weryfikowany doświadczalnie)
obliczeń schematem ruch płynu nielepkiego na zewnątrz warstwy + warstwa przyścienna
jest kilku procentowy... Podkreślamy: gdy kontur jest „lotniczy” i kąt natarcia niewielki...
Dla dużych kątów natarcia oderwanie wystąpi na znacznej części brzegu i idea warstwy
przyściennej traci sens.

Dla ruchów trójwymiarowych – wokół bryły – ruch potencjalny płynu nielepkiego
prowadzi do paradoksu D’alembarta.
Paradoks ten sprowadza się do stwierdzenia: przy pontencjalnym ruchu na zewnątrz
bryły, gdy prędkość nieskończoności jest wszędzie taka sama, BRAK (jakiejkolwiek)
REAKCJI. Bryła ma skończone wymiary.

Przy opływie konturu – mamy kompletnie inną sytuacje. Ruch na zewnątrz jest -
oczywiście – potencjalny i, pomimo to, występuje niezerowa reakcja (gdy Γ≠0 to
wirowość – formalnie – występuje w „zakrytym” opływanym ciałem początku układu
odniesienia..). Ale: kontur jest bryłą o nieograniczonym wymiarze w kierunku
prostopadłym do płaszczyzny ruchu...
Taka – nieskończenie wielka – bryła wprowadza zaburzenie jednorodnego pola ciśnienia
w sposób prowadzący do niezerowej reakcji.. (Jeśli wymiary bryły są skończone – to
zmiana pola ciśnienia nie jest taka, jak przy bryle nieograniczonej). W wyniku mamy
brak siły przy ruchu trójwymiarowym i niezerową siłę dla ruchu płaskiego. W obu
przypadkach pola prędkości są – w zewnętrzu opływanych ciał – potencjalne..

Elementarna Dynamika Gazów

Przedmiotem naszych zainteresowań będzie jednowymiarowe ruchy gazu.
Termin „jednowymiarowe” oznacza wystepowanie jednej (niezerowej) skałdowej
prędkości zależnej od jednej współrzędnej – ewentualnie od czasu.

Zamin przejdziemy do szczegółów przypomnimy zasadnicze fakty znane z ogólych
równań. Gazy są najprostszymi (fizycznie) ciałami. Aby określić ich stan trzeba podać
dwa parametry. Trzeci parameter wynika z równania stanu.
Najprstrze równanie stanu to równanie Clapeyrona:

p

RT

ρ

=

. Stała gazowa R to B

μ

,

z uniwersalną wielkością B (=8315 J/Kmol

o

K) i miara kilomola, μ. Określa się ciepło

właściwe Cp i Cv dla stalego ciśnienia i stałej objętości. Cp/Cv = k = wykaznik

izentropy =

2

n

n

+

, n – ilość stopni swobody (...) i R=Cp-Cv. Określa się tez funkcje

termodynamiczne:

entalpie

di

CpdT

=

energia wewnetrzna

w

de

CvdT

=

eentropia

dq

ds

T

=

(I jeszcze wiele innych...)

Mamy I-a zasade termodynamiki

1

1

w

dp

de

pd

di

dp

ρ

ρ

⎛ ⎞

=

+

= −

⎜ ⎟

⎝ ⎠

Druga zasada termodynamiki – w jednym ze sformulowan – brzmi:

„W ukladzie izolowanym entropia nie maleje...”

Tyle na poczatek. Szczegoly beda podane w dobrym wykladzie. W ruchach gazu
dominuja sily cisnieniowe i sily bezwladnosci. Tarcie odgrywa role albo w warstwie

przysciennej albo wowczas, gdy analizowany ruch przez bardzo dlugi przewod...
Mozemy tez, poza specjalnymi przypadkami, odrzucic oddzialywanie cieplne zachodzace
miedzy rozwiazanym gazem a jego otoczeniem. (To otoczenie stanowia ciala stale
organiczujace obszar wypelniony gazem).

Wobec tego opis ruchu i stanu gazu moze byc dokonany w prosty sposob: odrzucam
tarcie, przewodzenie ciepla i zaniedbujemy przekarywanie ciepla do / od plynacego gazu.
Mamy wiec:

Rownanie Ciaglosci:

( )

0

p

div

V

t

ρ

uv

∂

+

=

∂

( )

1

V

V

dV

gradp

∂

⎡

⎤

=

+

⋅∇

= −

⎢

⎥

u

Rownanie Eulera:

dt

t

ρ

∂

⎣

⎦

v

uuuuv uv

Rownanie energi:

( )

2

2

1

d

v

v

p

i

V

i

⎛

⎞

⎛

⎞

2

2

dt

t

t

ρ

∂

∂

⎡

⎤

+ =

+

⋅∇

+ =

⎜

⎟

⎜

⎟

⎢

⎥

∂

∂

⎣

⎦

⎝

⎠

⎝

⎠

uv

N.B: W jakich okolicznosciach jest:

( )

2

?

v

dp

const

+

=

∫

2

?

v

i

const

+ =

2

2

p

ρ

Jak pamietamy, z rownania Eulera i rownania energii wynika stalosc entropii *. Trzeba

jednak zalozyc, ze

dq

ds

T

=

, czyli brak procesow nieodwracalnych wewnatrz gazu.

Charakterystyczna cecha gazow jest powstawanie fal cisnienia (gestowsc, temperatury).
Fale te – jak wszystkie fale – poruszuja sie wzgledem osrodka w ktorym zaistnialy. Fale
cisnienia sa falami podluznymi. Fala podluzna ma kierunek ruchu zgodny z kierunkiem
zmian. (Czytelnik ma tez fale poprzeczne, dla ktorych kierunek ruch i kierunek zmian sa
prostopadle). Dla fal rozchodzacych sie w przestrzen okreslamy powierzchnie stalej
fazy. Powierzchnia ta zmienia sie z uplywem czasu. Wektor prostopadly do tej
powierzchni moze byc zgodnie z predkoscia rzchodzenia sie fali. Moze tez byc
ortogonalny do predkosci...
Fale moga miec rozmaite amplitudy. Fala cisnieniowa o znikomej amplitudzie to fala
dzwiekowa (akustyczna). Znajdujemy predkosc rozchodzenia sie fal akustycznych.
Wczesniej – okreslamy rownanie falowe.

( )

( )

,

,

F t x

f

x at

ξ ξ

=

= ±

Niech pewna wielkosc fizyczna bedzie okreslona tak:

( )( )

( )( )( )

2

2

F

Znajdujemy pochodne:

,

F

f

f

a

f

a

a

t

t

t

ξ

∂

∂

∂

∂

ξ

ξ

ξ

∂

∂ ∂

∂

′

′′

=

⋅

=

±

=

±

±

Czyli

( )

2

2

2

F

a

f

t

ξ

∂

′′

=

⋅

∂

. Podobnie:

( )

2

2

2

2

,(

1)

F

d F

f

bo

ξ

ξ

∂

∂

′′

x

d

x

ξ

=

=

=

∂

∂

* Mnozymy rownianie Eulera (skalarami) przez V

uv

:

2

1

2

dV

d v

V

V gradp

dt

dt

ρ

=

= −

uv

uv

uv

i

odejmujemy od rownania energii. Powstanie:

( )

1

1

d

d

i

V

p

dt

t

dt

ρ

ρ

∂

⎡

⎤

=

+

⋅∇

=

⎢

⎥

∂

⎣

⎦

uv

p

lub

1

0

0

di

dp

Tds

ds

ρ

= −

=

⇒

=

Eliminujemy

( )

f

ξ

′′

. Otrzymujemy:

2

2

2

2

F

a

2

F

x

t

∂

∂

=

∂

∂

rownanie falowe.

Poniewaz

, to gdy

( )

( )

(

,

F t x

f

f x at

ξ

=

=

±

)

x

at

const

= ± +

to f, a wiec i F, nie ulega

zmiane. Stala wartosc funkcji F „przemieszcza sie” z predkoscia

a

±

.

Dla ruchu wielowymiarowego jest tak:

2

2

2

2

2

2

2

2

F

F

F

a

2

F

x

y

z

t

⎛

⎞

∂

∂

∂

∂

+

+

=

⎜

⎟

∂

∂

∂

∂

⎝

⎠

lub

2

2

2

F

a

F

t

∂

= Δ

∂

Rownanie falowe.

Czytelnik sprawdzi, ze wozwiazaniem jest:

(

)

( )

, , ,

,

F t x y z

f

k r

at

ξ ξ

=

= ⋅ ±

v v

z wektorem

takim, iz k

k

v

2

= 1. Fala przemeszcza sie w kierunku okreslony, przez z predkoscia a.

k

v

Wyznaczamy prdkosci fali cisnieniowj o znikomej amplitudzie
Zwiazemy uklad odmieszczenia z tuchowym gazem. Gaz porusza sie lokalnie ze stala
predkoscia. Zaburzenie cisnienia jest male. Podobnie zaburzenie gestosci: Rowniez
zaburzenia predkosci wywalane zmiana cisnienia i gestossci jest niewielkie. Wobec tego
– w ruchowym ukladzie – jest:

V

V ′

=

uv uv

,

1

p

p

p′

=

+

,

1

ρ ρ ρ

′

=

+

, z malymi , ,

V

p i

ρ

′ ′ ′

uv

.

Piszemy:

1

V

V

V

V

1

ρ

ρ

ρ

ρ

′

′

′

=

+ ⋅

≈

uv

uv

uv

uv′

i wobec tego rownianie ciaglosci mozna napisac tak:

1

0

divV

t

ρ

ρ

′

∂

+

≅

∂

uv

Rownanie ruchu uproszcimy , bo

( )

0

V

V

V

V

⎛

⎞

′

′

⋅∇

=

⋅∇

≈

⎜

⎟

⎝

⎠

uv

uv

uv

uv

.

1

1

dV

gradp

dt

ρ

′

′

≅ −

uuv

Eliminujemy

V

. W tym celu biezemy divergencje uproszczonego rownania ruchu:

′

uv

1

1

divV

divgradp

t

ρ

∂

′

′

= −

∂

uv

Z rownania ciaglosci wynika:

2

2

1

1

1

1

d

divV

divV

dt

t

u

ρ

ρ

ρ

ρ

′

′

∂

∂

′

′

≡ −

⇒

=

∂

∂

uuv

uuv

Laczymy dwa ostatnie rownania:

2

2

2

2

divgradp

p

p

t

x

y

ρ

′

⎛

∂

∂

∂

2

2

2

2

z

⎞

∂

′

′

′

=

= Δ =

+

+

⎜

⎟

∂

∂

∂

⎝

⎠

∂

Pozostaje powiazac

ρ

′

z

. Dla fal akustycznych postulujemy

p′

1

1

,

p

dp

p

d

ρ

ρ

ρ

′

′

=

⋅ (

1

1

...

dp

p

p

p

d

ρ

ρ

′

+

=

+

⋅ +

′

→ zaburzenie cisnienia

...

dp

p

d

ρ

ρ

′

′

=

⋅ + )

Wielkosci

dp

d

ρ

jest obliczone dla wielkosci niezaburzonych, to znaczy dla p

1

i ρ

1

. A

wiec

,

p

dp

d

ρ

ρ

jest obliczane. Otrzymujemy:

1

1

2

2

,

p

dp

t

d

ρ

ρ

ρ

ρ

′

∂

′

=

Δ

∂

To Rownanie Falowe

Predkosc rozchodzenia sie fali okresla pochodna

dp

d

ρ

. Fala o znikomej amplitudzie (

ρ

′

,

, i

V

sa male) nie zaburza rownowagi termodynamicznej.

p′

′

uv

Wobec tego pchodna

dp

d

ρ

trzeba obliczyc przy przemianie odwracalnej, a wiec prz stalej

entropii. * Dla stalej entropii jest

k

p

const

ρ

=

. Logamytujemy i obliczamy pochodna

logoratmiczna:

ln

ln

p

k

const

ρ

=

+

1

1

s

dp

k

d

ρ ρ

ρ

=

⇒

s

dp

p

k

kR

d

ρ

ρ

=

T

A wiec predkosc dzwieku to:

s

p

dp

a

k

kRT

d

ρ

ρ

=

=

=

Opuscilismy oznaczenie „1” – bo wartosci p, i ρ (oraz T) moga byc dowolne.

* Newton (w jego czasach nic nie wiedziano o odwrotnosci termodynamicznej) obliczyl
predkoswc fali zakladajac T=const. Otrzymamy:

( )

t const

dp

p

RT

RT

d

ρ

ρ

=

=

⇒

=

wynik byl niezgodny z pomiarem...

Podkreslamy: Fala porusza sie wzgledem gazu, ktory ma predkosc V

uv

. A wiec lacznie,

predkosc fali wzgledem neruchomego ukladu odniesienia, jst suma predkosci gazu i
predkosci fali wzgledem gazu.. Dla sytuacji w ktorej gaz ma jedyna nezereowa
skaldowa predkosci skierowana wzdluz osi x (oznaczamy ja u) mamy:

Predkosc wali wedlug nieruchomego ukladu

u

a

= ±

Pomnozymy rownanie falowe okreslajace

ρ

′

przez stala a

2

. Poniewaz

2

p

a

ρ

′

′

=

, to

wynik jest nastepujacy:

2

2

2

p

a

p

t

′

∂

′

= Δ

∂

Dalej: gradient

podzielony przez stala

p′

1

1

ρ

okresla

V ′

uv

. A wiec:

2

2

2

V

a

V

t

′

∂

′

= Δ

∂

uv

uv

Kazde z wielkosci

ρ

′

,

, i

V

podlega zaburzeniom falowym rochodzacym sie

dokladnie tak samo...

p′

′

uv

Fala o znikomej amplitudzie jest oczywiscie, najprostsza z mozliwych fal poruszajacych
sie w gazach. Predkosc jej wzchodzenia nie zalezy od amplitudy (ta ostatnia jest zawsze
znikoma) ani, ewentualnie od czestotliwosci.
Fale o skonczonej amplitudzie maja predkosci rozchodzenia sie zalezne od amplitudy.
Osrodek, w ktorym predkosc fal zalezy od czestotliwosci nazywamy dyspersyjnym.
Tamikm osrodkiem jest np. Woda licznymi bablami gazu albo gaz ze znaczacym
udzialem plynu lub mikroskopijnych kropli cieczy (mgla, aerosol).
Znajduimy predkosci diczyki w powietrzu. Dla kilku temperatur mamy:
T 300 600 1000 1500
a 347 490 634 776 Powietrze
a 429 607 784 960 H

2

O

a

1321 1869 2412 2954 H

2

Powietrze R=287 m

2

/S

2

K, para wodna (R=462, K=1.33), i wodor (R=4157.5, K=1.4)

Predkosc fali o znikomej amplitduzie – a wiec Predkosc dzwieku stanowi stala
predkosci dla gazow. To Naturalna skala predkosci. Definiujemy:

u

M

a

=

=

v

=Liczba Macha

Predkosc w danym miejscu
Predkosc w tym miejscu

Gdy M<1 to ruch jest poddzwiekowy, a dla M>1 – naddzwiekowy. Z rownania energii –
w formie elgebraicznej – wynika:

2

2

2

2

u

u

i

const

CpT

const

+ =

⇒

+

=

Ale, poniewaz

1

kR

Cp

k

=

−

, to

2

1

1

kRT

a

CpT

k

k

=

=

−

−

, i mozna napisac:

2

2

2

2

0

0

0

2

1

1

a

a

u

a

const

k

k

+

=

= +

=

1

k

−

−

−

Oznaczylismy tu

0

0

u

a

=

= a . Jest to predkosc dzwieku w nieruchomym gazie (przy

zachowaniu energii; tzn. Gaz zatrzymal sie nie wymieniajac energii z otoczeniu).

Zapamietajmy:

2

2

2

0

2

1

a

u

a

k

k

+

=

1

−

−

Maksymalna predkosc jaka moza osiagnac gaza to ruchu ustalonym. Wynosi:

(

)

2

2

2

max

0

max

0

0

2

2

1

1

a

u

a

u

a

k

k

k

=

+

=

⇒

=

−

−

−1

Poniewaz

, to

u

M a

=

⋅

2

2

0

0

1

1

2

a

T

k

M

a

T

−

⎛

⎞

+

=

=

⎜

⎟

⎝

⎠

To jest tempereatura gazu nieruchomego (przy zachowaniu energii). Przepisujemy
rownanie okreslajace ulamach temperatury:

2

0

1

1

1

2

T

k

T

M

=

−

+

T

0

nazywamy „temperatura calkowita,” to temperatura w bezruchu, energia jest

zachowana.
Jesli Gaz podlega przemianie oduracalnej to:

1

0

0

1

2

1

1

1

2

k

k

k

k

p

T

p

T

k

M

−

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

−

⎛

⎞

+

⎜

⎟

⎝

⎠

1

1

1

0

0

1

2

1

1

1

2

k

k

T

T

k

M

ρ

ρ

−

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

−

⎛

⎞

+

⎜

⎟

⎝

⎠

p

0

i ρ

0

sa cisnieniem i masa wlasciwa w bezruchu – gdy proces hamowania jest

odwracalny.
p

0

i ρ

0

nazywamy cisnieniem i masa wlasciwa spietrzenia.

Podkreslmy: zachowanie energii nie jest rownoznaczne odwracalnosci.

Tylko wowczas, gdy gaz w izolowanym od wplywow zewnetrznych ruchu podlega
izentropie (tzn. Przemianie odwracalnej) to cisnienie (i masa wlasciwa) osiagaja
wartosci spietrzenia...

Zadania

1. Powietrze wyplywa ze zbiornika. Predkosc wynosi u=500m/s, temperatura 250K.

Jaka jest temperatura w zbiorniku?

2

0

1

1

,

,

2

k

u

T

T

M

M

a kRT

a

−

⎛

⎞

=

+

=

⎜

⎟

⎝

⎠

. Oblicamy: a≈317m/s, M≈1.578, T

0

≈374K

2. Przez izolowany przewod plynie gaz. W dwu przekrojach liczby Macha wynosza

M

1

i M

2

. Jak (i u mamy) zmienia sie predkosc?

Energia gazu jest zachowana:

2

2

2

2

1

1

2

2

2

1

2

1

u

a

u

a

const

k

k

+

=

=

+

−

−

. Poniewaz a=u/M,

to

2

2

2

2

2

2

1

2

1

1

2

2

2

2

1

2

1

1

1

2

2

1

1

2

1

1

1

1

1

u

k

u

M

u

M

k

k

u

k

M

−

−

+

⎛

⎞

−

⎛

⎞

⎛

⎞

+

=

+

→

=

⎜

⎟

⎜

⎟

⎜

⎟

−

−

⎝

⎠

⎝

⎠

⎝

⎠

+

−

M

3. Gaz porusza sie przewodem ogrzewanym / chlodzonym, temperatura jest stala.

Napisac rownanie Bernoulliego.

Jak pamietamy, rownanie Bernoulliego mozna napisac wtedy gdy

( )

p

p

ρ

=

albo

( )

p

ρ ρ

=

. Poniewaz T=const, to

p

RT

ρ

=

, RT=const. Ogolna forma rownania

Bernoulliego to

2

2

v

dp

const

ρ

+

=

∫

.

W naszym przypadku

2

2

ln

2

2

u

dp

u

RT

RT

p

p

+

=

+

=

∫

const

.

4. Obliczyc zmiane energii 1kg gazu dla przypadku z zadania 3.

Energia 1kg:

2

2

u

e

i

=

+

2

2

2

2

1

1

2

1

2

2

2

2

u

u

u

u

e

e

e

i

i

⎛

⎞ ⎛

⎞

Δ = − =

+

−

+

=

−

⎜

⎟ ⎜

⎟

⎝

⎠ ⎝

⎠

2

2

, bo i = CpT = const.

Piszemy rownanie Bernoulliego:

2

2

2

2

1

2

2

1

1

2

1

ln

ln

ln

2

2

2

2

u

u

u

u

RT

p

RT

p

RT

2

p

p

+

=

+

⇒

−

=

Wynika stad:

2

1

ln p

e

RT

p

Δ =

5. W zbiorniku z powietrzem cisnienia wynosi 2b. Temperatura 300K. Do jednej –

conajmniej – predkosci mozna rozpedzic gaz przy wyplywu do atmosfery w
ktorej p=1b?

0

1

2

1

1.05

1

1

2

k

k

p

M

p

k

M

−

=

⇒

−

⎛

⎞

+

⎜

⎟

⎝

⎠

≅

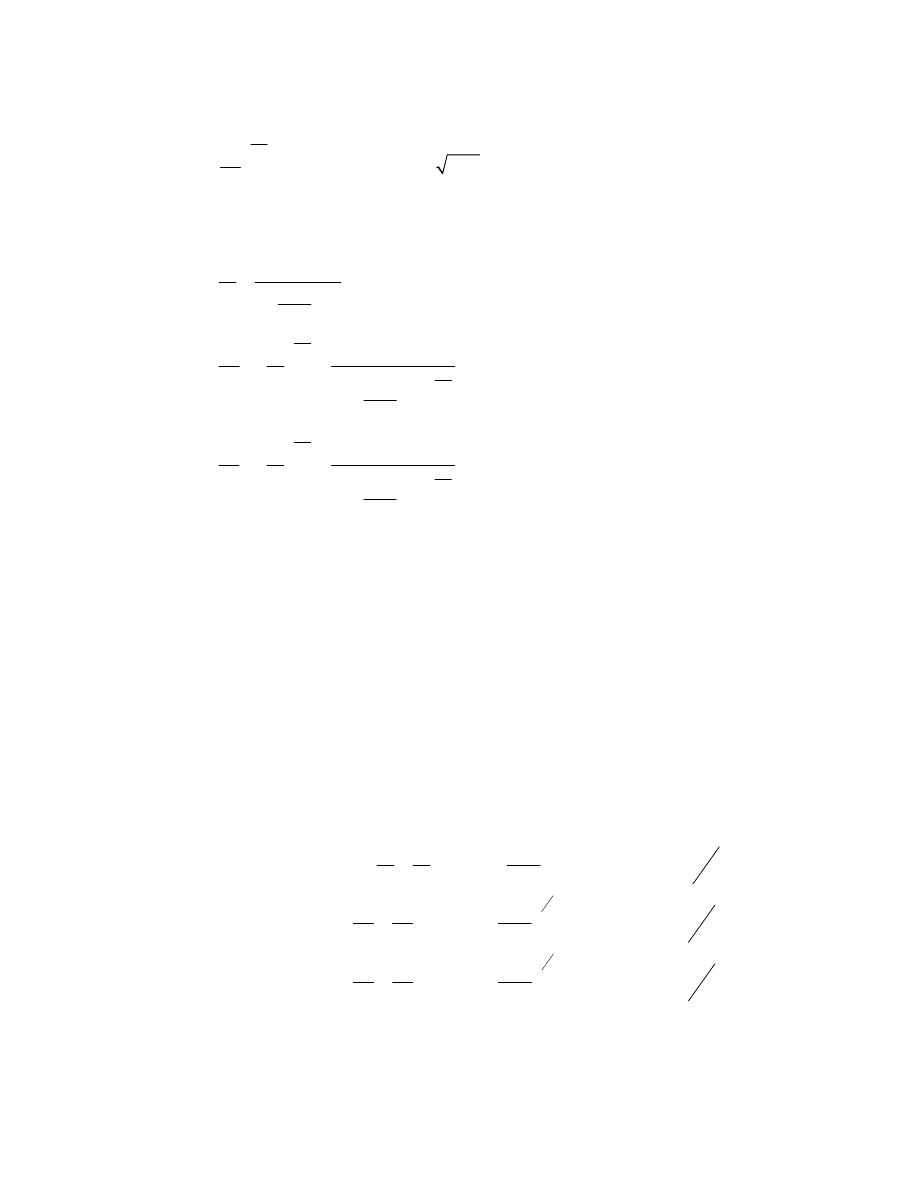
Temperatura wyplywajacego gazu:

1

0

0

246

k

k

p

T

T

K

p

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

330

u

M a

M kRT

=

⋅ =

≅

m/sek

Piszemy ponownie wzory okreslajace parametry termodynamiczne w zaleznosci od
liczby Macha (str. 30):

2

0

1

1

1

2

T

k

T

M

=

−

+

Obowiazuje wtedy, gdy energia masy jednostkowej jest stala.

1

0

0

1

2

1

1

1

2

k

k

k

k

p

T

p

T

k

M

−

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

−

⎛

⎞

+

⎜

⎟

⎝

⎠

Przemiana termodynamiczna jest izentropa.

1

1

1

0

0

1

2

1

1

1

2

k

k

T

T

k

M

ρ

ρ

−

−

⎛

⎞

=

=

⎜

⎟

⎝

⎠

−

⎛

⎞

+

⎜

⎟

⎝

⎠

Przemiana termodynamiczna jest izentropa.

Przypomniemy jeszcze to, ze T

0

, p

0

, i ρ

0

okresla sie dla gazu nieruchomego.

p

0

i ρ

0

otrzymamy wtedy, gdy przejscie do bezruchu odbywa sie odwracalnie.

a T

0

– gdy zachowana jest energia.

Oczywiscie odwracalnosc implikuje zachowanie energii. (Zdanie odwrotne nie jest
prawdziwe... )

Obliczano wyrazen w prawych stronach wypisanych zwiazkow nie jest trudne, ale
wymaga kilku nascinac klawiszy. (Przy uzyciu komputera – zaprogramowanie jest
banalne.. ) Przy obliczeniach sazerzych (nie warto pisac program gdy saczny rachunek
trwa krotko... ) wypadnie uzyc wzkoaniw.

Poslugiwanie sie wykresem jest elementarnie proste. Wane wartosci ulamkow

0

0

/ , /

, _ /

T T

i

p p

0

ρ ρ

otrzymamy dla M=1.

Mowimy: parametry dla M=1 nazywamy krytycznymi, oznaczamy je symbolem „*.”
I tak:

Dla k=1.4

(

)

*

0

0

2

1

1

T

T

M

T

T

k

=

= =

+

*

0

0.833

T

T

≅

(

)

1

1

*

0

0

2

1

1

k

M

k

ρ

ρ

ρ

ρ

−

⎛

⎞

=

= = ⎜

⎟

+

⎝

⎠

*

0

0.634

ρ

ρ

≅

(

)

1

*

0

0

2

1

1

k

k

p

p

M

p

p

k

−

⎛

⎞

=

= = ⎜

⎟

+

⎝

⎠

*

0

0.528

p

p

≅

Znajdujemy jeszcze zwiazek pomiedzy a

0

i a

*

. Predkosc a

*

odpowiada ruchowi przy

M=1, czli sytuacji, w ktorej u = a i u = a = a

*

= u

*

. (u

*

jest predkoscia – rowna predkosci

dziweku – przy M = 1). Mamy:

2

2

2

2

0

*

*

1

2

1

2

1

M

a

a

a

u

a

k

k

=

⎛

⎞

+

=

+

=

⎜

⎟

1

k

−

−

−

⎝

⎠

Wynika wiec taka zaleznosc:

2

2

*

0

2

1

a

a

k

=

+

Zestawione wzory pozwaluja wyznaczyc ruch gazu przez przewod o zmiennym
przekroju

.

Mamy ruch ustalony. Mozna napisac:

1. Zasada zachowania masy
2. Rownanie ruchu
3. Rownanie energii – wyrazajace jej stalosc

Ale – z rownania ruchu i rownania energii, przy braku tarcia i zrodel ciepla oraz
przewodzenie – wynika izentropowosc. Mozna wiec wziac rownanie Bernoulliego i
rownanie przemiany. Tyle ze przy izentropowosci rownanie Bernoulliego staje sie
rownaniem energii...
Z tego rownania wynika zwiazek

(

0

0

T

T

)

M

T

T

=

. Przy izentropowosci mamy

( )

0

0

p

p

M

p

p

=

i

(

0

0

)

M

ρ

ρ

ρ

ρ

=

. A wiec, poslugujac sie staloscia plynacej masy

gazu

piszemy:

n

V dA

const

ρ

=

∫

V

n

oznacza rzut predkosci na normalna. Jesli przewod zmienia lagodnie przekroj, to

V

n

≈ u , i u nie zmienia sie na przekroju. Podobnie ρ oraz p sa w przekroju ≈ stale.

Przyblizony (tym lepiej, im lagodniej zmienia sie przekroj A) zwiazek wyznaczajacy
zachowanie masy jest wiec taki:

uA

const

ρ

=

( = wydatek masowy)

Oczywiscie, ten sam wydatek masowy plynie (ewentualnie... ) przez przekroj, w ktorym
M=1, a wiec

* * *

uA

a A

ρ

ρ

=

Mozemy napisac:

( )

( )

*

*

*

*

*

0

0

0

0

1

1

a

a

A

1

A

u

a

T

M

M

T

M

ρ

ρ

ρ

ρ

ρ

ρ

=

=

Bo u = Ma i

*

*

*

0

0

1

1

a

a

a

a

u

aM

a

M

a

=

=

⋅

⋅

.

Prawa strona jest funkcja wylacznie liczby Macha. Jasne, ze gdy M = 1 to

*

1

A

A

= . Dla

M→0 otrzymujemy

*

A

A

→ ∞ . Podobnie, gdy M→∞,

*

A

A

jest nieograniczone.

Wykres funkcji

( )

( )

*

*

A

A

M

F M

A

A

=

=

przedstawia szkic.

Zauwazamy:
Danej liczbie macha odpowiada jedna wartosc

*

A

A

. Jesli jest zadana wartosc

*

A

A

- to

otrzymujemy dwie liczby macha: odpowiadajaca ruchowi poddziekowemu (<1) i druga
dla ruchu naddziekowego.
Wykres

( )

( )

*

A

M

F M

A

=

pozwala przeprowadzic wazna dyskusja zmian liczby

mahca pry zmnianie przekroju

.

Zmieniajac przekroj * powodujemy:
Wzrost M gdy M<1 spadek M gdy M>1. Odrwotnie, gd przekroj wzrasta – M rosnia dla
M>1 i M maleje, jesli M<1.

Mozemy teraz rozpatrzyc wyplyw ze zbiornika prze zwezajaca sie rure. Nazywamy ja
„dysza zbiezna.” Predkosc w zbiorniku jest bliska zeru. Gaz wyplywajac do rury
zwieksza predkosc od bliskiej zeru – w zbiorniku – do predkosci w przekroju wlotowym
rury. Nie ma powodow by predkosc wlotowa byla predkoscia naddziekowa, bo
wymagalo by to znacznego spadku cisnienia...
A wiec w przekroju wlotowym jest M<1. Zwezenie przewodu powoduje wzrost liczby
Macha wzdluz dyszy... (przy ruchu poddzwiekowym). Wnioskujemy: w przekroju
wylotowym liczba Macha jest – conajwyzej – rowne 1:

1

wylot

M

≤

* Oczywiscie A

*

= const to pole przekroju tam, gdzie M=1...)

Jak znalezc liczba macha w przekroju wylotowym?
Jasne, ze o ruchu gazu decyduja cisnienia: zewnetrzne p

zew

i zbiornikowe. To ostatnie

mozna uznac ze cisnienie spietrzenia p

0

(zdladno przeciez izentropowosc... )

Jesli p

zew

= p

0

– to ruch nie pojawi sie. Gdy p

zew

< p

0

– to oczywiscie w miare malenia

cisnienia zewnetrznego, gaz wyplywa coraz szybciej.
Cisnienie w przekroju wylotowym jest rowne cienieniu zewnetrzynemu...
Ale – gdy

To dalszy spadek cniesnienia zewnetrznego nie powoduje wzrostu

liczby macha – bo w dyszy zbieznej moze ona wzrosnac tylko do jednosci...

1

wylot

M

=

Zapiszemy to tak:

wyl

zew

p

p

=

gdy

1

wyl

M

<

wyl

zew

p

p

≥

gdy

1

wyl

M

=

Jasne, ze dla

1

wyl

M

=

(

)

*

0

0

1

wyl

p

0

p

p

M

p

p

p

=

= =

A wiec:

Gdy

*

*

0

0

zew

p

p

p

p

>

=

p

to

i M

1

wyl

M

<

wyl

wynika z dostosowanie cisnien:

(

)

0

0

1

wyl

wyl

p

p

M

M

p

p

=

= ⇒

Jezeli zas

*

zew

p

p

≤ - to

.

1

wyl

M

=

Zadania

1. Po strzelaninie na pokladnie samolotu powstalo 30 otworow o srednicy 8mm

kazdy. Ile kilogramow powietrza trzeba dostarczyc – conajwyzej do kabiny?
Warunki komfortu: 295K, p=0,95 bar.

W otworze – conajmniej – jest M=1. Znajdujemy:

*

*

* *

* *

0 0

0

0

masowy

a

Q

m

u A

a A

A

a

a

ρ

ρ

ρ

ρ

ρ

= =

=

=

&

Poslwaujemy sie definicja predkosci dzwieku i rownaniem stanu:

0 0

0

0

1,12 344 385, 6

o

p

a

kRT

RT

ρ

=

⋅

≅

⋅

≅

(kg/sek m

2

)

Poniewaz

*

0

0,624

ρ

ρ

≅

i

*

*

0

0

0,913

a

T

a

T

=

≅

oraz

3

1,5 10

A

−

≅

×

to:

1

5,82 10

masowy

Q

m

−

= ≅

×

&

kg/sek

Jak widac – jest to calkiem malo...
Gdyby zawiedly sprezarki, to przy objetosci kabiny rzedu 1000m

3

czas wyplywu

polowy powietrza jest rzedu wielu minut... samolot zdazy obnizyc wysokosc..

2. Samolot SR 71 porusza sie z liczba macha 3.5. Temperatura atmosfery wynosi

230K. Do jednej – conajwyzej – temperatury rozpnac sie moga fragmenty
pokrycia samolotu?

Na krawedziach natarcia predkosc gazu wzgledu samolotu ≈0.
Piszemy rownanie energii:

2

2

2

2

0

0

2

0

1

1

2

1

2

1

1

2

u

a

u

a

T

k

k

k

T

M

∞

∞

∞

∞

+

=

+

⇒

=

−

−

−

+

Maksymalna temperatura gazu wynosi

2

0

1

1

793

2

k

T

M

T

∞

∞

−

⎛

⎞

= +

≅

⎜

⎟

⎝

⎠

K

Jest to temperatura wykluczajace uzycia stopow aluminium – jesli lot jest
dlugotrwaly.
MIG 25 (M

maks

=3.2) moze leciec z maksymalna predkoscia przez 7 minut. W tym

czasie przeleci ok. 420km.

3. W zbiorniku panuje cisnienie 1.5 bara. Gaz (azot) wyplywa do atmosfery (p

zew

=1

bar). Wyznaczyc predkosc tam, gdzie przekroj dyszy zbeiznej jest rowny
podwojonemu przekroju wylotowemu. T

0

= 300K.

Oznaczamy przekroj nas interesujacy symbolem x. Jest Ax = 4Aw.

Poniewaz

*

0

0

0, 667

0,528

zew

p

p

p

p

≅

>

=

to M

w

< 1.

Znajdujemy M

w

:

(

)

0

0, 667

0, 77

W

W

p

M

M

p

=

⇒

≅

Tej liczbie macha odpowiada

*

*

1, 08

W

A

A

A

A

=

=

W przekroju x:

( )

*

*

4

x

W

x

x

A

A

F M

M

A

A

=

=

⇒

Oderytanie M

x

(znamy

*

x

A

A

) dla M

x

≈ 0,5

Uwaga: wykorzystalismy niezmiennosc A

*

.

Predkosc w przekroju x:

( )

( )

0

0

0

0

x

x

x

x

x

x

x

a

a

u

a

M

M

a

M

M

M

kRT

a

a

=

⋅

=

⋅ ⋅

=

⋅

Poniewaz

m

2

297

N

R

≅

2

/s

2

K, to przy

( )

0

0,97

x

x

a

M

M

a

⋅

≅

otrzymamy

171 /

x

u

m s

≅

ek

A

⎤⎦

4. W butli z tlenem panuje cisnienie 150b. Temperatura 300K. Po utraczeniu

zaworu powstal otwor o powierzchni 10cm

2

. Jaka sila dziala na butle? Na

zewnatrz 1bar.

Sila:

. Wyplyw odbywa sie z M = 1.

(

)

2

a

F

u

p

p

ρ

⎡

=

+

−

⎣

3

*

0

0

0,634 192 122

/

w

kg m

ρ

ρ

ρ

ρ

=

≅

⋅

≈

.

,

5

5

0,528 150 10

79, 2 10

w

p

P

=

⋅

×

=

×

a

2

2

2

4

*

0

0

2

2

9 10

1

1

u

a

a

kRT

k

k

=

=

=

≅ ×

[ ]

4

4

... 10 10

1,88 10

F

N

−

=

⋅ ×

≅

×

+

,

+

Istotna kwestia dla dysz – zbieznej albo innej – jest wydatek masowy. Wydatek ten
zalezy oczywiscie od przekroju wylotowego. Ozaczamy go Q

m

i obliczymy:

(

)

m

wylot

Q

m

uA

ρ

= =

&

Proste przkesztalcenie jedne zastosujemy to dzielenie i mnozenie:

(

)

0

0

0

0

m

w

w

w

w

u

a

Q

m

a

A

a

a

ρ

ρ

ρ

= =

⋅

⋅

⋅

⋅

&

Wyrazenie w nawiasie okraglym

(

)

0

0

a

ρ

⋅

jest stale – gdy stale sa warunki panujace w

zbiorniku zasilajacym dysze. Oczywiscie A

w

tez jest stala. Pozostale czynniki sa zalezne

od liczby macha w przekroju wylotowym. Otrzymalismy:

( )

( )

0

0

0

0

0

m

w

w

w

p

a

Q

m

M

M

M

kRT

A

a

RT

ρ

ρ

⎛

⎞

= =

⋅

⎜

⎟

⎝

⎠

&

w

Dla niezmiennego cisnienia p

0

i niezmiennej temperatury T

0

jedyna zmienna niezalezna

moze byc cisnienie zewnetrzne. Oznaczamy ta wielkosc p

z

. Interesuje na przypadek p

z

<

p

0

, bo gdy p

z

= p

0

, to ruch nie wystepuje. Spadek p

z

do wartosci p

*

powoduje wzrost M

w

do wartosci odpowiadajacej temu cisnieniu czyli do jednosci. Dla nizszych cisnien
zewnetrznych model jest M

w

= 1 i nic sie nie zmienia.

A wiec maksymalny wydatek okresla wyrazenie:

(

)

*

*

_ max

max

0 0

*

0

0

1

m

w

a

Q

m

a

A

a

m

Q

ρ

ρ

ρ

=

=

⋅ ⋅

=

&

Mowimy: wydatek krytyczny. Oczywiscie,

*

m

m

Q

Q

<

. Wydatek krytyczny odpowiada

M

w

=1. Dla dyszy zbeiznej A

w

– przekroj wylotowy – jest zarazem przekrojem

minimalnym dyszy.

Jesli zmienic sytuacje i rownac zmiana wydatku przy zmnianie cisnienia w zbiorniuku –

to wyplyw zachodzi dla p

z

< p

0

. Jesli

0

*

1

z

z

p

p

p

p

=

to pojawia sie wyplyw krytyczny. Dla

dalszego wzrostu p

0

(stala p

z

). W przekroju koncowym nadal jest M

w

=1. Dla wyplywu

krytycznego jest:

( )

0

*

*

0

0

0

0

1

m

w

p

a

Q

m

M

kRT

A

a

RT

ρ

ρ

⎛

⎞

= =

⋅ ⋅

⎜

⎟

⎝

⎠

&

w

.

Jak widac

.

0

m

Q

p

Czytelnik z latwiascia narysuje wykres zmiennosci wydateku dla

*

0

0

z

p

p

p

p

≤

w funkcji

temperatury w zbiorniku... (oczywiscie, T

0

> minimalnej – ktora jest zblizona do

temperatury otoczenia...)

Wyciagnjmy wnioski. Kluczowa wielkoscia sluzaca do obliczenia wydatku jest liczba

Macha w przekroju wylotowym, czyli M

w

. Dla ulamka

*

0

0

z

p

p

p

p

≤

jest

.

1

w

M

=

Jesli zas

*

0

0

1

z

p

p

p

p

<

<

To M

w

okresla rownanie:

( )

0

0

z

w

w

p

p

M

M

p

p

=

⇒

Po znalezieniu M

w

obliczamy

( )

(

0

0

,

w

a

)

w

M

M

a

ρ

ρ

i z latwoscia znajduejmy wydatek.

Obydwa rozazane przypadki i odpowiadajace im szlice wynainic roznia sie. W
pierwszym przypadku stale jest p

0

(i T

0

). W drugim p

z

, a zmienia p

0

. Mamy wiec

zasilanie gazem o roznych cechach. To powoduje roznice...

Nastepnym nadziejem dyszy jest dysza zbeizno – rozbiezna albo dysza Lavala.
Zbadany ruch gazu wyplywajacego ze zbiornika przez taka dysze. Uzywamy za zadane
dwa przekroje: wylotowy A

w

i minimalny A

min

. Okaza sie, ze w istocie potrzeba tylko

ulamka

min

w

A

A

,

Bo wszystkie dysze o takiej cesze reakuja identycznie (- z dokladnoscia do skali) ruch
gazu.
Tak jak poprzednio w zbiornuku zasilajacym (jest tam niemial bezruch) zadajemy
cisnienie i temperature. Zadane jest tez cisnienie zewnetrzne p

z

.

Przypuscimy, ze p

z

jest nieznacznie mniejsze od p

0

. Spodziewamy sie powolnego – a

wiec poddzwiekowego – ruchu w przekroju wylotowym. Poniewaz jest wtedy M

w

< 1, to

cisnienie zewnetrzne p

z

i cisnienie w przekroju wylotowym sa rozne:

z

w

p

p

=

1

w

M

<

Otrzymamy:

( )

0

0

0

1

w

z

w

p

p

p

M

p

p

p

=

=

⇒

To, po prostu, dostosowanie poddzwiekowego strumienia wyplywajacego z dyszy do
otoczenia.
W czesci wzbiezniej – gdy ruch jest poddzwiekowy – mamy zmniejszenie sie liczby
macha. A wiec najwieksza wartosc tego porwadu wystapi w przekroju minimalnym.
Graniczne wartoscia M w tym (minimalnym) przekroju jest jedynka.

min

max

1

A

M

=

Jesli

min

1

A

M

= to

. Znajdujemy M

*

min

A

= A

w

odpowiadujaca tej sytuacji. Jest:

( )

1

1

min

*

,

1

w

w

A

A

F M

M

A

A

=

=

<

Oczywiscie,

1

w

M

M

=

. Jesli obliczymy cisnienie wylotow, to:

( )

( )

1

1

0

0

0

w

w

p

0

p

p

p

M

M

p

p

p

=

=

=

p

Podkreslamy: Gdy

min

1

A

M

= to przy wyplywie poddzwiekowy

(

1

1

w

M

M

)

=

< oraz

. Oczywiscie,

1

z

p

p

=

(

)

1

1

*

1

p

p M

>

<

Zmiennosc cisnienia w dyszy jest naszkicowana obok. Najnizsze cienienie = p

*

wystepuje w przekroju minimalnym. Wszedzie poza tym przekroju M<1 i p>p

*

.

Jesli cisnienie zewnetrzne p

z

jest wieksze od p

1

(i oczywiscie nizsze od p

0

), tzn

1

0

z

p

p

p

>

>

To w przekroju minimalnym liczba macha jest mniejsza od jednosci:

min

1

A

M

<

Wtedy, , bo gaz zmienia liczbe macha w czesci rozbieznej. W przekroju
koncowym jest p

1

w

M

=

w

= p

z

i, wobec tego:

( )

( )

0

0

1

z

w

w

p

p

M

M

p

p

=

=

⇒

<

Jaka jest liczba macha w przekroju minimalnym?

(

)

( )

( )

min

min

min

min

*

*

1

w

w

A

A

w

A

A

A

F M

F M

M

A

A

A

=

⋅

=

⋅

⇒

<

Czytelnik zauwazyl, ze wazna wielkoscia jest taka liczba macha M

w

, ktorej odpowiada

M=1 w przewroju minimalnym. Sposob jej okreslenia opisalismy na poprzeczniej
stronie.

Mozna przypuszczas ze dla niskich cisnien zewnetrznyh w rozbieznej czesci dyszy
pojawi sie ruch naddziwiekowy. Oczywiscie, w przewezeniu dyszy jest M = 1 a

A

min

= A

*

. Poniewaz znamy

(

min

*

w

w

w

A

A

)

F M

A

A

=

=

z rozwiazaniem M

w

>1 – to odwracajac

zaleznosc (dla czesci naddzwiekowej) znajdujemy M

w

(>1).

Znajdujemy cisnienie wylotowe:

(

2

0

0

0

w

w

p

p

p

M

p

p

p

=

=

)

(p

o

– zadane... )

Jest to ulamek (znacznie) mniejszy od

*

0

p

p

(gdy

min

1

w

A

A

>

w istotny sposob).

Zauwazamy, ze p

2

zalezy tylko od geometrii dyszy.

Cisnienie zewnetrzne

odpowiadajace p

2

okresla prawidlowa prace dyszy. Jesli

2

z

p

p

<

to ruch w dyszy nie

ulegnie zmianie. Jest tak, bo to, co dzieje sie wewnatrz niej zalezy wylacznie od
geometrii..
Strumien, w ktorym w „ostatnim” przekroju dyszy panuje cisnienie p

w

rozpwa sie na

zewnatrz. Moze sie przy tym znacznie rozszerzyc.

Zilistrujemy podane rownanie przykladem.
Niech dysza Lavala o przekroju wylotowym A

w

wiekszym od minimalnego 1.5 razy

bedzie polaczone ze zbiornikiem. Cisnienie zewnetrzne wynosi 1 bar. Wyznaczyc:

1. Cisnienie w zbiorniku odpowiadujace maksymalnej, poddzwiekowej liczbie

macha w przekroju wylotowym

2. Cisnienie w zbiorniku odpowiadajace prawidlowej, naddzwiekowej pracy dyszy
3. Liczba macha w przekroju wylotowym dla cisnienia zbiornikowego 1.1 bara.
4. Liczba macha w przekroju minimalnym dla warunkow z pytania 3.

1.

. Poniewaz w przewezeniu jest M=1 to

1

1

wyl

M

M

=

<

min

*

A

A

=

. Mamy

( )

1

*

wyl

A

F M

M

A

=

⇒

1

. Odczytujemy:

.

1

0, 41

M

=

Dalej:

( )

(

1

0

0

0

w

w

z

w

p

p

p

p

p

M

M

p

p

p

=

⇒

=

=

)

, i nastepnie:

( )

0

0

0

1

1

1

1 1,166

0,86

w

z

w

w

p

p

p

p

p

M

p

p

=

=

=

⋅ =

2.

. Postepujac analogiczne otrzymamy

2

1

wyl

M

M

=

>

2

1,85

M

=

Dalej:

( )

0

2

0

1

1

1 6, 62

1,51

z

p

p

p

M

p

=

=

⋅ ≅

b

z

3. W tym przykladzie

. A wiec wszedzie jest ruch poddzwiekowy. W

przewezeniu M<1 i nie jest to „przekroj krytyczny.” M

1

z

p

p

>

w

wynika z warunku:

w

p

p

=

lub

( )

0

0

0

0

0,38

0,91

w

z

z

w

w

p

p

p

p

M

M

p

p

p

p

⎛

⎞

=

=

⇒

=

=

⎜

⎟

⎝

⎠

4. Wykozystamy dane:

min

min

min

min

*

*

w

w

w

w

A

A

A

A

A

A

A

A

A

A

=

⋅

⇒

=

⋅

(Oczywiscie, ze

. Nie znamy tego przekroju – ale wiemy, ze istnieje... )

*

mi

A

A

<

n

Dalej:

(

)

( )

1

:

1,5

przewaz

w

przewaz

F M

F M

M

=

⇒

Ponewaz

( )

(

)

(

)

0,38

1,52

1, 013

w

w

F M

F

F M

=

=

⇒

=

yl

1

. Wynika stad

0,86

przewaz

M

≈

Znajac liczbe macha latwo okresliamy cisnienie, temperature, predkosc, itp.

Czytelnik zauwazyl istotna roznice pomiedzy maksymalnie rozpedzonym gazem
plynacym z predkoscia poddwiekowa i ruchem naddwiekowym w czesci rozbieznej
dyszy zachodzi pytanie o ruch w sytuacji gdy

. Jak mozna opisac wzrost

cisnienia w czesci rozbieznej? Jest potrzebny bo

. Wzrost ten dostosuje warunki

wyplywu do sytuacji panujacej w otoczeniu. Jesli za przewezeniem zaistnieje – nawet na
malym odcinku – ruch naddzwiekowy, to dalej wzdluz dyszy liczba macha rosnie a
cisnienie spada. Nie ma innej mozliwosci...

2

z

p

p p

<

2

z

p

p

>

Nie ma wtedy, gdy stosujemy teorje dyszy Lavala. Jakie zalozenia ruczywilismy?
Odmcilismy lepkosc i sile zewnetrzna. To sensowne, bo dysza jest krotka, a sily te nie
graja istotnej roli. Zachowana jest energia. To oczywiste, nie ma dostarczanego albo
odbiaracego ciepl, i nie ma wykazowanej / dostarczanej pracy.

Co jeszcze? Uzywamy hipotezy o izentropowosci. Ta hipoteza wynika z ciaglosci...
Czy moga pojawic sie nieciaglosci?

Wyobrazmy sobie znikoma sprezenie gazu. Cialo fali zgeszczenia (wywalanej
sprazenem) prusza sie z predkoscia dzwieku. Nastepnia znikome zageszczenie tworzy
fale pruszajaca sie w gazie juz nieco zageszczonym, a wiec o wyzszej temperaturze.

Predkosc rozchodzenia sie nastepnej fali zageszczenionej jest nieco wieksze, niz
predkosc fali poprzedniej.

Wnikoskujemy: fale zageszczeniowe dopedzaja sie. Co w rezultacie otrzymamy? Suma
zageszczen. Moze po dodaniu, skok gestosci bedzie mial znaczna amplituda? Nie ma
powodow, bo bylo inaczej. A wiec, moga pojawic sie nieciaglosci. Jest nieciaglosc
zaistnieje w plynacym gazie (preciwne skierowane predkosci) to nieciaglosc moze nie
premieszczac sie w inacjalnym ukladzie odwieszenia.

Rozwiamy nieciaglosc: to skok wartosci parametrow gazu. Zwiazamy uklad odniesienia
z ta nieciagloscia. Gaz przed nieciagloscia ma parametry z indeksem (1) a za
nieciagloscia dwojka. Jest zachowana masa, ped, i energia. Piszemy:

1 1

2 2

u

u

ρ

ρ

=

(1) zachowanie Masy

2

2

1 1

1

2 2

2

u

p

u

p

ρ

ρ

+

=

+

(2) zachowanie pedu

2

2

1

1

2

1

2

2

1

2

1

u

p

u

p

k

k

k

2

k

ρ

ρ

+

=

+

−

−

(3) zachowanie energii

Te trzy rownania pozwalaja uyznaczyc

2

2

2

,

,

u p

ρ

jesli sa znane

1

1

, ,

u p

1

ρ

.

Jedno (byc moze z wielu: rownania sa nieliniowe) rozwiazanie otrzymujemy
natychmiast: to Tautologia:

2

1

2

1

2

,

,

u

u p

p

1

ρ

ρ

=

=

=

. Taki wynik nie jest interesujacy:

brak nieciaglosci...
Sa inne rozwiazania. Jestli wyznaczymy je – to trzeba sprawdzic czy maja sens.
(Oczywiscie: musza byc rzeczywiste i dodatne). Sensowne sa te rozwiazania, ktore nie
sa sprzeczne z nieuwzglenionymi w rownaniach prawach fizyki..
Otoz – nasz uklad jest izolowany – bo energia jest stala. W ukladzie izolowanym
entropia

nie moze malec. Zbadamy przemiane termodynamiczna i wynikajaca z niej

zmiane entropii. Aby otrzymac odpowiedni zwiazek wyeliminujemy predkosci. Dzielac
rownianie (2) przez rownanie (1)

(

)

0

u

ρ

>

otrzymamy:

1

2

2

1

2

1

2

1 1

2 2

2 2

1 1

p

p

p

u

u

u

u

u

u

u

1

p

u

ρ

ρ

ρ

+

=

+

⇒ −

=

−

ρ

Trzecie rownanie mozna przepisac tak:

(

)(

)

2

1

1

2

1

2

2

1

2

1

p

p

k

u

u

u

u

k

ρ

ρ

⎛

⎞

−

+

=

−

⎜

⎟

− ⎝

⎠

Podstawiamy roznice predkoci i mnizymy przez

1

u

u

2

+ . Ale – na mocy rozwiazania (1)

mozna wymieniac

1 1

u

ρ

na

2 2

u

ρ

:

(

)

2

1

2

1

2

1

1

2

1

1

2

2

2 2

1 1

1 1

1 1

2 2

2 2

p

p

p

p

p

p

u

u

u

u

u

u

u

u

u

u

u

u

ρ

ρ

ρ

ρ

ρ

ρ

⎛

⎞

−

+

=

−

+

−

⎜

⎟

⎝

⎠

=

2

1

2

1

2

1

1

1

2

2

2

1

2

1

p

p

p

p

p

p

k

k

ρ

ρ

ρ

ρ

ρ

ρ

⎛

⎞

=

−

+

−

=

−

⎜

⎟

− ⎝

⎠

Podkreslone postac rowniania nie zawiera predkosci. Trzeba tylko doprowadzic je do

sensownej postaci. Chcemy wyzanczyc

2

1

p

p

z funkcji

2

1

ρ

ρ

- jak zwykle termodynamice.

Piszemy – po pomnozeniu przez

1

1

p

ρ

:

2

2

1

1

2

1

1

1

2

2

1

2

2

1

1

1

p

p

p

k

p

p

k

p

ρ

ρ

ρ

ρ

ρ

ρ

⎛

⎞

= − +

−

=

−

⎜

⎟

− ⎝

⎠

albo

1

1

2

2

2

1

2

2

1

1

1

1

p

k

k

k

p

k

1

2

ρ

ρ

ρ

ρ

ρ

ρ

⎛

⎞

−

−

=

− −

⎜

⎟

−

−

⎝

⎠

Obliczamy

2

1

p

p

:

1

2

2

2

1

2

1

2

1

1

1

1

1

1

1

1

1

1

1

k

k

p

k

k

k

k

p

k

k

1

ρ

ρ

ρ

ρ

ρ

ρ

ρ

ρ

+

+

−

−

−

−

=

=

+

+

−

−

−

−

zamapietamy:

2

2

1

2

1

1

1

1

1

1
1

k

p

k

k

p

k

ρ

ρ

ρ

ρ

+

−

−

=

+

−

−

Adiabata

Hugonita.

Poniewaz energia jest stala - to przemiana termodynamiczna opisana tym rownaniem jest

adiabatyczna

. Nazywamy ta adiabata Hugoniota. Jak widac, dla

( )

2

1

1

,

1

1

k

k

ρ

ρ

+

=

>

−

jest

asymptota pionowa. Oczywiscie, gdy

2

1

1

ρ

ρ

=

to

2

1

1

p

p

=

.

Napiszmy:

1

1

,

1

1

x

k

y

k

α

α

α

−

+

=

=

−

−

I znajdziemy pochodna dla x = 1. Prosty rachunek dla

1

1
1

x

y

k

α
α

=

+

′

=

=

−

. Izentropa to:

2

2

1

1

k

k

p

y

x

p

ρ

ρ

⎛

⎞

= =

=

⎜

⎟

⎝

⎠

Porownajmy te przemiany: izentropa nie ma asymptoty pionowej. Dla x = 1 pochodne sa
rowne. Czytelnik sprowadzi rownosc drugich pochodnych (gdy x = 1). Mowimy: dla

x=y=1

2

2

1

1

1

p

p

ρ

ρ

⎛

⎞

=

=

⎜

⎝

⎠

⎟ krzywe sa scisle styczne. A wiec z dokladnoscia trzeciego rzedu

jedna moze zastapic druga. (trzeciego rzedu wzgledem (x-1), tzn.

2

1

1

ρ

ρ

⎛

⎞

−

⎜

⎟

⎝

⎠

(

)

3

2

2

1

1

1

.

hug

izen

p

const x

p

ρ

ρ

−

=

−

+ ..

gdy x ≈ 1).

Przypominamy definicjie entropii wlasciwej:

1

1

1

1

Cp

p

ds

dq

di

dp

d

dp

T

T

R

ρ

ρ

⎛

⎞

⎛ ⎞

=

=

−

=

−

⎜

⎟

⎜ ⎟

⎝

⎠

⎝ ⎠

ρ

= .. wykonaj rachunki.. =

dp

d

Cp

Cv

p

ρ

ρ

−

.

Wynika stad:

2

1

2

2

1

1

ln

ln

k

s

s

p

s

Cp

Cp

p

ρ

ρ

⎛

⎞

⎛

⎞

−

Δ

=

=

−

⎜

⎟

⎜

⎟

⎝

⎠

⎝

⎠

Jesli ∆s > 0 to

2

2

1

1

k

p

p

ρ

ρ

⎛

⎞ ⎛

⎞

>

⎜

⎟ ⎜

⎟

⎝

⎠ ⎝

⎠

, a wiec tam, gdzie adiabata Hugoniota sytunje sie nad

izentropa – to mamy wzrost entropii. Jesli rozwiazac ta czesc wykresu ktora odpowiada

2

1

1

ρ

ρ

<

czyli rozprezaniu to ∆s < 0. Eliminujemy wiec „rozprezaniowa” czesc

otrzymanej przemiany.

Mamy dopuszalny obszar:

2

2

1

1

1,

1

p

p

ρ

ρ

≥

≥

.

Powtazamy: kryterium eliminuajcym jest II-a zasada termodynamiki. Zla rozprezania w
nieciaglosci entropia maleje. To niedopuszczalne. Nieciaglosc „rozwecheniowa” nie
moze istniec...
Zrekapitulujmy: w nieciaglosci rosnie masa wlasciwa i cisnienie, rosnie entropia.

Maleje predkosc (bo

1

2

1

2

u

u

ρ

ρ

=

i

2

u

u

1

< ). Poniewaz zachowana jest energia – to, przy

nadajacej predkosci – rosnie entalpia (i temperatura). Ale – entalpia calkowita i
temperatura calkowita pozostaje niezmienione.