Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

1

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Rozwi zywanie równa ró niczkowych zwyczajnych

Równaniem ró niczkowym zwyczajnym n-tego rz du b dziemy nazywa równanie postaci:

F x,y, dy

dt

, d

2

y

dx

2

, d

3

y

dx

3

, , d

n

y

dx

n

0

Ogólnie równanie takie mo e by spełnione przez wiele funkcji y (x ) — aby mo liwe było jednoznaczne wyznaczenie

rozwi zania konieczne jest podanie dodatkowych informacji — warto ci funkcji y (x) i ewentualnie jej pochodnych dla

jakiej warto ci x. Koniecznych b dzie n takich warto ci. Je li podano je wszystkie dla tego samego punktu x

0

to mamy

zagadnienie pocz tkowe, je li wchodzi w gr wi cej ni jedna warto x to zagadnienie takie nazywamy brzegowym.

Zazwyczaj w przypadku równa ró niczkowych zwyczajnych wy szych rz dów mo liwe jest dokonanie podstawienia

n –1 nowych zmiennych (za wy sze pochodne) i wówczas równanie wy szego rz du zostaje zamienione na układ n równa

rz du pierwszego. Dlatego te omawia si zwykle tylko metody rozwi zywania równa rz du pierwszego.

Rozwi zania numeryczne, które b dziemy otrzymywa nie b d oczywi cie w postaci funkcji analitycznych — b d

to warto ci zbli one do warto ci rozwi zania obliczone dla pewnej sko czonej liczby punktów x

i

. Odległo ci pomi dzy

dwoma s siednimi punktami b dziemy oznacza przez h (na razie zakładamy, e s one stałe, mo liwo zmiany kroku

b dzie omawiana oddzielnie).

Zagadnienia pocz tkowe

Rozwini cie w szereg Taylora

Jedn z metod rozwi zywania równa ró niczkowych zwyczajnych postaci

jest wyra enie

dy dx

f x,y

rozwi zania y (x) w postaci szeregu Taylora w otoczeniu punktu x

0

:

y x

0

h

y x

0

h f x

0

,y x

0

h

2

2!

f x

0

,y x

0

h

3

3!

f x

0

,y x

0

Je li jako warunek pocz tkowy podano y (x

0

) to f (x

0

,y (x

0

)) otrzymamy bezpo rednio z równania ró niczkowego, a

pozostałe pochodne mo na wyliczy . Po dan ilo wyrazów nale y wstawi do badanego równania i scałkowa . Niestety

w ogólnym przypadku obliczenia kolejnych pochodnych staj si zbyt skomplikowane.

Metoda Eulera

Jest to najprostsza (w swej klasycznej postaci) z metod numerycznych. Odpowiada ona rozwi zaniu za pomoc

rozwini cia w szereg Taylora, w którym zachowano tylko pierwsze pochodne. Rozwi zywane równanie ró niczkowe

przekształcimy do postaci:

dy

dx

f x,y

i zało ymy, e podano nam pocz tkow warto funkcji y

0

(x

0

).

Działanie metod Eulera (podstawowej i jej obu modyfikacji) b dzie ilustrowane na dwóch przykładowych równaniach

ró niczkowych:

dy
dx

y

2x

y

i

dy
dx

x

y

Równania te b d rozwi ywane wszystkimi trzema metodami w przedziale <0,1>, dla warunku pocz tkowego y(0) = 1

i z trzena ró nymi krokami h wynosz cymi 0.2, 0.1 i 0.05.

Klasyczna metoda Eulera

Mo emy zastosowa nast puj cy algorytm:

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

2

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

1

y x

0

h f x

0

,y x

0

y

i 1

y

i

h f x

i

,y

i

i >0

za pomoc którego wychodz c od znanych warto ci pocz tkowych x

0

,y

0

mo na obliczy kolejno warto ci szukanej funkcji

we wszystkich dalszych punktach x

i

. Mo na udowodni , e bł d (zdefiniowany jako ró nica rozwi zania analitycznego

i obliczonych warto ci przybli onych) d y do zera dla h d

cego do zera. Metoda Eulera jest metod zbie n o

dokładno ci rz du O(h) (chodzi tu o bł d globalny — tzn. po przej ciu wszystkich kroków — bł d lokalny —

odpowiadaj cy przej ciu od jednej warto ci do s siedniej — jest rz du O(h

2

)).

Zmodyfikowane metody Eulera

Pierwsza modyfikacja metody Eulera polega na obliczeniu najpierw warto ci po rednich:

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

3

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

x

i

1
2

x

i

h
2

y

i

1
2

y

i

h
2

f x

i

,y

i

f

i

1
2

f x

i

1
2

,y

i

1
2

a nast pnie wykorzystaniu ich do obliczenia kolejnej warto ci y

i+1

:

y

i 1

y

i

h f

i

1
2

Druga modyfikacja metody Eulera (zwana te metod Heuna) polega na obliczeniu najpierw warto ci „wst pnie

przybli onych”:

y

i 1

y

i

h f x

i

,y

i

f

i 1

f x

i 1

,y

i 1

po czym oblicza si warto ci y

i+1

:

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

4

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

i 1

y

i

h

f

i

f

i 1

2

W obu modyfikacjach odrzucona reszta rozwini cia w szereg Taylora jest rz du O(h

3

) (jest to bł d lokalny — tzn.

odpowiadaj cy przej ciu pomi dzy dwiema kolejnymi warto ciami przybli enia).

W praktyce przyjmuje si , e bł d uzyskanego rozwi zania jest równy ró nicy pomi dzy rozwa anym rozwi zaniem,

a innym rozwi zaniem tego samego zagadnienia otrzymanym dla dwa razy wi kszego kroku h.

Bł d rozwi zania mo na te szacowa na podstawie tzw.

kryterium Rungego — wynosi on ró nicy rozwa anego

rozwi zania i rozwi zania otrzymanego dla kroku dwukrotnie wi kszego.

Porównanie metod Eulera

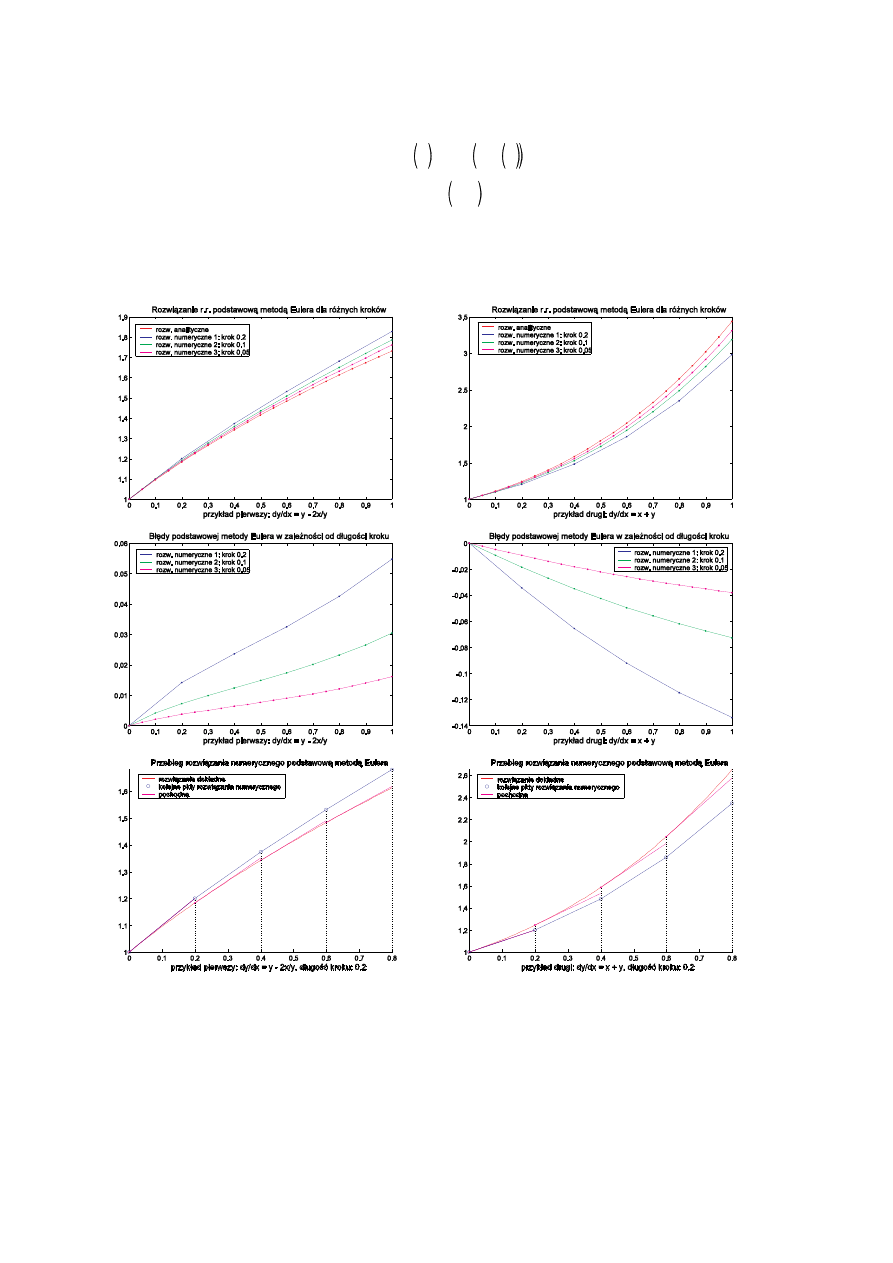
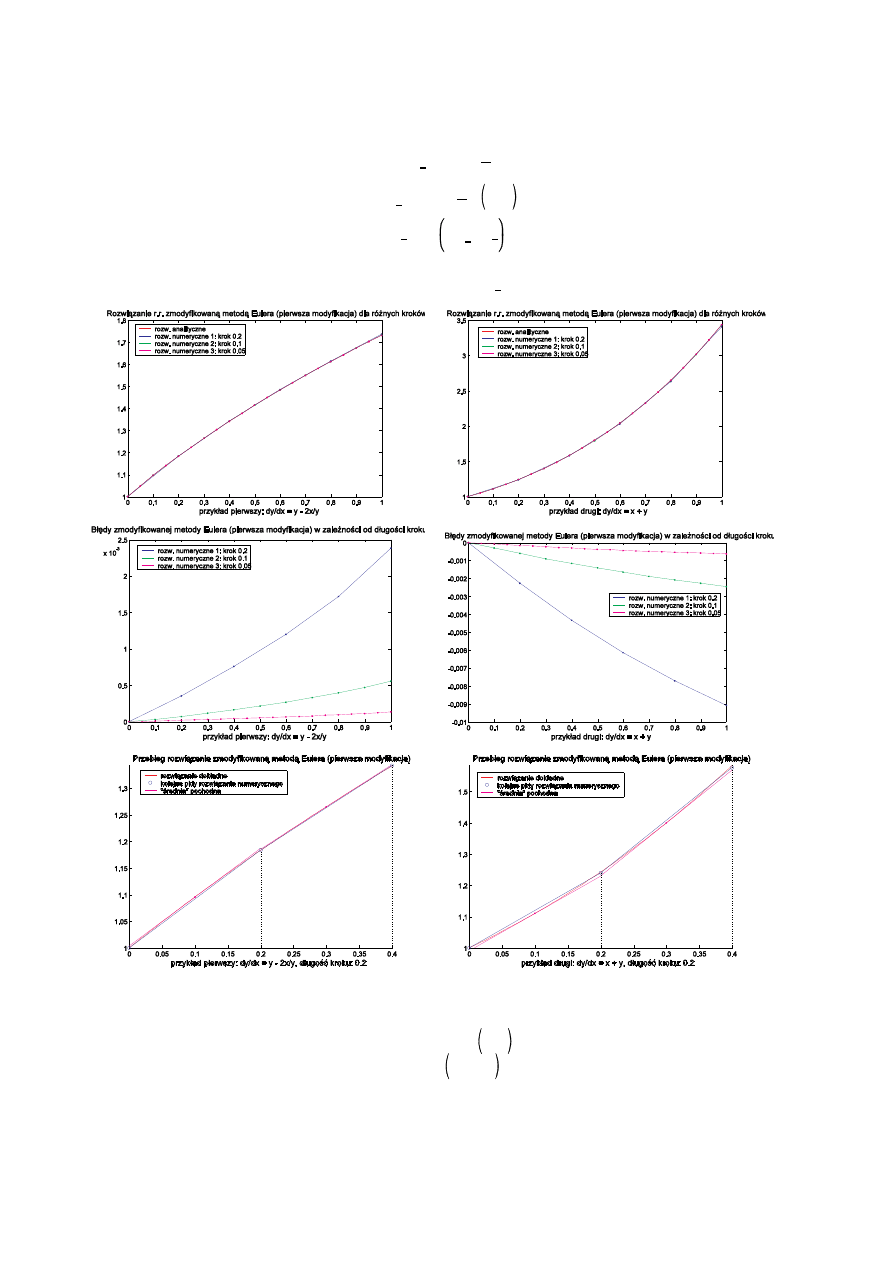
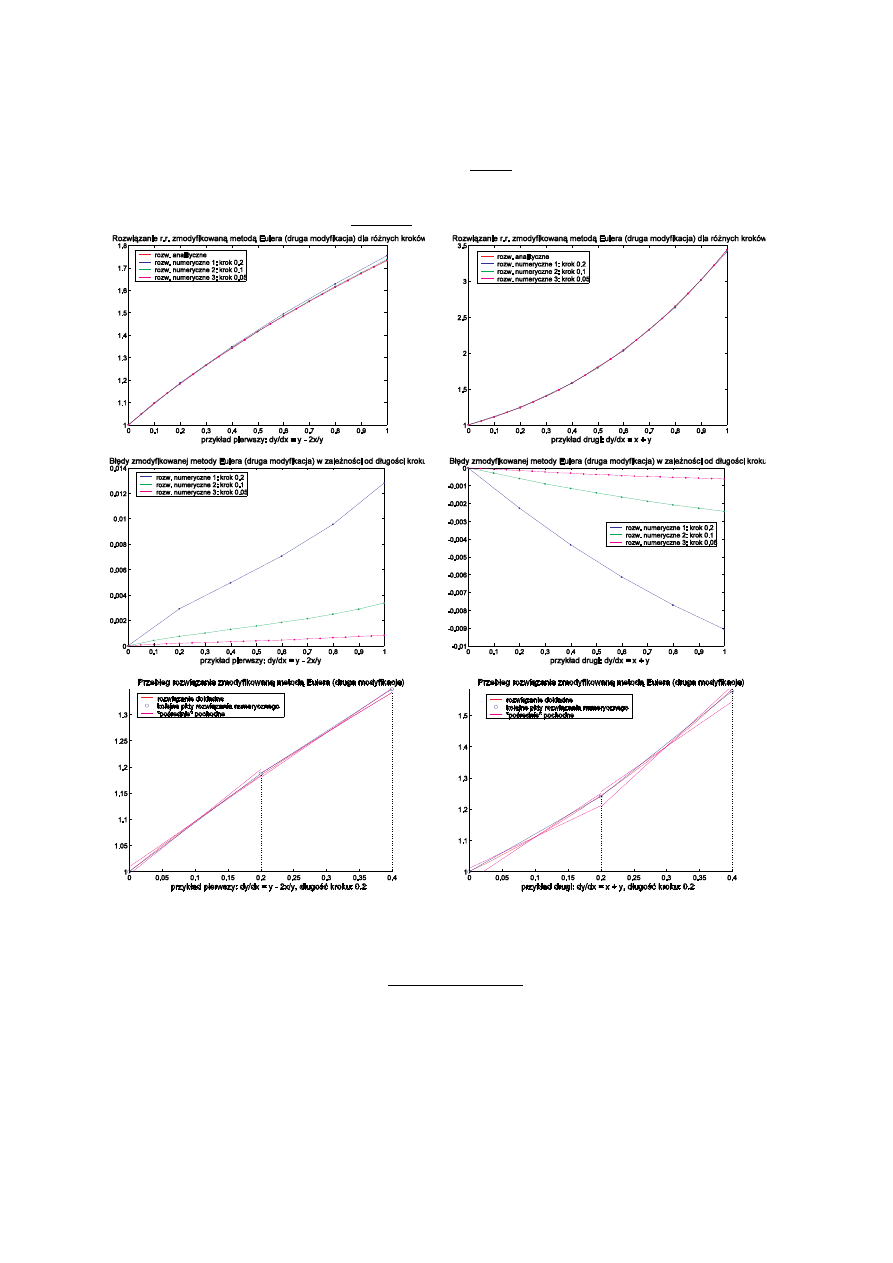
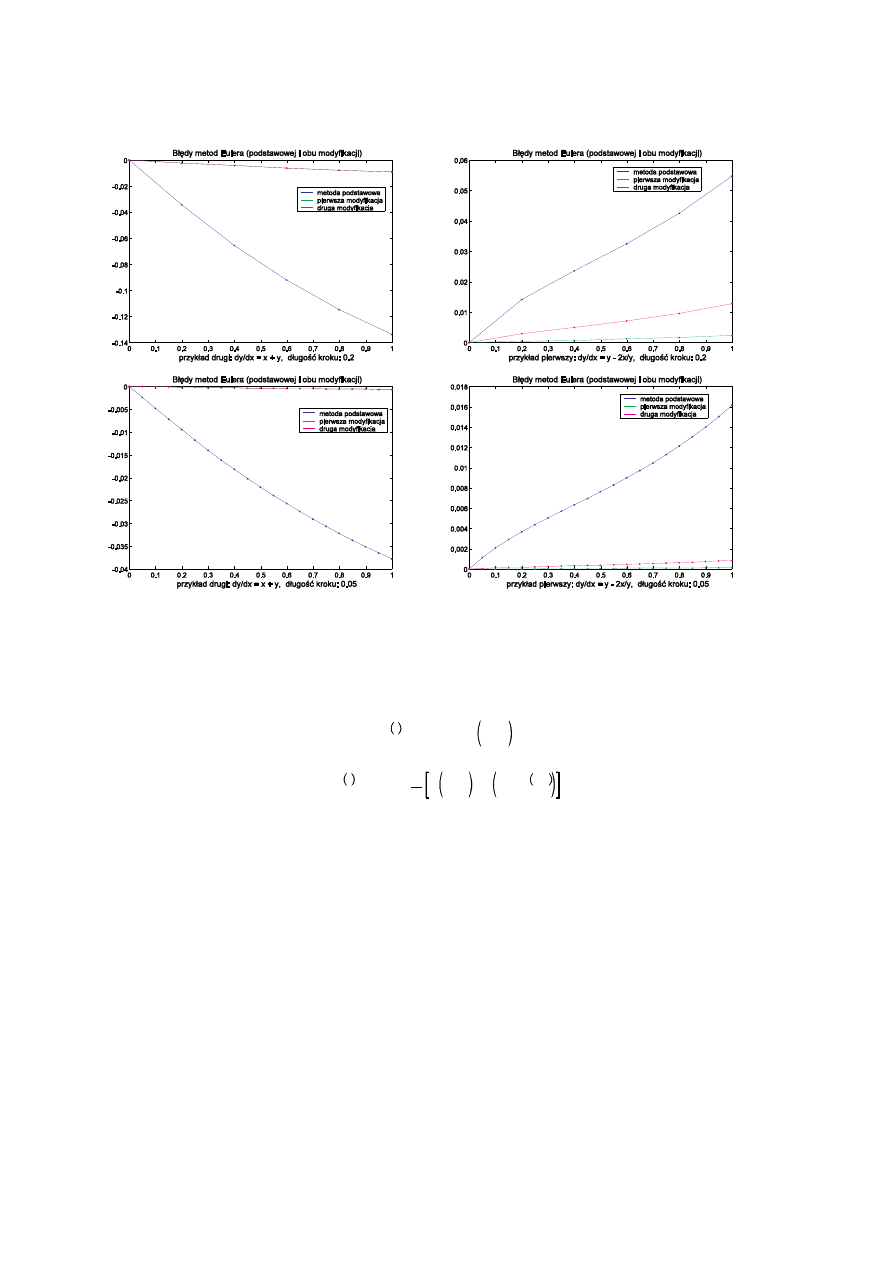
Poni ej znajduj si wykresy przedstawiaj ce rozwi zania oraz warto ci bł dów rozwi za otrzymanych

poszczególnymi metodami dla ró nych długo ci kroków.

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

5

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Jak wida nie mo na jednoznacznie stwierdzi , która z modyfikacji metody Eulera jest lepsza — zale y to od

konkretnego rozwi zywanego zagadnienia.

Metoda Eulera z iteracj

Metod Eulera mo na udokładni stosuj c dla ka dej obliczonej warto ci y

i

dodatkowo proces iteracyjny. Traktuj c

warto obliczon klasyczn metod Eulera jako zerowe przybli enie:

y

0

i 1

y

i

h f x

i

,y

i

zastosujemy nast puj cy proces iteracyjny:

y

k

i 1

y

i

h
2

f x

i

,y

i

f x

i 1

,y

k 1

i 1

który b dzie powtarzany, a dwa kolejne wyniki b d zgodne z zadan ilo ci cyfr znacz cych, wtedy ostatni z nich

przyjmiemy za y

i+1

.

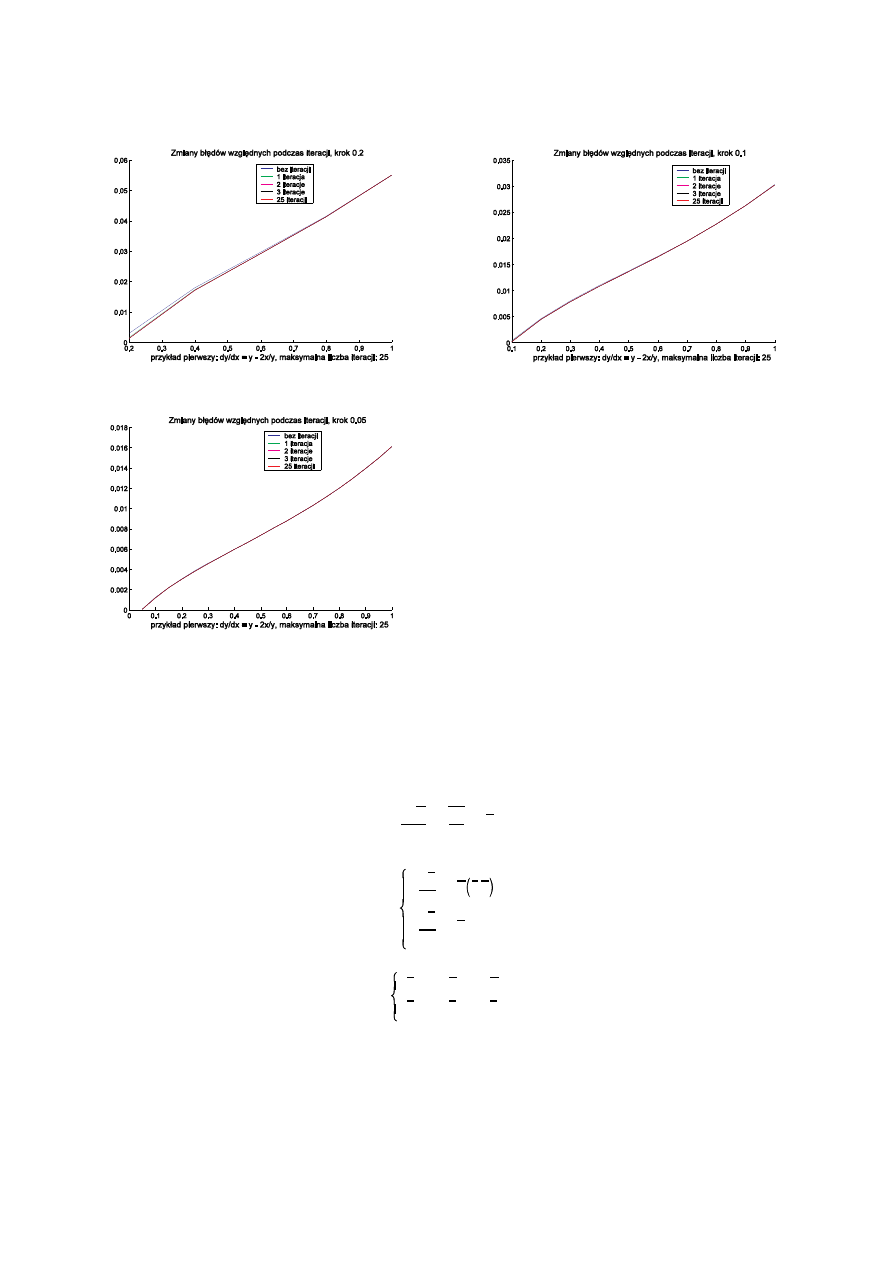
Zazwyczaj proces taki jest szybkozbie ny (tzn. zadowalaj cy wynik powini my otrzyma ju po kilku iteracjach) —

je li po 3-4 iteracjach nie uzyskujemy zbie no ci nale y zmniejszy krok h.

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

6

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Rozwi zywanie równa ruchu

Bardzo cz stym przypadkiem jest rozwi zywanie równa ruchu (dla jednego lub bardzo wielu ciał) — s to oczywi cie

równania drugiego rz du. Ka de takie równanie (drugiego rz du) mo na zapisa jako układ dwóch równa pierwszego

rz du. Poni sze równania zostały zapisane wektorowo — z punktu widzenia rozwi zania numerycznego liczba

wyst puj cych w problemie wymiarów sprowadza si do wymiaru tablic wykorzystywanych do przechowywania

rozwi zania.

Podstawow posta równania ruchu:

d

2

R

dt

2

F

m

a

Przepiszemy w nieco innej postaci:

dv

dt

a r,v

dr

dt

v

Typowy algorytm Eulera b dzie mie wówczas tak posta :

v

i 1

v

i

a

i

r

i 1

r

i

v

i

Algorytm Eulera-Cromera

Pewn modyfikacj algorytmu Eulera jest algorytm nazywany algorytmem Eulera-Cromera. Modyfikacja polega na tym,

e do obliczenia kolejnej warto ci poło enia wykorzystuje si obliczon przed chwil warto pr dko ci:

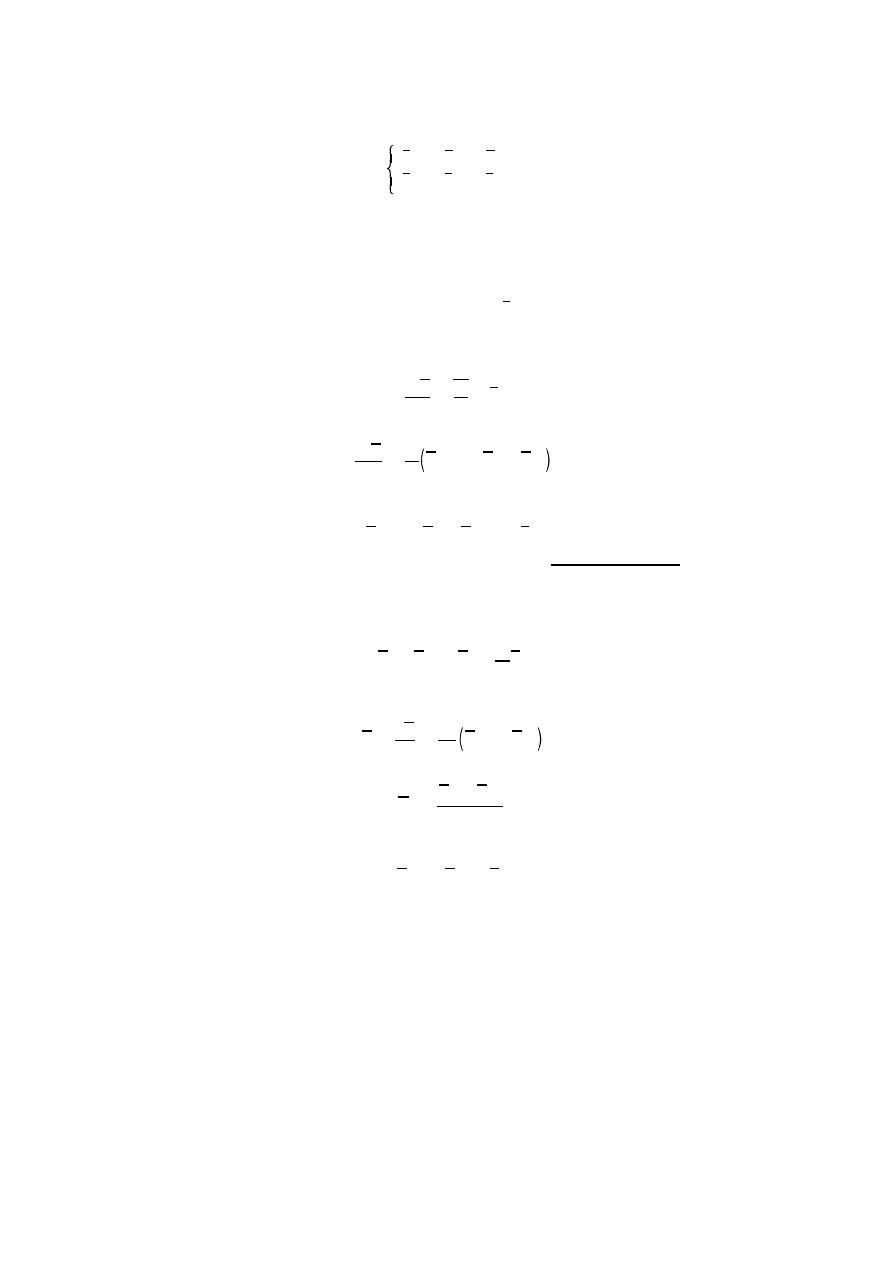
Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

7

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

v

i 1

v

i

a

i

r

i 1

r

i

v

i 1

Jest to bardzo niewielka zmiana (co do zasady identyczna z modyfikacj Seidla, któr poznali my w przypadku układów

równa ), jednak w wi kszo ci przypadków algorytm Eulera-Cromera zdecydowanie góruje nad typowym algorytmem

Eulera.

Algorytm Verlet’a

Załó my, e mamy do rozwi zania równanie ruchu (albo równania — dla wielu ciał). Poniewa jest to równanie 2-go

stopnia rozwi zujemy je jako układ dwóch równa rz du pierwszego. Je li interesuje nas przede wszystkim trajektoria

ciała, to mo na byłoby twierdzi , e rozwi zanie pierwszego z równa — daj ce pr dko — jest dla nas strat czasu.

W sytuacji takiej zastosowanie znajduje algorytm Verlet’a.

Jeszcze raz równanie ruchu:

d 2

R

dt

2

F

m

a

Drug pochodn zapiszemy w postaci ró nicowej:

d

2

R

dt

2

1

2

R

n 1

2R

n

R

n 1

gdzie n oznacza numer kolejny kroku czasowego, a jest jego długo ci .

Proste przekształcenie doprowadza nas do:

R

n 1

2R

n

R

n 1

2

a

n

Jak wida z wzoru na R

n+1

do „uruchomienia” tego algorytmu potrzebne s dwie kolejne warto ci pocz tkowe poło e .

W problemach fizycznych z jakimi mo emy si spotka , zazwyczaj b dziemy zna tylko jedn warto poło enia — w

chwili pocz tkowej i odpowiadaj c jej warto pr dko ci. Dla „uruchomienia algorytmu konieczne b dzie

„wygenerowanie” drugiej potrzebnej warto ci — najpro ciej mo na to zrobi zakładaj c stało przyspieszenia w

pierwszym odcinku czasu . W takim przypadku warto R

1

b dzie taka jak dla ruchu jednostajnie przyspieszonego:

R

1

R

0

V

0

2

2

a

0

Gdyby potrzebna była równie pr dko cz stki to j równie mo emy zapisa w postaci ró nicowej (skorzystamy

z wzoru centralnego):

V

dR

dt

1

2

R

n 1

R

n 1

sk d otrzymamy:

V

n

R

n 1

R

n 1

2

Jak wida wzór ten mo e w pewnych sytuacjach by „niepor czny” — obliczana pr dko jest „opó niona” w

stosunku do poło enia o jeden krok czasowy. Mo na temu zaradzi obliczaj c j wprost z działaj cej siły:

V

n 1

V

n

a

n

znacznie dokładniejsze wyniki uzyskamy wykorzystuj c do oblicze zamiast a

n

redni wyznaczon z a

n

i a

n+1

(a

n+1

b dziemy zna bo „przed chwil ” obliczyli my poło enie R

n+1

).

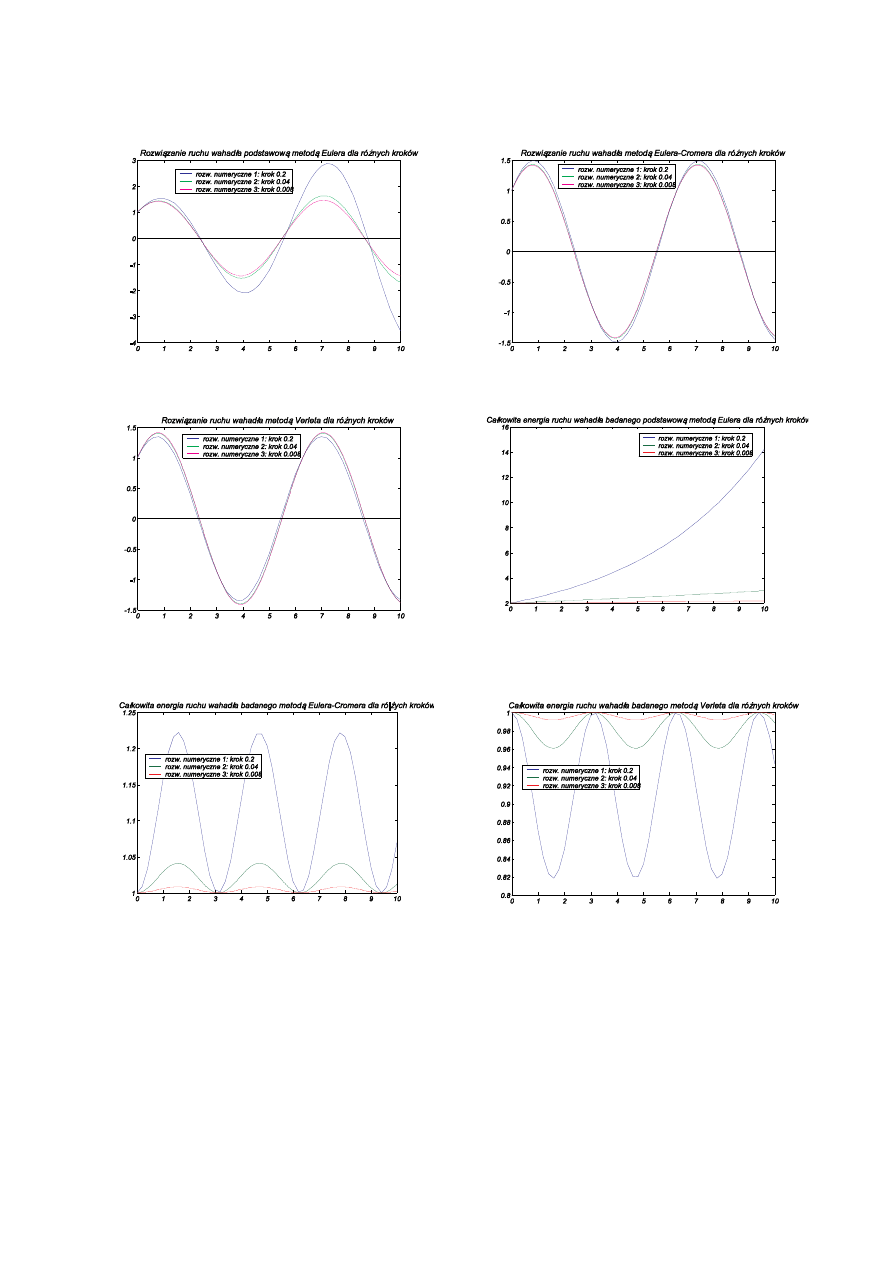
Poni ej przedstawiono rozwi zania prostego zagadnienia: harmonicznego ruchu wahadła bez oporów, tłumienia i

wymuszenia. Dragj ca masa jest jednostkowa, współczynnik spr ysto ci te jest jednostkowy.

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

8

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

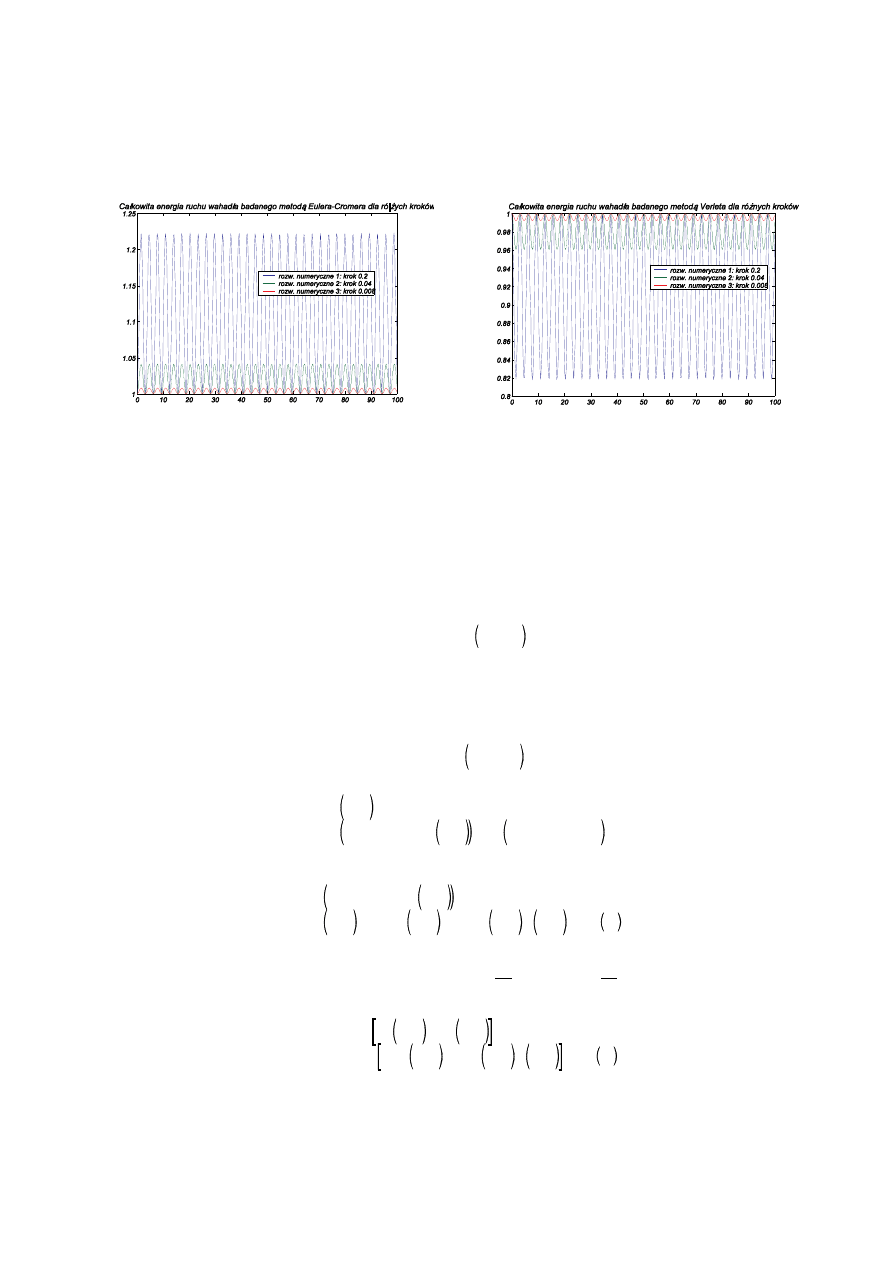
Pierwsze trzy rysunki przedstawiaj wykres poło enia drgaj cej masy w funkcji czasu. W przypadku podstawowej

metody Eulera ju „na oko” wida , e wyniki s złe — wiemy, e energia, a co za tym idzie i amplituda, opisywanego

układu powinny by stałe. Jednak wybór której z pozostałych dwóch metod mo e by trudny. Aby lepiej je oceni

wyznaczymy całkowit energi układu i zbadamy jej zmiany z czasem. Przy rzyj tych parametrach (jednostkowa masa

i współczynik spr ysto ci) całkowita energia wynikaj ca z warunków pocz tkowych równie jest jednostkowa. Fakt, e

energia ta ewidentnie nie jest stała podczas trwania ruchu, nie musi od razu dyskwalifikowa metody — ze wzgl du na

ró nego rodzaju bł dy nie mo emy oczekiwa rzeczywistej stało ci całkowitej energii — decyduj cym kryterium b dzie

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

9

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

to czy obliczona energia całkowita waha si w ograniczonym zakresie czy te amplituda jej waha wzrasta. Oczywi cie

celem wyboru metody nale ałoby sporz dzi te wykresy dla du o dłu szego czasu — poni ej czas przedłu ono

dziesi ciokrotnie:

Metody Rungego-Kutty

Metod Eulera otrzymujemy dzi ki rozwini ciu szukanej funkcji w szereg Taylora i odrzuceniu wyrazów

zawieraj cych pochodne rz du wy szego ni pierwszy — bł d lokalny jest wówczas rz du O(h

2

). Zachowanie wy szych

pochodnych jest mo liwe tylko dla bardzo szczególnych postaci równa , w ogólnym przypadku b d one zbyt

skomplikowane. Mo liwe jest jednak stworzenie metody jednokrokowej (tzn. wymagaj cej znajomo ci tylko jednego

wcze niejszego punktu) o dokładno ci lokalnej wy szego rz du. S to metody Rungego-Kutty.

Ogólnie algorytm metod Rungego-Kutty jest nast puj cy:

y

i 1

y

i

h

x

i

,y

i

,h

funkcja (x,y,h) jest odpowiednio dobran aproksymacj funkcji f (x,y ) na przedziale (x

i

,x

i+1

).

Metoda Rungego-Kutty rz du drugiego

Załó my, e funkcj (x,y,h ) zdefiniujemy jako redni z dwóch przybli e pochodnej f (x,y ), oznaczymy je przez

k

1

i k

2

: (x,y,h) = ak

1

+ bk

2

. Wówczas algorytm Rungego-Kutty (drugiego rz du) b dzie mie posta :

y

i 1

y

i

h ak

1

bk

2

Załó my dalej, e:

k

1

f x

i

,y

i

k

2

f x

i

ph,y

i

qhf x

i

,y

i

f x

i

ph,y

i

qhk

1

gdzie p i q s stałymi, które wyznaczymy pó niej.

Rozwi my k

2

w szereg Taylora opuszczaj c wszystkie wyrazy zawieraj ce pot gi h wy sze ni pierwsza:

k

2

f x

i

ph,y

i

qhf x

i

,y

i

f x

i

,y

i

phf

x

x

i

,y

i

qhf x

i

,y

i

f

y

x

i

,y

i

O h

2

Szereg Taylora dla funkcji dwóch zmiennych:

f (x r,y s)

f (x,y)

rf

x

sf

y

r

2

2

f

xx

rsf

xy

s

2

2

f

yy

Podstawiaj c definicj k

1

i rozwini cie k

2

do algorytmu otrzymamy:

y

i 1

y

i

h af x

i

,y

i

bf x

i

,y

i

h

2

bpf

x

x

i

,y

i

bqf x

i

,y

i

f

y

x

i

,y

i

O h

3

Nast pnie rozwiniemy w szereg Taylora funkcj b d c rozwi zaniem dokładnym:

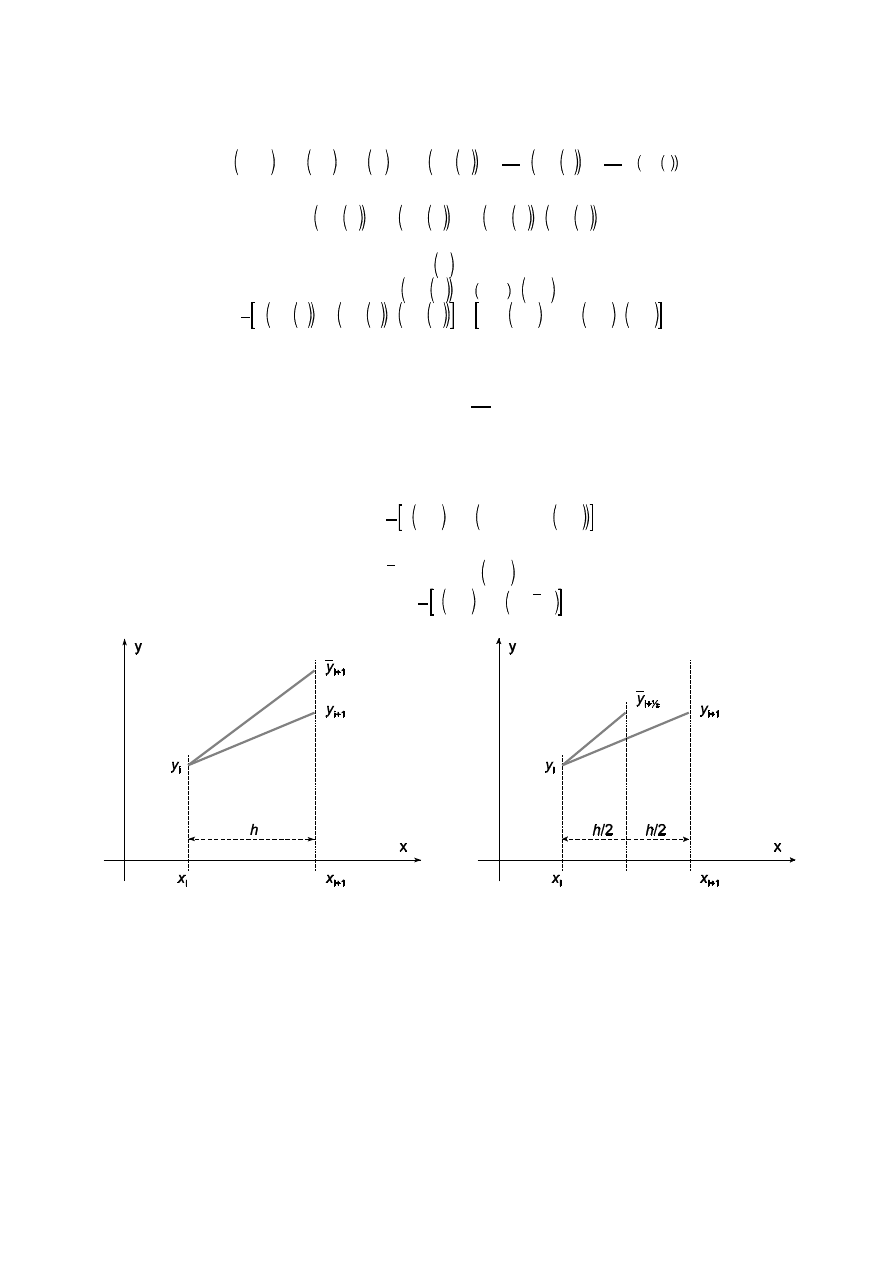
Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

10

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y x

i

h

y x

i 1

y x

i

hf x

i

,y x

i

h

2

2

f x

i

,y x

i

h

3

3!

f

,y

gdzie jest liczb z przedziału (x

i

,x

i+1

). Pochodna f (x

i

,y(x

i

)):

f x

i

,y x

i

f

x

x

i

,y x

i

f

y

x

i

,y x

i

f x

i

,y x

i

Je li teraz za damy, aby współczynniki przy odpowiednich pot gach h były równe to otrzymamy:

y x

i

y

i

f x

i

,y x

i

a b f x

i

,y

i

1
2

f

x

x

i

,y x

i

f

y

x

i

,y x

i

f x

i

,y x

i

bpf

x

x

i

,y

i

bqf

y

x

i

,y

i

f x

i

,y

i

Je li zało ymy y

i

= y (x

i

) i za damy, aby dla wszystkich funkcji współczynniki przy h

2

były równe otrzymamy

a + b = 1, bp = ½ oraz bq = ½, a zatem:

a

1

b

p

q

1

2b

Poniewa mamy tylko trzy równania, a cztery niewiadome, mo emy jedn z nich wybra dowolnie, najcz ciej

przyjmuje si b = ½ albo b = 1.

W przypadku b = ½ otrzymamy a = ½, p = 1 i q = 1. Algorytm b dzie mie wówczas posta :

y

i 1

y

i

h
2

f x

i

,y

i

f x

i

h,y

i

hf x

i

,y

i

co mo na zapisa równie w postaci:

y

i 1

y

i

hf x

i

,y

i

y

i 1

y

i

h
2

f x

i

,y

i

f x

i 1

,y

i 1

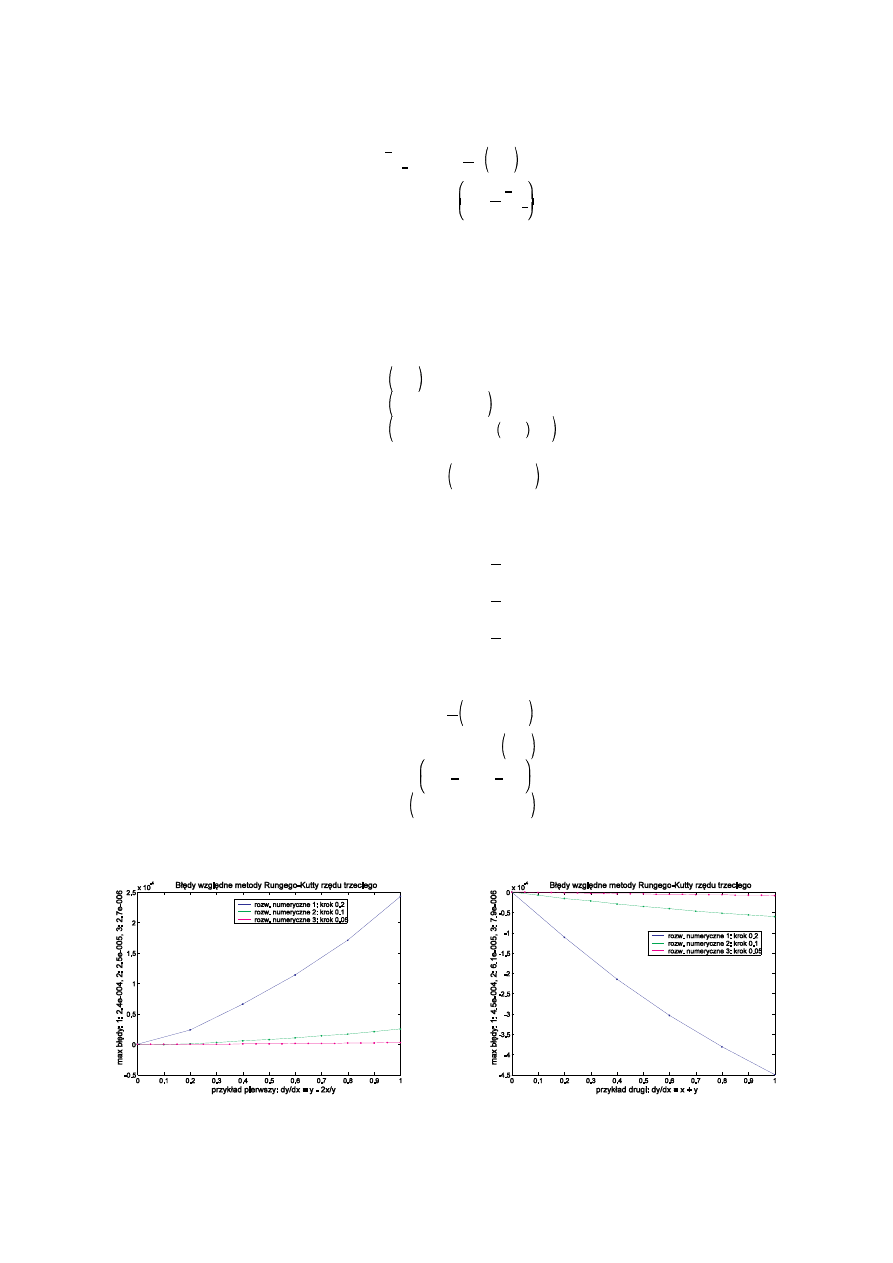
Jest to metoda identyczna z podan wcze niej drug modyfikacj metody Eulera. Metody tego typu nazywane s

metodami predyktor-korektor, poniewa najpierw za pomoc metody daj cej gorsze przybli enie przewidujemy warto

y

i+1

(jest to warto jak y

i+1

miałoby gdyby nachylenie (pochodna) wynosiło k

1

), a nast pnie uzyskujemy skorygowan

warto y

i+1

(jako redni wa on z warto ci f na obu ko cach przedziału (x

i

,x

i+1

). Metoda ta jest znana równie pod nazw

metody Heuna. Ilustruje j lewy rysunek powy ej.

Dla b = 1 otrzymamy a = 0, p = ½ i q = ½ i algorytm przyjmie posta :

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

11

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

i

1
2

y

i

h
2

f x

i

,y

i

y

i 1

y

i

hf x

i

h
2

,y

i

1
2

Ten algorytm z kolei odpowiada przedstawionej ju pierwszej modyfikacji metody Eulera. Najpierw za pomoc

normalnej metody Eulera otrzymujemy warto y w połowie przedziału (x

i

,x

i+1

), a nast pnie znajdujemy warto f w tym

punkcie i wykorzystujemy j do obliczenia y na ko cu przedziału. Ilustruje to prawy rysunek powy ej.

Metoda Rungego-Kutty rz du trzeciego

Metody Rungego-Kutty wy szych rz dów wyprowadza si analogicznie. Dla metody rz du trzeciego funkcja ma

posta : = ak

1

+ bk

2

+ ck

3

, gdzie k

1

, k

2

i k

3

s przybli eniami warto ci pochodnej w ró nych punktach wewn trz przedziału

(x

i

,x

i+1

):

k

1

f x

i

,y

i

k

2

f x

i

ph,y

i

phk

1

k

3

f x

i

rh,y

i

shk

2

r s hk

1

Algorytm jest wi c dany wzorem:

y

i 1

y

i

h ak

1

bk

2

ck

3

Aby wyznaczy stałe a, b, c, p, r i s rozwijamy k

2

i k

3

oraz funkcj y w szeregi Taylora wokół punktu (x

i

,y

i

) odrzucaj c

wyrazy zawieraj ce pot gi h wy sze ni trzecia i przyrównujemy odpowiednie wyrazy. Otrzymamy układ równa :

a

b

c

1

bp

cr

1
2

bp

2

cr

2

1
3

cps

1
6

Dwie z tych stałych mo na przyj dowolnie. Kutta dokonał wyboru, przy którym algorytm dla metody trzeciego rz du

jest nast puj cy:

y

i 1

y

i

h
6

k

1

4k

2

k

3

k

1

f x

i

,y

i

k

2

f x

i

1
2

h,y

i

1
2

hk

1

k

3

f x

i

h,y

i

2hk

2

hk

1

W powy szych wzorach przyj to a = c = 1/6, b = 4/6, p = ½, r = 1 i s = 2.

Poni ej przedstawiam bł dy metody Runge-Kutty trzeciego rz du zastosowanej do identycznych jak poprzednio dwóch

równa przykładowych:

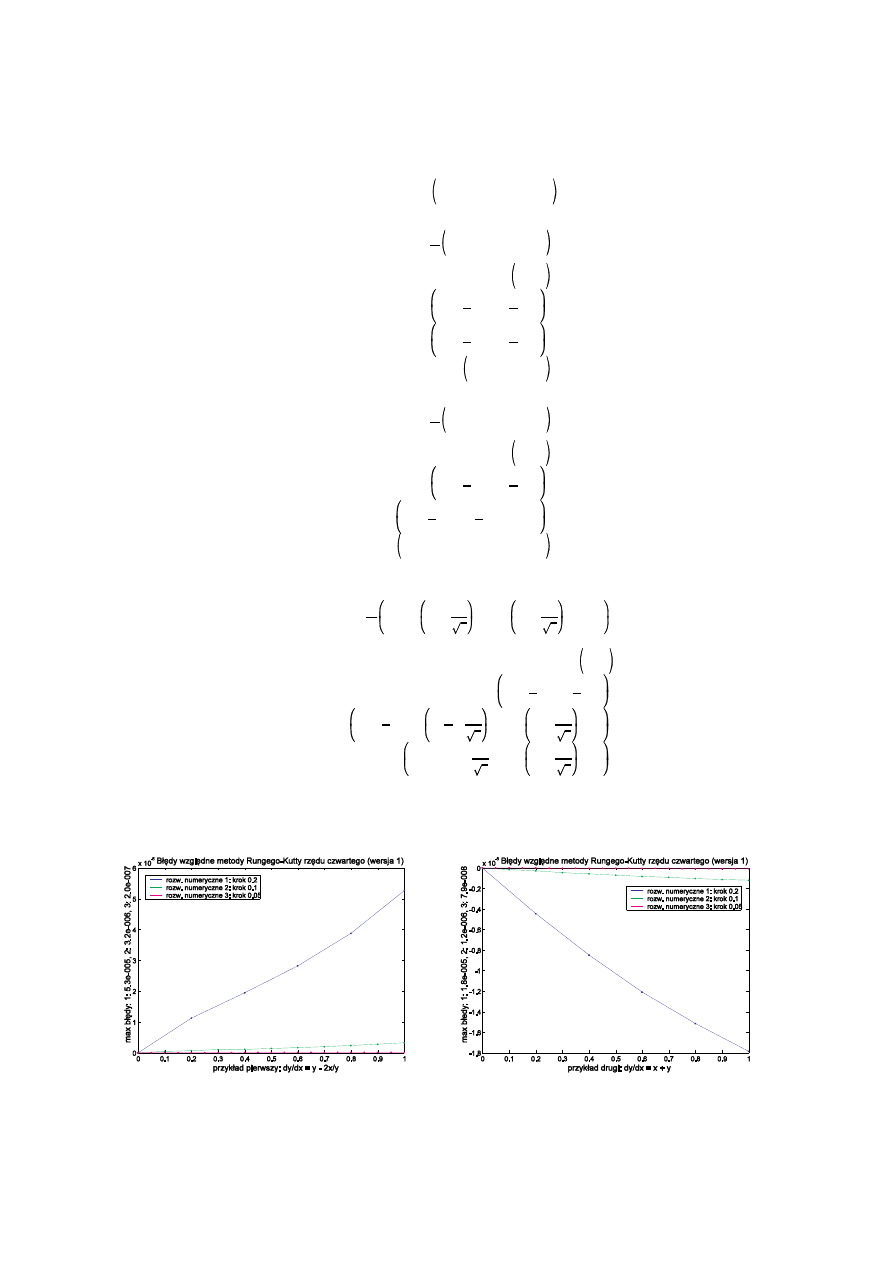
Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

12

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Metoda Rungego-Kutty rz du czwartego

Algorytm metod rz du czwartego jest oczywi cie nast puj cy:

y

i 1

y

i

h ak

1

bk

2

ck

3

dk

4

U ywanych jest kilka algorytmów, autorem dwu poni szych jest Kutta:

y

i 1

y

i

h
6

k

1

2k

2

2k

3

k

4

k

1

f x

i

,y

i

k

2

f x

i

1
2

h,y

i

1
2

hk

1

k

3

f x

i

1
2

h,y

i

1
2

hk

2

k

4

f x

i

h,y

i

hk

3

albo

y

i 1

y

i

h
8

k

1

3k

2

3k

3

k

4

k

1

f x

i

,y

i

k

2

f x

i

1
3

h,y

i

1
3

hk

1

k

3

f x

i

2
3

h,y

i

1
3

hk

1

hk

2

k

4

f x

i

h,y

i

hk

1

hk

2

hk

3

Jednak najcz ciej wykorzystywan metod czwartego rz du jest metoda Gilla:

y

i 1

y

i

h
6

k

1

2 1

1

2

k

2

2 1

1

2

k

3

k

4

k

1

f x

i

,y

i

k

2

f x

i

1
2

h,y

i

1
2

hk

1

k

3

f x

i

1
2

h,y

i

1
2

1

2

hk

1

1

1

2

hk

2

k

4

f x

i

, h,y

i

1

2

hk

2

1

1

2

hk

3

Poni ej przedstawiam bł dy metody Runge-Kutty czwartego rz du zastosowanej do identycznych jak poprzednio

dwóch równa :

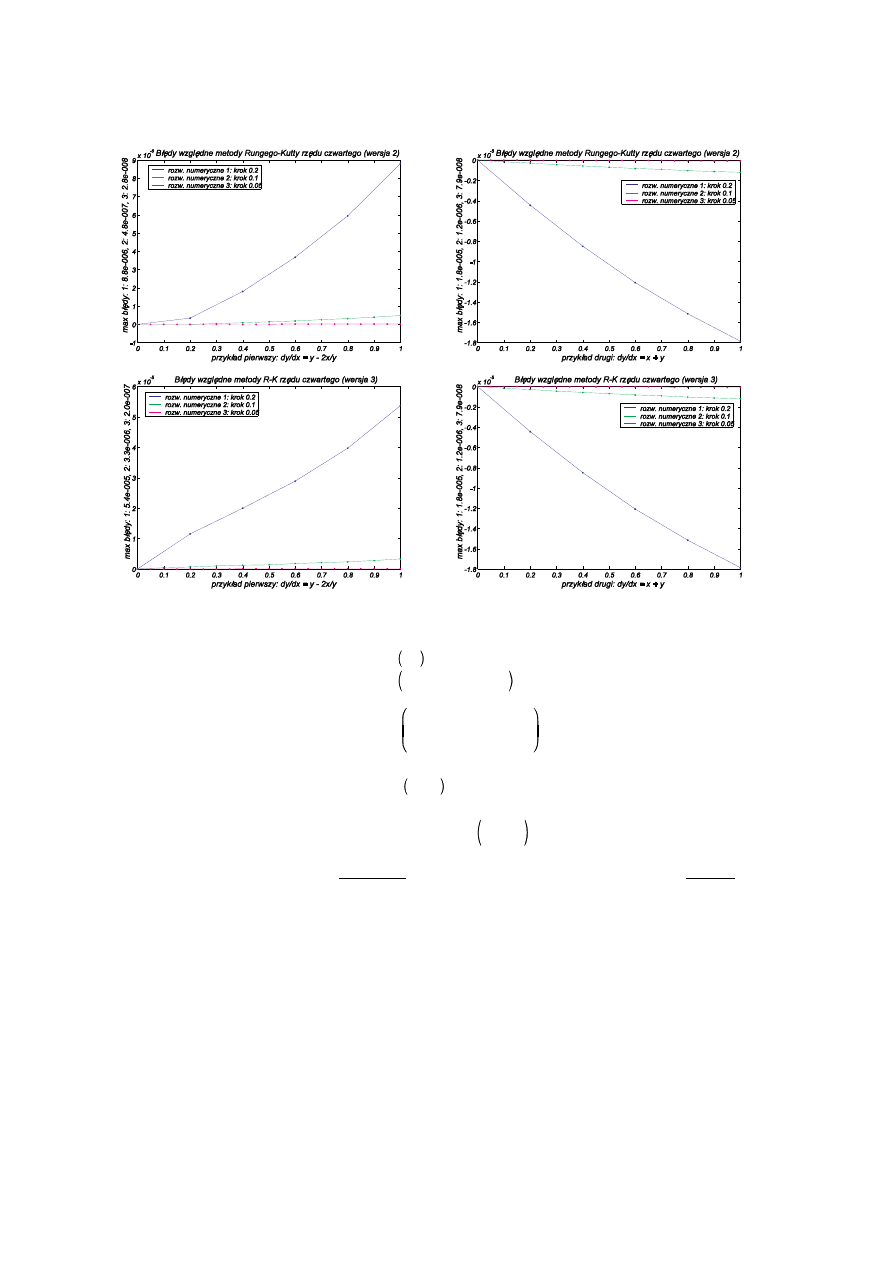
Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

13

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

k

1

f x,y

k

2

f x c

2

h, y ha

2,1

k

1

k

s

f x c

s

h, y h

s 1

j 1

a

s,j

k

j

x,y,h

s

i 1

b

i

k

i

y

k 1

y

k

h

x

k

,y

k

,h

Ogólny schemat metod Runge-Kutta

Ogólny wzór podany przez Rungego:

Odnosi si on w gruncie rzeczy do wszystkich metod Runge-Kutta. Indeks s odpowiada tu rz dowi metody. W

literaturze mo na spotka taki zapis zmiennych wyst puj cych w tym schmacie:

0

c

2

a

2,1

c

3

a

3,1

a

3,2

c

s

a

s,1

a

s,2

a

s,s 1

b

1

b

2

b

s 1

b

s

Ogólnie rzecz bior c podczas „własnor cznego” tworzenia jakiego schematu tego typu potrzebne b d rozwini cia

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

14

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

f x

1

,x

2

, ,x

n

f a

1

,a

2

, ,a

n

n

i 1

f

x

i a

1

,a

2

, ,a

n

x

i

a

i

1

2!

n

i 1

n

j 1

2

f

x

i

x

j a

1

,a

2

, ,a

n

x

i

a

i

x

j

a

j

R

m

x

1

,x

2

, ,x

n

Taylora funkcji kilku zmiennych. Ogólny wzór na takie rozwini cie funkcji f w pobli u punktu a jest nast puj cy:

Bł dy metod Rungego-Kutty

Ogólnie bł d w metodach Rungego-Kutty mo na okre li nast puj co. Załó my, e bł d zdefiniujemy jako ró nic

pomi dzy warto ci rozwi zania analitycznego y (gdyby było znane), a warto ci otrzyman przy kroku h

1

lub h

2

w

wyniku scałkowania równania na przedziale (x

i

,x

i+1

):

1

y

y

1

m

h

m 1

1

x

i 1

x

i

h

1

2

y

y

2

m

h

m 1

2

x

i 1

x

i

h

2

Dziel c oba powy sze równania stronami otrzymamy:

y

y

1

y

2

h

1

h

2

m

1

h

1

h

2

m

co dla h

2

= h

1

/2 przechodzi w:

y

y

1

2

m

y

2

1 2

m

Podstawiaj c t warto do pierwszego lub drugiego wyra enia na bł d otrzymamy:

1

2

m

y

2

y

1

2

m

1

2

y

2

y

1

2

m

1

gdzie m jest rz dem metody, a y

1

i y

2

s warto ciami otrzymanymi odpowiednio dla kroków h

1

i h

2

= h

1

/2. Oczywi cie taki

sposób obliczania bł du wymaga praktycznie potrojenia ilo ci oblicze , nie nadaje si wi c do praktycznego zastosowania.

W przypadku metod nieparzystego rz du istnieje mo liwo przeprowadzenia po ka dym cyklu cyklu odwrotnego (tzn.

ponownego obliczenia warto ci y

i

na podstawie wła nie obliczonej warto ci y

i+1

). Po takim obliczeniu jako bł d mo na

przyj połow ró nicy mi dzy obliczonymi w obu kierunkach warto ciami y

i

.

Wybór długo ci kroku

Collatz podał praktyczne jako ciowe kryterium doboru kroku całkowania dla pierwszego z podanych algorytmów

Kutty czwartego rz du: po ka dym kroku nale y obliczy warto wyra enia: k

3

– k

2

/ k

2

– k

1

. Je eli przekracza ona

kilka setnych to długo kroku nale y zmniejszy .

Cz sto stosowana jest metoda polegaj ca na obliczaniu (co jak liczb kroków) warto ci przybli onej bł du:

= y

1

– y

2

/ 15. Je li warto jest mniejsza od po danej dokładno ci obliczenia prowadzone s dalej. Je li jest

mniejsza ni 1/50 zało onej dokładno ci krok powi ksza si dwukrotnie. Je li jest wi ksza — obliczenia powtarza si (od

miejsca gdzie ostatnio sprawdzano ) z krokiem dwukrotnie mniejszym.

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

15

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Najcz ciej spotykan metod oblicze ze zmiennym krokiem jest metoda Runge-Kutta-Fehlberg (o której dalej).

W przypadku programu maj cego mo no zmiany długo ci kroku musimy oczywi cie poda dopuszczalny zakres

tych zmian, a wi c poda jego maksymaln i minimaln

dopuszczaln długo . Oczywi cie wektor wynikowy takiego

programu (zawieraj cy obliczone warto ci y

i

) ma nieprzewidywaln długo . Co wi cej, konieczne b dzie zapisanie w

pami ci równie wektora „chwil czasu”, którym odpowiadaj wyznaczone warto ci funkcji — zatem cały program mo e

okaza si bardziej „pami cio erny”. Z drugiej jednak strony, je li charakter funkcji nie wymusi skracania kroku, a

umo liwi jego wydłu anie, mo emy zaoszcz dzi i na pami ci i na czasie (a przynajmniej na cyklach oblicze ). Je li oka e

si , e uzyskane rozwi zania nie wypadaj w punktach, na których nam zale ało b dziemy musieli przeprowadzi

interpolacj .

Stabilno metod jednokrokowych

Przykład: Rozwa my znowu równanie:

dy
dx

f x,y

x

y

którego rozwi zanie analityczne ma posta :

y x

x 1 1 x

0

y x

0

e

x x

0

Przy warunku pocz tkowym y (0) = –1 jego rozwi zaniem analitycznym jest: y (x ) = –x – 1. Jak wida przy takim

warunku pocz tkowym składnik eksponencjalny w rozwi zaniu analitycznym znika, ale nawet minimalna zmiana warunku

pocz tkowego, np. na –0,99999 spowoduje w ko cu znaczn zmian warto ci y dla du ych x. Tymczasem rozwi zywanie

równa ró niczkowych metodami jednokrokowymi sprowadza si w ka dym kroku do rozwi zywania kolejnego

zagadnienia pocz tkowego — wynik uzyskany w kroku i staje si warunkiem pocz tkowym dla obliczenia wyniku i +1.

Tego rodzaju niestabilno jest cech konkretnego równania i jego warunku pocz tkowego, a nie zale y od tego jaki

konkretny algorytm jednokrokowy zostanie wykorzystany.

Metoda Runge-Kuta-Fehlberg

Metoda ta jest znana równie jako „RKF45" (funkcja „ODE45" Matlaba wykorzystuje t wła nie metod ). Jest to

metoda o zmiennym kroku, jednak w celu doboru długo ci kroku nie stosuje si w niej porównywania wyników

otrzymanych przy dwóch ró nych długo ciach kroków — zamiast tego porównuje wyniki trzymane dla dwóch ró nych

rz dów metody obliczeniowej (czwartego i pi tego).

Algorytm.

Kolejne współczynniki:

k

1

hf t

i

,y

i

k

2

hf t

i

1
4

h,y

i

1
4

k

1

k

3

hf t

i

3
8

h,y

i

3

32

k

1

9

32

k

2

k

4

hf t

i

12
13

h,y

i

1932
2197

k

1

7200
2197

k

2

7296
2197

k

3

k

5

hf t

i

h,y

i

439
216

k

1

8k

2

3680

513

k

3

845

4104

k

4

k

6

hf t

i

1
2

h,y

i

8

27

k

1

2k

2

3544
2565

k

3

1859
4104

k

4

11
40

k

5

Kolejne przybli enie (obliczenia rz du 4):

y

i 1

y

i

25

216

k

1

1408
2565

k

3

2197
4104

k

4

1
5

k

5

Lepsze rozwi zanie (obliczenia rz du 5):

z

i 1

y

i

16

135

k

1

6656

12825

k

3

28561
56430

k

4

9

50

k

5

2

55

k

6

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

16

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Nast pny krok wyznacza si badaj c nast puj c wieko :

s

Tol h

2 z

i 1

y

i 1

1
4

0.84

Tol h

z

i 1

y

i 1

1
4

Długo kroku mo emy regulowa na kilka sposobów:

• metod „konserwatywn ”: Je li s < 3/4 — krok zmniejszamy o połow , je li s > 3/2 — krok zwi kszamy dwukrotnie

— jak łatwo zauwa y przy zastosowaniu tej metody przez wi kszo czasu krok pozostanie stały

• metod „dynamiczn ”: Sprowadzamy warto s do wybranego zakresu (np. <0.1,4.0> — tzn. je li s < 0.1 to

podstawiamy s = 0.1 i je li s > 4 to podstawiamy s = 4), a nast pnie mno ymy dotychczasowy krok przez s (post pujemy

tak w ka dym kroku).

• metod „mieszan ”: Post pujemy tak jak w metodzie „konserwatywnej”, ale zmian kroku uzyskujemy mno c jego

aktualn długo przez obliczon warto s.

Oczywi cie niezale nie od zastosowanej metody w programie powinny by narzucone granice dopuszczalnych zmian

długo ci kroku — tzn. maksymalna i minimalna nieprzekraczalna długo kroku.

Podane warto ci granic przedziałów warto ci współczynnika s wynikaj z praktyki, mo emy je dobra do konkretnego

rozwi zywanego zagadnienia

Istnieje pogl d, e jako wynik procedury nale y, zamiast wektora y, przedstawia obliczany równolegle wektor z.

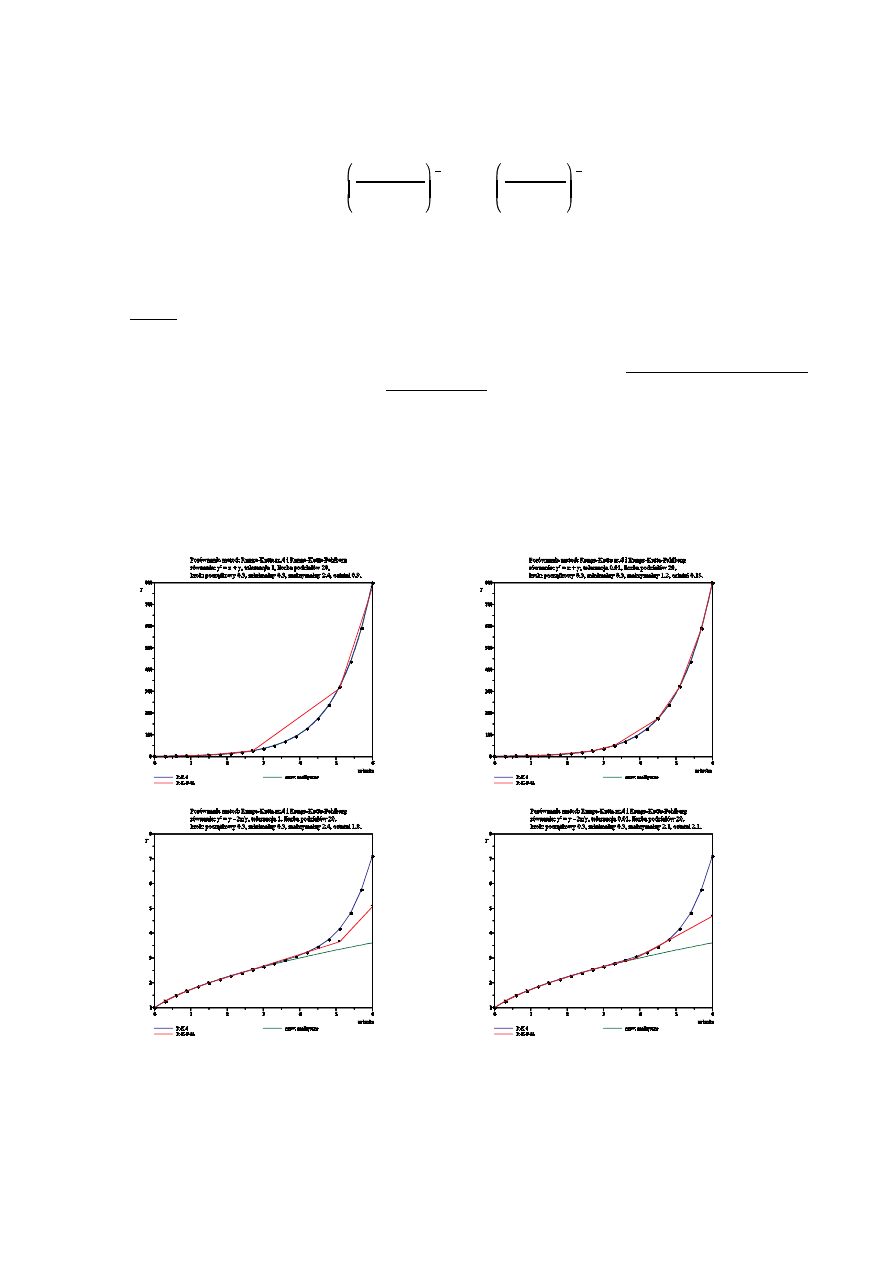
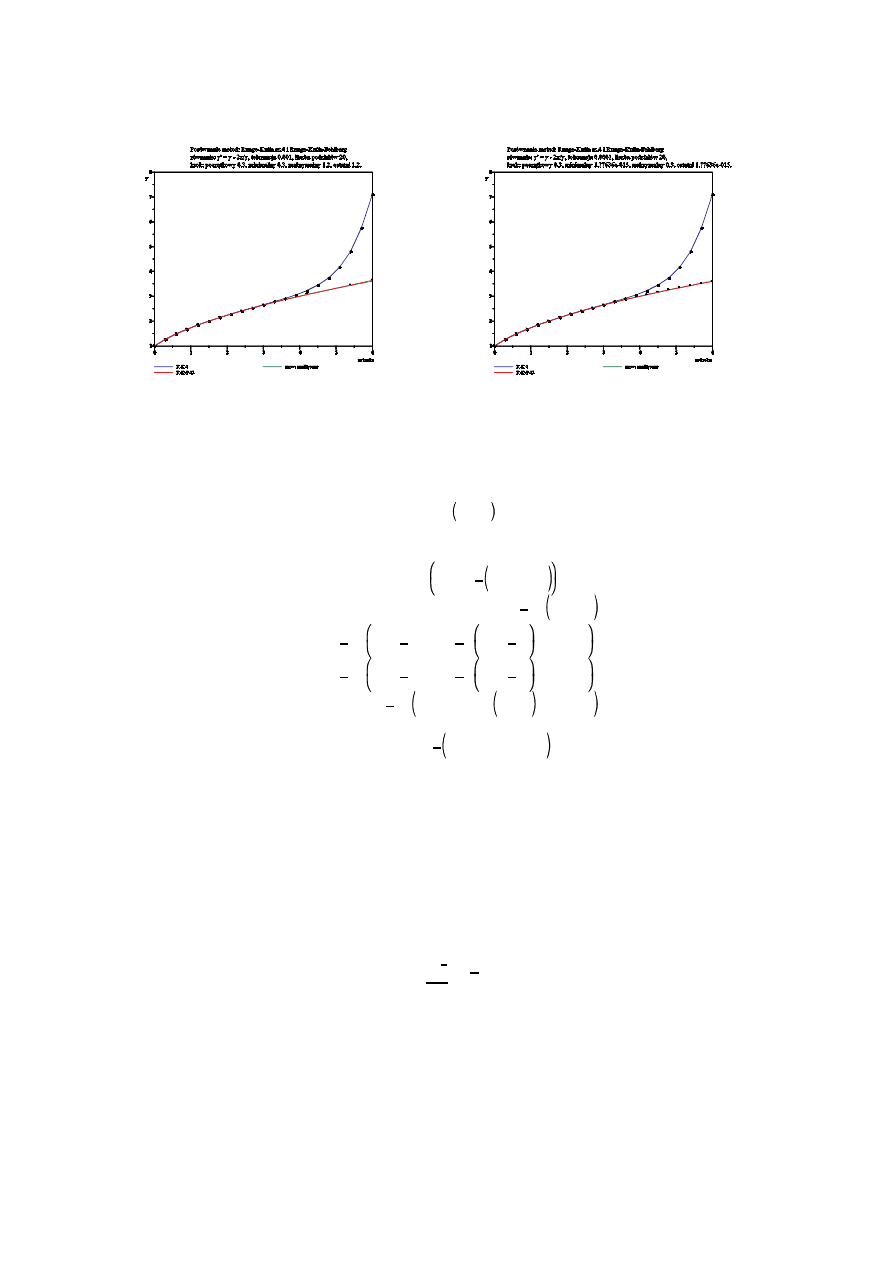
Poni sze wykresy przedstawiaj porównanie metody Runge-Kutta rz du 4 i metody Runge-Kutta-Fehlebrg

(wykorzystuj c przedstawion wy ej „konserwatywn ” metod zmiany kroku) zastosowanych do ju wcze niej podanych

dwóch równa przykładowych. Pocz tkowy krok zastosowany w metodzie RKF był taki sam jak krok u ywany przez cały

czas oblicze w metodzie RK4. Warto zauwa y , e zastosowanie w metodzie RKF zbyt du ej tolerancji mo e prowadzi

do znacznych bł dów.

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

17

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Metoda Runge-Kutta-Nyström

Jak wcze niej powiedziano liniowe równania wy szych rz dów mo emy zast powa układami równa ni szych

rz dów i rozwi zywa je kolejno. Jednak w przypadku równa rz du drugiego opracowano metod czwartego rz du,

b d c adaptacj metody Runge-Kutta. Metoda ta stosuje si do równa postaci:

y

f x,y,y

Zakładamy, e znane s warto ci funkcji i jej pochodnej w punkcie pocz tkowym. Dla równoodległych punktów x

i

(krok

równy h) algorytm jest nast puj cy:

y

n 1

y

n

h y

n

1
3

k

1

k

2

k

3

k

1

1
2

hf x

n

,y

n

,y

n

k

2

1
2

hf x

n

1
2

h , y

n

1
2

h y

n

1
2

k

1

, y

n

k

1

k

3

1
2

hf x

n

1
2

h , y

n

1
2

h y

n

1
2

k

1

, y

n

k

2

k

4

1
2

hf x

n

h , y

n

h y

n

k

3

, y

n

2k

3

y

n 1

y

n

1
3

k

1

2k

2

2k

3

k

4

W metodzie tej mo na stosowa opisany ju wcze niej dla metody Runge-Kutta sposób zmieniania długo ci kroku

h w trakcie oblicze , z tym, e oprócz ró nicy warto ci y

1

i y

2

nale y kontrolowa równie ró nice pomi dzy

odpowiednimi pochodnymi (i tak przecie obliczanymi); wydłu enie kroku jest mo liwe gdy zarówno warto ci funkcji

jak i pochodnych spełniaj warunek.

Zastosowanie metod jednokrokowych do układów równa

Jak ju wcze niej wspominałem, podr czniki nie omawiaj sposobów rozwi zywania równa ró niczkowych rz dów

wy szych ni pierwszy, poniewa zawsze mo na je sprowadzi do układu odpowiedniej liczby równa rz du pierwszego.

Rozwa my równanie ruchu (czyli równanie rz du drugiego):

2

r

t

2

a

podstawiaj c now zmienn (pr dko ) otrzymamy układ dwóch równa (wektorowych) rz du pierwszego (albo sze ciu

równa skalarnych):

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

18

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

r

t

v

v

t

a

x

t

v

x

y

t

v

y

z

t

v

z

v

x

t

a

x

v

y

t

a

y

v

z

t

a

z

W dalszym ci gu b d omawia skalarne równanie drugiego rz du, które po przekształceniu do układu dwóch równa

rz du pierwszego zapiszemy wektorowo:

d

2

r

dt

2

a

dr

dt

v

dv

dt

a

d

dt

r
v

v

a

Gdyby my rozwa ali ruch w trzech wymiarach we wzorach powy ej mieliby my wektory nie dwu- ale sze cioelementowe.

Aby zastosowa metod Runge-Kutty trzeciego rz du wła ciwe dla niej wzory zapiszemy w postaci wektorowej:

k

1

f t

i

, y

i

f t

i

,

r

i

v

i

v

i

a(r

i

)

k

2

f t

i

1
2

h, y

i

1
2

h k

1

f t

i

1
2

h,

r

i

v

i

1
2

h

v

i

a(r

i

)

f t

i

1
2

h,

r

i

1
2

hv

i

v

i

1
2

ha(r

i

)

v

i

1
2

ha(r

i

)

a(r

i

1
2

hv

i

)

k

3

f t

i

h, y

i

2h k

2

h k

1

f t

i

h,

r

i

v

i

2h

v

i

1
2

ha(r

i

)

a(r

i

1
2

hv

i

h

v

i

a(r

i

)

f t

i

h,

r

i

2hv

i

h

2

a(r

i

) hv

i

v

i

2ha(r

i

1
2

hv

i

) ha(r

i

)

v

i

2ha(r

i

1
2

hv

i

) ha(r

i

)

a(r

i

2hv

i

h

2

a(r

i

) hv

i

I ostateczne rozwi zanie:

y

i 1

y

i

h
6

k

1

4 k

2

k

3

Warto zwróci uwag , e do zapisania tych wzorów w Scilabie wyniki przekształce widoczne po prawej stronie

przedstawionych powy ej wzorów nie b d potrzebne — funkcj f zdefiniujemy jako przyjmuj c dwa argumenty, z

których pierwszym b dzie skalar (czas), a drugim wektor zawieraj cy wszystkie niewiadome.

Analogicznie b dziemy post powa w przypadku ka dej innej metody.

Metody wielopunktowe

Wszystkie metody przedstawione powy ej s nazywane jednopunktowymi — a to dlatego, e do prowadzenia oblicze

wystarczy znajomo tylko jednej warto ci szukanej funkcji. Podanie warunku pocz tkowego jest wystarczaj ce. W

przeciwie stwie do nich metody wielopunktowe wymagaj znajomo ci warto ci funkcji w kilku punktach pocz tkowych.

Zazwyczaj jednak warunek pocz tkowy zadany jest w jednym punkcie, wówczas mo liwe jest rozpocz cie oblicze któr

z przedstawionych powy ej metod jednopunktowych, obliczenie niezb dnej liczby warto ci pocz tkowych, a nast pnie

kontynuowanie oblicze metod wielopunktow .

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

19

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Metoda Adamsa

Załó my, e dla zagadnienia y = f(x,y) z warunkiem pocz tkowym y(x

0

) = y

0

znamy trzy kolejne warto ci

y

1

= y(x

1

) = y(x

0

+h), y

2

= y(x

2

) = y(x

0

+2h), y

3

= y(x

3

) = y(x

0

+3h) — obliczone w inny sposób.

Rozwi zanie znajdujemy w dwóch etapach: w pierwszym dokonujemy ekstrapolacji znanych punktów i znajdujemy

przybli on warto punktu kolejnego:

y

i 1

y

i

h

24

55f

i

59f

i 1

37f

i 2

9f

i 3

A nast pnie, wykorzystuj c obliczon warto y

i+

*

1

do obliczenia f

i+

*

1

w etapie drugim dokonujemy jej udokładnienia:

y

i 1

y

i

h

24

9f

i 1

19f

i

5f

i 1

f

i 2

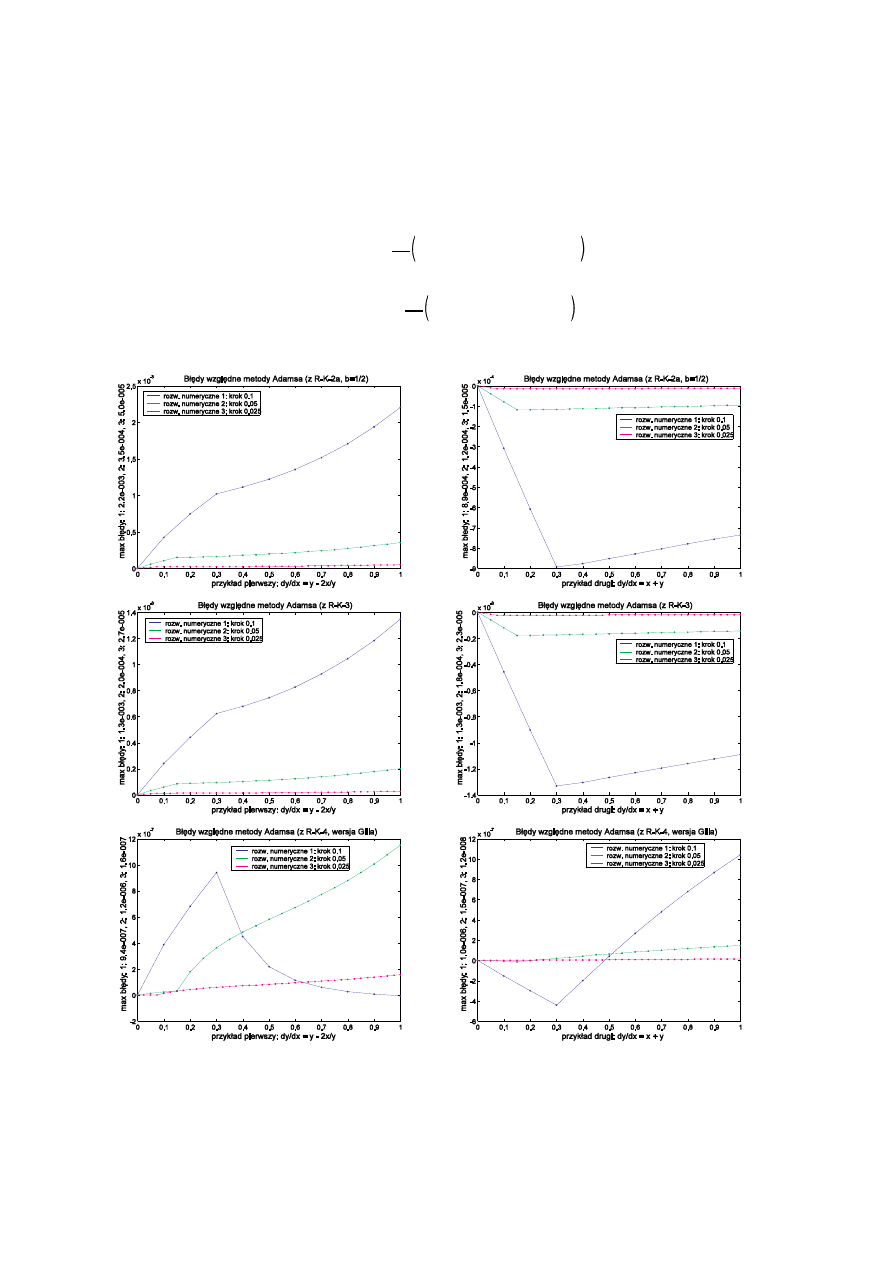
Poni ej przedstawiam bł dy metody Adamsa zastosowanej do identycznych jak poprzednio dwóch równa , do

obliczenia punktów pocz tkowych wykorzystano metod Runge-Kutty drugiego, trzeciego i czwartego rz du:

Metoda Milne'a

Metoda ta działa analogicznie jak przedstawiona powy ej metoda Adamsa — obliczenia przeprowadzamy równie

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

20

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

w dwóch etapach:

y

i 1

y

i 3

4h

3

2f

i 2

f

i 1

2f

i

y

i 1

y

i 1

h
3

f

i 1

4f

i

f

i 1

Jest to metoda 4-go rz du. Przyjmuje si , e bł d bezwzgl dny warto ci udokładnionej (obliczonej w drugim etapie)

jest równy w przybli eniu 1/29 ró nicy pomi dzy warto ci uzyskan w pierwszym etapie a warto ci z etapu drugiego

— mo liwe jest wi c wygodne kontrolowanie dokładno ci podczas oblicze .

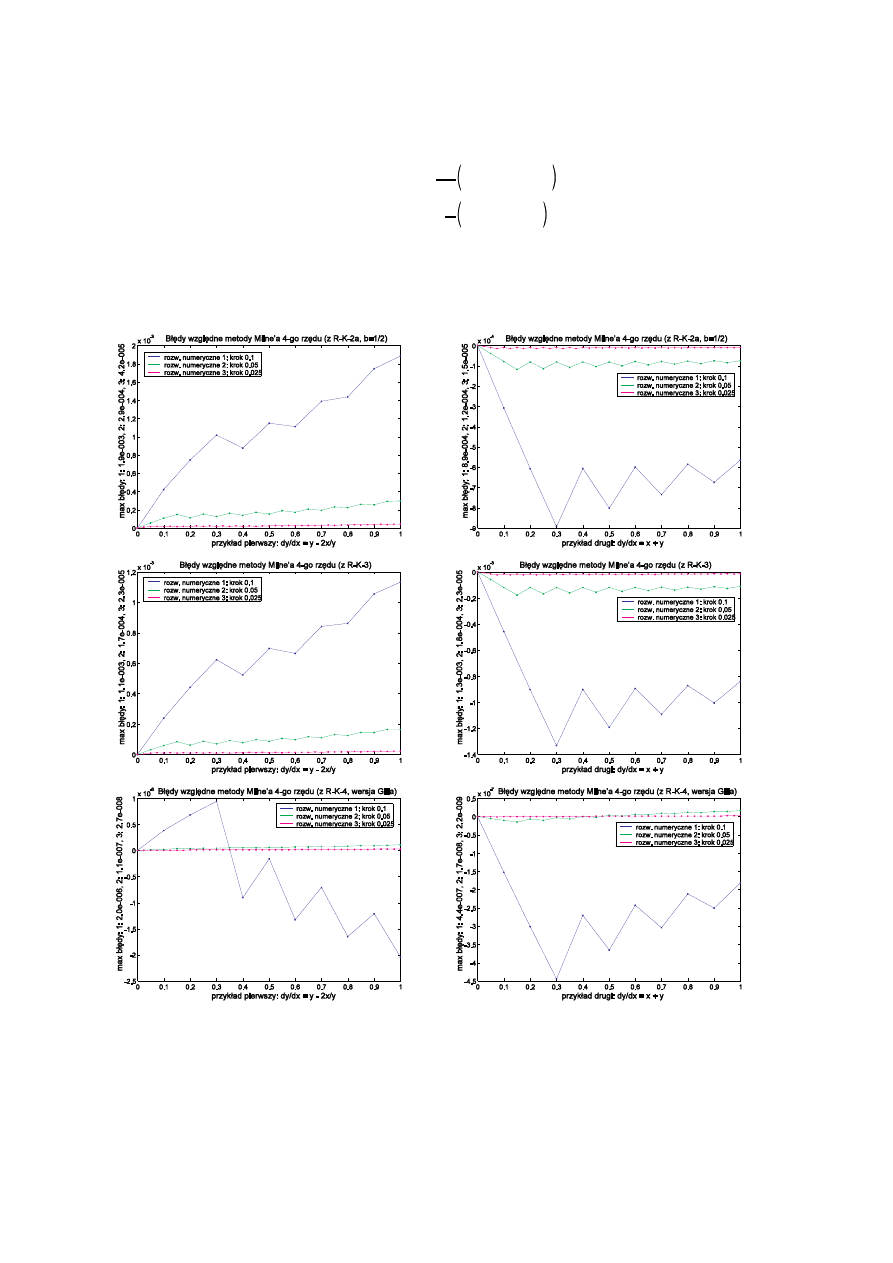
Poni ej przedstawiam bł dy metody Milne’a czwartego rz du zastosowanej do identycznych jak poprzednio dwóch

równa , do obliczenia punktów pocz tkowych wykorzystano metod Runge-Kutty drugiego, trzeciego i czwartego rz du:

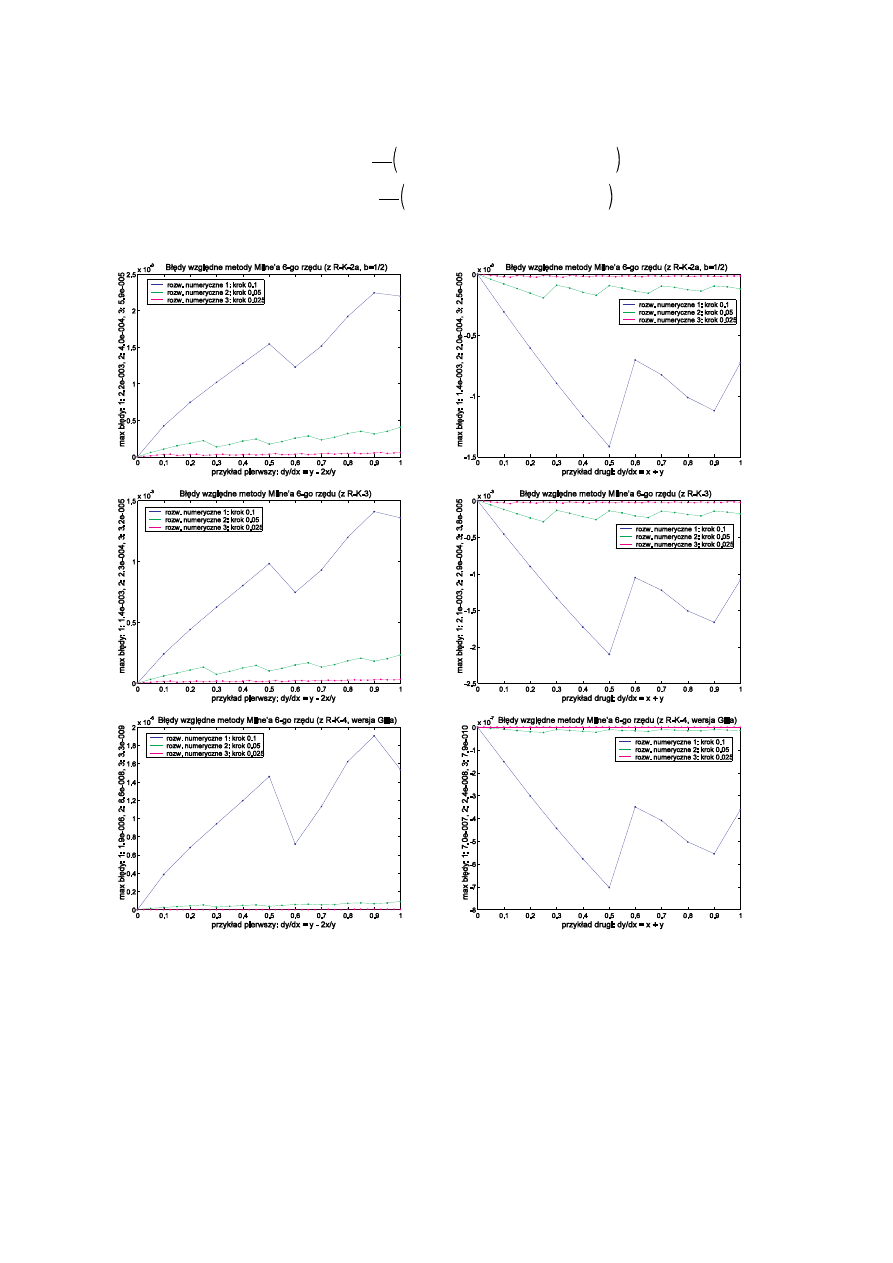
Istnieje tak e metoda Milne'a rz du 6-go:

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

21

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

i 1

y

i 5

3h

10

11f

i

14f

i 1

26f

i 2

14f

i 3

11f

i 4

y

i 1

y

i 3

2h

45

7f

i 1

32f

i

12f

i 1

32f

i 2

7f

i 3

Poni ej przedstawiam bł dy metody Milne’a szóstego rz du zastosowanej do identycznych jak poprzednio dwóch

równa , do obliczenia punktów pocz tkowych wykorzystano metod Runge-Kutty drugiego, trzeciego i czwartego rz du:

Dokładno rozwi zania a dokładno punktów pocz tkowych

Jak wida na powy szych wykresach, w przypadku metody Milne’a (i ogólnie w przypadku wszystkich metod

wielokrokowych) obliczenie warto ci pocz tkowych ze zbyt mał dokładno ci mo e uczyni całe rozwi zanie

bezu ytecznym.

Metody "półanalityczne"

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

22

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Rozwa my zagadnienie Cauchy-ego dla równania ró niczkowego z warunkiem pocz tkowym:

y

f x,y

;

y x

0

y

0

Metoda kolejnych przybli e polega na znalezieniu y(x) jako granicy ci gu funkcji y

n

(x) znajdowanych za pomoc

wzoru rekurencyjnego:

y

n

x

y

0

x

x

0

f x ,y

n 1

x dx

Udowodniono, e je li w pewnym obszarze R (okre lonym jako: x – x

0

a oraz y – y

0

b) spełniony jest warunek:

f x,y

1

f x,y

2

N y

1

y

2

gdzie N jest jak stał , to niezale nie od wyboru funkcji pocz tkowej y

0

(x) kolejne przybli enia y

n

(x) w pewnym

przedziale (x,x+h) d

do poszukiwanego rozwi zania zagadnienia.

Bł d n-tego przybli enia w tym przedziale mo na oszacowa nast puj co:

n

y x

y

n

x

MN

n

x x

0

n 1

n 1 !

gdzie M jest okre lone jako:

M

max

x,y R

f x,y

a h jest okre lone jako:

h

min a, b

M

Metod t mo na równie łatwo zastosowa do układów równa ró niczkowych.

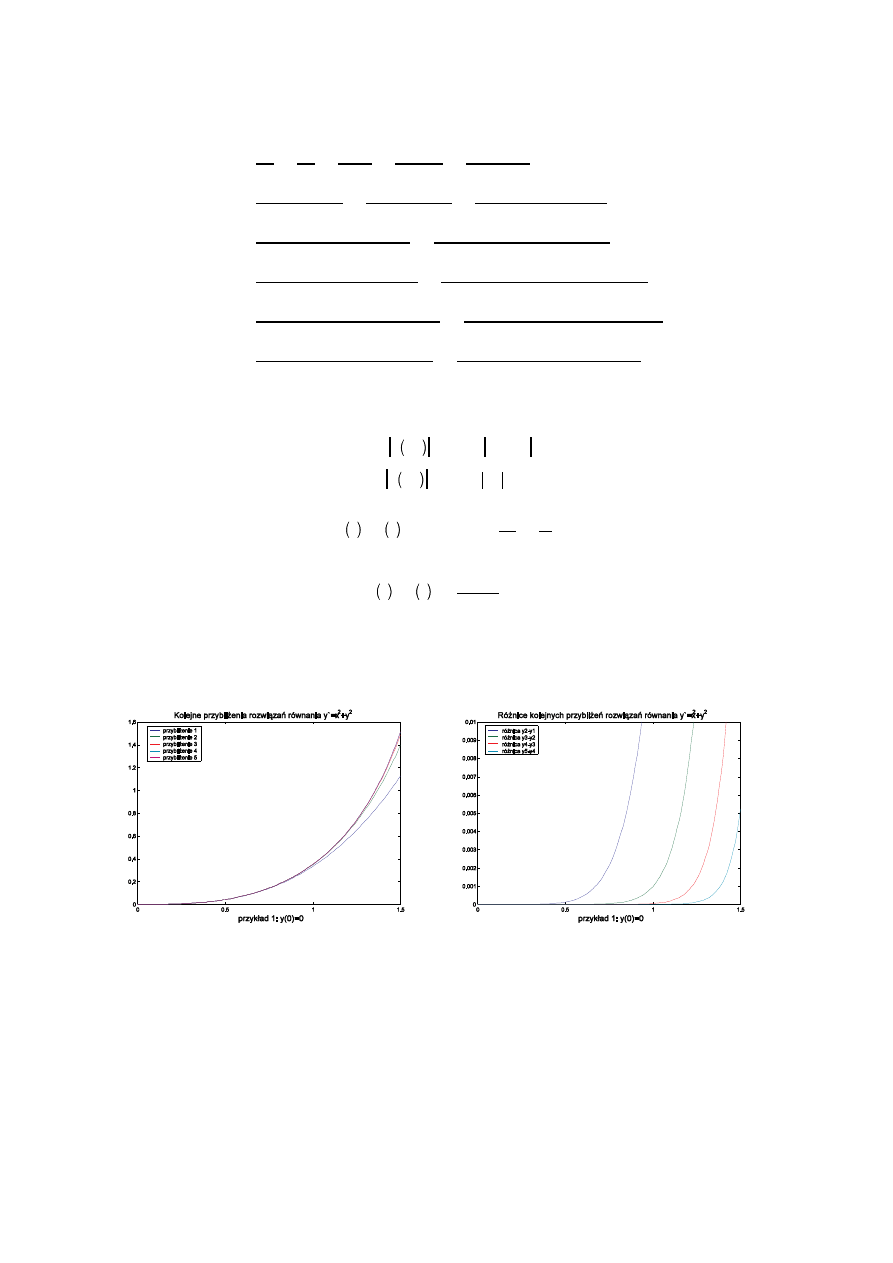
Przykład: Znale kilka kolejnych przybli e rozwi zania równania: y = x

2

+ y

2

dla warunku pocz tkowego y(0) = 0.

Zapiszmy równanie w postaci całkowej:

y x

x

0

x

2

y

2

dx

Jako przybli enie wyj ciowe przyjmiemy y

0

(x) 0. Kilka kolejnych przybli e b dzie mie nast puj c posta :

y

0

0

y

1

x

3

3

y

2

x

3

3

x

7

63

y

3

x

3

3

x

7

63

2x

11

2079

x

15

59535

y

4

x

3

3

x

7

63

2x

11

2079

13x

15

218295

82x

19

37328445

662x

23

10438212015

4x

27

3341878155

x

31

109876902975

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

23

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

5

x

3

3

x

7

63

2x

11

2079

13x

15

218295

46x

19

12442815

7382x

23

39665205657

428x

27

50998121559

17853193x

31

52289648987481675

738067298x

35

60394544580541334625

10307579354x

39

26851414520508677374275

6813116x

43

667791107219128471425

89797289962x

47

407191917287292044684671125

1159084x

51

308193360994502430591375

721012x

55

15328564533673936679413125

8x

59

21664518085681213656375

x

63

760594829864786522589375

Okre limy bł d przybli enia numer 3. Przyjmijmy a = 1 i b = 0,5 (mog to by dowolne liczby jako e funkcja x

2

+ y

2

jest okre lona i ci gła na całej płaszczy nie xy). Otrzymamy wówczas:

M

max f x,y

max x

2

y

2

1,25

N

max f x,y

max 2y

1

sk d wynika, e h = 0,4. Dla przedziału (0;0,4) otrzymamy:

y x y

3

x

1,25 1

3

x

4

4!

5

96

x

4

i dla całego przedziału:

m a x

(0;0,4)

y x y

3

x

5 0,4

3

96

0,00133

Obliczone w powy szy sposób bł dy poszczególnych przybli e s nast puj ce: n=2 — 0.1, n=3 — 0.01(3), n=4

— 0.001(3), n=5 — 0.00010(6). Jak wida dla ka dego kolejnego przybli enia bł d maleje o rz d wielko ci.

Zastosowany wzór na bł d cz sto daje wynik zbyt ostro ny (tzn. obliczony bł d jest zbyt du y). W praktyce obliczenia

prowadzi si do chwili, gdy kolejne y

n

i y

n–1

zgadzaj si z wymagan dokładno ci .

Na rysunku przedstawiaj cym ró nice kolejnych przybli e znacznie powi kszono skal osi y. O x obejmuje nieco

zbyt du y zakres — do oblicze przyj to zakres x-ów od –1 do +1. Je li chcemy aby rozwi zanie było dokładne dla

wi kszego zakresu x musimy posłu y si przybli eniem wy szego rz du. W sytuacji dost pno ci programów całkuj cych

metoda ta mo e by bardzo u yteczna.

Przykład: Zamiast przyj jako funkcj wyj ciow funkcj to samo ciowo równ zeru (jak w poprzednim przykładzie)

mo na znale funkcj bardziej zbli on do poszukiwanego rozwi zania. Na przykład dla równania y = x + 0,1y

2

z

warunkiem pocz tkowym y(0) = 1 funkcj wyj ciow mo e by :

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

24

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

0

x

y

0

y 0

1!

x

y 0

2!

x

2

Powy szy wzór uzyskali my rozwijaj c y(x) wokół punktu x

0

=0 (wówczas x jest odległo ci od x

0

) w szereg Taylora

ograniczony do drugich pochodnych. Z warunków pocz tkowych i z równania otrzymamy wówczas:

y

0

1

y 0

0,1y

2

0

0,1

y 0

1

0,2y

0

y

0

1,02

zatem ostatecznie b dzie to funkcja:

y

0

x

1

0,1x

0,51x

2

Zagadnienia brzegowe

W przypadku zagadnie pocz tkowych dysponowali my pełn informacj o szukanej funkcji w jednym wybranym

punkcie pocz tkowym (tzn. znali my warto funkcji i warto ci odpowiedniej liczby jej pochodnych — zale nie od

stopnia rozwi zywanego równania). W przypadku zagadnie brzegowych tak informacj nie dysponujemy, jest ona

„rozło ona” pomi dzy dwa punkty ograniczaj ce interesuj cy nas obszar, w którym chcemy znale rozwi zanie.

Wprawdzie rozwi zywanie zagadnie pocz tkowych jest w pewnym sensie łatwiejsze (mo liwe jest zastosowanie du o

prostszych metod) to jednak kolejne obliczane warto ci funkcji s obarczone coraz to wi kszymi bł dami, w kra cowych

przypadkach mo e to powodowa konieczno porzucenia prostych metod rozwi zywania. W przypadku zagadnie

brzegowych ograniczenia narzucone na oba kra ce przedziału powoduj bardziej równomierne rozło enie bł dów

znalezionych rozwi za .

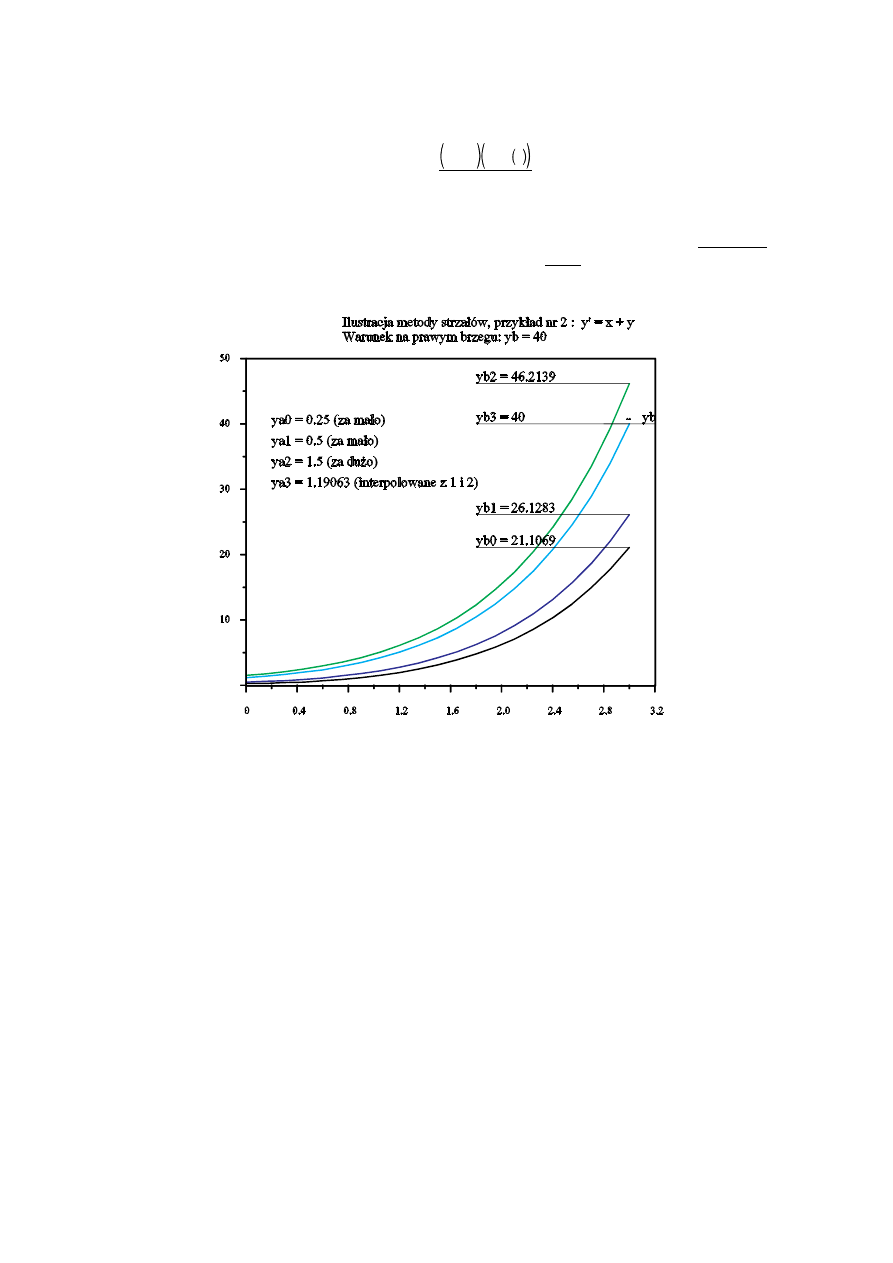
Metoda strzałów

Metoda ta jest logiczn konsekwencj ch ci zastosowania do zagadnie brzegowych metod opracowanych dla

zagadnie pocz tkowych (a wi c w zasadzie nie nadaj cych si do takiego zastosowania). Czasami nazywana jest metod

prób i bł dów.

Załó my, e interesuje nas zagadnienie brzegowe dla równania drugiego rz du. W przypadku zagadnienia

pocz tkowego oczekiwaliby my warto ci funkcji i jej pochodnej w punkcie pocz tkowym, natomiast w przypadku

zagadnienia brzegowego b dziemy dysponowa warto ciami funkcji na obu kra cach przedziału (oznaczmy je

odpowiednio przez a i b oraz przez f(a) i f(b)) natomiast nie b dzie dana adna warto pochodnej szukanej funkcji..

Je li odgadniemy (oboj tne czy bior c warto z sufitu czy

te szacuj c na podstawie jakich sensownych przesłanek)

warto pochodnej na jednym z kra ców (oznaczmy j przez

c

1

), to b dziemy mogli zastosowa któr z wcze niej

opisanych metod i za jej pomoc obliczy wszystkie warto ci

szukanej funkcji a do drugiego brzegu wł cznie (warto t

oznaczymy przez f

1

). Nie oczekujemy oczywi cie, e obliczona

w ten sposób warto funkcji w punkcie b b dzie zgadza si

z wynikaj c z warunków zadania warto ci brzegow . Jednak

uzyskamy w ten sposób par warto ci: zało ona warto

pochodnej i otrzymana warto funkcji na drugim brzegu.

Teraz mo emy przyj inn warto pochodnej na brzegu (c

2

)

i znów przeprowadzi obliczenia (otrzymuj c f

2

).

Je li b dziemy mie szcz cie jedna z otrzymanych

warto ci b dzie za du a a druga za mała. Wtedy warto c

3

wyznaczymy cho by za pomoc interpolacji liniowej:

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

25

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

c

3

c

1

c

2

c

1

f

1

f b

f

1

f

2

(przy zało eniu, e f

1

było za du e a f

2

za małe).

Pierwszy przykład nie jest wła ciwie zagadnieniem brzegowym — rozwi zywane jest równanie pierwszego rz du,

jednak podano warunek (warto funkcji szukanej) nie dla pocz tku lecz dla ko ca przedziału. Mo na byłoby oczywi cie

rozwi za to zagadnienie któr kolwiek z poznanych ju metod stosuj c krok o ujemnej warto ci jednak i w takim

przypadku mo na zastosowa metod strzałów.

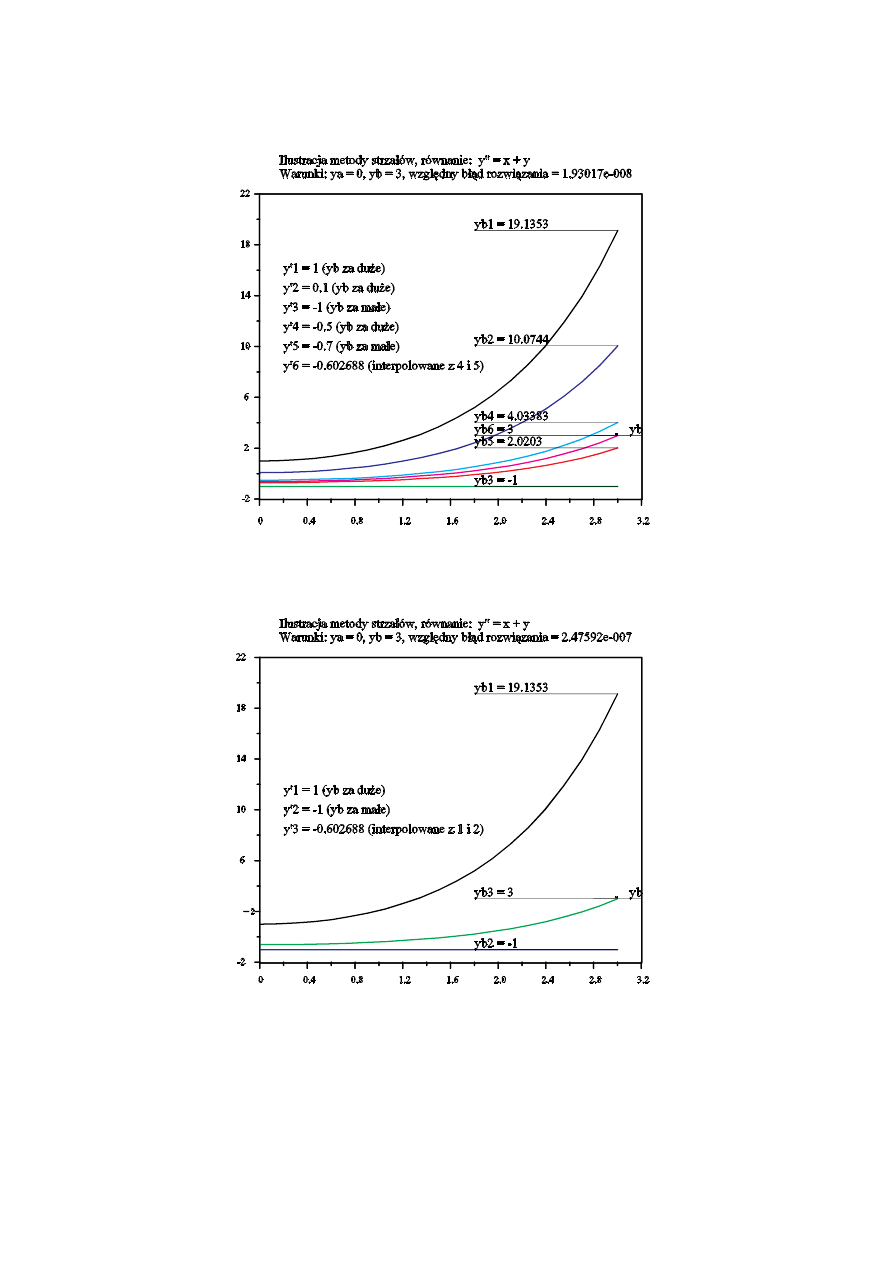
Kolejne przykłady dotycz równania drugiego rz du z podanymi warto ciami funkcji szukanej na obu kra cach

przedziału (jest to ju wi c zagadnienie brzegowe). Jak wida całkiem niezł dokładno rozwi zania mo na uzyska

nawet bez nadmiernej dbało ci o dokładno poszukiwanej warto ci pocz tkowej pierwszej pochodnej.

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

26

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Metody ró nicowe

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

27

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

Metody ró nicowe w odniesieniu do zagadnie brzegowych dla równa ró niczkowych zwyczajnych s takie same

jak w przypadku równa ró niczkowych cz stkowych, rozwi zania s jednak prostsze, bo mamy do czynienia tylko z

jedn zmienn niezale n . Zastosowane mog by praktycznie wszystkie wzory podane dla równa ró niczkowych

cz stkowych.

Metoda passage

Dla równania liniowego drugiego rz du mo liwe jest wyprowadzenie wzorów z uwzgl dnieniem dowolnych warunków

brzegowych (trzeciego rodzaju — zawieraj cych i warto funkcji i warto pochodnej na brzegu przedziału). Załó my,

e rozwi zywany problem ma posta :

y

p(x)y

q(x)y

f(x)

0

y(a)

1

y (a)

A

0

y(b)

1

y (b)

B

gdzie p(x), q(x) i f(x) s znanymi funkcjami, a i b s warto ciami granicznymi zmiennej x za

0

,

1

,

0

,

1

, A i B s

znanymi stałymi. Zakładamy dalej, e odcinek a–b został podzielony na N kroków o długo ci x, przy czym w zeł nr 0

odpowiada lewej granicy, a w zeł nr N — granicy prawej.

Wówczas oznaczaj c:

m

i

2q

i

x

2

4

2 p

i

x

;

k

i

2 p

i

x

2 p

i

x

mo emy przeprowadzi obliczenia jak nast puje. Najpierw obliczamy stałe c

1

i d

1

:

c

1

1

0

x

m

1

1

0

x

k

1 1

d

1

2f

1

x

2

2 p

1

x

k

1

A x

1

0

x

nast pnie wyznaczamy pozostałe stałe a do c

N

i d

N

:

c

i

1

m

i

k

i

c

i 1

d

i

2f

i

x

2

2 p

i

x

k

i

c

i 1

d

i 1

Na podstawie c

N

i d

N

obliczamy y

N

:

y

N

2B x

1

d

N

c

N 1

d

N 1

2

0

x

1

c

N 1

1

c

N

po czym kolejne warto ci y

i

(to, e wzory przewiduj mo liwo obliczenia warto ci y

o

wynika z faktu, e warunki

brzegowe mog nie zawiera warto ci funkcji na brzegu — gdy nie s to warunki pierwszego rodzaju):

y

i

c

i

d

i

y

i 1

y

0

1

y

1

A x

1

0

x

Wyprowadzenie: Rozwi zywane równanie ma posta :

y

p x y

q x y

f x

a warunki brzegowe:

0

y a

1

y a

A

0

y b

1

y b

B

W postaci ró nicowej:

Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

28

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

i 1

2y

i

y

i 1

h

2

p

i

y

i 1

y

i 1

2h

q

i

y

i

f

i

0

y

0

1

y

1

y

0

h

A

0

y

N

1

y

N 1

y

N 1

2h

B

Warto zauwa y , e do zapisania prawego warunku brzegowego (dla x=b) wykorzystano ró nic centraln — zapis

ró nicowy nie jest wi c symetryczny wzgl dem x i nale y oczekiwa , e wyniki mog by ró ne w zale no ci od tego od

którego ko ca przedziału zaczniemy rozwi zywa .

Po przekształceniu otrzymamy:

y

i 1

m

i

y

i

k

i

y

i 1

i

gdzie:

m

i

2q

i

h

2

4

2 hp

i

;

k

i

2 hp

i

2 hp

i

;

i

2h

2

f

i

2 hp

i

Jest to oczywi cie układ równa opisany macierz trójdiagonaln . Załó my, e dla i = 1,2,...,n–1 mo liwe jest zapisanie

rozwi za w postaci:

y

i

c

i

d

i

y

i 1

Je li jest to prawd , to mo emy podstawi taki wzór na y

i–1

do ró nicowej postaci rozwi zywanego równania:

y

i 1

c

i 1

d

i 1

y

i

y

i 1

m

i

y

i

k

i

c

i 1

d

i 1

y

i

i

co po przekształceniach daje:

y

i

1

m

i

k

i

c

i 1

i

k

i

c

i 1

d

i 1

y

i 1

czyli:

c

i

1

m

i

k

i

c

i 1

;

d

i

i

k

i

c

i 1

d

i 1

Dla i = 1 otrzymamy:

y

2

m

1

y

1

k

1

y

0

1

Z warunku brzegowego dla x = a mamy:

0

y

0

1

y

1

y

0

h

A

y

0

Ah

1

y

1

0

h

1

po podstawieniu:

y

2

m

1

y

1

k

1

Ah

1

y

1

0

h

1

1

i po przekształceniu:

m

1

1

k

1

o

h

1

y

1

y

2

1

k

1

Ah

0

h

1

y

1

0

h

1

m

1

0

h

1

1

k

1

1

k

1

Ah

0

h

1

y

2

co daje nam warto ci c

1

i d

1

. Na podstawie wzorów na c

i

i d

i

mo emy obliczy wszystkie kolejne warto ci współczynników

c i d. Nast pnie rozwa ymy układ równa (który umo liwi nam wyeliminowanie z oblicze warto ci y

N+1

):

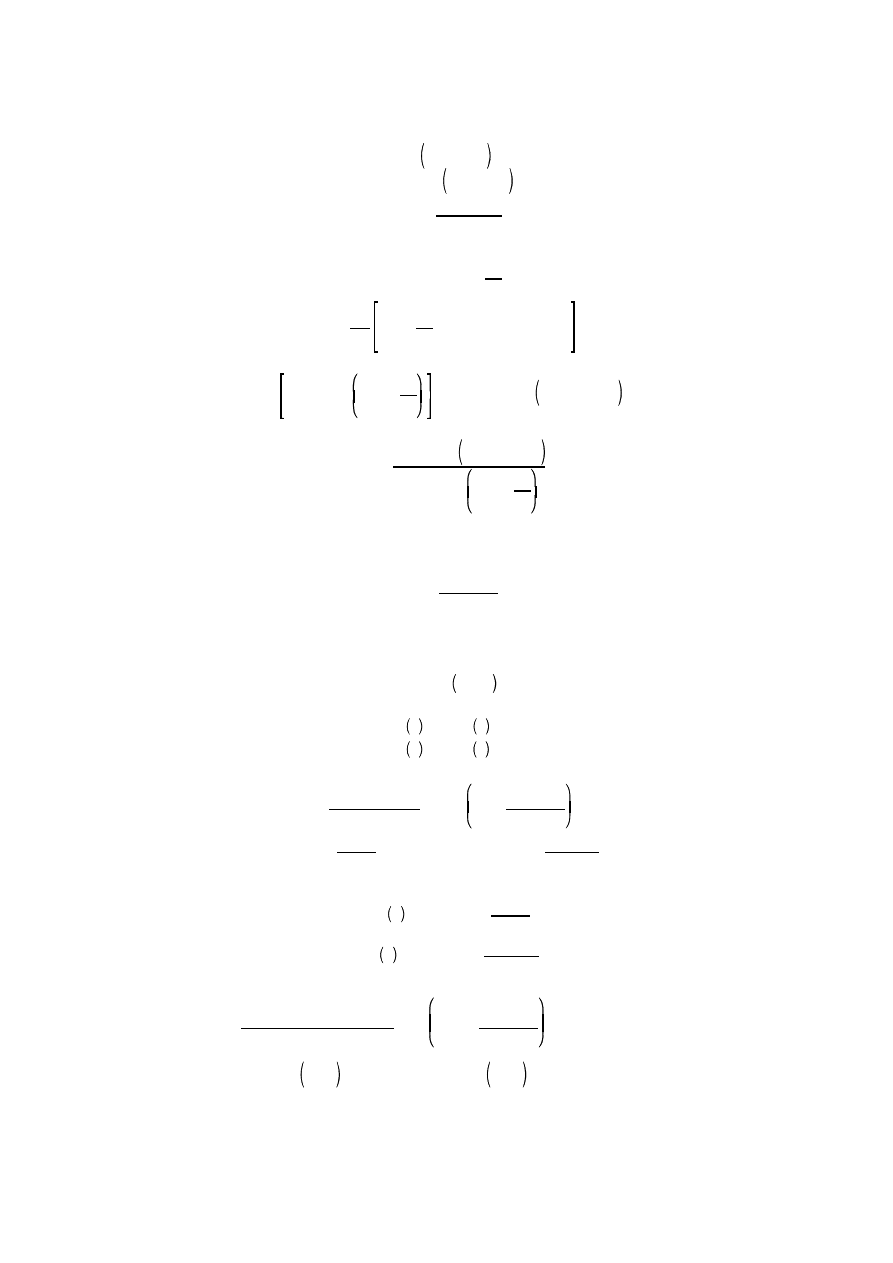
Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

29

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

y

N

c

N

d

N

y

N 1

y

N 1

c

N 1

d

N 1

y

N

0

y

N

1

y

N 1

y

N 1

2h

B

po przekształceniach otrzymamy:

y

N 1

d

N

y

N

c

N

0

y

N

1

2h

d

N

y

N

c

N

c

N 1

d

N 1

c

N 1

y

N

B

i dalej:

2h

0

1

c

N 1

1

c

N

y

N

2hB

1

c

N 1

d

N 1

d

N

Ostatecznie warto y

N

wyniesie:

y

N

2hB

1

c

N 1

d

N 1

d

N

2h

0

1

c

N 1

1

c

N

Po obliczeniu y

N

mo emy „cofaj c” si obliczy wszystkie pozostałe warto ci y, a do y

1

.

Lewy warunek brzegowy zapisany w postaci ró nicowej mo emy przekształci do postaci umo liwiaj cej obliczenie

y

0

:

y

0

Ah

1

y

1

1

0

h

Metoda ró nicowa dla równa nieliniowych drugiego rz du

Rozwa my teraz zagadnienie brzegowe dla nieliniowego równania drugiego rz du:

y

f x,y,y

z warunkami brzegowymi:

0

y a

1

y a

A

0

y b

1

y b

B

Równanie ró niczkowe zast pimy nast puj cym równaniem ró nicowym:

y

i 1

2y

i

y

i 1

h

2

f x

i

,y

i

,

y

i 1

y

i 1

2h

0

y

0

1

y

1

y

0

h

A

;

0

y

N

1

y

N

y

N 1

h

B

Jest to równanie nieliniowe, rozwi zujemy je metod iteracyjn . Oznaczmy:

0

y

0

y

0

1

y

1

y

0

h

N

y

0

y

N

1

y

N

y

N 1

h

iteracje b d mie posta (indeks górny (r) oznacza numer iteracji):

y

(r 1)

i 1

2y

(r 1)

i

y

(r 1)

i 1

h

2

f x

i

,y

(r )

i

,

y

(r )

i 1

y

(r )

i 1

2h

;

i 1, ,N 1

0

y

(r 1)

i

A

(i 0)

;

N

y

(r 1)

i

B

(i N )

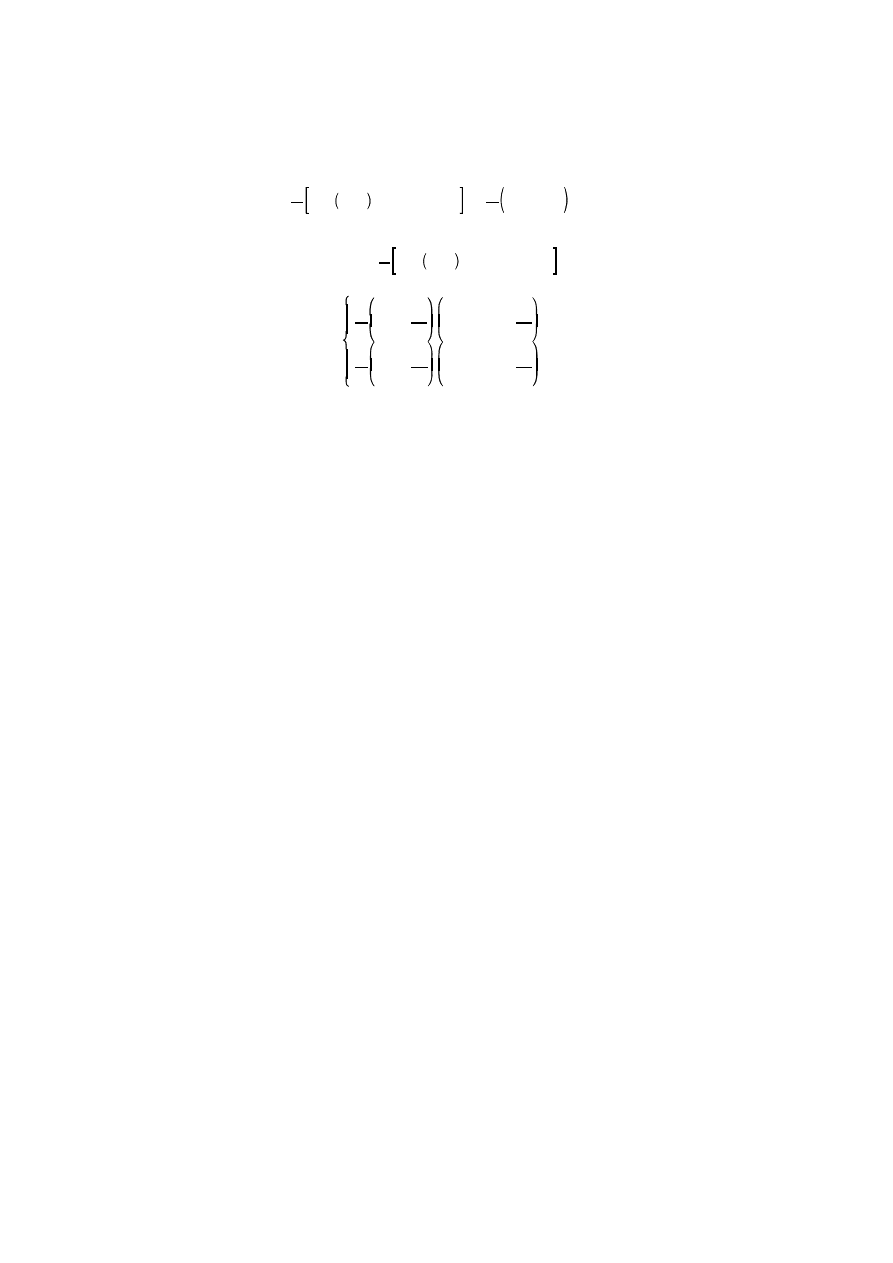
Metody Numeryczne w Fizyce 1

Rozwi zywanie ODE

30

© Andrzej Brozi, Instytut Fizyki Politechniki Łódzkiej

W ramach ka dej z iteracji musimy rozwi za układ równa algebraicznych. Rozwi zanie to mo na przedstawi w

postaci:

y

(r 1)

i

h A

0

b a

A

1

1

B

i

0

B A

0

h

2

N 1

j 1

g

ji

f

(r)

j

gdzie g

ji

i obliczane s jako:

1
h

0 0

b a

0 1

1 0

g

ji

1 j

0

1

h

i

0

0

N

1

h

j i

1 i

0

1

h

j

0

0

N

1

h

j>i

Warto zauwa y , e we wzorze iteracyjnym tylko warto f

j

zale y od numeru iteracji.