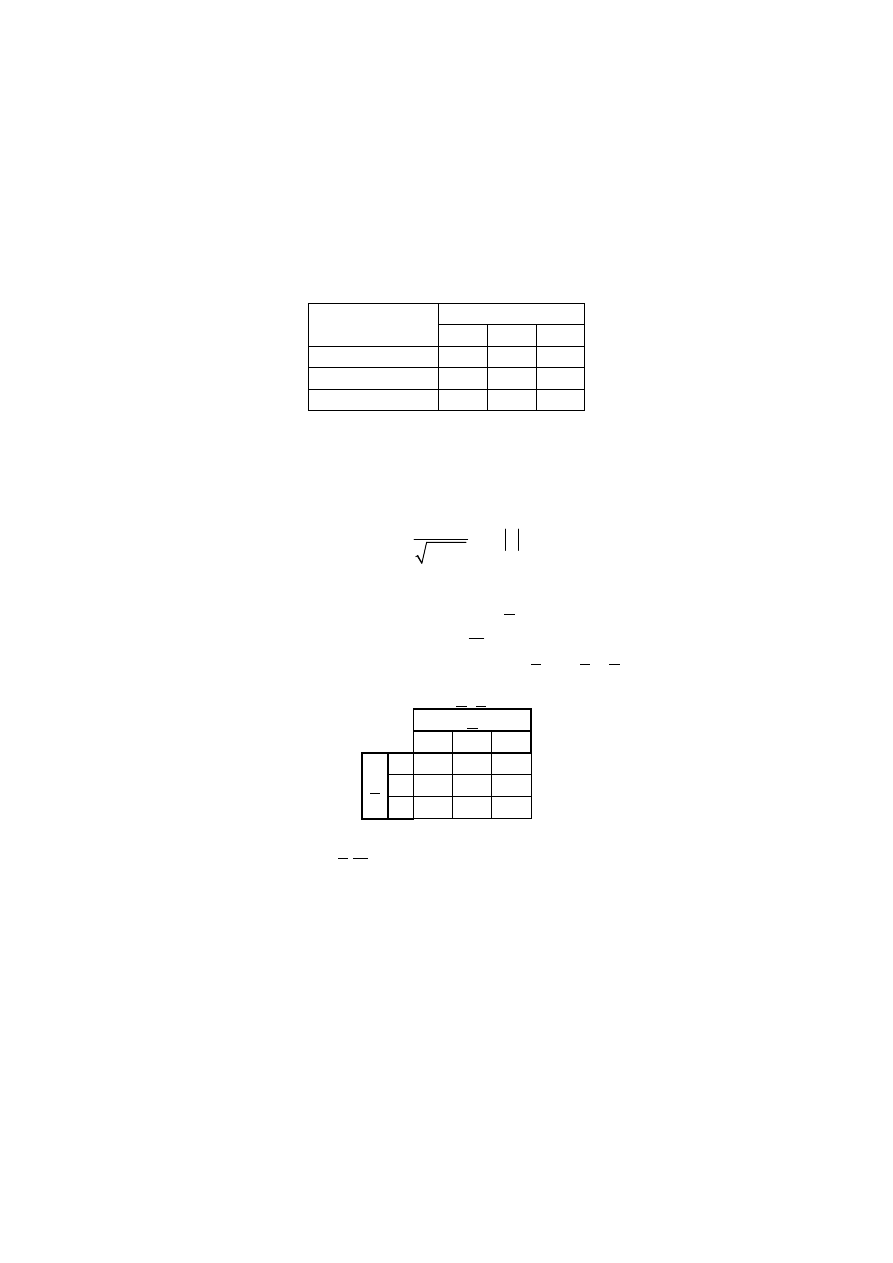
Część zadaniowa

Zadanie 1 Ile można utworzyć liczb parzystych siedmiocyfrowych takich, że cyfra zero nie
występuje na pierwszym miejscu oraz cyfry w danej liczbie się nie powtarzają (2 punkty).

Zadanie 2 Kanałem łączności nadaje się tylko 3 rodzaje ciągów liter: AAAA, BBBB, CCCC
odpowiednio z prawdopodobieństwami 0.4, 0.3 i 0.3. Litery te (sygnały) podlegają niezależ-
nie losowym zakłóceniom (przekłamaniom) w rezultacie czego np. litera A może być odebra-
na jako B albo C (zamiast A). Prawdopodobieństwa poprawnego przesłania albo przekłama-
nia podaje tablica.

Sygnały odebrane

Sygnały nadane

A

B

C

A

0.8

0.1

0.1

B

0.1

0.8

0.1

C

0.1

0.1

0.8

a)

znaleźć prawdopodobieństwo odebrania na wyjściu sygnału AAAA (2 punkty),

b)

na wyjściu odebrano sygnał ACAA, oblicza prawdopodobieństwo, że został nadany
jako AAAA (2 punkty).

Zadanie 3 Dobrać tak stałą C by funkcja

( )

2

dla

1

1

0 poza tym

C

x

p x

x



<



=

−







była gęstością prawdopodobieństwa zmiennej losowej X (1 punkt), a następnie: a) wyznaczyć
jej dystrybuantę (2 punkty), b) obliczyć

(

)

0

1/ 4

P

X

≤ <

(2 punkty), c) obliczyć wartość

ś

rednią (2 punkt), d) wyznaczyć gęstość zmiennej losowej Y jeśli Y = X

5

(3 punkty)

Zadanie 4 Dany jest rozkład zmiennej losowej (X, Y) w postaci tabeli

X

2

3

4

1 1/6 1/6 1/6
2

0

1/6

0

Y

3 1/6

0

1/6

a) obliczyć dystrybuantę (2 punkty) b) znaleźć rozkłady brzegowe (1 punkt) c) sprawdzić nie-
zależność zmiennych losowych X Y (1 punkt)

Część teoretyczna (na oddzielnej kartce)

1.

Podaj i opisz twierdzenie Bayesa (3p)

2.

Podaj definicję i wymień właściwości dystrybuanty zmiennej losowej (5p)

3.

Podaj częstościową definicję prawdopodobieństwa (2p)