POLITECHNIKA ŁÓDZKA

Katedra Techniki Cieplnej i Chłodnictwa

TECHNOLOGIE

INFORMATYCZNE

MATLAB

Część I

Temat: Środowisko programu, podstawowe operacje

Opracował: dr inż. Artur Gutkowski

Łódź - 2008

Katedra Techniki Cieplnej i Chłodnictwa

90-924 Łódź; ul. Stefanowskiego 1/15
tel. [phone]; fax [phone]; e-mail: [e-mail]

2

Spis Treści

1. Wstęp ...............................................................................................................................................3

2. Wygląd MATLAB-a ........................................................................................................................3

3. Wprowadzanie liczb i proste operacje na nich.................................................................................5

4. Wprowadzanie łańcuchów i proste operacje na nich.....................................................................11

5. Literatura........................................................................................................................................13

3

1. Wstęp

MATLAB jest obecnie jednym z najczęściej wykorzystywanych programów do obliczeń

naukowych i technicznych. Czynnikiem odpowiedzialnym za tą popularność jest w głównej mierze
prostota jego obsługi oraz szeroka baza bibliotek, którymi dysponuje. Pierwsza wersja programu
pojawiła się w 1985, ale jego początki sięgają lat siedemdziesiątych. Innowacyjną zmianą,
odróżniającą go od innych aplikacji tego typu było traktowanie każdej liczby jako macierzy
(pojedyncza liczba jest macierzą o wymiarach 1×1), stąd też wzięła się nazwa pakietu (MATrix
LABoratory). Oprócz obliczeń macierzowych pozwala on także na analizę numeryczną,
przetwarzanie sygnałów, obliczenia symboliczne oraz obróbkę obrazów. Wyniki pracy MATLAB’a
mogą być przedstawione za pomocą dwu lub trójwymiarowych wykresów a nawet filmów
animowanych.

Pracę z MATLAB’em możemy podzielić na dwa podstawowe tryby: bezpośredni i pośredni.

Pierwszy tryb przypomina dialog. Użytkownik w oknie poleceń pisze komendę lub „zapytanie”
a pakiet wyświetla wynik lub „odpowiedź”. Pośredni tryb polega na uruchomieniu programu
napisanego w języku pakietu MATLAB. Drugi sposób wykorzystujemy zwłaszcza wtedy, gdy
podczas pracy często pojawia się problem wielokrotnego wpisywania (z wiersza poleceń) szeregu
tych samych poleceń, proces ten może być zautomatyzowany poprzez stworzenie m-pliku (plik
z rozszerzeniem .m). M-pliki są skryptami (plikami tekstowymi) obsługiwanymi przez MATLAB.
Lista poleceń znajdująca się w takim pliku jest uruchamiana jedną komendą. W skrypcie może
znajdować się procedura, funkcja lub wiele funkcji. Do napisania skryptu nie potrzebujemy
MATLABA, może to tego celu posłużyć prawie każdy edytor tekstowy np. Notepad, lub Wordpad.

W tym opracowaniu skoncentrujemy się na podstawowych operacjach na liczbach

i łańcuchach, które także mogą być wykorzystywane podczas pracy z macierzami.

2. Wygląd MATLAB-a

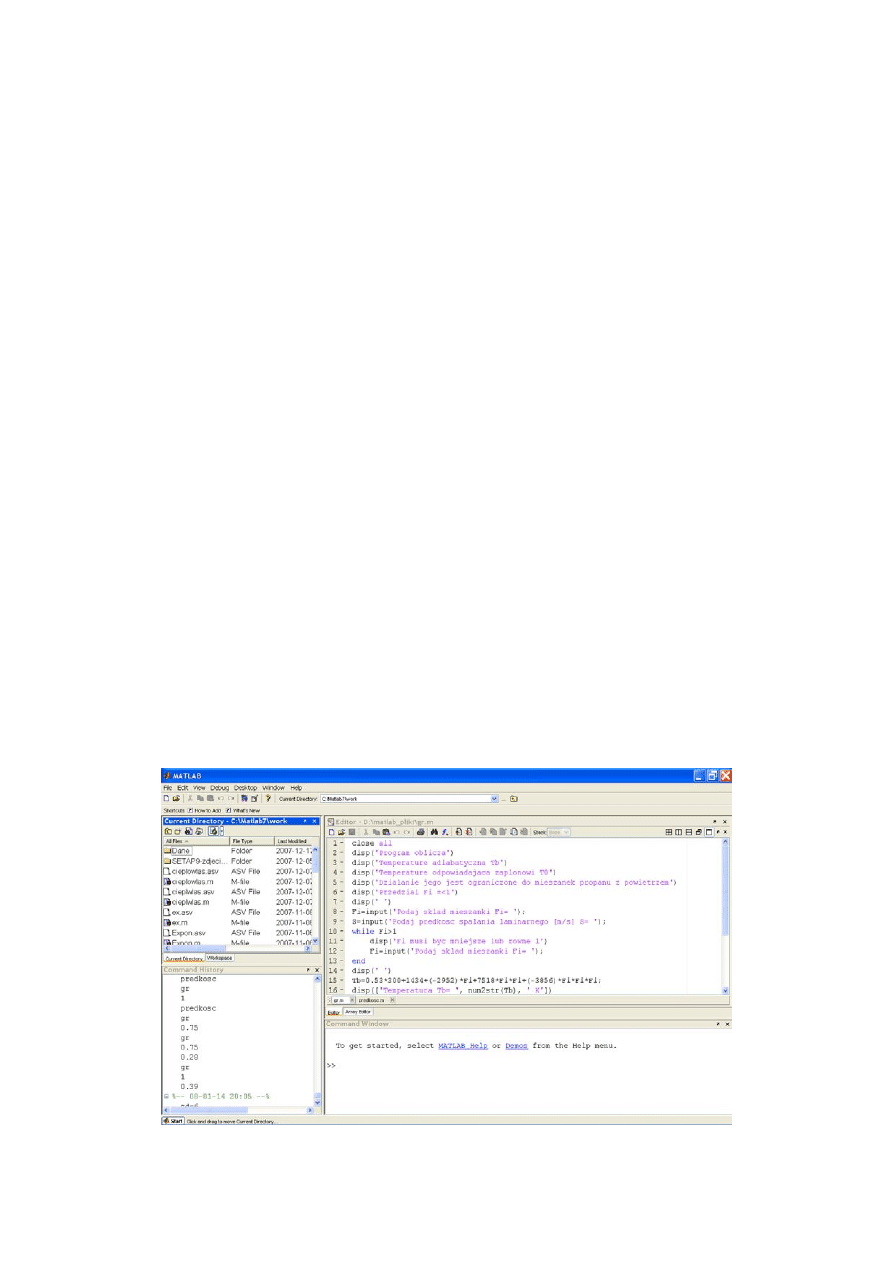
Po otwarciu MATLABA-a ukazuje się domyślny interfejs (rys. 1) składający się z kilku

podstawowych okien:

Rys. 1. Domyślny interfejs MATLAB-a.

4

- Command Window – okno poleceń,
- Command History – okno poprzednich poleceń,
- Current Directory – okno katalogu roboczego,
- Workspace – informacje o zmiennych w przestrzeni roboczej.

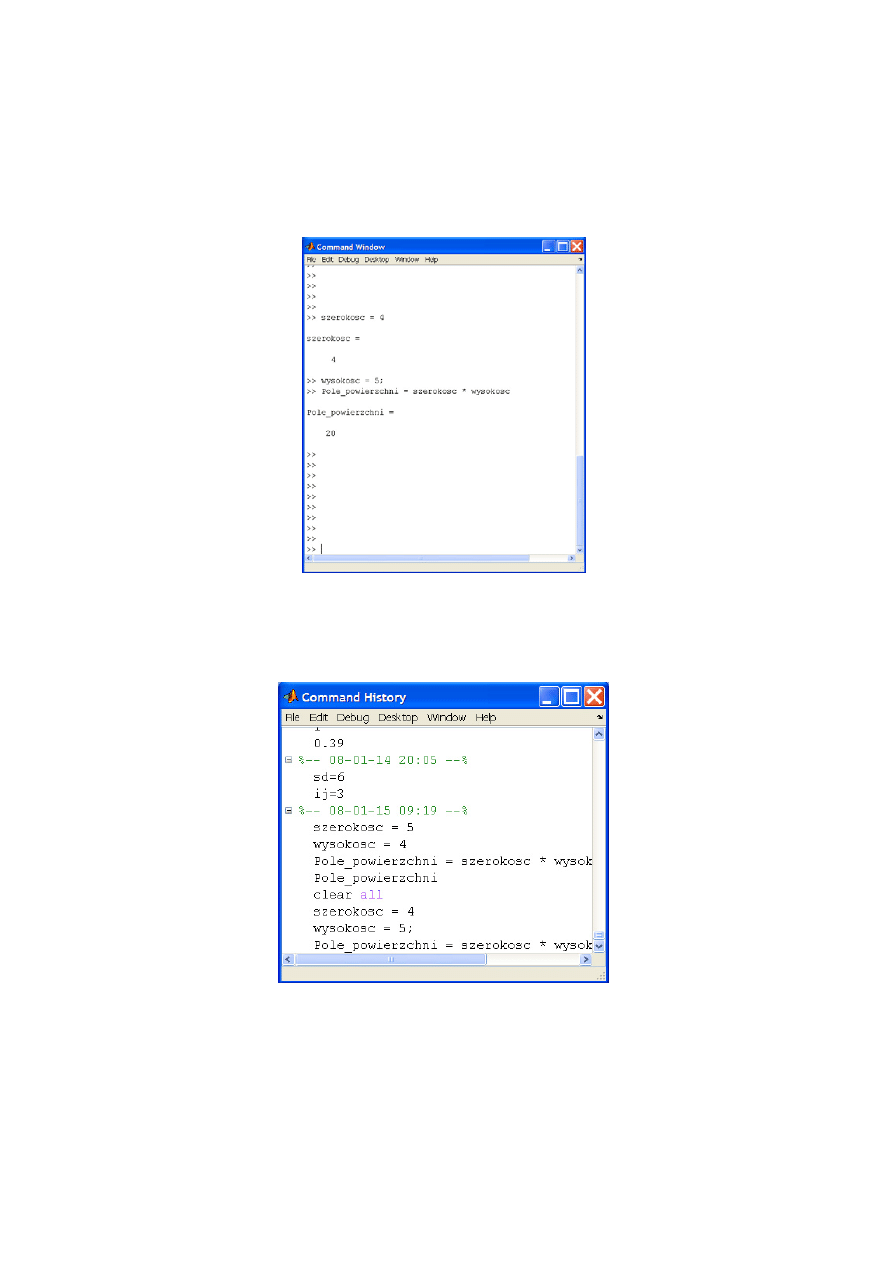
Sercem programu jest okno poleceń (Command Window) (rys. 2), to tutaj wpisujemy

większość poleceń i funkcji, także tutaj otrzymujemy odpowiedzi i wyniki.

Rys. 2. Okno poleceń.

Command History (rys. 3) pokazuje wszystkie komendy, które zostały wpisane w oknie

poleceń. W oknie tym nie ma wyników ich działania.

Rys. 3. Okno historii.

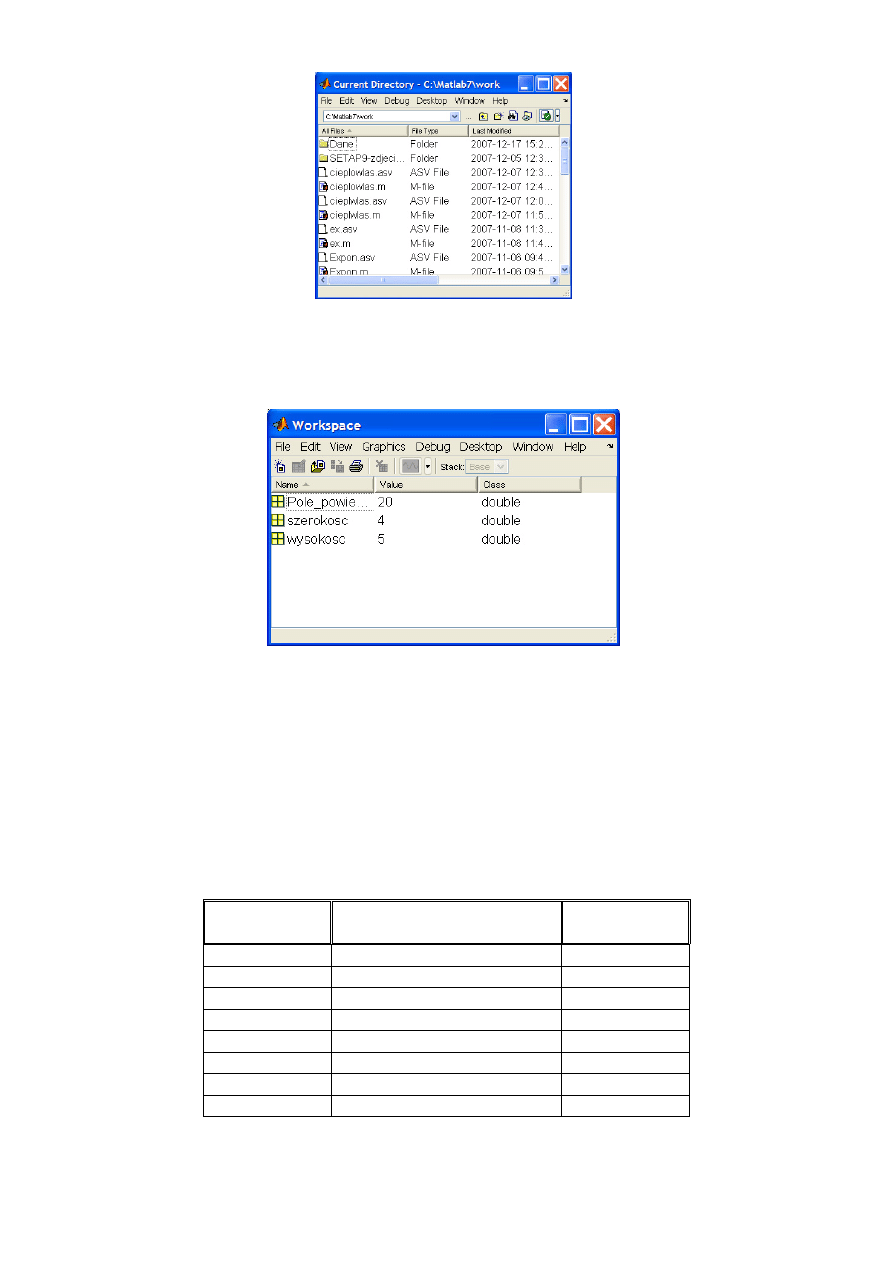
Okno katalogu roboczego (Current Directory) (rys. 4) zawiera opcje, które ułatwiają

otwieranie, edytowanie i zapisywanie plików.

5

Rys. 4. Okno katalogu roboczego.

Workspace (rys. 5) pokazuje zmienne, które zostały stworzone w danej sesji. Można tam

znaleźć także informacje dotyczące ich rozmiaru oraz rodzaju.

Rys. 5. Okno przedstawiające informacje o zmiennych.

3. Wprowadzanie liczb i proste operacje na nich

Do podstawowych działań arytmetycznych w MATLAB-ie wykorzystujemy dwa rodzaje

operatorów: macierzowe i tablicowe (Tabela 1). Pierwsze wykonują operacje na całych macierzach
drugie na konkretnych elementach macierzy.

Tabela 1. Operatory wykorzystywane w MATLAB-ie.

Operator

macierzowy

Opis

Operator

tablicowy

+ dodawanie +

– odejmowanie –
* mnożenie .*

/ dzielenie

prawostronne ./

\ dzielenie

lewostronne .\

^ potęgowanie .^

’ sprzężenie nie

ma

.’ transpozycja

nie

ma

6

Zawsze musimy zdawać sobie sprawę o jakie działanie nam chodzi, w pewnych przypadkach

nie będzie miało znaczenia, który z operatorów użyjemy np. gdy będziemy chcieli pomnożyć przez
siebie dwie liczby (dwie macierze jednostkowe).

Po uruchomiania MATLABA-a pojawia się symbol zachęty (>>), oznacza on, że program

czeka na wpisanie polecenia, które zatwierdzane jest klawiszem ENTER.

Spróbujmy dodać do siebie dwie liczby

>> 2 + 4
ans =

6

>>

Widzimy, że MATLAB wykonał operację, a wynik przypisał do tymczasowej zmiennej ans.

Gdybyśmy chcieli otrzymany wynik podzielić przez 2, możemy to zrobić następująco

>> ans/2
ans =

3
>>

Istnieją dwa znaki dzielenie prawostronny i lewostronny, operacje te dają różne wyniki np.:

>> 15/3
ans =

5
>> 15\3
ans =

0.2000
>>

Dużym ułatwieniem podczas pracy z MATLAB-em jest to, że nie wymaga on deklaracji

zmiennych, czynność ta jest wykonywana automatycznie (program przydziela jej domyślny obszar
pamięci)

>> dlugosc = 5
dlugosc =

5
>>

Każda nazwa powinna się rozpoczynać od litery alfabetu, po której może być umieszczony

dowolny znak alfanumeryczny (maksymalna ilość znaków – 31). Należy pamiętać, że MATLAB
rozróżnia małe i duże litery.

Po zatwierdzeniu ENTER-em MATLAB wyświetla nazwę zmiennej w kolejnym wierszu

a w następnym jej wartość. Jeżeli chcemy uniknąć ponownego wyświetlania nazwy i przypisanej jej
wartości, na końcu wyrażenia wstawiamy średnik np.

>> dlugosc = 5;
>> szerokosc = 6;

>> pole_pow = długość * szerokosc
pole_pow =
30

>>

7

Gdy podczas pracy postanowimy zmienić wartość zdefiniowanej poprzednio wielkość,

MATLAB przeprowadzi to w sposób dynamiczny jednocześnie przyporządkowując jej wymagany
obszar pamięci np.:

>> dlugosc = 5;
>> szerokosc = 6;

>> pole_pow = długość * szerokosc
pole_pow =
30

>>
>> pole_pow = 2340

%Ponowne zdefiniowanie wielkości pole_pow

pole_pow =
2340

>>

Jeżeli w oknie poleceń, lub w skrypcie chcemy umieści komentarz, który nie będzie widoczny

dla interpretera MATLABA-a to poprzedzamy go znakiem %.

Istnieje także możliwość zapisu kilku instrukcji w jednej linii – oddzielamy je przecinkiem.

>> a = 2; , b = 3;

>> a + b
ans =

5
>>

MATLAB wyświetla domyślnie liczby z dokładnością do czterech cyfr po przecinku. Jeżeli

chcemy zmienić postać prezentowanych liczb możemy to zrobić za pomocą polecenia format.
Dyrektywa ta zmienia tylko sposób wyświetlania liczb a nie ma wpływu na dokładność obliczeń
(wszystkie obliczenia wykonywane są w podwójnej precyzji). Spróbujmy prześledzić sposób
wyświetlania przez MATLAB następującej liczby:

>> a = 1.2345678910
a =

1.2346
>>

format

long

%zmieniamy format

>> a
a =
1.23456789100000

>>

format

short

e

%zmieniamy format

>> a

a =
1.2346e+000

>>

format

long

e

%zmieniamy format

>> a
a =

1.234567891000000e+000
>>

Oczywiście można to także zapisać w taki sposób:

>> a = 1.2345678910
a =

1.2346

8

>>

format

long,

a

%zmieniamy format

a =

1.23456789100000
>> format short e, a

%zmieniamy format

a =

1.2346e+000
>> format long e, a

%zmieniamy format

a =
1.234567891000000e+000

>>

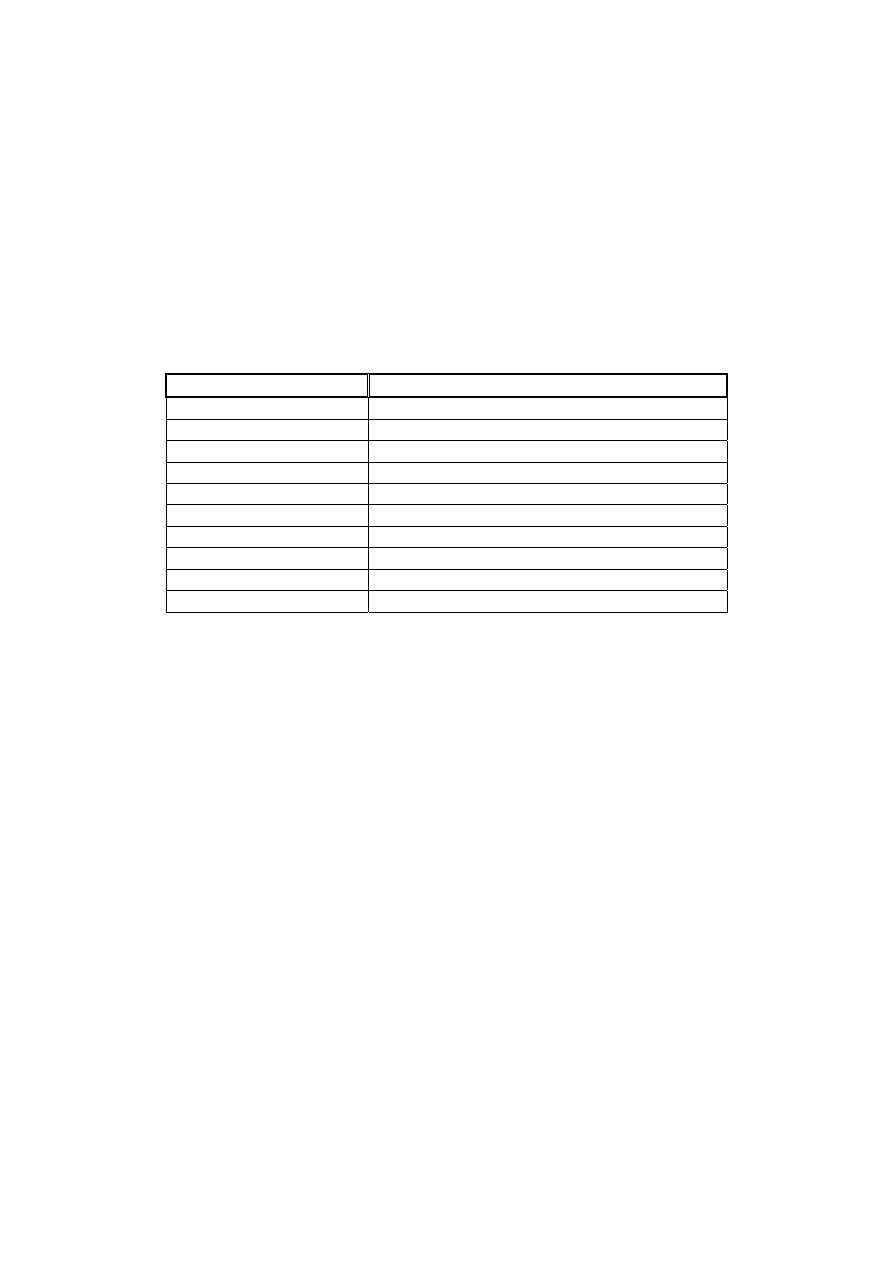
W Tabeli 2 zestawiono funkcje formatujące sposób wyświetlania wyników.

Tabela 2. Rodzaje formatowania w MATLAB-ie.

Polecenie Opis

format short

5 cyfr, reprezentacja stałoprzecinkowa

format long

15 cyfr, reprezentacja stałoprzecinkowa

format short e

5 cyfr, reprezentacja zmiennoprzecinkowa

format long e

15 cyfr, reprezentacja zmiennoprzecinkowa

format short g

5 cyfr, reprezentacja stało- lub przecinkowa

format long g

15 cyfr, reprezentacja stało- lub przecinkowa

format hex

liczba w układzie szesnastkowym

format bank

2 liczby dziesiętne

format rat

przybliżona wartość liczby w postaci ułamka

format +

informacja o znaku liczby

Jeżeli wpisywana zależność jest zbyt długa możemy ją przenieść do następnego wiersza

wstawiając po znaku operacji trzykropek (…) np.

>> a = 1/10 + 2/10 + 3/10 + 4/10 +5/10 + ...
6/10 + 7/10 + 8/10 + 9/10

a =
4.5000

>>

Spróbujmy teraz policzyć objętość walca znając jego promień i wysokość (

h

r

V

⋅

⋅

=

2

π

).

Załóżmy, że promień wynosi 2cm (4cm) a wysokość 10cm.

>> Promien = 2;
>> Wysokosc = 10;
>> Objetosc = pi * Promien * Promien * Wysokość

%pi stała MATLAB-a

Objętość =
125.6637

>>
>> Promien = 4;

%zmieniamy wartość promienia

>> Objetosc = pi * Promien * Promien * Wysokość

%używamy

%klawiszy

Objętość =

%do ponownego

502.6548

%przywołania tej komendy

9

Aby uniknąć wpisywania tych samych komend, możemy do nich wrócić za pomocą

kombinacji klawiszy i użyć ich w nie zmienionej formie lub je zmodyfikować. W Tabeli 3 podano
kombinacje klawiszy służące do edycji linii poleceń.

Tabela 3. Kombinacje klawiszy służące do edycji linii poleceń w MATLAB-ie.

Kombinacja klawiszy

Funkcja

Przywołanie poleceń

↑ <Ctrl>

+

<P>

Przywołuje poprzednią linię (komendę)

↓ <Ctrl>

+

<N>

Przywołuje następną linię (komendę)

Przesunięcie kursora

←

<Ctrl> + <B>

Przesuwa w lewo o jeden znak

→

<Ctrl> + <F>

Przesuwa w prawo o jeden znak

<Ctrl> + →

<Ctrl> + <R>

Przesuwa w prawo o jedne słowo

<Ctrl> + ←

<Ctrl> + <L>

Przesuwa w lewo o jedne słowo

<Home>

<Ctrl> + <A>

Przesuwa na początek linii

<End>

<Ctrl> + <E>

Przesuwa na koniec linii

Usuwanie

<Del>

<Ctrl> + <D>

Usuwa znak w miejscu kursora

<Backspace> <Ctrl> + <H>

Usuwa znak przed kursorem

<Ctrl> + <K>

Usuwa do końca linii

<Esc>

<Ctrl> + <U>

Usuwa całą bieżącą linię

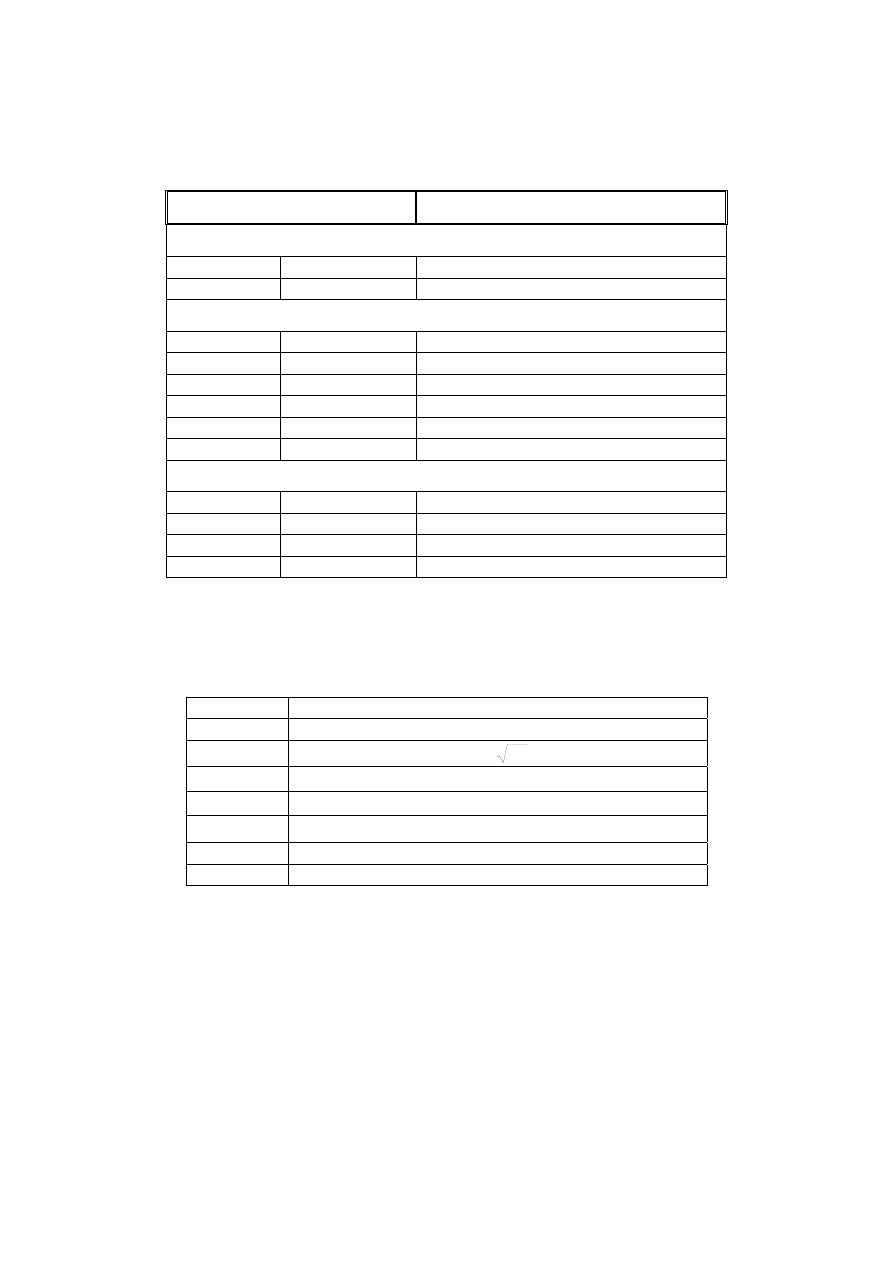
Nie jest konieczne wpisywanie wartości liczbowej π istnieje w MATLAB-ie funkcja

specjalna pi, która robi to za nas. Inne funkcje specjalne zostały podane w Tabeli 4.

Tabela 4. Zmienne specjalne i stałe w MATLAB-ie.

ans

zmienna robocza

pi

3.1415926….

i, j

jednostka liczby urojonej -

1

−

eps

precyzja zmiennoprzecinkowa -

52

2

−

=

ε

realmin najmniejsza dostępna liczba rzeczywista -

1022

2

−

realmax największa dostępna liczba rzeczywista -

1023

2

)

2

(

ε

−

inf

nieskończoność

NaN

wartość nie oznaczona – (not a number)

Nazwy te nie są jednak zastrzeżone dlatego jest możliwość zmiany ich wartości. Znak inf

pojawia się na przykład przy dzieleniu przez zero.

>> 2/0

Warning: Divide by zero.
ans =

Inf
>>

Wyrażenie NaN pojawia się przy działaniach typu 0/0 i Inf-Inf.

Jeżeli chcemy usunąć z przestrzeni roboczej MATLAB-a jakąś zmienną robimy to za pomocą

komendy clear. Komenda clc czyści okno poleceń.

10

>> clear Promien

%usuwa z pamięci roboczej zmienną „Promien”

>> clear all

%usuwa z pamięci roboczej wszystkie zmienne

>>

Podczas wprowadzania części urojonej liczby zespolonej, nie stosujemy znaku mnożenia. Do

wyświetlenia części rzeczywistej i urojonej służą dwie funkcje real i imag.

>> a = 1 + 2i;

>>real(a)

%wyświetla część rzeczywista liczby zespolonej

ans =

1
>>imag(a)

%wyświetla część urojona liczby zespolonej

ans =

2
>>

Wartość bezwzględną liczby (moduł) obliczamy za pomocą funkcji abs

>> abs(2)
ans =

2
>> abs(-2)

ans =
2

>> abs(1 + 2i)
ans =

2.2361
>>

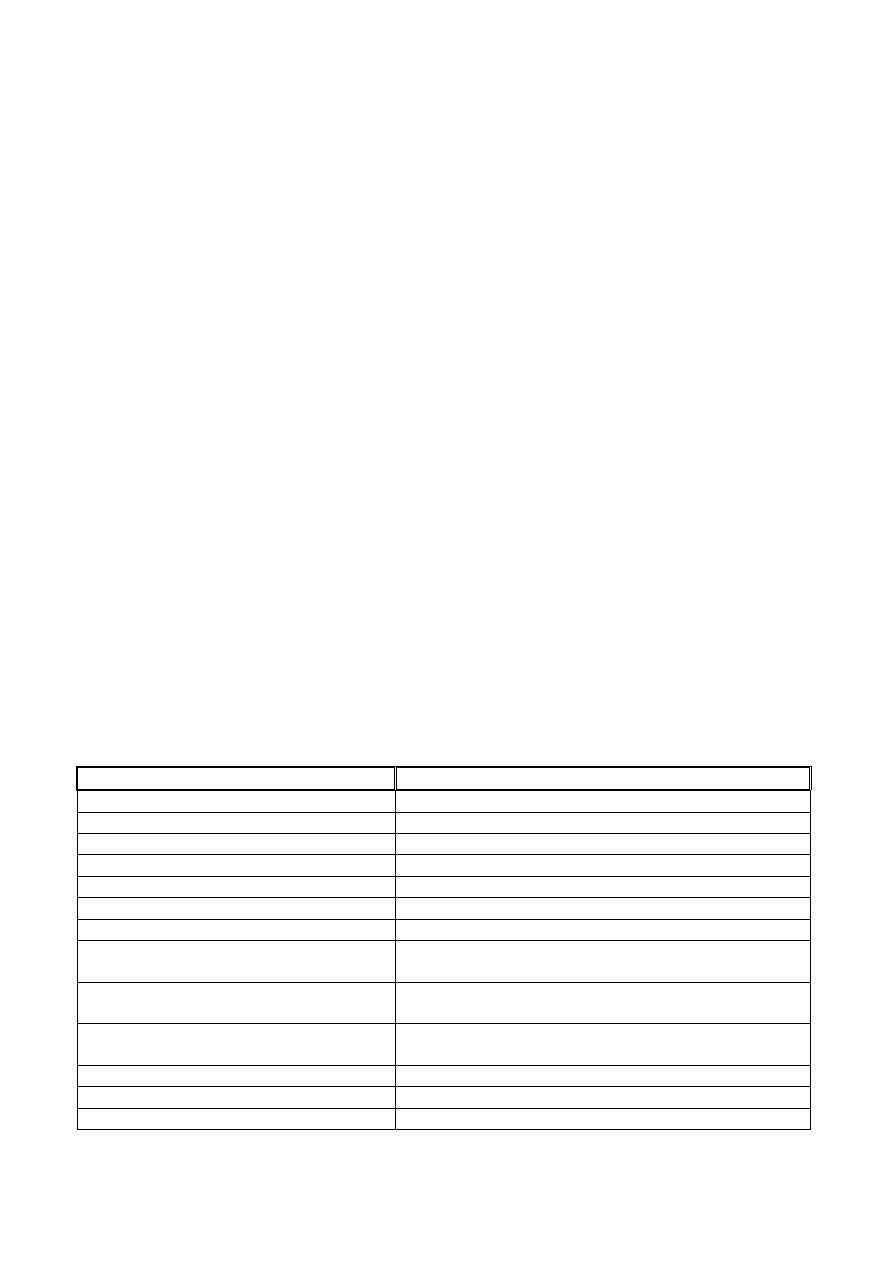
Oczywiście MATLAB zawiera dużo więcej funkcji matematycznych. Kilkanaście z nich

zostało przedstawionych w Tabeli 5.

Tabela 5. Elementarne funkcje matematyczne w MATLAB-ie.

Nazwa funkcji

Objaśnienie

sqrt(x)

pierwiastek

abs(x)

wartość bezwzględna

exp(x)

e do potęgi x

log(x)

logarytm naturalny

log2(x)

logarytm o podstawie 2

log10(x)

logarytm o podstawie 10

sign(x)

zwraca -1 jeżeli x<0, 0 jeżeli x=0 i 1 jeżeli x>0

sin(x), cos(x), tan(x),

cot(x)

funkcje trygonometryczne

sinh(x), cosh(x), tanh(x),
coth(x)

funkcje hiperboliczne

asin(x), acos(x), atan(x),

acot(x)

funkcje odwrotne do trygonometrycznych

gcd(x, y)

największy wspólny podzielnik

lcm(x, y)

najmniejszy wspólny podzielnik

rem(x, y)

reszta z dzielenia

11

Oto

przykład użycia funkcji matematycznych służących do obliczenia poniższych wielkości:

2

3

=

x

,

2

/

2

2

1

x

e

y

−

⋅

=

π

>> x = sqrt(3)/2
x =

0.8660

>> y = exp(-(x^3)/2)/sqrt(2*pi)
y =

0.2883
>>

MATLAB udostępnia także szereg funkcji służących do zaokrąglania, (patrz przykład poniżej

i Tabela 6).

>> A = 2.31;
>> ceil(A)

ans =
3
>> floor(A)

ans =
2

>> fix(A)
ans

2
>> round(A)
ans

2
>>

Tabela 6. Funkcje zaokrągleń w MATLAB-ie.

Funkcja Opis

ceil(x)

zaokrągla w górę (+∞)

floor(x)

zaokrągla w dół (–∞)

fix(x)

zaokrągla w kierunku zera

round(x)

zaokrągla do najbliżej liczby całkowitej

4. Wprowadzanie łańcuchów i proste operacje na nich

Możemy także wprowadzać do MATLAB-a tekst (string) jako ciąg znaków (characters)

w tym celu używamy apostrofów np.

>> A = ‘K’
A =

K
>>

albo

12

>> B = ‘Lodz to ciekawe miasto.’
B =

Lodz to ciekawe miasto.
>>

Możliwe jest dodawanie do siebie wyrazów (funkcja strcat) np.

>> A = ‘Lodz’;
>> B = ‘to ciekawe miasto.’;

>> C = strcat(A, B)
C =
Lodzto ciekawe miasto.

>>

Widzimy, że potrzebny jest odstęp pomiędzy pierwszym a drugim członem, możemy to

uzyskać wstawiając spację za pierwszym wyrazem a apostrofem, lub w drugim wyrazie za
apostrofem a początkiem wyrazu.

>> A = ‘Lodz ’;

>> B = ‘to ciekawe miasto.’;
>> C = strcat(A, B)

C =
Lodz to ciekawe miasto.

>>

Bardzo często będzie wykorzystywana funkcja ischar w celu sprawdzenia czy dana

wielkość jest znakiem (łańcuchem) czy liczbą. Funkcja ta zwraca: prawdę (1) jeżeli jest to wyraz,
w pozostałych przypadkach – fałsz (0).

>> A = ‘Lodz’;

>> B = 5;
>> ischar(A)

ans =
1

>> ischar(B)
ans =
0

>>

Możemy także zmieniać litery w wyrazie na małe (lower) lub duże (upper), także tutaj

może być stosowana funkcja length liczącą ilość znaków w wyrażeniu lub macierzy.

>> A = ‘Lodz’
ans =

Lodz
>> lower(A)
ans =

lodz
>> upper(A)

ans =
LODZ

>> length(A)
ans =

4

13

Odwołanie się do poszczególnych znaków w wyrażeniu może być zrobione następująco:

>> A = ‘Lodz’;
>> A(1)

ans =
L
>> B = A(2)

B =
o

>>

Jak z powyższego wynika operacja ta wyświetla znaki łańcucha odpowiadające liczbom

umieszczonym w nawiasie, licząc od lewej strony łańcucha.

5. Literatura

1.

http://www.mathworks.com

2.

Kuncicky D. C.

MATLAB programming, Person Education, Inc, 2004,

3.

Mrozek B., Mrozek Z.

MATLAB i Simulink – Poradnik użytkownika, Helion, Warszawa, 2004,

4.

Zalewski A., Cegieła R.

MATLAB – obliczenia numeryczne i ich zastosowanie, Wydawnictwo

Nakom, Poznań, 1996,