Ćwiczenie nr 2, strona 1

Ćwiczenie nr 2

− „Potencjał sił masowych, powierzchnie ekwipotencjalne, rozkłady ciśnienia”.

Równania równowagi płynu
Zależności pomiędzy składowymi siły masowej

]

,

,

[

z

y

x

f

f

f

f

=

r

a ciśnieniem hydrostatycznym p

obowiązujące dla płynu znajdującego się w stanie równowagi mają postać

x

f

x

p

⋅

ρ

=

∂

∂

,

y

f

y

p

⋅

ρ

=

∂

∂

,

z

f

z

p

⋅

ρ

=

∂

∂

.

We współrzędnych cylindrycznych równania równowagi przyjmują postać:

r

f

r

p

⋅

ρ

=

∂

∂

,

θ

⋅

ρ

=

θ

∂

∂

f

p

r

1

,

z

f

z

p

⋅

ρ

=

∂

∂

.

kierunek promieniowy

kierunek obwodowy

kierunek osiowy

Potencjał sił masowych
Funkcja skalarna współrzędnych przestrzennych jednoznacznie opisująca pole sił masowych:

x

f

x

U =

∂

∂

,

y

f

y

U =

∂

∂

,

z

f

z

U =

∂

∂

.

Potencjał sił masowych istnieje tylko wtedy, kiedy praca wykonana w polu sił masowych nie zależy
od drogi, po której nastąpiło przesunięcie jednostkowej masy od punktu "A" do punktu "B".

A

B

B

A

B

A

U

U

r

d

f

W

−

=

⋅

=

∫

→

→

r

r

,

gdzie r

dr to wektor różniczkowego przesunięcia wzdłuż obranej drogi. Do sił masowych, które

mają potencjał zaliczamy m.in. siły: grawitacji, bezwładności, elektrostatyczne.
Jeżeli płyn znajduje się stanie równowagi to istnieje związek pomiędzy różniczką zupełną ciśnienia
a różniczką zupełną potencjału sił masowych

dU

dp

⋅

ρ

=

.

Równanie to wskazuje, że powierzchnie stałego potencjału (U=const) są jednocześnie
powierzchniami stałego ciśnienia (p=const). Kierunek najszybszego wzrostu ciśnienia potencjału sił
masowych wyznaczają odpowiednio wektory:













∂

∂

∂

∂

∂

∂

=

z

p

y

p

x

p

p

,

,

grad

,













∂

∂

∂

∂

∂

∂

=

z

U

y

U

x

U

U

,

,

grad

U

p

grad

grad

⋅

ρ

=

.

Związek pomiędzy potencjałem sił masowych a ciśnieniem można wykorzystać do obliczenia
rozkładu ciśnienia:

A

B

p

p

U

U

dp

B

A

−

=

ρ

∫

,

kiedy gęstość jest funkcją ciśnienia )

( p

ρ

=

ρ

− płyn barotropowy,

)

(

A

B

A

B

U

U

p

p

−

⋅

ρ

=

−

,

kiedy gęstość jest stała

const

=

ρ

− płyn nieściśliwy.

Wyznaczanie rozkładu potencjału z dokładnością do stałej
1. Całkowanie po dowolnie obranej drodze wyrażenia

r

d

f

r

r

⋅

, np. wzdłuż drogi składającej się z

odcinków równoległych do osi układu współrzędnych (x,y,z)

∫

∫

∫

+

+

+

=

B

A

B

A

B

A

z

z

B

B

z

y

y

A

B

y

x

x

A

A

x

A

B

dz

z

y

x

f

dy

z

y

x

f

dx

z

y

x

f

U

U

)

,

,

(

)

,

,

(

)

,

,

(

.

2. Całkowanie równań równowagi płynu.

)

,

(

)

,

,

(

)

,

(

)

,

,

(

)

,

,

(

z

y

C

z

y

x

F

z

y

C

dx

f

z

y

x

U

z

y

x

f

x

U

x

x

x

+

=

+

=

→

=

∂

∂

∫

,

)

(

)

,

,

(

)

(

)

,

(

)

,

,

(

z

C

z

y

x

F

z

C

dy

y

F

f

z

y

C

z

y

x

f

y

U

y

x

y

y

+

=

+















∂

∂

−

=

→

=

∂

∂

∫

,

Ćwiczenie nr 2, strona 2

C

z

y

x

F

C

dz

z

F

z

F

f

z

C

z

y

x

f

z

U

z

y

x

z

z

+

=

+













∂

∂

−

∂

∂

−

=

→

=

∂

∂

∫

)

,

,

(

)

(

)

,

,

(

.

W rezultacie uzyskuje się rozwiązanie ogólne o postaci

C

z

y

x

F

z

y

x

F

z

y

x

F

z

y

x

U

z

y

x

+

+

+

=

)

,

,

(

)

,

,

(

)

,

,

(

)

,

,

(

Zadanie 1
Prostopadłościenny zbiornik wypełniony częściowo cieczą porusza się poziomo ze stałym
przyspieszeniem. Wyznaczyć:
a) potencjał sił masowych i równanie powierzchni ekwipotencjalnej,
b) maksymalne przyspieszenie, przy którym ciecz się nie przeleje przez krawędź zbiornika,
c) rozkład ciśnienia w cieczy.

Zadanie 2
Otwarta wirówka wolnoobrotowa jest częściowo wypełniona cieczą. Wyznaczyć:
a) potencjał sił masowych i równanie powierzchni ekwipotencjalnej,
b) maksymalną prędkość obrotową, przy której ciecz się nie przeleje przez krawędź zbiornika,
c) objętość cieczy, która się wyleje do momentu aż powierzchnia swobodna dotknie dna zbiornika,
d) rozkład ciśnienia w cieczy,

Zadanie 3
Zamknięta wirówka szybkoobrotowa jest wypełniona częściowo dwiema nie mieszającymi się
cieczami o różnej gęstości. Wyznaczyć:
a) kryterium określające kiedy można zaniedbać wpływ sił grawitacji,
b) potencjał sił masowych i rozkład ciśnienia w wirówce przy pominięciu sił grawitacji.

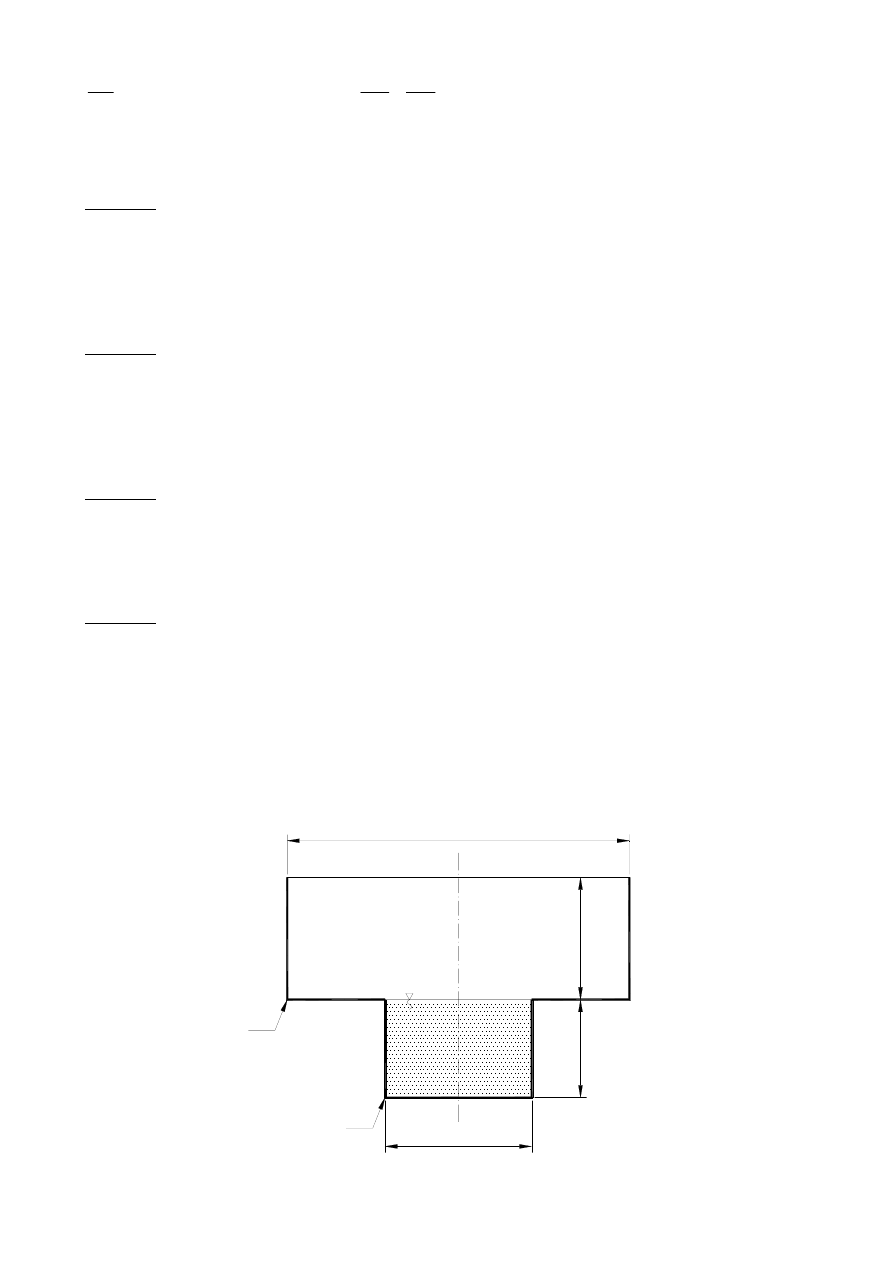
Zadanie 4
Dolną część wirówki przedstawionej na rysunku wypełniono całkowicie cieczą o gęstości

ρ.

Średnica i wysokość dolnej części wirówki wynoszą odpowiednio d i h, zaś średnica i wysokość
górnej części wirówki wynoszą odpowiednio D i H. Wirówkę wprawiono w ruch obrotowy wokół
jej osi symetrii. Wyznaczyć:
a) maksymalną częstość obrotów, przy której ciecz nie przeleje się przez górną krawędź wirówki,
b) objętość cieczy jaka pozostanie w dolnej części wirówki oraz ciśnienie w punktach A i B, kiedy
powierzchnia swobodna cieczy osiągnie górną krawędź wirówki.
W obliczeniach przyjąć: d=0.3 m, D=0.7 m, h=0.2 m, H=0.25 m,

ρ=1200 kg/m

3

.

d

h

H

D

B

A