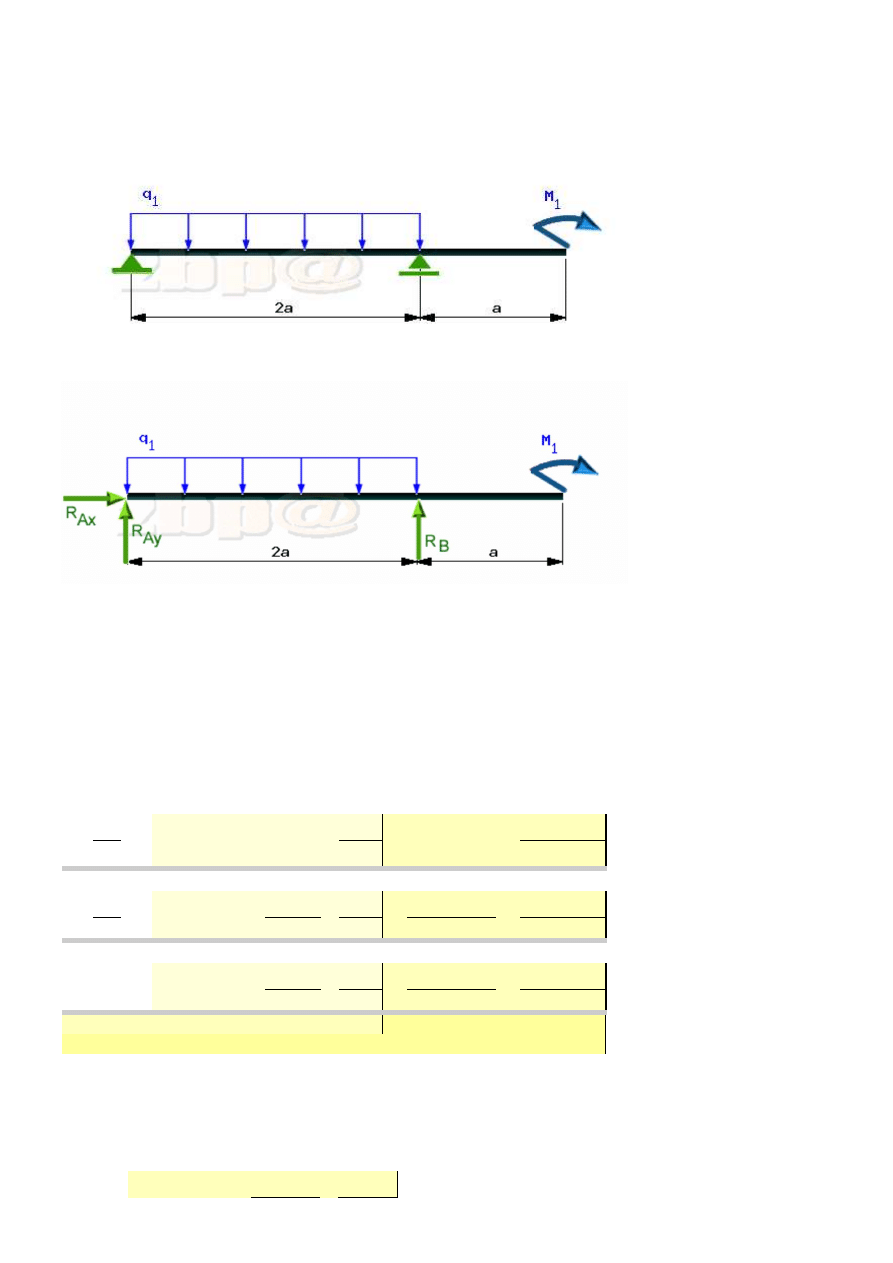
Dla belki przedstwionej na rysunku i obciążonej w podany sposób wyznaczyć ugięcie i jej kąt
obrotu

gdy:
a=500 mm
q

1

= 1 N/mm

M

1

= 0.4q

1

a

2

= 100000 Nmm

Po uwolnieniu od więzów, możemy napisać warunki równowagi

ΣM

iA

= + M

1

+ q

1

—2a—a - R

B

—2a = 0

ΣM

iB

= + M

1

- q

1

—2a—a + R

Ay

—2a = 0

Wyznaczone reakcje z powyższego układu równań wynoszą:

R

Ay

= 0.8 q

1

a = 400

N,

R

B

= 1.2 q

1

a = 600

N

Równanie różniczkowe ugięcia belki, oraz kolejne całkowania tego równania zapisz w
następującej postaci

EJ

z

d

2

y

=

+ R

Ay

—x -

q

1

—x

2

+ R

B

—(x-2a) +

q

1

—(x-2a)

2

dx

2

2

2

EJ

z

dy

=

C +

R

Ay

—x

2

-

q

1

—x

3

+

R

B

—(x-2a)

2

+

q

1

—(x-2a)

3

dx

2

6

2

6

EJ

z

y = D + C—x +

R

Ay

—x

3

-

q

1

—x

4

+

R

B

—(x-2a)

3

+

q

1

—(x-2a)

4

6

24

6

24

0 < x < 2 a

2 a < x < 3 a

Do wyznaczenia stałych całkowania wykorzystaj warunki brzegowe

podpora A to x=0 (występuje w przedziale 1) ugięcie w niej wynosi y=0. Ten warunek można
opisać równaniem:

EJ

z

0 = D

+ C—0 + R

Ay

—(0)

3

- q

1

—(0)

4

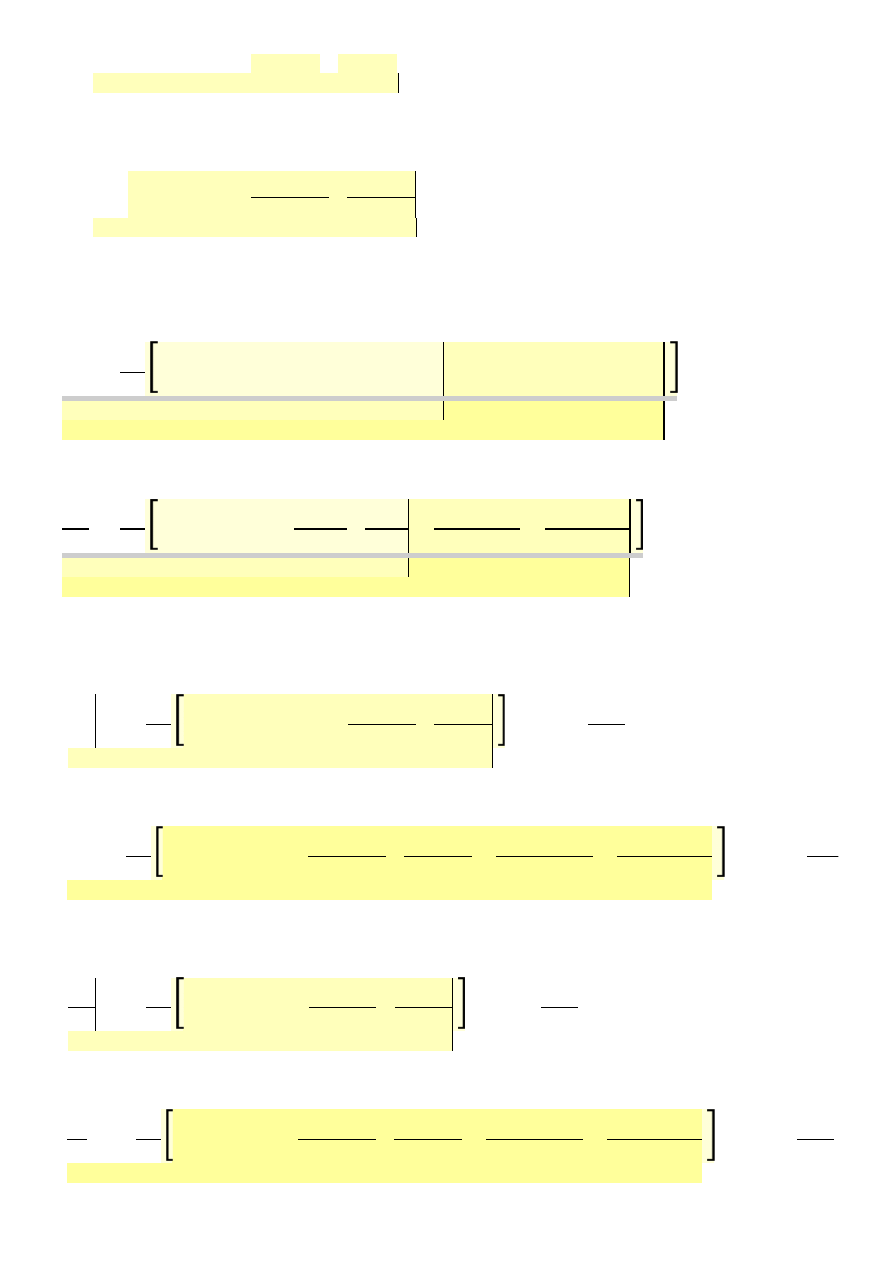
6

24

0 < x < 2 a

podpora B to x=2a (występuje w przedziale 1) ugięcie w niej wynosi y=0. Ten warunek można
opisać równaniem:

EJ

z

0 = D + C—2a +

R

Ay

—(2a)

3

-

q

1

—(2a)

4

6

24

0 < x < 2 a

Z ostatnich dwu równań wyznaczasz stałe całkowania D=0 i C=-0.2q

1

a

3

Teraz równanie ugięcia belki wygląda następująco:

y =

1

+ -0.200—q

1

a

3

—x +

R

Ay

—x

3

-

q

1

—x

4

+

R

B

—(x-2a)

3

+

q

1

—(x-2a)

4

EJ

z

6

24

6

24

0 < x < 2 a

2 a < x < 3 a

a równanie katów obrotu:

dy

=

1

-0.200—q

1

a

3

+

R

Ay

—x

2

-

q

1

—x

3

+

R

B

—(x-2a)

2

+

q

1

—(x-2a)

3

dx

EJ

z

2

6

2

6

0 < x < 2 a

2 a < x < 3 a

ugięcia dla x=500, 1500 mm.

x=a

(x=500)

to przedział 1 ugięcie wynosi zatem

y

x=1a

=

1

+ -0.200q

1

a

3

—a +

R

Ay

—(a)

3

-

q

1

—(a)

4

= -0.108

q

1

a

4

EJ

z

6

24

EJ

z

0 < x < 2 a

x=3a

(x=1500)

to przedział 2 ugięcie wynosi zatem

y

x=3a

=

1

+

-0.200q

1

a

3

—3a

+

R

Ay

—(3a)

3

-

q

1

—(3a)

4

+

R

B

—(3a-2a)

3

+

q

1

—(3a-2a)

4

= -0.133

q

1

a

4

EJ

z

6

24

6

24

EJ

z

2 a < x < 3 a

katy obrotu dla x=500, 1500 mm.
x=a

(x=500)

to przedział 1 ugięcie wynosi zatem

dy

x=1a

=

1

-0.200q

1

a

3

+

R

Ay

—(a)

2

-

q

1

—(a)

3

= 0.033

q

1

a

3

dx

EJ

z

2

6

EJ

z

0 < x < 2 a

x=3a

(x=1500)

to przedział 2 ugięcie wynosi zatem

dy

x=3a

=

1

-0.200q

1

a

3

+

R

Ay

—(3a)

2

-

q

1

—(3a)

3

+

R

B

—(3a-2a)

2

+

q

1

—(3a-2a)

3

= -0.333

q

1

a

3

dx

EJ

z

2

6

2

6

EJ

z

2 a < x < 3 a

maksymalne ugięcie belki f

max

=0.006 (-0.133)

q

1

a

4

EJ

z

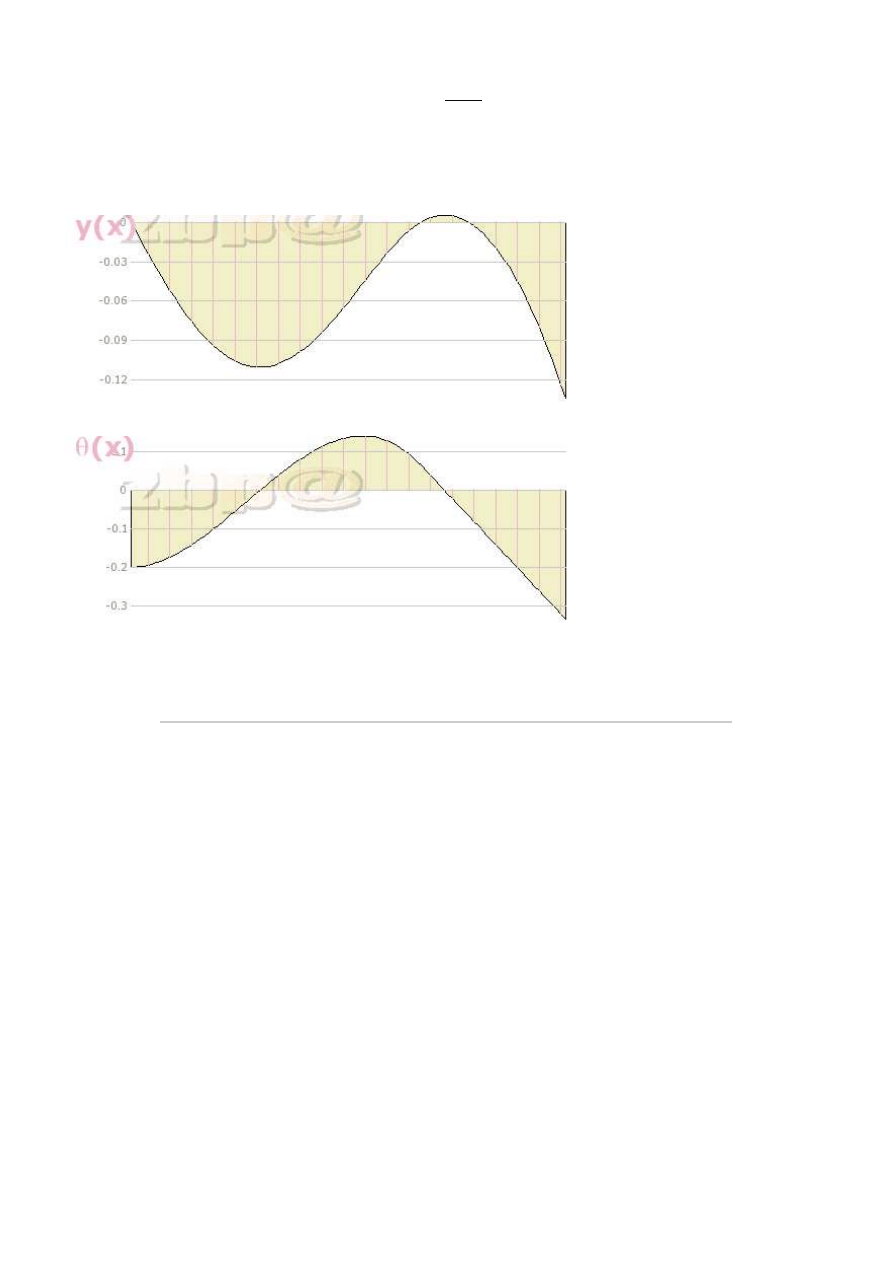
Ugięcie jak i kąt obrotu belki możemy obliczyć w dowolnym jej punkcie, a te wyniki
przedstawić na wykresach poniżej

©2009-2010 SoM. All Rights Reserved.