
STATYSTYCZNA ANALIZA DANYCH
STATYSTYCZNA ANALIZA DANYCH
V semestr studiów inżynierskich w PJWSTK,
V semestr studiów inżynierskich w PJWSTK,
2008/09
2008/09
Prowadząca: dr hab. Elżbieta Ferenstein, profesor PJWSTK
Cel wykładu
- poznanie podstaw analizy
danych
•
statystyka opisowa
statystyka opisowa
•
modelowanie probabilistyczne
modelowanie probabilistyczne
•
wnioskowanie statystyczne
wnioskowanie statystyczne

Tematyka wykładu SAD
Metody graficzne prezentacji danych jakościowych i
ilościowych. Statystyki próbkowe. Histogramy a gęstości
prawdopodobieństwa, kwantyle, wykresy kwantylowe.
Prawdopodobieństwo, niezależność zdarzeń, twierdzenie
Bayes’a.
Zmienne losowe, rozkłady prawdopodobieństwa i ich
parametry, wybrane rozkłady prawdopodobieństwa.
Podstawowe statystyki i ich własności, przedziały ufności,
testy parametryczne dla średnich i wariancji jednej i dwu
populacji, regresja liniowa jednowymiarowa.


Zaliczenie ćwiczeń:
skala punktowa: 100 punktów = 75
punktów za 3 kolokwia i 25 punktów za aktywność na
zajęciach
Ocena z ćwiczeń
: 91 pkt: bdb; 81pkt: db+; 71: db;
61: dost +; 51: dost.
Ocena dostateczna zalicza ćwiczenia i jest warunkiem
dopuszczenia do egzaminu. Niepowodzenie: 2 x egzamin?
Ćwiczenia laboratoryjne - 30% czasu, 70% czasu – ćwiczenia
rachunkowe.
Na ćwiczeniach obowiązuje znajomość materiału
omawianego na wykładach.
Egzamin:
zadania z zakresu wykładu i ćwiczeń.
Wymagania wstępne
: Analiza I i II, Matematyka Dyskretna.
Software
: pakiet SAS, Excel.

Literatura podstawowa:
J acek Koronacki, J an Mielniczuk: Statystyka dla studentów kierunków
technicznych i przyrodniczych, Wydawnictwa Naukowo-Techniczne
2001.
Elżbieta Ferenstein: Statystyczna Analiza Danych, slajdy na FTP
(public), katalog elaw, folder SAD2008/09
Literatura uzupełniająca:
J anina J óźwiak, J arosław Podgórski: Statystyka od podstaw, PWE,
Warszawa 2001(3), wyd. V (VI).
Przemysław Grzegorzewski i inn.: Rachunek prawdopodobieństwa i
statystyka, WSISiZ, Warszawa 2001.
Amir D. Aczel: Statystyka w zarządzaniu, PWN, Warszawa 2000.
K. Bobecka, P. Grzegorzewski, J . Pusz: Zadania z rachunku
prawdopodobieństwa i statystyki, WSISiZ, Warszawa 2003.
Mieczysław Sobczyk: Statystyka, PWN 2005.
Marek Cieciura, J anusz Zacharski: Metody probabilistyczne w ujęciu
praktycznym, Vizja 2007.
STATYSTYKA OPISOWA
Techniki wstępnej analizy danych i ich
prezentacji:
•
gromadzenie
gromadzenie
,
,
przechowywanie danych, analiza danych
surowych
•
p
p
rezentacja
rezentacja
danych: tabele, wykresy, parametry
liczbowe
obliczane
dla danych
.
Cel:
•
charakteryzacja
charakteryzacja
danych - w
zwięzłej formie
odzwierciedlająca pewne ich
cechy
, np. średni dochód,
średnie zużycie paliwa, ..
•
odnalezienie
odnalezienie
różnego rodzaju
regularności
( nieregularności ) ukrytych w danych,
zależności
między podzbiorami danych.

Obejrzenie danych surowych – nieprzetworzonych,
niepogrupowanych, niezorganizowanych.
Poznanie sposobu i celu zebrania danych:
jaką cechę mierzono ( obserwowano ) ?,
w jakich jednostkach ?,
ile wykonano obserwacji ( liczebność zbioru danych ), w jakich
warunkach – czy nie zgubiono części danych, dane brakujące, czy
jest możliwość przekłamań ?
czy celem zebrania danych ma być odpowiedź na konkretne pytania ?

Cel badania statystycznego: poznanie charakterystyk dużej zbiorowości
obiektów ( osoby, przedmioty, zjawiska, możliwe wyniki
eksperymentów ... ) na podstawie obserwacji cech (danych ) jedynie
niektórych wylosowanych obiektów
Populacja:
zbiór obiektów badanych ze względu na określoną cechę
nazywaną
zmienną
Próbka:
zbiór cech zbadanych obiektów populacji

Populacja
badana cecha zebrane dane
(zmienna) ( próbka )
zbiór detali jakość detalu zbiór jakości zbadanych
detali
zbiór komputerów liczba awarii kompu- zbiór liczb awarii wybranych
w sieci tera w danym okresie komputerów w danym czasie
zbiór projektów ocena projektu zbiór ocen wybranych
przysłanych na konkurs projektów
zbiór osób w staż pracy zbiór staży pracy (lat pracy)
zespole pracowników wylosowanych osób

P
r
z
y
k
ł
a
d
.
W
3
0
r
z
u
t
a
c
h
k
o
s
t
k
ą
s
z
e
ś
c
ie
n
n
ą
o
t
r
z
y
m
a
n
o
lic
z
b
y
o
c
z
e
k
:
3
5
6
1
4
6
2
3
5
6
2
6
5
3
5
4
6
6
5
1
5
2
4
3
6
1
1
2
1
3
3
6
w
a
r
t
o
ś
ć
(
l
i
c
z
b
a
o
c
z
e
k
)
1
2
3
4
5
6
l
i
c
z
n
o
ś
ć
(
l
i
c
z
b
a
w
y
s
t
ą
p
i
e
ń
)
5
4
6
3
5
7
c
z
ę
s
t
o
ś
ć
30
5
30
4
30
6
30
3
30
5
30
7
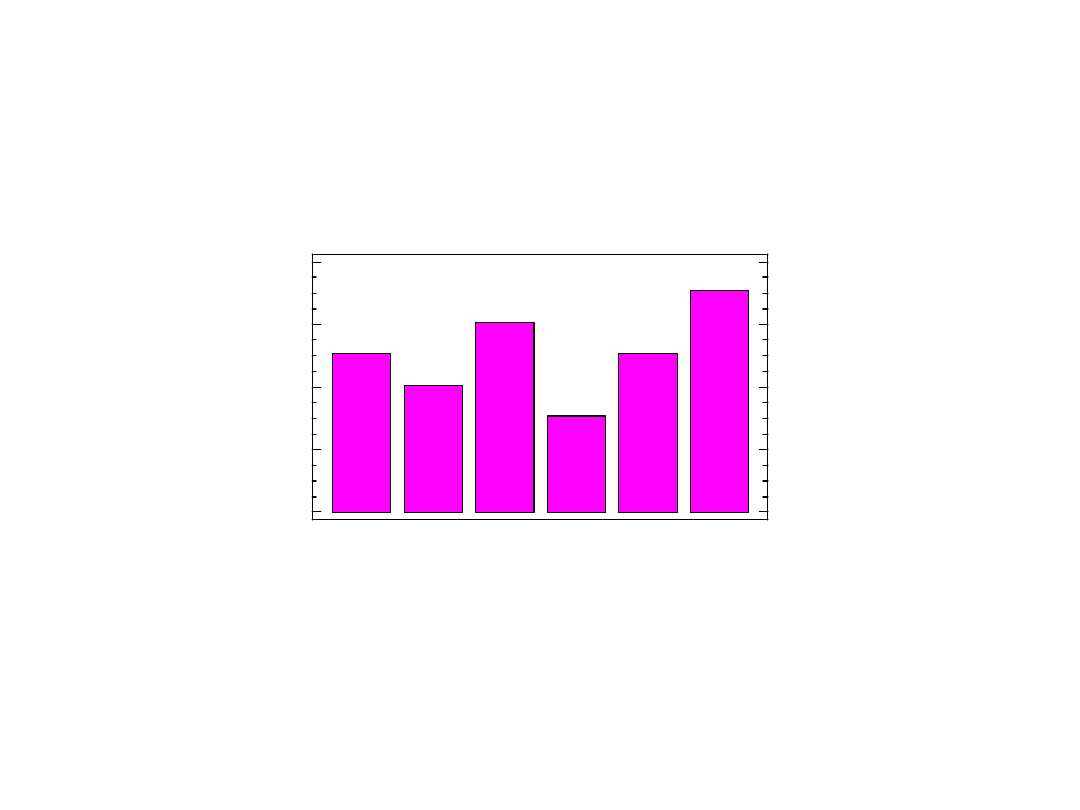
Diagram
liczebności
0
2
4
6
8
1
2
3
4
5
6
Liczba oczek
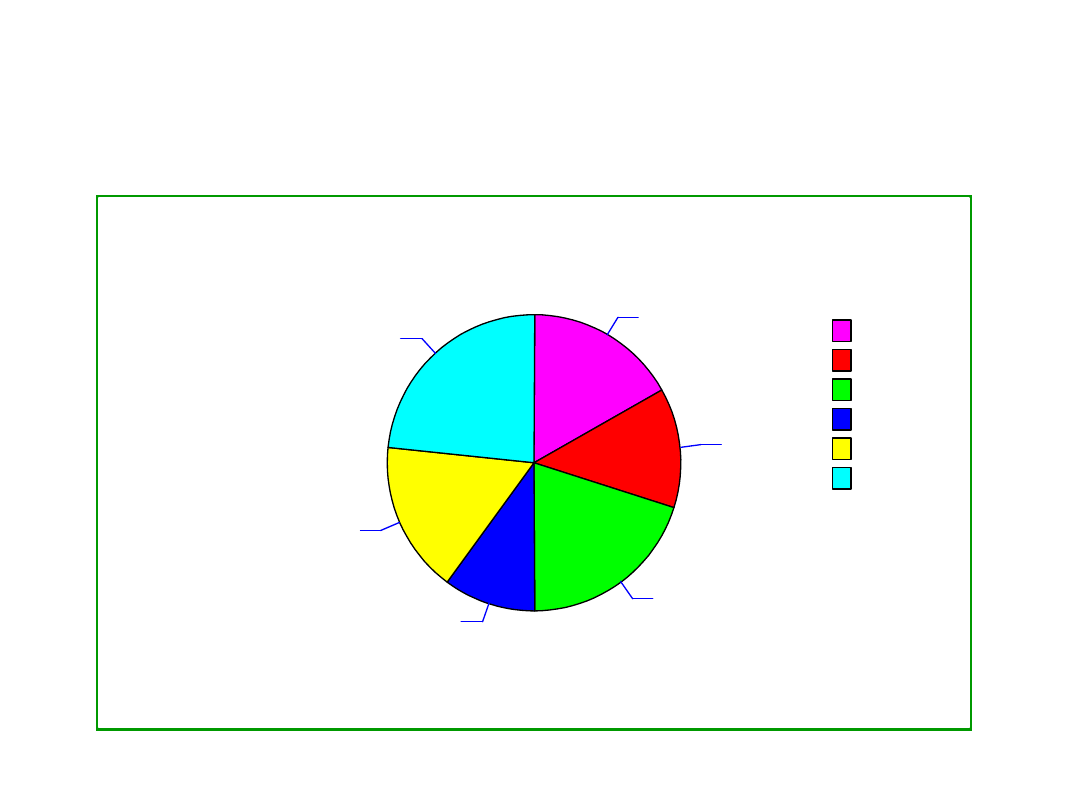
Wykres kołowy
1
2
3
4
5
6
16,67%
13,33%
20,00%
10,00%
16,67%
23,33%
Metody opisu danych
jakościowych
wykres słupkowy, wykres
kołowy
Przykład.
Liczby studentów w kraju na różnych
kierunkach studiów w roku ak. 1990/91 oraz 1997/98
podane są w tabeli. Wykonamy:
wstępną analizę danych
wykresy słupkowe (procentowe, ilościowe)
wykresy kołowe

1. pedagogiczne 99 552 18,3 91 100
14,0
2. humanistyczne 69 088 12,7 110 565
8,1
3. prawne i nauki 133 824 24,6
566 475
41,5
społeczne
4. nauki ścisłe i
144 704 26,6
292 110
21,4
przyrodnicze
5. medyczne 81 600 15,0 95 550
7,0
6. pozostałe 15 232 2,8 109 200
8,0
ogółem
ogółem
544 000
100
1 365 000
100
Grupa rok 1990/91 rok
Grupa rok 1990/91 rok
1997/98
1997/98
kierunków
kierunków
liczba % liczba
liczba % liczba
%
%
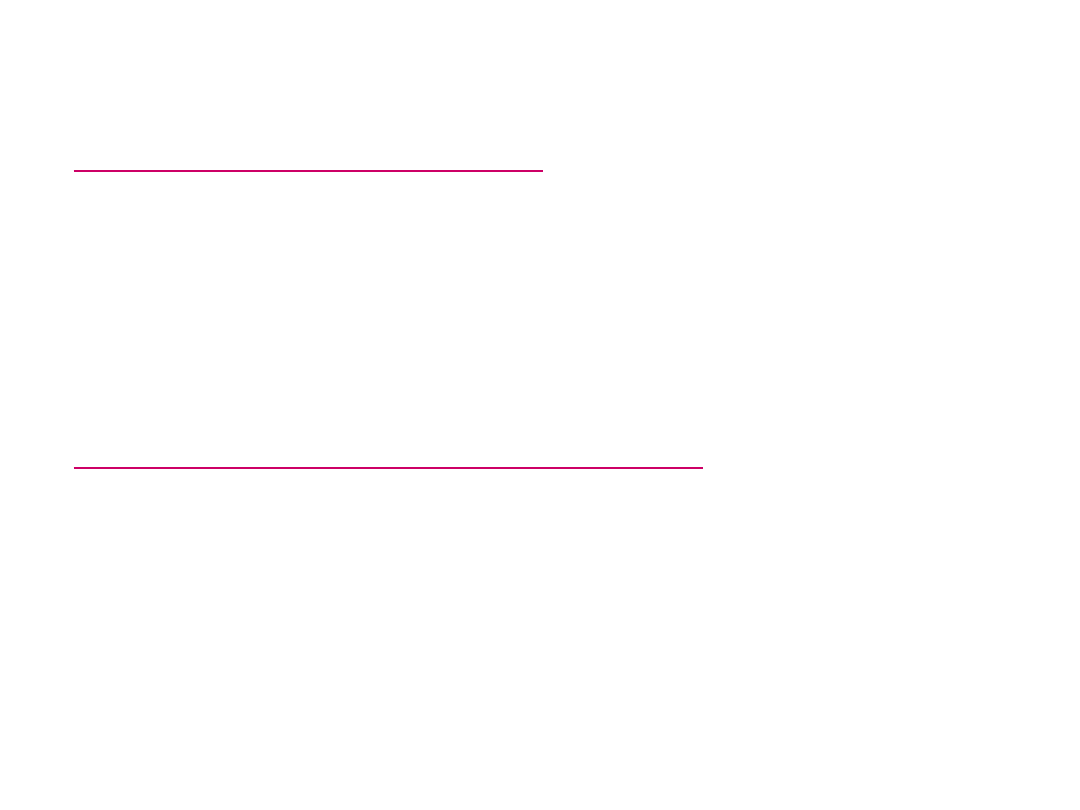
Wstępna analiza danych
Wstępna analiza danych
Opis danych surowych:
2 próbki
o liczebnościach n = 544000 oraz m =
1365000
•
cecha jakościowa
:
:
grupa kierunków studiów
•
6 kategorii
( klas, atrybutów ) cechy
•
atrybuty
: grupa kierunków pedagogicznych,
humanistycznych, medycznych, ....
Najliczniejsze grupy kierunków:
nauki ścisłe i przyrodnicze
nauki ścisłe i przyrodnicze
w 1990/91
w 1990/91
roku
roku
prawo i nauki społeczne
prawo i nauki społeczne
w 1997/98 roku
w 1997/98 roku
Procentowy udział klasy =
( liczność klasy/ liczebność próbki ) x
100% =
częstość x 100%
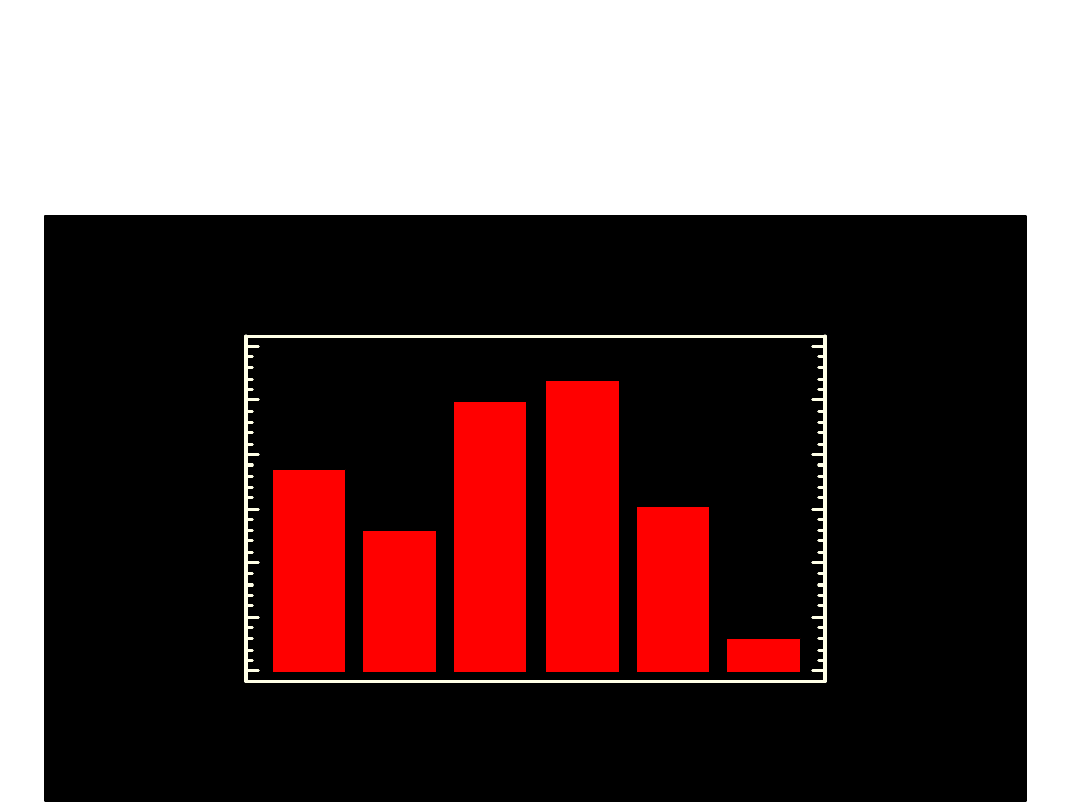
p
ro
ce
n
t
0
5
10
15
20
25
30
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
Wykres słupkowy procentowego
udziału grup kierunków studiów
w r. ak.
1990/91
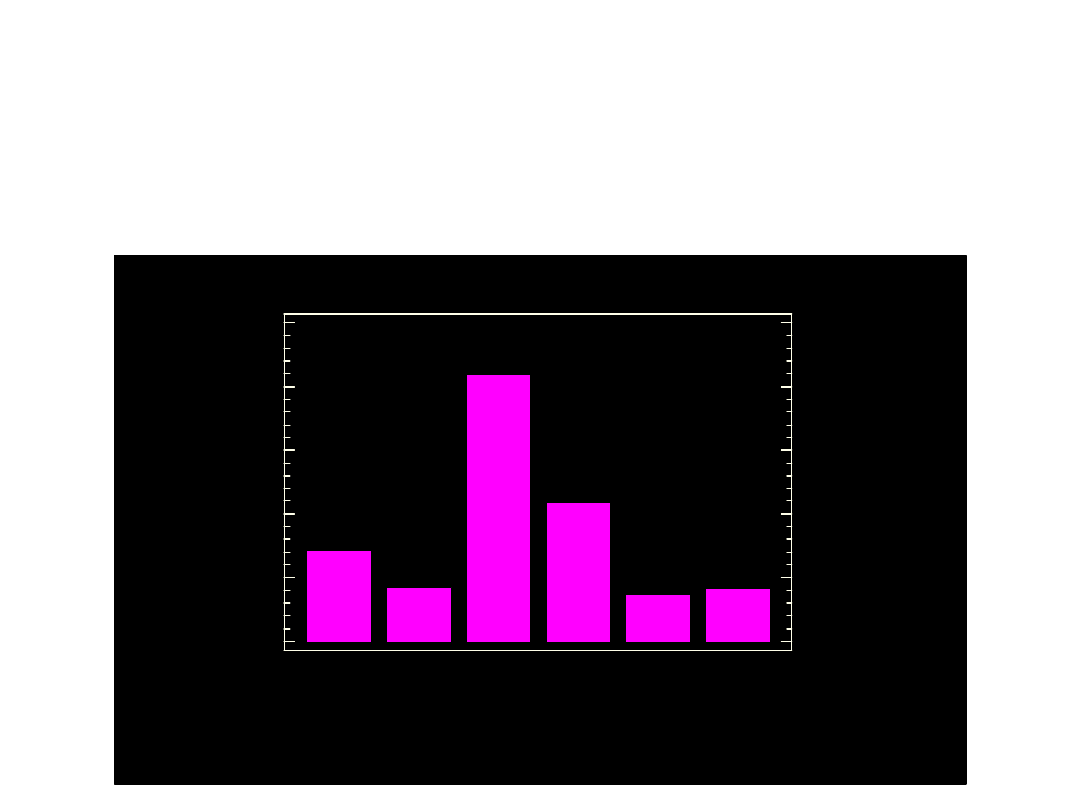
p
ro
ce
n
t
0
10
20
30
40
50
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
Wykres słupkowy procentowego
udziału grup kierunków studiów
w r. ak. 1997/98
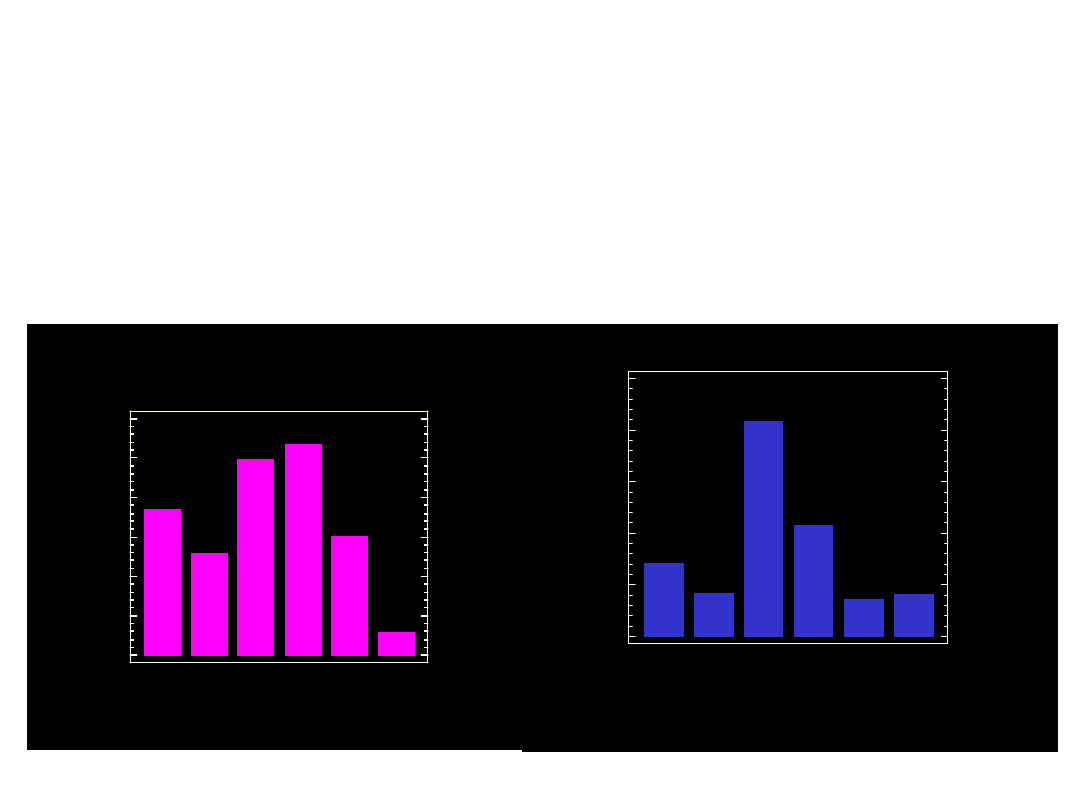
p
ro
ce
n
t
0
5
10
15
20
25
30
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
p
ro
ce
n
t
0
10
20
30
40
50
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
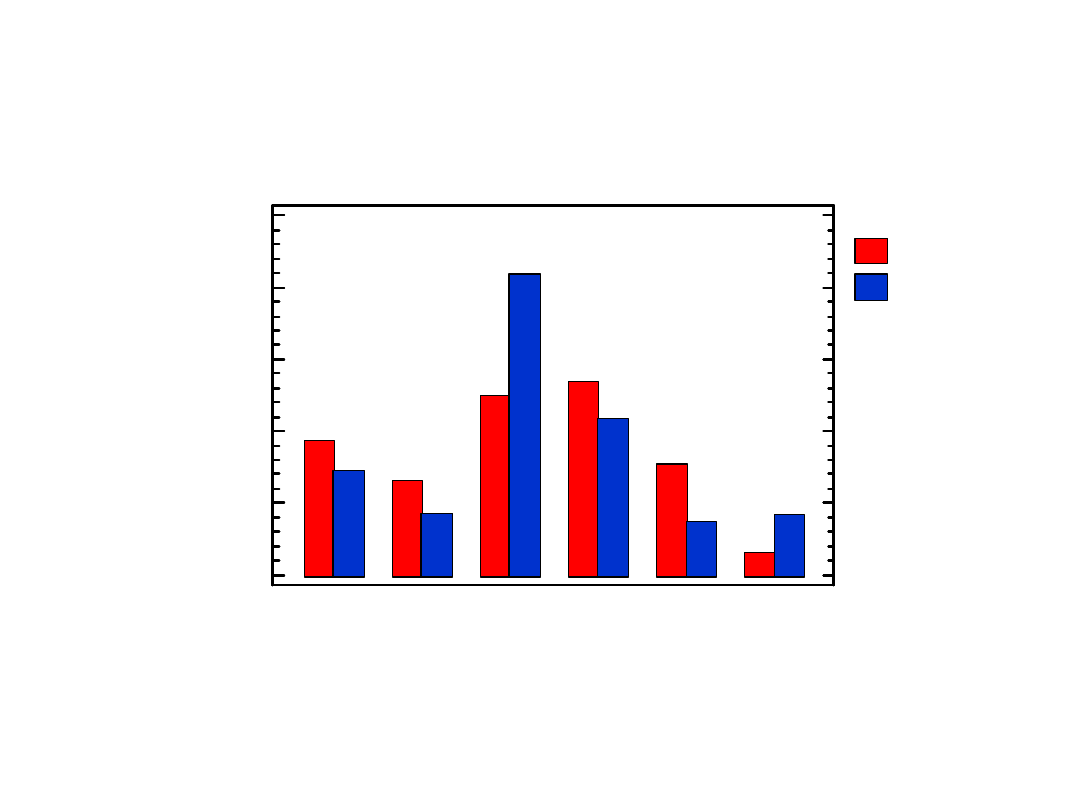
Wykresy słupkowe
1990/91
1997/98
p
ro
ce
n
t
1990/91
1997/98
0
10
20
30
40
50
pedag
.
huma
n.
prawne,sp
oł.
ścisłe,przyr.
med
..
inne
Połączony wykres
słupkowy

pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
1990/91
1997/98
0
1
2
3
4
5
6
(X 100000)
Połączony wykres
słupkowy
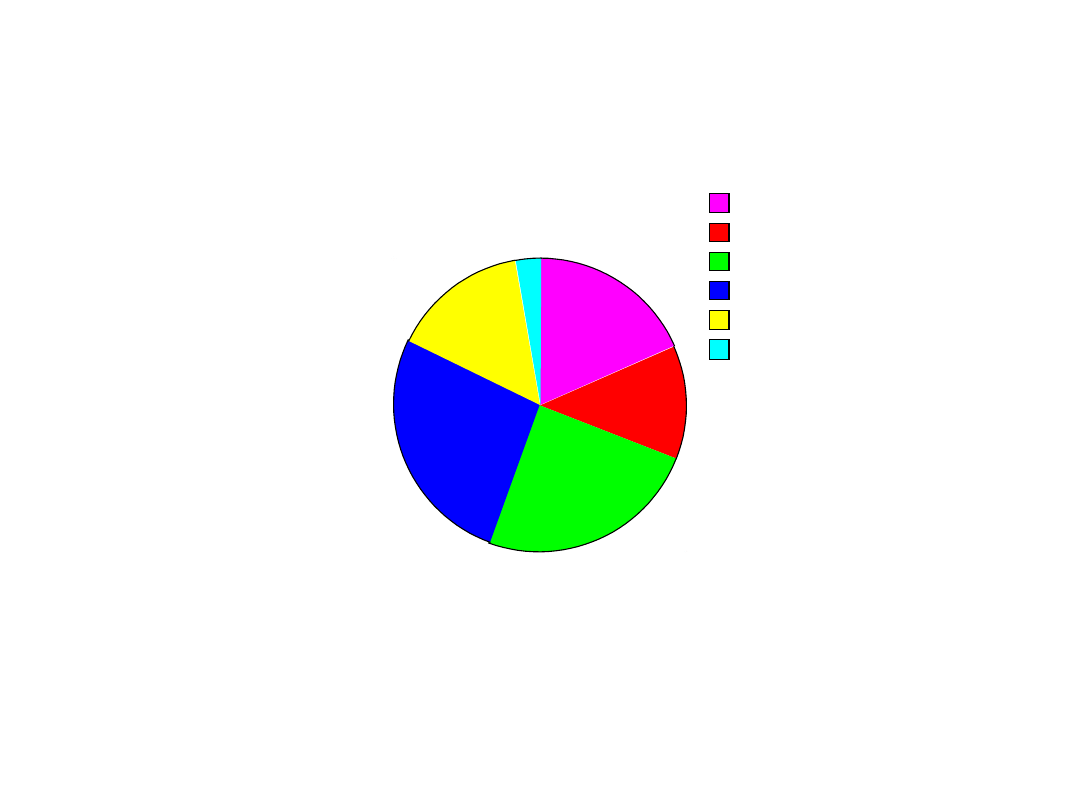
kierunki
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
18,30%
12,70%
24,60%
26,60%
15,00%
2,80%
1990/91
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
18,30%
12,70
%
24,60%
26,60%
15,00%
2,80%

K ą t w y c i n k a k o ł a d l a g r u p y h u m a n i s t y c z n e j =
K ą t w y c i n k a k o ł a
o d p o w i a d a j ą c e g o o k r e ś l o n e j k a t e g o r i i =
L i c z e b n o ś ć k a t e g o r i i / l i c z e b n o ś ć p r ó b k i )
.
360
o
c z ę s t o ś ć k a t e g o r i i x 1 0 0 % =
= ( p o l e w y c i n k a / p o l e k o ł a ) x 1 0 0 %
o
o
72
,
45
360
127
,
0
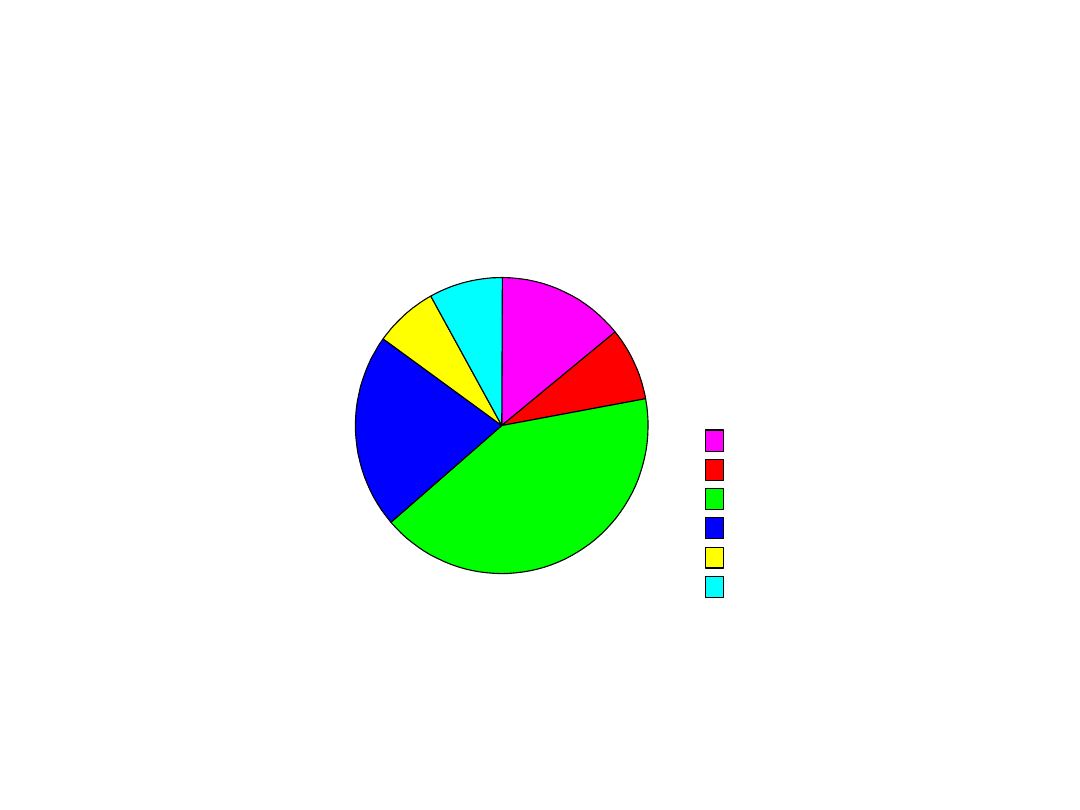
pedag.
human.
prawne,spol
scisle,przyr.
med.
inne
14,00%
8,10%
41,50%
21,40%
7,00%
8,00%
1997/98

Ograniczenia wykresów kołowych
:
można przedstawić jedynie dane procentowe
w próbce musi być co najmniej 1 obserwacja
każdej kategorii ( bo łączna suma pól wycinków
musi stanowić 100 % pola koła )
mało czytelne przy dużej liczbie kategorii
analiza dwóch wykresów kołowych bardziej
kłopotliwa niż połączonego wykresu słupkowego
.
METODY OPISU DANYCH ILOŚCIOWYCH
SKALARNYCH
Wykresy:
diagramy, histogramy, łamane częstości
,
wykresy przebiegu.
Przykład
.
W stu kolejnych rzutach kostką sześcienną
otrzymano wyniki (próbkę cechy dyskretnej o liczności
100):
5 2 2 6 3 2 5 3 1 2 5 3 6 2 5 4 4 6 1 6 4 5 5 2 4 6 1 4 4 3 4 2 4 2 4 4
1 1 4 5 3 1 5 6 5 6 1 5 6 2 4 5 5 2 5 4 5 5 1 1 2 2 5 5 2 6 3 5 5 4 1 4
5 5 1 4 3 2 1 2 6 1 2 1 6 5 1 3 6 1 5 6 6 2 2 3 5 5 2 4
Rozkład liczby oczek w próbce
Wartość (l. oczek)
1 2 3 4 5 6
Liczność (l. wystąpień)
16 19 9 17 25 14
Rozkład częstości liczby oczek w próbce
Wartość (l. oczek)
1 2 3 4 5 6
Częstość
0,16 0,19 0,09 0,17 0,25 0,14
Zwięzły opis próbki:
rozkład cechy w próbce
, tzn. zapisanie
jakie
wartości wystąpiły w próbce i ile razy, lub z jaką częstością.
Diagram liczebności
Diagram częstości

Przykład.
Wiek
25
osób, które ubezpieczyły się w III filarze
emerytalnym w pewnym zakładzie pracy: 30,
49
, 33, 35, 37,
20
, 31, 30, 36, 46, 39, 40, 38, 41, 35, 37, 24, 27, 36, 43, 45,
25, 32, 29, 28.
21 różnych wartości
: diagram rozkładu lat nieczytelny.
Agregacja danych
: przedziały wiekowe zawierające
wszystkie obserwacje, liczba obserwacji w tych przedziałach.

Przedział Obserwacje Liczność Częstość
(klasa)
[18,23) 20 1 1/25 = 0,04
[23,28) 24, 27, 25 3 3/25 = 0,12
[28,33) 30, 30, 31, 32, 29, 28 6 6/25 = 0,24
[33,38) 33, 35, 37, 36, 35, 37, 36 7 7/25 = 0,28
[38,43) 39, 40, 38, 41 4 4/25 = 0,16
[43,48) 43, 45, 46 3 3/25 = 0,12
[48,53) 49 1 1/25 = 0,04
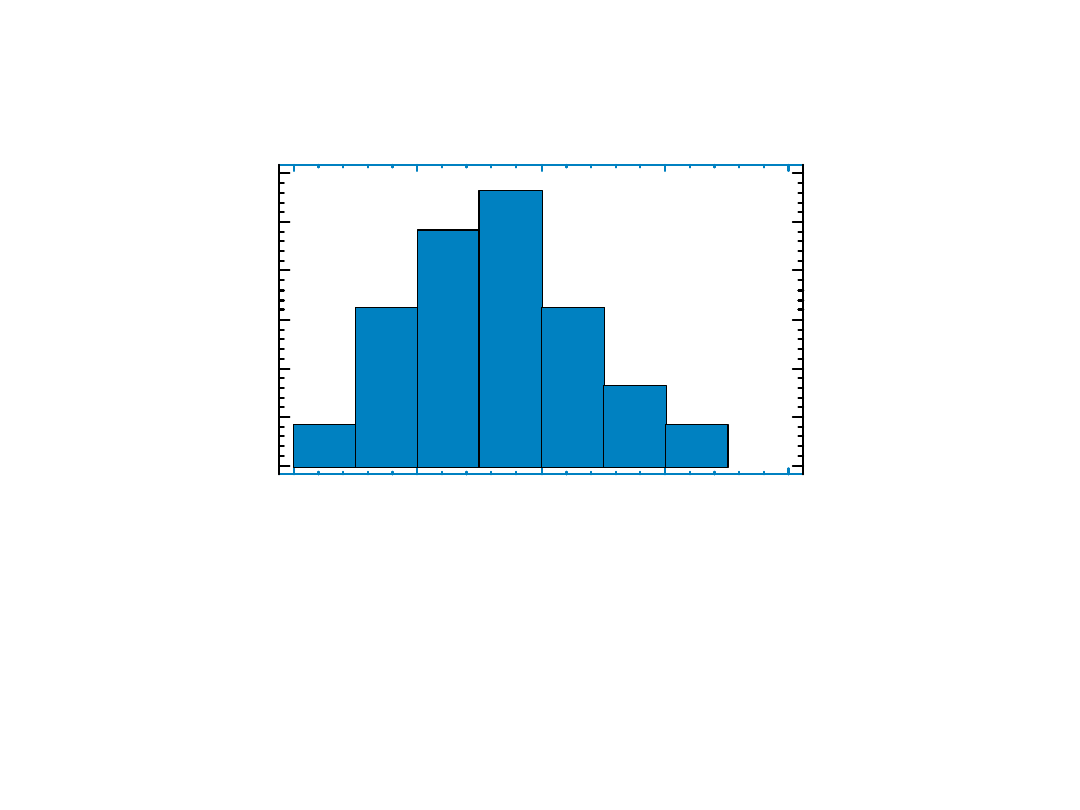
Histogram
wiek
p
ro
ce
n
t
18
28
38
48
58
0
5
10
15
20
25
30
28+16+12+4=60%
pracowników ma co najmniej
33 lata

Na osiach poziomych: granice klas wiekowych ( przedziałów)
wysokości słupków = procentowy udział każdej klasy w próbce
Wysokość słupka = częstość klasy
x
100%.
Pole słupka
=
stała długość przedziału
x
częstość
x
100
Histogram
liczebności:
wysokość słupka =
liczność klasy
Histogram
częstości
: wysokość słupka =
częstość klasy
KONSTRUKCJA HISTOGRAMU
P o c z ą tk o w y
w y b ó r d łu g o ś c i
p r z e d z ia łó w :
3
/
1
64
,
2
n
IQR
h
n = lic z n o ś ć p ró b k i, I Q R = ro z s tę p m ię d z y k w a rty lo w y = z a k re s 5 0 %
" ś ro d k o w y c h " w a rto ś c i w p ró b c e
Obserwacja wpływu stopniowego
zwiększania lub
zmniejszania
długości przedziałów na kształt histogramu:
,...
,
2
h
h
lub
,...
,
2
1
h
h
;
1

Mała
długość przedziału to :
nieregularność
histogramu
Duża
długość przedziału to: za duże
wygładzenie
histogramu
Przy ustaleniu kompromisu pomiędzy zbyt dużym wygładzeniem histogramu
(redukcją informacji) a dużą nieregularnością histogramu pomocne są dodatkowe
informacje o naturze obserwowanego zjawiska, np. obserwacje z kilku różnych
populacji mogą dawać histogramy wielomodalne.
Początek histogramu
: najmniejsza obserwacja stanowi
środek pierwszego przedziału. Uśredniając kilka
histogramów o nieznacznie przesuniętych początkach
można
uniezależnić się od
wpływu początku histogramu na jego
kształt.
WSKAŹNIKI SUMARYCZNE
W S K AŹ N I K I P O Ł O Ż E N I A
(
m i a r y p oł o ż e n i a
,
p a r a m e t r y
p oł o ż e n i a
) c h a r a k t e r y z u ją n a j b a r d z i e j r e p r e z e n t a t y w n e
d a n e , c e n t r a l ną „ t e n d e n c ję ” d a n y c h , o k r e ś l a j ą „ ś r o d e k ”
p r ó b k i
:
N i e c h : x
1
, x
2
, . . . , x
n
- p r ó b k a o l i c z n oś c i n .
W a r t oś ć ś r e d n i a w p r ó b c e
(
ś r e d n i a p r ó b k o w a , ś r e d n i a
p r ó b k i
)
n
i
i
n
x
n
x
x
x
n
x
1
2
1
1
)
...
(
1

x
med
=
,
)
2
/
)
1
((
n
x
gdy n jest nieparzyste
x
med
=
),
(
2
1
)
1
2
/
(
)
2
/
(
n
n
x
x
gdy n jest parzyste.
Mediana w próbce
(
mediana próbki
,
mediana
próbkowa
)
Niech
)
(
)
1
(
)
2
(
)
1
(
...
n
n
x
x
x
x
uporządkowane w sposób rosnący wartości próbki:
x
(1)
= min{ x
1
, x
2
, ...,x
n
}, ... , x
(n)
= max{ x
1
, x
2
, ...,x
n
}

Przykład.
Miesięczny dochód 11-tu
osób:
Dochód (PLN)
2000
2500
3500
19000
Liczba osób
4
4
2
1
Ś re d n ie w y n a g ro d z e n ie te j g ru p y o s ó b to :
)
19000
3500
2
2500
4
2000
4
(
11
1
x
4 0 0 0
2000, 2000, 2000, 2000, 2500,
2500,
2500, 2500, 3500, 3500,
19000
Mediana = 2500
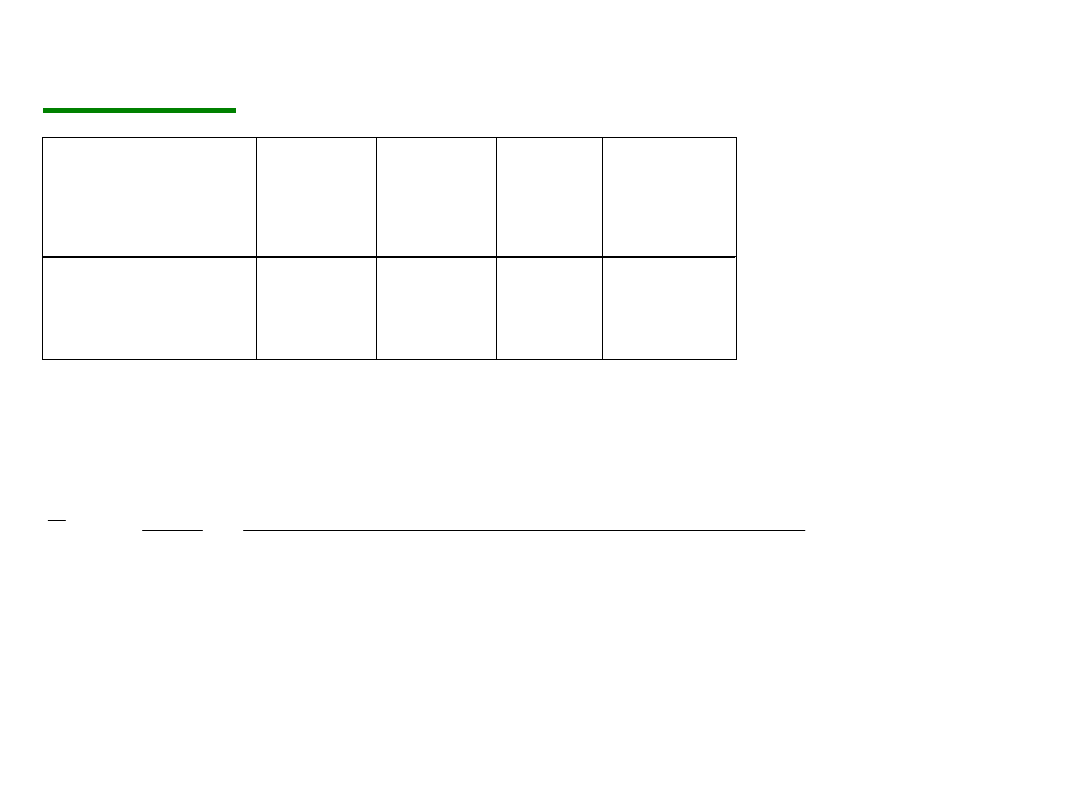
P r z y k ł a d .
M i e s i ę c z n y d o c h ó d 1 0 - c i u
o s ó b ( w t y s . P L N ) :
D o c h ó d ( P L N )
[ 1 , 1 , 5 )
[ 1 , 5 , 2 )
[ 2 , 2 , 5 )
[ 2 , 5 , 3 )
L i c z b a o s ó b
2
2
4
2
Ś r e d n i a n a p o d s t a w i e d a n y c h z g r u p o w a n y c h :
k
i
i
i
n
x
n
x
1
10
75,
2
2
25,
2
4
75,
1
2
25,
1
2
~
= 2 , 0 5

Ś r e d n i a w r a ż l i w a n a o b s e r w a c j e o d s t a j ą c e :
)
10
(
3500
4000
x
x
,
19000
)
11
(
x
-
ś r e d n i a n i e o d z w i e r c i e d l a
„ t y p o w e g o ” d o c h o d u .
M e d i a n a o d p o r n a ( m a ł o w r a ż l i w a ) n a o b s e r w a c j e
o d s t a j ą c e :
2500
)
6(
x
x
med
-
m e d i a n a j e s t l e p s z ą m i a r ą p r z e c i ę t n e g o
w y n a g r o d z e n i a n i ż ś r e d n i a

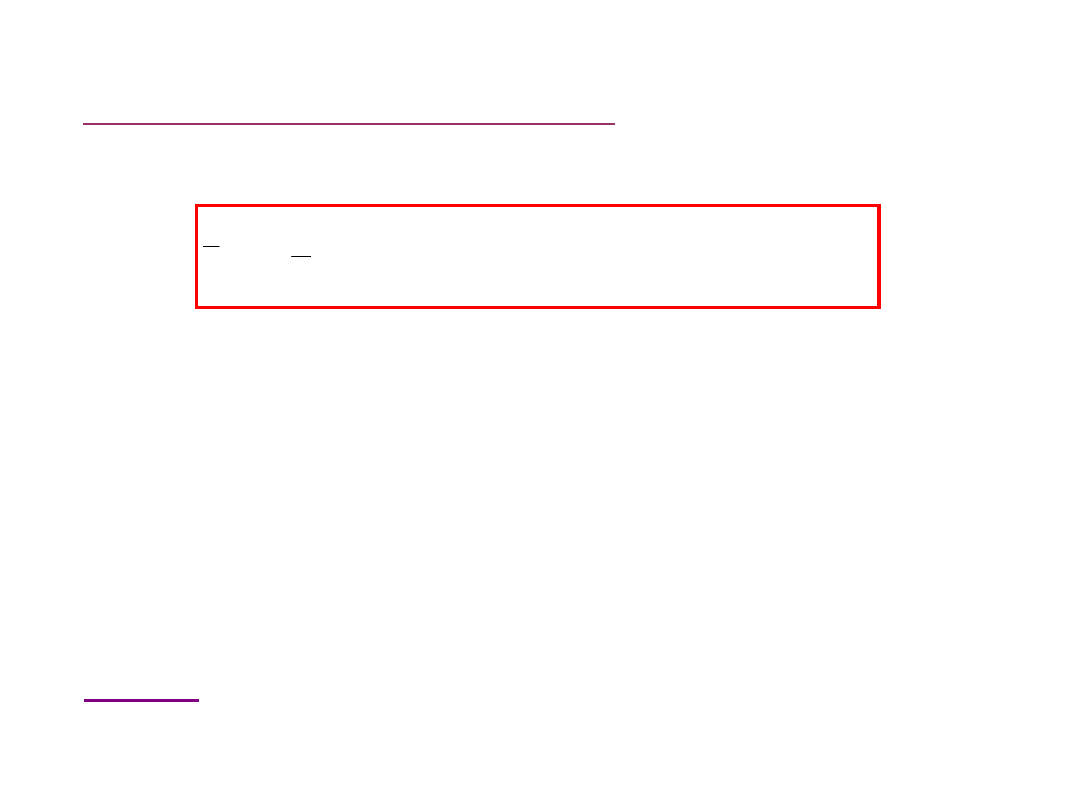
Ś r e d n ia u c in a n a
(
u c ię ta
) ( z p a r a m e tr e m k )
k
n
k
i
i
tk
x
k
n
x
1
)
(
2
1
,
s to s o w a n a g d y w a r toś c i o d s ta ją c e s ą w y n ik ie m b łę d u
( błę d n e p r z e tw o r z e n ie d a n y c h lu b b łę d y p r z y r z ą d ó w
p o m ia r o w y c h ) .
O s tr z eż e n ie : o b s e r w a c je o d s ta ją c e m o g ą b y ć b a rd z o
is to tn e , n p . są w y n ik ie m r o z r e g u lo w a n ia p r o c e s u
p r o d u k c ji
Średnia winsorowska
( z parametrem k )
1
2
)
(
)
(
)
1
(
)
1
(
1
1
k
n
k
i
k
n
i
k
wk
x
k
x
x
k
n
x
Stosowana w sytuacjach gdy wartości skrajne ( k najmniejszych lub k
największych ) niepewne co do ich prawdziwych wartości (np. zostały
utracone z bazy danych; nie mogły być zaobserwowane w przypadku
badania czasu życia lub czasu bezawaryjnej pracy urządzenia gdy
eksperymentator ma ograniczony czas obserwowania zjawiska.
Moda
–
najczęściej występująca wartość (lub wartości) w
próbce.
WSKAŹNIKI ROZPROSZENIA
(
miary rozproszenia
,
parametry rozproszenia
) charakteryzują rozrzut danych,
rozproszenie wartości próbki wokół parametru położenia.
Rozstęp próbki
)
1
(
)
(
x
x
R
n
,
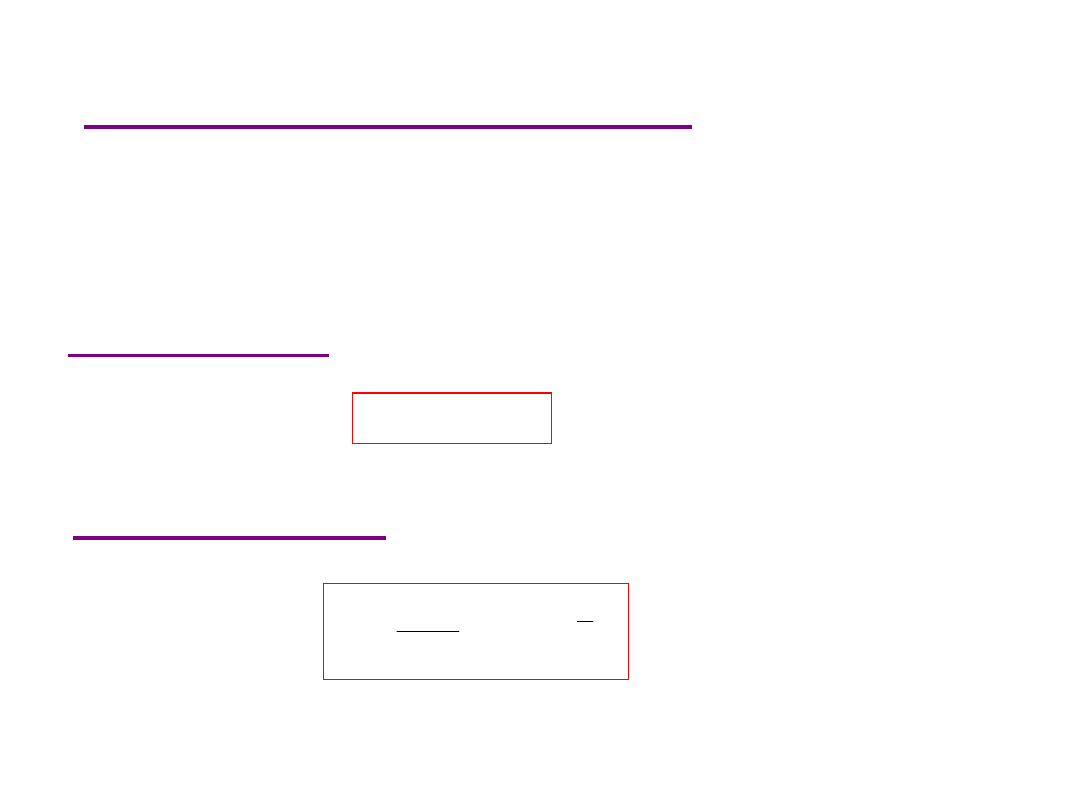
Wariancja próbki
(
w próbce
)
n
i
i
x
x
n
s
1
2
2
)
(
1
1
,
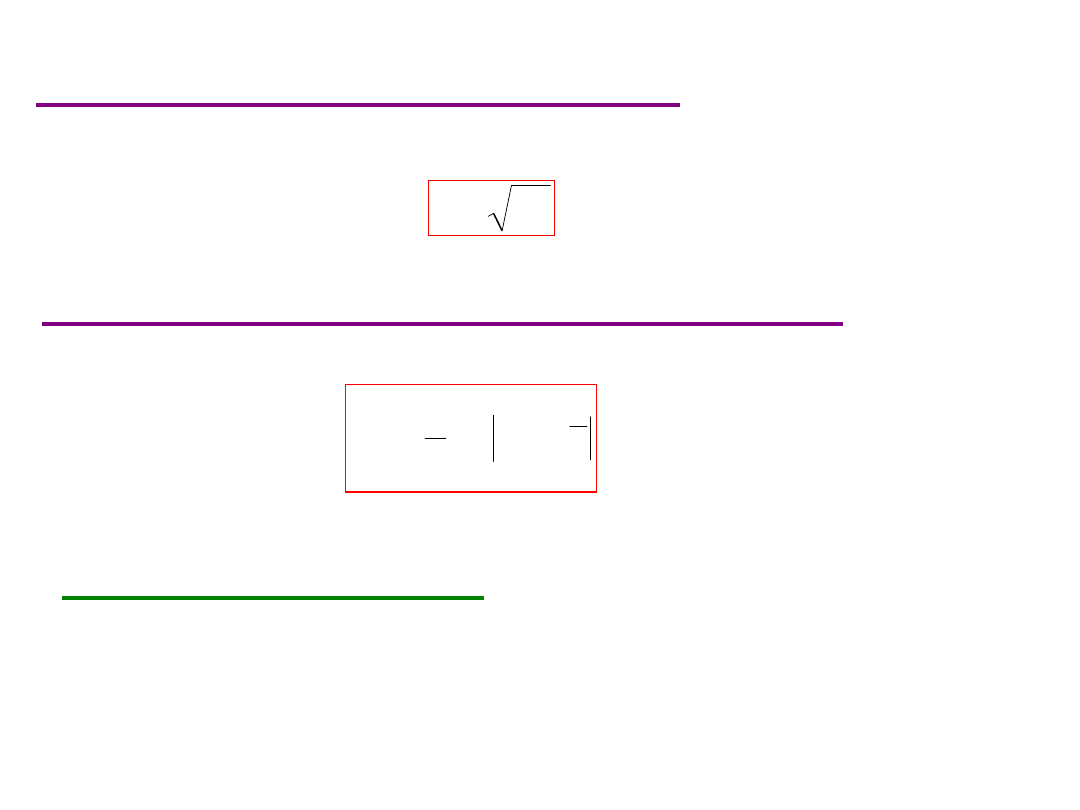
O dc h ylenie s tandardo w e w pró bc e
(próbki)
2
s
s
Odchylenie przeciętne od wartości średniej
n
i
i
x
x
n
d
1
1
1
D
o
l
n
y
(
p
i
e
r
w
s
z
y
)
k
w
a
r
t
y
l
1
Q
=
m
e
d
i
a
n
a
p
o
d
p
r
ó
b
k
i
s
k
ł
a
d
a
j
ą
c
e
j
s
i
ę
z
e
l
e
m
e
n
t
ó
w
p
r
ó
b
k
i
„
m
n
i
e
j
s
z
y
c
h
”
o
d
m
e
d
i
a
n
y
x
m
e
d
.

G
ó
rn
y (trz
e
c
i) k
w
a
rtyl
3
Q
=
m
e
d
ia
n
a
p
o
d
p
ró
b
k
i sk
ła
d
a
ją
ce
j się
z e
le
m
e
n
tó
w
p
rób
ki „
w
iększy
ch
”
od
m
ed
ian
y.
R ozstęp m iędzy kw arty low y :
1
3
Q
Q
IQR
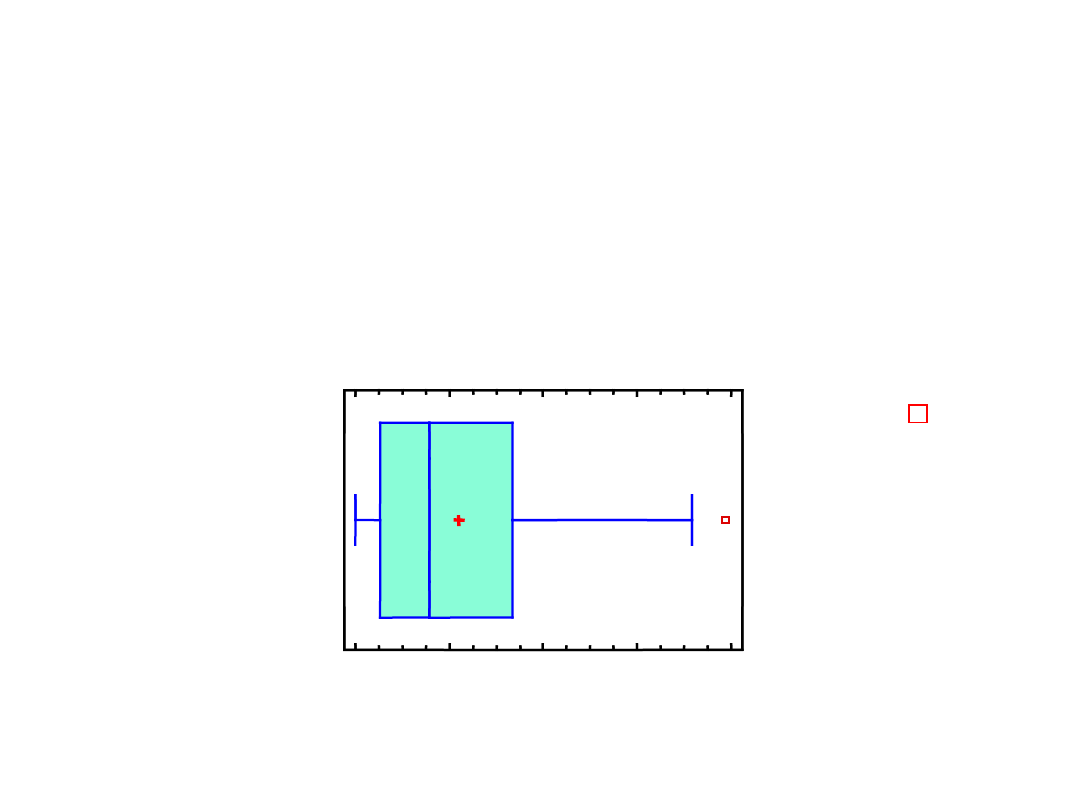
W Y K R E S R A M K O W Y
( p u d e ł k o w y )
i l u s t r u j e w z a j e m n e p o ł o ż e n i e p i ę c i u w s k a ź n i k ó w s u m a r y c z n y c h :
max
)
n
(
med
min
)
(
x
x
,
Q
,
x
,
Q
,
x
x
3
1
1
.
0
0,4
0,8
1,2
1,6
Obserwacja
potencjalnie
odstająca

Z wykresu odczytujemy następujące wskaźniki:
Q
1
= 0,1 = rzut na oś poziomą lewego boku prostokąta
Q
2
= 0,7 = rzut na oś poziomą prawego boku prostokąta
Q
3
= 0,3 = rzut na oś poziomą pionowego odcinka
wewnątrz prostokąta
IQR
= długość podstawy prostokąta
Wąsy wykresu ramkowego = linie po obu stronach
prostokąta.
Rzut lewego wąsa na oś poziomą = przedział
[x
*
, Q
1
],
gdzie
x
*
= min{ x
k
: Q
1
– 3/2 IQR x
k
Q
1
},
podobnie określamy rzut prawego wąsa = przedział
[x
*
, Q
1
],
gdzie
x
*
= max{ x
k
: Q
3
x
k
Q
3
+ 3/2 IQR }
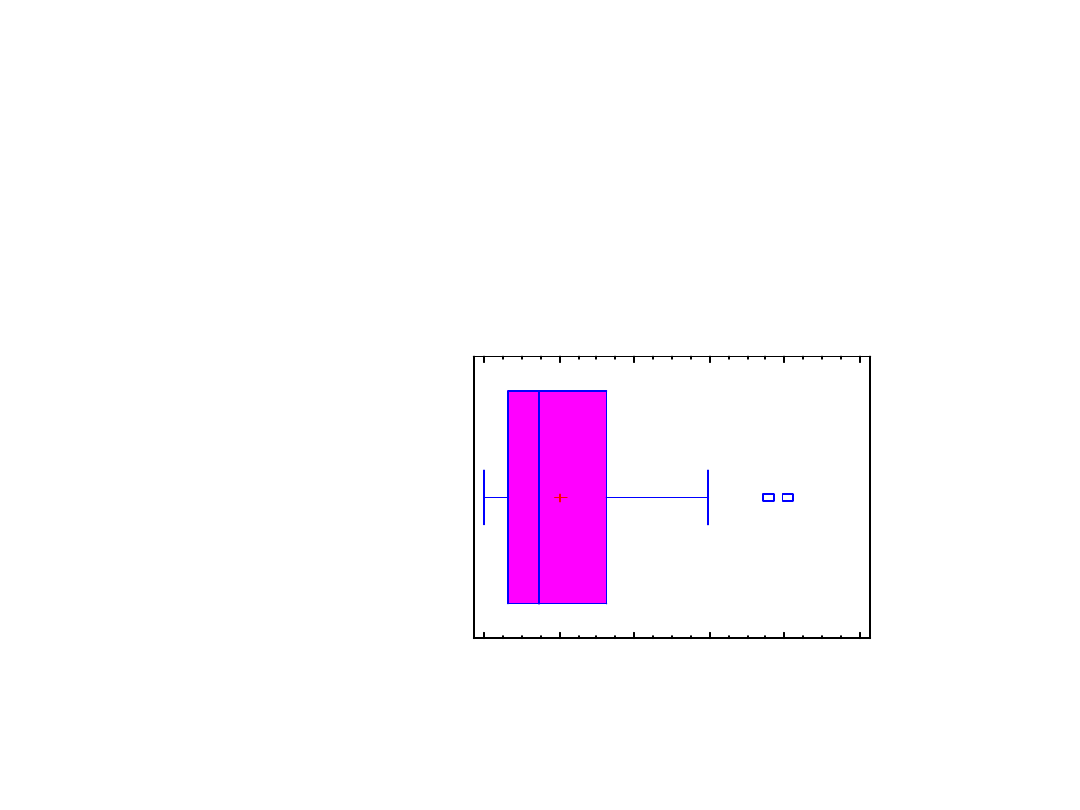
Box-and-Whisker Plot
0
2
4
6
8
10
Col_1
Count =
100
Average =
2,02544
M
edian =
1,46467
Variance =
3,16395
Standard deviation =
1,77875
M
inim
um
=
0,0150559
M
axim
um
=
8,05684
Range =
8,04179
Lower quartile =
0,638618
Upper quartile =
3,23695
Interquartile range =
2,59833
Coeff. of variation =
87,8206%
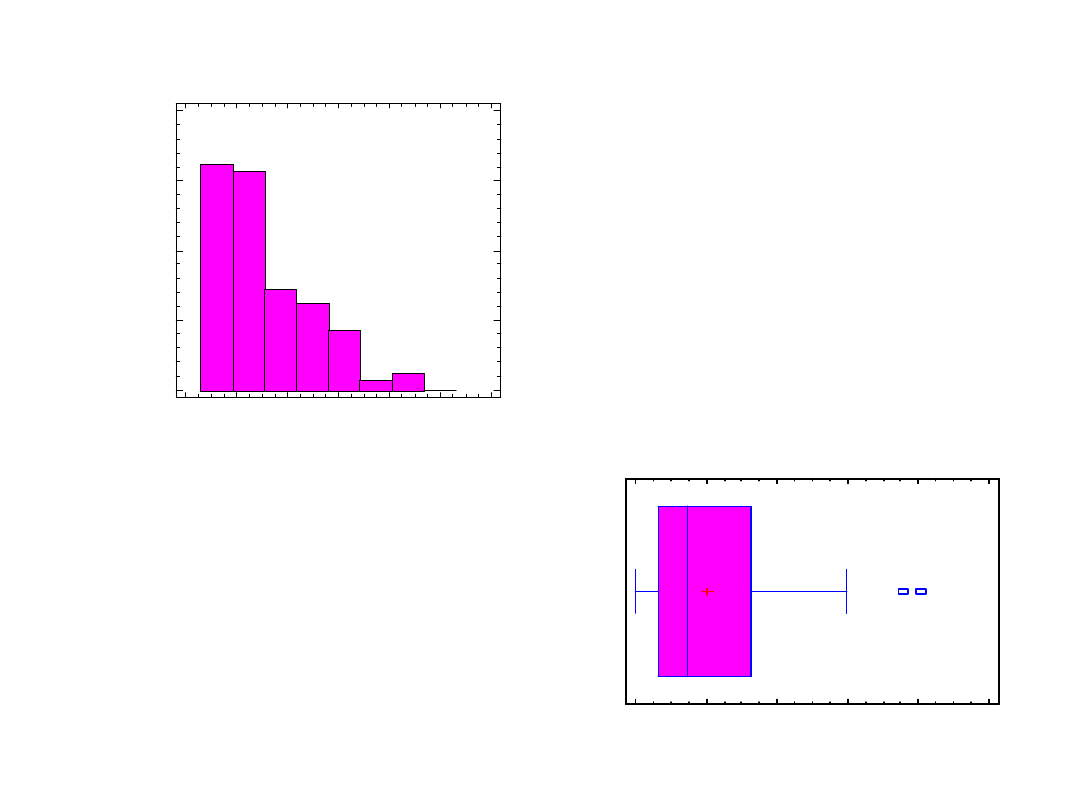
Box-and-Whisker Plot
0
2
4
6
8
10
Col_1
Histogram
-1
1
3
5
7
9
11
Col_1
0
10
20
30
40
fr
e
q
u
e
n
c
y
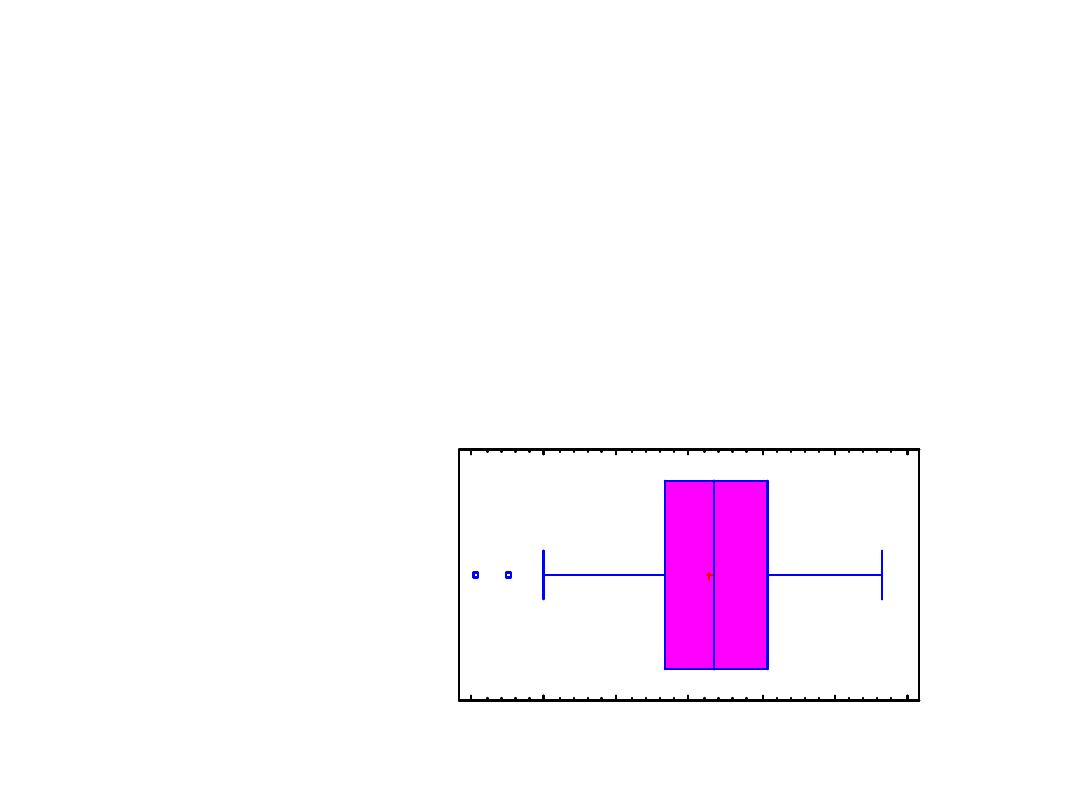
Box-and-Whisker Plot
-3,4
-2,4
-1,4
-0,4
0,6
1,6
2,6
RAND1
Summary Statistics for RAND1
Count = 100
Average = -0,110696
Median = -0,0516888
Variance = 1,07775
Standard deviation = 1,03815
Minimum = -3,36516
Maximum = 2,26235
Range = 5,62751
Lower quartile = -0,726224
Upper quartile = 0,680553
Interquartile range = 1,40678
Stnd. skewness = -1,86072
Coeff. of variation = -937,836%
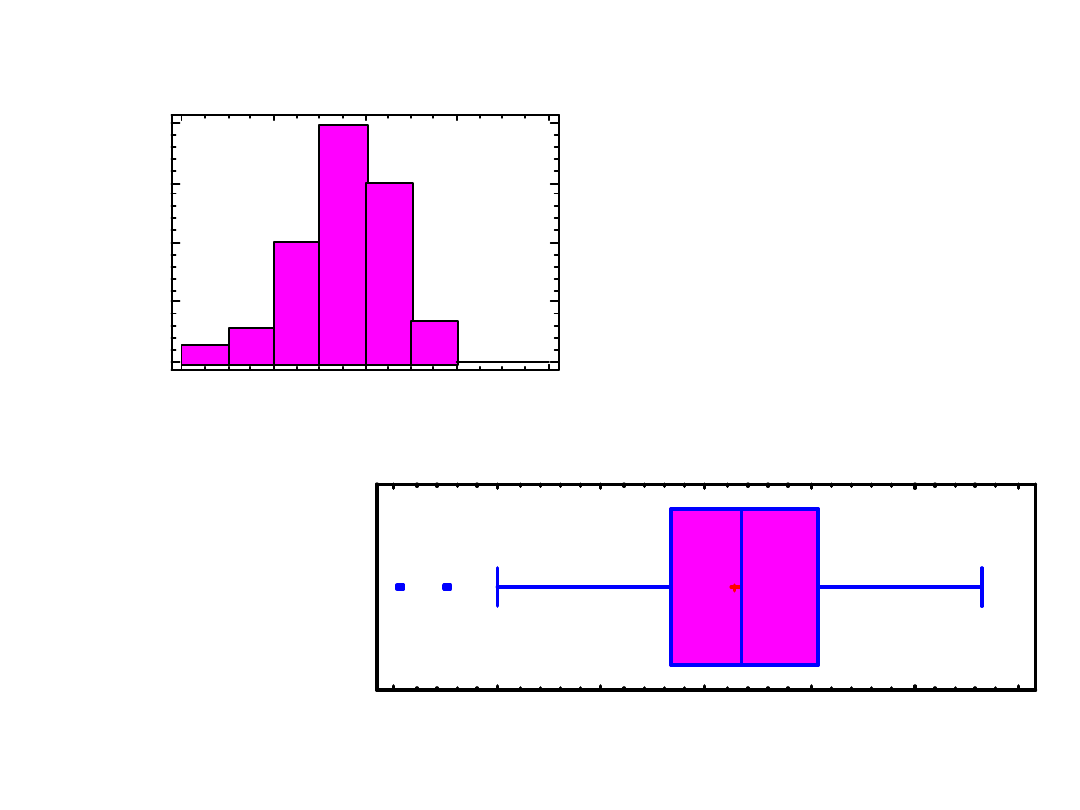
Histogram
-3,7
-1,7
0,3
2,3
4,3
RAND1
0
10
20
30
40
fr
e
q
u
e
n
cy
Box-and-Whisker Plot
-3,4
-2,4
-1,4
-0,4
0,6
1,6
2,6
RAND1
Document Outline
- STATYSTYCZNA ANALIZA DANYCH
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- STATYSTYKA OPISOWA
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Diagram liczebności
- Wykres kołowy
- Metody opisu danych jakościowych
- Slide 14
- Wstępna analiza danych
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- WSKAŹNIKI SUMARYCZNE
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Średnia winsorowska ( z parametrem k )
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
Wyszukiwarka
Podobne podstrony:
sąd1
Wojciech SAD1
więcej podobnych podstron