ŚREDNIA 

ARYTMETYCZNA

DOMINANTA

MEDIANA

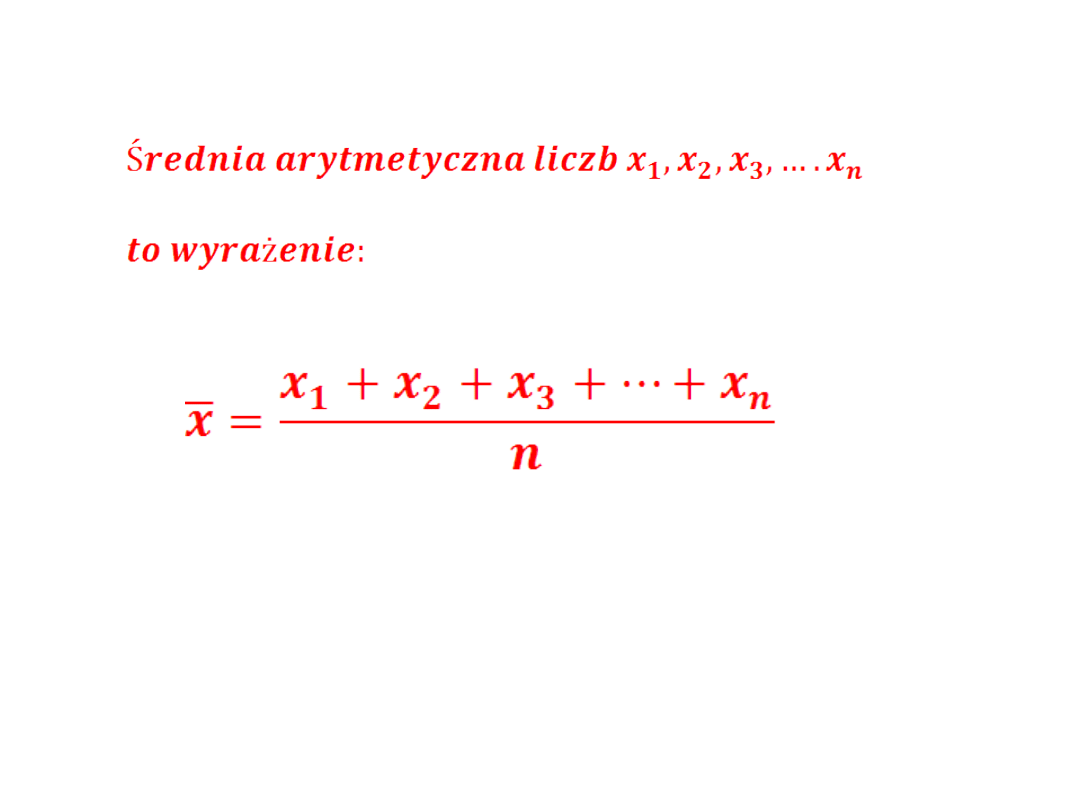
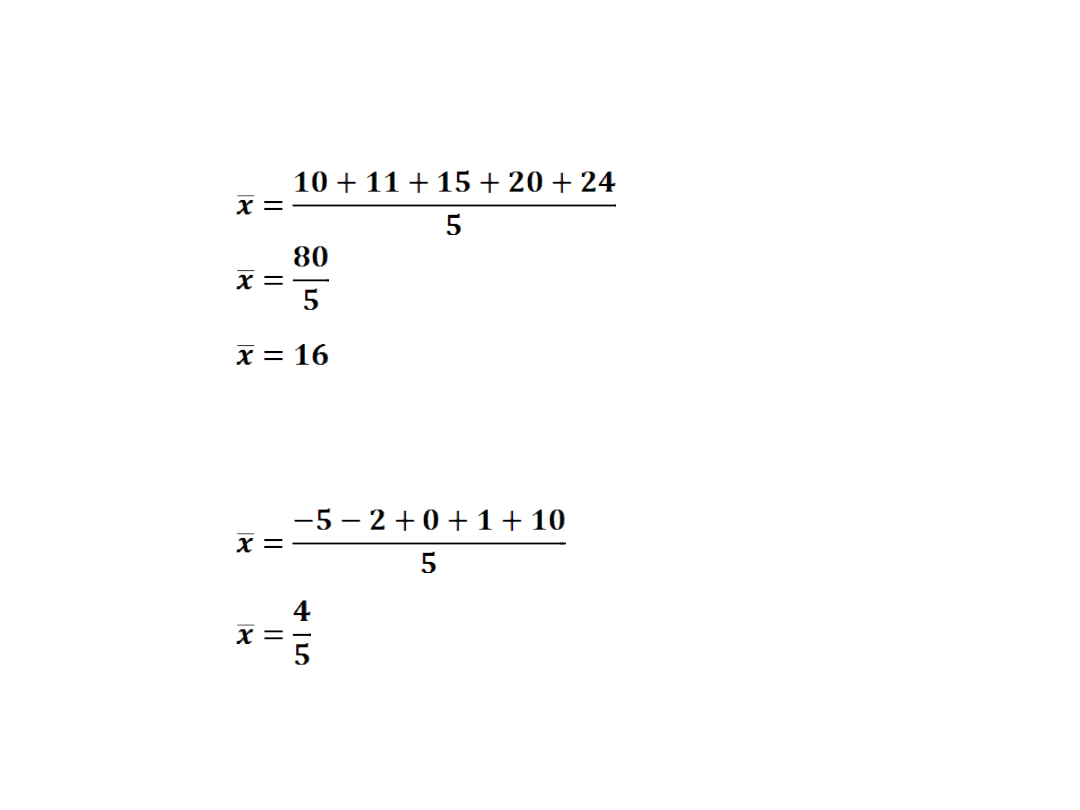
Ćw.1: Oblicz średnią arytmetyczną liczb:

a)10,11,15,20,24

b)-5,-2,0,1,10

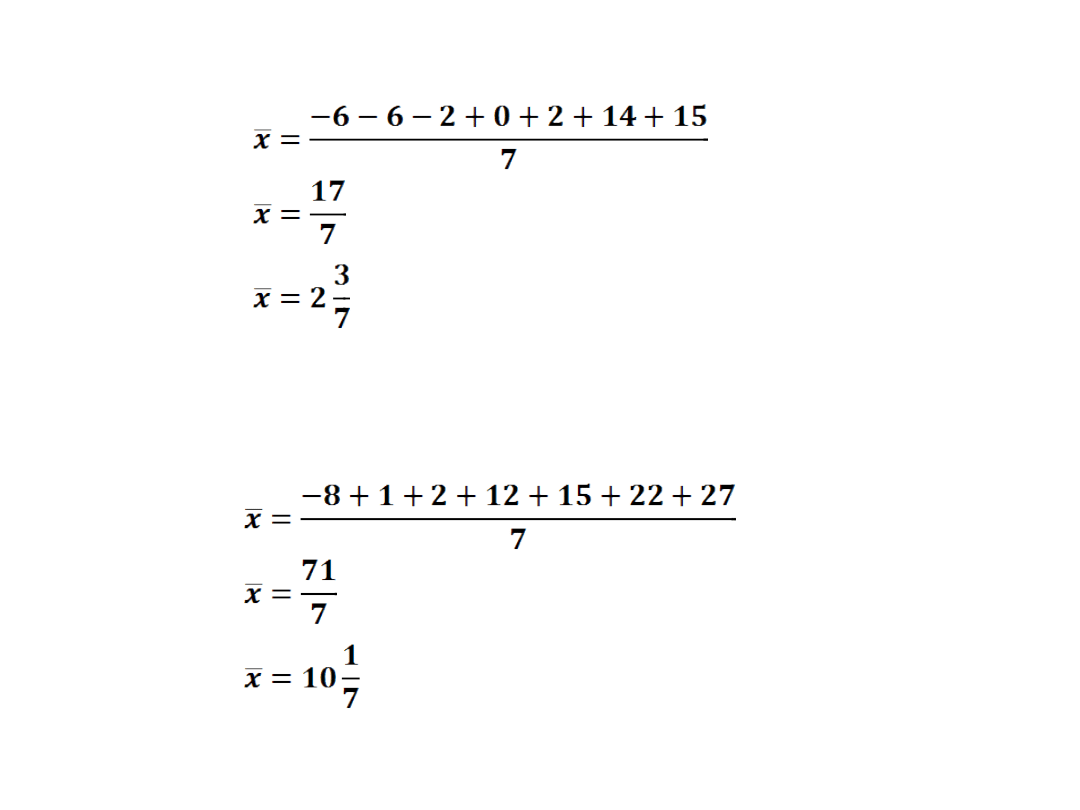
c) -6, -6,-2,0,2,14,15

 

d)  -8,1,2,12,15,22,27

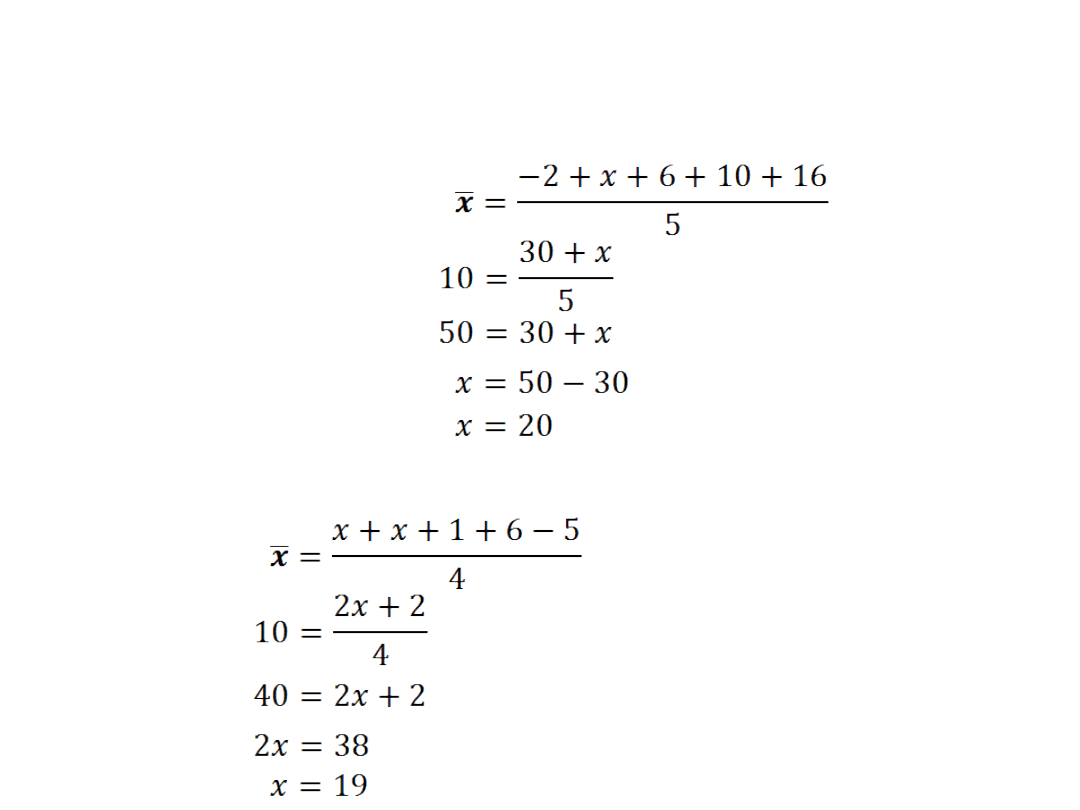
Ćw.2: Oblicz liczbę x, wiedząc że średnia arytmetyczna 
podanych 
        liczb wynosi 10.

a)-2,x,6,10,16

                                                  Szukaną liczbą x jest 20.

b)x,x+1,6,-5

                                                   Szukaną liczbą x jest 19.

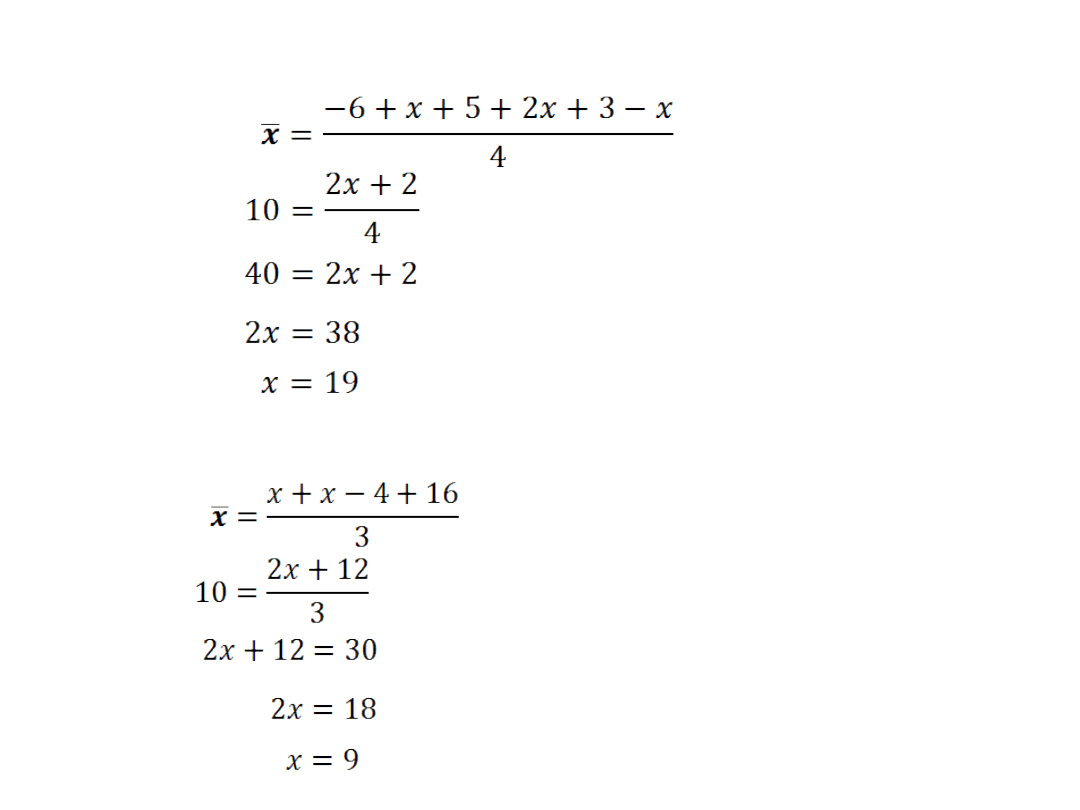
c) -6,x+5,2x,3-x

                                    

Szukaną liczbą x jest 19.

d)   x,x-4,16,

                                        Szukaną liczbą x jest 9.

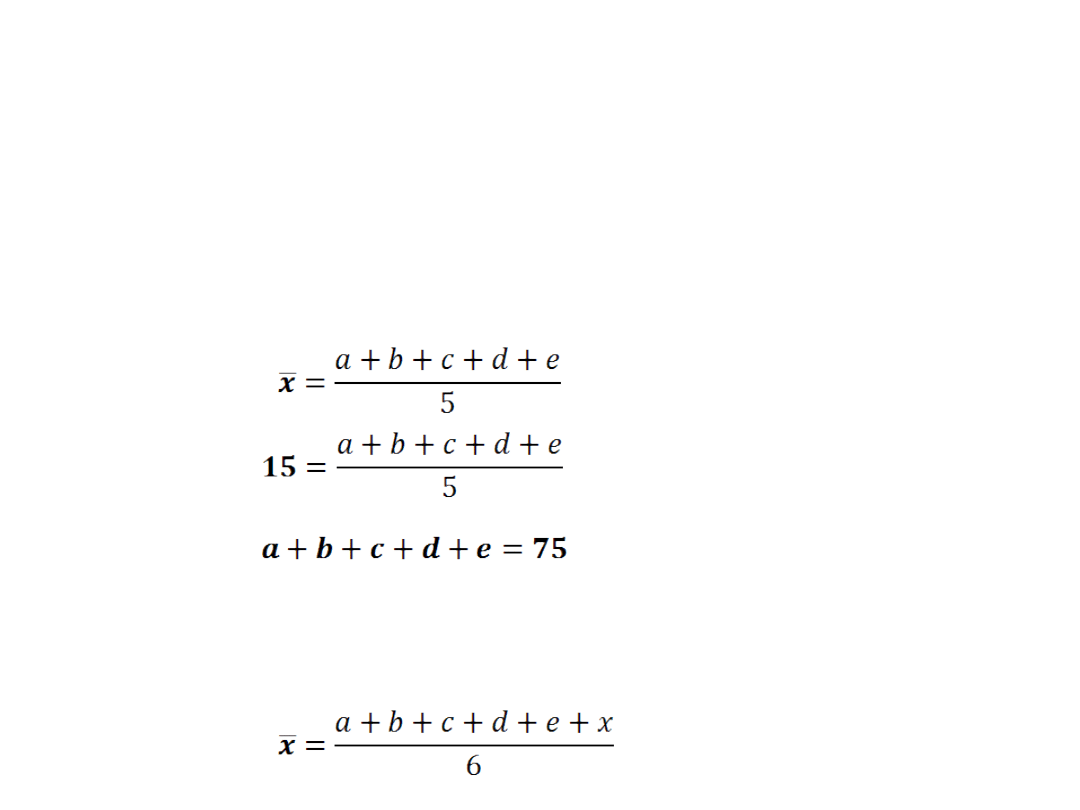
Ćw.3: Średnia pięciu dowolnych liczb wynosi 15, średnia 
sześciu liczb wynosi 24. Oblicz szóstą liczbę.

Oznaczmy pięć liczb dowolnymi literkami alfabetu: a, b, 
c, d, e.

Wiemy że średnia tych liczb wynosi 15.

Nieznaną szóstą liczbę oznaczymy przez x i zapiszemy 
odpowiedni warunek dotyczący średniej liczb.

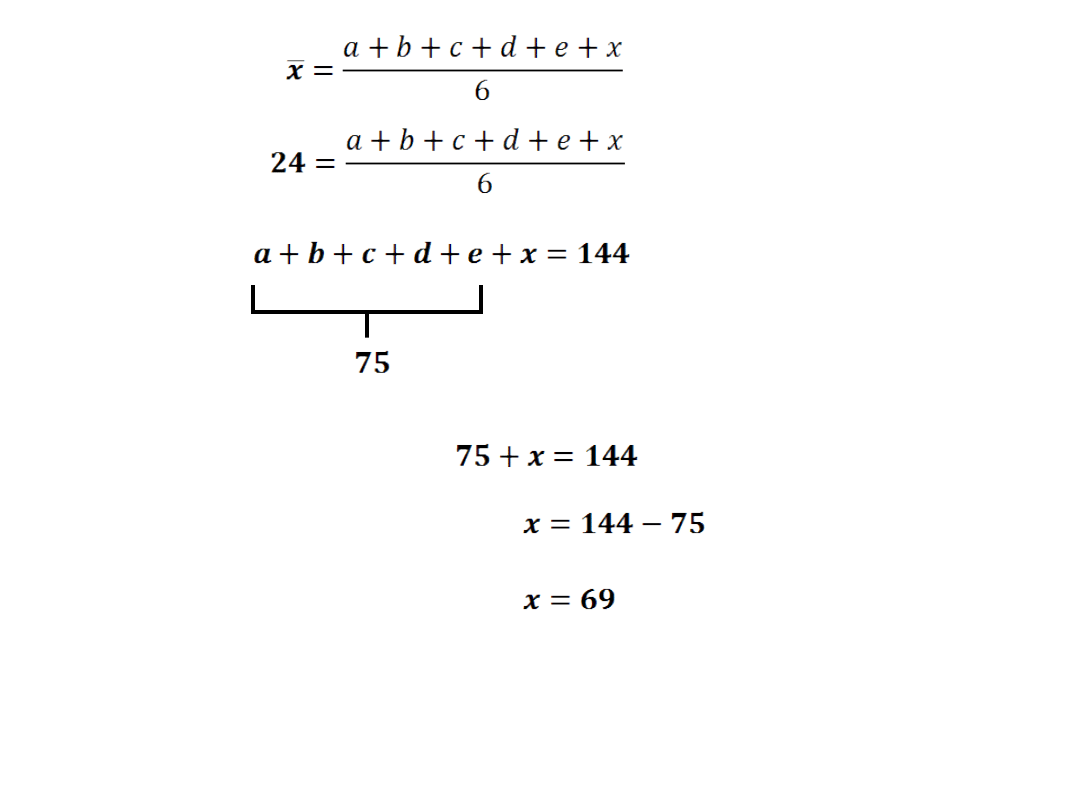
Nieznana szósta liczba to 69.

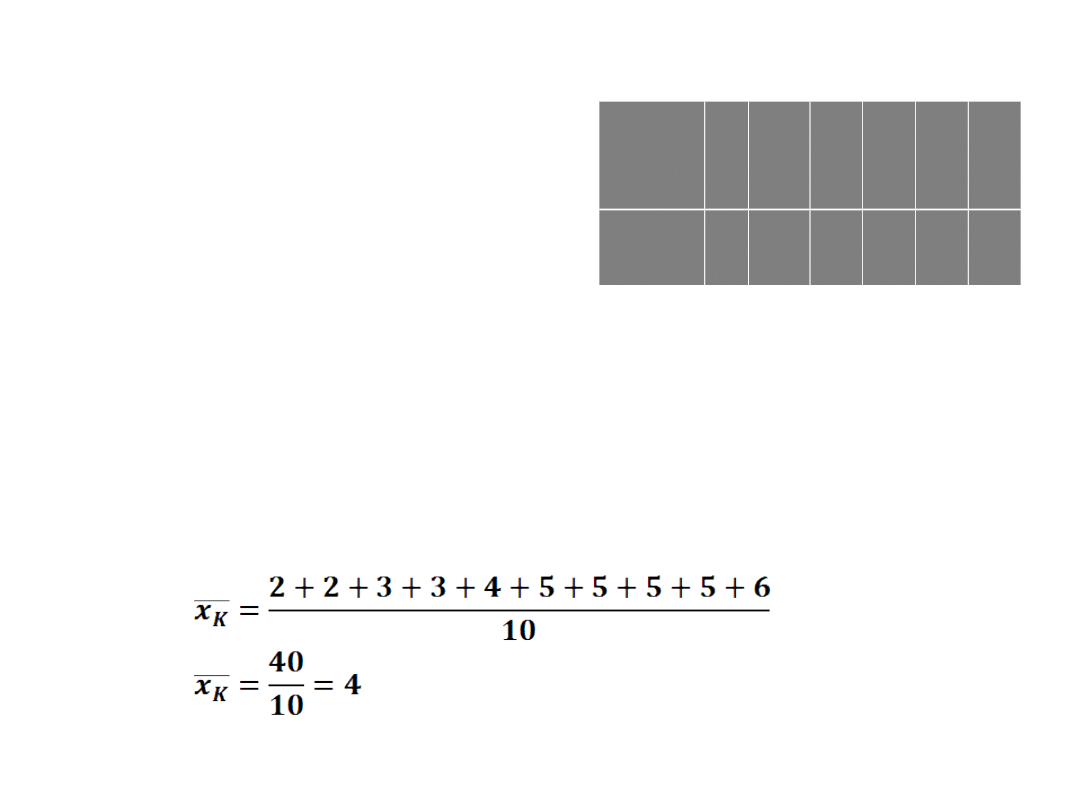
Ćw.4: Liczba poszczególnych ocen na świadectwie Kasi  
       umieszczona jest w tabelce:

a)ile przedmiotów ma Kasia?
b)wyznacz średnią ocen Kasi,
c)oblicz ile piątek ma na 
    świadectwie Asia, (druga tabela) jeśli ma 12 
przedmiotów i jej średnia jest o pół stopnia wyższa od 
średniej Kasi.

Ad a) 0+2+2+1+4+1=10
       Kasia ma 10 przedmiotów.

Ad b) 

Kasia ma średnią 4.

ocen

a

1

2

3

4

5

6

ilość 

ocen

0

2

2

1

4

1

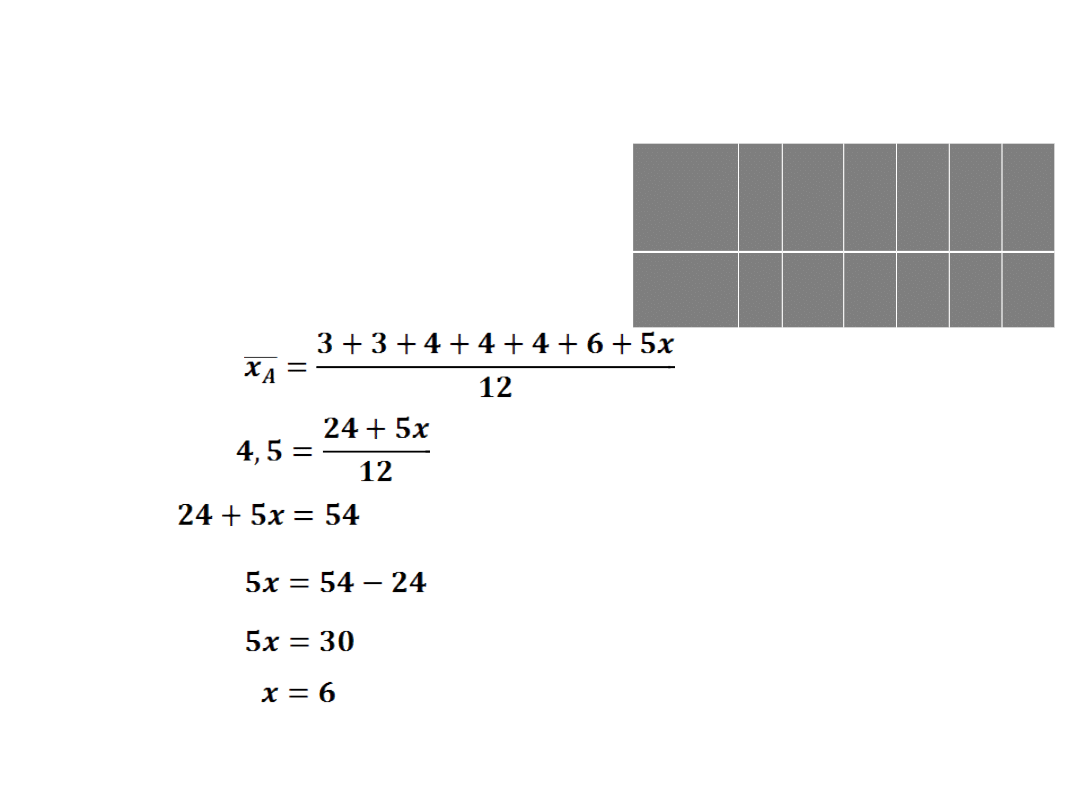
Ad c) Asia ma średnią o pół stopnia wyższą od   
       średniej Kasi, więc jej średnia wynosi 4,5. 
       Ilość poszczególnych ocen 
       dziewczynki przedstawia tabela:

 

Asia ma 6 piątek na świadectwie.

ocen

a

1

2

3

4

5

6

ilość 

ocen

0

0

2

3

x

1

Mediana liczb x

1

, x

2

, x

3

, … x

n

 to wartość środkowa tych 

liczb.

Liczby należy uporządkować od wartości najmniejszej do 
największej.

Mediana dzieli dane na dwie równoliczne grupy – dane w 

jednej 

grupie są od niej mniejsze lub równe, liczby w drugiej 

grupie są 

od niej większe lub równe.

Medianą nieparzystej liczby danych jest wartość 

znajdującą się

dokładnie na środku tych liczb.

W przypadku parzystej liczby danych medianą jest 

średnia

arytmetyczna dwóch sąsiednich wartości środkowych. 

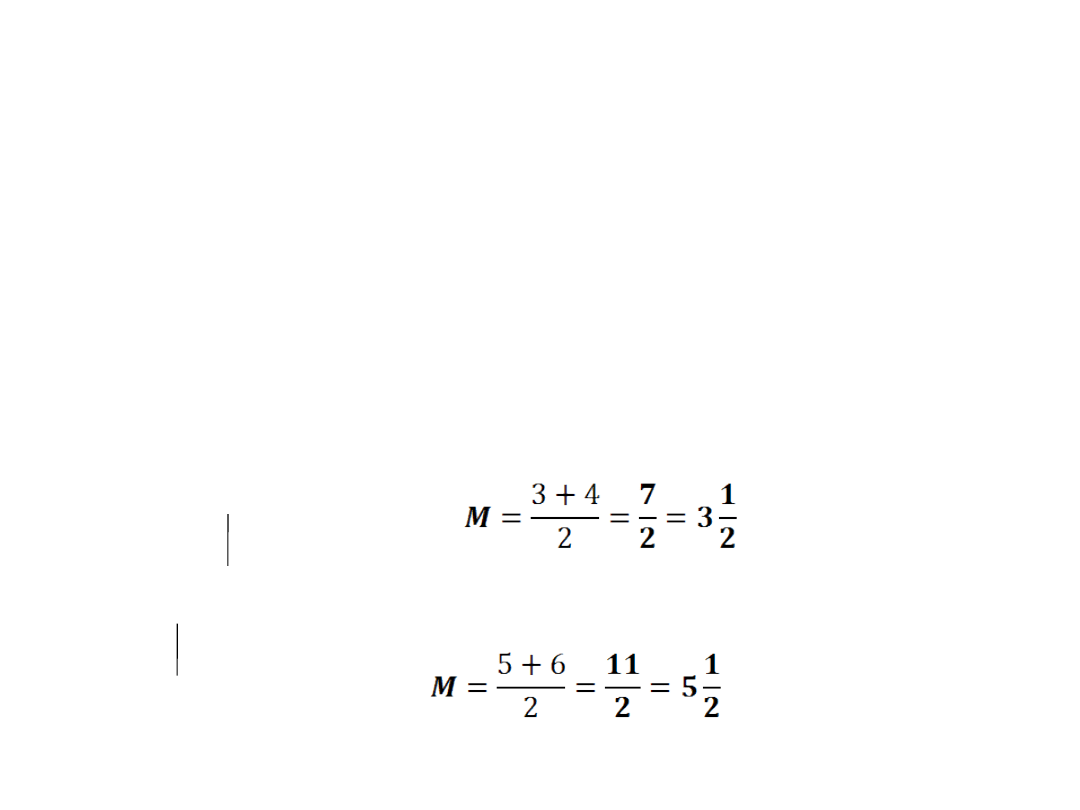
Ćw.5: Wyznacz medianę liczb:

a) -3,10,0,-5,2
   -5,-3,

0

,2,10         M=0

b)  2,3,4,4,5,

6

,6,6,7,8,10           M=6       

c) 4,4,4,5,-2,0,1,3

   -2,0,1,

3  4

,4,4,5

d) 0,0,

5

  

6

,7,8

Dominanta to wartość, która występuje wśród danych 

najczęściej.

Dominanta nazywana jest również wartością modalną 

lub modą.

Jeżeli wśród danych kilka liczb występuje z tą samą, 

najwyższą

częstością to przyjmuje się że każda z tych liczb jest 

dominantą.

Jeżeli wszystkie liczby występują tak samo często, to 

przyjmuje

się że nie ma dominanty.

Ćw.6: Wyznacz dominantę liczb:

a) -2,0,1,1,4,5,1,7              D=1
b) 1,1,3,5,3,3,7,4,1           D



{1,3}

c) 2,2,2,5,5,5,10,10,10     brak dominanty
d) 5,6,6,6,-5,-5,5,-5,6      D=6
e) 1,1,1,1,1,5,5,5,5          D=1

Ćw.7: Dane w tabeli przedstawiają dzienną liczbę godzin 
przeznaczonych na oglądanie telewizji przez uczniów klasy 
pierwszej.
                                 Oblicz:
                                     a) ile jest uczniów w klasie,
                                     b) oblicz średnią liczbę godzin 
                                        przypadających na jednego ucznia
                                     c) wyznacz medianę
                                     d) wyznacz dominantę

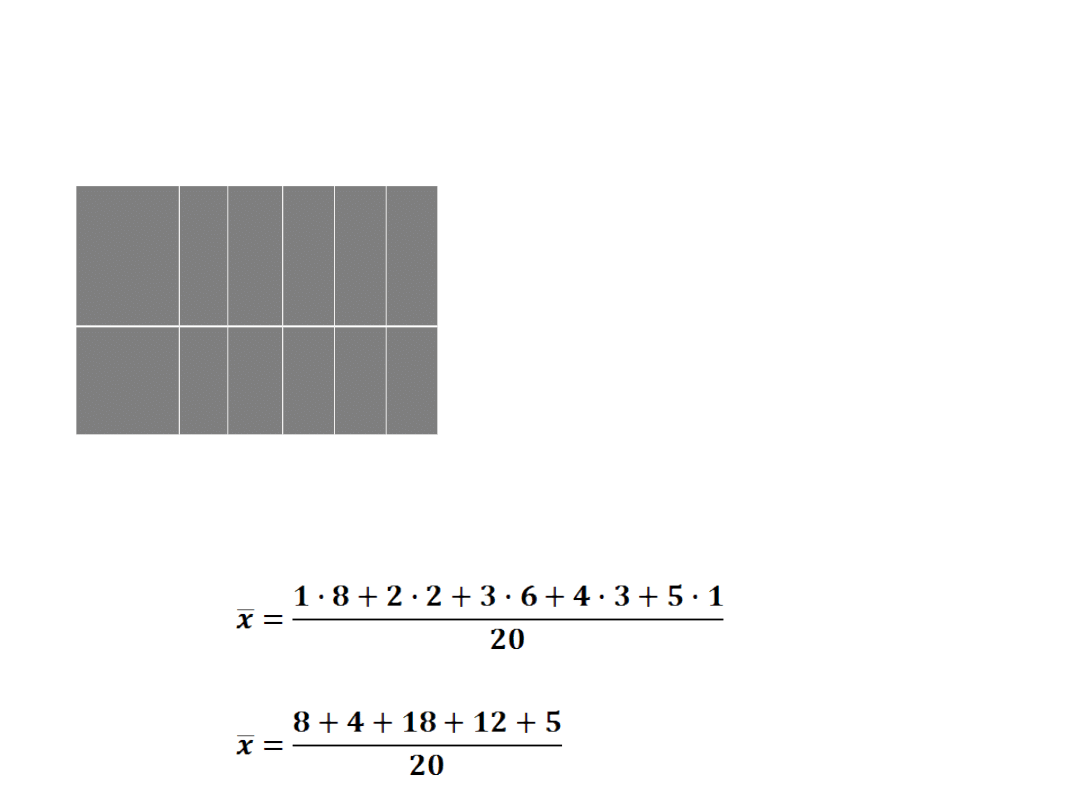
Ad a) 8+2+6+3+1=20
        W klasie jest 20 uczniów.

Ad b) średnia oglądalność: 

liczb

a 

godzi

n

1

2

3

4

5

liczb

a 

osób

8

2

6

3

1

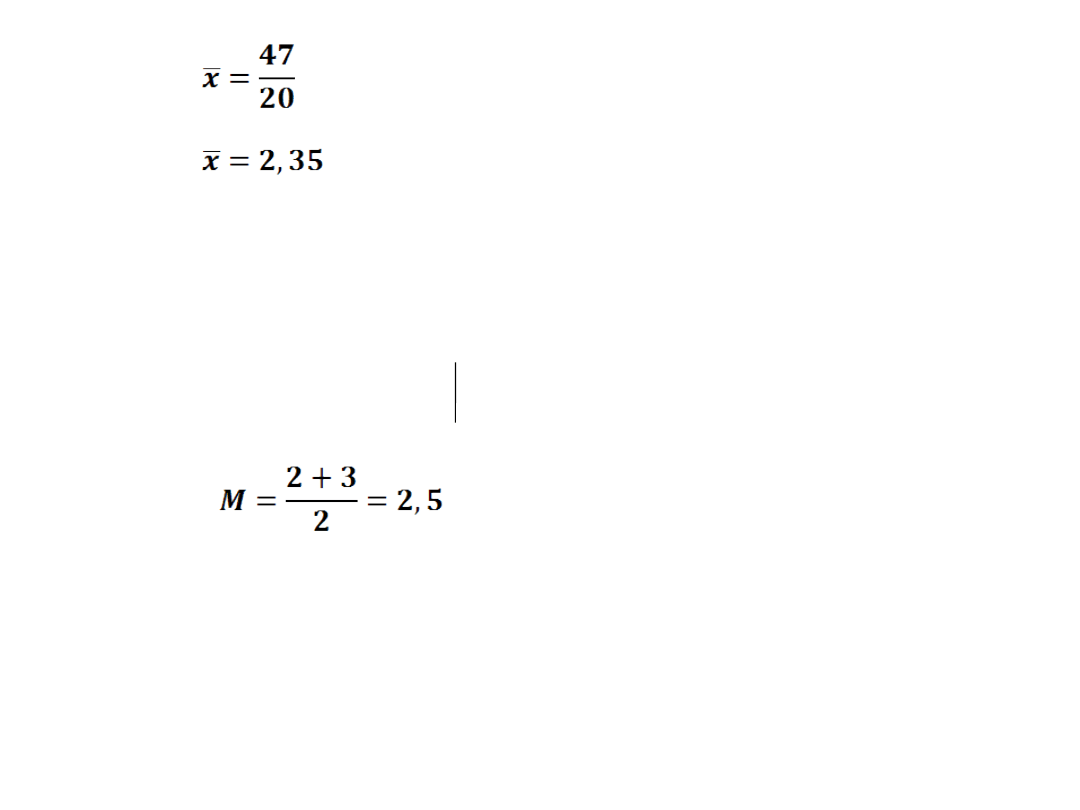
Średnio 2,35 godziny dziennie każdy uczeń klasy 
pierwszej ogląda telewizję.

Ad c)  1 1 1 1 1 1 1 1 2 

2

 

3

 3 3 3 3 3 4 4 4 5

Ad d) 

             D=1

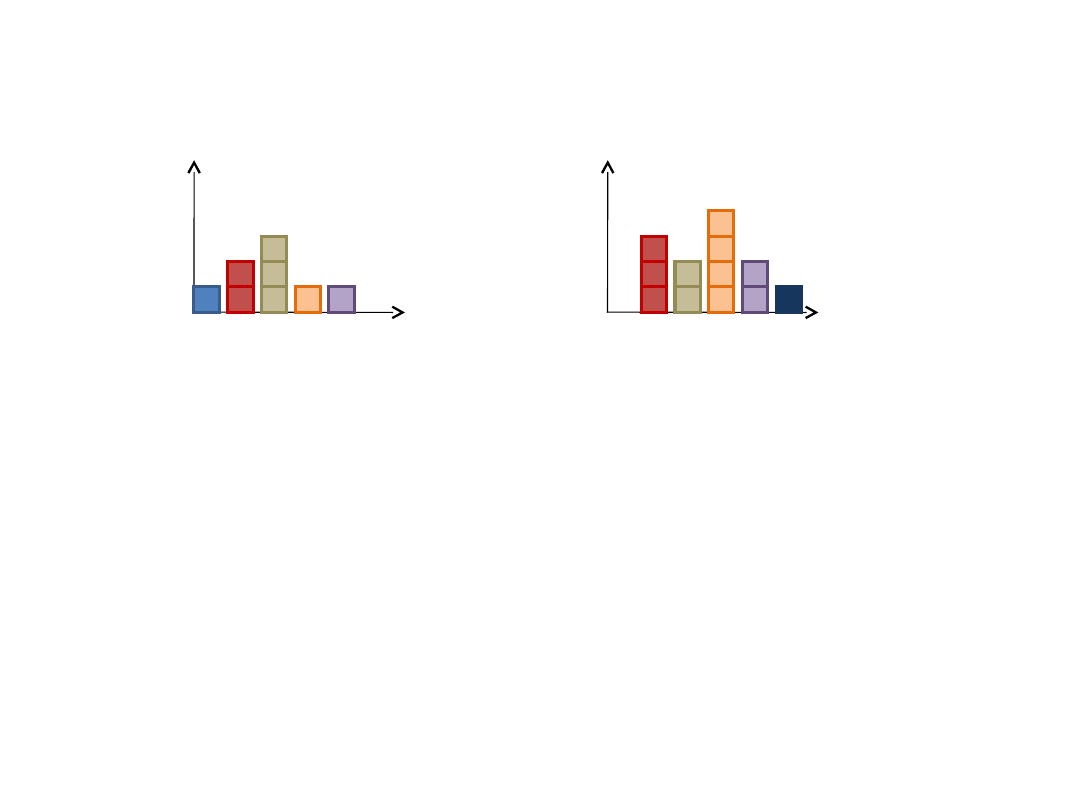
Ćw.8: Na wykresie przedstawiono ilość ocen z klasówki 
     z matematyki w poszczególnych grupach: dziewcząt i 
chłopców.

            

grupa dziewcząt                            grupa chłopców

a) ilu jest chłopców, dziewcząt, ile jest uczniów w klasie,
b) przedstaw w tabeli liczebność w poszczególnych 
grupach,
c) oblicz średnią ocen w grupie chłopców,
d) oblicz średnią ocen w grupie dziewcząt,
e) oblicz średnią ocen w klasie,
f) wyznacz medianę i dominantę w całej klasie i 
poszczególnych 
   grupach,

 1     2     3    4     5   
  6

 1     2     3    4     5   
  6

liczb
a 
ocen

liczb
a 
ocen

ocen
y

ocen
y

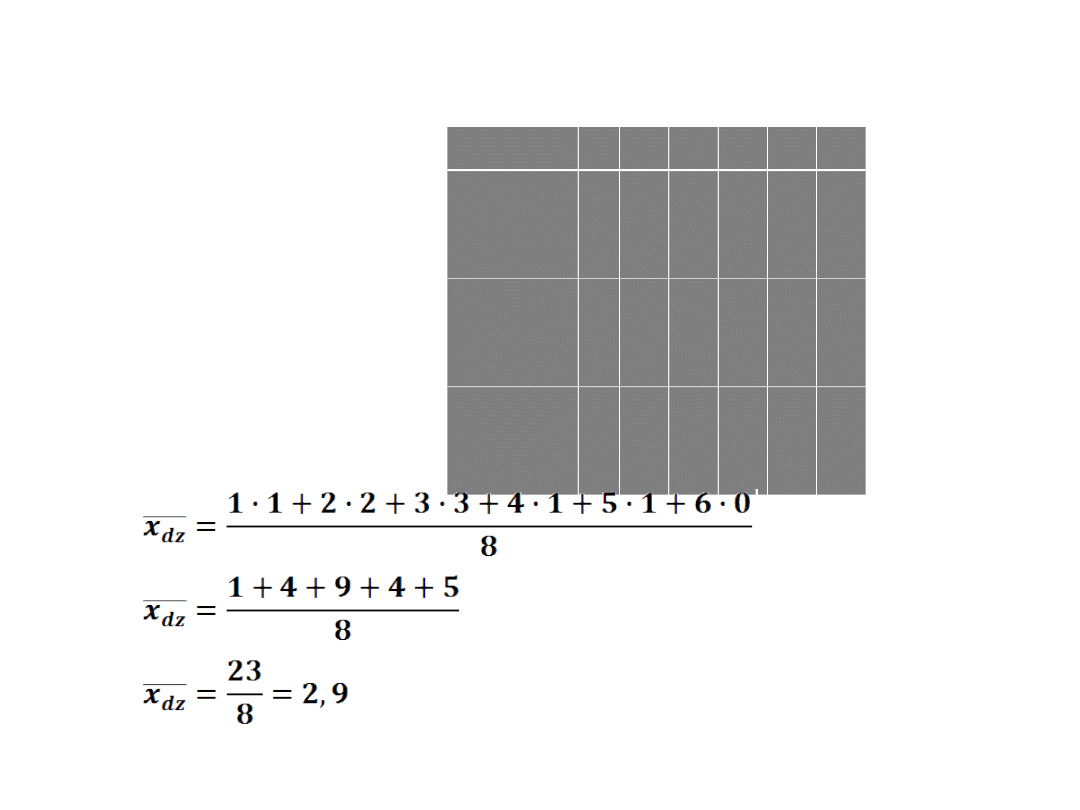
Ad a) W klasie jest 20 uczniów: 8 dziewcząt, 12 chłopców.

Ad b) tabela liczebności: 

Ad c)

ocena

1 2 3 4 5 6

liczba 

dziewc

ząt

1 2 3 1 1 0

liczba 

chłopc

ów

0 3 2 4 2 1

liczba 

ucznió

w

1 5 5 5 3 1

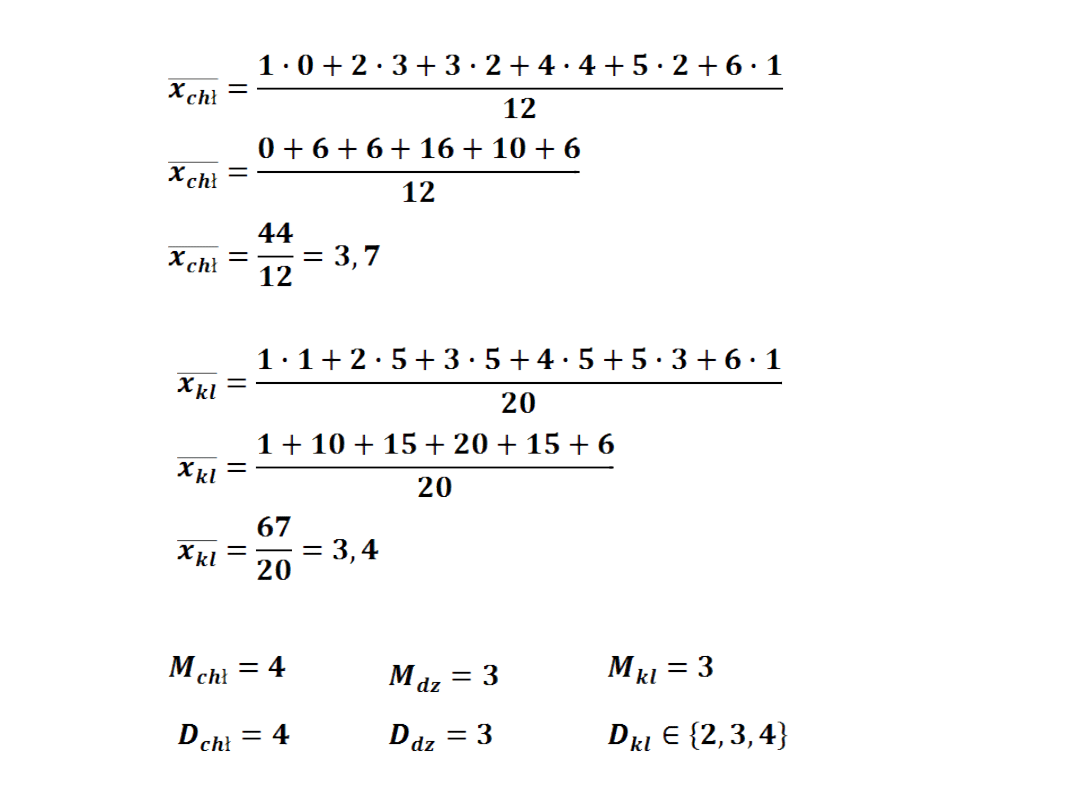
Ad d) 

Ad e)  

Ad f)       

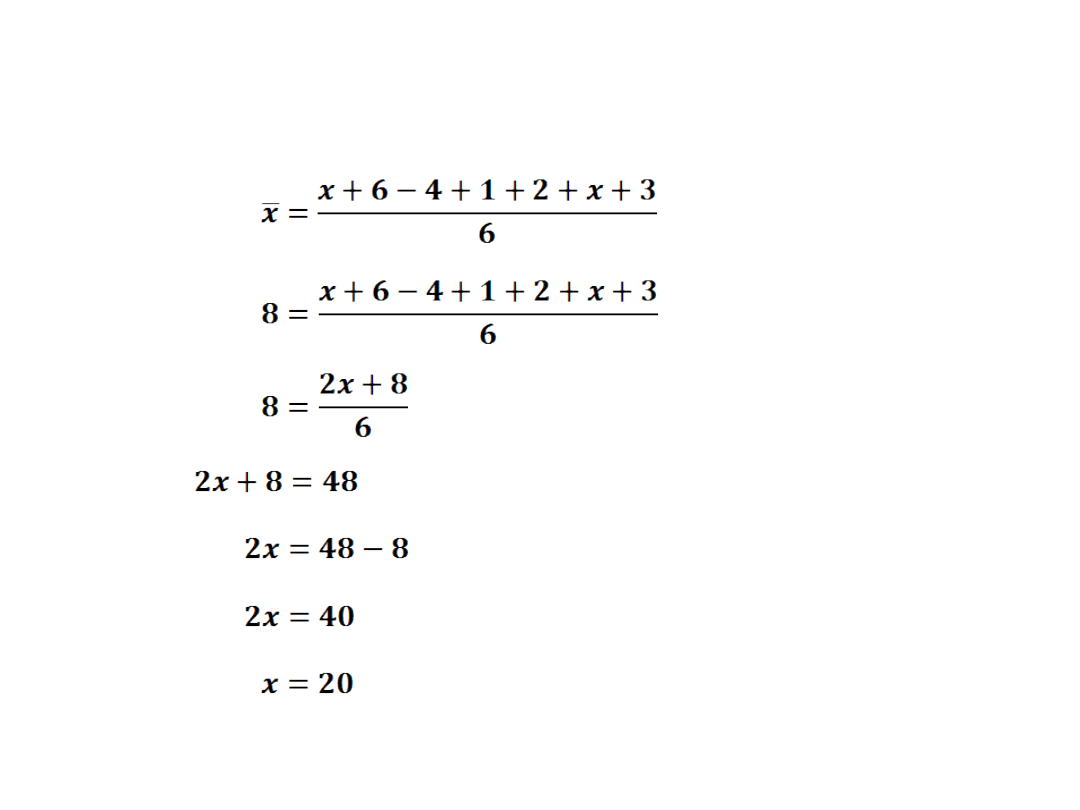
Ćw.9: Oblicz x wiedząc, że średnia arytmetyczna liczb:
        x,6,-4,1,2,x+3 jest równa 8.

Szukaną liczbą x jest liczba 20.

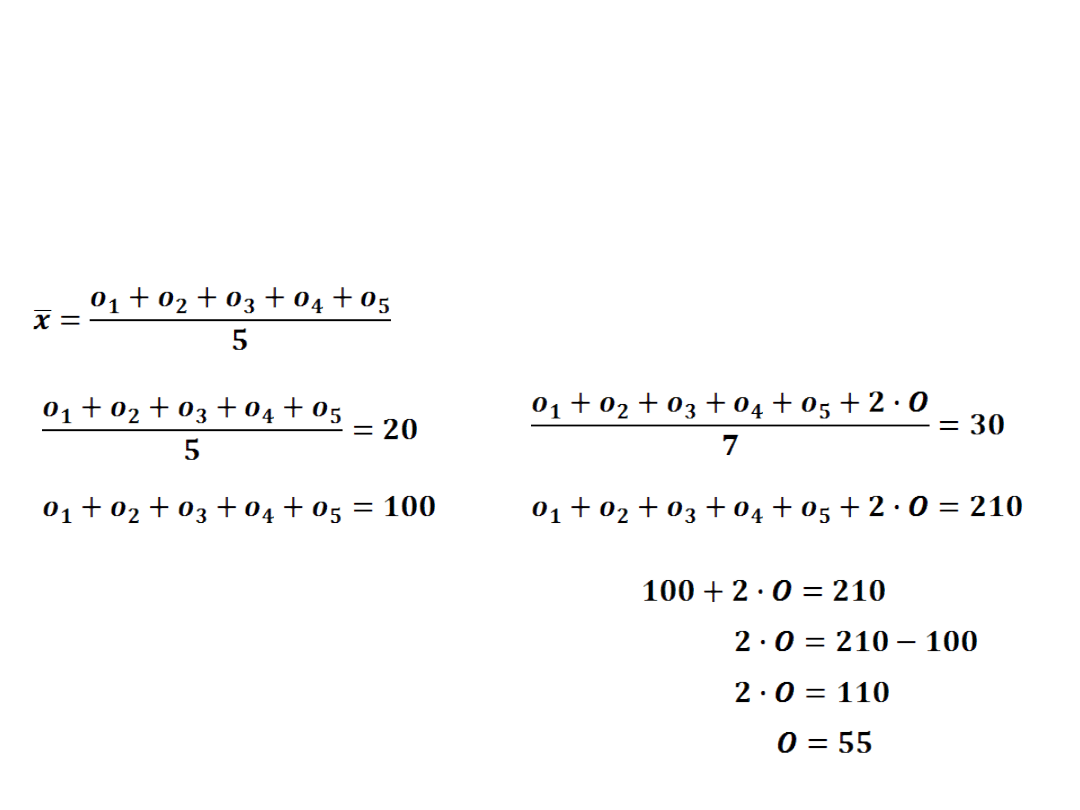
Ćw.10: Średnia waga 5 owiec jest równa 20kg. Jeśli 
zważymy owce 
       i dwa jednakowej wagi owczarki to średnia waga 
zwierząt 
       będzie równa 30kg. Ile waży owczarek?

O-owczarek   o

..

 –kolejne owce

Owczarek waży 55kg.