

1. Ralston A.: Wstęp do analizy numerycznej.
PWN Warszawa 1975.
2. Fortuna Z., Macukow B., Wąsowski J.: Metody numeryczne.
WNT Warszawa 1982.
3. Bjorck A., Dahlquist G.: Metody numeryczne.
PWN Warszawa 1983.
4. Pozrikidis C.: Numerical Computation in Science
and Engineering.
Oxford University Press 1998.
Zapis liczb w maszynie cyfrowej
Liczby całkowite
p
0
i
i
i
2
e
znak
n
gdzie e
i
=0 lub 1.
Jeżeli na zapis liczby przeznaczymy d bitów, to
pierwszy bit - znak,
następne d-1 bitów - zapis liczby
czyli mając do dyspozycji rejestr d bitowy p=d-2 i możemy
zapisać liczbę całkowitą:
1
2
n
2
1
d
1
d
w Pascalu mamy reprezentacje:

1 byte = 8 bitów
1 byte
shortint : -2
7
n 2
7
-1 -128 n 127
tylko nieujemne:
byte : 0 n 2
8
-1
0 n 255
2 byte = 16 bitów
integer : -2
15
n 2
15
-1 -32768 n 32767
tylko nieujemne:
word : 0 n 2
16
-1 0 n 65535
4 bite = 32 bity
longint : -2
31
n 2
31
-1 -2147483648 n 2147483647
W podanych zakresach liczby całkowite są reprezentowane
w maszynie cyfrowej dokładnie.
Przekroczenie zakresu dla danego typu liczb całkowitych
powoduje najczęściej błędne obliczenia.
Liczby rzeczywiste
c
2
m
x
m – mantysa, c – cecha. Przyjmuje się, że
1
m
2
1
Reprezentacja zmiennoprzecinkowa:
Mantysa m jest obliczana z zależności:
1
i
i
i
2
e
m
W maszynie cyfrowej mamy do dyspozycji skończoną liczbę
bitów wynoszącą t i mantysa maszynowa m
t
jest:
t
)
1
t
(
t
1
i
i
i
t
2
e
2
e
m
a więc popełniamy błąd zaokrąglenia mantysy:
t
1
t
1
i
i
1
t
m
1
t
i
i
1
t
i
i
i
1
i
i
i
t
1
i
i
i
t
m
2
2
1
1
1
2
2
2
2
2
e
2
e
2
e
m
m

c - cecha
Przykład:
x=znak liczby |mantysa |znak cechy |cecha
x=0|1110|011
00
.
7
2
875
.
0
2
2
1
0
2
1
1
2
1
1
2
1
1
1
x
3
2
1
2
1
1
4
3
2
1
0
zmieniamy jeden bit: x=0|1111|011
i mamy:
50
.
7
2
9375
.
0
2
2
1
1
2
1
1
2
1
1
2
1
1
1
x
3
2
1
2
1
1
4
3
2
1
0
Spróbujmy przedstawić w tej maszynie liczbę x=7.25
cecha: 2
3
i mantysa m=7.25/8=0.90625
reprezentacja dwójkowa mantysy:
4
1
i
i
i
2
e
m
czyli
0
e
e
5
.
2
1
e
25
.
0
1
e
2
1
e
e
25
.
1
2
1
e
2
1
e
625
.
0
1
e
2
1
e
2
1
e
e
625
.
1
2
1
e
2
1
e
2
1
e
8125
.
0
1
e
2
1
e
2
1
e
2
1
e
e
8125
.
1
2
1
e
2
1
e
2
1
e
2
1
e
90625
.
0
4
4
4
3
4
3
2
4
3
2
2
4
3
2
3
4
2
3
2
1
3
4
2
3
2
1
4
4
3
3
2
2
1
Przy ośmiu bitach dla zapisu liczb rzeczywistych - liczb
między 7.00 i 7.50 nie rozróżniamy.
Rzeczywiście mamy: błąd mantysy 2
-4
=0.0625, maksymalna
cecha 8, czyli 0.0625*8=0.5.
Błąd względny :
x
x
x
przyb
czyli
0357
.
0
7
7
25
.
7
lub inaczej
1
x
x
przyb
Maksymalny błąd względny przy najostrzejszym oszacowaniu,
to:
0625
.
0
8
8
5
.
7
ale
0625
.
0
2
1
4
W Pascalu stosujemy reprezentacje:
single – 4 byte w tym 1 byte cecha
czyli o wielkości błędu względnego decyduje liczba bitów
przeznaczonych na mantysę.
błąd względny reprezentacji:
7
23
10
2
.
1
2
a więc 7 do 8 prawidłowych cyfr znaczących.
Zakres reprezentowanych liczb:
max
min
c
c
2
x
2
2
1
gdzie
1
2
c
2
c
7
max
7
min
38
39
127
129
10
x
10
2
x
2

real – 6 byte
cecha – 1 byte
błąd względny reprezentacji:
74
.
11
39
10
2
około 10 do 12 cyfr znaczących dokładnie.
Zakres reprezentowanych liczb jak dla single czyli
1
2
c
2
c
7
max
7
min
38
39
127
129
10
x
10
2
x
2
double – 8 byte
cecha 11 bitów
1
2
c
2
c
10
max
10
min
308
308
1023
1025
10
9
.
0
x
10
6
.
3
2
x
2
błąd względny reprezentacji:
65
.
15
52
10
2
około 15 do 16 cyfr znaczących dokładnie.
Zakres reprezentowanych liczb:
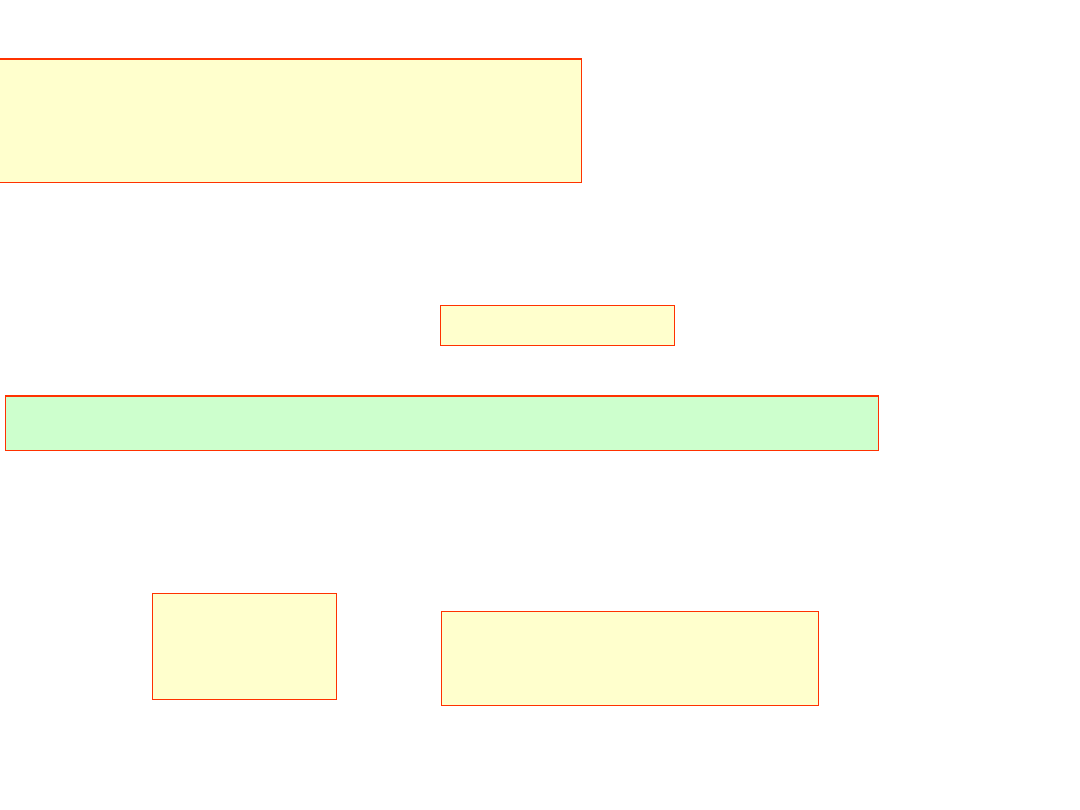
extended – 10 byte
cecha – 15 bitów
błąd względny reprezentacji:
26
.
19
64
10
2
około 19 do 20 cyfr znaczących dokładnie.
1
2
c
2
c
14
max
14
min
4932
4932
16383
16385
10
1
.
1
x
10
4
.
3
2
x
2
Zakres reprezentowanych liczb:
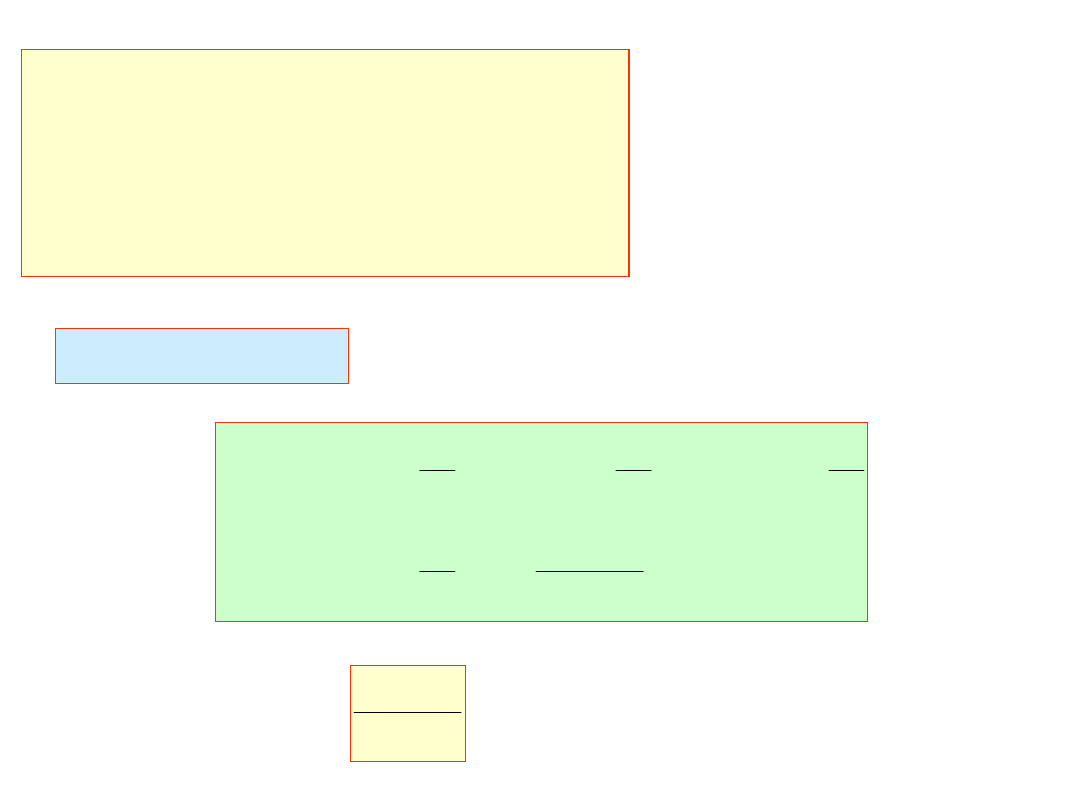
Rodzaje błędów:
1. błędy danych wejściowych,
2. błędy obcięcia,
3. błędy zaokrągleń.
Błąd obcięcia
!
1
N
x
O
!
n
x
1
e
!
n
x
1
!
n
x
1
!
n
x
1
e
1
N
N
0
n
n
n
x
1
N
n
n
n
N
0
n
n
n
0
n
n
n
x
Błąd obcięcia:
!
1
N
x
1
N

Błąd obcięcia będzie dyskutowany przy poszczególnych
metodach
Błąd danych wejściowych może być np. spowodowany
błędami popełnionymi przy pomiarach np. wymiarów
geometrycznych, itp..
Kilka uwag na temat organizacji obliczeń
Obliczyć wartość wielomianu stopnia n:
n
1
n
1
n
1
n
n
a
x
a
x
a
x
x
P
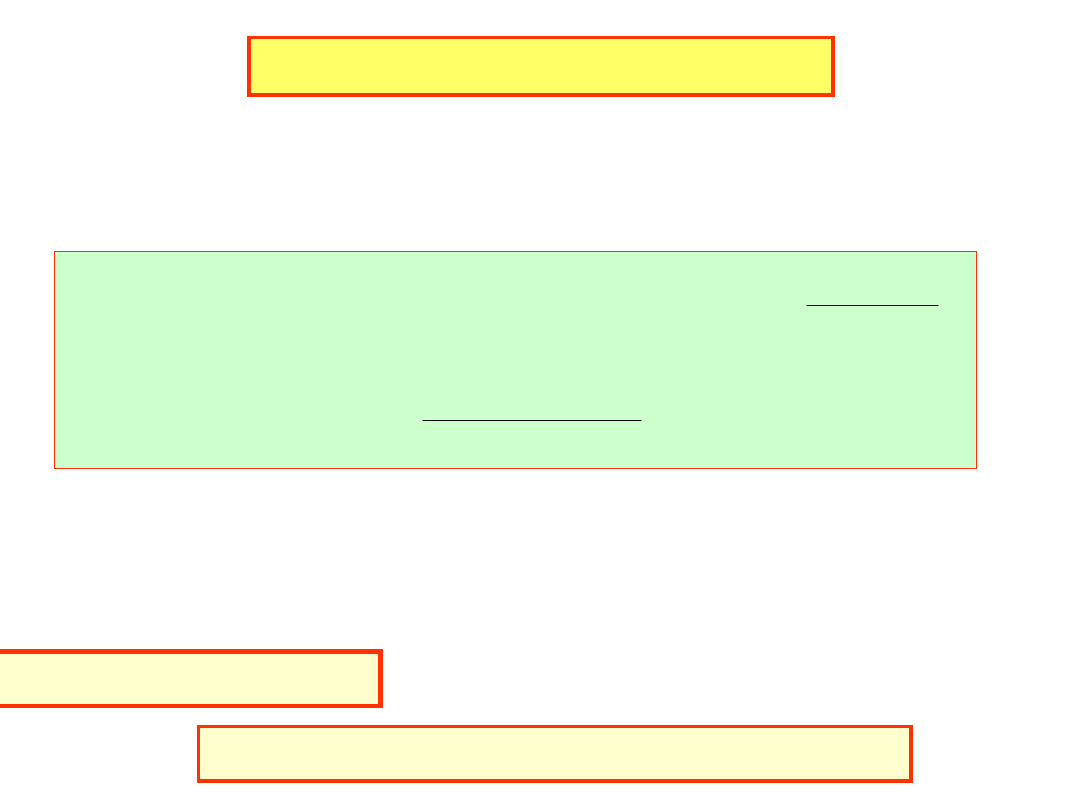
n
1
n
1
n
1
n
n
a
x
a
x
a
x
x
P
Obliczenia klasyczne:
Liczba mnożeń –
2
2
n
1
n
2
1
n
n
1
n
1
2
2
n
1
n
1
n
Liczba dodawań - n
Dla n=100 mamy 5049 mnożeń i 100 dodawań.
Schemat Hornera:
n
1
n
2
1
a
x
a
x
a
x
a
x
x
P
n
1
n
2
1
a
x
a
x
a
x
a
x
x
P
Liczba działań:
mnożeń – n-1
dodawań - n
Schemat łatwy do realizacji w pętli:
w=x+a
1
for k=2 to n
w=wx+a
k
P(x)=w
Po zakończeniu pętli mamy obliczoną wartość wielomianu.
Obliczanie sum
Sumę nieskończoną w obliczeniach numerycznych zastępujemy
sumą skończoną:
k
0
k
k
dok
a
S
Obliczenia numeryczne:
N
k
1
k
k
p
a
N
S
Błąd obliczeń szacujemy:
100
kN
S
kN
S
N
S
N
er
p
p
p
gdzie k najczęściej przyjmuje się =2.
Przykład:
125
.
0
1
k
4
k
0
S
k
1
k
2
2
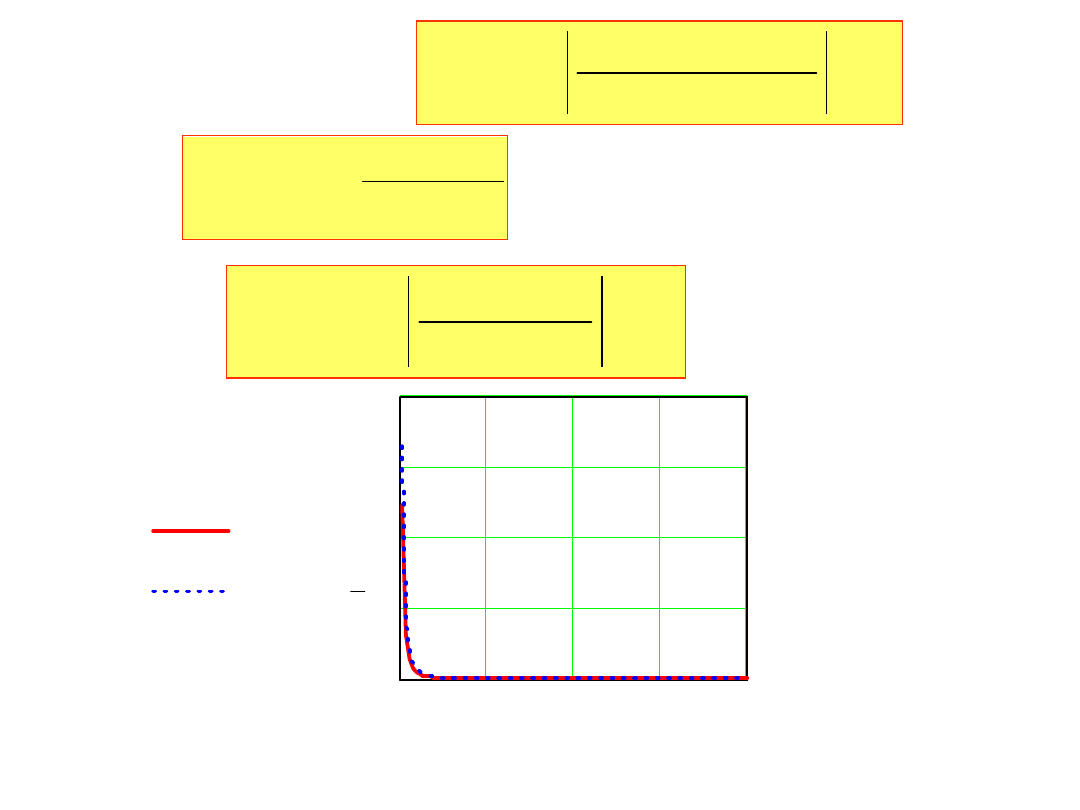
i porównajmy błędy:
ep N
( )
Sp N
( ) Sp 2 N
(
)
Sp 2 N
(
)
100
gdzie
N
k
1
k
2
2
1
k
4
k
N
Sp
z błędem: ep0N
( )
Sp N
( ) S0
S0
100
0
2.5
5
7.5 10
0
7.510
4
0.0015
0.00225
0.003
ep K
( )
ep0K
( )
K 10
3
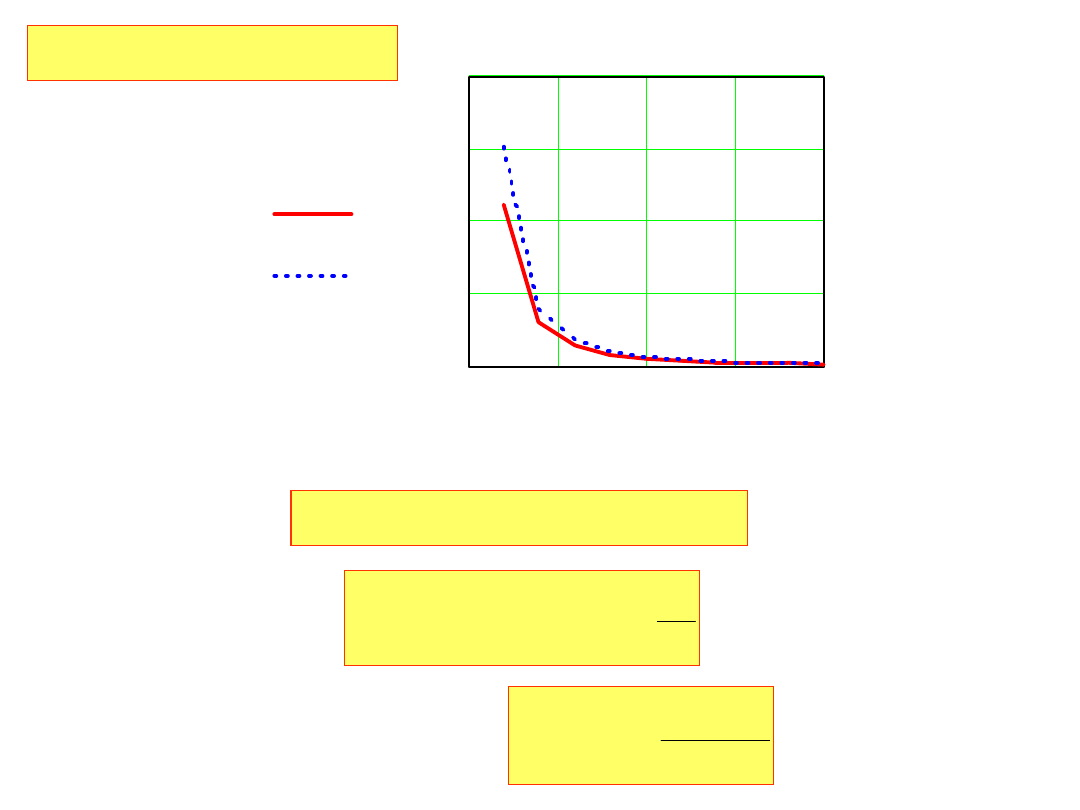
0
25
50
75 100
0
0.075
0.15
0.23
0.3
ep K
( )
ep0K
( )
K
dla K=10,20..100
Kolejność sumowania
1
k
k
1
k
k
x
1
)
x
1
ln(
i obliczmy dla x=1 czyli
1
k
1
k
k
1
)
2
ln(
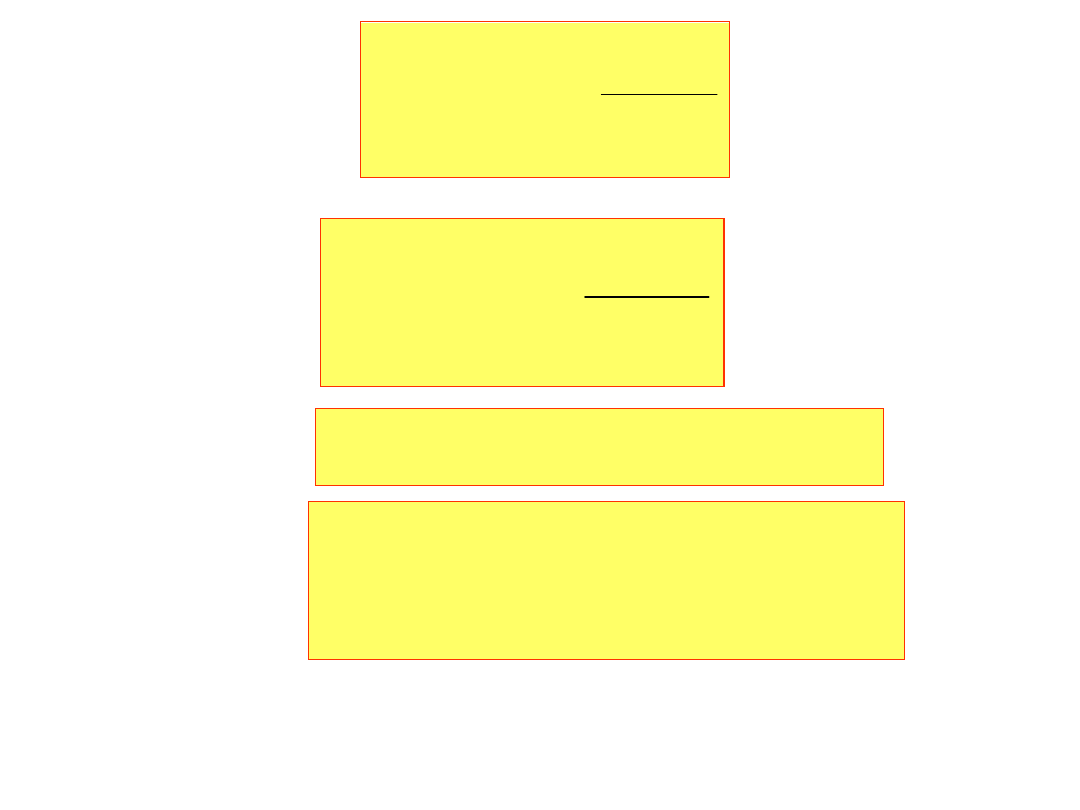
i obliczamy:
Sg N
( )
1
N
n
1
( )
n 1
n
�
oraz
Sd N
( )
N
1
n
1
( )
n 1
n
�
ln 2
( )
0.693147180559945
Sg 100
(
)
0.688172179310195
Sd 100
(
)
0.688172179310195

ln 2
( )
0.693147180559945
Sg 1000
(
)
0.692647430559822
Sd 1000
(
)
0.69264743055982
Sg 5000
(
)
0.693047190559951
Sd 5000
(
)
0.693047190559945
Sg 10000
(
)
0.693097183059958
Sd 10000
(
)
0.693097183059945
Sg 20000
(
)
0.693122181184958
Sd 20000
(
)
0.693122181184945

Przyśpieszenie zbieżności:
N
k
1
k
1
k
1
k
1
k
1
k
1
k
1
k
2
k
2
1
)
N
(
0
S
1
k
2
k
2
1
1
k
2
1
k
2
1
k
1
0
S
ln 2
( )
0.693147180559945
S0 100
(
)
0.690653430481824
Sg 100
(
)
0.688172179310195
S0 1000
(
)
0.692897243059939
Sg 1000
(
)
0.692647430559822
S0 10000
(
)
0.693122181184947
Stabilność algorytmu
Przykład niestabilnego algorytmu (Kincaid i Cheney, 1996r)
Rozpatrzmy ciąg liczbowy:
2
k
x
3
4
x
3
13
x
3
1
x
1
x
2
k
1
k
k
1
0
równoważny ciągowi:
0
k
3
1
x
k
k
Dowód metodą
indukcji matematycznej
Algorytm I
Algorytm II
Wyniki obliczeń w arytmetyce 32 bitowej według:
Algorytmu I
Algorytmu II
x
1
=1.00000000000000
x
1
=1.00000000000000
x
2
=0.333333333333333
x
2
=0.333333333333333
x
3
=0.111111111111111
x
3
=0.111111111111111
x
4
=0.037037037037036
x
4
=0.037037037037037
………………………..
………………………..
x
10
=0.000016935074827 x
10
=0.000016935087808
x
20
=-0.000013611585443 x
20
=0.000000000000000
x
30
=-14.273082546213100x
30
=0.000000000000000
Algorytmu I
Algorytmu II
x
40
=-1.496641180397794e7
x
40
=0.000000000000000
x
100
=-4.973443391573326e42
x
100
=0.000000000000000
Algorytm obliczeń rekurencyjnych:
2
k
x
3
4
x
3
13
x
3
1
x
1
x
2
k
1
k
k
1
0
jest numerycznie niestabilny
i nie może być zastosowany do
obliczeń numerycznych.

Układy równań liniowych
N
M
NM
k
Nk
2
2
N
1
1
N
k
M
kM
k
kk
2
2
k
1
1
k
2
M
M
2
k
k
2
2
22
1
21
1
M
M
1
k
k
1
2
12
1
11
b
x
a
...
x
a
...
x
a
x
a
.
..
..........
..........
..........
b
x
a
...
x
a
...
x
a
x
a
.
........
..........
..........
b
x
a
...
x
a
...
x
a
x
a
b
x
a
...
x
a
...
x
a
x
a
Jeżeli N<M, układ równań jest nieokreślony,
N=M – określony
N>M - nadokreślony
Rozważymy tylko przypadek N=M

Układ NxM liczb rzeczywistych bądź zespolonych zapisujemy
w formie tablicy.
Taką tablicę nazywamy macierzą NM wymiarową
lub macierzą prostokątną.
NM
Nk
2
N
1
N
kM
kk
2
k
1
k
M
2
k
2
22
21
M
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
wiersz macierzy
wiersz k-ty macierzy
kolumna
macierzy
k-ta kolumna
macierzy
a
ik
– wyraz macierzy położony we wierszu i-tym i kolumnie k-tej
NM
Nk
2
N
1
N
kM
kk
2
k
1
k
M
2
k
2
22
21
M
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
Macierz symbolicznie zapisujemy w postaci jednego znaku, np.: A
podając liczbę wierszy i kolumn w opisie.
Inny skrócony zapis to:
ik
a
A
i=(1,N); k=(1,M)
Jeżeli N=M, to macierz jest macierzą o jednakowej liczbie wierszy
i kolumn. Mówimy, że jest to macierz kwadratowa stopnia N,
lub macierz stopnia N.

NN
Nk
2
N
1
N
kN
kk
2
k
1
k
N
2
k
2
22
21
N
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
Macierz kwadratowa stopnia N.
Operacje na macierzach
Mnożenie macierzy przez liczbę c.
c – liczba rzeczywista lub zespolona.
Dwie macierze A i B są równe czyli A=B, jeżeli mają jednakową
liczbę wierszy i kolumn i zachodzi a
ij
=b
ij
dla wszystkich par (i,j).

NM
Nk
2
N
1
N
kM
kk
2
k
1
k
M
2
k
2
22
21
M
1
k
1
12
11
ca
.
ca
.
ca
ca
.
.
.
.
.
.
ca
.
ca
.
ca
ca
.
.
.
.
.
.
ca
.
ca
.
ca
ca
ca
.
ca
.
ca
ca
cA
lub krótko B=cA=[ca
ik
]
wymiary macierzy B są identyczne jak wymiary macierzy A.
Dodawanie (odejmowanie) dwóch macierzy A i B.
Obie macierze muszą mieć tę samą liczbę wierszy i kolumn.

NM
Nk
2
N
1
N
kM
kk
2
k
1
k
M
2
k
2
22
21
M
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
NM
Nk
2
N
1
N
kM
kk
2
k
1
k
M
2
k
2
22
21
M
1
k
1
12
11
b
.
b
.
b
b
.
.
.
.
.
.
b
.
b
.
b
b
.
.
.
.
.
.
b
.
b
.
b
b
b
.
b
.
b
b
B

suma:
NM
NM
Nk
Nk
2
N
2
N
1
N
1
N
kM
kM
kk
kk
2
k
2
k
1
k
1
k
M
2
M
2
k
2
k
2
22
22
21
21
M
1
M
1
k
1
k
1
12
12
11
11
b
a
.
b
a
.
b
a
b
a
.
.
.
.
.
.
b
a
.
b
a
.
b
a
b
a
.
.
.
.
.
.
b
a
.
b
a
.
b
a
b
a
b
a
.
b
a
.
b
a
b
a
B
A
lub krótko C =A+B=[a
ij
+b
ij
]
lub w postaci realizacji na maszynie: c
ij
=a
ij
+b
ij
dla i=(1,N), j=(1,M):
for i:=1 to N do
for j:=1 to M do
C[i,j]:=A[i,j]+B[i,j]
Suma macierzy jest przemienna, czyli A+B=B+A

różnica:
NM
NM
Nk
Nk
2
N
2
N
1
N
1
N
kM
kM
kk
kk
2
k
2
k
1
k
1
k
M
2
M
2
k
2
k
2
22
22
21
21
M
1
M
1
k
1
k
1
12
12
11
11
b
a
.
b
a
.
b
a
b
a
.
.
.
.
.
.
b
a
.
b
a
.
b
a
b
a
.
.
.
.
.
.
b
a
.
b
a
.
b
a
b
a
b
a
.
b
a
.
b
a
b
a
B
A
C
lub krótko C =A-B=[a
ij
-b
ij
]
lub w postaci realizacji na maszynie: c
ij
=a
ij
-b
ij
dla i=(1,N), j=(1,M):
for i:=1 to N do
for j:=1 to M do
C[i,j]:=A[i,j]-B[i,j]

Iloczyn dwóch macierzy
Dane dwie macierze prostokątne:
A o wymiarze N
A
xM
A
i B o wymiarze N
B
xM
B
Obliczyć iloczyn C=AB.
Macierz będącą iloczynem można obliczyć tylko wtedy, jeżeli
liczba kolumn pierwszego czynnika – czyli M
A
– jest równa
liczbie wierszy drugiego czynnika – czyli N
B
, a więc warunkiem
wykonalności mnożenia dwóch macierzy prostokątnych jest
M
A
=N
B
Macierz C będzie miała N
A
wierszy i M
B
kolumn.
Jeżeli A i B są macierzami kwadratowi tego samego stopnia N
mnożenie jest zawsze wykonalne.

Wyrazy macierzy C=[c
ik
] będącej iloczynem macierzy AB
obliczamy z zależności:
B
A
M
n
1
n
nk
in
ik
M
1,
k
oraz
N
1,
i
dla
b
a
c
A
Przykład:
1
0
0
1
2
0
3
0
2
0
3
1
A
liczba wierszy 4
liczba kolumn 3
1
2
0
0
0
0
0
4
3
0
0
1
2
0
2
B
liczba wierszy 3
liczba kolumn 5

Macierz C=AB będzie macierzą o 4 wierszach i 5 kolumnach
1
0
0
1
2
0
3
0
2
0
3
1
A
1
2
0
0
0
0
0
4
3
0
0
1
2
0
2
B
c
11
=a
11
b
11
+a
12
b
21
+a
13
b
31
=1·2+3 ·0+0 ·0=2
c
12
=a
11
b
12
+a
12
b
22
+a
13
b
32
=1 ·0+3 ·3+0 ·0=9
c
13
=a
11
b
13
+a
12
b
23
+a
13
b
33
=1 ·(-2)+3 ·4+0 ·0=10
c
14
=a
11
b
14
+a
12
b
24
+a
13
b
34
=1 ·1+3 ·0+0 ·2=1
c
15
=a
11
b
15
+a
12
b
25
+a
13
b
35
=1 ·0+3 ·0+0 ·1=0
c
21
=a
21
b
11
+a
22
b
21
+a
23
b
31
=(-2) ·2+0 ·0+3 ·0=-4
itd…

1
2
0
0
0
1
2
8
6
0
3
4
4
0
4
0
1
10
9
2
C
Iloczyn dwóch macierzy, również kwadratowych,
nie jest przemienny czyli AB≠BA
4
3
2
0
5
0
0
4
2
A
1
2
0
2
0
2
0
2
0
B
10
4
6
10
0
10
8
4
8
AB
4
7
2
8
2
0
0
10
0
BA
Jeżeli zachodzi AB=BA mówimy, że macierze są przemienne.
Macierz jednostkowa I – jest to macierz kwadratowa o wymiarze
N, której wyraz δ
ik
jest zdefiniowany następująco:
k
i
dla
0
k
i
dla
1
ik
czyli np. macierz jednostkowa 5-go stopnia ma postać:
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
0
0
0
0
0
1
I
Wykazać, że AI=IA=A
Ograniczymy nasze rozważania tylko do macierzy kwadratowych
stopnia N
O wyrazach a
ii
macierzy A mówimy, że leżą na głównej przekątnej
NN
kk
22
11
a
.
0
.
0
0
.
.
.
.
.
.
0
.
a
.
0
0
.
.
.
.
.
.
0
.
0
.
a
0
0
.
0
.
0
a
A
a macierz A, która ma niezerowe wyrazy tylko na głównej
przekątnej nazywamy macierzą diagonalną
NN
Nk
2
N
1
N
kN
kk
2
k
1
k
N
2
k
2
22
21
N
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
Jeżeli w macierzy A
NN
kN
N
2
N
1
Nk
kk
k
2
k
1
2
N
2
k
22
12
1
N
1
k
22
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
zamienimy wiersze z kolumnami, to tak otrzymaną macierz
nazywamy macierzą transponowaną i oznaczamy A
T
zapisując symbolicznie możemy napisać: [a
ik
]
T
=[a
ki
]
Przykład:
3
2
0
0
0
0
0
1
2
1
0
4
0
2
3
1
A
3
0
2
0
2
0
1
2
0
0
0
3
0
1
4
1
T
A
Zachodzą związki:
T
T
T
A
B
AB
Przykład:
4
1
1
2
0
3
2
1
3
A
3
1
1
0
5
2
4
1
0
B
16
10
6
18
5
2
18
0
0
AB
16
18
18
10
5
0
6
2
0
T
AB
4
1
1
2
0
3
2
1
3
A
4
2
2
1
0
1
1
3
3
T
A
3
1
1
0
5
2
4
1
0
B
3
0
4
1
5
1
1
2
0
T
B
16
18
18
10
5
0
6
2
0
T
T
A
B
16
18
18
10
5
0
6
2
0
T
AB
A
A
T
T
Dla każdej macierzy zachodzi

T
T
T
T
T
T
T
T
T
AA
AA
AA
A
A
AA
Macierz B, dla której zachodzi równość: nazywamy
macierzą symetryczną
T
B
B
Macierz B=AA
T
jest macierzą symetryczną.
5
1
1
3
0
4
3
1
0
0
2
4
0
0
1
2
A
5
0
0
0
1
4
0
0
1
3
2
1
3
1
4
2
T
A
30
2
14
7
2
26
10
5
14
10
20
10
7
5
10
5
T
AA
Wyznacznik
Dla danej macierzy kwadratowej A:
NN
Nk
2
N
1
N
kN
kk
2
k
1
k
N
2
k
2
22
21
N
1
k
1
12
11
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
.
.
.
.
.
.
a
.
a
.
a
a
a
.
a
.
a
a
A
definiujemy liczbę:
N
1
j
ij
ij
j
i
det
a
1
det
A
A
gdzie detA
ij
jest wyznacznikiem macierzy stopnia N-1 otrzymanej
przez skreślenie z macierzy A wiersza i-go i kolumny j-ej.
Jest to definicja rekurencyjna i dlatego musimy zdefiniować
wyznacznik macierzy kwadratowej stopnia N=1, czyli A=[a
11
].
Wyznacznik tej macierzy jest: detA=a
11
.
Dla macierzy drugiego stopnia mamy:
22
21
12
11
a
a
a
a
det
A
Zgodnie ze wzorem
N
1
j
ij
ij
j
i
det
a
1
det
A
A
mamy:
21
12
2
1
22
11
1
1
a
det
a
1
a
det
a
1
det
A
czyli dla macierzy drugiego stopnia mamy:
21
12
22
11
a
a
a
a
det
A
Wyznacznik drugiego stopnia obliczamy bezpośrednio:
12
21
22
11
22
21
12
11
a
a
a
a
a
a
a
a
dla obliczenia wyznacznika
musimy wykonać dwa mnożenia
Wyznacznik macierzy trzeciego stopnia:
33
32
31
23
22
21
13
12
11
a
a
a
a
a
a
a
a
a
A
Zgodnie ze wzorem:
N
1
j
ij
ij
j
i
det
a
1
det
A
A
mamy:
12
21
33
11
23
32
13
22
31
32
21
13
31
23
12
33
22
11
22
31
32
21
13
23
31
33
21
12
23
32
33
22
11
32
31
22
21
13
3
1
33
31
23
21
12
2
1
33
32
23
22
11
1
1
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
1
a
a
a
a
a
1
a
a
a
a
a
1
det
A
Liczba mnożeń, którą trzeba wykonać wynosi 9=3!
Wyznacznik 3-go stopnia możemy łatwo obliczyć metodą Sarrusa
12
21
33
11
23
32
13
22
31
32
21
13
31
23
12
33
22
11
32
31
33
32
31
22
21
23
22
21
12
11
13
12
11
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
a
+ +
+
-
-
-

Obliczenie wyznacznika N-go stopnia wymaga wykonania N!
mnożeń.
Obliczanie wyznaczników stopnia 4-go i wyższych jest operacją
czasochłonną,
Macierz odwrotna
Macierz odwrotną do macierzy kwadratowej A będziemy
oznaczać A
-1
.
Macierz A
-1
jest macierzą odwrotną do macierzy A tylko
wtedy jeżeli
I
i
I
1
1
A
A
AA
Jeżeli wyrazy macierz odwrotnej oznaczymy przez b
ik
a wyrazy
macierzy A przez a
ik
, to dla wyznaczenia wyrazów macierzy
odwrotnej mamy N
2
równań:
k
i
dla
0
k
i
dla
1
b
a
N
j
1
j
jk
ij

Wyrazy macierzy odwrotnej można wyznaczyć ze wzorów
analitycznych:
A
A
det
det
1
b
ij
j
i
ij
gdzie detA – wyznacznik macierzy A,
A
ij
– oznacza macierz stopnia N-1 otrzymaną z macierzy
A przez skreślenie i-go wiersza i j-ej kolumny, a
detA
ij
jest wyznacznikiem macierzy A
ij
.
Z powyższego wzoru wynika, że warunkiem istnienia macierzy
odwrotnej jest aby wyznacznik główny detA≠0
Podanego wzoru praktycznie nigdy nie stosujemy do obliczenia
macierzy odwrotnej, gdyż prowadzi on do olbrzymiej liczby
obliczeń. Szacując tylko liczbę mnożeń mamy dla obliczenia
wyznacznika głównego N!. Dla obliczenia N
2
wyrazów macierzy
odwrotnej (N-1)! mnożeń, a więc N!+N
2
(N-1)!=(N+1)! mnożeń.

Rozwiązywanie układów równań liniowych
Dany jest układ równań liniowych:
B
AX
A – macierz (tablica) o wymiarze NxN,
a
ij
– element macierzy A leżący w i-tym wierszu i j-tej kolumnie
.
.
.
.
.
.
.
.
.
.
.
.
a
.
.
.
.
.
.
.
.
.
.
.
.
wiersz
ty
i
kolumna
ta
j
ij

X – wektor (tablica jednokolumnowa) niewiadomych
o N składowych
Zapis:
.
x
.
x
x
i
1
i
X
Często wygodniej zapisywać w postaci:
N
i
1
T
x
.
x
.
x
X
Formalnie rozwiązanie równania AX=B możemy zapisać w postaci:
B
A
X
1
i ponieważ obliczenie macierzy odwrotnej wymaga (N+1)! mnożeń,
więc w przybliżeniu taki byłby nakład pracy przy rozwiązaniu w ten
sposób. Niestety jest to niewykonalne dla dużych układów równań.
Przestrzeń R
n
jest utworzona przez n - wymiarowe wektory X
Definiujemy normy dla wektora:
.
x
.
x
x
i
1
i
X
jako
n
2
1
1
x
x
x
X
lub norma euklidesowa:
2
1
2
n
2
2
2
1
2
x
x
x
X
norma maksimum:
n
2
1
x
,
,
x
,
x
max
X
Normy wektorów są równoważne, co oznacza, że jeżeli ciąg
norm jest zbieżny do zera według jednej z norm
to jest zbieżny również względem pozostałych.
,
x
,
x
2
1

Macierz A o m wierszach i n kolumnach:
m
n
AX
X
wektorom X
(m)
przestrzeni R
m
przyporządkowuje wektory X
(n)
przestrzeni R
n
. Mówimy, że mamy operator liniowy A
przekształcający przestrzeń R
m
w R
n
.
Normę operatora definiujemy:
m
n
nm
max
X
AX
A
0
X
Jeżeli przyjmiemy w obu przestrzeniach normę
n
2
1
1
x
x
x
X
to
m
i
1
i
ij
n
,
,
2
,
1
j
1
a
max
A
maksymalna suma
modułów w kolumnie
Jeżeli w obu przestrzeniach jest stosowana norma euklidesowa:
2
1
2
n
2
2
2
1
2
x
x
x
X
to normę macierzy najczęściej ocenia się za pomocą normy:
m
1
i
n
1
j
2
ij
E
a
A
zwanej normą euklidesową.
Dla normy maksimum w obu przestrzeniach
n
2
1
x
,
,
x
,
x
max
X
norma macierzy jest
m
j
1
j
ij
m
,
,
2
,
1
i
a
max
A
maksymalna suma
we wierszu

Metoda Gaussa
bez wyboru elementu wiodącego
5
10
0
30
x
x
x
x
4
1
2
0
1
10
0
2
.
0
2
0
5
1
0
2
.
0
1
4
4
3
2
1
Przykład:
5
4
1
2
0
10
1
10
0
2
.
0
0
2
0
5
1
30
0
2
.
0
1
4
Zapisujemy w postaci macierzy dołączonej:

157894737
.
8
578947368
.
3
021052632
.
1
0
0
421052632
.
8
021052632
.
1
989473684
.
9
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1
0
2
.
0
1
4
/
1
5
4
1
2
0
5
.
8
1
99
.
9
05
.
0
0
5
.
7
2
05
.
0
75
.
4
0
5
.
7
0
05
.
0
25
.
0
1
5
4
1
2
0
10
1
10
0
2
.
0
0
2
0
5
1
30
0
2
.
0
1
4

157894737
.
8
578947368
.
3
021052632
.
1
0
0
421052632
.
8
021052632
.
1
989473684
.
9
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1
5
4
1
2
0
5
.
8
1
99
.
9
05
.
0
0
5
.
7
2
05
.
0
75
.
4
0
5
.
7
0
05
.
0
25
.
0
1
2
05
.
0
75
.
4
/
1
2971549
.
7
474582663
.
3
0
0
0
842992624
.
0
102212856
.
0
1
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1

100152913
.
2
1
0
0
0
842992624
.
0
102212856
.
0
1
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1
Redukcja górnej trójkątnej:
W wyniku przeprowadzonej redukcji otrzymujemy układ
równań w postaci:
1
.
2
x
843
.
0
x
102
.
0
x
5789
.
1
x
421
.
0
x
0105
.
0
x
5
.
7
x
0
x
05
.
0
x
25
.
0
x
4
4
3
4
3
2
4
3
2
1
100152913
.
2
1
0
0
0
628329997
.
0
0
1
0
0
45660828
.
2
0
0
1
0
185835002
.
7
0
0
25
.
0
1
100152913
.
2
1
0
0
0
628329997
.
0
0
1
0
0
46322228
.
2
0
010526316
.
0
1
0
5
.
7
0
5
.
0
25
.
0
1
1
.
2
x
628
.
0
x
463
.
2
x
0105
.
0
x
5
.
7
x
05
.
0
x
25
.
0
x
4
3
3
2
3
2
1
1
.
2
x
628
.
0
x
4566
.
2
x
5
.
7
x
25
.
0
x
4
3
2
2
1
3897439
.
2
1
0
0
0
5987301
.
0
0
1
0
0
5788529
.
2
0
0
1
0
1147767
.
8
0
0
0
1
ostatnia kolumna zawiera rozwiązanie:
=
X
8.1147767
2.5788529
0.5987301
2.3897439
1
.
2
x
628
.
0
x
4566
.
2
x
5
.
7
x
4
3
2
1
Liczba działań w metodzie Gaussa:
mnożeń: n
3
/3+n
2
-n/3n
3
i dodawań: n
3
/3+n
2
/2-5n/6n
3
ogólnie około n
3
działań.
Licząc ze wzorów Cramera
(wyznaczniki) potrzeba
działań
!
1
n
np. n=100 w metodzie Gaussa daje 10
6
działań. Jeżeli maszyna
wykonuje 10
7
mnożeń na sekundę, to układ zostanie rozwiązany
w czasie 0.1s.
Wzorami Cramera potrzeba
159
3
.
2
101
203
5
.
101
10
51
.
2
10
10
51
.
2
101
exp
101
2
!
101
t.j. około 10
152
s,
rok około 3.1·10
7
s
a więc około 145 lat

30
10
0
5
x
x
x
x
0
2
.
0
1
4
1
10
0
2
.
0
2
0
5
1
4
1
2
0
4
3
2
1
Rozważmy układ równań
który jest układem już rozwiązanym po zmianie pierwszego
i ostatniego wiersza:
5
10
0
30
x
x
x
x
4
1
2
0
1
10
0
2
.
0
2
0
5
1
0
2
.
0
1
4
4
3
2
1
Nie może układ wierszy wpłynąć na istnienie rozwiązania!

Metoda Gaussa z częściowym wyborem elementu
podstawowego
30
10
0
5
x
x
x
x
0
2
.
0
1
4
1
10
0
2
.
0
2
0
5
1
4
1
2
0
4
3
2
1
Największy element w kolumnie pierwszej znajduje się we wierszu
czwartym i dlatego zamieniamy te dwa wiersze miejscami:
5
10
0
30
x
x
x
x
4
1
2
0
1
10
0
2
.
0
2
0
5
1
0
2
.
0
1
4
4
3
2
1

Przeprowadzamy eliminację:
157894737
.
8
578947368
.
3
021052632
.
1
0
0
421052632
.
8
021052632
.
1
989473684
.
9
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1
0
2
.
0
1
4
/
1
5
4
1
2
0
5
.
8
1
99
.
9
05
.
0
0
5
.
7
2
05
.
0
75
.
4
0
5
.
7
0
05
.
0
25
.
0
1

2971549
.
7
474582663
.
3
0
0
0
842992624
.
0
102212856
.
0
1
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1
100152913
.
2
1
0
0
0
842992624
.
0
102212856
.
0
1
0
0
578947368
.
1
421052632
.
0
010526316
.
0
1
0
5
.
7
0
05
.
0
25
.
0
1
Jeszcze raz rzut oka na otrzymany układ równań:
1
.
2
x
843
.
0
x
102
.
0
x
5789
.
1
x
421
.
0
x
0105
.
0
x
5
.
7
x
0
x
05
.
0
x
25
.
0
x
4
4
3
4
3
2
4
3
2
1

3897439
.
2
1
0
0
0
5987301
.
0
0
1
0
0
5788529
.
2
0
0
1
0
1147767
.
8
0
0
0
1
100152913
.
2
1
0
0
0
628329997
.
0
0
1
0
0
45660828
.
2
0
0
1
0
185835002
.
7
0
0
25
.
0
1
100152913
.
2
1
0
0
0
628329997
.
0
0
1
0
0
46322228
.
2
0
010526316
.
0
1
0
5
.
7
0
5
.
0
25
.
0
1
i redukcja górnej trójkątnej:
i ostatnia kolumna zawiera
rozwiązanie.

Rozkład LU. Metoda Croute’a.
Rozkład na macierze trójkątne
Dana jest macierz A i przedstawiamy ją w postaci:
A=LU
gdzie macierz L jest macierzą dolną trójkątną:
55
54
53
52
51
44
43
42
41
33
32
31
22
21
11
l
l
l
l
l
0
l
l
l
l
0
0
l
l
l
0
0
0
l
l
0
0
0
0
l
L
lub ogólnie:
i
j
dla
obliczane
i
j
dla
0
u
u
ij
ij
U
Macierz U górna trójkątna:
55
45
44
35
34
33
25
24
23
22
15
14
13
12
11
u
0
0
0
0
u
u
0
0
0
u
u
u
0
0
u
u
u
u
0
u
u
u
u
u
U
lub ogólnie:
j
i
dla
obliczane
j
i
dla
1
j
i
dla
0
l
l
ij
ij
L
Jeżeli
A=LU
, to dla układu równań
AX=b
mamy:
b
LY
Y
UX
b
LUX
Rozwiązanie układu LY=b z dolną macierzą trójkątną jest łatwe:
1
i
1
j
j
ij
i
ii
i
11
1
1
y
l
b
l
1
y
l
b
y
i=2,3,...,N
i rozwiązanie równania UX=Y z górną macierzą trójkątną
jest łatwe:
N
1
i
j
j
ij
i
ii
i
NN
N
N
x
u
y
u
1
x
u
y
x
i=N-1,N-2,...,1
Duża zaleta:
Znając rozkład LU możemy go wykorzystać wielokrotnie dla
różnych prawych stron.
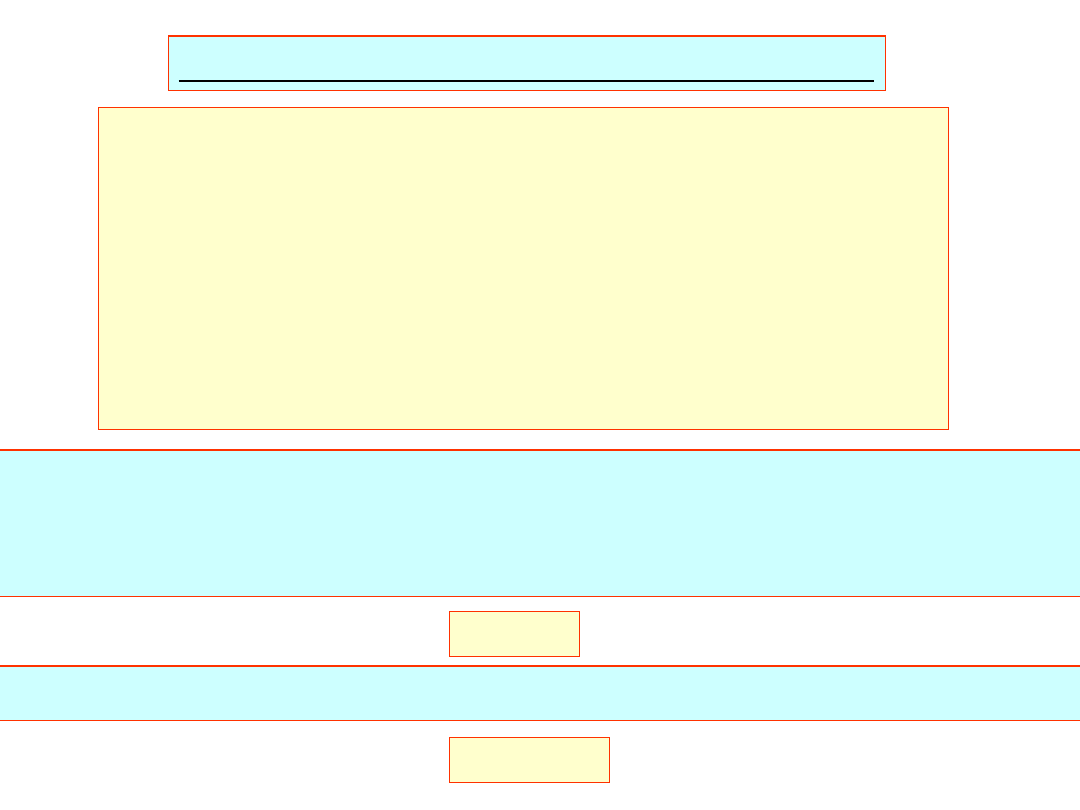
Obliczanie wyrazów macierzy L i U
NN
kN
kk
N
2
k
2
22
N
1
k
1
12
11
1
N
,
N
Nj
1
N
1
k
,
k
1
k
21
u
0
0
0
0
0
.
.
.
.
.
.
u
.
u
.
0
0
.
.
.
.
.
.
u
.
u
.
u
0
u
.
u
.
u
u
1
l
.
l
.
l
.
.
.
.
.
.
0
.
1
l
.
l
.
.
.
.
.
.
0
0
0
0
1
l
0
0
0
0
0
1
w wyniku mnożenia obu macierzy mamy macierz B=[b
ij
]
Zaczynamy kolejno:
pierwszy wiersz macierzy L razy k-ta kolumna macierzy U:
k
1
k
1
u
b
k-ty wiersz macierzy L razy pierwszy wiersz macierzy U:
1
k
11
1
k
b
u
l
NN
kN
kk
N
2
k
2
22
N
1
k
1
12
11
1
N
,
N
Nj
1
N
1
k
,
k
1
k
21
u
0
0
0
0
0
.
.
.
.
.
.
u
.
u
.
0
0
.
.
.
.
.
.
u
.
u
.
u
0
u
.
u
.
u
u
1
l
.
l
.
l
.
.
.
.
.
.
0
.
1
l
.
l
.
.
.
.
.
.
0
0
0
0
1
l
0
0
0
0
0
1
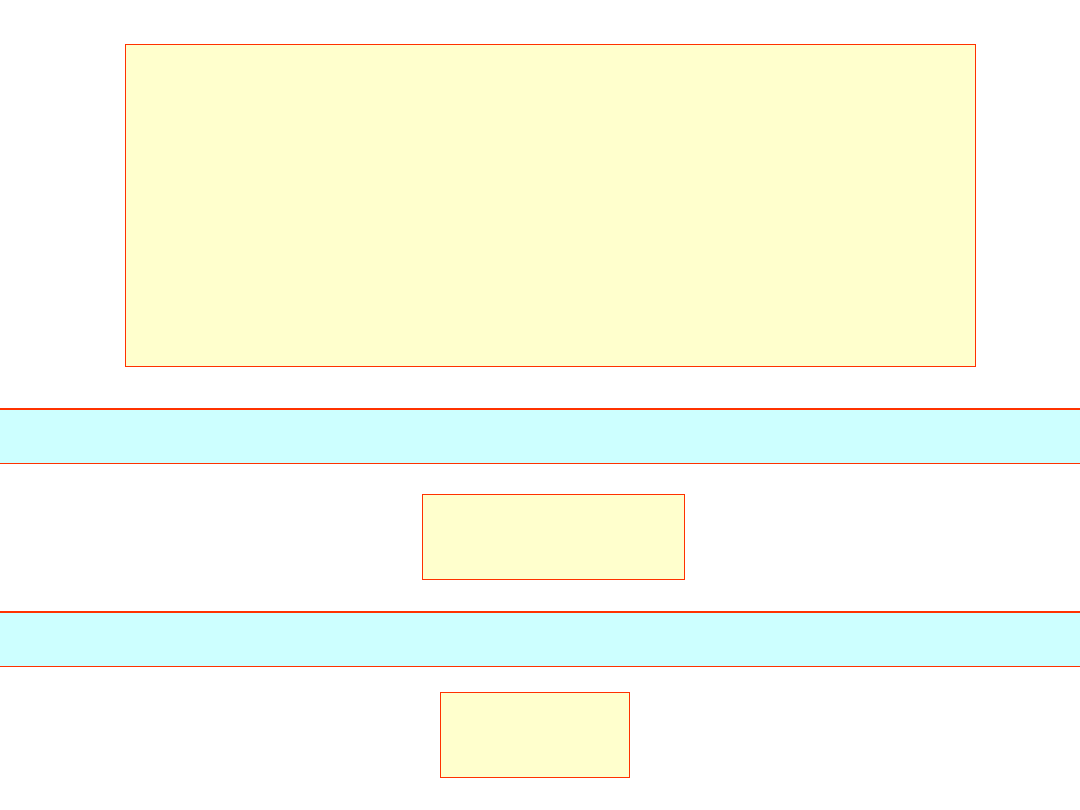
k-ty wiersz macierzy L razy j-ta (jk) kolumna macierzy U:
kj
kj
1
k
i
1
i
ij
ki
b
u
u
l
j-ty wiersz (j>k) macierzy L razy k-ta kolumna macierzy U:
jk
k
i
1
i
ik
ji
b
u
l
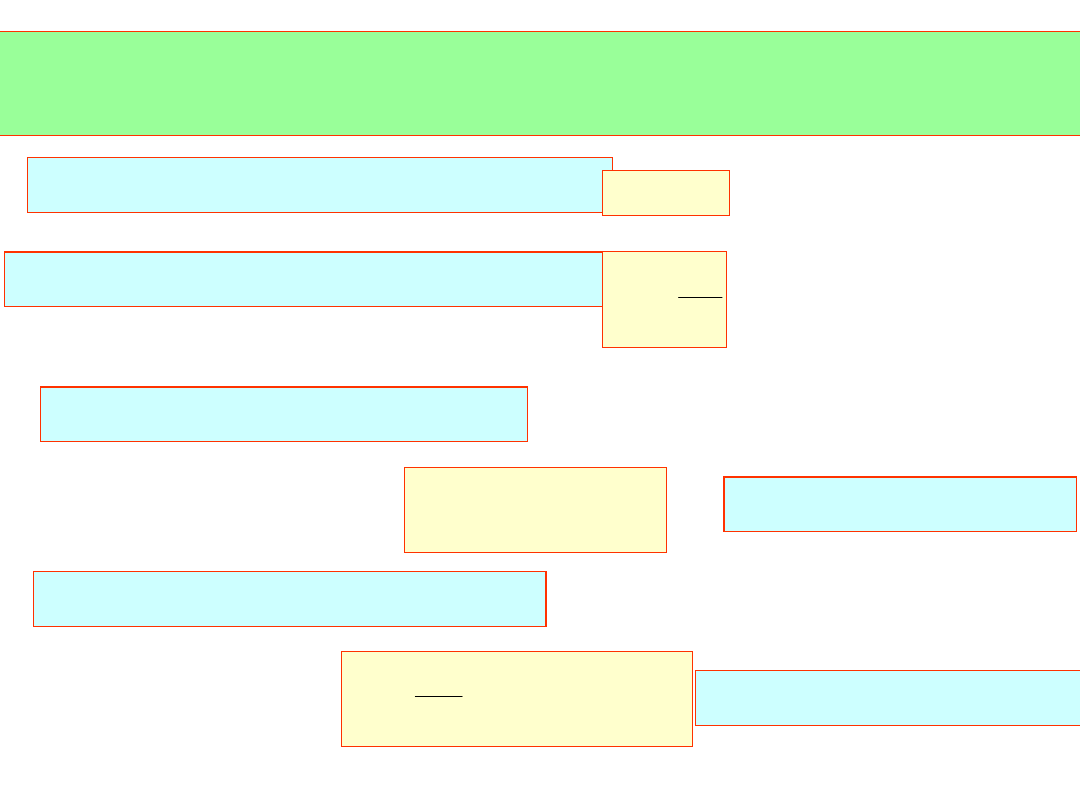
ponieważ musi zachodzić B=A, czyli b
ij
=a
ij
dla (i,j=1,2,...,N)
stąd otrzymujemy kolejno:
Pierwszy wiersz macierzy U:
k
1
k
1
a
u
pierwsza kolumna macierzy L:
11
1
k
1
k
u
a
l
k-ty wiersz macierzy U:
1
k
i
1
i
ij
ki
kj
kj
u
l
a
u
dla j=k,k+1,...,N
k-ta kolumna macierz L:
1
k
i
1
i
ik
ji
jk
kk
jk
u
l
a
u
1
l
dla j=k+1,k+2,...,N

Przykład:
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
Zgodnie z:
k
1
k
1
a
u pierwszy wiersz macierzy U:
.
0
0
0
0
.
.
0
0
0
.
.
.
0
0
.
.
.
.
0
0
0
2
1
4
U

Pierwsza kolumna macierzy L zgodnie z
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
11
1
k
1
k
u
a
l
gdzie u
11
=4
1
.
.
.
0
0
1
.
.
0
0
0
1
.
0
0
0
0
1
5
.
0
0
0
0
0
1
L

10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
drugi wiersz macierzy U zgodnie ze wzorem:
1
i
1
i
ij
i
2
j
2
j
2
u
l
a
u
j=2,3,4,5
.
0
0
0
0
.
.
0
0
0
.
.
.
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
.
.
0
0
1
.
.
0
0
0
1
.
0
0
0
0
1
5
.
0
0
0
0
0
1
L
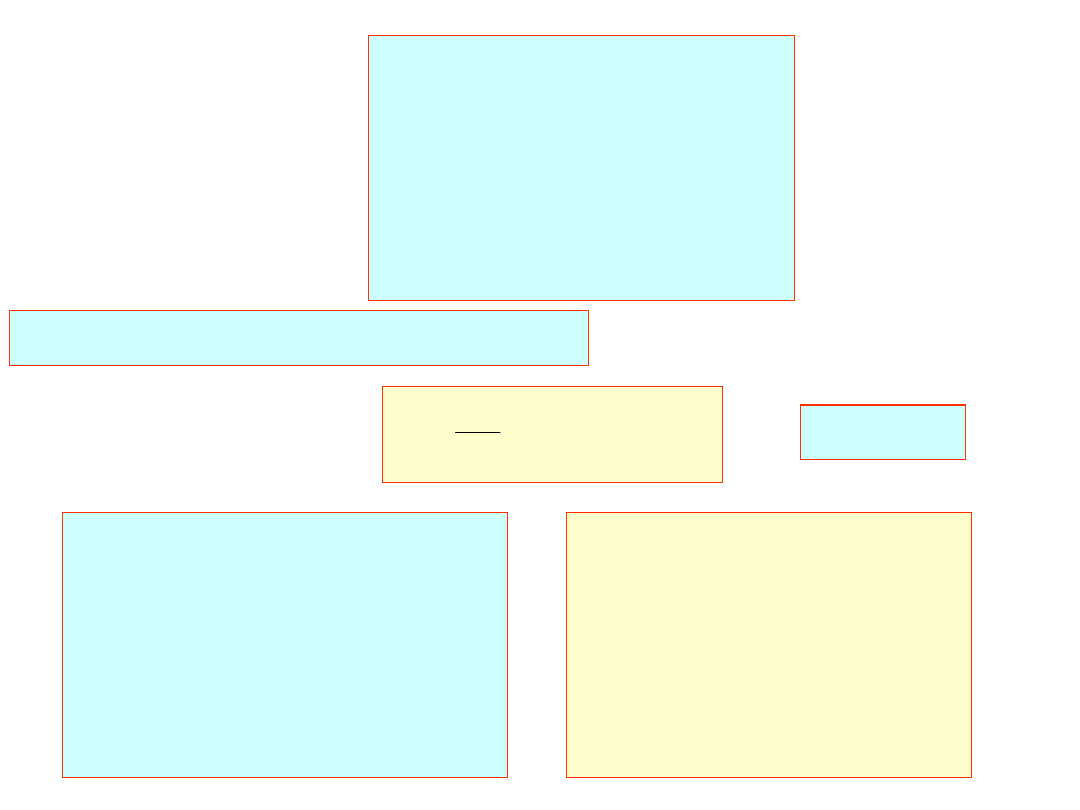
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
j=3,4,5
.
0
0
0
0
.
.
0
0
0
.
.
.
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
.
0
0
0
1
.
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
1
i
1
i
2
i
ji
2
j
22
2
j
u
l
a
u
1
l
Druga kolumna macierzy L:

10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
trzeci wiersz macierzy U zgodnie ze wzorem:
2
i
1
i
ij
i
3
j
3
j
3
u
l
a
u
j=3,4,5
.
0
0
0
0
.
.
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
.
0
0
0
1
.
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
.
0
0
0
0
.
.
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
1
.
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
j=4,5
2
i
1
i
3
i
ji
3
j
33
3
j
u
l
a
u
1
l
trzecia kolumna macierzy L:
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
czwarty wiersz macierzy U zgodnie ze wzorem:
3
i
1
i
ij
i
4
j
4
j
4
u
l
a
u
j=4,5
1
.
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
.
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U

10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
j=5
3
i
1
i
4
i
ji
4
j
44
4
j
u
l
a
u
1
l
czwarta kolumna macierzy L:

1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
.
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U

Dla sprawdzenia czy nie popełniliśmy błędu obliczamy: B=LU
1
15476
.
0
0
0
0
0
1
692308
.
1
0
0
0
0
1
18182
.
0
0
0
0
0
1
5
.
0
0
0
0
0
1
L
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
B
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
B
Mając macierz A=LU możemy rozwiązać równanie LUX=b
dla dowolnego wektora prawej strony.

Znając rozkład LU macierzy łatwo obliczyć wyznacznik
główny |A| macierzy A=LU. Mamy:
U
L
LU
A
ale
1
L
a
N
1
i
ii
u
U
i ostatecznie:
N
i
1
i
ii
u
A
10
1
0
0
0
4
8
4
0
0
1
8
2
1
0
0
3
1
5
2
0
0
2
1
4
A
35714
.
10
0
0
0
0
30769
.
2
46158
.
6
0
0
0
1
54545
.
8
36364
.
2
0
0
0
3
2
5
.
5
0
0
0
2
1
4
U
3480
A
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
- Slide 61
- Slide 62
- Slide 63
- Slide 64
- Slide 65
- Slide 66
- Slide 67
- Slide 68
- Slide 69
- Slide 70
- Slide 71
- Slide 72
- Slide 73
- Slide 74
- Slide 75
- Slide 76
- Slide 77
- Slide 78
- Slide 79
- Slide 80
- Slide 81
- Slide 82
- Slide 83
- Slide 84
- Slide 85
- Slide 86
- Slide 87
- Slide 88
Wyszukiwarka
Podobne podstrony:
Wyklad mn no 8 piątek
więcej podobnych podstron