
Podstawy rachunku
macierzowego
Definicja macierzy
Macierz to układ m • n liczb
rozmieszczonych w m wierszach i n
kolumnach.
mn
m
m
n
n
a
a
a
a
a
a
a
a
a
A
2
1
2
22
21
1
12
11
Macierze i krakowiany to liczby
zespołowe.
Dodawanie i odejmowanie liczb
zespołowych:
13
9
9
4
10
3
7
4
5
3
7
1
6
5
4
1
3
2
A + B = C
c
ij
=
a
ij
+ b
ij
1
1
1
2
4
1
7
4
5
3
7
1
6
5
4
1
3
2
A - B = C
c
ij
=
a
ij
- b
ij

Mnożenie macierzy:
)
,
(
)
,
(
)
,
(
p
m
p
n
n
m
C
B
A
n
k
kj
ik
ij
b
a
c
1
25
4
5
3
1
1
2
4
3
1
5
1
2

Przykład mnożenia macierzy:
C
B
A
1
3
2
4
7
5
5
2
4
3
-
70
9
-
1
8
3
Kontrole sumowe przy mnożeniu:
2
1
3
2
6
4
7
5
9
5
5
2
4
3
-
7
9 8 10
0 -1 3 2
-7 8 1
1
12

Transponowanie macierzy:
6
7
5
4
3
2
6
5
3
7
4
2
A
A
T
Rozkład macierzy na czynniki
trójkątne:
G
H
A
g
g
g
g
g
g
h
h
h
h
h
h
a
a
a
a
a
a
a
a
a
a
a
a
T
34
24
23
14
13
12
33
32
31
22
21
11
34
33
32
31
24
23
22
21
14
13
12
11
1
0
0
1
0
1
0
0
0
G
H
A
T
_
1
0
0
_
_
1
0
_
_
_
1
_
_
_
0
_
_
0
0
_
14
20
7
2
0
10
5
2
4
12
8
4
4
2 3 -1
2 1
4
2
2 3
2
5

Rozkład macierzy na czynniki
trójkątne = wzory:
1
1
i
i
a
h
11
1
1
h
a
g
j
j
1
1
j
n
nj
in
ij
ij
g
h
a
h
ii
i
n
nj
in
ij
ij
h
g
h
a
g
1
1

Zastosowanie rozkładu macierzy na
czynniki – rozwiązywanie układu
równań liniowych
0
0
2
2
2
1
2
1
2
1
1
1
c
x
b
x
a
c
x
b
x
a
0
14
10
4
0
6
4
2
2
1
2
1
x
x
x
x
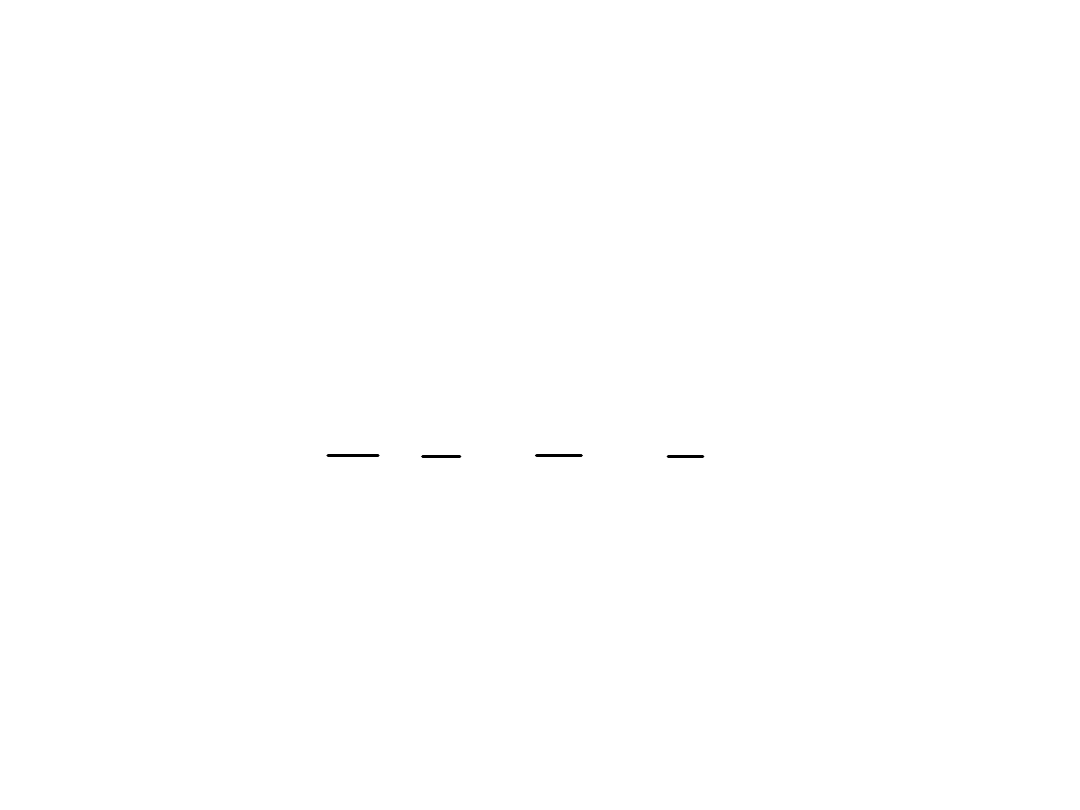
Zapis macierzowy:
0
14
10
4
0
6
4
2
2
1
2
1
x
x
x
x
0
L
x
A
0
0
14
6
10
4
4
2
2
1
x
x
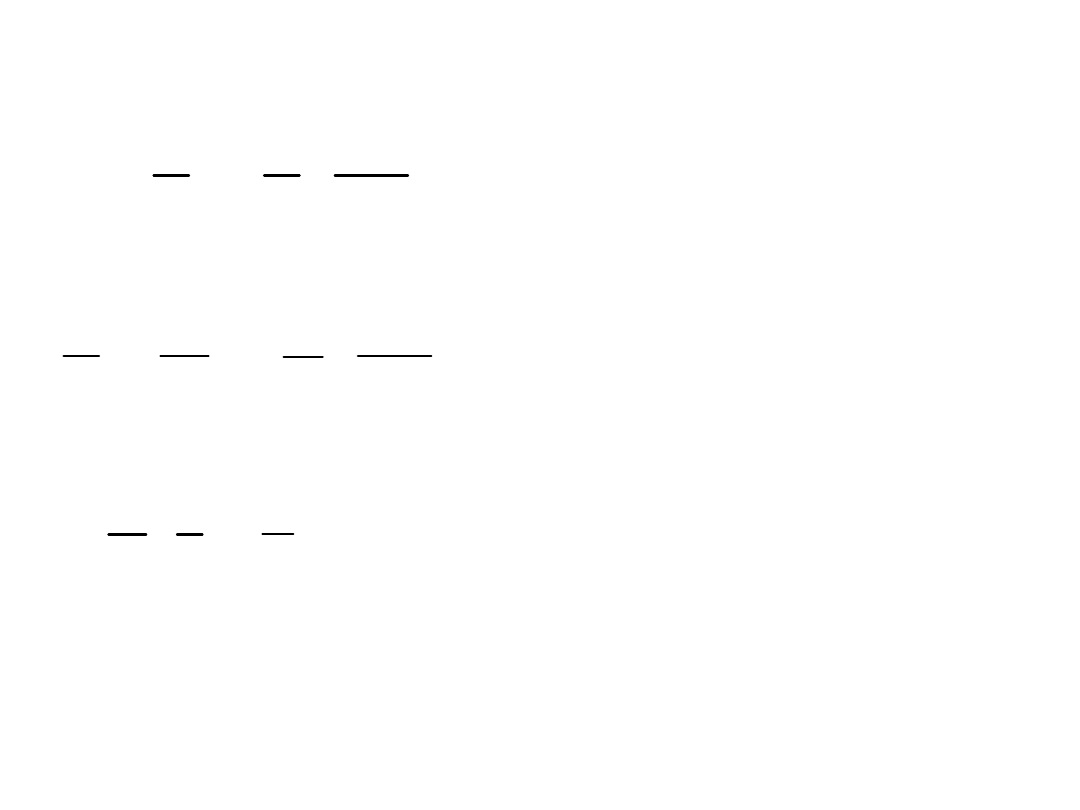
Macierzowy zapis rozwiązania:
L
A
B
|
14
6
10
4
4
2
'
| L
G
H
B
T
1
1
0
3
2
1
2
4
0
2
'
L
x
G
1
3
1
0
2
1
2
1
x
x
1
1
k
i
n
in
n
i
i
g
x
l
x
1
dla i=k, k-1, ... ,
1
Document Outline
Wyszukiwarka
Podobne podstrony:
MES I EL RACH MAC1
mac1
więcej podobnych podstron