Sld 18.1. Zaawansowane

techniki

1.Algorytmy typu „dziel-i-

rządź”(“conquer and divide”)

2.Algorytmy „zachłanne“ (“żarłoczne”,

“greedy”)

3.Algorytmy dynamiczne

Sld 18.2. Algorytmy typu „dziel-i-

rządź“

Programowanie typu „dziel-i-rządź" polega na wykorzystaniu

podstawowej cechy rekurencji:

1. dekompozycji

problemu

na

pewną

skończoną

ilość

podproblemów tego samego typu,

2. rozwiązania podproblemów,
3. połączeniu częściowych rozwiązań w celu odnalezienia

rozwiązania globalnego.

 

Jeśli oznaczymy problem do rozwiązania przez Pb, a rozmiar danych

przez N, to zabieg wyżej opisany da się przedstawić za pomocą zapisu:

 

Pb(N) → Pb(N

1

) + Pb(N

2

) + ...+ Pb(N

k

) + KOMB(N).

 

Problem „rzędu" N został podzielony na k podproblemów.
Funkcja KOMB(N) nie jest rekurencyjna.

•

Technika „dziel-i-rządź" pozwala w wielu przypadkach na zmianę klasy

algorytmu (np. z O(n) do O(log

2

N) ).

•

Istnieje grupa zadań, dla których zastosowanie metody „dziel-i-rządź"

nie spowoduje przyspieszenia.

 

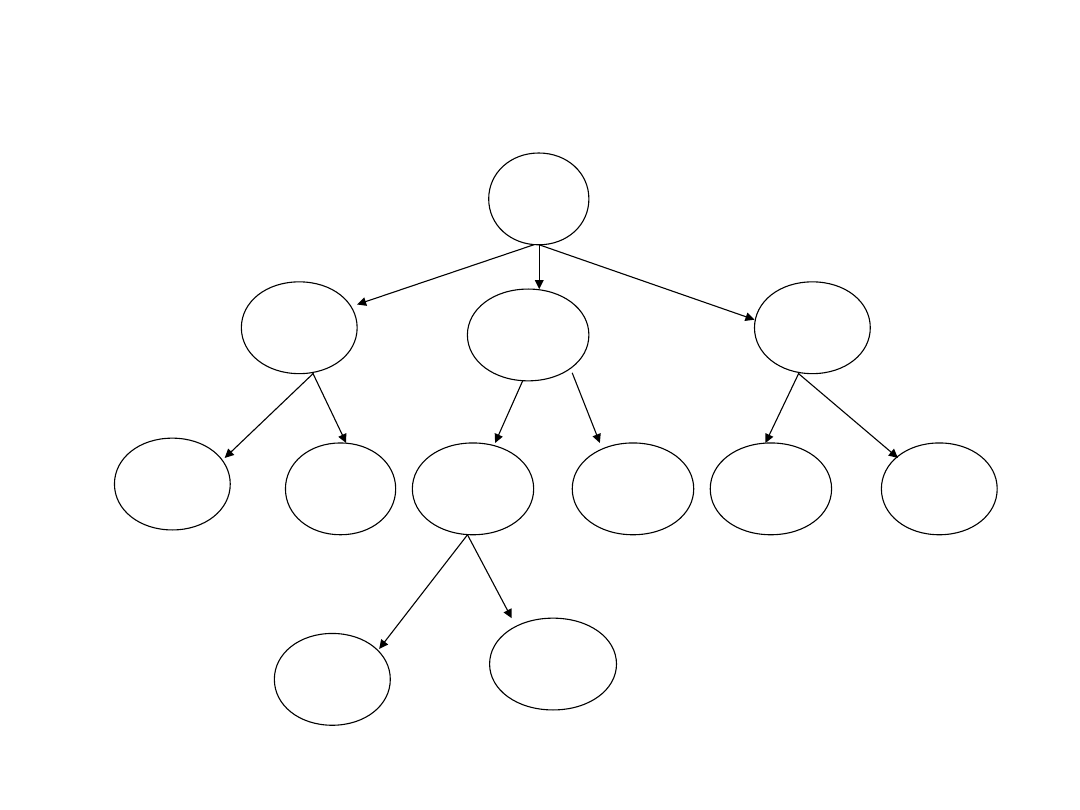
Sld 18.3. Algorytmy typu „dziel-i-

rządź“ - 2

Pb

0

Pb

1

Pb

i

Pb

n

Pb

1,1

Pb

1,k

Pb

i,1

Pb

i,l,

Pb

n,1

Pb

n,s

Pb

i,1,t

Pb

i,1,1

.

°°°

°°°

°°°

°°°

°°°

°°°

° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° ° °

° ° ° ° ° ° ° ° °

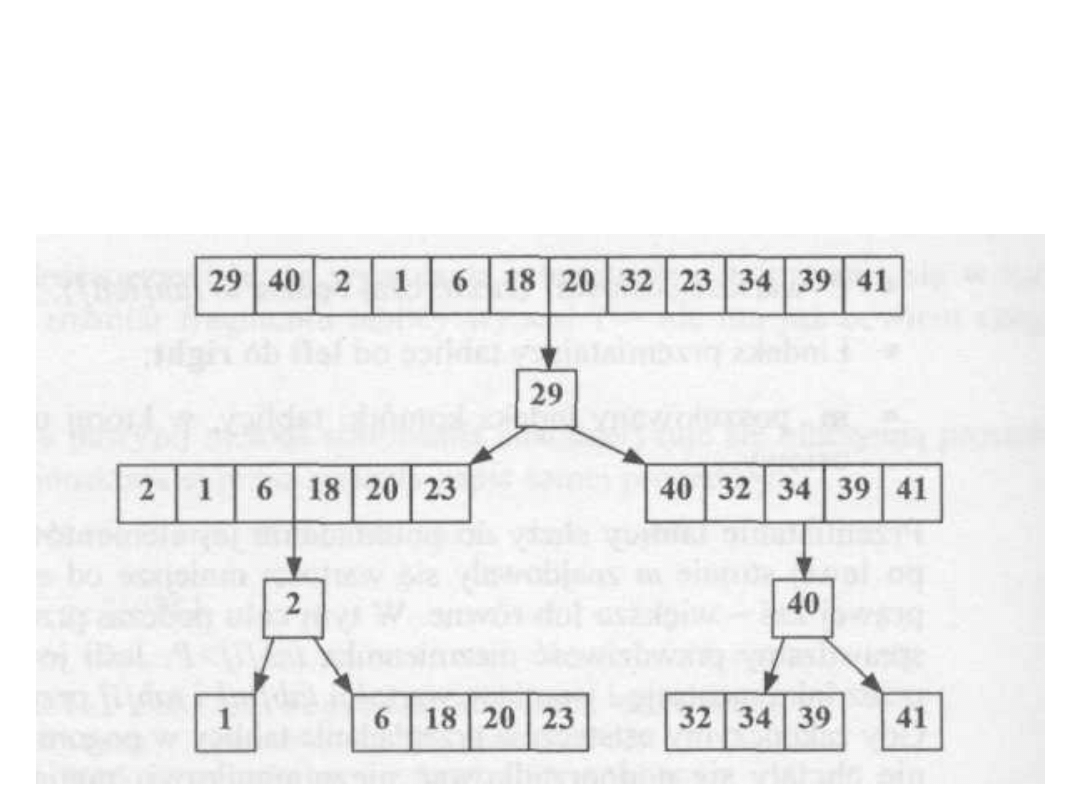
Sld 18.4. Quicksort

Złożoność O(n

log

2

n)

Sld 18.5. Przeszukiwanie binarne

Złożoność O(n log

2

n)

Binarne przeszukiwanie elementu

27

w liście



2 4 7 8 8 9 10 11 14 15 17 20 21 25 27 37 41 57 69 73 92 94



2 4 7 8 8 9 10 11 14 15 17

20 21 25 27 37 41 57 69 73 92 94



2 4 7 8 8 9 10 11 14 15 17

20 21 25 27 37

41 57 69 73 92 94



2 4 7 8 8 9 10 11 14 15 17 20 21 25

27 37

41 57 69 73 92 94



2 4 7 8 8 9 10 11 14 15 17 20 21 25

27

37 41 57 69 73 92 94

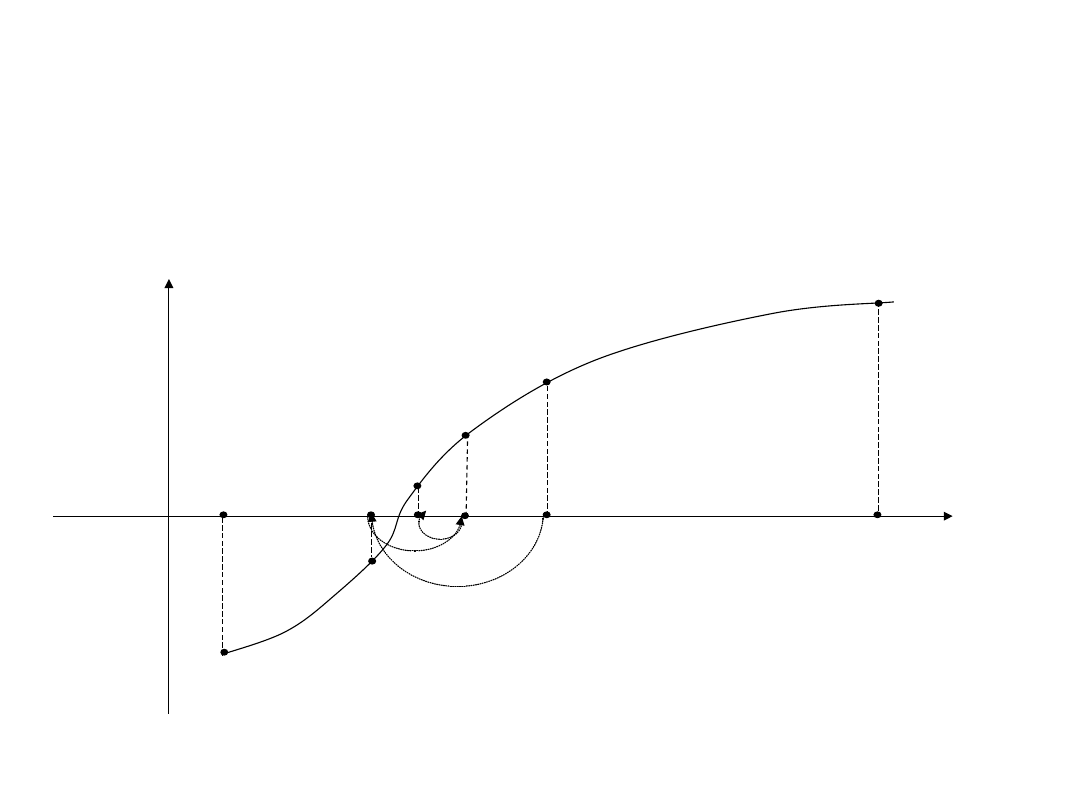
Sld 18.6. Znajdowanie zera

funkcji metodą

połowienia przedziału

a

b

x

3

x

4

x

2

x

1

y

x

1

= a+½(b - a); y >

0;
x

2

= a+½(x

1

- a); y <

0;
x

3

= x

2

+½(x

1

- x

2

); y >

0;
x

4

= x

2

+½(x

3

- x

2

); y >

0;
. . . . . . . . . . . . . . . . . .
. . .

x

Ilość iteracji i = log

2

((b – a)/ Δ;

Δ – dokładność obliczeń

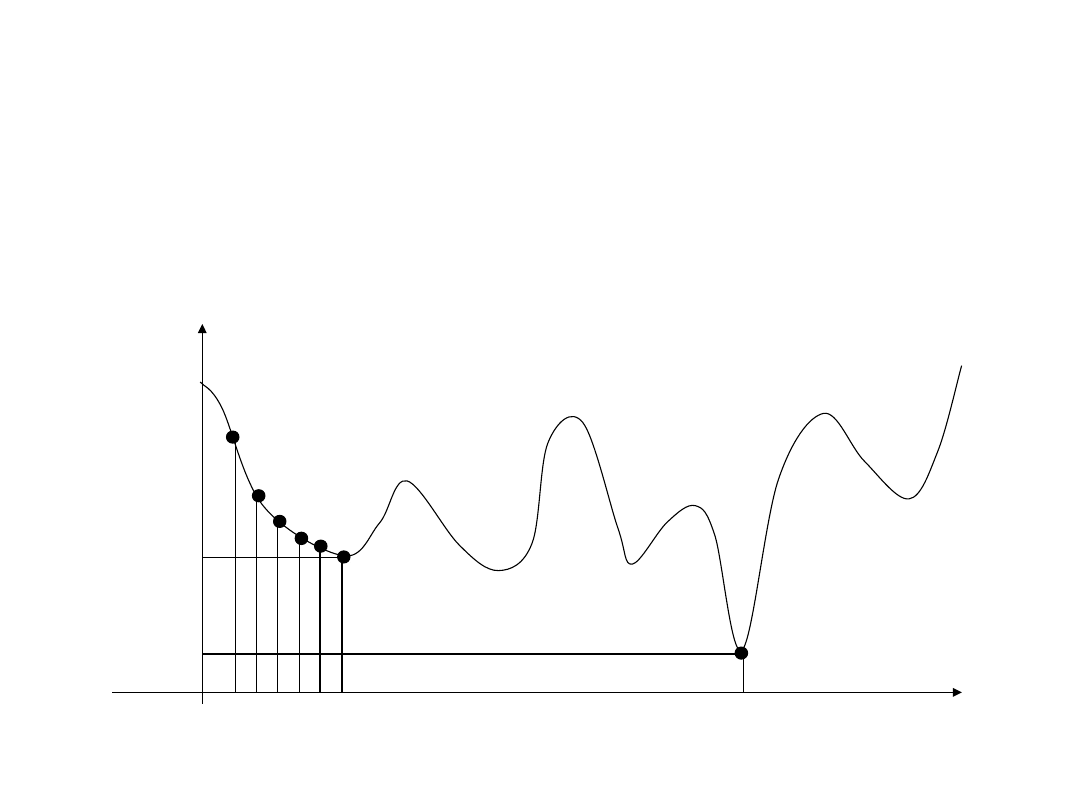
Sld 18.7. Algorytmy „zachłanne“

(“żarłoczne“, ”greedy”)

• Cechą szczególną algorytmu „zachlannego" jest to, że w każdym

etapie poszukiwania rozwiązania wybiera on opcję lokalnie

optymalną. W zależności od tego doboru, rozwiązanie globalne

może być również optymalne, ale nie jest to gwarantowane.

y

x

Δ =
1,2,3,4,5,6

x

opt

y

min

y

min,loc

Sld 18.8. Ogólny problem

plecakowy

•Polega on na zapakowaniu do plecaka o ograniczonej pojemności możliwie

najbardziej wartościowych rzeczy. W innych zastosowaniach, może to dotyczyć

pakowania walizek, paczek, samochodu, samolotu itp.

• Dane:

   n rzeczy R

1

R

2

, ..., R

n

, każda w nieograniczonej ilości;

  rzecz R

i

waży w

i

i ma wartość p

i

.

   maksymalna pojemność plecaka, wynosząca W

max

.

• Wyniki:

Ilości n

i

, n

2

,..., n

n

, poszczególnych rzeczy (mogą być zerowe), których

całkowita waga W

nie przekracza W

max

i których sumaryczna wartość P jest

największa.

• W

= ∑ n

i

w

i

= n

1

w

1

+ n

2

w

2

+ ... +

n

n

w

n

≤ W

max

• P

= ∑ n

i

p

i

= n

1

p

1

+ n

2

p

2

+ … + n

n

p

i

→ max

 

Sld 18.9. Algorytm zachłanny dla

ogólnego problemu plecakowego

W decyzjach ścierają się ze sobą trzy kryteria

wyboru kolejnych rzeczy do zapakowania:

1.

wybierać najcenniejsze rzeczy, czyli w kolejności

nierosnących wartości p

t

;

2.

wybierać rzeczy zajmujące najmniej miejsca,

czyli w kolejności niemalejących wag w

i

3.

wybierać rzeczy najcenniejsze w stosunku do

swojej wagi, czyli w kolejności nierosnących

wartości ilorazu p

i

/w

i

.

Sld 18.10. Przyklad problemu

plecakowego

R

i

1

2

3

4

5

6

p

i

6

4

5

7

10

2

w

i

6

2

3

2

3

1

p

i

/w

i

6/6

4/2

5/3

7/2

10/3

2/1

Kryteria

n

1

p

1

n

1

w

1

n

2

p

2

n

2

w

2

n

3

p

3

n

3

w

3

n

4

p

4

n

4

w

4

n

5

p

5

n

5

w

5

n

6

p

6

n

6

w

6

? n

i

p

i

? n

i

w

i

1

0

0

0

1×7

1×2

7×10

7×3

0

77

23

2

0

0

0

0

0

23×2

23×1

46
23

3

0

0

0

11×7

11×2

0

1×2

1×1

79

23

W

max

= ∑ n

i

w

i

≤ 23

Sld 18.11. Programowanie

dynamiczne

1. koncepcja:
• dla danego problemu P stwórz rekurencyjny model

jego rozwiązania (wraz z jednoznacznym określeniem

przypadków elementarnych);

• stwórz tablicę, w której będzie można zapamiętywać

rozwiązania przypadków elementarnych i rozwiązania

podproblemów, które zostaną obliczone na ich

podstawie;

2. inicjacja:
• wpisz do tablicy wartości numeryczne, odpowiadające

przypadkom elementarnym;

3. progresja:
• na podstawie wartości numerycznych wpisanych do

tablicy używając formuły rekurencyjnej, oblicz

rozwiązanie problemu wyższego rzędu i wpisz je do

tablicy;

• postępuj w ten sposób do osiągnięcia pożądanej

wartości.

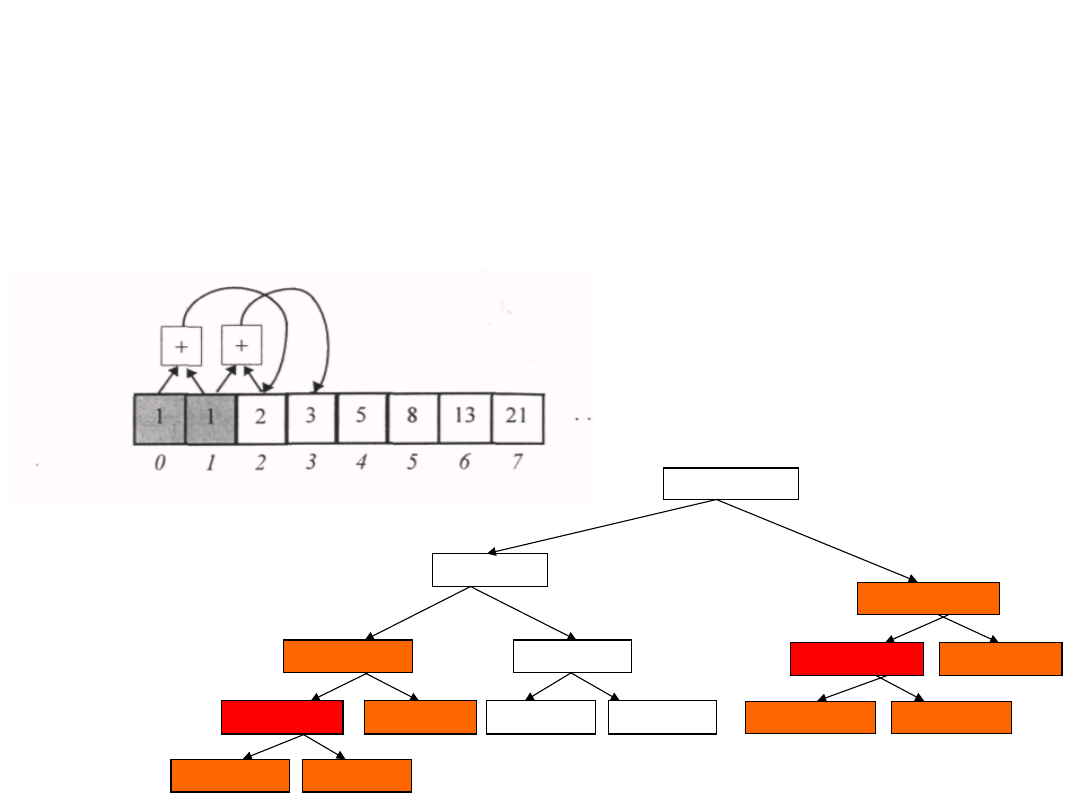
Sld 18.12.

Ciąg Fibonacciego

fib(4)=
5

fib(1)=
1

fib(1)=
1

fib(2) =
2

fib(1)=
1

fib(0)=
1

fib(3)=3

fib(2)=
2

fib(1)=
1

fib(5)=8

fib(1)=
1

fib(0)=1

fib(3)=3

fib(2)=2

fib(1)=
1

fib(0) = 1,

fib(1) = 1,

fib(n) = f(n - I) + fib(n - 2) gdzie n ≥ 2; N

f

= 1, 1, 2, 3, 5, 8, 13, 21, 34,

55, ...

Tablica dla zapamiętywania rozwiązania podproblemów:

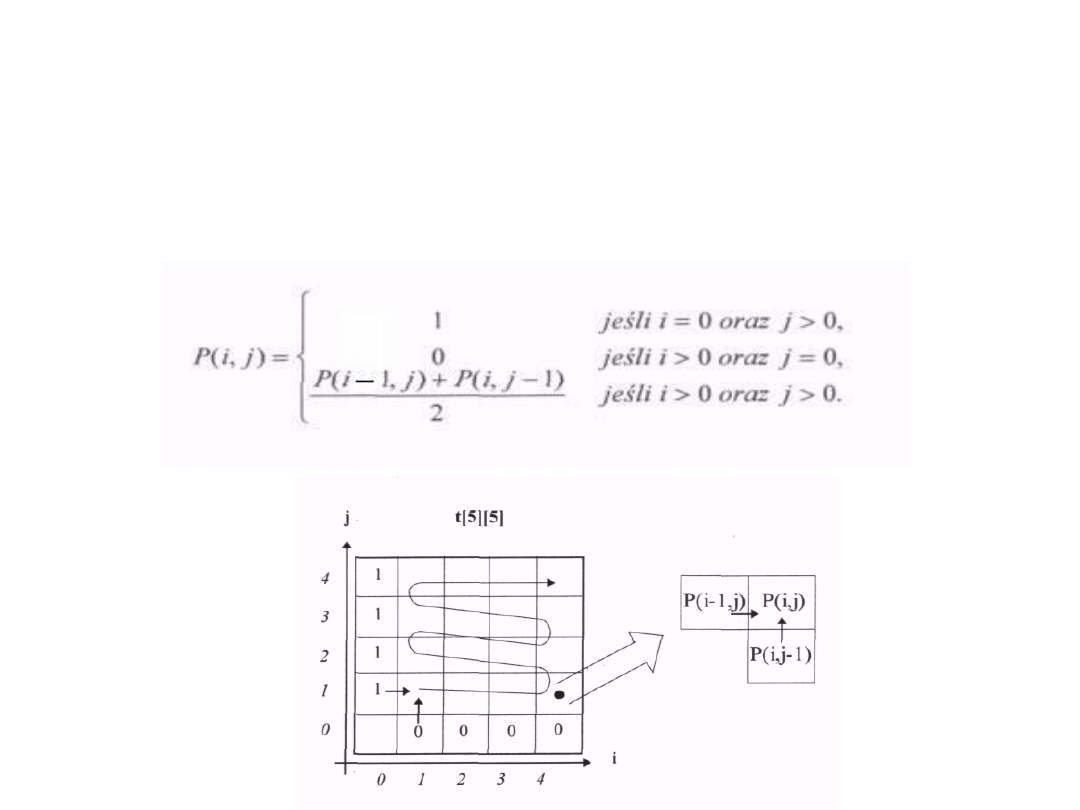
Sld 18.13. Dwuwymiarowy wzór

rekurencyjny.

Do obliczenia wartości P(i, j) potrzebna jest znajomość

dwóch sąsiednich komórek: dolnej - P(ij-l) oraz tej

znajdującej się z lewej strony - P(i-l,j). Naturalnym

sposobem obliczania wartości P(i,j) będzie posuwanie się

„zygzakiem" zaznaczonym na rysunku.

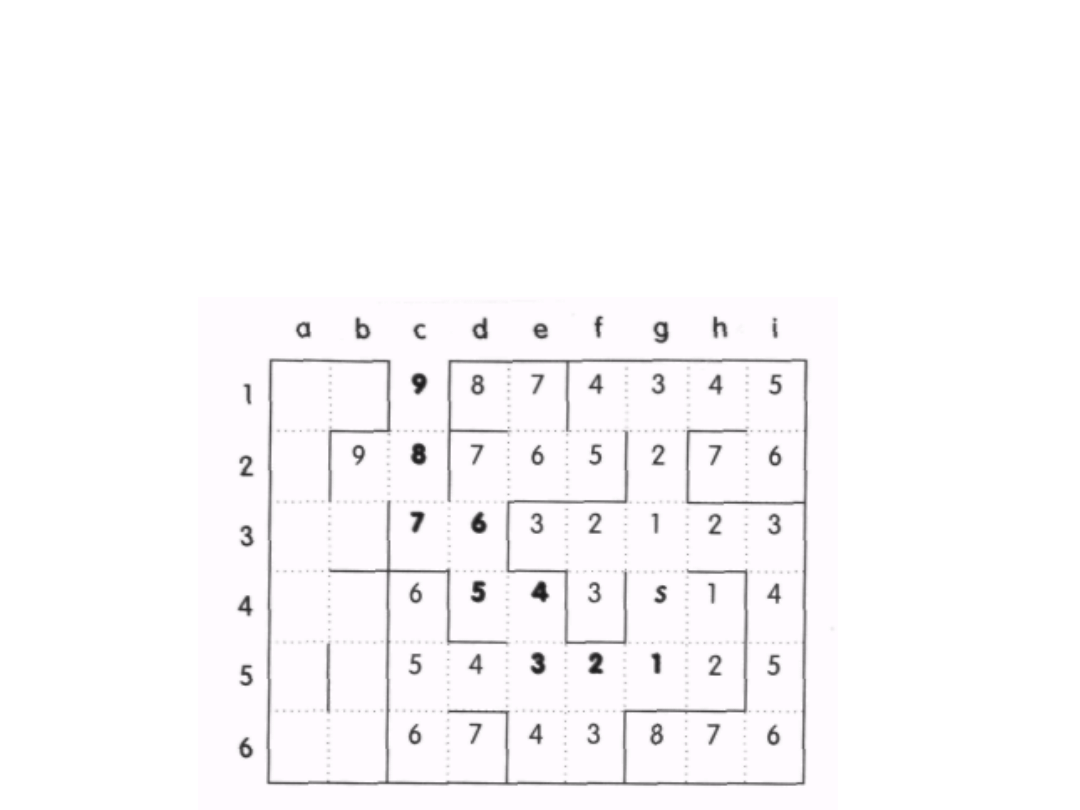
Sld 18.14. Znajdowanie

najkrótszej drogi do wyjścia z

labiryntu

1.

Rozpowszechnianie fali od pola S.

2.

Zwinięcie fali od pola wyjścia C1.

Sld 18.23. Literatura

1. P.Wróblewski. Algorytmy.

Struktury danych i techniki

programowania. Helion. 2001.

2. K.A.Lambert, D.W.Nance, T.L.Naps.

Introduction to Computer Science

with C++. Books/Cole, 2000.

3. M.M. Syslo. Algorytmy. Warszawa,

WSP, 1997.