Testowanie prostych

hipotez

statystycznych

Testing simple hypotheses

Agnieszka Piernik

Etapy procesu weryfikacji hipotez statystycznych

1. Formułowanie hipotezy zerowej H

0

oraz odpowiadającej jej

hipotezy alternatywnej H

1

:

H

0

: nie ma różnicy

H

1

: istnieje różnica

2. Wybór odpowiedniego do postawionej hipotezy zerowej testu
i
obliczenie jego wartości w oparciu o dane pochodzące z próby
3. Przyjęcie odpowiedniego poziomu istotności i podjęcie decyzji
o przyjęciu lub odrzuceniu hipotezy zerowej:

- akceptujemy H

1

, jeśli p(H

0

)  0.05

Agnieszka Piernik

Jaki rodzaj testu zastosować?

Testy parametryczne

-rozkład normalny pomiarów

-rozkład normalny różnic m. parami
pomiarów

Testy nieparametryczne

Do porównania

dwóch średnich

t-
test

Do porównania

dwóch wariancji

F-
test

1

2

2

2

1

2

x x

t

N

s

s

-

=

+

2

1

2

2

F

s
s

=

Do porównania

dwóch rozkładów

Do porównania

obserwacji i

oczekiwań

Chi

2

-

test

2

2

1

(

)

k

i

i

i

i

Obs Exp

Exp

c

=

-

=

�

2

2

1

(

)

k

i

i

i

i

Obs Exp

Exp

c

=

-

=

�

Chi

2

-

test

Kolmogorov -

Smirnov-test

max(

)

cum

cum

KS

Obs

Exp

=

-

Chi

2

-

test

Do porównania

wielu średnich

ANOVA

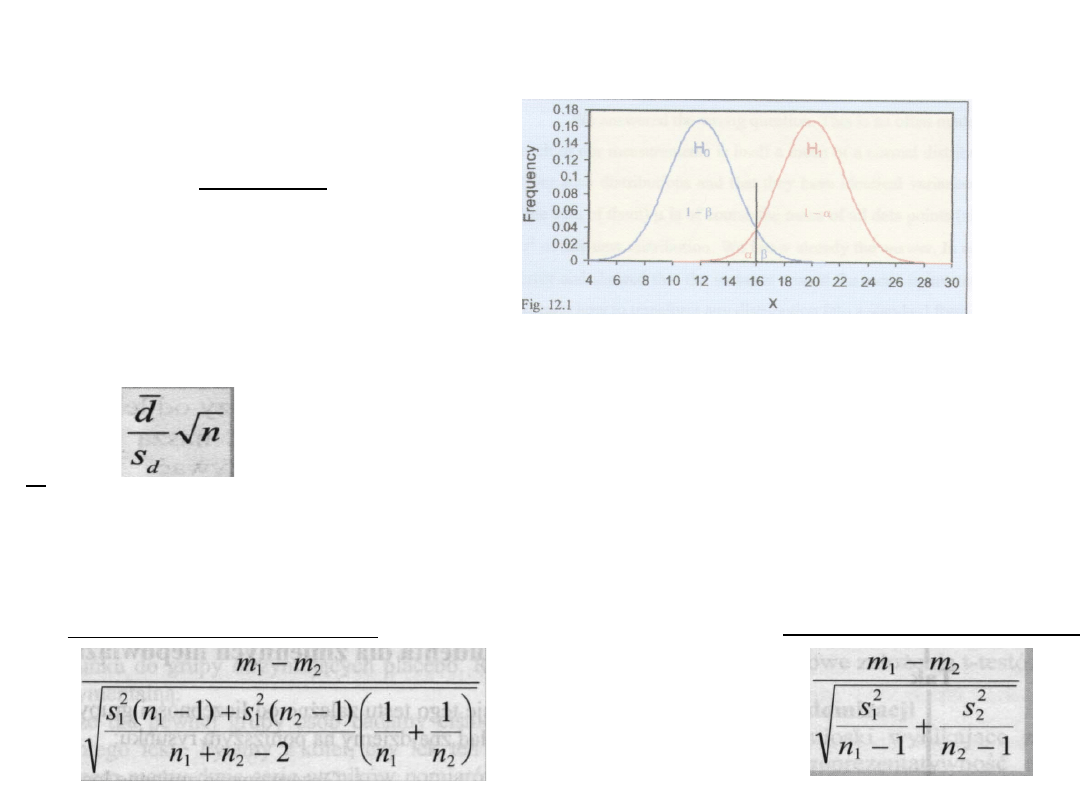
Porównywanie różnic między dwoma

średnimi

1. Dla zmiennych powiązanych:

d - średnia różnica,

s

d

- odchylenie standardowe różnic

zmienna ma rozkład t-Studenta o liczbie stopni swobody n-1

t =

Testy t - Studenta

t = n

1

- 

2





1

2

+ 

2

2



1

, 

2

- średnie populacji



1

2

+ 

2

2

- wariancje

2. Dla zmiennych niepowiązanych:

a. Przy równych wariancjach

t =

m - średnia
s - odchylenie standardowe
n - liczebność

b. Przy różnych wariancjach

t =

Statystyka ma rozkład t-Studenta o n

1

+ n

2

- 2 stopniach swobody

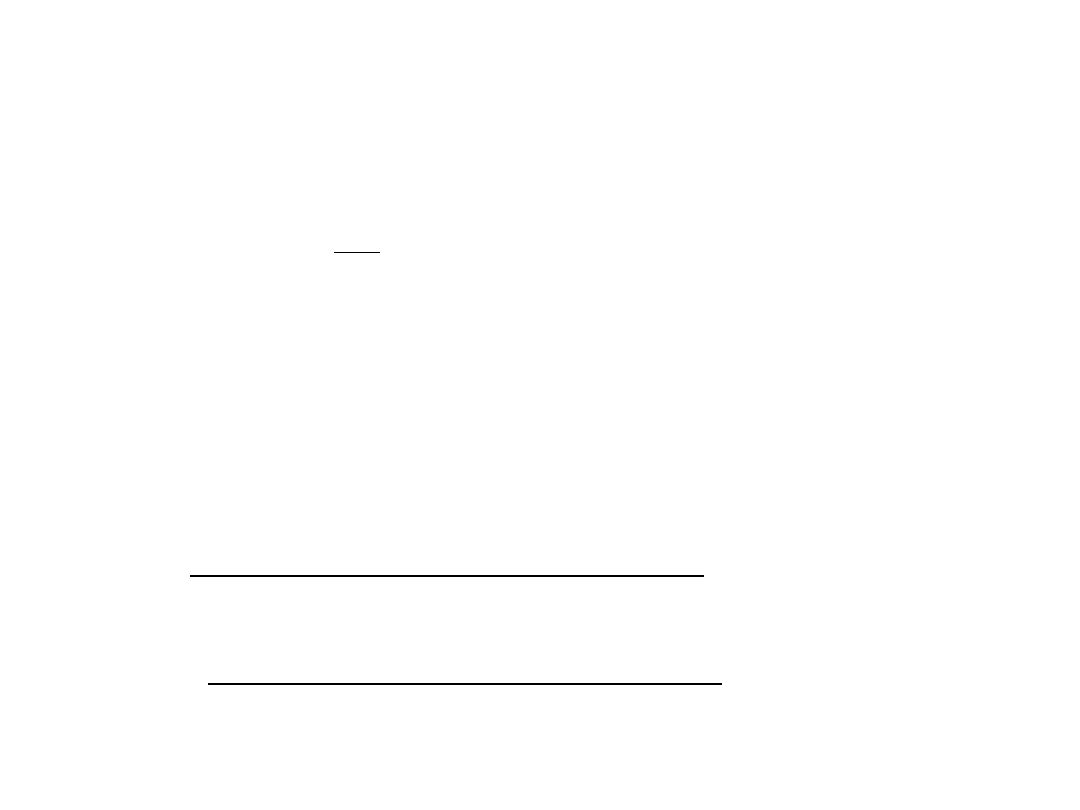
Porównywanie rozkładów cech

(obserwacji i oczekiwań)

Test 

2

(wartość oczekiwana - wartość obserwowana)

2



2

= 

wartość oczekiwana

1

k

(frekwencja oczekiwana - frekwencja obserwowana)

2



2

= N 

frekwencja oczekiwana

1

k

k - liczba obserwacji, k-1 liczna stopni swobody, N - wielkość próby

Testowanie hipotezy o braku różnic

między wariancjami

F =



1

2



2

2

Test Fishera - Snedecora



2

- wariancja

liczba stopni swobody n

1

+ n

2

- 2