
1
ZAGADNIENIA WYMIANY CIEPŁA W PRZEGRODACH
ZAGADNIENIA WYMIANY CIEPŁA W PRZEGRODACH
BUDOWLANYCH
BUDOWLANYCH.
•
1. UWAGI WSTĘPNE.
•
2.PODSTAWY TEORII WYMIANY CIEPŁA.
•
3.PRZEWODNOŚĆ CIEPLNA MATERIAŁÓW BUDOWLANYCH.
•
4. JEDNOWYMIAROWE, USTALONE PRZEWODZENIE CIEPŁA.
•
5. DWUKIERUNKOWY PRZEPŁYW CIEPŁA.

2
1. UWAGI WSTĘPNE.
Budynek w swym wnętrzu tworzy mikroklimat o wymaganych dla człowieka
parametrach (tem-
peratura, wilgotność, szybkość ruchu i czystość powietrza itp..). Zadaniem przegród
zewnętrznych
jest oddzielenie stworzonego mikroklimatu wnętrza od zmiennego klimatu
zewnętrznego. (Zimno,
upał, śnieg, deszcz, wiatr, hałasy itp..).
Ciągle ulepszane rozwiązania konstrukcyjne i architektoniczne, wprowadzane nowe
materiały i
technologie np. lekkie ściany osłonowe, duże powierzchnie przeszklone, cienkie
wielowarstwowe
przegrody, stwarzają wiele nowych problemów z zakresu ruchu ciepła i masy przez
przegrody. W
wielu przypadkach wymagania fizyki budowli są decydujące o przyjęciu lub
odrzuceniu rozwiąza-
nia.
Z zagadnieniami fizyki budowli są związane problemy ochrony cieplnej budynków,
problemy
wielkości zużycia energii na stworzenie i utrzymanie mikroklimatu wnętrza.
LITERATURA:
1.W. Żenczykowski. BUDOWNICTWO OGÓLNE. Wa-wa. Arkady
.
2.W.Płoński, J. A. Pogorzelski. FIZYKA BUDOWLI. Wa-wa. Arkady.
3.PN-EN ISO 6946:1999 Opór cieplny i współczynnik ciepła. Metoda obliczania.
4.PN-83/B 02402 Temperatury ogrzewanych pomieszczeń w budynkach.
5.PN-82/B 02403 Temperatury obliczeniowe zewnętrzne.
6.PN-B-02025 Obliczanie sezonowego zapotrzebowania na ciepło do ogrzewania
budynków…..

3
2.PODSTAWY TEORII WYMIANY CIEPŁA.
Ciepło jest jedną z form energii jak np. energia mechaniczna, chemiczna, świetlna,
elektryczna
itp.. Energia cieplna wywołuje drgania cząstek lub ich ciągły ruch. Szybkość ruchu
cząstek ciała
nagrzanego zależy od ilości dostarczonej energii. Możemy powiedzieć że ciepło to
wymiana ener-
gi wewnętrznej lub entalpii, zdefiniowana równaniami bilansu tych wielkości. W
układach otwar-
tych pojęcie ciepła nie jest jednoznaczne. Niekiedy tradycyjnie ciepło utożsamia się z
energią
wewnętrzną lub entalpią tj. energią kinetyczną bezładnego ruchu cząstek oraz
energią potencja-
lną ich wzajemnego oddziaływania.
Entalpia – zawartość cieplna – wielkość fizyczna
skalarna określana jako funkcja
stanu układu
termodynamicznego równa sumie jego energii wewnętrznej oraz iloczynu ciśnienia i
objętośći.
Ilość energii cieplnej zakumulowanej w jednostce masy danego ciała zależy przede
wszystkim
od temperatury rozpatrywanego ciała – od szybkości ruchu cząstek ciała nagrzanego.
Temperatura – intensywna funkcja stanu o następującej właściwości: jeśli układ w
stanie równo-
wagi termodynamicznej składa się z dwóch części odgraniczonych od siebie
diatermicznie, to
wartości tej funkcji dla tych części są równe. (Miernik aktywności termicznej.)
Przyjmuje się teoretycznie, ze ruch cząstek materii ustaje jeżeli temperatura
osiągnie O K czyli
-273,16
o
C ( temperatura zera bezwzględnego).
Rozróżnia trzy zasadnicze rodzaje wymiany ciepła:
1.Przewodzenie,
2.Konwekcja,
3.Promieniowanie.

4
Przewodzenie ciepła – przenoszenie energii cieplnej wewnątrz makroskopowo
nieruchomego oś-
rodka materialnego w wyniku oddziaływań międzycząsteczkowych. Sposób
charakterystyczny dla
ciał stałych. W ciałach stałych porowatych wymiana ciepła zachodzi również przy udziale
konwek-
cji i promieniowania.
Konwekcja – albo unoszenie ciepła występuje wówczas gdy makroskopowe cząstki
ośrodka
zmieniają swoje położenie. Zjawisko charakterystyczne dla cieczy i gazów, przy czym
przenosze-
nie energii odbywa się na wskutek wymieszania się gazu lub cieczy a w niewielkim
stopniu przez
przewodzenie. Rozróżnia się konwekcję naturalną i wymuszoną.
Konwekcja naturalna- wywołana jest różnicą gęstości spowodowaną wzrostem
objętości przy og-
rzniu powietrza lub cieczy. Konwekcyjną wymianę ciepła między powierzchnią a
powietrzem opisuje
równanie Newtona:
q
k
=
k
(t
i
-
i
) [W/m
2
]
gdzie:
q
k
– gęstość strumienia cieplnego W/m
2
,
k
– współczynnik przejmowania ciepła przez konwekcję W/(m
2.
K),
t
i
– temperatura ośrodka
0
C (K),
i
– temperatura powierzchni
0
C (K).
Konwekcja wymuszona – powodowany mechanicznie (pompa, wentylator itp.) ruch
cząstek cie-
czy lub gazu. Zjawisko wykorzystywane w wentylacji, klimatyzacji, ogrzewaniu itp..

5
Promieniowanie – przenoszenie energii w ośrodku gazowym lub próżni między
dwoma promie-
niującymi powierzchniami za pomocą fal elektromagnetycznych, przy czym następuje
dwukrotna
wymiana energii cieplnej na falę elektromagnetyczną na powierzchni ciała
wypromieniowującego
i odwrotnie na powierzchni ciała pochłaniającego ciepło.
Powierzchnie ciał o temperaturze powyżej zera bezwzględnego promieniują cieplnie
o natężeniu
zależnym od właściwości i temperatury powierzchni.
Promieniowanie takie charakteryzuje współczynnik promieniowania C, który określa
ilość ciepła
wypromieniowanego z 1m
2
powierzchni w ciągu 1h do próżni absolutnej przy
temperaturze po-
wierzchni 100K.
Natężenie promieniowania ciała absolutnie czarnego określa wzór Boltzmanna –
Stefana:
E
0
=C
0
[T/100]
4
;
C
0
– współczynnik promieniowania ciała absolutnie czarnego C
0
=5,77W/
(m
2
/K
4
),
T – temperatura bezwzględna powierzchni w K.
Materiały budowlane są materiałami szarymi, w odróżnieniu od ciał absolutnie
czarnych wypro-
mieniowują mniej ciepła, a padający na nie strumień ciepła jest częściowo
pochłaniany a częścio-
wo odbity.
Przejmowanie ciepła między powierzchnią a powietrzem charakteryzuje się
oporami przejmo-
wania ciepła względnie współczynnikami przejmowania ciepła.
Współczynniki przejmowania ciepła określają gęstość ustalonego strumienia ciepła
przepływają-
cego między powietrzem a powierzchnią przegrody przy różnicy temperatur równej
1K.

6
Oznaczamy je:
i
– współczynnik napływu ciepła do przegrody W/(m
2.
K),
α
e
– współczynnik odpływu ciepła od przegrody W/(m
2.
K),
Na powierzchniach przegród budowlanych następuje złożona wymiana ciepła,
równocześnie
przez konwekcję i promieniowanie. Możemy napisać że gęstość strumienia cieplnego
na powierz-
chni wynosi:
q = q
c
+ q
r
[W/m
2
]
gdzie:
q
c
– gęstość strumienia cieplnego przekazywanego przez konwekcję
W/m
2
,
q
r
– gęstość strumienia cieplnego przekazywanego przez promieniowanie
W/m
2
.
W przypadku pomieszczenia z jedną przegrodą zewnętrzną, przy jednokierunkowej
emisyj-
ności i temperaturze wszystkich pozostałych powierzchni można napisać że gęstość
strumienia
wynosi:
q =
c
(t
i
-
i
) -
r
(t
i
-
i
) [W/m
2
]
gdzie:
c
– współczynnik przejmowania ciepła przez konwekcję W/(m
2.
K),
r
– współczynnik przejmowania ciepła przez promieniowanie W/(m
2.
K).

7
W warunkach stacjonarnych gdzie temperatura powierzchni wewnętrznej niewiele
się różni od
powietrza wewnętrznego można w przybliżeniu napisać, że:
q = (
c
+
r
)
.
(t
i
-
i
) =
i
(t
i
-
i
) [W/m
2
],
gdzie:
i
– jest umownym współczynnikiem przejmowania ciepła przez
konwekcję i promie-
niowanie. Zależy on głównie od różnicy temperatury powietrza w pomieszczeniu t
i
i
wewnętrznej
powierzchni przegrody
i
oraz od współczynnika promieniowania tej powierzchni.
[W/m
2.
K].
e
– współczynnik odpływu ciepła (oddawania) ciepła zależy głównie od
prędkości
wiartu w pobliżu powierzchni. [W/(m
2.
K].
Do praktycznych obliczeń zapotrzebowania ciepła, wymiany ciepła między
powierzchnią przegro-
dy a otaczającym powietrzem norma PN-EN ISO 6936:1998 podaje wartości R
si
i R
se
R
si
= 1/
i
; R
se
= 1/
e
[m
2.
K/
Podane wartości dotyczą kierunku poziomego, w górę i w dół. W przypadku
powierzchni z wystę-
pami o specjalnych warunkach brzegowych należy korzystać ze wzoru na opór
przejmowania cie-
pła:
R
s
= 1/(h
c
+ h
r
) [m
2.
K/W]
gdzie:
h
c
– współczynnik przejmowania ciepła przez konwekcję W/(m
2.
K)
h
r
– współczynnik przejmowania ciepła przez promieniowanie W/(m
2.
K).
W przypadku powierzchni zewnętrznych h
c
=h
ce
przy czym
h
ce
= 4 + 4 [ W/(m
2.
K)
- prędkość wiatru w pobliżu powierzchni m/s.
Uwaga: Procedura obliczeń, wielkości pomocnicze podane są w przywołanej
normie.

8
Przewodzenie ciepła w dowolnym ciele stałym, układzie ciał, komponencie
budowlanym itp. spro-
wadza się do określenia pola temperatur, tj. podania zależności funkcyjnej
temperatury od współ-
rzędnych (najczęściej w układzie prostokątnym) i czasu:
t = f(x,y,z,) ,
gdzie:
t – temperatura,
- czas,
x, y, z, -współrzędne prostokątne.
Jeżeli temperatura zależy od czasu, to pole temperatur nosi nazwę nieustalonego
(niestacjonarne-
go). Jeżeli temperatura w każdym punkcie pola jest stała w czasie:
/
.
f(x,y,z,,) = 0
to pole temperatur nazywa się ustalonym (stacjonarnym). W tym przypadku określa go
funkcja:
t = f(x,y,z,)
By uprościć obliczenia praktyczne przyjmuje się, że temperatura elementu nie ulega
zmianom
wzdłuż współrzędnych leżących w płaszczyźnie elementu (y,x) tj. t/y = t/z = 0 stąd
w stanie
nieustalonym:
t = f(x,) ,

9
a w stanie ustalonym:
t = f(x).
Takie pole nazywamy jednowymiarowym.
Opisane powyższymi równaniami pole temperatur znajduje się jako rozwiązanie
równania różnicz-
kowego cząstkowego zwanego równaniem Fouriera lub równaniem przewodnictwa
cieplnego:
t/ = a
.
2
/x
2
gdzie:
a – współczynnik wyrównania temperatury m
2
/s,
a = /(c
.
)
w którym:
- wsp. przewodności cieplnej W/(m
.
K)
c – ciepło właściwe kJ/kg
.
K,
- gęstość materiału kg/m
3
.
Wzór ten można napisać w postaci:
t/ = a
2
t,
lub jako empiryczny wzór zwany prawem Fouriera:
q = - dt/dx = - grad t
. [W/m
2
]

10
w których:
2
- symbol operatora Laplace’a (nabla),
q – natężenie strumienia ciepła,
dt/dx – gradient temperatury.
Ilość ciepła przeniesionego w jednostce czasu przez jednostkę powierzchni
jest proporcjo-
nalna do gradientu temperatury mierzonego wzdłuż kierunku przepływu
ciepła.
Znak minus oznacza, że ciepło przepływa z obszaru o temperaturze wyższej do
obszaru o tempe-
raturze niższej a mierzonemu odcinkowi dx odpowiada ujemna wartość przyrostu
temperatury dt.
3. PRZEWODNOŚĆ CIEPLNA MATERIAŁÓW BUDOWLANYCH.
Definicja przewodności cieplnej.
Przewodność cieplna jest podstawową cechą decydującą o zastosowaniu materiału w
przegro-
dach izolacyjnych.
Przewodność cieplną określa współczynnik W/(m
.
K), który można zdefiniować:
I. Współczynnik przewodności cieplnej - gęstość ustalonego strumienia
ciepła przepływa-
jącego przez materiał jeżeli spadek temperatury t w stosunku do
grubości d wynosi 1K.
II. Współczynnik przewodności cieplnej jest to ilość ciepła przepływająca
przez materiał
o grubości 1m i powierzchni 1m
2
w ciągu 1 godziny przy różnicy
temperatur 1K.
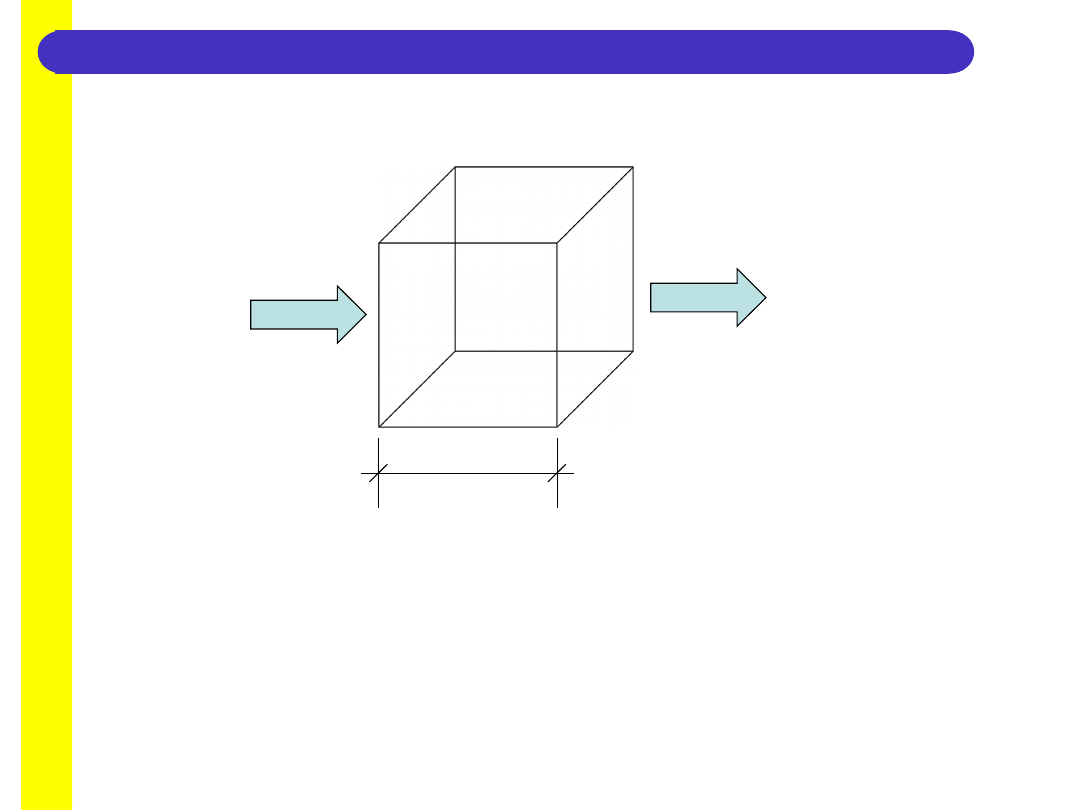
11
q =
1,0m
2
1,0m
2
1,0m
t = 1K
Znając ilość ciepła Q przepływającą w ustalonych warunkach przez próbkę materiału o
określonych wy-
miarach oraz czas przepływu i różnicę temperatur przeciwległych płaszczyzn, prostopadłych
do kierunku
przepływu, możemy obliczyć współczynnik z zależności:
= Q
.
d / (t
.
A
.
)
gdzie:
Q – ilość przepływającego ciepła [J] A – powierzchnia próbki [m
2
]
d – grubość próbki [m] - czas przepływu ciepła [h].
t – różnica temperatur [K]

12
Przewodność cieplna materiałów budowlanych zależy od wielu czynników jak:
- gęstość pozorna,
-struktura materiału,
-wilgotność,
-temperatura.
Ze wzrostem gęstości pozornej rośnie przewodność cieplna materiałów. Materiały lekkie o
gęstości
=20200kg/m
3
(styropian, pianka poliuretanowa, wełna mineralna) mają współczynnik
=0,050,035
w/(m
2.
K). Materiały kamienne =2800kg/m
3
, =3,5W/(m
.
K), dla stali =7800kg/m
3
, =58W/
(m
.
K).
W materiałach z tych samych substancji ale o różnej gęstości występuje zróżnicowanie
współczynników np. dla betonu:
=1900kg/m
3
=1,0W/(m
.
K)
=2400kg/m
3
=1,5W/(m
.
K).
W materiałach anizotropowych (o budowie włóknistej lub krystalicznej) wartość
współczynnika zależy
od kierunku przepływu ciepła. Np. drewno sosnowe o gęstości =550kg/m
3
wzdłuż włókien =0,30W/(m
.
K)
w poprzek włókien =0,16W/(m
.
K).
Współczynnik przewodności cieplnej powietrza jest mały =0,020,31W/(m
.
K), w
porównaniu do współczynnika szkieletu materiałowego, dlatego też ze wzrostem ilości
porów wypełnionych powie-trzem maleje przewodność cieplna materiału.
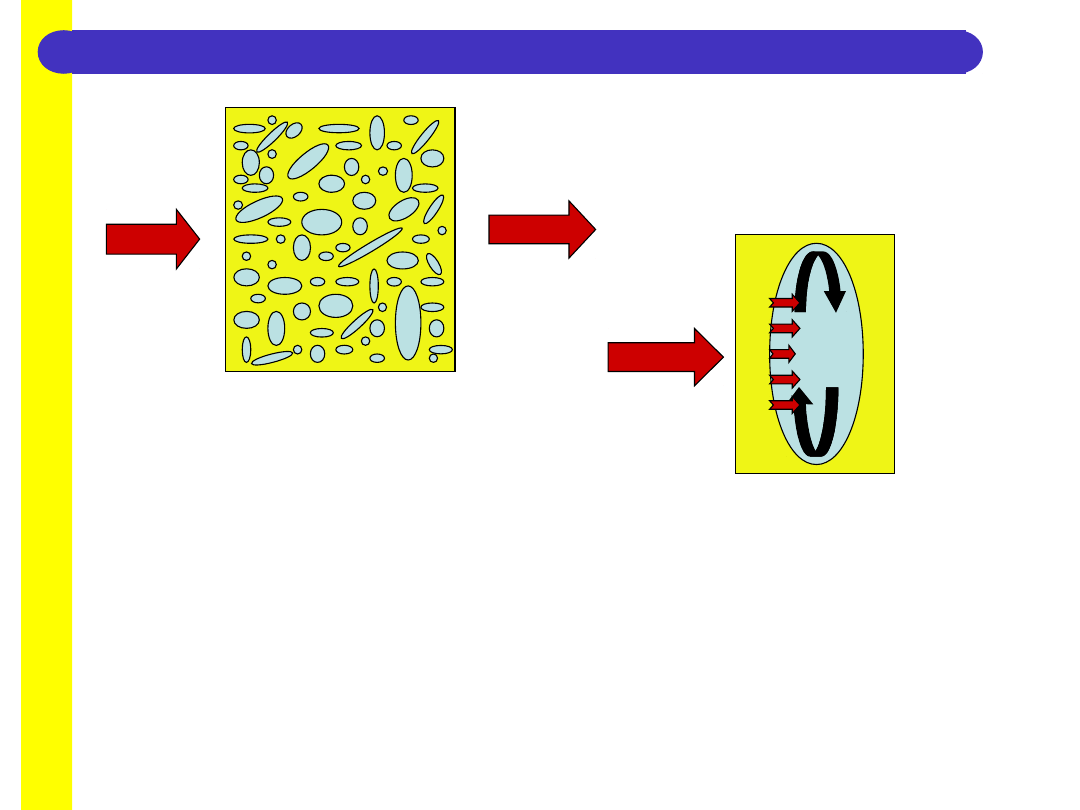
13
Lepsze są pory drobne
rozmieszczone w całej strukturze
materiału niż pory duże w których
może wystąpić ruch i
konwekcyjna wymiana ciepła.
Wzrost wilgotności materiału to pory wypełnione wodą o współczynniku =0,56W/(m
.
K)
czyli dwa razy
większym od powietrza, co powoduje pogorszenie właściwości termoizolacyjnych.
Dodatkowo na przewodność cieplną materiału ma wpływ dyfuzja pary wodnej z którą
połączone jest przenoszenie ciepła i kapilarne przemieszczanie się wody. Np. w betonach
komórkowych wzrost wilgot-
ności o 1% powoduje wzrost współczynnika o 45%.
W temperaturze ujemnej po zamarznięciu wody następuje dalsze obniżenie wartości
termoizolacyjnej materiału (dla lodu =2,30W/(m
.
K) ).

14
Przy wzroście temperatury wzrasta współczynnik , szczególnie dla materiałów włóknistych
i ziarnistych.
Wzrost ten jest jednak niewielki, ma znaczenie dopiero dla temperatur powyżej 500
0
C.
Chcąc go uwzglę-
dnić dla temperatur od 0100
0
C można posłużyć się wzorem:
t
=
0
(1+
.
t)
gdzie:
t
– współczynnik przewodności cieplnej materiału w określonej
temperaturze t
0
C,
0
– współczynnik przewodności cieplnej materiału w temperaturze
t=0
0
C,
t – temperatura dla której określane jest
t
,
- współczynnik temperatury równy ok. 0,0025.
Dla zakresu temperatur 20 60
0
C zmiany są małe i można je praktycznie pominąć.
Uwaga:
Uwaga:
Wartości obliczeniowe właściwości fizycznych materiałów , wyrobów i komponentów, w
przypadku gdy
znany jest ich producent ( dostawca ), bierzemy z norm lub aprobat technicznych. W
przypadku gdy nie można ich określić przyjmuje się je według tablicy NC1 w załączniku do
normy PN- EN ISO 6946 : 1999.
15
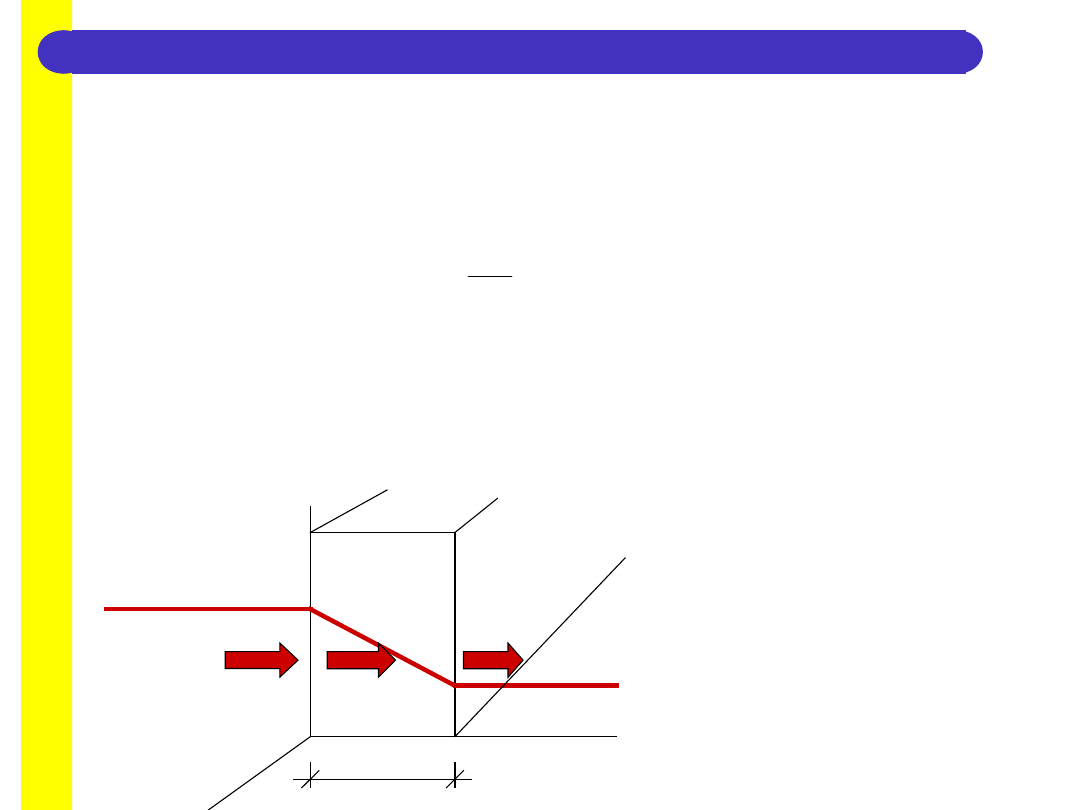
4. JEDNOWYMIAROWE, USTALONE
PRZEWODZENIE CIEPŁA.
Najprostszy przypadek przewodzenia ciepła tj. przy przepływie jednokierunkowym,
prostopadle do płaszczyzn ograniczających warstwę, w stanie ustalonym, opisuje równanie:
0
2
2
dx
t
d
Ogólne rozwiązanie równania:
t=C
1
x+C
2
Stałe całkowania wyznacza się z warunków brzegowych dla:
x=0 t
(x)
=
i
x=d t
(x
)=
e
q
1
q
2
q
3
i
e
t
i
t
e
z
X
y
0
d
d

16
Po wyznaczeniu stałych całkowania C
1
i C
2
oraz wstawieniu do równania otrzymamy
rozwiązanie:
x
d
t
e
i
e
e
Rozwiązanie to przedstawia liniową zależność temperatury od współrzędnej X co jest
charakterystycz-
ne dla ustalonego jednokierunkowego przepływu ciepła w ścianie jednorodnej.
Po zróżniczkowaniu powyższego rozwiązania otrzymany gradient temperatury dt/dx.
Wstawiając tą
różniczkę do wzoru Fouriera otrzymamy wzór do obliczenia strumienia ciepła:
d
dx
dt
q
e
i
Przez przegrodę w warunkach ustalonego przepływu ciepła, zgodnie z prawem
Fouriera, prze-
pływa strumień ciepła q o stałej gęstości.
W rozpatrywanym przypadku, zgodnie ze stwierdzeniem jak wyżej dla przegrody jednorodnej
napiszemy:
q
1
=q
2
=q
3
=q
ale podstawimy:
- ciepło napływające q
1
=
i
(t
i
-
i
)
- ciepło przepływające
- ciepło odpływające q
3
=
e
(
e
-t
e
).
Powyższe wyrażenia przekształcimy otrzymując je w postaci:
d
q
e
i
2

17
i
i
i
q
t
1
1
d
q
e
i
2
e
e
e
q
t
1
3
Po dodaniu stronami mamy:
e
i
e
i
d
q
t
t
1
1
lub:
e
i
e
i
d
t
t
q
1
1
Wprowadzając pojęcie oporu cieplnego warstwy jednolitej i pojedynczej:
d
R
[m
2.
K/W]
gdzie:
d – grubość warstwy materiału m,
- obliczeniowy współczynnik przewodzenia ciepła materiału W/(m
.
K)
oraz znane już:
i
si
R
1
e
se
R
1
;
Otrzymamy opór cieplny przegrody jednowarstwowej (jednomateriałowej):
R
T
=R
si
+ R + R
se

18
Opór cieplny przegrody składającej się z termicznie jednorodnych warstw prostopadłych do
kierunku prze-
pływu ciepła wynosi:
R
T
= R
si
+ R
1
+ R
2
+…….+R
n
+ R
se
gdzie:
R
si
– opór przejmowania ciepła na wewnętrznej powierzchni,
R
1
; R
2
;….R
n
– obliczeniowe opory cieplne każdej warstwy,
R
se
– opór ciepła na wewnętrznej powierzchni.
Stąd dla całej przegrody gęstość strumienia ciepła wyniesie:
T
e
i
R
t
t
q
T
e
i
R
q
t
t
lub
W komponencie, w przegrodzie budowlanej obliczamy temperatury na granicach warstw i
sporządzamy
wykres temperatur. Można to robić w dwojaki sposób:
1. Odejmując od poprzedzającej temperatury iloczyn ciepła q i oporu R poprzedniej
warstwy.
2. Odejmując od temperatury powietrza w pomieszczeniu iloczyn sumy wszystkich
oporów od
warstwy wewnętrznej do danej warstwy, oraz ilości ciepła q.
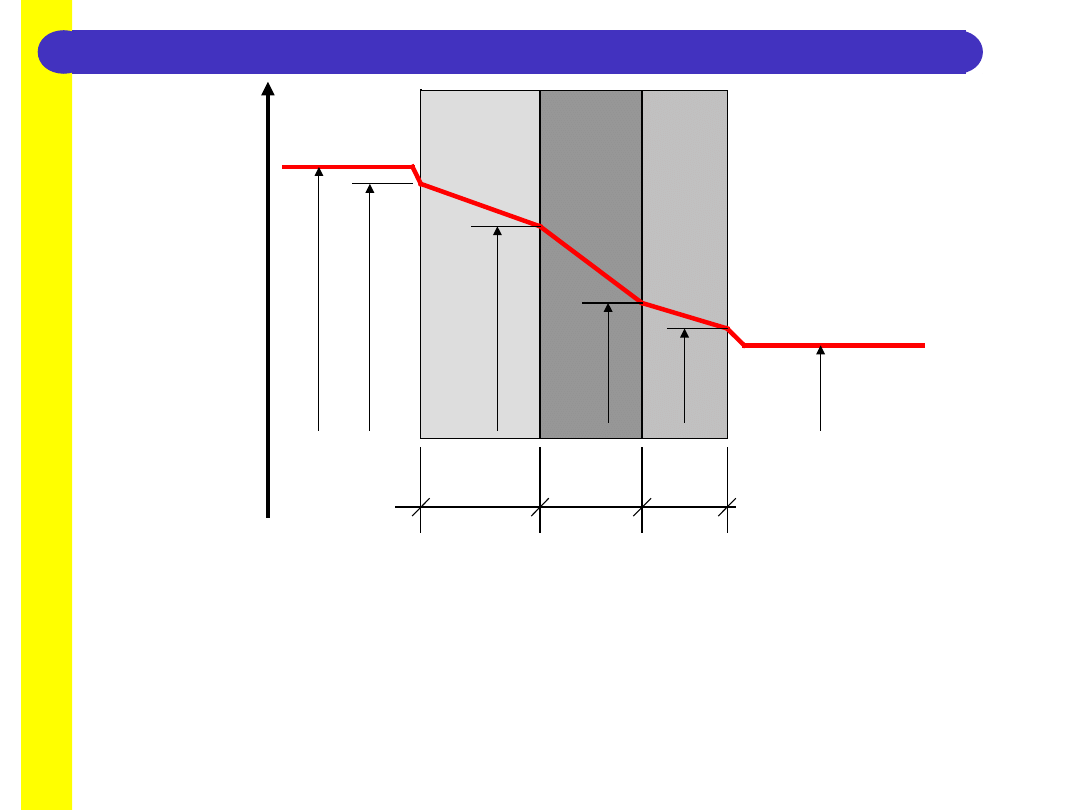
19
t
0
C
d
1
d
2
d
3
R
1
R
2
R
3
1
2
3
t
i
i
1
2
e
t
e
Przyjmując oznaczenia jak na rysunku obliczamy temperatury:
i
= t
i
– q
.
R
si
1
=
i
– q
.
R
1
= t
i
– q
.
(R
si
+ R
1
)
2
=
1
– q
.
R
2
= t
i
– q
.
(R
si
+ R
1
+ R
2
)
e
=
2
– q
.
R
3
= t
i
– q
.
(R
si
+ R
1
+ R
2
+ R
3
)
t
e
=
e
– q
.
R
se
= t
i
– q
.
(R
si
+ R
1
+ R
2
+ R
3
+ R
se
).
R
si
R
se

20
W praktyce posługujemy się odwrotnością oporu przenikania ciepła przegrody R
T
nazywając ją współ-
czynnikiem przenikania ciepła U.
T
R
1
=
U
[W/(m
2.
K)]
Charakteryzuje on przegrodę pod względem izolacyjności cieplnej. Można go zdefiniować:
1. Współczynnik przenikania ciepła U jest to stosunek gęstości ustalonego
strumienia cieplnego
do różnicy temperatur po obu stronach przegrody.
e
i
t
-
t
q
=
U
[W/(m
2.
K)]
2. Współczynnik przenikania U wyraża ilość ciepła jaka przenika przez przegrodę o
powierzchni 1m
2
w ciągu jednej godziny przy różnicy temperatur po obu stronach
przegrody wynoszącej 1K.

21
Temperaturę na powierzchni przegrody, od strony napływu można wyliczyć ze wzoru:
i
= t
i
– q
.
R
si
[
0
C ]
ale wiemy że:
q = U
.
( t
i
– t
e
)
podstawiając otrzymamy:
i
= t
i
– U(t
i
– t
e
)
.
R
si
[
0
C]
Temperaturę na dowolnej płaszczyźnie przegrody można wyliczyć ze wzoru:
n
= t
i
– U(t
i
– t
e
)
.
(R
n
+ R
si
) [
0
C]
gdzie:
R
n
– suma oporów od strony napływu ciepła do płaszczyzny n.
Różnica temperatur na płaszczyznach ograniczających n-tą warstwę wynosi:
=
n-1
-
n
= q
.
R
n
= [(
i
-
e
):R]
.
R
n
= U(t
i
– t
e
)
.
R
n
[
0
C]

22
5. DWUKIERUNKOWY PRZEPŁYWY CIEPŁA
W przegrodach o skomplikowanym kształcie (zmiany grubości, naroża itp..), wykonanych z
różnych ma-
teriałów i o różnej konfiguracji zachodzi konieczności określenia pola temperatur przy
dwukierunkowym
przepływie ciepła ( np. dla mostka termicznego).
Przy założeniu ustalonego pola temperatur i zastąpieniu w równaniu Fouriera-Laplace’a
(
2
t/=a
2
t )
różnicami skończonymi wzór przyjmuje postać:
0
=
y
Δ
t
Δ
+
x
Δ
t
Δ
2
2
2
2
Wykorzystując elektroniczną technikę obliczeń i stosując metodę elementów skończonych,
można uzys-
kać pole temperatur.
W obliczeniach praktycznych na obszar w którym chcemy określić pole temperatury
nakładamy siatkę prostokątną, węzły numerując kolejno. Siatkę dobieramy tak by jej węzły
leżały wewnątrz i na brzegu roz-
patrywanego obszaru, oraz w punktach charakterystycznych.
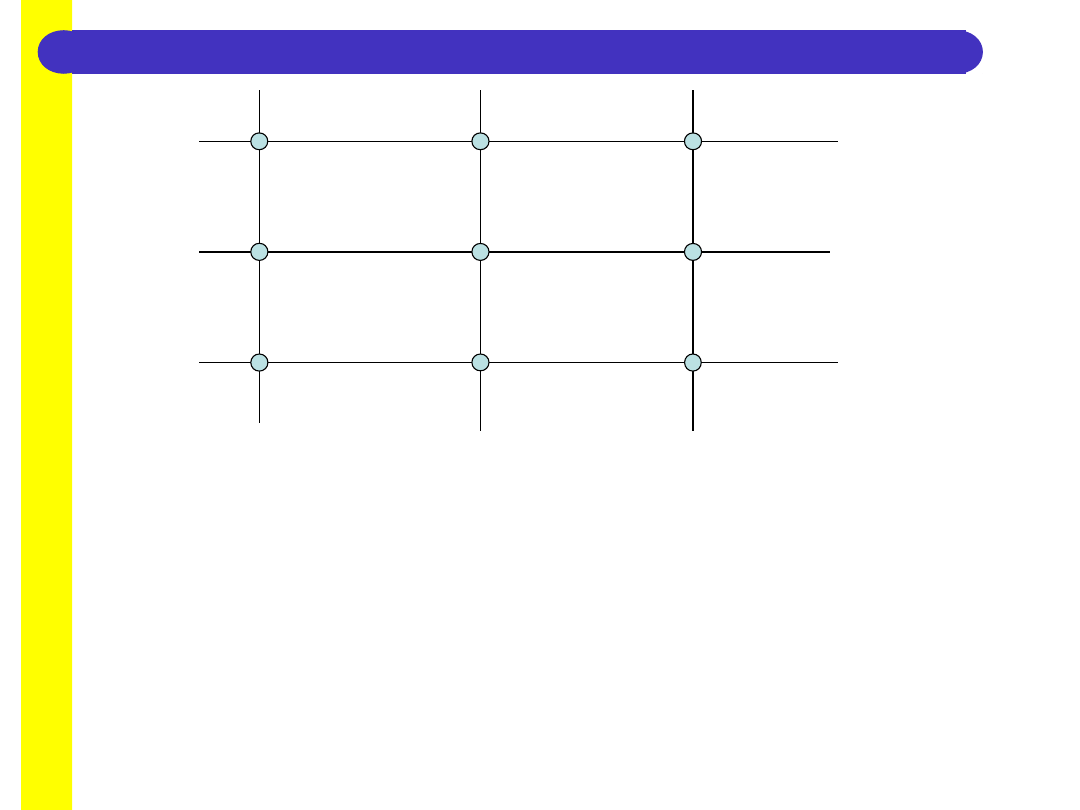
23
t
i;j+1
t
i;k
t
i;j+1
t
i-1;j-1
t
i-1;j
t
i-1;j-1
t
i+1;j+1
t
i+1;j
t
i+1;j+1
Następnie układa się równania wyrażające zależność temperatury w poszczególnych
punktach przecię-
cia od temperatury sąsiednich najbliżej usytuowanych czterech punktów. W ten sposób
otrzymuje się n
równań z n liczbą niewiadomych temperatur.
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
Wyszukiwarka
Podobne podstrony:
IZOLACYJNOŚĆ TERMICZNA WIELOWARSTWOWYCH PRZEGRÓD BUDOWLANYCH
Labolatorium Wymiany Ciep
certyfikacja przegrody budowlane
Izolacyjność termiczna wielowarstwowych przegród budowlanych, budownictwo ogólne
więcej podobnych podstron