

Dr inż. JANUSZ LICHOTA

PODSTAWY AUTOMATYKI

regulatory optymalne

Wydział Mechaniczno-
Energetyczny

PLAN WYSTĄPIENIA

• Optymalizacja statyczna

sterowania

• Optymalizacja dynamiczna

sterowania

REGULACJA OPTYMALNA
Optymalizacja oznacza wybór

Wybór
• najlepszej strategii
• najlepszych parametrów
• najlepszego sygnału

sterującego

• najlepszej estymaty

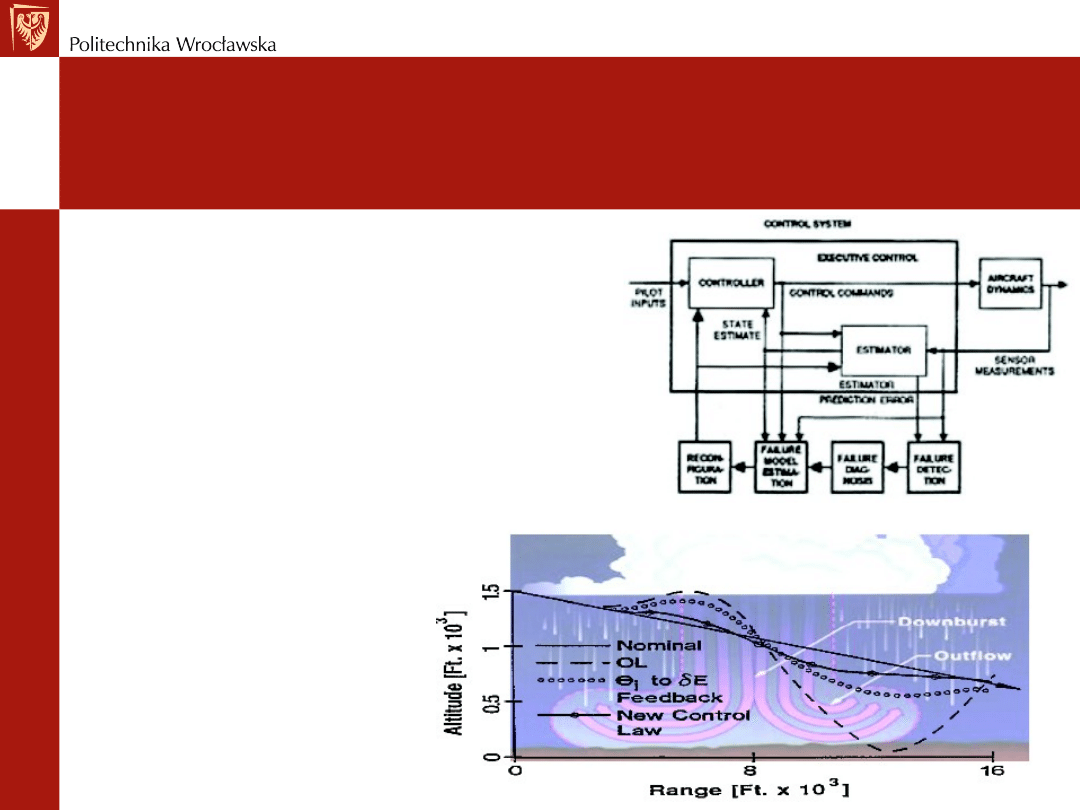
Trajektoria samolotu i
wpływ zakłóceń (chmury)

REGULACJA OPTYMALNA
Optymalizacja oznacza wybór

• Optymalne rozwiązanie jest

ograniczone przez fizyczne
własności obiektu

• Optymalne wskaźniki jakości

regulacji są ograniczone przez
sygnały sterujące

• Celem jest minimalizacja funkcji

kosztu, która

jest

kompromisem pomiędzy jakością
regulacji i sygnałem sterującym

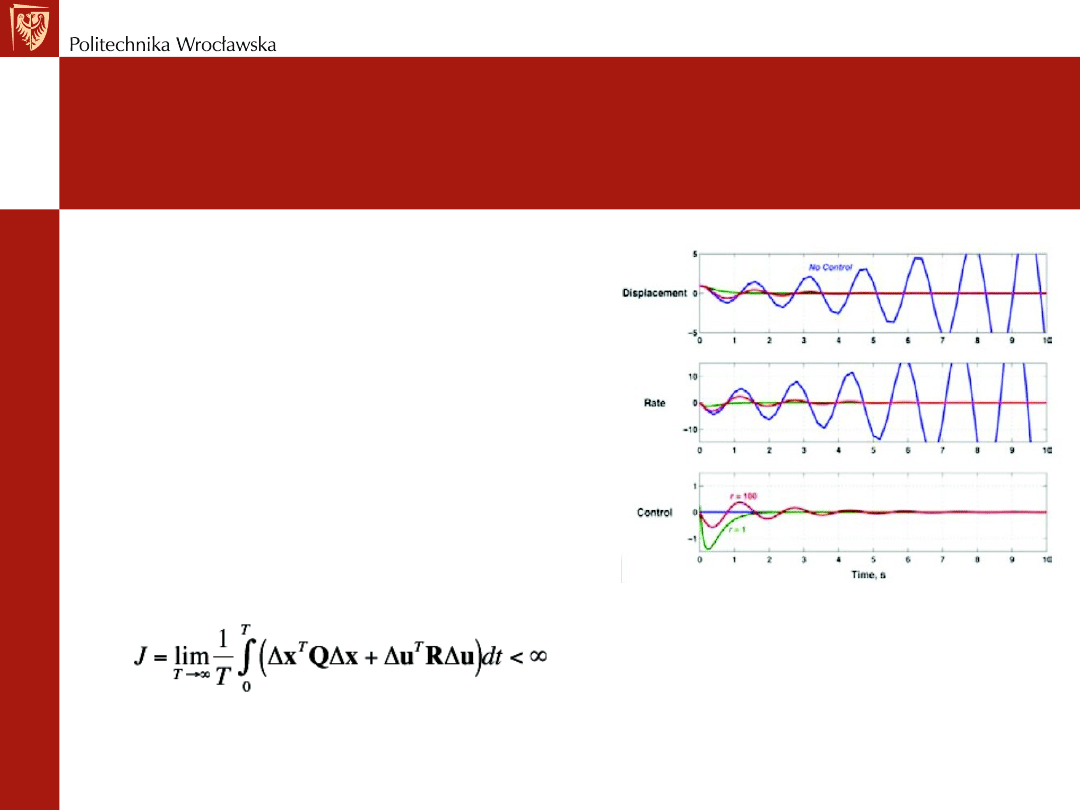
Duże u, dobry x (najmniejszy)

Średnie u, średni x

u=0, najgorszy x (największy)

REGULACJA OPTYMALNA
Optymalizacja statyczna i
dynamiczna

• Statyczna: optymalny stan i sygnał

sterujący są stałe niezależne od czasu

J

*

=J(x

*

, u

*

)

- minimalizacja lub

maksymalizacja funkcji

- optymalizacja parametrów

• Dynamiczna: optymalny stan i sygnał

sterujący są ciągle zależne od czasu

J

*

=J(x

*

(t), u

*

(t))

- optymalna trajektoria
- optymalna strategia sprzężenia

zwrotnego

• Funkcja kosztów J

*

jest w obu

przypadkach skalarem (liczbą
rzeczywistą)

REGULACJA OPTYMALNA

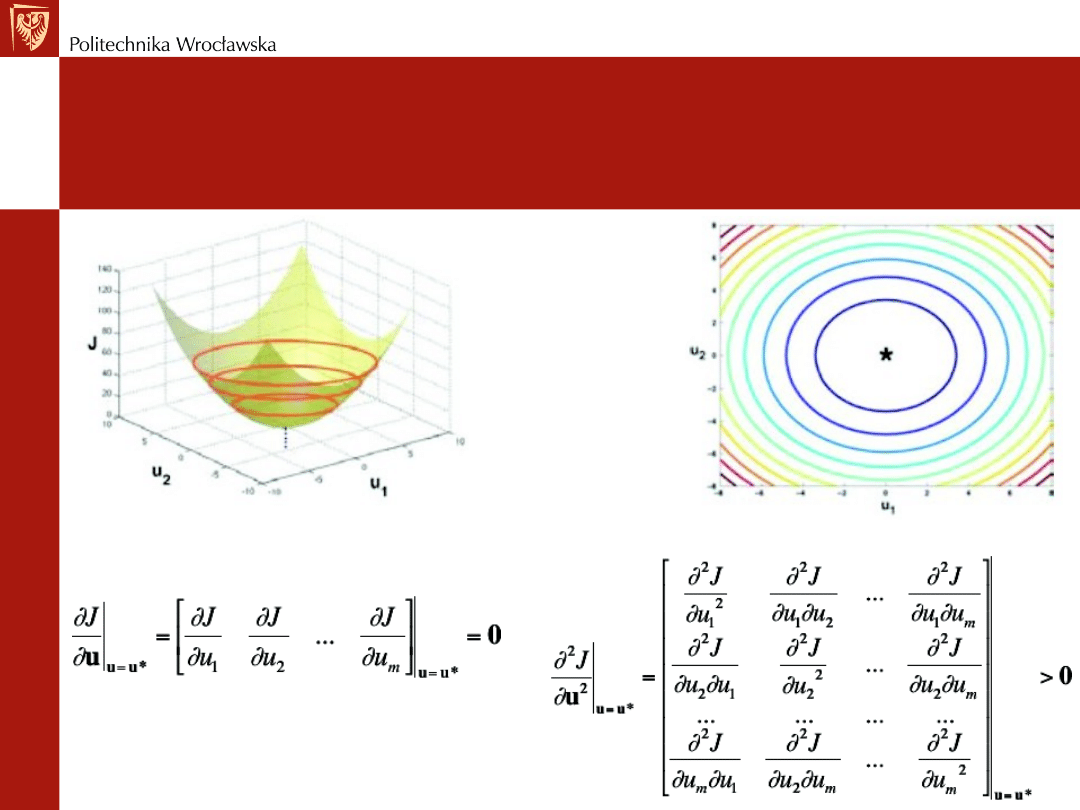
Warunki konieczne i dostateczne istnienia
minimum
w optymalizacji statycznej

1) Gradient wskaźnika jakości (wektor 1 x m)=0

2) Hesjan jest dodatni

REGULACJA OPTYMALNA

Ograniczenia równościowe

• Zminimalizuj J(u’) wzdłuż krzywej c(u’)=0

-dim (c) = [ n x 1]

-dim(u’) = [(m + n) x1]

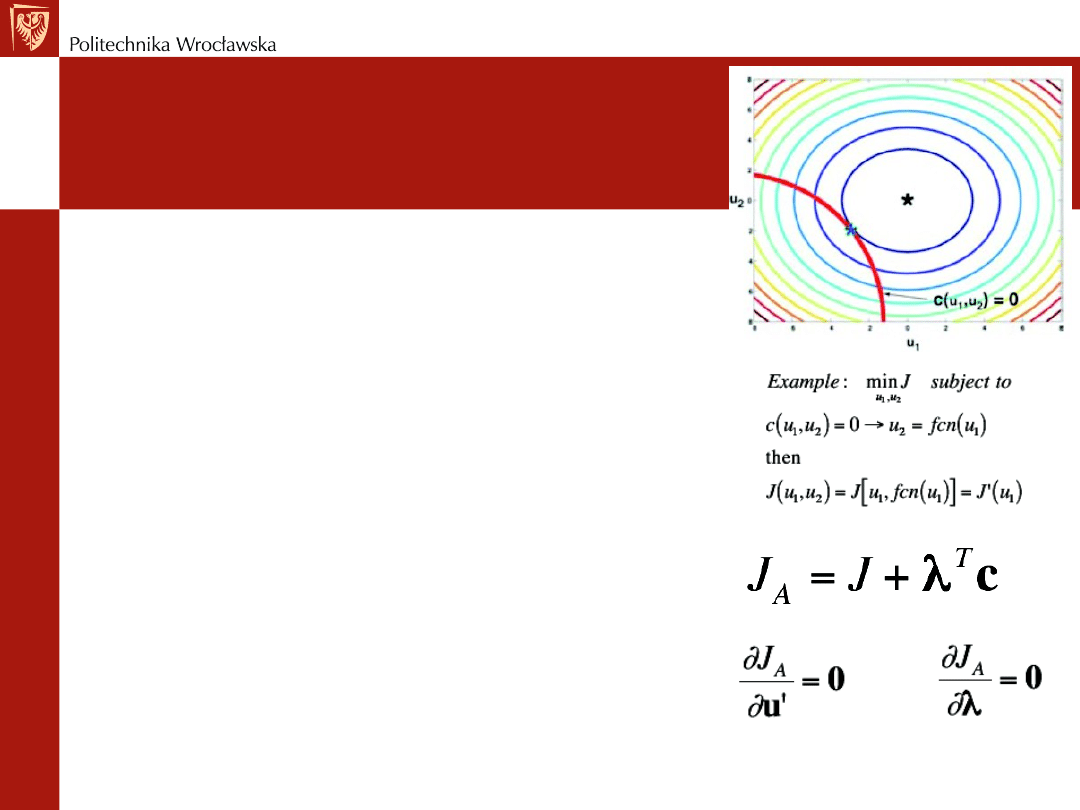
REGULACJA OPTYMALNA

Dwa podejścia do rozwiązania

1) Wykorzystaj ograniczenie do redukcji wymiaru sterowania

2) Wykorzystaj J(u’) do zbadania przebiegu krzywej c(u’)=0

- wprowadź mnożnik Lagrange’a, , jako nieznaną stałą

-  ma ten sam wymiar co ograniczenie c, dim()=[n x 1]

- w minimum

- J

A

jest stacjonarne tj. gradient u’ oraz  jest równy 0

- spełnione jest ograniczenie równościowe c=0

Należy rozwiązać 2n+m, aby znaleźć optymalne parametry x,u, 

REGULACJA OPTYMALNA

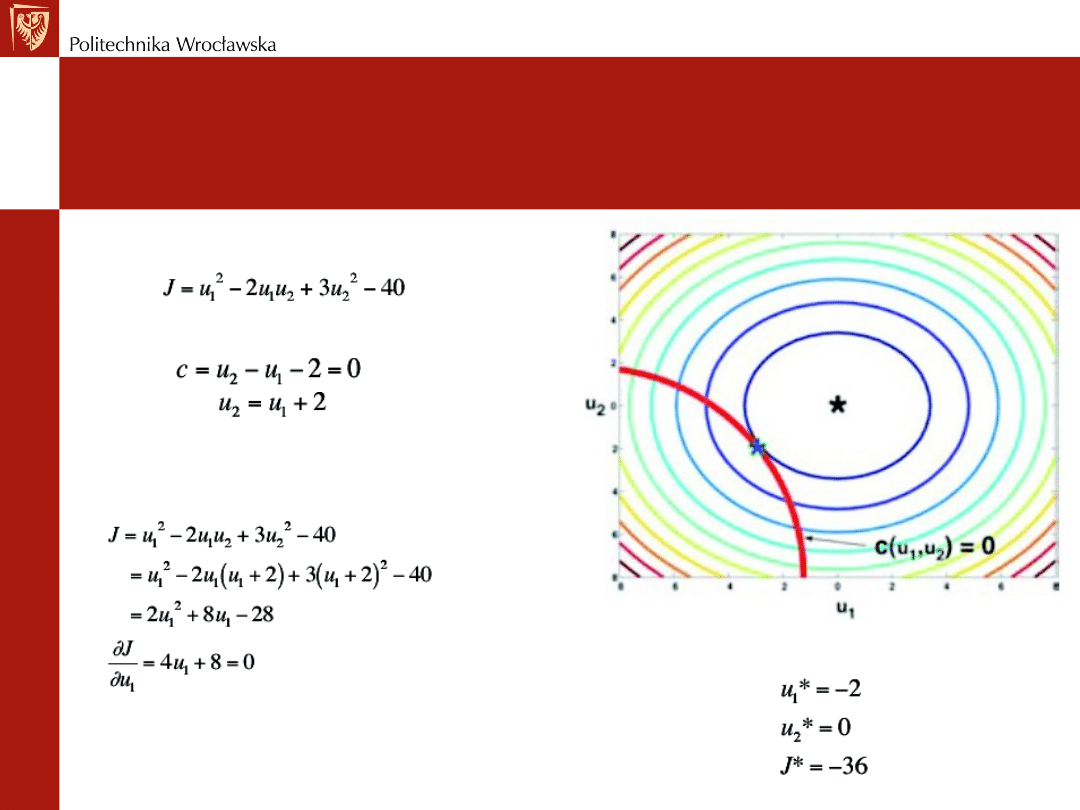
Przykład pierwszego rozwiązania

Funkcja kosztów

Ograniczenie

Funkcja kosztów

Rozwiązanie optymalne

REGULACJA OPTYMALNA

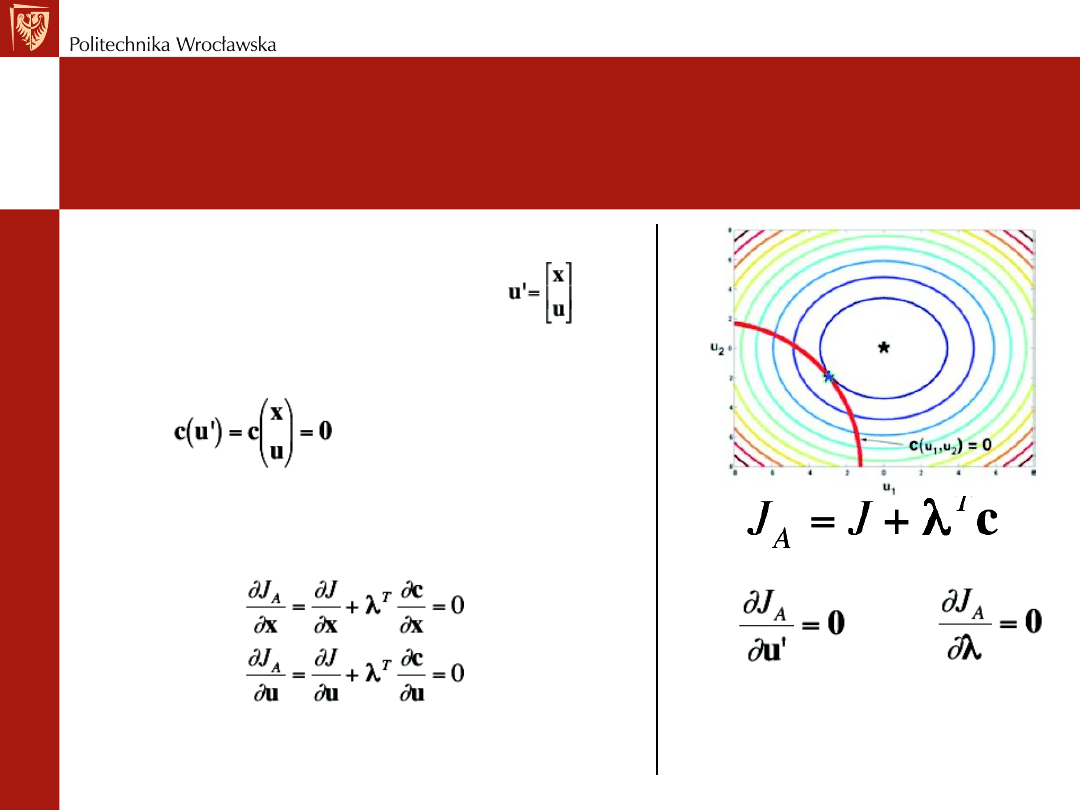
Przykład drugiego rozwiązania

Podziel u’ na stan x oraz sterowanie u

-dim(x)=[n x 1]

-dim(u)=[m x 1]

-Wtedy

-Gradient odniesiony do u’ tworzy dwa równania

-W minimum

REGULACJA OPTYMALNA

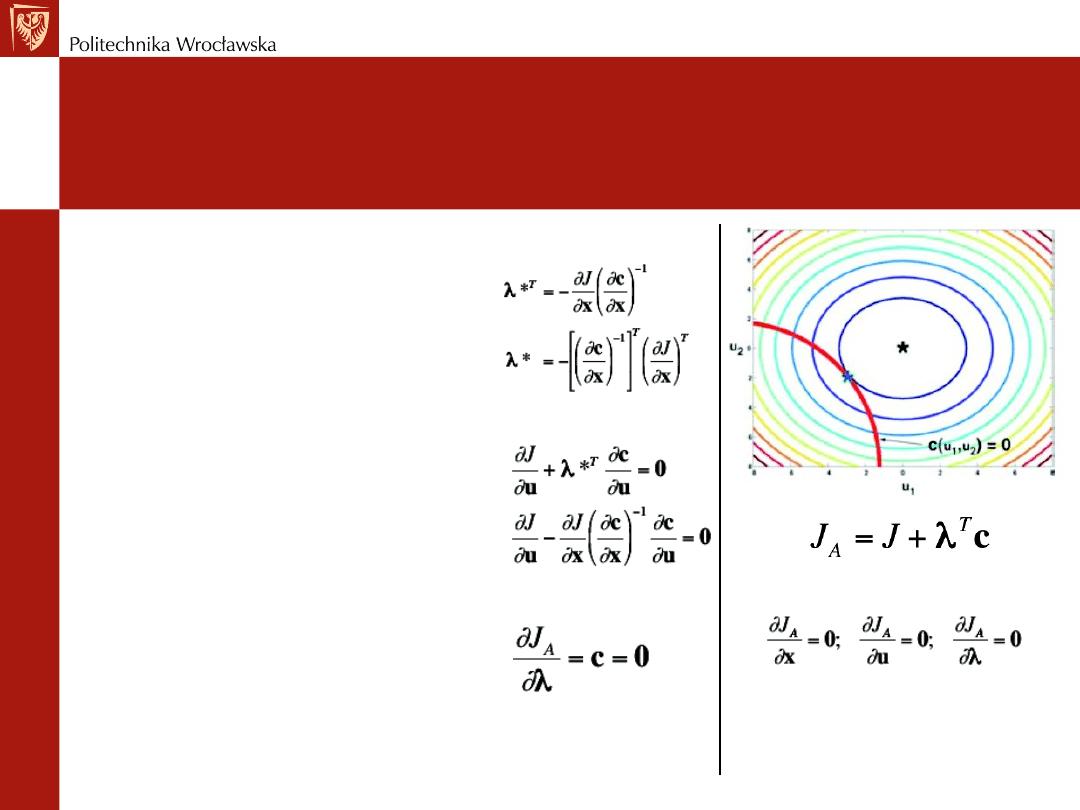
Przykład drugiego rozwiązania

Rozwiąż pierwsze równanie znajdując
mnożniki Lagrange’a (n równań)

Drugie równanie pozwala na obliczenie
m sygnałów sterujących u

Pozostałe n równań jest określone przez
ograniczenie równościowe

REGULACJA OPTYMALNA

Przykład drugiego rozwiązania

Funkcja kosztu

Ograniczenie

Pochodne cząstkowe

Z pierwszego równania

Z drugiego równania

Z ograniczenia

Rozwiązanie optymalne

REGULACJA OPTYMALNA

Optymalizacja dynamiczna

Minimalizacja funkcji kosztów końcowych i całki z kosztów bieżących

L - lagranżian

w funkcji sterowania u(t) w czasie (t

o

, t

f

) z ograniczeniem dynamicznym

Warunek początkowy x(t

o

) jest zadany.

dim(x)=[n x 1]
dim(f)=[n x 1]
dim(u)=[m x 1]

REGULACJA OPTYMALNA

Optymalizacja dynamiczna

Wykorzystaj funkcję kosztów J(u’) do zbadania przebiegu ograniczenia

dynamicznego

- wprowadź mnożnik Lagrange’a, , jako nieznany zależny od czasu wektor
-  ma ten sam wymiar co ograniczenie c, dim()=[n x 1]

Dołącz ograniczeni dynamiczne do całki z zastosowaniem mnożnika Lagrange’a

- ograniczenie =0 wtedy, gdy jest spełnione równanie

Zdefiniuj Hamiltonian

REGULACJA OPTYMALNA

Wykorzystaj Hamiltonian

Wstaw hamiltonian do równania kosztów

Optymalny koszt jest wynikiem optymalnego sterowania, stanu i mnożnika Lagrange’a

REGULACJA OPTYMALNA

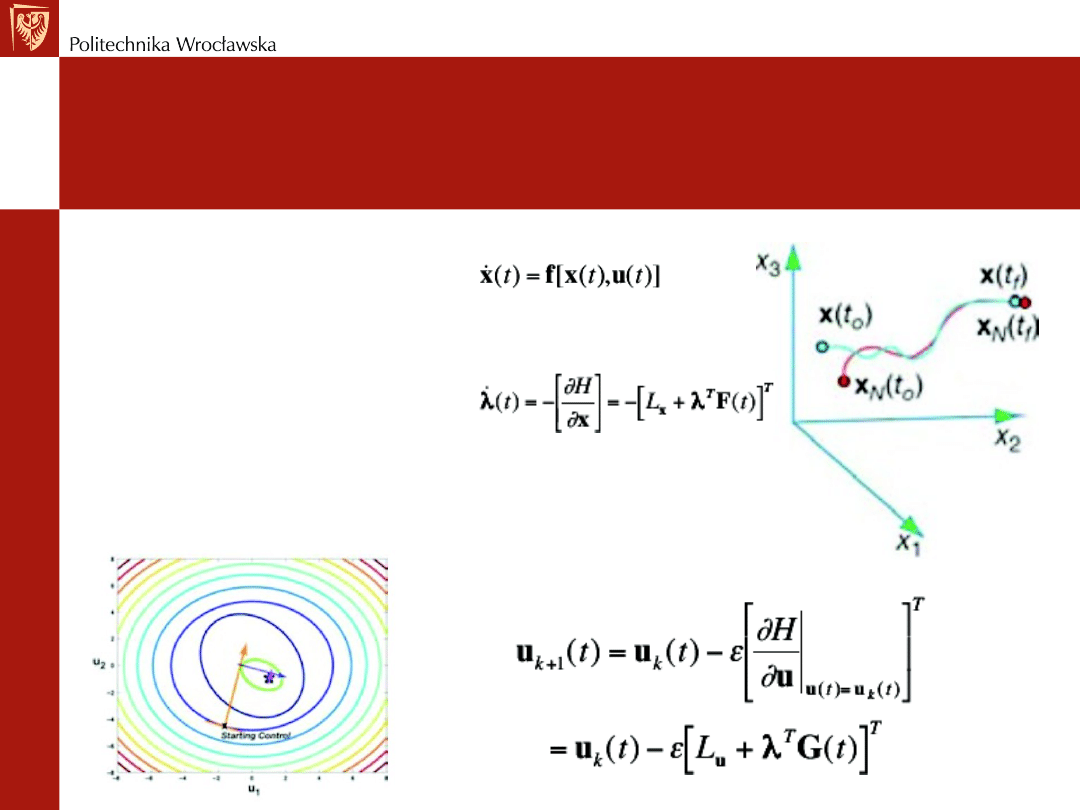
Sterowanie optymalne

Koszt wzdłuż optymalnej trajektorii J

*

powinien być niewrażliwy na małe zmiany sterowania

Przyjmując  J

*

=0 otrzymujemy trzy równania Eulera-Lagrange’a (warunki konieczne optymalności)

REGULACJA OPTYMALNA

Optymalizacja numeryczna za pomocą
gradientowego algorytmu największego spadku

Procedura

-rozwiązanie w przód, x(t)

-rozwiązanie wstecz, (t)

-algorytm największego spadku
w poszukiwaniu u(t)

x(t

o

) zadany

(t

f

)

zadany

REGULACJA OPTYMALNA

Programowanie dynamiczne

Cel: zminimalizuj wartość kosztu V

o

od chwili

bieżącej do końcowej poprzez wybór łuków

Każdy łuk reprezentuje koszt L

k+1

Poszukiwanie w dwóch kierunkach

-proces iteracyjny

Łańcuch w przód propaguje koszty od początku
Łańcuch wstecz propaguje koszty od końca
(koszt końcowy ścieżki)

REGULACJA OPTYMALNA

Przykład – optymalny kąt natarcia promu
kosmicznego

Kąt natarcia = kąt pomiędzy osią samolotu i wektorem prędkości

Początkowe koncepcje promu były oparte o DC-3 =60°.

Problemem jest przejście od dużego kąta natarcia do małego
podczas lądowania.

REGULACJA OPTYMALNA

Przykład – równania ruchu promu

Zmienne używane w optymalizacji, x

1

=v prędkość, kąt ścieżki lotu x

2

=g, wysokość x

3

=h i zasięg

lotu x

4

.

Optymalizowany jest kąt natarcia .

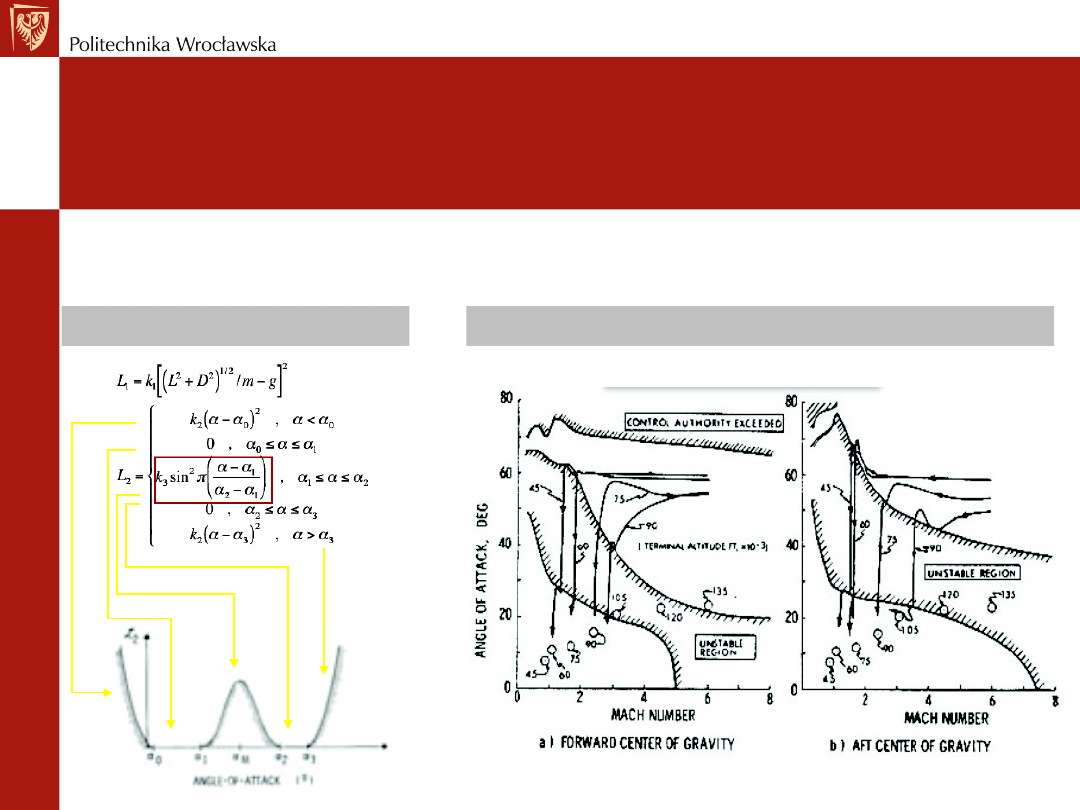
Kąt natarcia 

REGULACJA OPTYMALNA

Przykład – optymalna ścieżka lotu

Funkcja kosztów wprowadza funkcję kary w regionie niestabilnym
Są również spełnione dodatkowe warunki dla zmiennego czasu końcowego t

f

Składniki funkcji kosztu

Kąt natarcia w zależności od liczby Macha

REGULACJA OPTYMALNA

Przykład – rozpraszanie energii w czasie
powrotu

Rozwiązanie końcowe – skrzydło w kształcie 2

- wyeliminowano niestabilność kąta wniesienia promu

- wzrósł zasięg

Energia całkowita wynosi

Energia maleje monotonicznie na trajektorii powrotnej

REGULACJA OPTYMALNA

Przykład – trójwymiarowe równania ruchu

Zmiana zmiennych podlegających optymalizacji

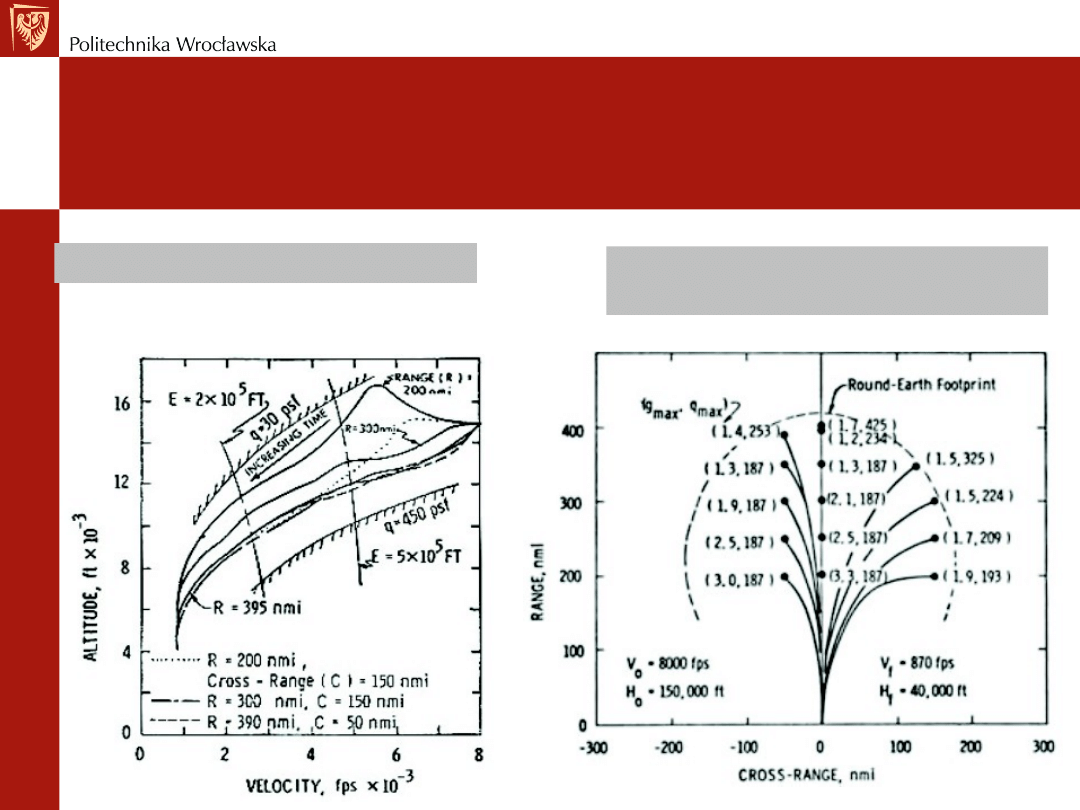
Wysokość w funkcji prędkości

Zasięg w funkcji poprzecznego
przesunięcia promu

REGULACJA OPTYMALNA

Przykład – optymalne prowadzenie promu

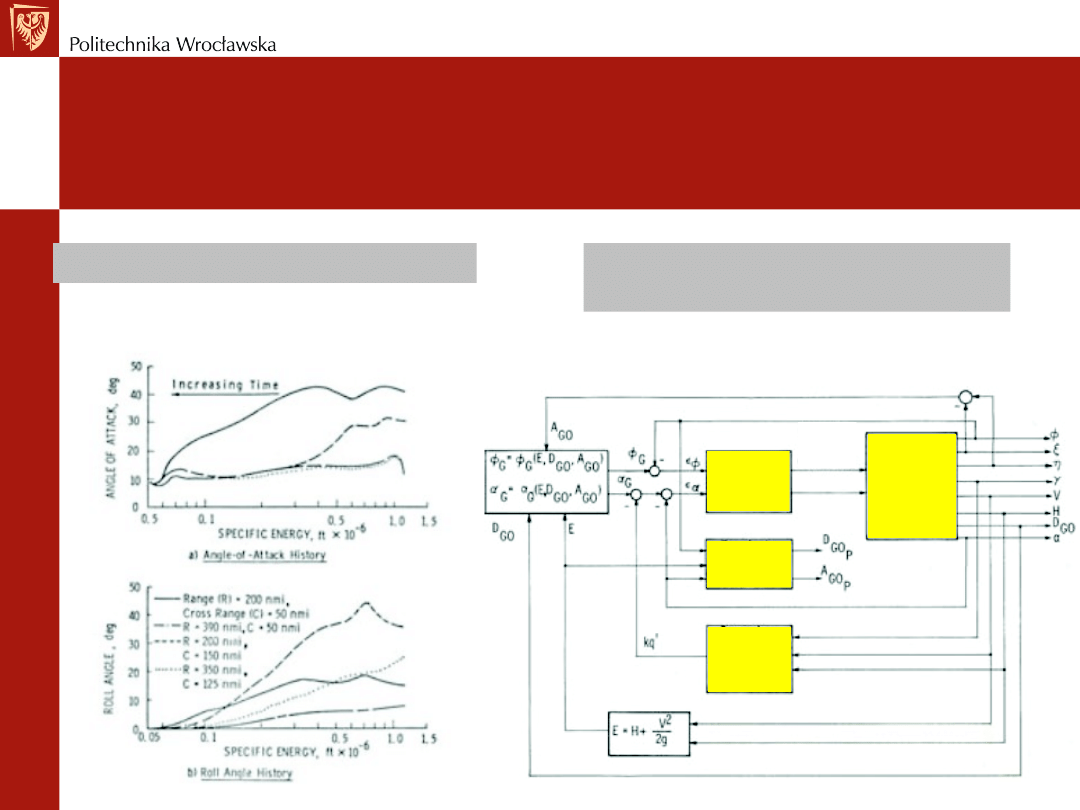
Kąt natarcia w funkcji energii

Układ sterowania w oparciu o
prawo zachowania energii

Logika
kontroli
lotu

Dynamika
samolotu

Predykcja
punktu
końcowego

Tłumienie
prędkości
zmian ciśnienia
dynamicznego

Komendy
powierzchni
kontrolnych

REGULACJA OPTYMALNA

Przykład – optymalne trajektorie ruchu

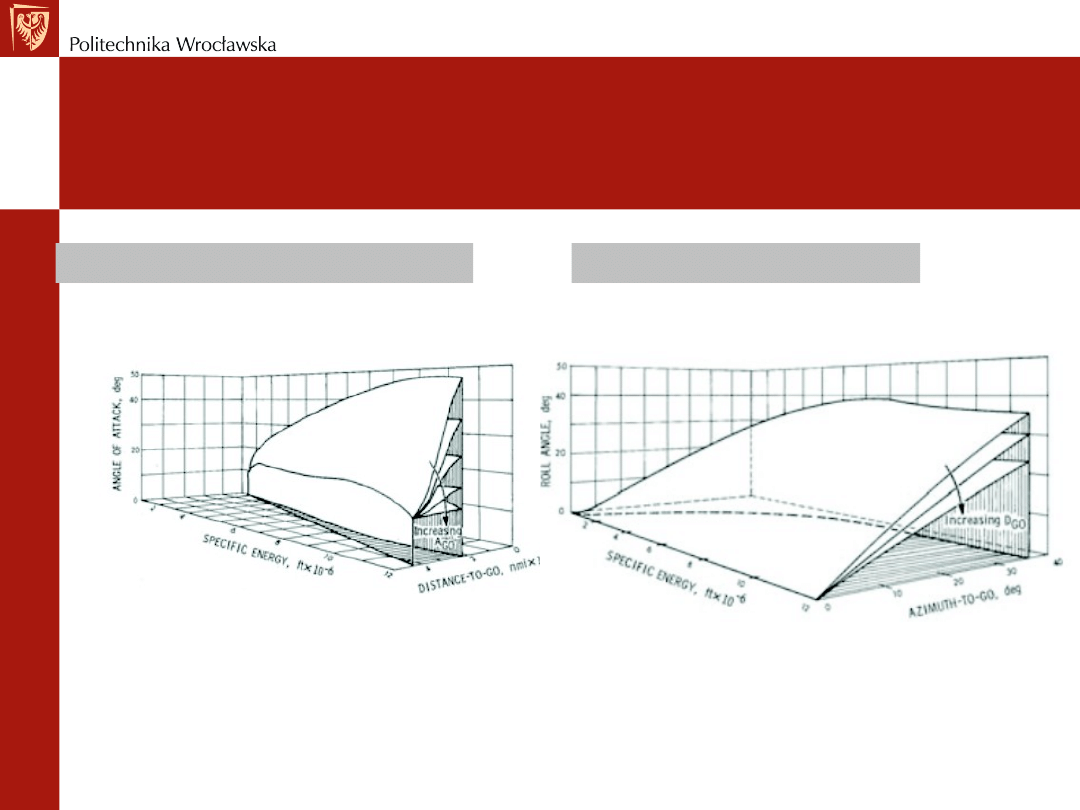
REGULACJA OPTYMALNA

Przykład – funkcje prowadzące prom do
lądowania

Funkcja zmiany kąta natarcia

Funkcja zmiany kąta ???

Sposoby rozwiązania układu sterowania

- programowanie dynamiczne

- nieliniowe sprzężenie zwrotne

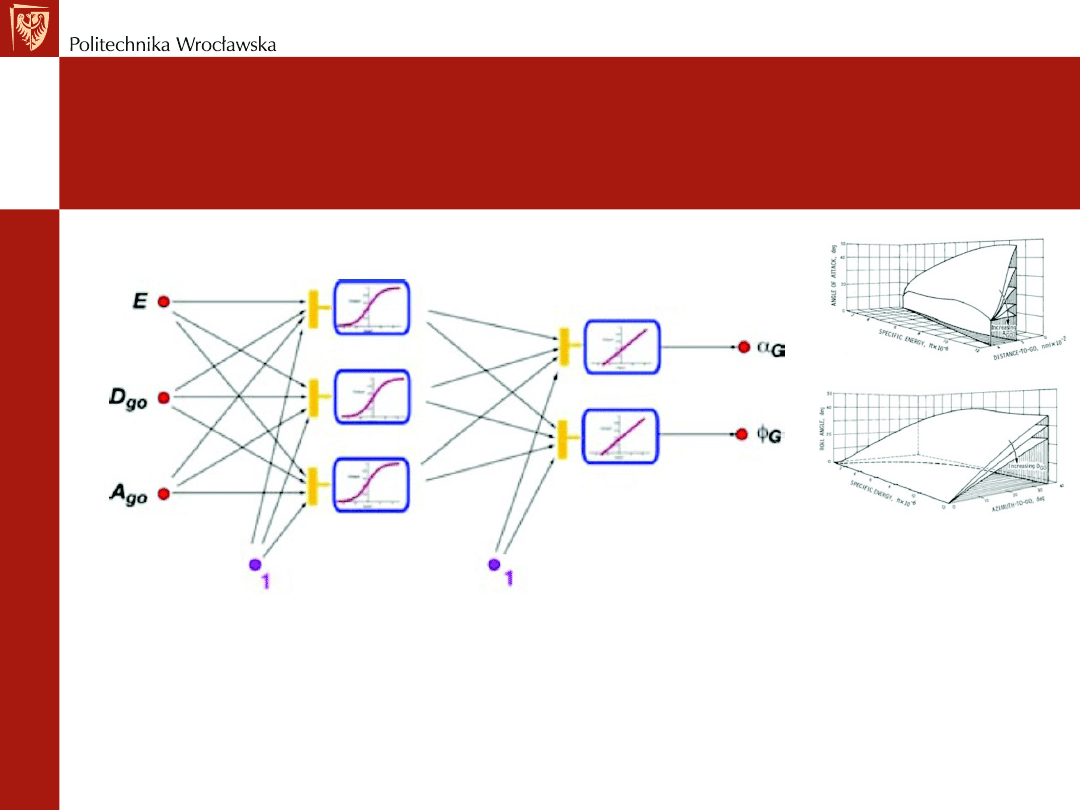
REGULACJA OPTYMALNA

Przykład – sieć neuronowa modelująca funkcje
prowadzące

REGULACJA OPTYMALNA

Przykład – optymalna terapia choroby

Do uzupełnienia

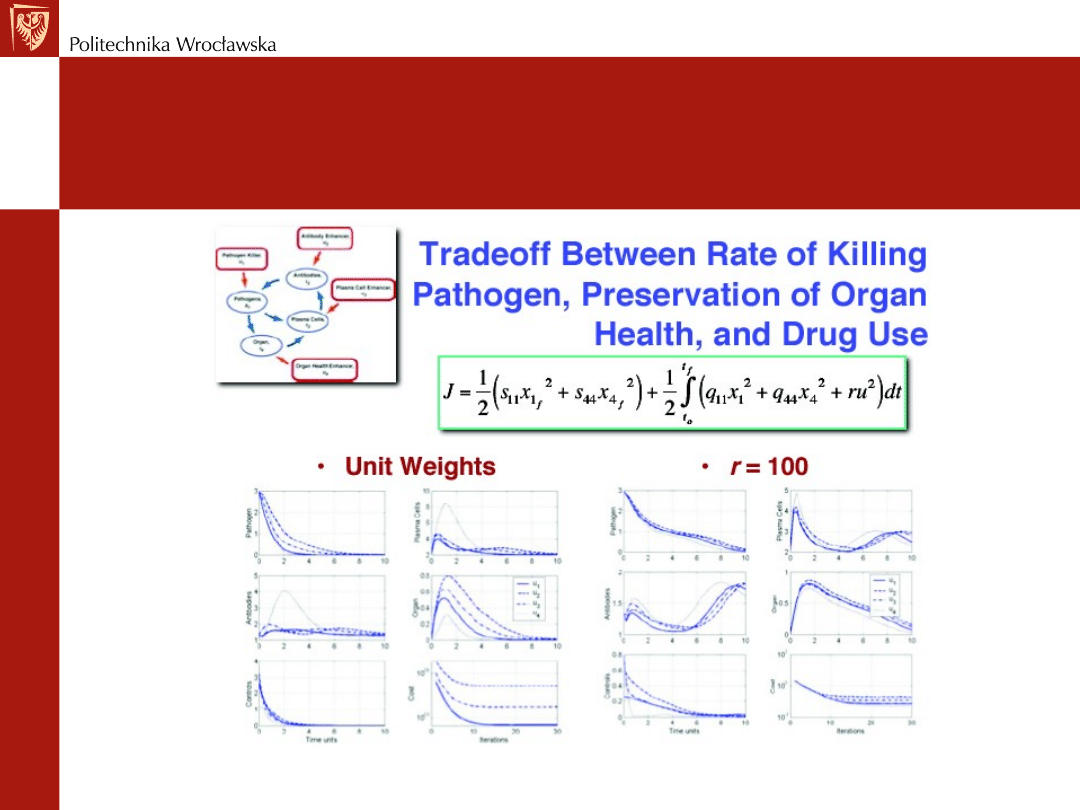
REGULACJA OPTYMALNA

Przykład – optymalna terapia choroby

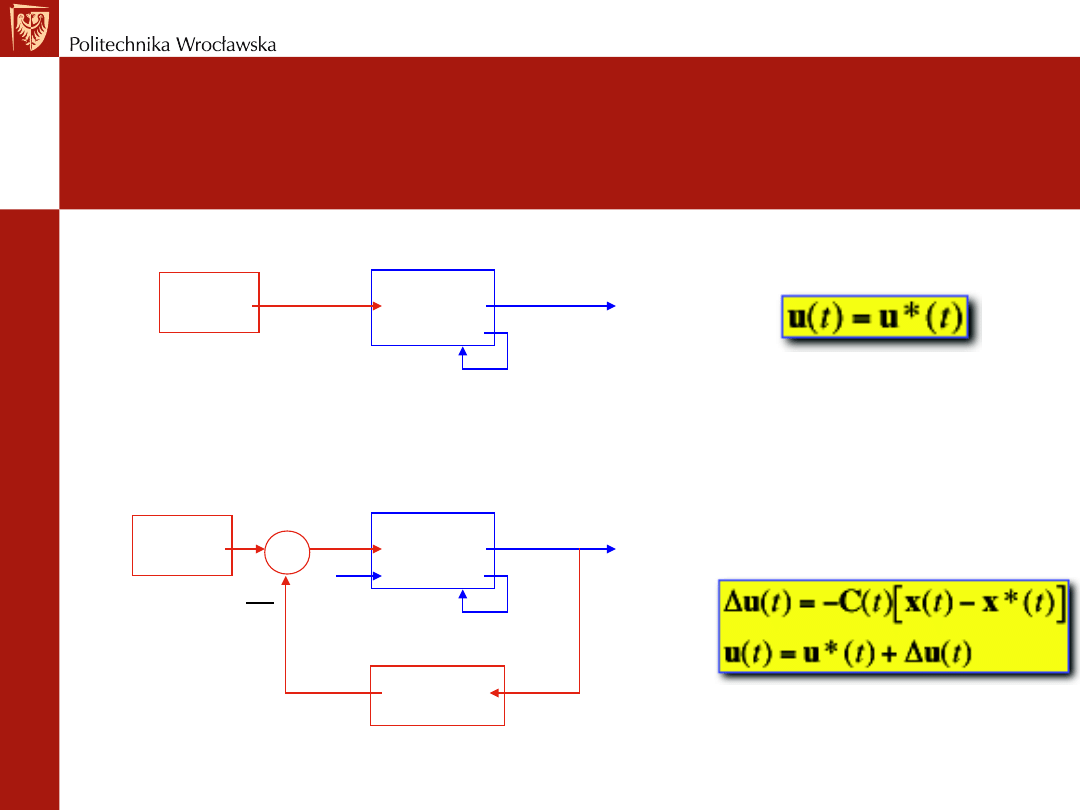
REGULACJA OPTYMALNA

Przykład – optymalna terapia choroby

Sterowanie optymalne może odbywać się w pętli otwartej

Sterowanie sub-optymalne odbywa się w pętli zamkniętej

Optymalny
sygnał
sterujący

Obiekt
dynamiczny
Wektor
Parametrów p

Stan
dynamiczny x

Sygnał wyjściowy y

Sygnał wejściowy u

Optymalny
sygnał
sterujący

Obiekt
dynamiczny
Wektor
Parametrów p

Stan
dynamiczny x

Sygnał wyjściowy y

Sygnał

wejściowy

u

Prawo regulacji
w sprzężeniu
zwrotnym

Zakłócenia w

REGULACJA OPTYMALNA

Przykład – algorytm sub-optymalny terapii
choroby

Rozwinięcie pierwszego rzędu równania dynamicznego,
z uwzględnieniem zakłóceń w

Zlinearyzowane w punkcie pracy, zmienne w czasie, równanie dynamiczne

REGULACJA OPTYMALNA

Przykład – deterministyczny regulator liniowo-
optymalny

Funkcja kosztów

Równania Eulera-Lagrange’a prowadzą do liniowego, zmiennego w czasie, optymalnego prawa regulacji

Równanie Riccatiego dla regulatora

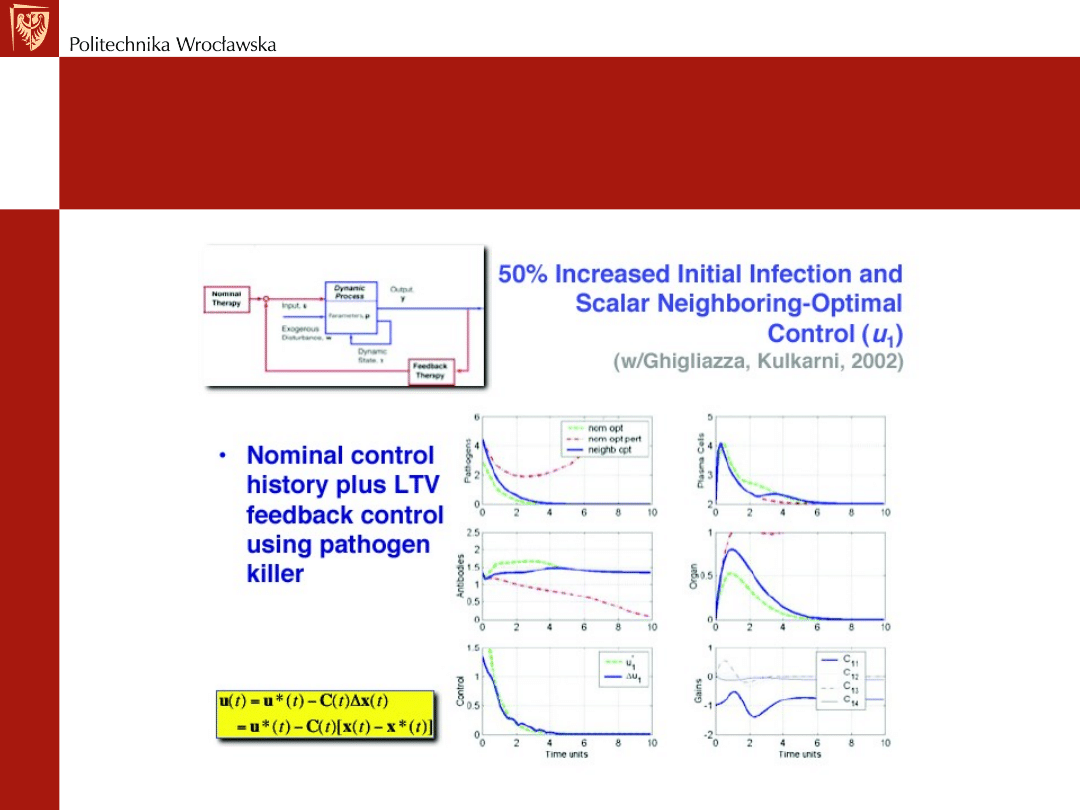
REGULACJA OPTYMALNA

Optymalne i sub-optymalne sterowanie

Dziękuję za uwagę i

zainteresowanie