Rozdział 13

BADANIE WŁASNOŚCI

ODCHYLEŃ LOSOWYCH

Sld.13.2. Badanie własności odchyleń

losowych

Przy szacowaniu parametrów modelu

ekonometrycznego czyni się wiele założeń
dotyczących odchyleń losowych. Czy przyjęcie
tych założeń było słuszne, rozstrzyga się na
etapie weryfikacji modelu. Analiza własności
odchyleń losowych pozwala także na ocenę
trafności doboru postaci analitycznej modelu
oraz zestawu zmiennych objaśniających.

Weryfikacja hipotez jest przeprowadzana

na

podstawie

ciągu

reszt

będących

oszacowaniami odchyleń losowych modelu.

Sld.13.3.

Weryfikacja

hipotezy

Weryfikacja hipotezy o losowości
rozkładu odchyleń losowych modelu
ma na celu ocenę trafności doboru
postaci analitycznej modelu.
Dla uporządkowanego ciągu reszt
oblicza się liczbę serii S reszt
modelu. Serią jest każdy podciąg
reszt

złożonych

wyłącznie

z

elementów dodatnich lub ujemnych.

Sld.13.4. Analiza rozkładu odchyleń

losowych

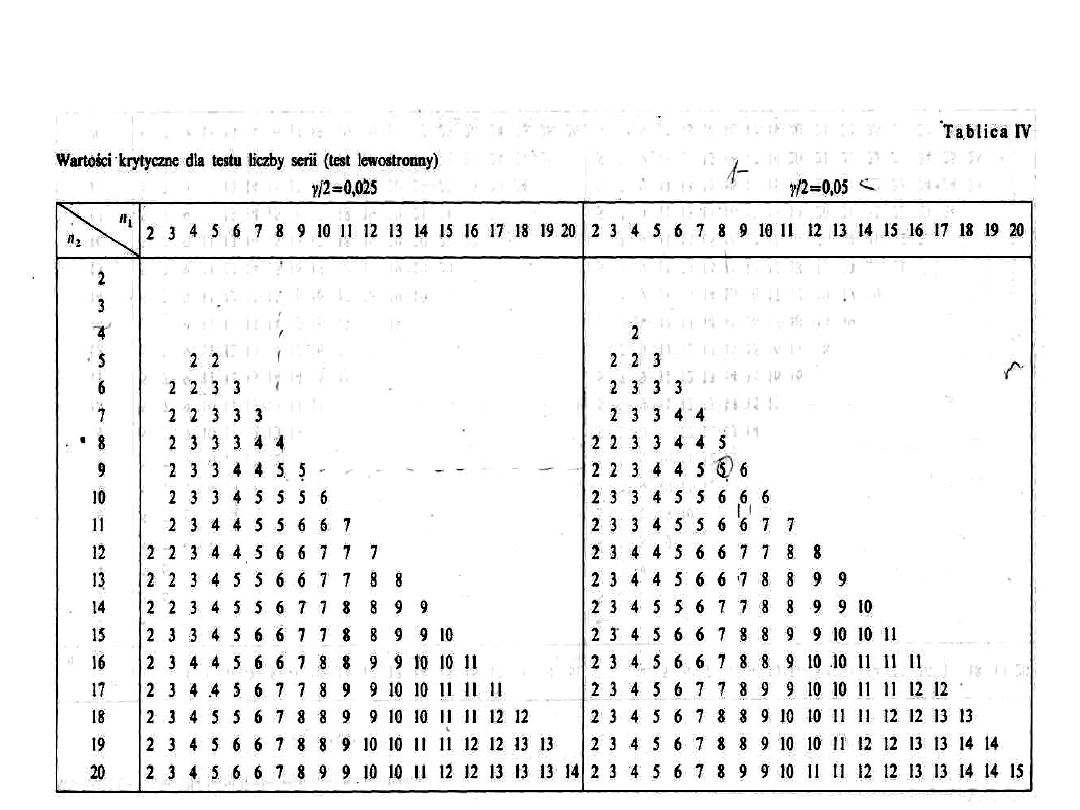
Z tablic testu liczby serii (tablica IV i tablica V)

dla danej liczby reszt dodatnich n

1

liczby reszt

ujemnych n

2

oraz przyjętego poziomu istotności

γ (dla γ/2 i 1- γ/2) odczytuje się dwie krytyczne
liczby serii: S

1

* i S

2

*. Jeśli

S

1

* < S < S

2

* ,

to nie ma podstaw do odrzucenia hipotezy -
postaci analityczną modelu . Oznacza to, że
rozkład odchyleń losowych jest losowy, a postaw
analityczna modelu została dobrana trafnie. Jeśli

S  S

1

* lub S  S

2

*,

to hipotezę należy odrzucić. W tym wypadku
rozkład odchyleń losowych jest nielosowy, a
postać analityczna modelu została dobrana
błędnie.

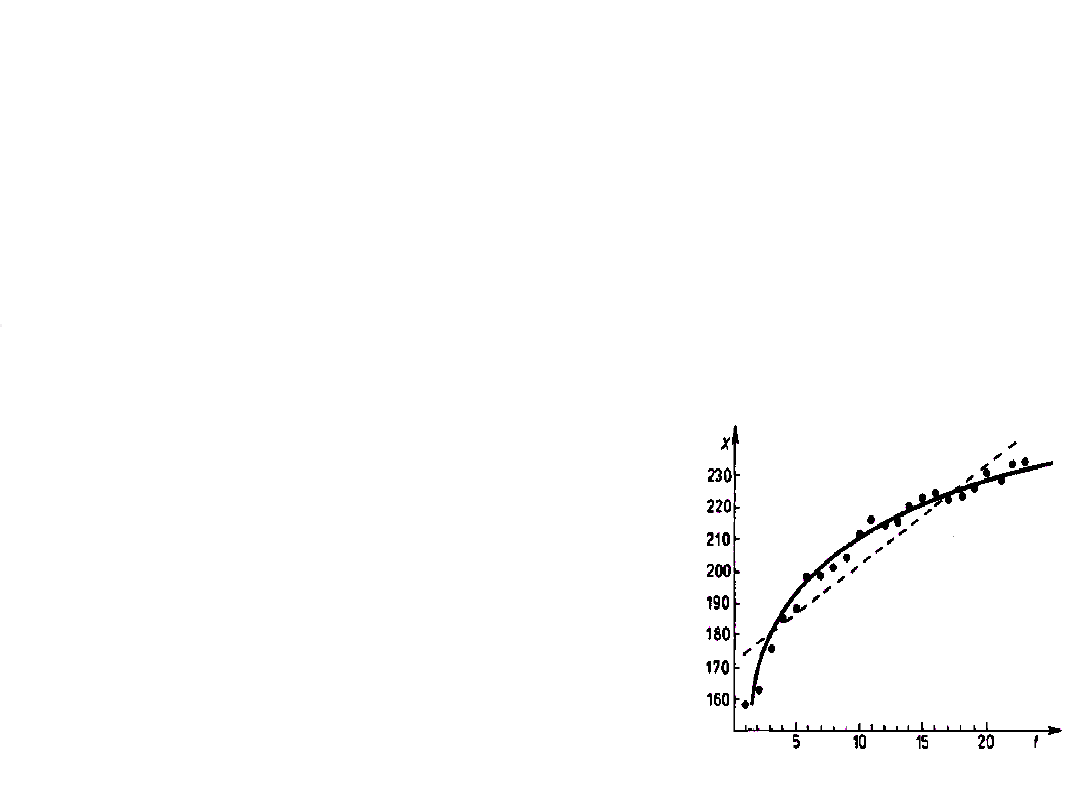
Sld.13.5. Przykład

Produkcja przedsiębiorstwa w tys sztuk X kształtowała się tak,

jak to podaje na rysunku. Do opisu rozwoju produkcji w czasie

zastosowano trend liniowy, który po oszacowaniu parametrów

przyjął postać:

X= 172 + 3,04 t.

Na poziomie istotności y = 0,10 zweryfikujemy hipotezę o

liniowości modelu tendencji rozwojowej produkcji. Reszty

badanego trendu e

t

(l) tworzą S = 3 serie. Dla danych: n

1

= 10, n

2

= 13, γ/2 = 0,05, 1-γ/2 = 0,95 w tablicach testu liczby serii

odnajdujemy wartości krytyczne: S*

1

= 8 i S*

2

= 16. Ponieważ S

< S*

1

hipotezę należy odrzucić. Rozkład odchyleń losowych

modelu nie jest losowy, a więc postać analityczna trendu

produkcji nie jest liniowa.

Zmieniamy postać analityczną modelu

tendencji

rozwojowej

produkcji

i

wyznaczamy

trend

logarytmiczny.

Po

oszacowaniu parametrów otrzymujemy: 

X = 149,73 + 60,3 log t.

Mamy S = 11, n

1

= 10, n

2

= 13. Ponieważ

8<11<16 nie ma podstaw do odrzucenia

hipotezy.

Rozkład

odchyleń

losowych

modelu jest losowy, a trend produkcji jest

trendem logarytmicznym.

 

Wartosci krytyczne dla testu liczby
serii

Wartosci krytyczne dla testu liczby serii

LITERATURA

1.E.Nowak. Zarys metod ekonometrii.

Warszawa 2002