Dr inż. JANUSZ LICHOTA

PODSTAWY AUTOMATYKI

Matlab

Wydział Mechaniczno-
Energetyczny

PLAN WYSTĄPIENIA

• Typowe sygnały wejściowe
• Równania różniczkowe obiektów

– mechanicznych
– elektrycznych
– elektromechanicznych
– silników prądu stałego
– hydraulicznych
– cieplnych
– wniosek

• Uogólnienie poprzez transmitancję – człony

podstawowe

• Linearyzacja równań różniczkowych
• Bonus

2

2

2

40

0 warunki początkowe (0)

20, (0) 0

d x

dx

x

x

x

dt

dt

+

+

=

=-

=

&

BONUS

Rozwiązać równanie różniczkowe przy pomocy programu Matlab

Rozwiązanie

Należy utworzyć dwa pliki. Jeden zawiera definicję równania różniczkowego,
drugi je rozwiązuje.

Rownanie.m – zawiera równanie różniczkowe jako układ równań 1-go rzędu
Rozwiaz.m – zawiera warunki początkowe równania, zakres rozwiązania i

procedurę rozwiązującą równanie

BONUS

function

zDot=diffX(t,z)

%
% równanie o postaci
% m d2x/dt2 + c dx/dt + k x = f(t)
% definicja stałych

m=1;
c=2;
k=40;
f=0;

% pobieranie wartości początkowych ze zmiennej z

x=z(1);
v=z(2);

% rozwiązanie równań różniczkowych 1-go rzędu

xDot=v;
vDot=(f-c*v-k*x)/m;

% i złożenie ich do tablicy (przekazywanie
% parametrów przez zmienną)

zDot=[xDot; vDot];

m=1;

Plik Rownanie.m

Plik Rozwiaz.m

% plik Rozwiaz.m
%
% Służy do rozwiązania równania różniczkowego
% zdefiniowanego w pliku DIFFX.M za pomocą metody zwanej
% ODE45
% Zmienne t0 = chwila początkowa
% tf = chwila końcowa obliczeń
% x0 = wartość początkowa przesunięcia
% v0 = wartość początkowa prędkości

t0=0

% chwila początkowa

tf=10

% chwila końcowa

T=[t0 tf]

% wektor T (poziomy)

x0=-20

% warunek początkowy przesunięcia

v0=0

% warunek początkowy prędkości

z0=[x0; v0]

% wektor z0 (pionowy)

[t,z]=ode45(

'diffX'

,T,z0)

% rozwiązanie znajdzie się w

% zmiennych t oraz z

x=z(:,1)

% ze zmiennej z pobierana jest pierwsza kolumna

v=z(:,2)

% ze zmiennej z pobierana jest druga kolumna

plot(t,x,

'b-'

)

% rysunek funkcji x(t) kolorem niebieskim

% (b-blue) linią ciągłą (-)

xlabel(

‘czas [s]'

)

% opis osi X

ylabel(

'x [m]'

)

% opis osi Y

title(

' model 2-go rzędu'

)

% tytuł wykresu

Grid

% siatka na rysunku

Należy uruchomić plik „rozwiaz”. Pliki powinny być w kartotece „work”

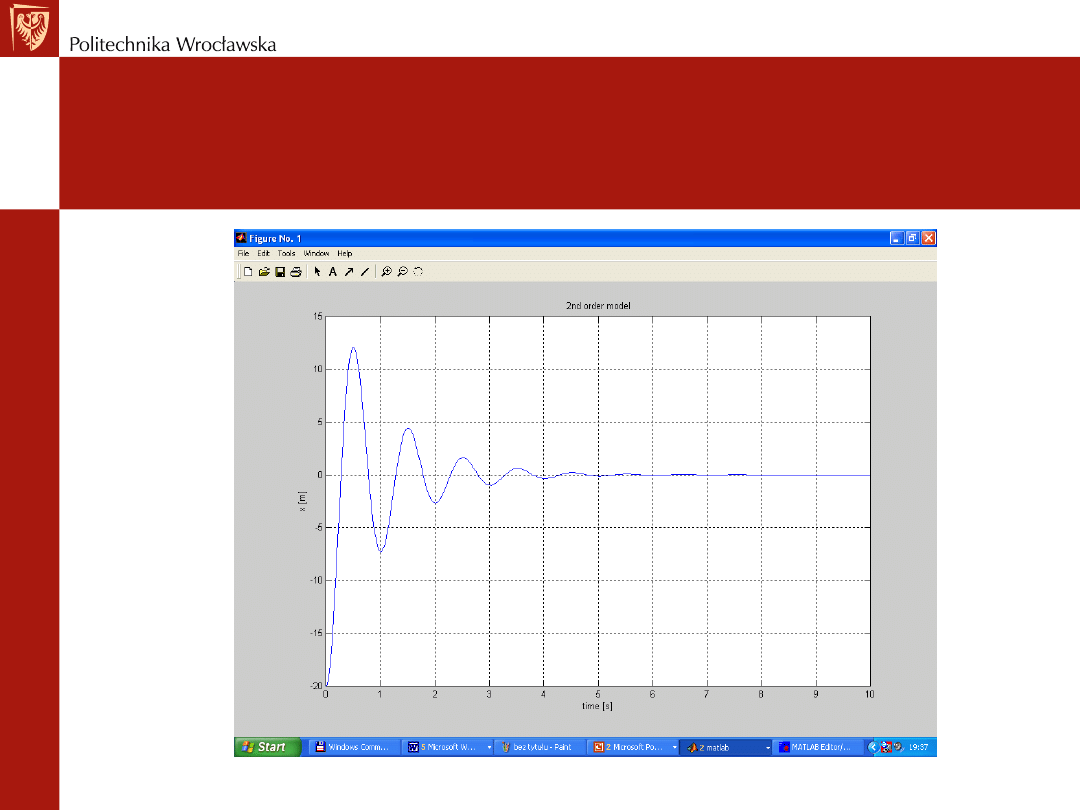
Matlab –

survival dla opornych

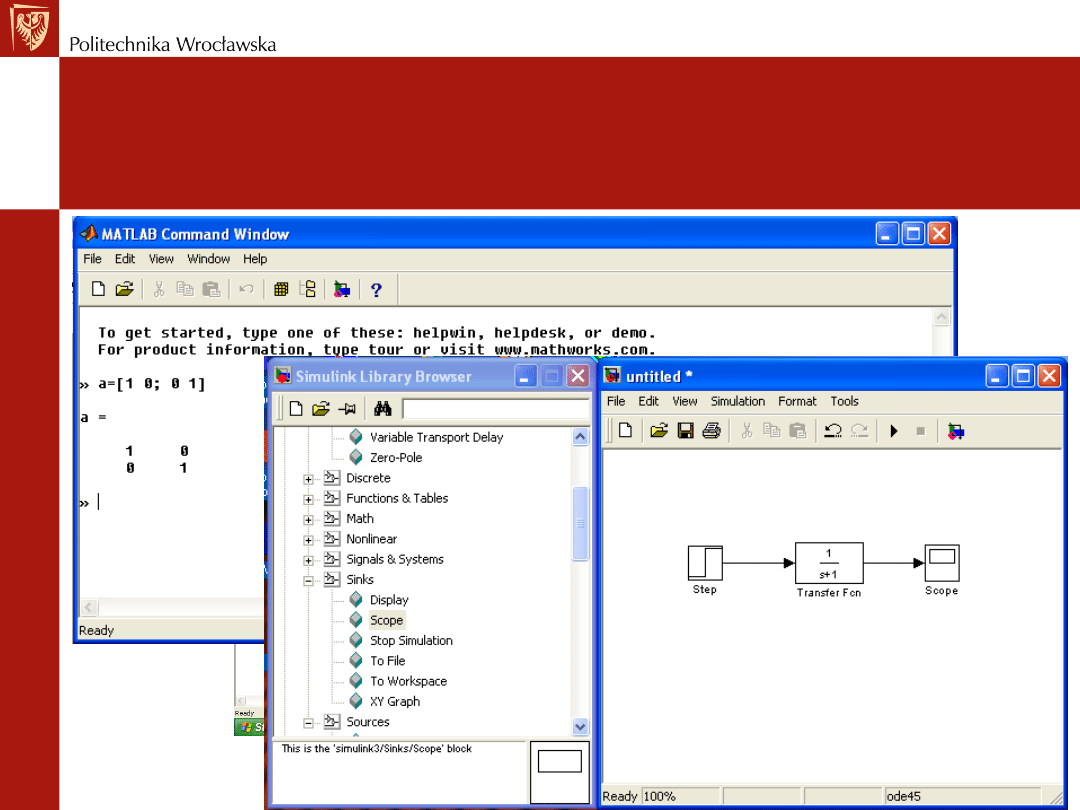
MATLAB
Polecenia systemowe

Kartoteki funkcji

Zestaw funkcji znajduje się
\MATLAB\toolbox\

xxxx\...

(np. matlab\..., simulink\..., compiler\..., fuzzy\...)

yyyy\...

(grupy funkcji)

W każdej kartotece xxxx\yyyy\ jest plik Contents z wykazem funkcji.
Komenda Help i menu pomocy
„help” – podaje wszystkie tematy (topic) w postaci: xxxx\yyyy (gdzie xxxx jest nazwą podkartoteki \MATLAB\toolbox)
„help yyyy” – podaje wszystkie funkcje z danego tematu (każdy temat jest umieszczony w oddzielnej podkartotece a
zestaw funkcji zawarty jest w pliku Contents)
„help nazwa” – wypisuje sposób użycia funkcji – początkowy komentarz z pliku funkcji (nazwa.m)
 
menu Help\Table of contents

(funkcje grupami)

menu Help\Index

(funkcje alfabetycznie)

Pliki i foldery

dir, ls, what

(listowanie wszystkich plików, funkcji)

type

nazwa

(pisz zawartość pliku w oknie)

delete nazwa

(kasuj plik)

cd

(zmień kartotekę)

which, lookfor
Matlabpath

Polecenia dla zmiennych

who, whos

(lista zmiennych z przestrzeni roboczej)

save a1.dat A -ascii

(zapamiętaj tablice A w pliku a1.dat)

load a1.dat

(wczytaj zmienne z pliku a1.dat)

save ses

(wszystkie zmienne robocze do ses.mat)

load ses

(wczytaj z ses.mat)

clear

(wyczyść przestrzeń zmiennych)

MATLAB
Polecenia systemowe

MATLAB
Zmienne i wyrażenia

Nazwy zmiennych
Pierwsza litera, 19 znaków, rozróżnia się duże i małe litery
Typy zmiennych
liczba

i=1, i=3*sin(1)

zmienna zespolona

a=3+2*j, a=3+2*i, a=r*exp(j*alfa), a=3+2i

wektor

a=[1 2 3 4 5]

tablica (macierz)

A=[1 2 0; 2 4 5]

łańcuch

s = ’ala’

Inicjowanie zmiennych w przestrzeni roboczej
Generowanie zmiennych
wprowadzenie listy
A=’ala’; C=1;
B=[11+11j 12+12j; 21+21j 22+22j];
B=[11 12; 21 22] + j * [11 12; 21 22];
wczytanie z pliku (binarny, ASCII)
load
generowanie tablic (wektorów, macierzy) przez funkcje
eye, linspace, logspace, meshgrid, ones, rand, randn, zeros, compan, magic, gallery,...
konstrukcja tablic za pomocą dwukropka (patrz znaki specjalne)
Rezerwacja miejsca w pamięci – zwykle generowanie przez funkcję (zeros, ones, eye)
A=ones(7)

(macierz jedynkowa 7*7)

ala=1:1:7

( [1 2 3 4 5 6 7] )

Odwołania do zmiennych
pojedyncze elementy tablic
B(1,2) – wiersz 1, kolumna 2
b) wybór wierszy i kolumn – patrz znaki specjalne - dwukropek
b) wielkość tablic i macierzy
ile = size(tablica) -> ile(1) – ilość wierszy, ile(2) – ilość kolumny
Nazwy specjalne

ans

zmienna robocza

computer
eps

dokładność obliczeń

flops

licznik operacji zmiennoprzecinkowej

i,j

jednostka urojona

Inf

nieskończoność

NaN

wartość nieokreślona

nargin

ilość argumentów wejściowych funkcji

nargout

ilość argumentów wyjściowych funkcji

pi

liczba 

realmax
realmin
clock
cputime
date
etime
tic,toc

MATLAB
Operatory

dodawanie,
odejmowanie

+, -

 

mnożenie,
potengowanie

*, ^

.*, .^

dzielenie prawo- i
lewostronne

/, \

./ , .\

sprzężenie i
transpozycja

‘,’

 

iloczyn tesorowy
Kronecker’a

kron

 

relacje

<, <=, >, >=,
==, ~=,

 

operacje logiczne

&, |, ~, xor

 

Lista znaków
=

przypisanie

[ ]

wektor, macierz

()

kolejność obliczeń

.

niejawna indeksacja wektorów i macierzy

..

katalog macierzysty (DOS)

...

kontynuacja w następnej linii

,

separacja indeksów, argumentów, poleceń

;

koniec wiersza macierzy; wstrzymanie wypisania odpowiedzi (brak echa)

:

generowanie wektorów, indeksowanie macierzy, wprowadzanie łańcuchów,

‘ , ’

transpozycja/sprzeżenie macierzy

%

komentarz

!

komenda SO

Średnik – przykłady
a) wprowadzanie macierzy, np. 2 wiersze, 3 kolumny -> a1=[1 2 3;1 2 3]
Dwukropek - przykłady
generowanie wektorów
j : k

=> [j, j+1, ..., k]

(przyrost o 1)

j : i : k

=> [j, j+1i, j+2i, ..., k]

(przyrost o i)

 
wybór żądanych wierszy, kolumn, elementów
A( : , j)

j-ta komuna

A( : , j:k)

kolumny A(j), A(j+1), ..., A(k)

A( i, : )

i-ty wiersz

A( : )

wszystkie elementy macierzy wypisane w jednej kolumnie

A( j:k)

elementy od j do k wypisane w jednym wierszu

A( : , [2,3]) = A( : , 2:3 )

Podstawowe funkcje matematyczne

abs, sqrt, round, fix, sign, rem, exp, log, log10
angle real, imag, conj
sin, cos, tan, asin acos, atan, atan2, sinh, cosh, tanh, asinh, acosh, atanh

- (kąt w radianach)

np. cos(2*pi-t)

MATLAB
Funkcje matematyczne

Grafika - wykresy
Okno wykresów
[nr =] figure

– otwórz nowe okno [i zapamiętaj jego numer]

figure(nr)

– uaktywnij wskazane okno

Wykresy 2-D
plot

– wykres liniowy

loglog

– wykres w skali podwójnie logarytmicznej o podstawie log

10

semilogx

– wykres w skali półlogarytmicznej (na osi x)

semilogy

– wykres w skali półlogarytmicznej (na osi y)

polar

– wykres biegunowy

 
plot(y), plot(x, y), plot(x, y, ’typ_linii’), plot(x1, y1, ’typ1’, x2, y2, ’typ2’,..)
gdzie

x, y

– wektory N-elementowe lub macierze N*M

typ_linii = np.’r:’ (czerwona kropkowana):

y – żółty, m – magenta, c – cyan, r – red, g – green, b – blue, w – white, k – black

. – punkt, o – okrąg, x,+,* – znaki, – – ciągła, : – punktowa,–.,– –

Wykresy 3-D
meshgrid(x1:dx:x2, y1:dy:y2)

– tworzenie dziedziny funkcji w postaci par liczb [x,y] (meshdom dla v.4)

mesh(z)

– wykres siatkowy 3-D nad dziedziną [x,y]

surf(z)

– wykres powierzchniowy

waterfall

– wodospad

 
mesh(z), mesh(z,[kąt,obrót], mesh(z, [kąt, obrót], [sx, sy,sz])
gdzie:

[kąt,obrót] – kąt prawo-lewo, obrót góra-dół
[sx,sy,sz] – skalowanie osi

Inne wykresy
fplot

– wykres funkcji ciągłej

bar

– wykres słupkowy na podstawie elementów wektorów

stairs

– jw. ale bez linii wewnętrznych

 
contour

– wykres konturowy (izolinie, „mapa z poziomicami”)

contour3

– wykres konturowy 3D

slice

– wykres plasterkowy

plot3(x, y, z)

– wykres krzywej w przestrzeni

pcolor

– wykres pseudokolorowy

quivier

– linie pola

fill3

– wielokąt

 
meshc, meshz

– wykres siatkowo-konturowy i siatkowy na płycie

surfc

– wykres powierzchniowo-konturowy i podświetlany

 
hist, rose,
fill,
stem, compass, feather, errorbar,
Edycja wykresu
axis([xmin,xmax,ymin,ymax])

– skalowanieosi x i y

ylabel(‘opis osi y’)
xlabel(‘opis osi x’)
title(‘tytul wykresu’)
text(xa,ya,napisa)

– na pozycji xa, ya wyświetla napisa

grid on, grid of

– włącz /wyłącz siatę na wykresie

hold on, hold of

– włącz / wyłącz czyszczenie wykresy w oknie

subplot(xm,ym,i)

– dzieli okno na xm wierszy i ym kolumn i wybiera i-ty wycinek

view(kąt, obrót)

– zmienia punkt widzenia (obrót= punkt widzenia góra dół)

legend

clg

– wyczyść okno

MATLAB
Grafika

Konstrukcje języka Matlab
Słowa kluczowe
catch, continue, break, else, elseif, end, error, for, if, return, switch, try, while
Pętla for

for indeks=poczatek:przyrost:koniec
instrukcje
end

for i = 1:n,
for j = 1:n,
A(i,j) = 1/(i+j-1);
end
end

Przerwanie pętli: break, przeskok do następnej pętli: continue
 
Pętla while

while wyrażenie
instrukcje
end

while i<10, i=i+1; a=a+2; end

Przerwanie pętli: break, przeskok do następnej pętli: continue
 
Warunek if

if warunek logiczny
instrukcje
end
if warunek_logiczny1
instrukcje1
elseif warunek_logiczny2
instrukcje2
else
instrukcje3
end

if i == j
A(i,j) = 2;
elseif ABS(i-j) == 1
A(i,j) = -1;
else
A(i,j) = 0;
end
 
if i==j, A(i,j)=2; else A(i,j)=0; end

MATLAB
Pętle

Funkcje wewnętrzne (wbudowane)
Wszystkie polecenia systemowe, np. clear, what, save,...
Funkcje zewnętrzne (dyskowe), tzw. M-pliki
Funkcje zewnętrzne występują w postaci plików tekstowych z rozszerzeniem *.m. Listę funkcji w danym katalogu można zobaczyć przez
polecenie: help katalog
Skrypty
Skrypty (pliki sterujące) działają na zmiennych globalnych.
Wywoływane są przez nazwę (bez argumentów).
Tworzone są najczęściej przez użytkownika:
przy pomocy zewnętrznego edytora plików tekstowych
przy pomocy polecenia diary (diary nazwa, diary of, diary on)
Funkcje
Funkcje działają na zmiennych lokalnych.
Zwykle są wywoływane przez nazwę z argumentami. np. gear(‘model’,10,[0 1 2])
Mogą być wywoływane z lewostronnym zdefiniowaniem wielkości oddawanych, np. [t]=gear(‘cos’,10,[0 1 2])
Tworzone przy pomocy zewnętrznego edytora (patrz Tworzenie własnych funkcji)
Tworzenie własnych funkcji

Inicjacja pracy:
input

- np. a=input(‘Podaj a ’)

keyboard,
menu,
pause

Polecenia:

eval

- wykonaj lancuch polecen matlab

feval

- wykonaj funkcje zapisana jako lancuch

global

- def zm.globalnych

nargchk

- okreslenie liczby parametrow funkcji

 
Nazwa pliku taka sama jak nazwa funkcji
function [lista arg wy] = nazwa fun. ( lista arg we)
 
np.:
M.-plik „ldata.m”:
function [x1,x2,x4] = ldata(fstr,n,ptr)
 
Wywołanie:
[a1, a2, a3] = ldata(‘leq’, 3, pscr)

MATLAB
Funkcje

Algorytmy całkowania Simulink’a
Dostępne metody Matlab4.2:
RK23, RK45, GEAR, EULER, LINSIM, SFUNC, DSFUNC, TRIM, LINMOD
ODE23, ODE45,
Patrz przykład odedemo (porownanie metod ode23 i ode45 z różnym krokiem)
 
Dostępne metody Matlab 5:
 
ODE15S Solve stif diferential equations, variable order method.
ODE23S Solve stif diferential equations, low order method.
ODE23TB Solve stif diferential equations, low order method.
ODE23T Solve moderately stif diferential equations, trapezoidal rule.
 
ODE23 Solve non-stif diferential equations, low order method.
ODE45 Solve non-stif diferential equations, medium order method.
ODE113 Solve non-stif diferential equations, variable order method.
 
ODE23S also solves problems M*y' = F(t,y) with a constant mass matrix M that is nonsingular and (usually) parse. Use ODESET to set
MassConstant 'on' if the ODE file is coded so that F([],[],'mass') returns a constant mass matrix M (see FEM2ODE).
 
ODE23T also solves problems M(t)*y' = F(t,y) with a mass matrix M(t) that is nonsingular and (usually) sparse. Use ODESET to set Mass 'on'
if the ODE file is coded so that F(T,[],'mass') returns M(T) (see FEM1ODE). Set MassConstant 'on' if F(T,[],'mass') returns a constant M.
 
ODE23TB also solves problems M(t)*y' = F(t,y) with a mass matrix M(t) that is nonsingular and (usually) sparse. Use ODESET to set Mass
'on' if the ODE file is coded so that F(T,[],'mass') returns M(T) (see FEM1ODE). Set MassConstant 'on' if F(T,[],'mass') returns a constant M.
 
Dla metod ODE15S, ODE23S, ODE23TB:
The Jacobian matrix dF/dy is critical to reliability and efficiency. Use ODESET to set JConstant 'on' if dF/dy is constant. Set Vectorized 'on' if
the ODE file is coded so that F(T,[Y1 Y2 ...]) returns [F(T,Y1) F(T,Y2) ...]. Set JPattern 'on' if dF/dy is a sparse matrix and the ODE file is coded
so that F([],[],'jpattern') returns a sparsity pattern matrix of 1's and 0's showing the nonzeros of dF/dy. Set Jacobian 'on' if the ODE file is
coded so that F(T,Y,'jacobian') returns dF/dy.
 

MATLAB
Algorytmy całkowania

Dziękuję za uwagę i

zainteresowanie