OCHRONA
KRYPTOGRAFICZNA

Data Encryption Standard – DES
Advanced Encryption Standard -
AES

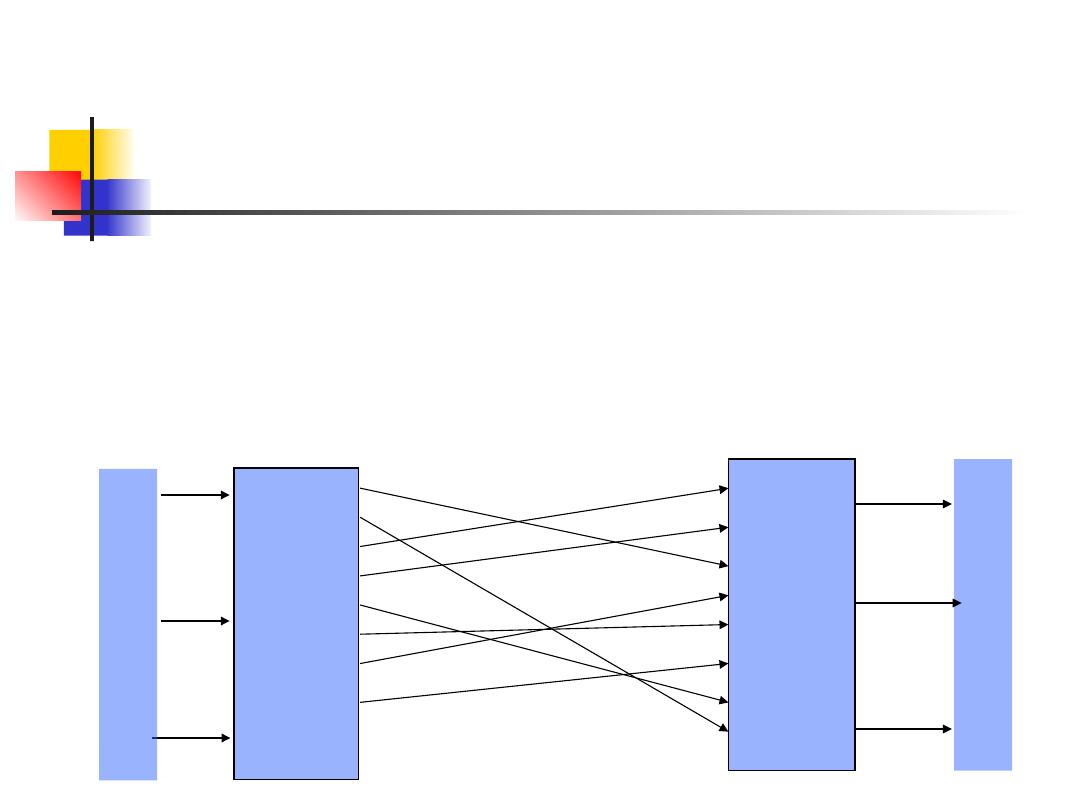
Teoria idealnej szyfracji

T

ra

n

sf

o

rm

a

c

je

b

in

a

rn

e

w

o

k

ta

ln

e

0

1

1

T

ra

n

sf

o

rm

a

c

je

o

k

ta

ln

e

w

b

in

a

rn

e

1

1

0

Shannon (1940) – nieskończony klucz, konfuzja i dyfuzja

Konfuzja (1)
Ma za zadanie tak poprzestawiać symbole, aby maksymalnie
utrudnić wnioskowanie o kluczu na podstawie tekstu otwartego.
Pomocne okazują się w tym zakresie substytucje nieliniowe,
rysunek i relacje T(a+b) -verte

 

Teoria Shannona – c.d.

Konfuzja (2)

C=T(a)+T(b), C’=T(a+b)

gdzie T – operator (tablica); a, b – sygnały wejściowe; C, C’ – ich odpowiedniki
wyjściowe;
Przykład:

C=T(001)+T(010)=111+000=111

C’=T(001+010)=T(011)=110 CC’

Dyfuzja
Ma za zadanie likwidować różnice statystyczne między symbolami i ich
kombinacjami. Można to zrobić drogą przetworzenia symboli symboli X

n

w Y

n

(tzw. wygładzanie)













1

0

24

.

),

mod(

s

i

i

n

n

s

np

s

X

Y

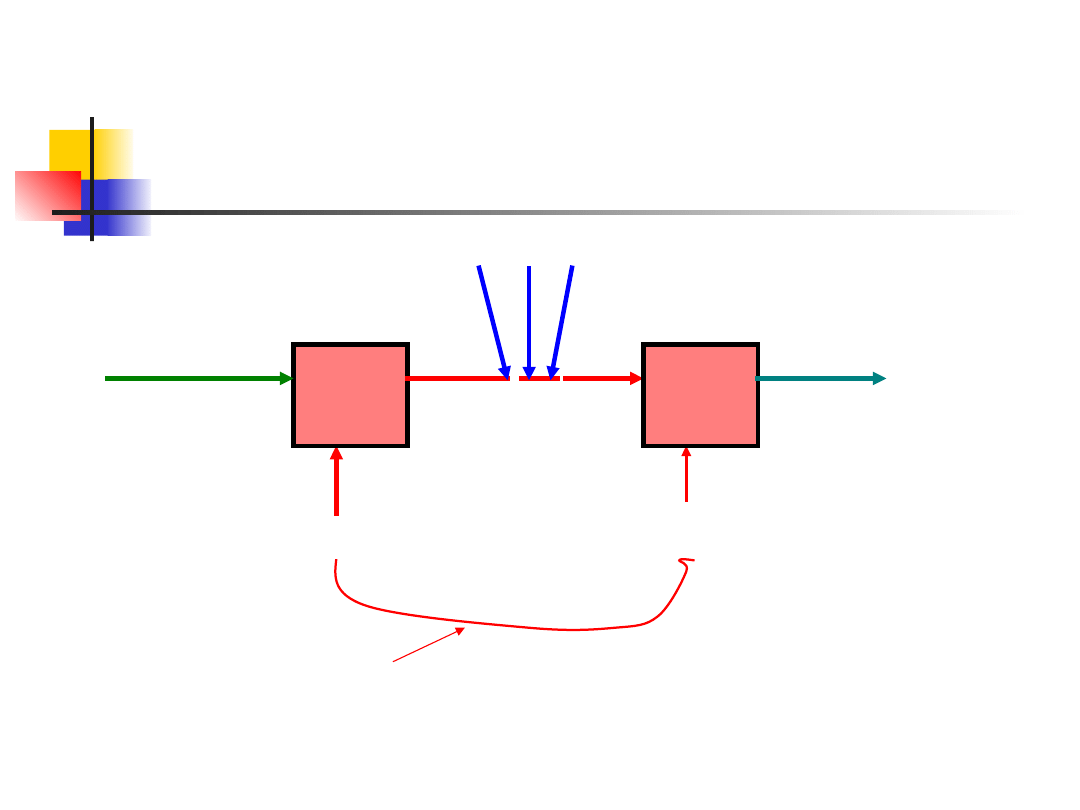
DES – schemat podstawowy

Dane 64 bity Klucz 56 Kanał 64 bity Klucz 56 Dane
rozszyfrowane

Kanał
tajny

DES

DES

Atak

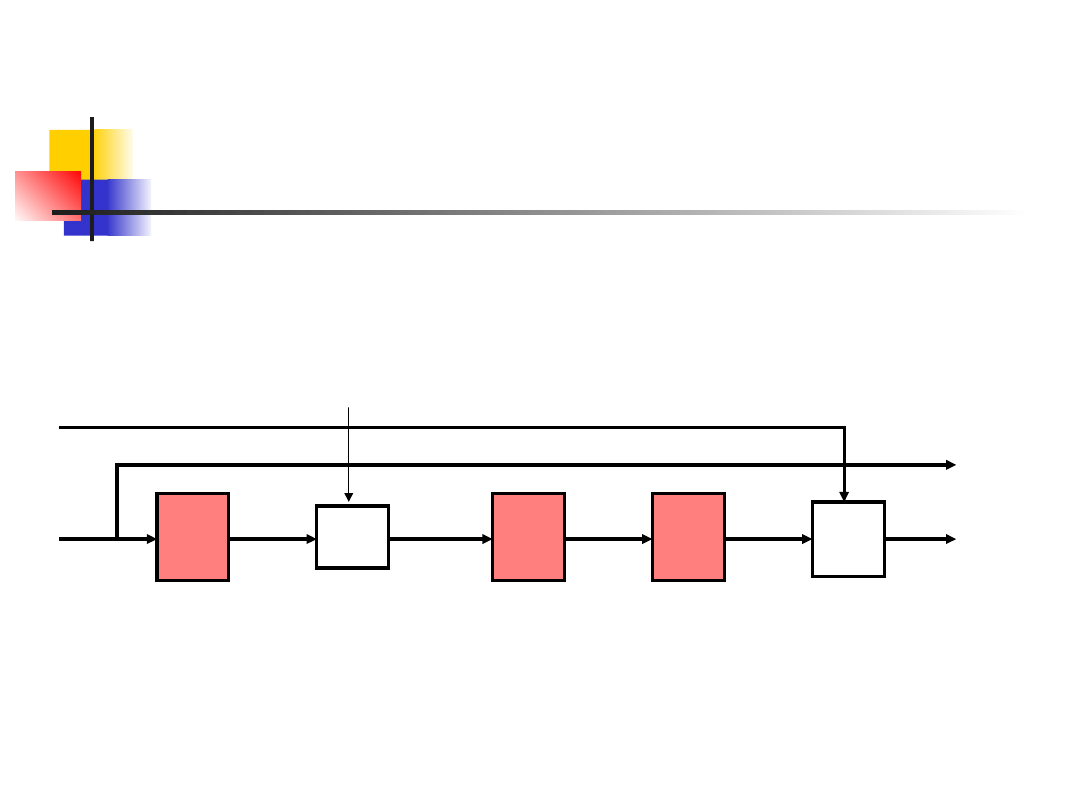
DES – moduł podstawowy

R

i-1

32 bity

48b 48b 32b 32b

R

i

32b

L

i-1

32 bity Klucz - 48b

L

i

32b

+

+

S

P

E

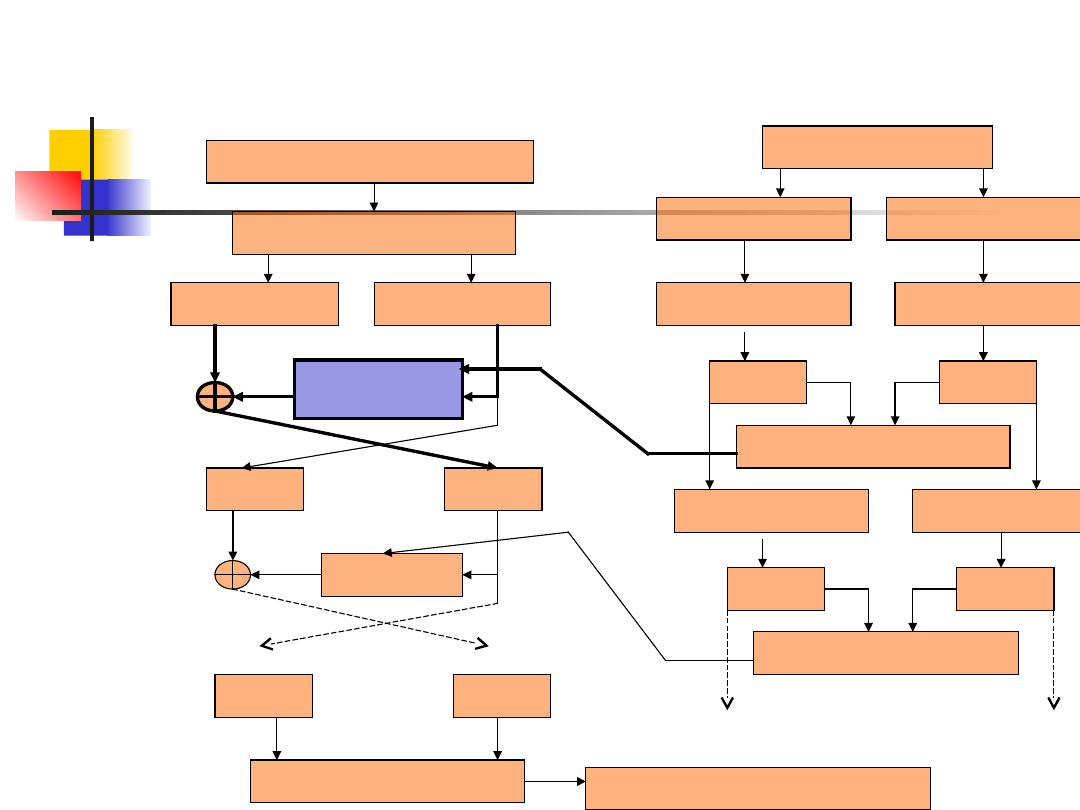
Algorytm

Tekst jawny 64 bity

Wstępna
permutacja

R

0

32 bity

L

0

32 bity

f(R

0

,

K

1

)

R

1

L

1

f(R

1

,K

2

)

Klucz 56 bitów

D

0

28 bitów

C

0

28 bitów

D

1

C

1

Przesunięci
e

Przesunięci
e

Permutacja

D

2

C

2

Przesunięci
e

Przesunięci
e

Permutacja

L

16

R

16

Finalna
permutacja

Tekst zaszyfrowany
64b

48b

David KAHN

Łamacze szyfrów

WNT 2004

Digital Communications

Fundamentals and Applications

C

hapter 14: Encryption and Decryption

Bernard SKLAR (UC), Prentice Hall 2001
(pp.890-944)