PODSTAWY
KONSTRUKCJI
MASZYN
Połączenia gwintowe
Opracował: dr hab. inż. Józef Salwiński prof.
n.

Rodzaje gwintów
Rozkład sił na gwincie
Sprawność i samohamowność gwintu
Przypadki obciążeń śrubowych
G
Momenty Tarcia
Uszkodzenia Gwintów
Wstęp

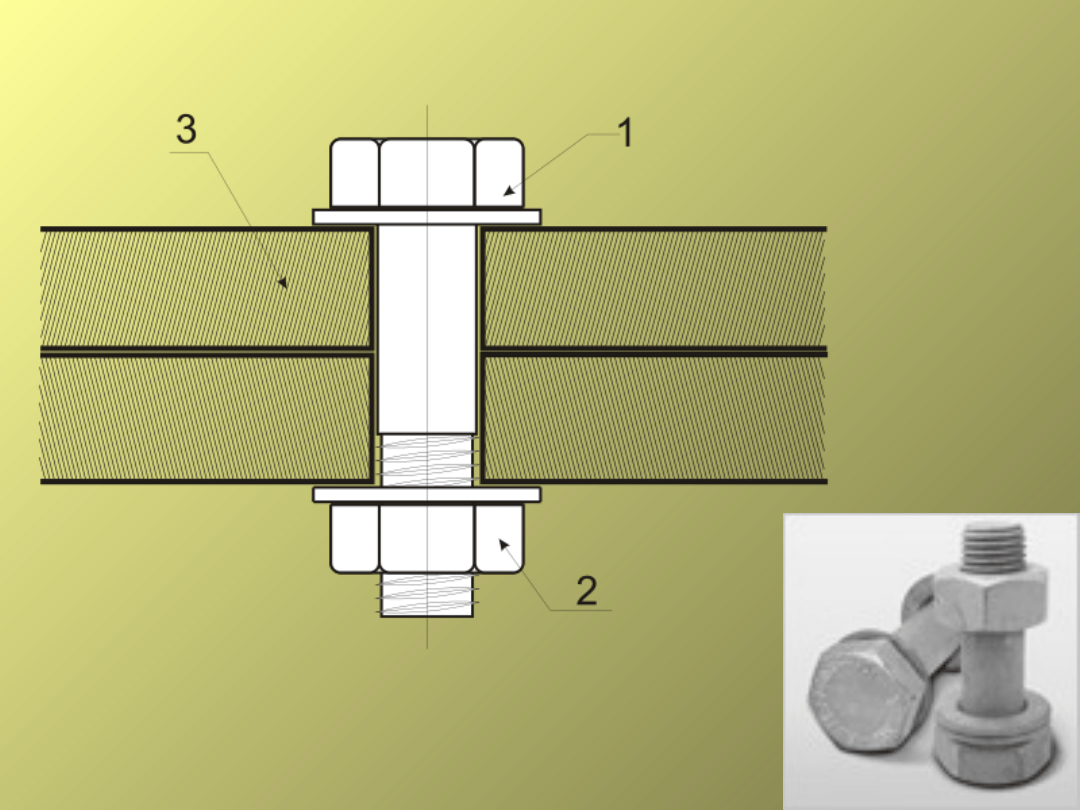
Pośrednie
- części maszyn łączy się za pomocą łącznika
składającego się ze śruby i nakrętki. Rolę nakrętki może
również spełniać gwintowany otwór w jednej z części.
Skręcenie śruby z nakrętką, tworzy połączenie śrubowe
Bezpośrednie
– gwint jest wykonany na łączonych częściach,
połączenie powstaje przez wkręcenie elementu z gwintem
zewnętrznym w otwór z gwintem wewnętrznym
Połączenia gwintowe
podział
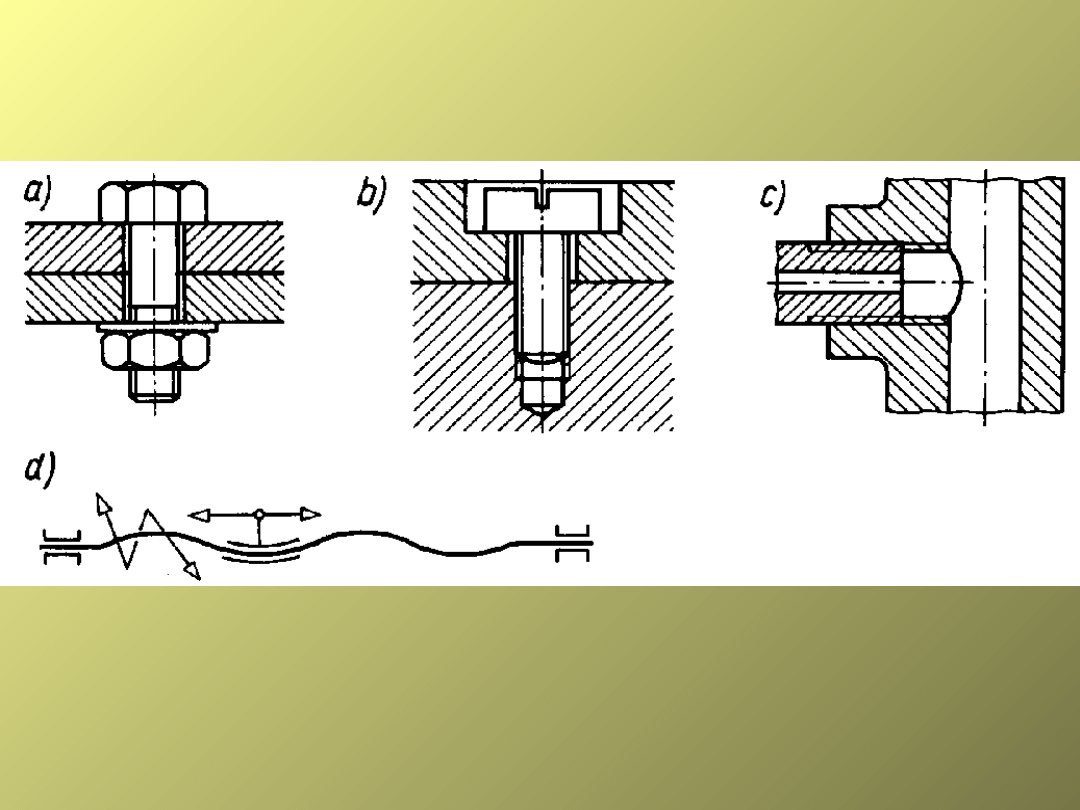
Połączenia gwintowe: a, b) pośrednie, c) bezpośrednie,
d) schemat mechanizmu śrubowego
Połączenia gwintowe
podział

Połączenia gwintowe mogą być:
połączeniami spoczynkowymi,
połączeniami ruchowymi.
Połączenia gwintowe
Gwint
Gwint
uzyskuje się przez wykonanie na powierzchni walcowej
lub stożkowej jednego lub kilku śrubowych rowków o
określonym kształcie. Powstałe występy oraz bruzdy,
obserwowane w płaszczyźnie przechodzącej przez oś
gwintu tworzą zarys gwintu
Połączenia gwintowe
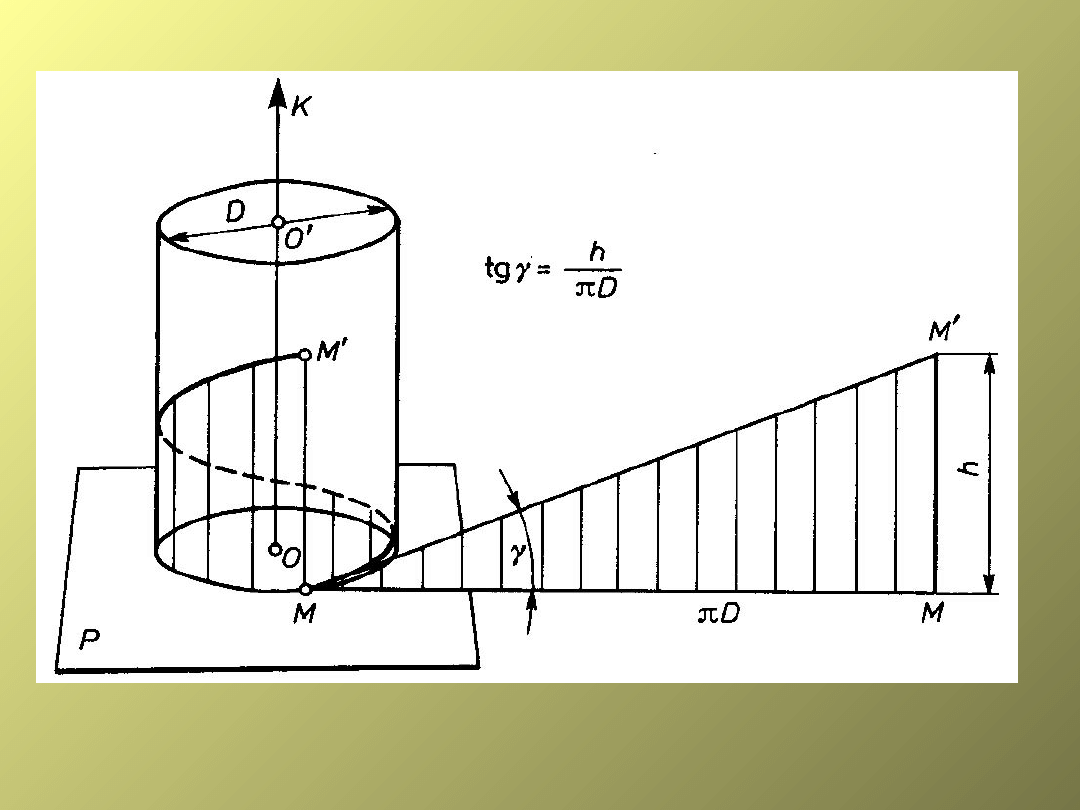
Powstawanie linii śrubowej

Połączenia gwintowe
Linią śrubową – nazywamy krzywą przestrzenną opisaną
na pobocznicy walca przez punkt poruszający się ruchem
jednostajnym wzdłuż osi walca (osi linii śrubowej) – przy
stałej prędkości obrotowej walca.
Linia śrubowa może być:
prawą lub lewą.
Linię śrubowa charakteryzuje
h – skok linii śrubowej - odcinek M – M’,
- kat wzniosu linii śrubowej.

Połączenia
gwintowe
zarys gwintu
W zależności od zarysu gwintu rozróżnia
się gwinty:
trójkątne,
trapezowe symetryczne,
trapezowe niesymetryczne.
prostokątne,
okrągłe.

Podziałką gwintu h
z
(P) nazywa się odległość
sąsiednich zarysów mierzoną wzdłuż osi gwintu
Skokiem gwintu h nazywa się przesunięcie
zarysu zwoju, wzdłuż osi po pełnym jego obrocie
h = h
z
gwint jednokrotny
h # h
z
gwint wielokrotny
Parametry gwintów
Połączenia gwintowe
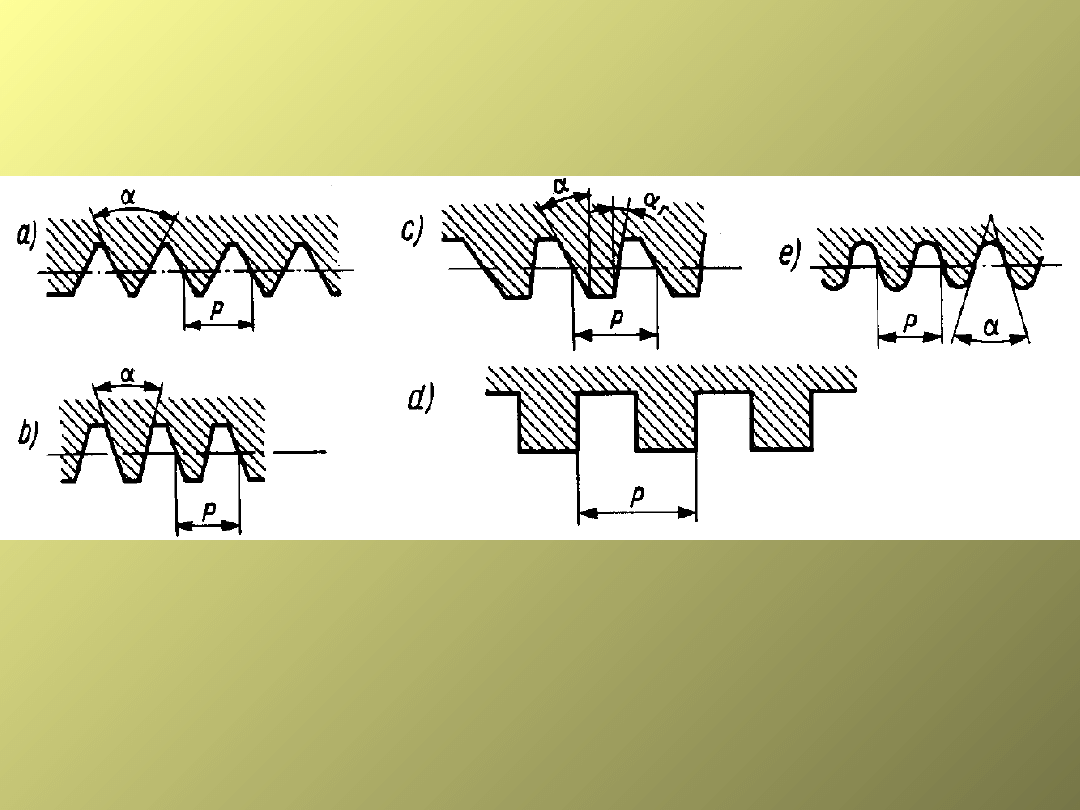
Zarysy gwintu:
a) trójkątny, b) trapezowy symetryczny,
b) c) trapezowy niesymetryczny, d) prostokątny, e)
okrągły
Połączenia
gwintowe
zarysy gwintów i ich
zastosowanie

Połączenia
gwintowe
sposób
wykonania
gwintów
Do nacinania gwintów zewnętrznych
używa się narzynek, głowic
gwinciarskich lub specjalnych
frezów.Gwinty zewnętrzne wykonuje
się również metodą walcowania.
Do wykonywania gwintów
wewnętrznych służą gwintowniki.
Gwinty można także wykonywać
metodami obróbki plastycznej i
odlewniczymi. Gwinty zarówno
wewnętrzne jak i zewnętrzne o
różnych średnicach nacina się
również na tokarkach.

Połączenia
gwintowe
sposób
wykonania
gwintów


Łączniki
gwintowe
elementy
ŚRUBY KATALOGOWE
Łączniki
gwintowe
elementy
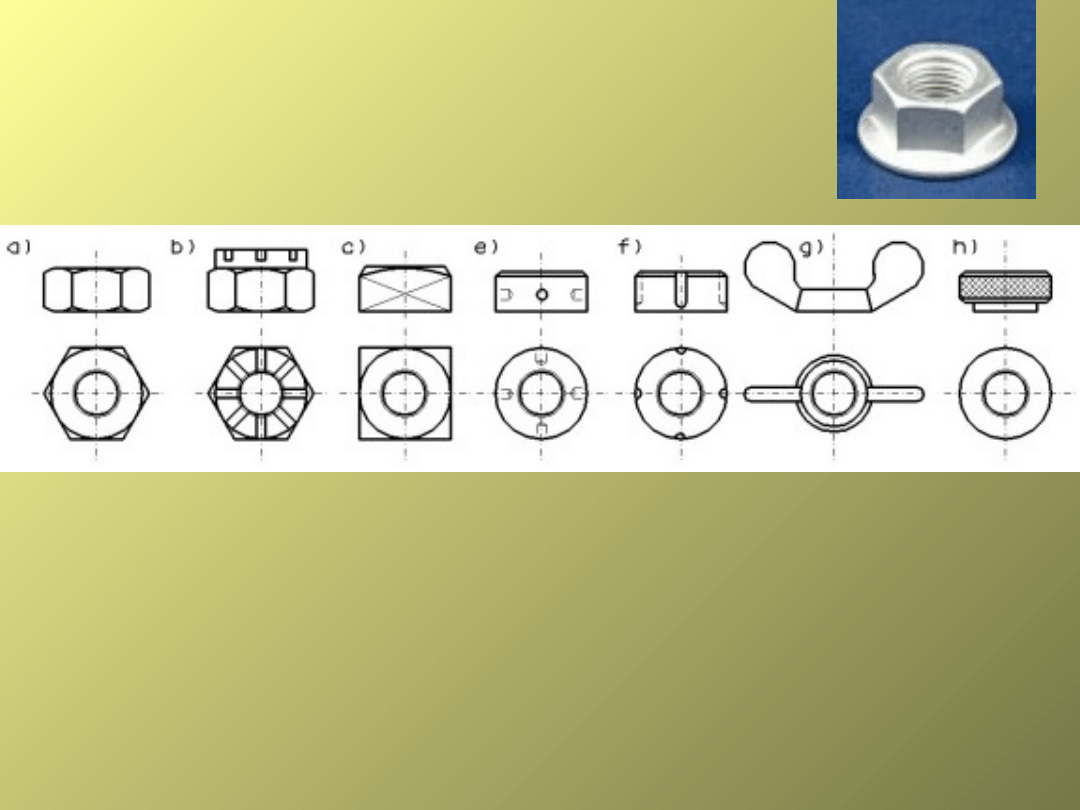
Ze względu na kształt nakrętki można
podzielić na:
a) sześciokątne, b) koronowe, c)
czworokątne
e) okrągłe otworowe, f) okrągłe rowkowe
g) skrzydełkowe, h) radełkowe

Łączniki
gwintowe
elementy
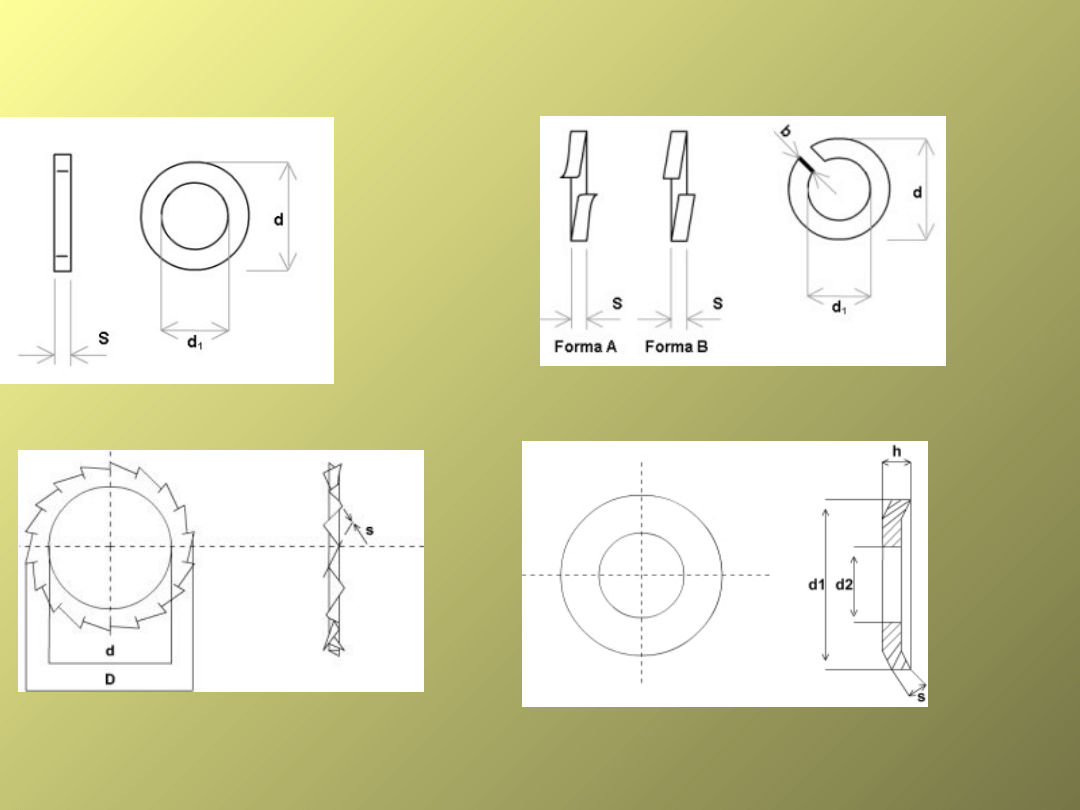
Łączniki
gwintowe
elementy
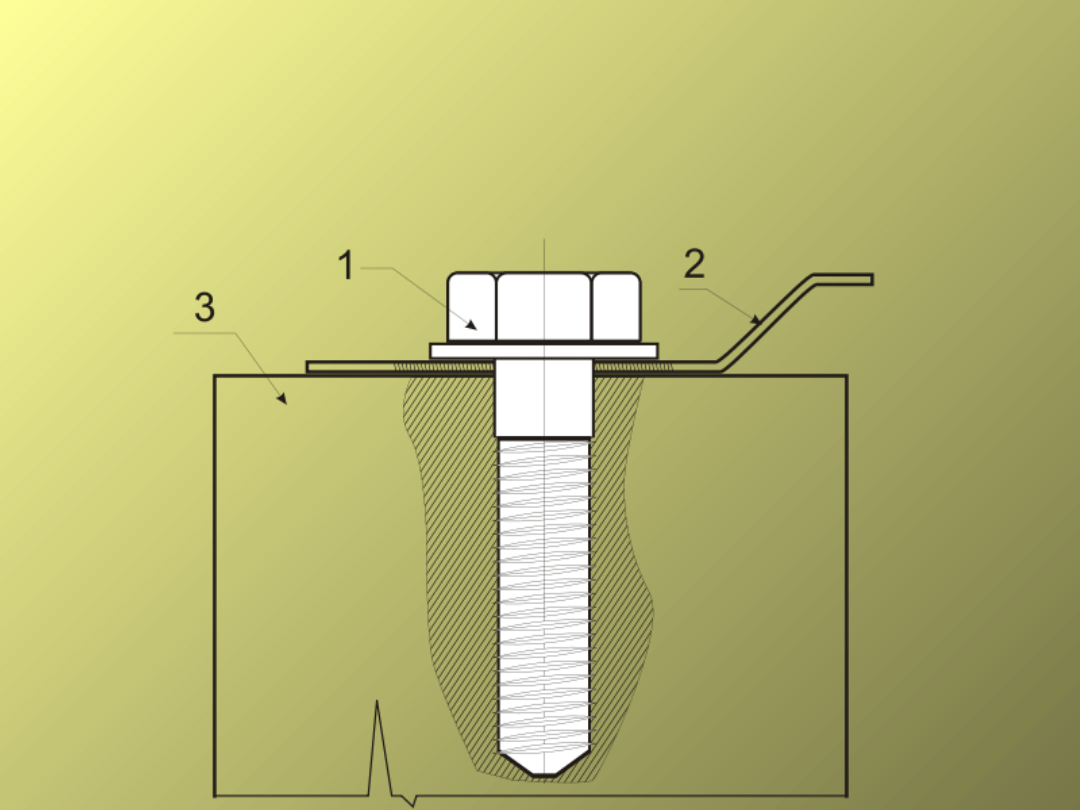
Łączniki gwintowe
Połączenie dociskowe
(wkrętowe)

Wkręt
– łącznik gwintowy, zwykle wkręcany jest
wkrętakiem i posiada nacięcie. Wkręt może być
samogwintujący.
Łby wkrętów mogą mieć kształt:
a) walcowy płaski
b) walcowy soczewkowy
c) stożkowy płaski
d) stożkowy soczewkowy
e) kulisty
f) bez łba
Nacięcie we łbie wkręta pod wkrętak może
mieć różny kształt:
g) proste
h) krzyżowe
i) kwadratowe
j) sześciokątne (inbusowe)
k) ośmiokątne
Wkręty
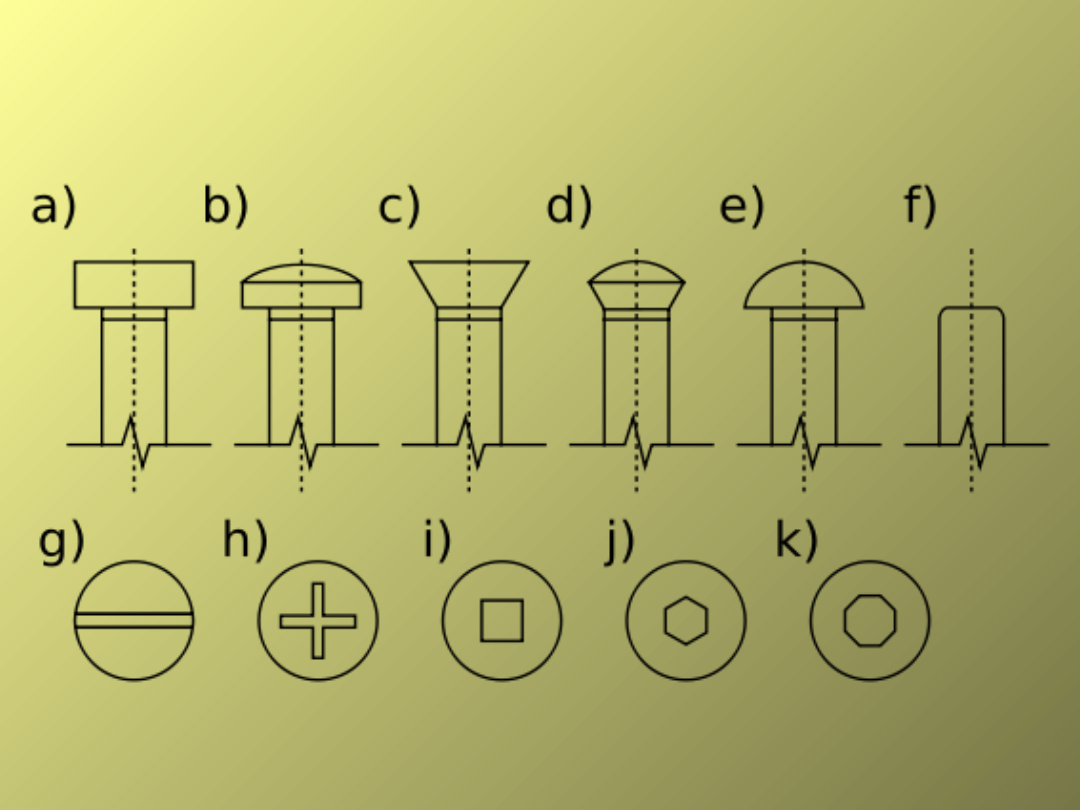
Wkręty
Łby i ich nacięcia

Wkręty
1 blachowkręt samowiertny, łeb z nacięciem PH, 2 wkręt do
materiałów warstwowych samowiertny (np. do przykręcania płyt
plastykowych do metalu), łeb z nacięciem PH, 3 wkręt montażowy,
łeb z nacięciem PH, 4 wkręt montażowy samowiertny, łeb z
nacięciem PH, 5 wkręt montażowy, łeb z nacięciem PZ, 6 wkręt do
drewna, łeb z nacięciem PZ, 7 wkręt montażowy, łeb sześciokątny z
nacięciem PH i prostym, 8 wkręt do pokryć blacharskich,
samowiertny, z uszczelką, łeb sześciokątny, 9 wkręt montażowy, łeb
sześciokątny z nacięciem prostym, 10 blachowkręt nierdzewny, łeb z
nacięciem prostym. a) końcówka samowiertna, b) skrzydełka
rozwiercające miękki materiał
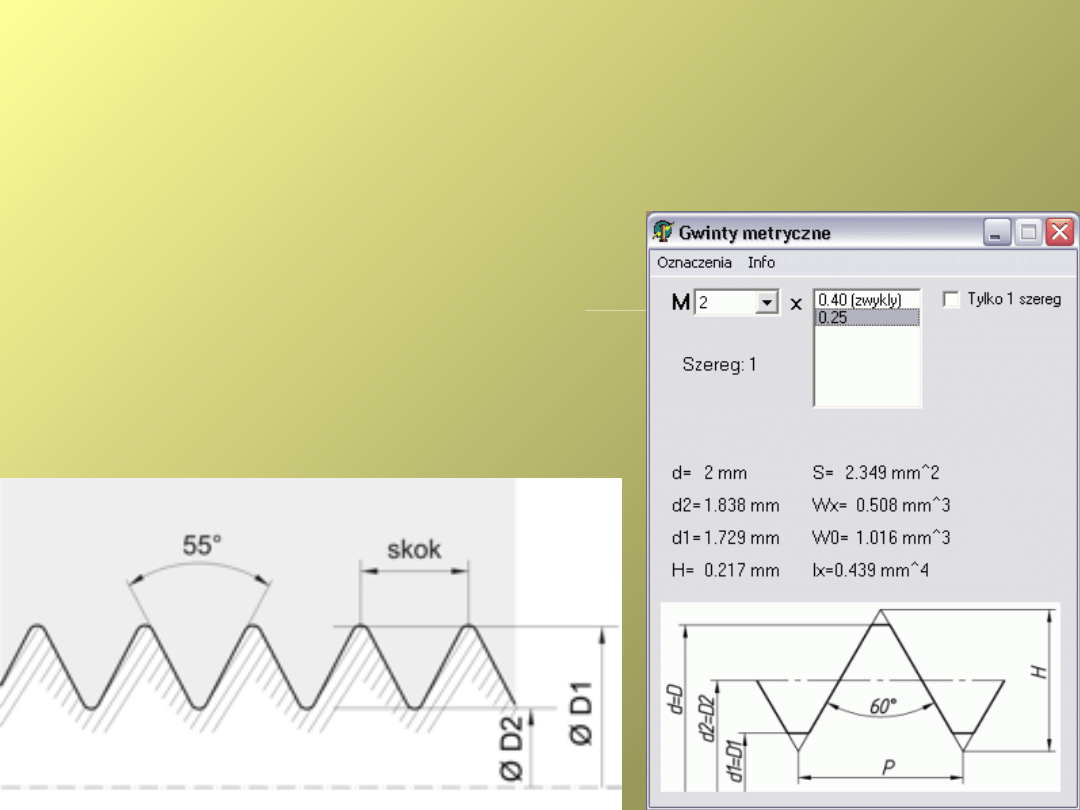
Gwinty trójkątne
Rodzaje:
Walcowe, stożkowe,
Metryczne ( 60
o
), calowe (55
o
)
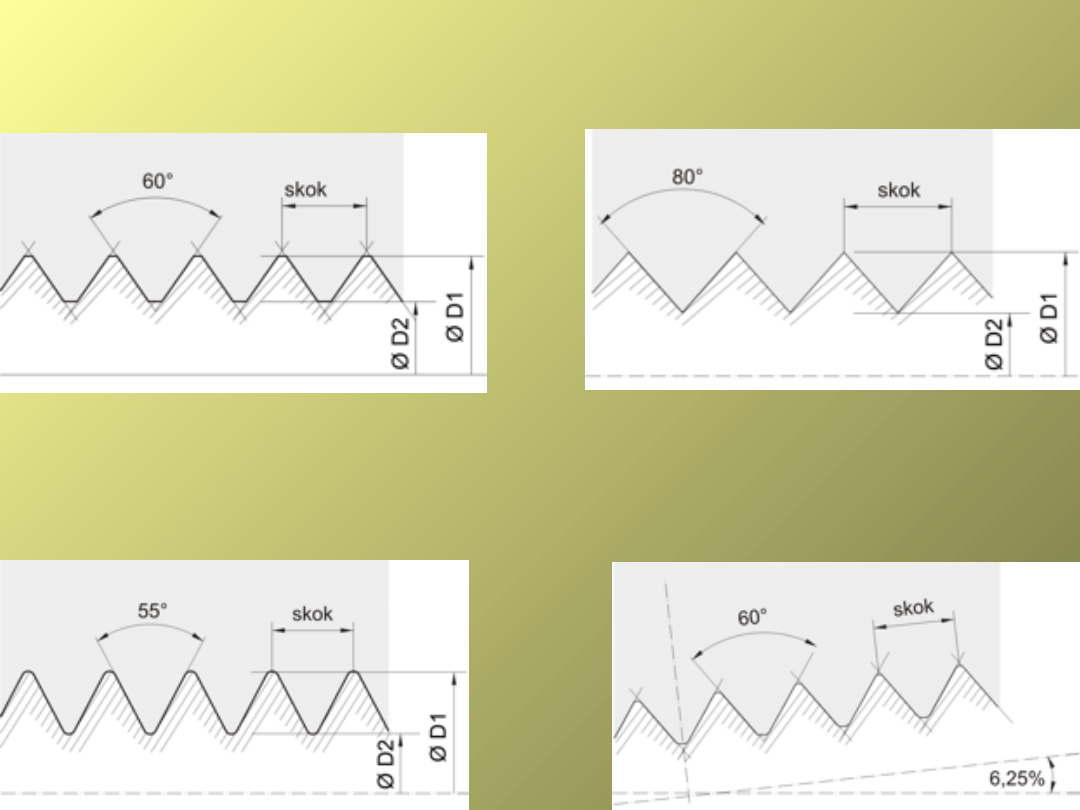
Gwint M, wg EN
60423
gwint metryczny
Gwinty
trójkątne
Gwint NPT, wg ANSI B2.1, ANSI
B2.2
gwint rurowy zwężany
Gwint G, wg DIN 259, ISO
228/I
gwint gazowy
Gwint PG, wg DIN
430430
gwint elektryczny
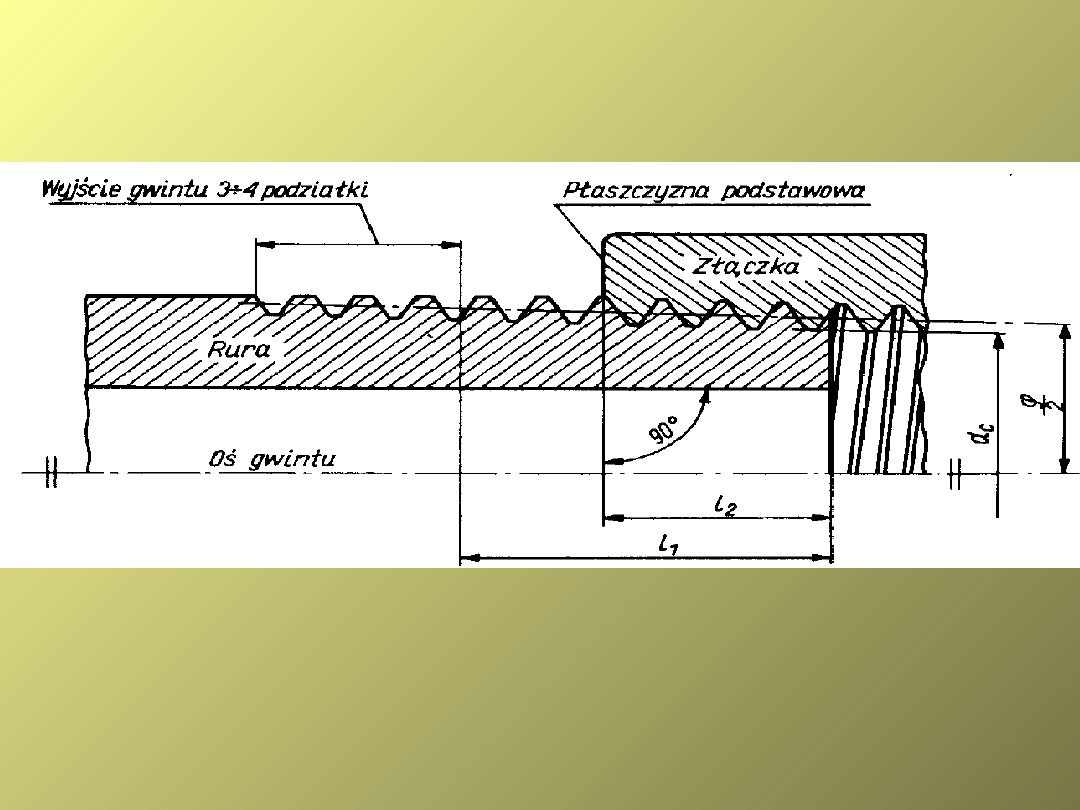
Gwint rurowy stożkowy (Briggsa)
Gwinty stożkowe

.
Powstaje podobnie jak gwint walcowy,
ale jest nacinany wzdłuż powierzchni
stożka.
W połączeniach normalnych gwint stożkowy
jest na rurze i w złączce.
W połączeniach uproszczonych gwint
walcowy stosuje się w złączce, a gwint
stożkowy tylko na rurze.
Gwinty stożkowe są stosowane do łączenia
przewodów rurowych wodnych, itp.
Zapewniają szczelność połączenia bez
stosowania dodatkowych materiałów
uszczelniających.
Gwinty stożkowe
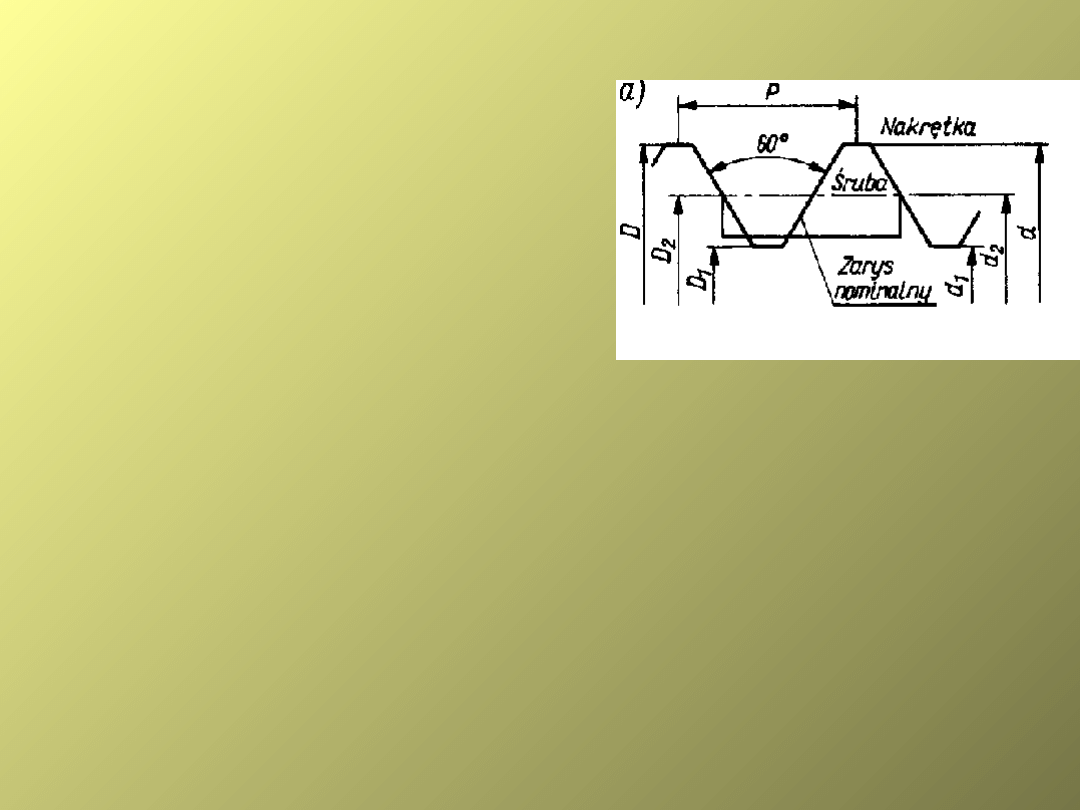
Zarys nominalny gwintu
metrycznego
d – średnica gwintu śruby;
d1 – średnica rdzenia śruby;
d2 – średnica podziałowa śruby;
D – średnica dna wrębów nakrętki D4;
D1 – średnica otworu nakrętki;
D2 – średnica podziałowa nakrętki (d2 = D2);
P – podziałka gwintu (h
z
)
P
h
– skok gwintu w gwintach wielokrotnych (P
h
= n
P);
n – krotność gwintu;
- kąt gwintu (między bokami zarysu);
- wznios gwintu równy wzniosowi linii śrubowej,
obliczany na średnicy linii podziałowej
Połączenia gwintowe

Gwinty
metryczne
Polska norma ustala 3 szeregi średnic
znamionowych gwintu
Dla odpowiednich zakresów średnic:
1 600 mm PN – 83/M – 02013,
0,25 0,9 mm PN – 74/M – 02012.
Skok gwintu metrycznego może być zwykły lub
drobnozwojny.
Gwint metryczny stosujemy głównie w połączeniach
spoczynkowych.
M20 – gwint zwykły
M20 x 2 – gwint metryczny drobny (drobnozwojny)
M16 – gwint metryczny (prawy)
LHM16 – gwint metryczny (lewy)

Gwinty
metryczne
Zalety gwintów metrycznych:
znaczna wytrzymałość,
samohamowność,
mała wrażliwość na niedokładność
wykonania.
Wady gwintów metrycznych:
niedokładność osiowania,
niska sprawność.

symetryczne – powierzchnie robocze
pochylone pod kątem = 15
niesymetryczne - Powierzchnie robocze są
pochylone pod kątem r = 3, powierzchnie
pomocnicze
p
= 30, ewentualnie
p
= 45.
Wśród nich rozróżnia się gwinty:
drobne,
zwykłe,
grube.
Tr 32 x 6 – gwint trapezowy symetryczny
S = 32 x 6 – gwint trapezowy niesymetryczny,
Odpowiednie oznaczenia: 32 – średnica gwintu, 6 – skok
Gwinty
trapezowe

Gwinty trapezowe są stosowane przeważnie
w połączeniach ruchowych (mechanizmach
śrubowych).
Charakteryzują się one dużą wytrzymałością ,
oraz wysoką sprawnością.
Gwinty trapezowe symetryczne – przenoszą
duże obciążenia obukierunkowe.
Dodatkową zaletą jest możliwość regulacji i
kasowania luzów poosiowych.
Gwinty trapezowe niesymetryczne –
charakteryzują się największą wytrzymałością.
Powinny pracować tylko przy jednokierunkowym
obciążeniu.
Gwinty
trapezowe

Nie jest znormalizowany.
Stosuje się go tylko w produkcji jednostkowej.
Zastępuje się go gwintem trapezowym, ponieważ
jest łatwiejszy do wykonania i przenosi większe
obciążenia.
Gwint
prostokątny

Jest gwintem trójkątnym.
Stosowany głównie do łączenia przewodów rurowych. Jest
to gwint calowy drobnozwojowy o kącie gwintu = 55.
Jako średnicę gwintu d podajemy średnicę otworu rury z
gwintem zewnętrznym (w calach).
Gwint rurowy walcowy

Gwint okrągły – PN – 84/M – 02035.
Posiada dużą wytrzymałość
zmęczeniową, zwłaszcza przy
obciążeniu udarowym.
Stosuje się go w połączeniach
spoczynkowych, często montowanych
i demontowanych, np. w przewodach
pożarowych, złączach wagonowych.
Rodzaje
gwintów

Zastosowanie gwintu
okrągłego

Zastosowanie gwintu
okrągłego
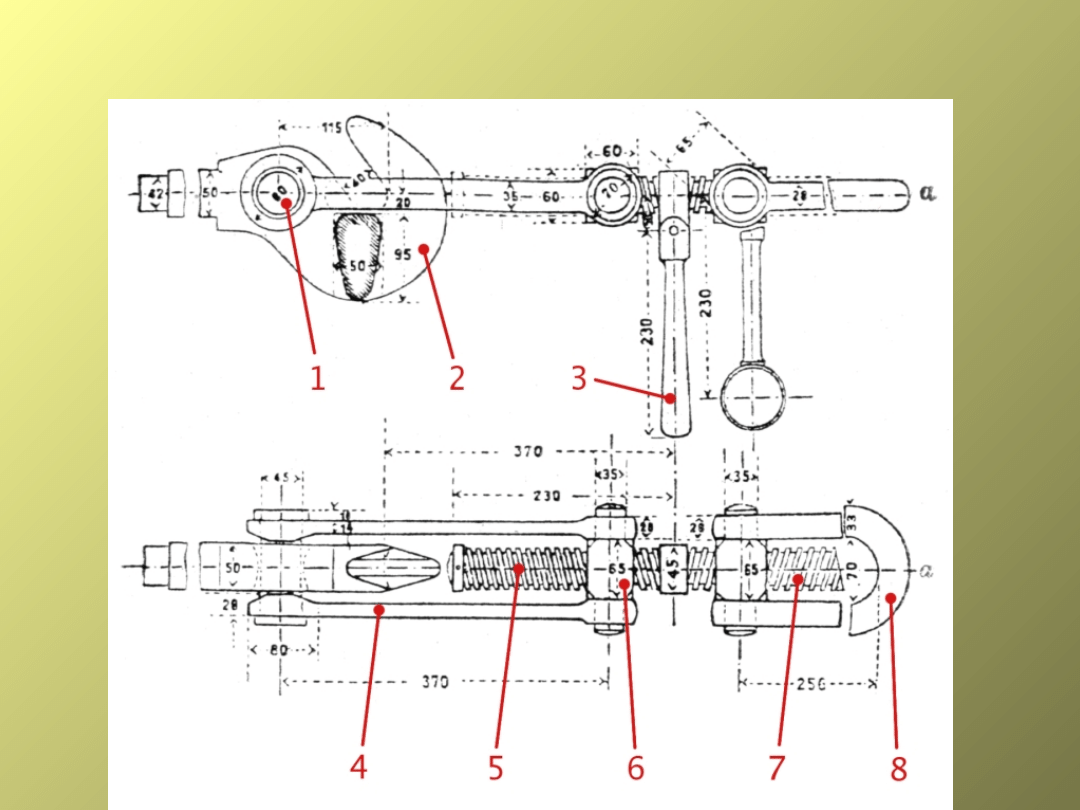
Zastosowanie gwintu
okrągłego
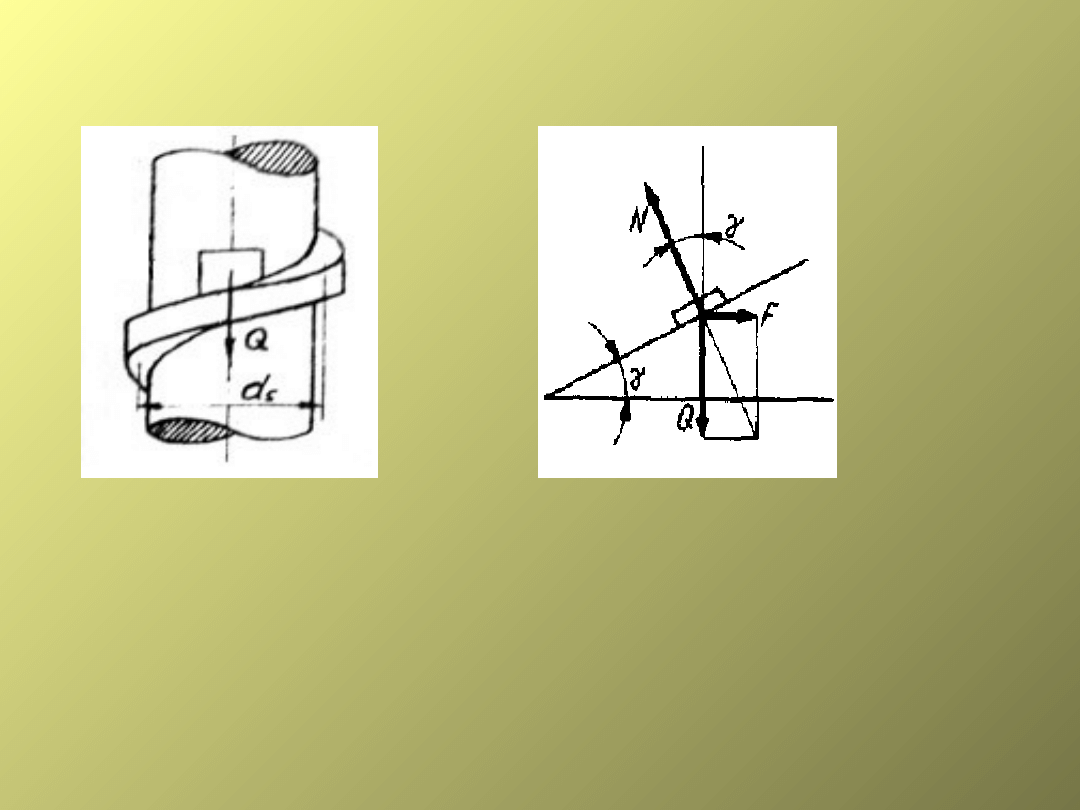
ROZKŁAD SIŁ NA GWINCIE
Śruba jako maszyna prosta
Q – skupione, umowne obciążenie działające na
gwint.
N - normalna reakcja podłoża, równoważąca
wypadkową Q i F.
tg = F/Q
F = Q tg
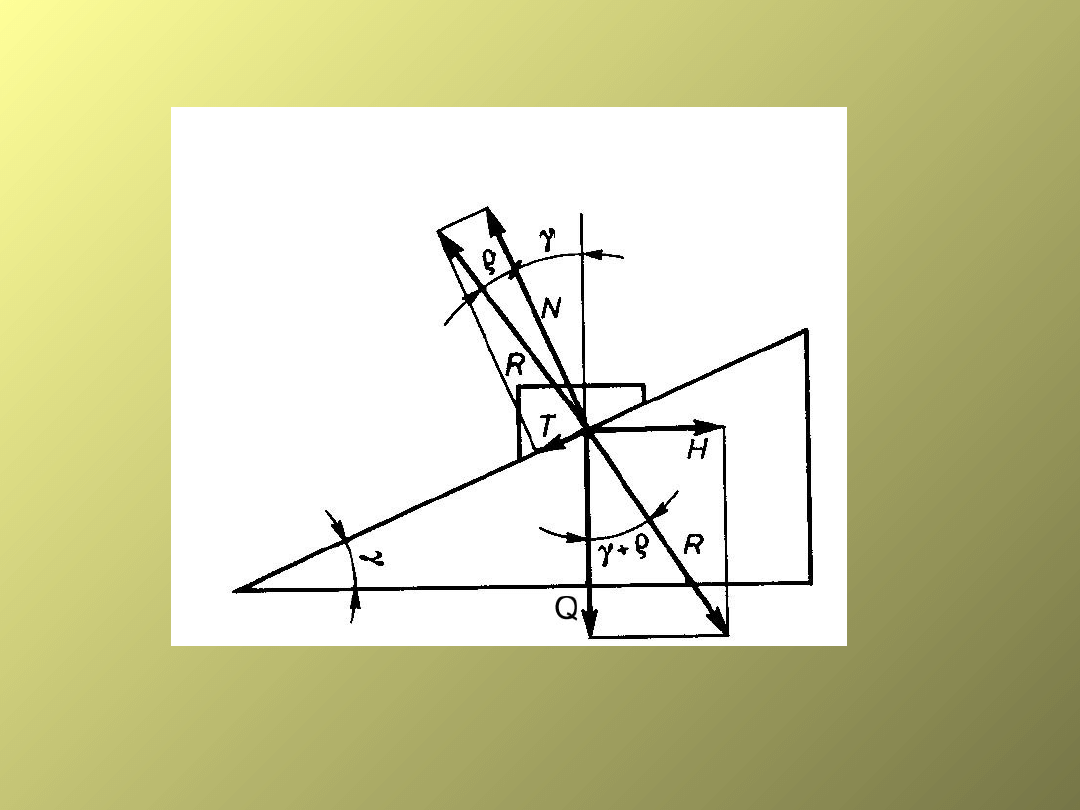
*napinanie złącza*
T – siła tarcia. T = N = N tg
H = Q tg ( + )
R=Q/cos( + )
ROZKŁAD SIŁ NA GWINCIE
Śruba jako maszyna prosta – podnoszenie
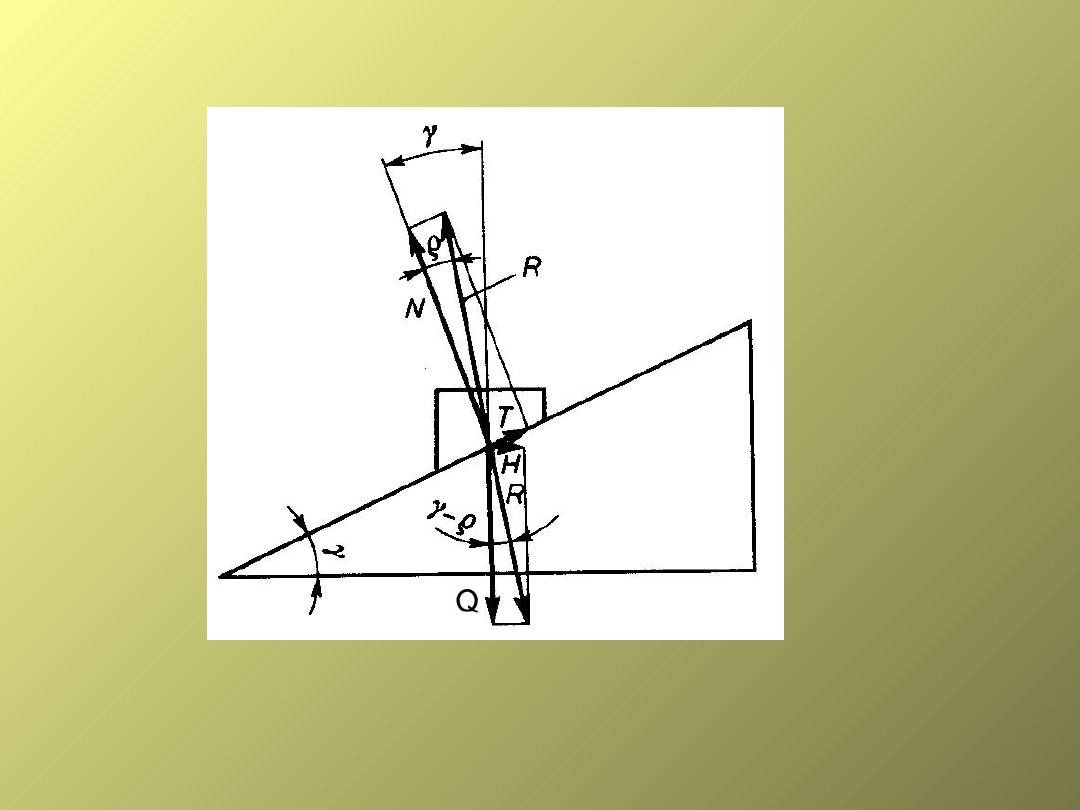
*luzowanie złącza* H = Q tg ( - )
R=Q/cos( - )
Zapis ogólny: H = Q tg ( )
(+) podnoszenie; (-) opuszczanie
ROZKŁAD SIŁ NA GWINCIE
Śruba jako maszyna prosta – opuszczanie
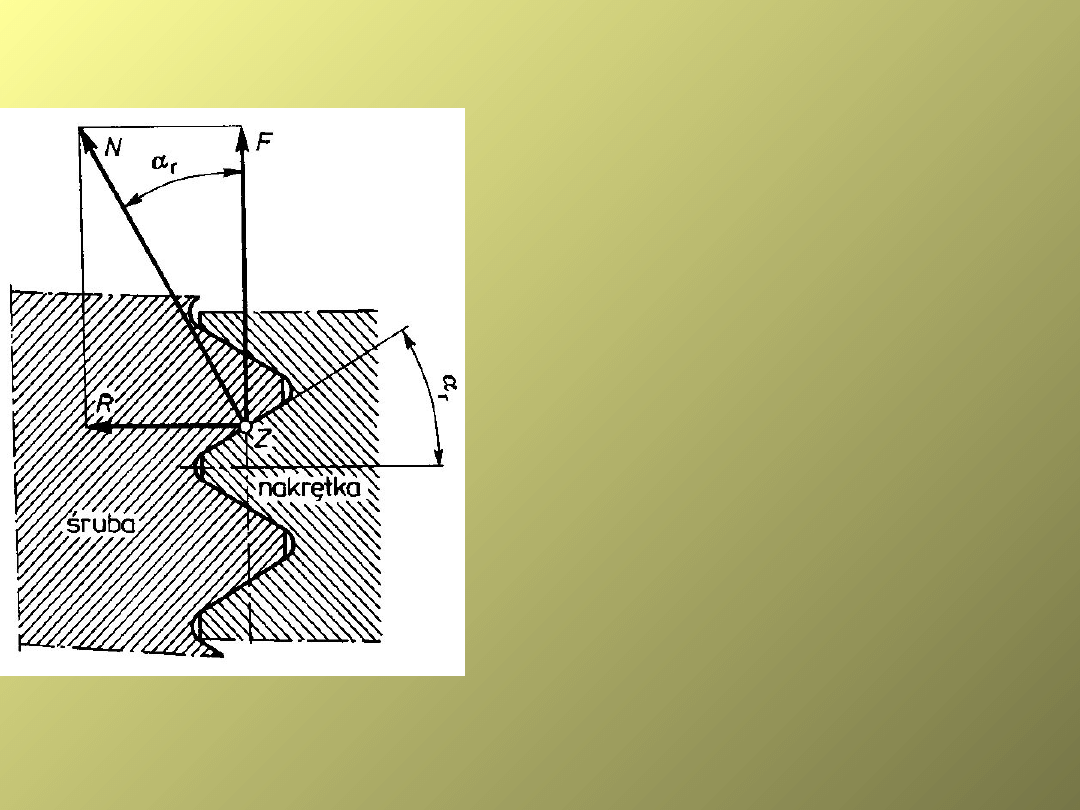
Gwint jest samohamowny jeśli:
< ’
T=N = (F /cos
r
)
= F
= tg= / cos
r
gdzie:
r
-kąt roboczy gwintu;
-pozorny współczynnik
tarcia
-pozorny kąt tarcia.
ROZKŁAD SIŁ NA GWINCIE
Przekrój osiowy

UWAGA!
Im większe jest
r
, tym większa jest siła
tarcia,
stąd wynika wniosek, że
w mechanizmach śrubowych należy
stosować gwinty o zarysie trapezowym i
prostokątnym,
a w połączeniach śrubowych - trójkątnym

SPRAWNOŚĆ I SAMOHAMOWNOŚĆ GWINTU
Praca uzyskana:
L
u
= Q * h = Q * π*d
s .
*tg
Praca włożona
:
L
w
= 2* π* Ms = Q * π*d
s .
*tg ( +
)
Sprawnością
g
– nazywamy stosunek pracy użytecznej,
uzyskanej do pracy włożonej
g
=L
u
/ L
w
= tg / tg( + )
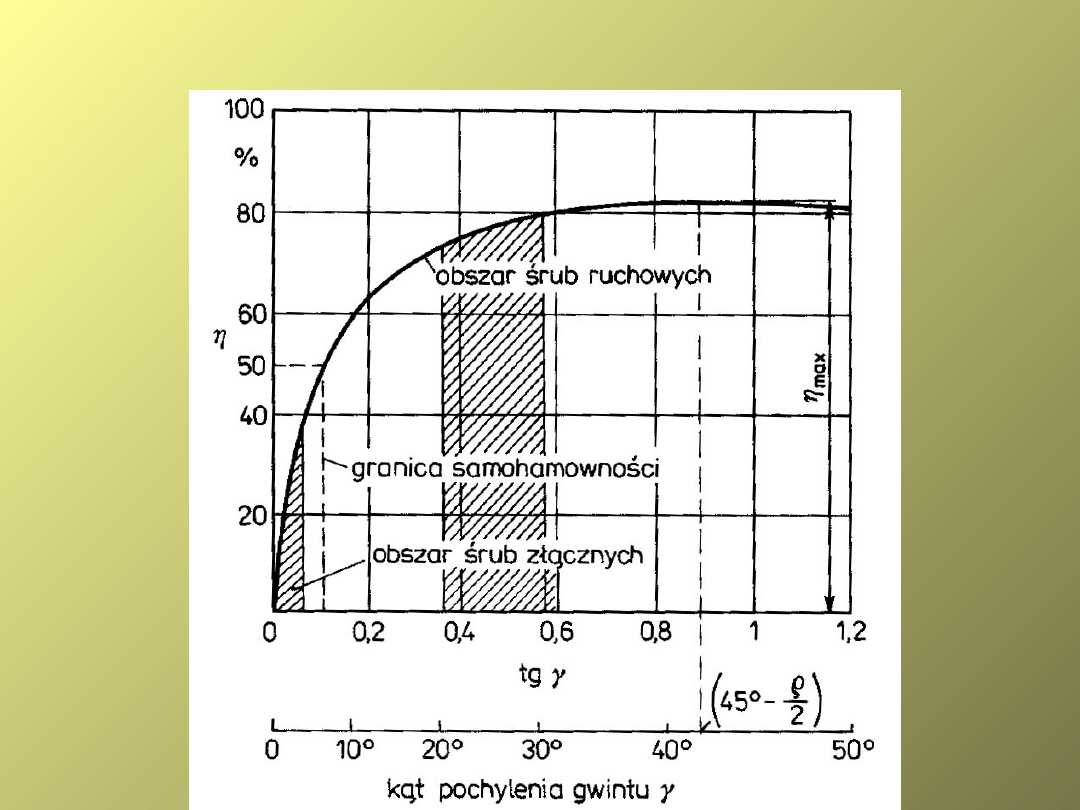
SPRAWNOŚĆ I SAMOHAMOWNOŚĆ GWINTU
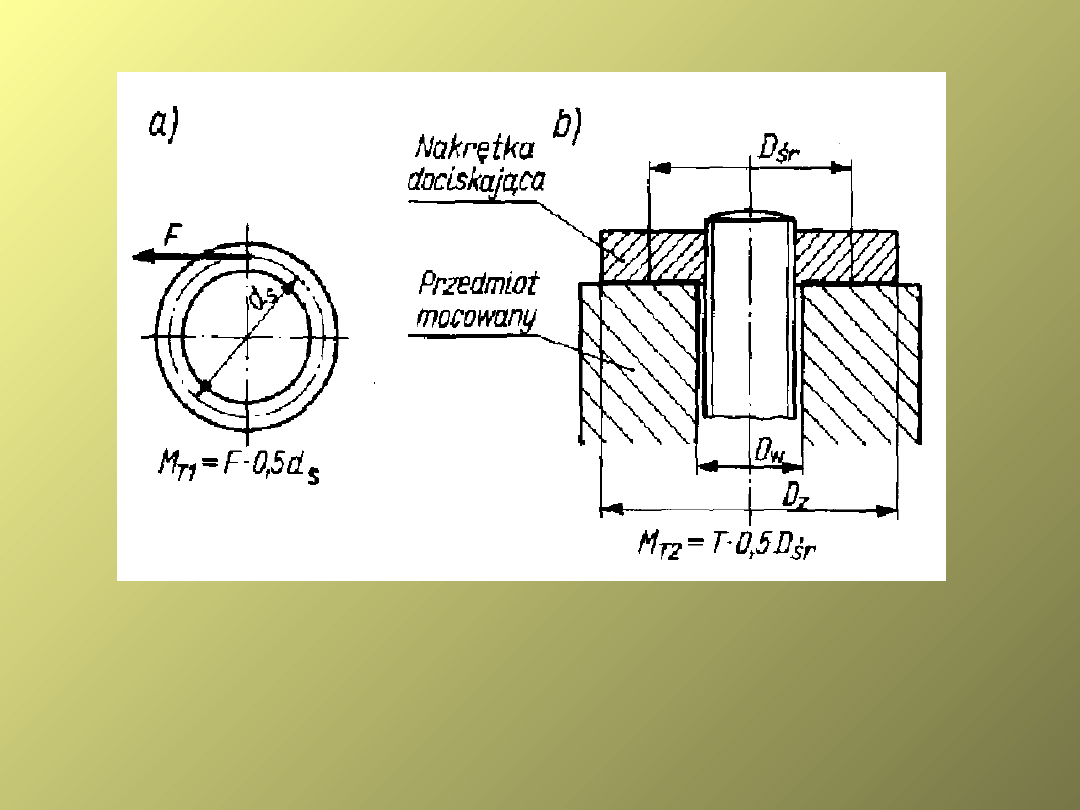
MOMENTY TARCIA
M
T1
=F*d
s
/2= 0,5Q ds
tg( )
M
T1
moment tarcia na
średnicy roboczej
gwintu
M
T2
= Q Dsr
0,5
M
T2
moment tarcia na
do-datkowej średnicy
oporowej

gdzie:
- współczynnik tarcia
r
śr
= (D
z
+D
w
)/4 - średni promień powierzchni styku
gwintu.
D
z
–średnica zewnętrzna powierzchni oporowej nakrętki
(dla
nakrętek sześciokątnych i kwadratowych – rozwartość
klucza)
D
w
–średnica wewnętrzna powierzchni oporowej (średnica
otworu
na śrubę).
Całkowity moment skręcający wynosi:
M
s
= M
T1
+ M
T2
= 0,5Q ds tg( ) + Q
r
śr
M
s
= F
r
l
– moment wywołany siłą ręki (100 300
N)
gdzie:
F
r
– Siłą ręki człowieka (100 300 N);
l
– czynna długość klucza.
MOMENTY TARCIA c. d.

Zniszczenie połączeń gwintowych może nastąpić w
wyniku:
nadmiernego obciążenie
wadliwego wykonanie gwintu
Gwint może być zgnieciony, ścięty lub złamany. W
pewnych warunkach może ulegać zużyciu
ściernemu.
Rdzeń śruby może podlegać rozciąganiu, ściskaniu,
skręcaniu, wyboczeniu lub obciążeniom złożonym.
W części niegwintowanej:
śruba ciasno pasowana może być ścięta a
powierzchnie boczne uszkodzone pod wpływem
nacisków.
śruba luźno pasowana narażona jest na zginanie i
naciski jw.
Dobór gwintu śruby zależy od wartości
nacisków na jego powierzchni i
wytrzymałość rdzenia śruby.
Obliczenia wytrzymałościowe śrub

UWAGA!
Z trzech rodzajów obciążeń działających na gwint:
zginanie
ścinanie
docisk
najbardziej niebezpieczny jest docisk.
W praktyce połączenia śrubowe projektuje
się tak, aby wytrzymałość gwintu była
większa niż wytrzymałość rdzenia śruby na
rozerwanie
Obliczenia
wytrzymałościowe
śrub

Połączenie śrubowe obciążone tylko
osiową siłą rozciągającą
Śruba obciążona siłą osiową i momentem
skręcającym
Połączenie z użyciem śrub napiętych
wstępnie
Połączenie śrubowe obciążone siłą
poprzeczną
Obliczenia wytrzymałościowe śrub
1.
Połączenie śrubowe obciążone tylko
osiową siłą rozciągającą
r
r
r
k
d
Q
4
2
e
e
r
X
R
k
z
rj
rj
X
Z
k
Xe= 2 - 2,3
Xz= 2,5 - 4
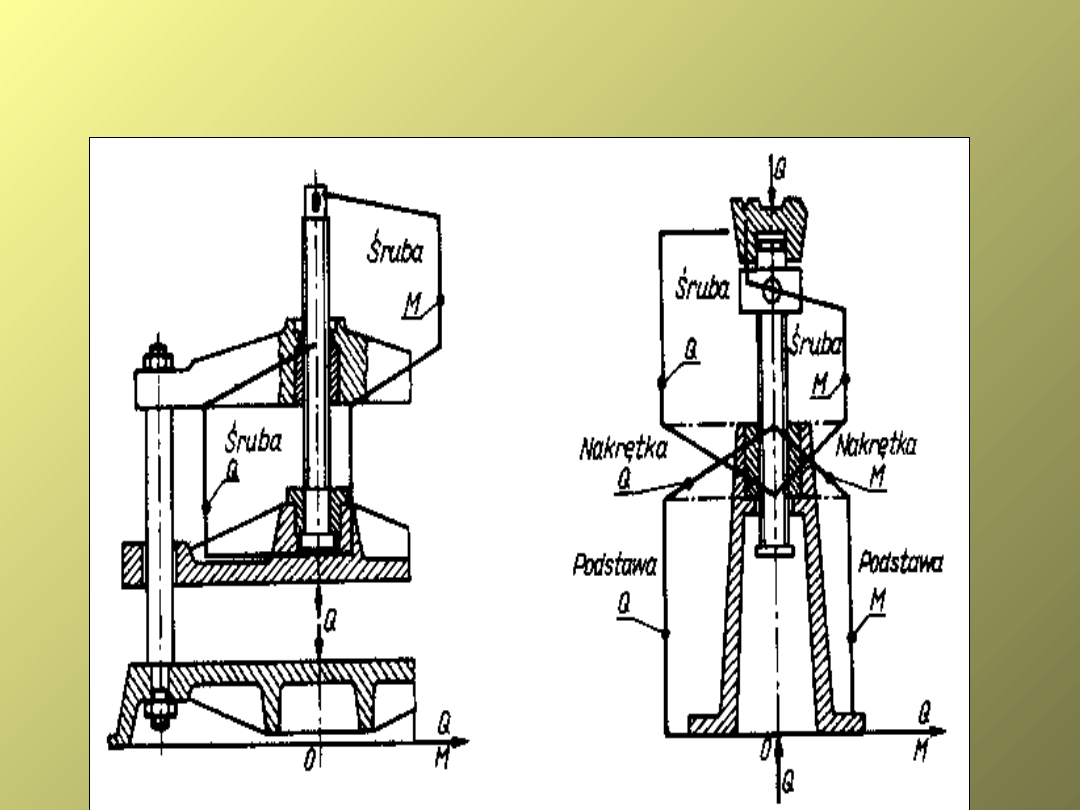
2. Śruba obciążona siłą osiową i momentem
skręcającym
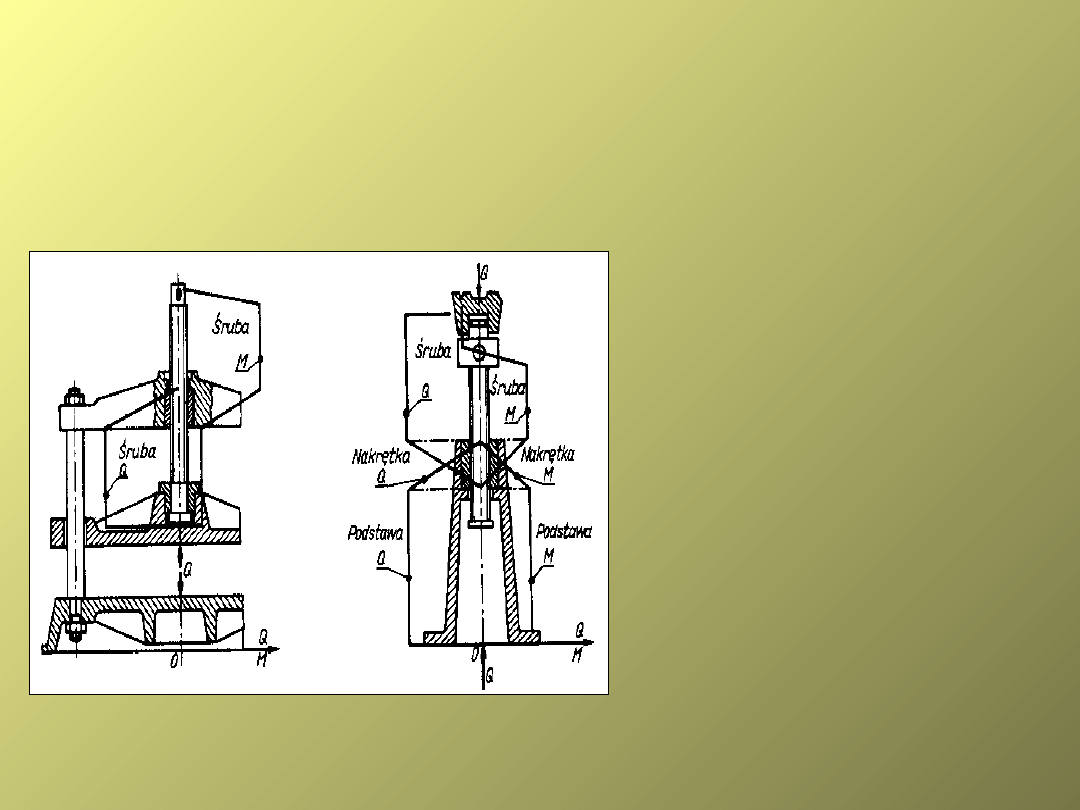
Połączenia obciążone
jednocześnie siłą osiową i
momentem skręcającym, mają
zastosowanie głównie w
połączeniach ruchowych .
W praktyce wykorzystujemy wzór
jak dla przypadku I, zamiast Q
przyjmuje się Qzastępcze.
Q
z
= 1,3*Q
Dobraną śrubę sprawdzam na
naprężenia zastępcze wg
hipotezy HUBERA .
2. Śruba obciążona siłą osiową i momentem
skręcającym
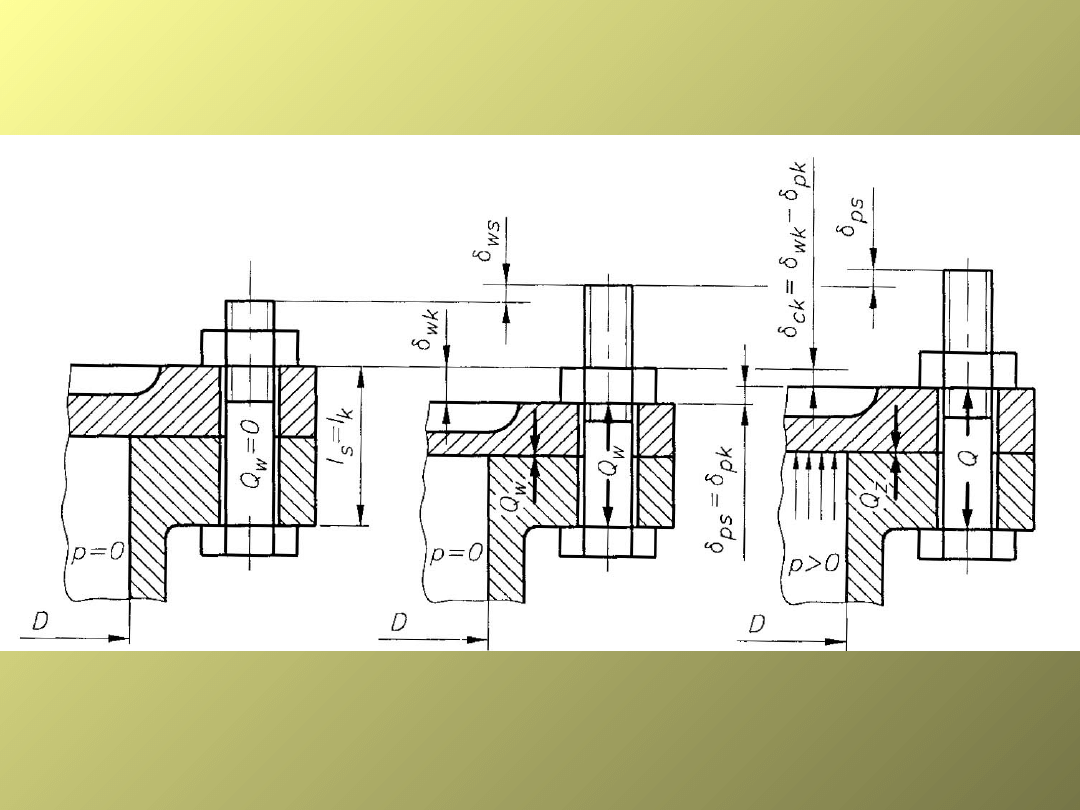
3.
Połączenie z użyciem śrub napiętych wstępnie
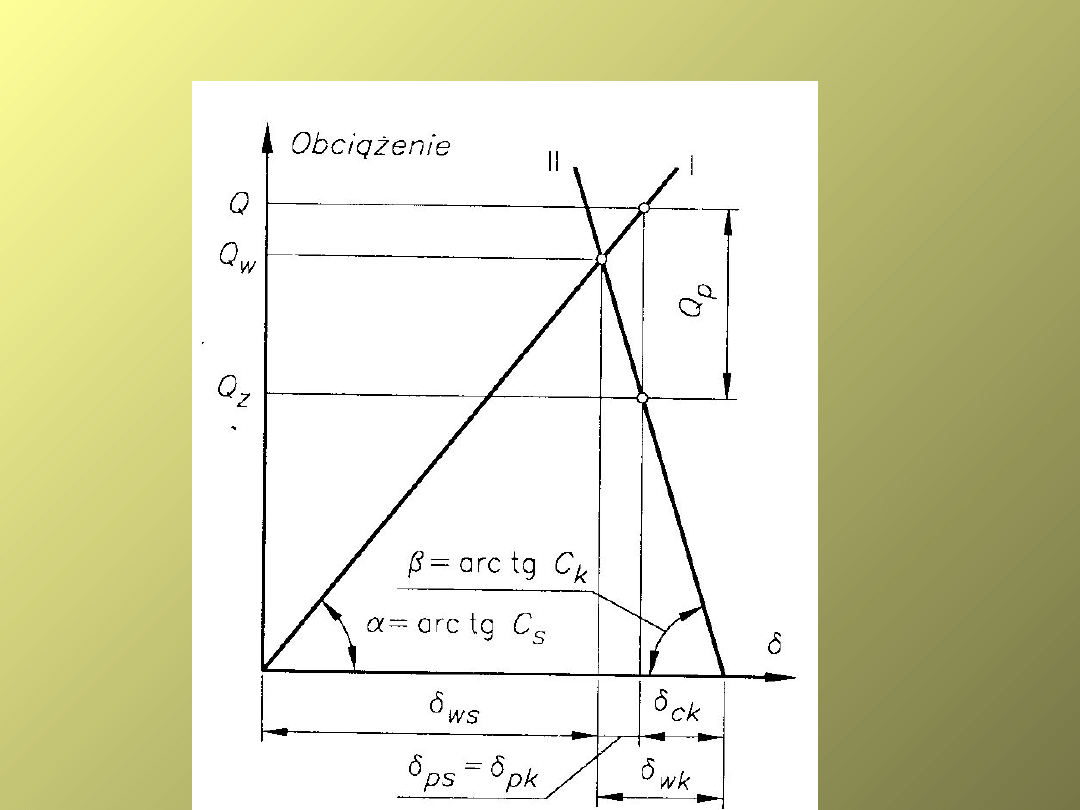
3.
Połączenie z użyciem śrub napiętych wstępnie
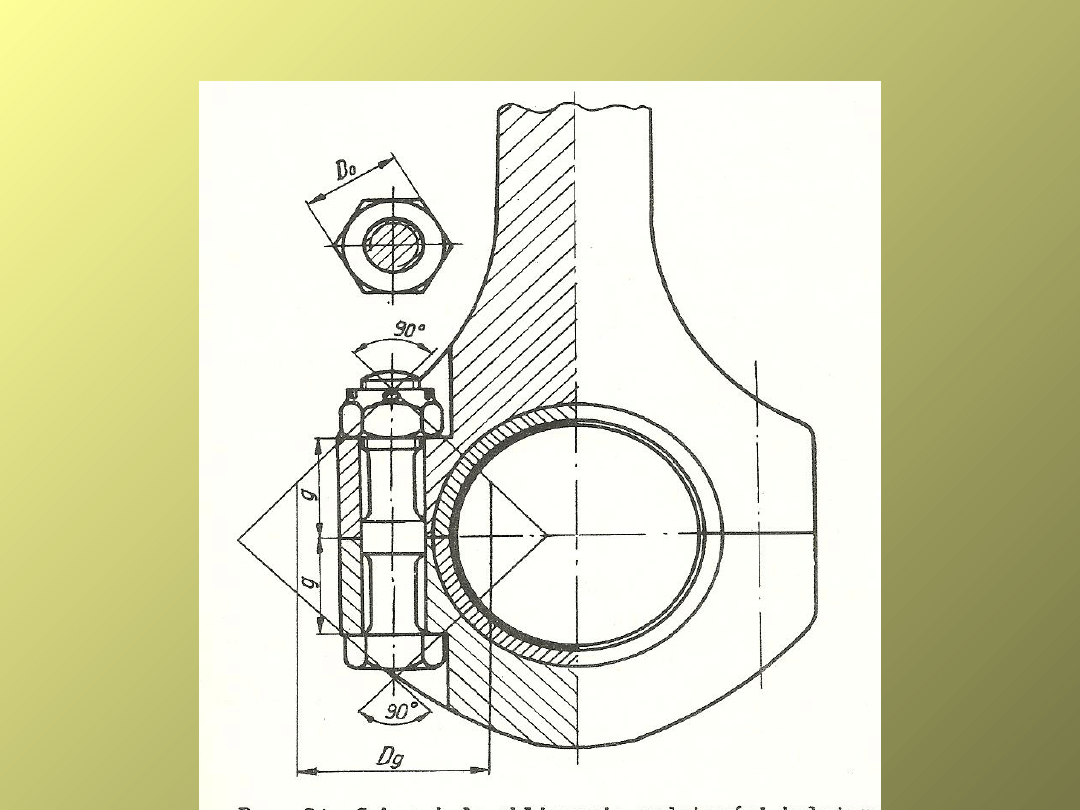
3.
Połączenie z użyciem śrub napiętych wstępnie
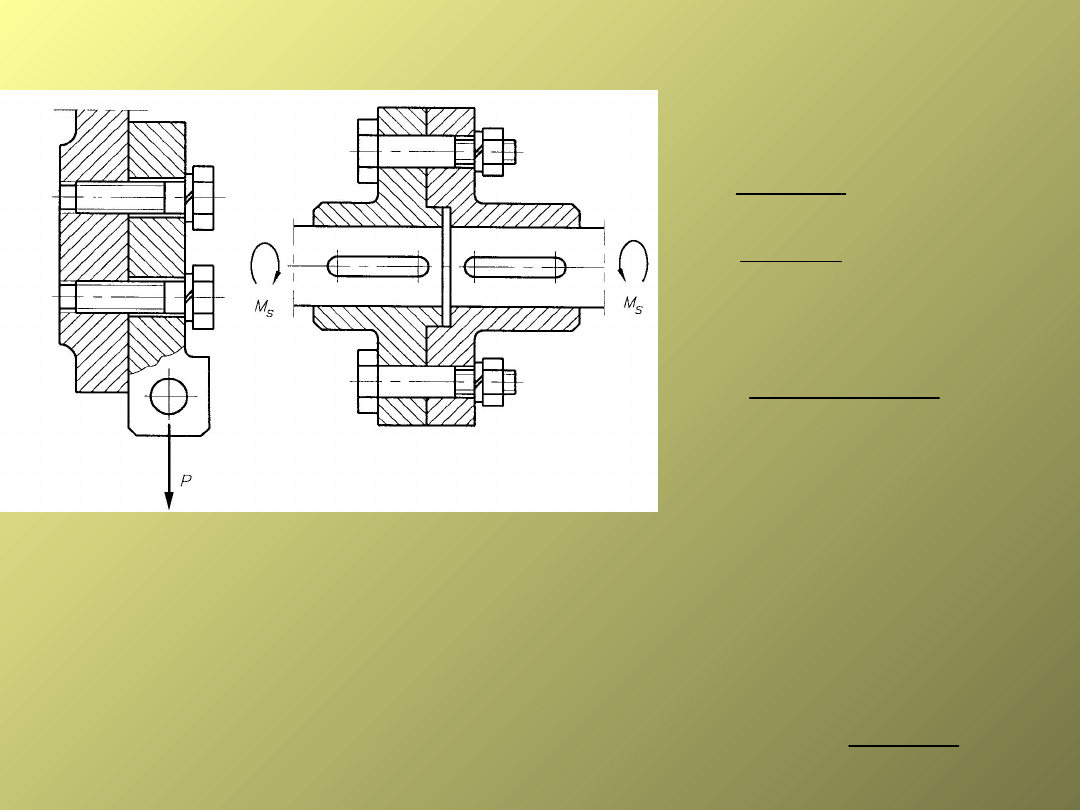
Śruby
pasowane:
Śruby
luźne:
t
o
k
d
P
4
2
dop
p
d
g
P
p
0
min
r
r
k
d
m
Q
P
Q
T
4
2
0
0
kt = 0,27 Rt – obc. stałe
kt = 0,22 Zgo – obc. pulsujące
kt = 0,16 Zgo – obc.
wahadłowe
4.
Połączenie śrubowe obciążone siłą poprzeczną
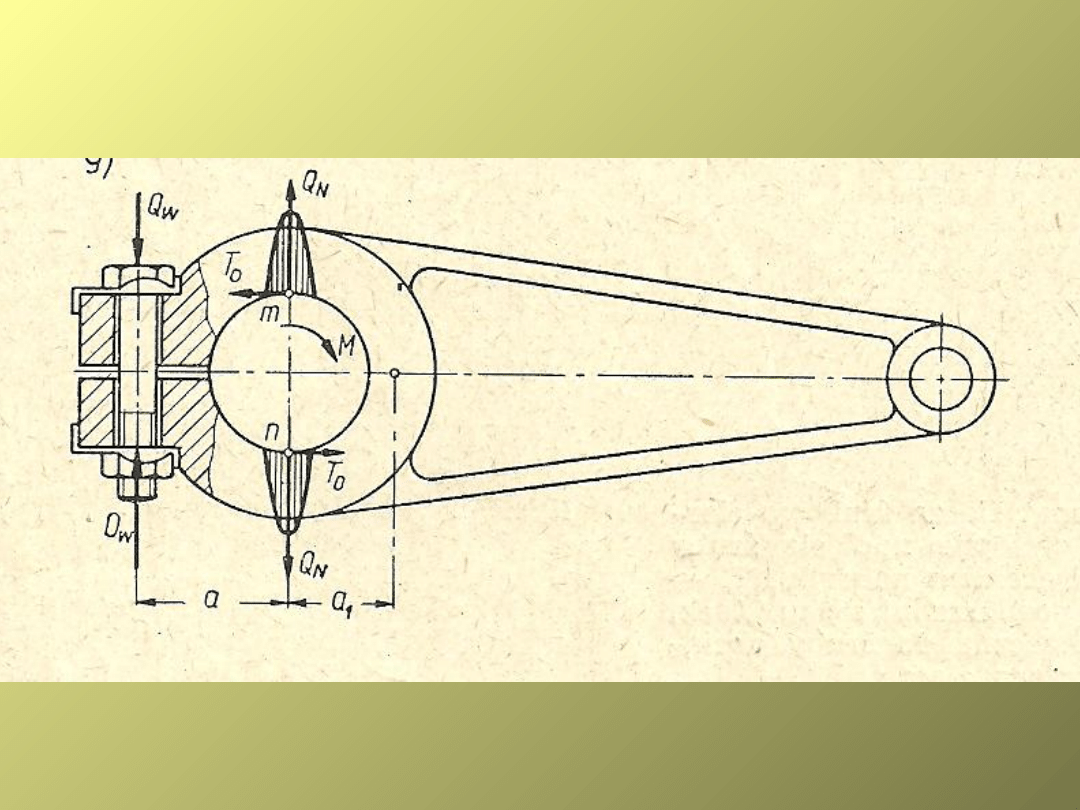
5.
Złącze czopowo-cierne obciążone siłą osiową
lub momentem skręcającym

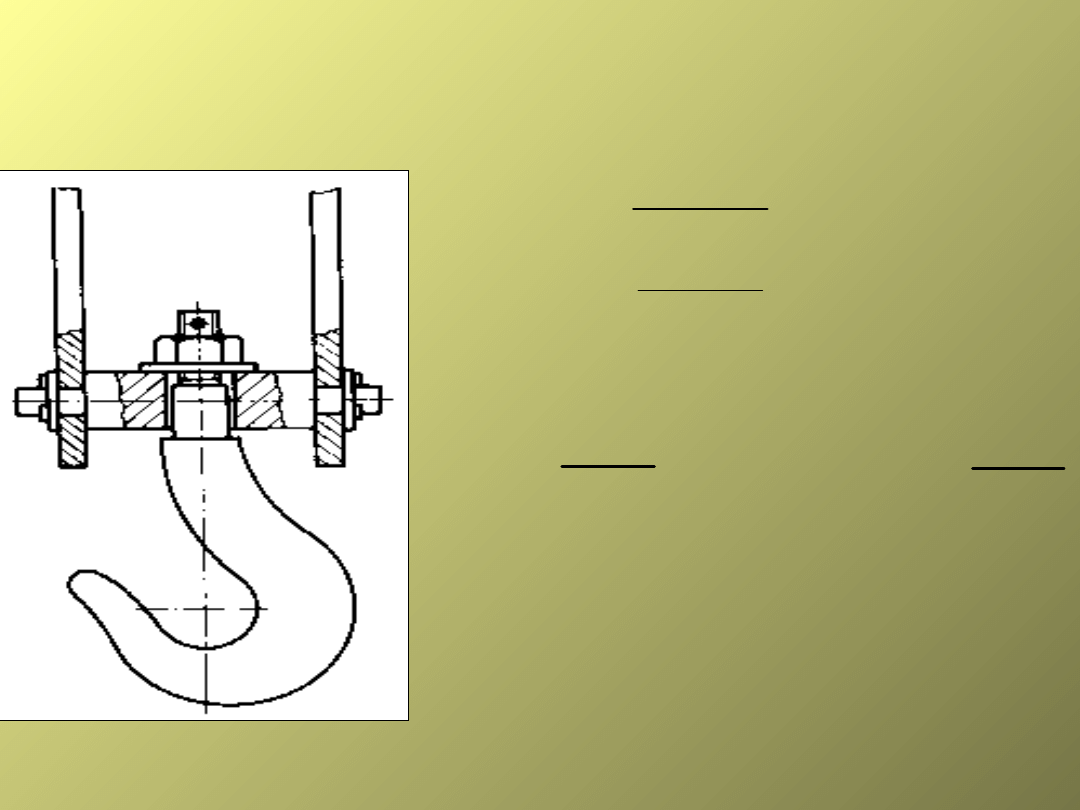
ODCIĄG ŚRUBOWY
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron