FIZYKA

Elementy Teorii 

Elementy Teorii 

Względności

Względności

dr inż. Marek Profaska

dr inż. Marek Profaska

 

 

 

 

E.T.W.

E.T.W.

   

Mechanika klasyczna

 (oparta na 

zasadach dynamiki Newtona) poprawnie 
opisuje zjawiska, w których prędkości ciał 
są małe w porównaniu z prędkością światła. 

   

Mechanika relatywistyczna oparta na 

szczególnej teorii względności 
(opracowanej przez Einsteina)

 - 

wykorzystuje się w zjawiskach atomowych, 
jądrowych i w astrofizyce gdzie prędkości 
są zbliżone do prędkości światła. 

 

 

E.T.W.

E.T.W.

   

   

Mechanika klasyczna nie jest 

sprzeczna z mechaniką 
relatywistyczną, a stanowi jej 
szczególny przypadek (dla 
małych prędkości). 

 

 

E.T.W.

E.T.W.

Zasada względności

    Gdy układ porusza się ze stałą prędkością po linii 

prostej to każde doświadczenie przebiega tak 

samo jak gdyby się nie poruszał. Jakakolwiek 

zmiana prędkości natychmiast jest do 

zaobserwowania.

    

Prawa przyrody (w szczególności fizyki) są 

takie same bez względu na to, czy 

obserwujemy je z układu nie poruszającego 

się, czy z ruchomego, ale poruszającego się 

bez przyśpieszenia (czyli układu 

inercjalnego).

 

 

E.T.W.

E.T.W.

Transformacja Galileusza

   

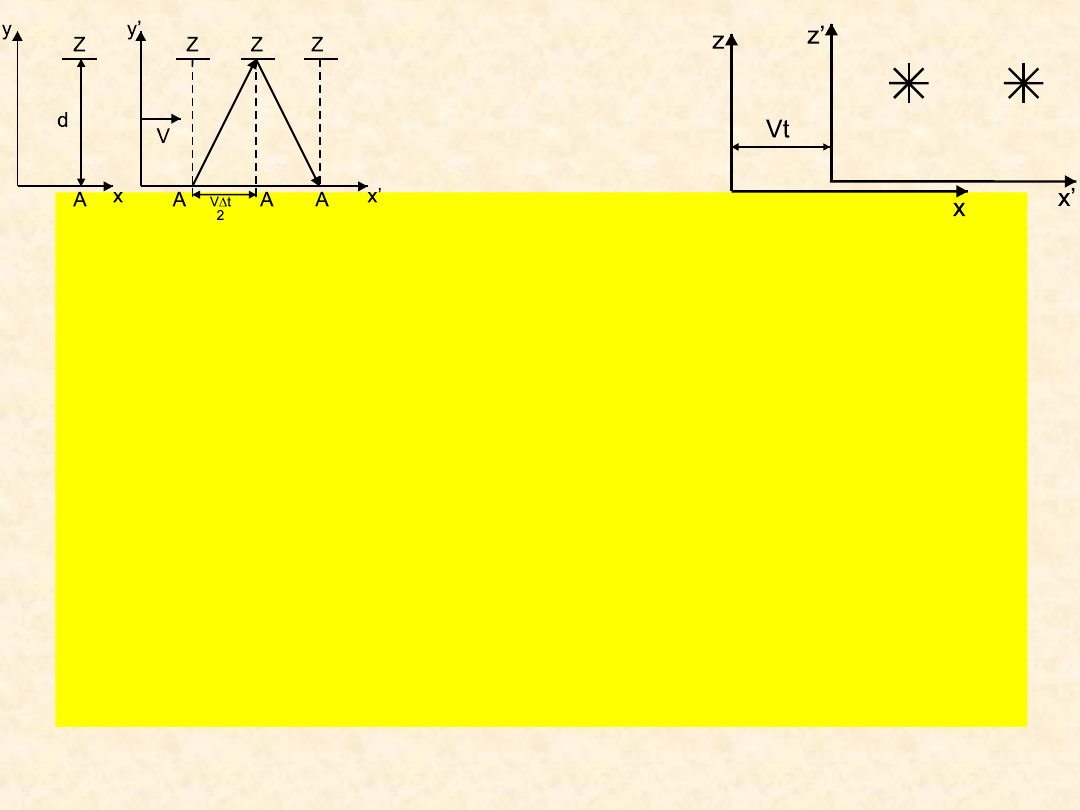
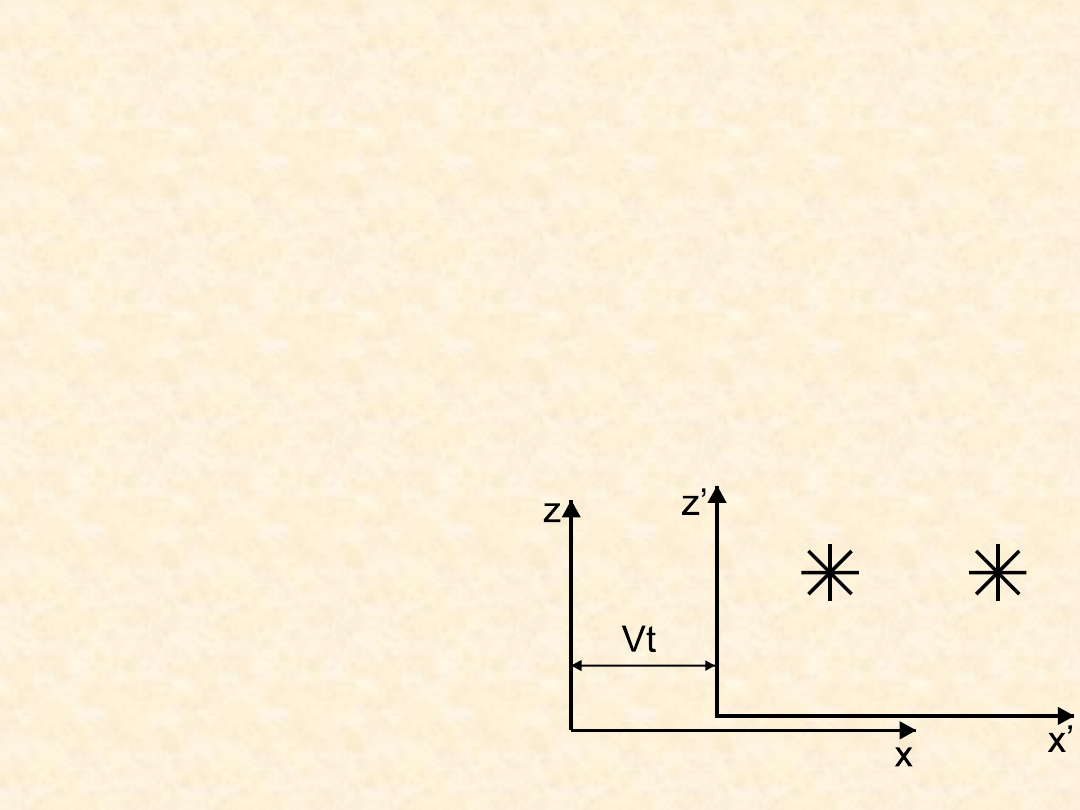
Wyobraźmy sobie, obserwatora na ziemi, który rejestruje dwa 

wybuchy na pewnej, jednakowej wysokości. Odległość między 
miejscami wybuchów wynosi, (według ziemskiego obserwatora) 
x, natomiast czas między wybuchami t. Dwa różne inercjalne 

układy odniesienia, poruszające się względem siebie.

     Te same dwa zdarzenia obserwowane są przez pasażera samolotu 

(prędkością V po linii prostej łączącej miejsca wybuchów - różnica 
położeń wybuchów x’, a różnica czasu t’).

Dwa różne inercjalne 
układy odniesienia, 
poruszające się 
względem siebie

 

 

E.T.W.

E.T.W.

 

 

E.T.W.

E.T.W.

t

t

z

z

y

y

Vt

x

x











'

'

'

'

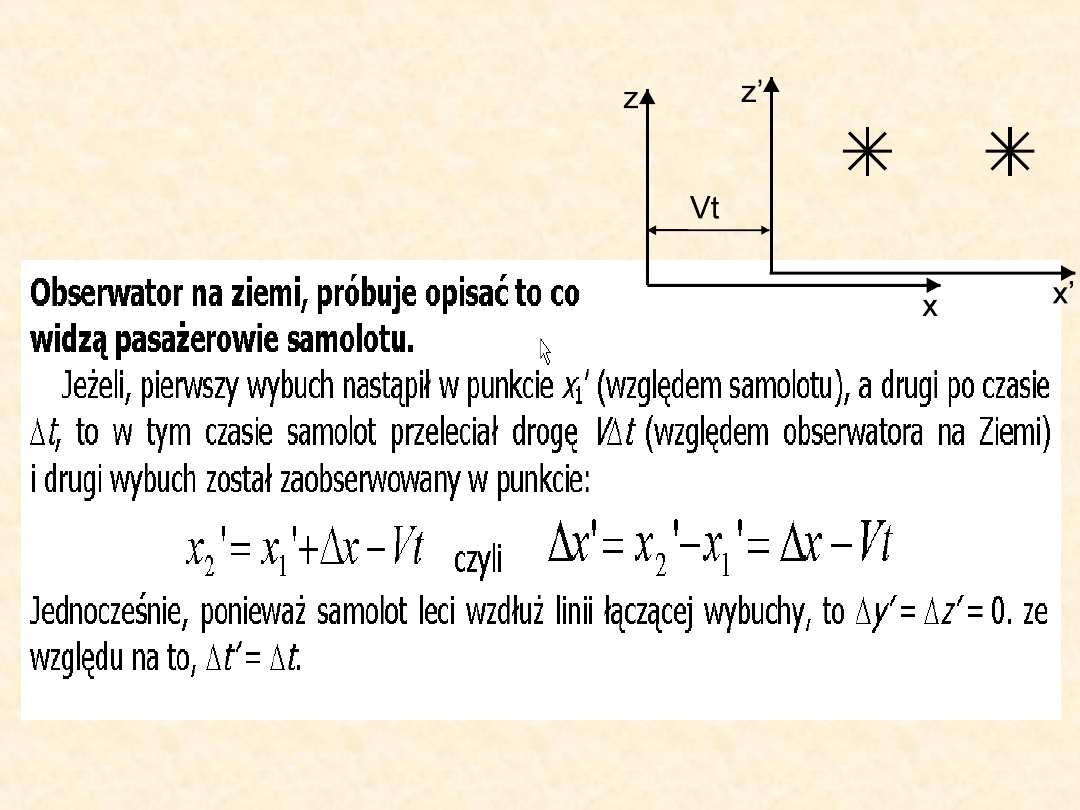
Wzory  przekładające  wyniki  obserwacji 
jednego  obserwatora  na  spostrzeżenia 
drugiego, 

równania 

noszą 

nazwę 

transformacji Galileusza

.

 

 

 

 

E.T.W.

E.T.W.

 

 

E.T.W.

E.T.W.

   

Wnioski wynikających ze stałości prędkości 

światła.

• Dylatacja czasu

    Przykład
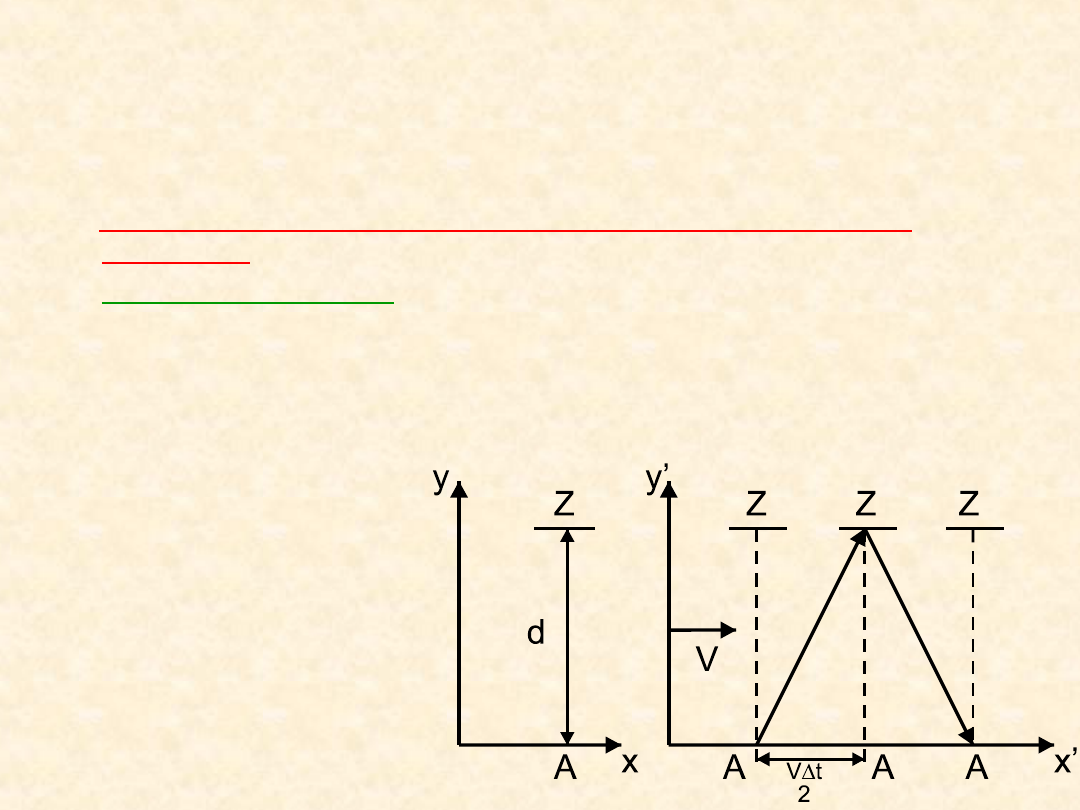
    Załóżmy, że w rakiecie znajduje się przyrząd 

wysyłający impuls światła z punktu A, który 

następnie odbity przez lustro Z, odległe od A o 

d powraca do punktu A, gdzie jest rejestrowany.

.

 

 

E.T.W.

E.T.W.

 

 

E.T.W.

E.T.W.

 

 

E.T.W.

E.T.W.

   

Każdy obserwator stwierdzi, że 

poruszający się zegar idzie wolniej 

niż identyczny zegar w spoczynku. 

   

Zjawisko 

dylatacji czasu

 jest 

własnością samego czasu i dlatego 

spowolnieniu ulegają wszystkie procesy 

fizyczne gdy są w ruchu. Dotyczy to 

również reakcji chemicznych, więc i np. 

biologicznego starzenia się.

 

 

E.T.W.

E.T.W.

Transformacja Lorentza

    Należy znaleźć (jak w przypadku transformacji 

Galileusza) wzory przekładające spostrzeżenia 
jednego obserwatora na obserwacje drugiego. 
Chcemy znaleźć transformację współrzędnych 
ale taką, w której obiekt poruszający się z 
prędkością równą c w układzie nieruchomym 
(x, y, z, t), również w układzie (x', y', z', t') 
poruszającym się z prędkością V wzdłuż osi x 
będzie poruszać się z prędkością c.

 

 

E.T.W.

E.T.W.

   

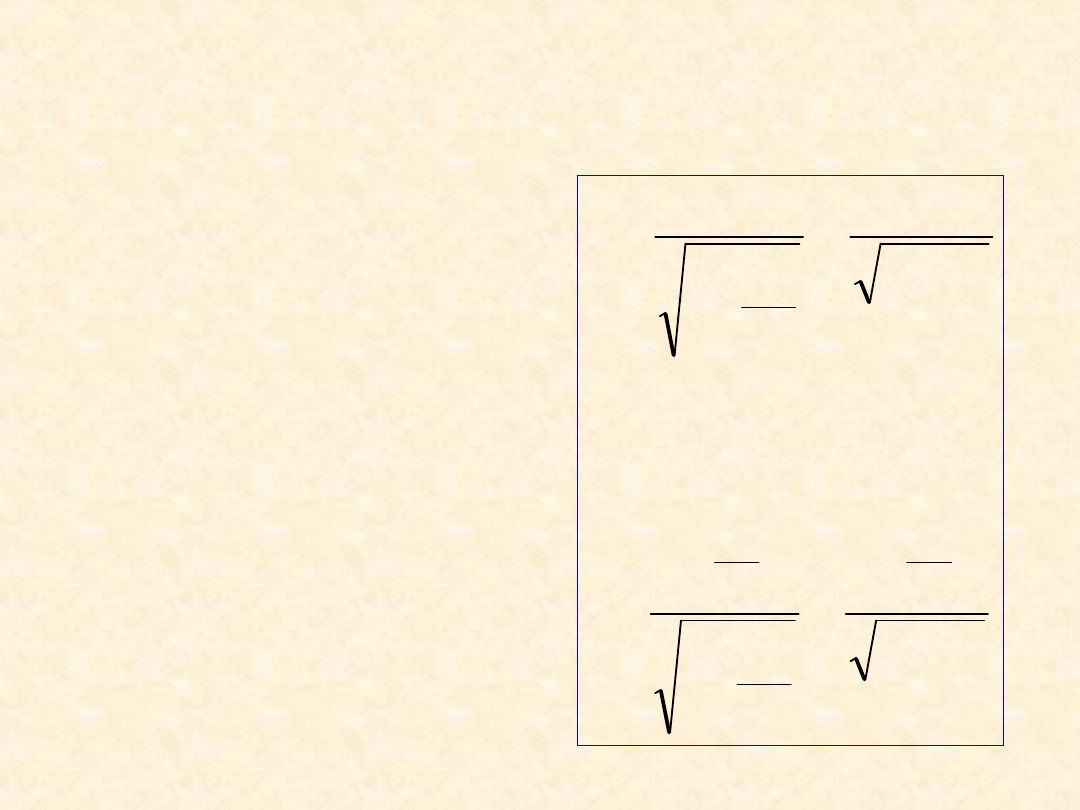
Transformacja 

współrzędnych

, która 

uwzględnia 

niezależność 

prędkości światła od 

układu odniesienia 

ma postać:

        gdzie 



 = V/c. 

   

Równania te noszą 

nazwę 

transformacji 

Lorentza.

2

2

2

2

2

2

2

2

1

1

'

'

'

1

1

'

































x

c

V

t

c

V

x

c

V

t

t

z

z

y

y

Vt

x

c

V

Vt

x

x

 

 

E.T.W.

E.T.W.

   

Wnioski wynikające z transformacji 

Lorentza.

• Jednoczesność

   Przyjmijmy, że według obserwatora w 

rakiecie poruszającej się wzdłuż osi x' (czyli 

także wzdłuż osi x, bo zakładamy, że te osie 

są równoległe) pewne dwa zdarzenia 

zachodzą równocześnie t' = t

2

' ‑ t

1

' = 0, ale 

w rożnych miejscach x

2

' ‑ x

1

' = x'  0. 

    Należy przeanalizować, czy te same 

zdarzanie są również jednoczesne dla 

obserwatora w spoczynku. 

 

 

 

 

E.T.W.

E.T.W.

 

 

 

 

 

 

E.T.W.

E.T.W.

 

 

 

 

 

 

 

 

 

 

Dziękuję za uwagę !!!