1

Wykład IX

Metody algorytmiczne

Algorytmy i struktury danych
Wyższa Szkoła Biznesu
Semestr III Informatyka
stosowana

2

Wiemy już prawie

wszystko, ale...

Wydaje się, że możemy teraz dalej pomyślnie podążać

naprzód w naszym algorytmicznym znoju.

– Wiemy jaką strukturę mają algorytmy i jak urządzić

obiekty, którymi manipulują;

– Wiemy również, jak je zapisać, aby wykonał je

komputer (języki programowania).

– Możemy zatem powiedzieć naszemu procesorowi,

co i kiedy ma robić.

Byłaby to jednak nazbyt naiwna ocena sytuacji i wkrótce

zobaczymy rozmaite tego przyczyny. Jedna z trudności

tkwi w fakcie, że nie podaliśmy żadnych metod,

których dałoby się użyć do wymyślenia algorytmu.

3

Od kawałków do całości

Łatwo się opowiada o konstrukcjach, z których
może korzystać algorytm (czyli o kawałkach, z
których może się składać), ale musimy
powiedzieć

nieco

więcej

o

sposobach

zabierania się do zbudowania całości z tych
kawałków.
Na tym wykładzie dokonamy przeglądu kilku
całkiem ogólnych metod algorytmicznych,
których może użyć projektant do znalezienia
rozwiązania zadania algorytmicznego.

4

Tworzenie algorytmów

to zadanie twórcze

Trzeba wszak zauważyć, że na obmyślanie przepisów nie ma

dobrych przepisów Każde takie zadanie stanowi ambitne

wyzwanie dla projektanta algorytmów.
Jedne zadania są proste, inne skomplikowane, a w wypadku

jeszcze innych nawet nadzieja na ich rozwiązanie jest

złudna.
Jedyne zatem co możemy pokazać to, że pewne algorytmy

całkiem zgrabnie wypływają z pewnych ogólnych wzorców.
Morałem niech będzie to, że projektant algorytmów

może odnieść korzyść wypróbowując właśnie te

wzorce w pierwszej kolejności. Jednak z całą pewnością

projektowanie algorytmów jest zajęciem twórczym, które

niekiedy może wymagać naprawdę ogromnej pomysłowości.

5

Poszukiwania i wędrówki

W wielu zadaniach algorytmicznych powstaje potrzeba

obejścia wszystkich elementów pewnej struktury.
Czasami struktura jest po prostu jedną z jawnie

dostępnych w algorytmie struktur danych;
Innym razem jest to jakaś struktura pośrednio w czymś

zawarta, której być może nie da się naprawdę

„zobaczyć”, ale która kryje się gdzieś pod powierzchnią;
Czasami szuka się w tej strukturze czegoś szczególnego

(„kto jest kierownikiem działu łączności z klientami?”);
Albo też pewną pracę należy wykonać w każdym

punkcie („oblicz średnią ocen wszystkich studentów”).

6

Przykłady

Na przykład widać od razu, że proste zadanie

sumowania zarobków z jednego z poprzednich

wykładów wymaga łatwego przejścia po danej liście

pracowników.
Z drugiej strony, o zadaniu, które dotyczyło jedynie

pracowników zarabiających więcej niż ich kierownicy

(patrz wykład: Algorytmy i dane), można pomyśleć,

że wymaga ono obejścia wyimaginowanej tablicy

dwuwymiarowej

o

wierszach

i

kolumnach

odpowiadających

poszczególnym

pracownikom.

Wykonując to obejście poszukujemy pewnych par

pracownik-kierownik.

7

Dobieramy odpowiednią

metodę obejścia

W takich przypadkach zadanie polega na

znalezieniu najbardziej naturalnego sposobu

obejścia

struktury

danych

(jawnej

bądź

niejawnej), z którą ma się do czynienia,

i wyprowadzeniu algorytmu właśnie stąd.
Kiedy w grę wchodzą wektory i tablice, wtedy

pojawiają się zwykle pętle i zagnieżdżone pętle,

co wyjaśniono na wykładzie Algorytmy i dane.
Kiedy w grę wchodzą drzewa, wtedy pojawia się

rekurencja, tak jak w przykładzie z sortowaniem

drzewiastym (ten sam wykład).

8

Pomysł nie zawsze jest

oczywisty

Co prawda, pomysł leżący u podstaw algorytmu

sortowania drzewiastego jest dosyć subtelny i nie

można nań wpaść wymyślając po prostu najlepszą

strukturę sterowania do obejścia danej struktury

danych.
Jeśli już jednak trafi się na ten pomysł, to

drobnostką jest zdanie sobie sprawy z tego, że

składanie odwiedzin za drugim przejściem, w

którym elementy wypisywane są według porządku,

nie jest niczym więcej niż pewnym sposobem

obejścia drzewa binarnego, skąd nietrudno dojść do

konkluzji, że należy użyć rekurencji.

9

Sposoby obchodzenia

drzew

Obejście wynikające z przyjęcia rekurencyjnej trasy

lewostronnej (sortowanie drzewiaste) bywa czasami

nazywane poszukiwaniem w głąb z nawracaniem, jako

że procesor „zanurza się” w drzewo próbując dostać się

najgłębiej, jak można, a kiedy nie może już dalej iść,

nawraca niechętnie, stale usiłując nurkować na nowo.

Jedyną dodatkowa cechą jest tu wymaganie, aby

nurkować jak najbardziej na lewo.
Są też inne sposoby obchodzenia drzew, z których jeden,

dualny wobec poszukiwania w głąb, otrzymał miano

poszukiwania wszerz. Obchodzenie wszerz oznacza, że

wyczerpuje się kolejno poziomy drzewa - najpierw korzeń,

potem całe jego potomstwo, następnie ich potomstwo itd.

10

Poszukiwanie -

Przykładowe zadania

Wiele

ciekawych

zadań

algorytmicznych

obraca się wokół pojęć geometrycznych, takich
jak punkty, linie i odległości, i stanowi zatem
część obszaru zagadnień znanych jako
geometria obliczeniowa.
Wiele problemów w tej dziedzinie wydaje się
wzrokowo

zwodniczo

„łatwymi”

do

rozwiązania, stanowią one jednak prawdziwie
ambitne zadanie dla projektantów algorytmów.

11

Oto jedno z prostszych

zadań

Przypuśćmy, że mamy prosty wielokąt wypukły

jak na rys. (następny slajd) i że interesuje nas

znalezienie takich dwóch punktów na jego

obwodzie, które dzieli największa odległość.
Przyjmujemy, że wielokąt jest przedstawiony jako

ciąg współrzędnych <X,Y> jego wierzchołków, w

kolejności zgodnej z ruchem wskazówek zegara.

Jako że największa odległość wystąpi dla dwóch

wierzchołków, nie ma potrzeby zwracania uwagi

na żadne inne punkty leżące wzdłuż boków

wielokąta różne od wierzchołków.

12

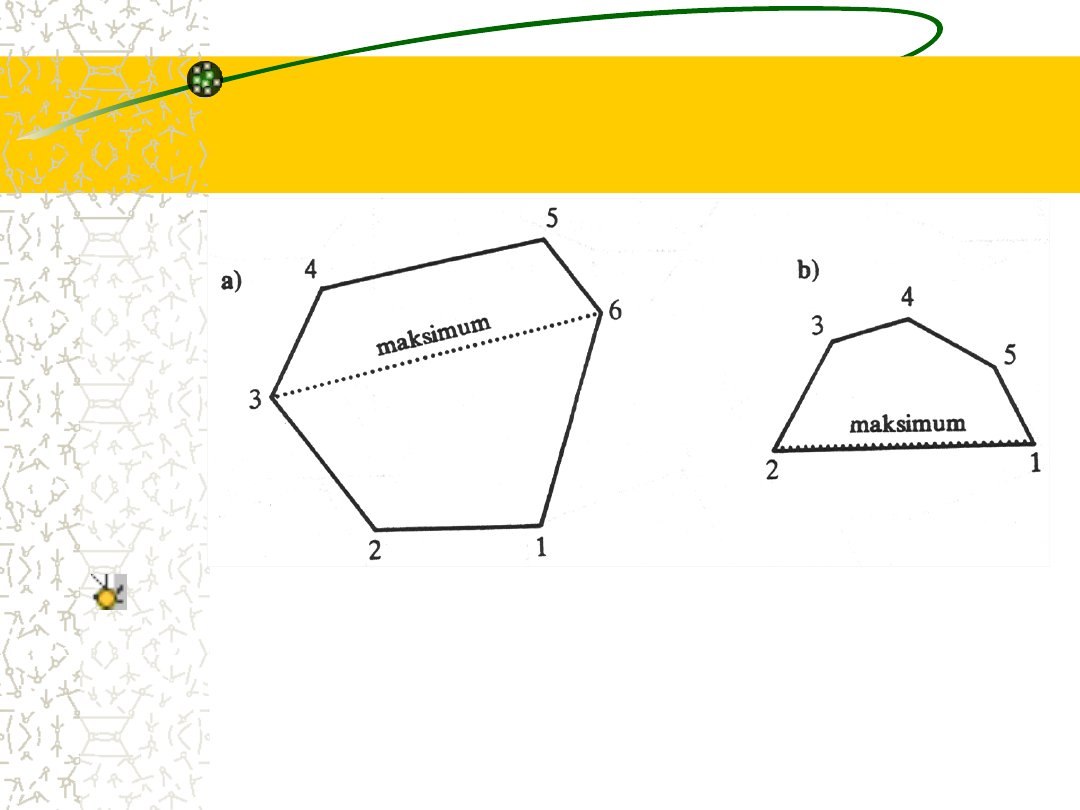
Dwa przykładowe

wielokąty wypukłe

Banalne rozwiązanie polegałoby na zbadaniu, w jakimś

porządku,

wszystkich

par

wierzchołków

i

przechowywałoby w zmiennych bieżące maksimum i

parę, która to maksimum osiąga.

13

Najprostsze rozwiązanie –

więcej szczegółów

Dla każdej nowej rozważanej pary w prosty sposób

oblicza się odległość, nową odległość porównuje się z

bieżącym maksimum i uaktualnia się zmienne, jeśli

okaże się, że jest ona większa, co oznacza, że stanowi

właśnie nowe maksimum.
Jeśli rozważymy przez chwilę to rozwiązanie, stanie się

jasne, że w istocie obchodzimy wyimaginowaną tablicę,

w której każdy wiersz i każda kolumna odpowiadają

pewnemu wierzchołkowi. Wyimaginowany element

danych tkwiący w pozycji <I, J> tej tablicy jest

odległością między wierzchołkami I a J. Obejścia można

łatwo dokonać przy pomocy dwóch zagnieżdżonych

pętli.

14

Czy istnieje lepsze

rozwiązanie ?

W tym rozwiązaniu jednak uwzględnia się o wiele za dużą liczbę

potencjalnych par; czyż nie powinno się rozważać tylko

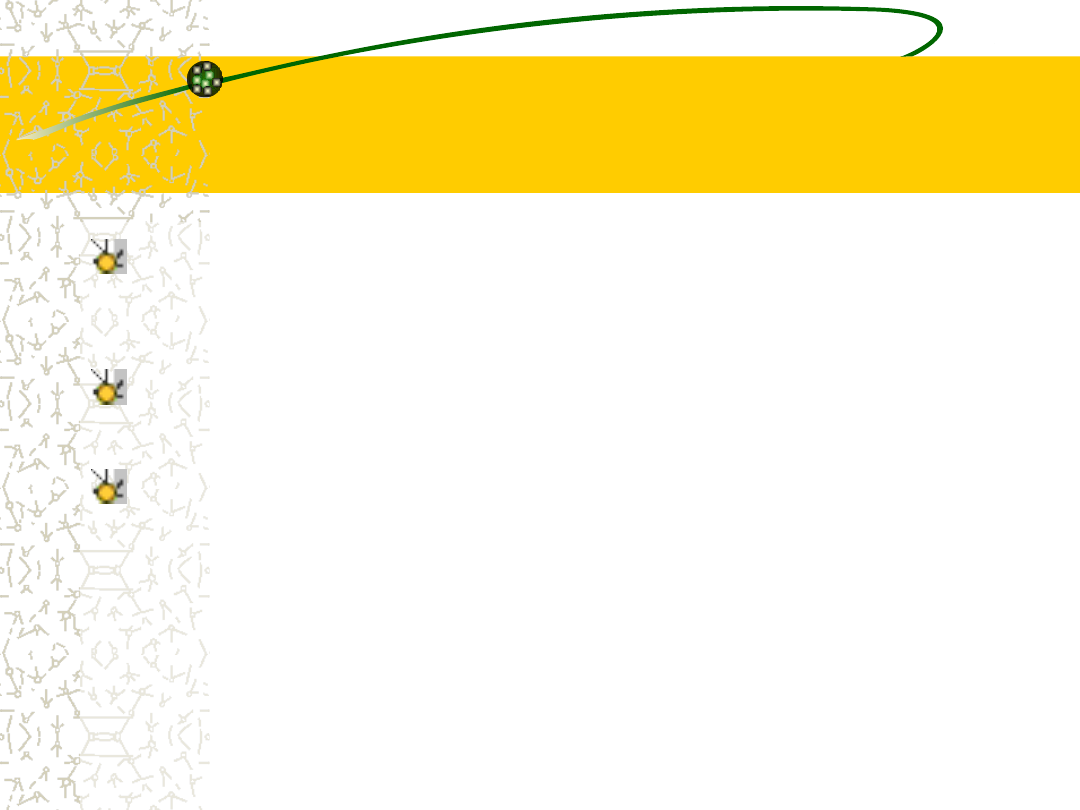
„przeciwległych” par punktów, takich jak <1,4>, <2,5> i <3,6)

z rys. a (dwa slajdy wstecz)?
Oznaczałoby to obejście jedynie wektora par „specjalnych”, a

nie tablicy wszystkich par, i dałoby oczywiście w wyniku

sprawniejszy algorytm, wymagający zaledwie pojedynczej pętli.
No cóż, nie jest to tak proste, jak się wydaje, ponieważ

przeciwległe pary, których sobie życzymy, nie muszą mieć

jednakowej liczby wierzchołków po każdej stronie; a na tym

samym rys. tylko w pkt. b pokazano wielokąt, w którym

maksimum występuje dla sąsiadujących wierzchołków, które

pominąłby algorytm rozważający tylko pary o przeciwległych

numerach.

15

Lepsze rozwiązanie

w którym rzeczywiście stosuje

się tylko jedną pętlę i rozważa

tylko „właściwy” gatunek

przeciwległych par,

przedstawiono na rys. obok.

Najpierw „rysuje” się linię

prostą wzdłuż krawędzi <1,2>,

czyli krawędzi między

wierzchołkami 1 i 2. Następnie

do wielokąta, z jego drugiej

strony, stopniowo przysuwa

przysuwa się linię równoległą do poprzedniej dopóty, dopóki
nie natrafi na jeden z wierzchołków. Za pierwsze
przybliżenie szukanego maksimum przyjmuje się większą z
odległości między tym wierzchołkiem a wierzchołkami 1 i 2.

16

Lepsze rozwiązanie

(cd.)

Potem rozpoczyna się ruch w kierunku zgodnym z obiegiem

wskazówek zegara. Każdy krok obejmuje obrót jednej z dwóch linii

tak, aby leżała wzdłuż krawędzi następnej w tym kierunku, i

dopasowanie drugiej linii tak, aby obie przebiegały równolegle. Którą

z linii obrócić, a którą dopasować, ustala się porównując wysiłek

niezbędny do wykonania obrotu; obraca się linię tworzącą mniejszy

kąt z następną krawędzią. Po zakończeniu obrotu mamy nowy

wierzchołek leżący na właśnie obróconej linii.
Obliczoną odległość między tym wierzchołkiem a wierzchołkiem

leżącym na linii dopasowanej porównuje się, jak poprzednio, z

bieżącym maksimum. Wszystko to wykonuje się dookoła całego

wielokąta. Wszelkie akcje wymagane przez ten algorytm obejmują

proste manipulacje numeryczne współrzędnymi wierzchołków,

wynikające z elementarnej geometrii analitycznej. Pozostałe rysunki

ilustrują kolejność przekształceń dokonywanych na tych liniach.

17

W poszukiwaniach

przydaje się wnikliwość

Wybrano ten przykład, aby dodatkowo
zilustrować fakt, że samo zauważenie
potrzeby obejścia czegoś i wymyślenie, co
naprawdę trzeba obejść, jest ważne i
może stanowić istotną pomoc, ale nie
zawsze

wystarczy

do

rozwiązania

trudniejszych zadań algorytmicznych.
Odrobina wnikliwości i sporo wiedzy z
danej dziedziny nigdy tu nie zawadzą.

18

Dziel i zwyciężaj

Często można uporać się z zadaniem sprowadzając je
do mniejszych zadań tego samego rodzaju i
rozwiązując je. Później można połączyć te częściowe
rozwiązania w rozwiązanie ostateczne pierwotnego
zadania.
Jeśli te mniejsze zadania są dokładnie tym samym
zadaniem, z którym mamy do czynienia, lecz
postawionym wobec „mniejszych” lub „prostszych”
danych, to oczywiście w algorytmie można użyć
rekurencji.
Nazwa tej metody jest oczywista: dziel i zwyciężaj.

19

„Dziel i zwyciężaj”

widzieliśmy w przykładzie

z Wieżami Hanoi

Sam

pomysł

widzieliśmy

już

pośrednio w przykładzie Wież
Hanoi: algorytm uporał się z
zadaniem

dla

N

krążków

rozwiązując,

w

odpowiednim

porządku

i

kontekście,

dwa

zadania dla N-1 krążków.

20

Inny przykład

zastosowania podziałów i

zwycięstw

Wyobraź sobie, że wręczono ci książkę telefoniczną o

porozrzucanych kartkach lub że - co zabrzmi

poważniej - otrzymałeś nieuporządkowaną listę L.
Interesuje nas nie posortowanie listy L, lecz tylko

znalezienie jej najmniejszego i największego

elementu. Jasne, że możemy po prostu raz przebiec

tę listę, przechowując w zmiennych bieżące

maksimum i minimum, i cały czas porównywać z

nimi każdy element.
Algorytm, który teraz podamy, opiera się na strategii

„dziel i zwyciężaj” i jest nieco lepszy niż naiwny

algorytm wspomniany powyżej.

21

Schemat algorytmu szukania

minimum i maksimum wg.

„dziel i zwyciężaj”

(1) jeśli lista L składa się z jednego elementu, to ten

element stanowi zarówno minimum, jak i maksimum;

jeśli składa się ona z dwóch elementów, to mniejszy z

nich stanowi minimum, a większy - maksimum;

(2) w przeciwnym razie wykonaj, co następuje:

(2.1)

podziel listę L na połowy, L

1

i L

2

;

(2.2)

znajdź ich skrajne elementy MIN1, MAX1, MIN2

i MAX2;

(2.3)

wybierz mniejszy z MIN1 i MIN2; to właśnie jest

element minimalny listy L;

(2.4)

wybierz większy z MAX1 i MAX2; to właśnie jest

element maksymalny listy L.

22

Zastosowanie rekurencji

wymaga zwrócenia przez

podprogram wyników

Wiersz (2.2) aż woła o wykonanie go rekurencyjnie, jako że

występujące tam zadania do rozwiązania są dokładnie zadaniami

min-i-max dla krótszych list L

1

i L

2

.

Zwykła próba sklecenia tej rekurencji nastręcza tylko pewną

drobną trudność: mianowicie to, że w tym miejscu, w

przeciwieństwie

do

procedury

Wież

Hanoi,

wywołanie

rekurencyjne musi dostarczyć wyników, których trzeba użyć w

dalszej części.
Procesor musi w jakiś sposób nie tylko zapamiętać swój adres

powrotny i to, jak przywrócić w swym otoczeniu sytuację

poprzedzającą wyprawienie się na tę rekurencyjną wycieczkę,

ale musi móc przywieźć z powrotem ze swej wyprawy wyniki. W

tym przypadku byłoby najkorzystniejsze, gdyby procesor mógł

powrócić z rekurencyjnego wywołania razem z żądanym

minimum i maksimum.

23

Rekurencyjne min-i-max

realizujące metodę dziel i

zwyciężaj

procedura znajdź-min-i-max-w L:
(1)jeśli lista L składa się z jednego elementu, to nadaj MIN i MAX

właśnie jego wartość; jeśli L składa się z dwóch elementów, to

nadaj MIN wartość mniejszego z nich, a MAX - większego;

(2)w przeciwnym razie wykonaj co następuje:

(2.1)

podziel listę L na połowy, L

1

i L

2

;

(2.2)

wywołaj znajdź-min-i-max-w L

1

; umieszczając

otrzymane w wyniku wartości w MIN1 i MAX1;

(2.3)

wywołaj znajdź-min-i-max-w L

2

, umieszczając

otrzymane w wyniku wartości w MIN2 i MAX2;

(2.4)

nadaj MIN mniejszą wartość z MIN1 i MIN2;

(2.5)

nadaj MAX większą wartość z MAX1 i MAX2;

(3)

wróć z wartościami MIN i MAX.

24

Nie tylko min i max

Zastosowanie paradygmatu „dziel i zwyciężaj” może

przynieść wiele dobrego przy sortowaniu listy, a nie

tylko przy znajdowaniu w niej skrajnych elementów.
Aby posortować listę L zawierającą co najmniej dwa

elementy, możemy podobnie podzielić ją na połówki L

1

i L

2

i posortować je rekurencyjnie.

Przypadek

pojedynczego

elementu

traktuje

się

oddzielnie, tak jak w przykładzie z min-i-max.
Aby otrzymać ostatecznie posortowaną wersję listy L,

dalej możemy scalić posortowane połówki. Aby scalić

dwie posortowane listy, w kółko wybieramy i dołączamy

do listy wynikowej mniejszy z dwóch elementów akurat

znajdujących się na obu początkach list.s

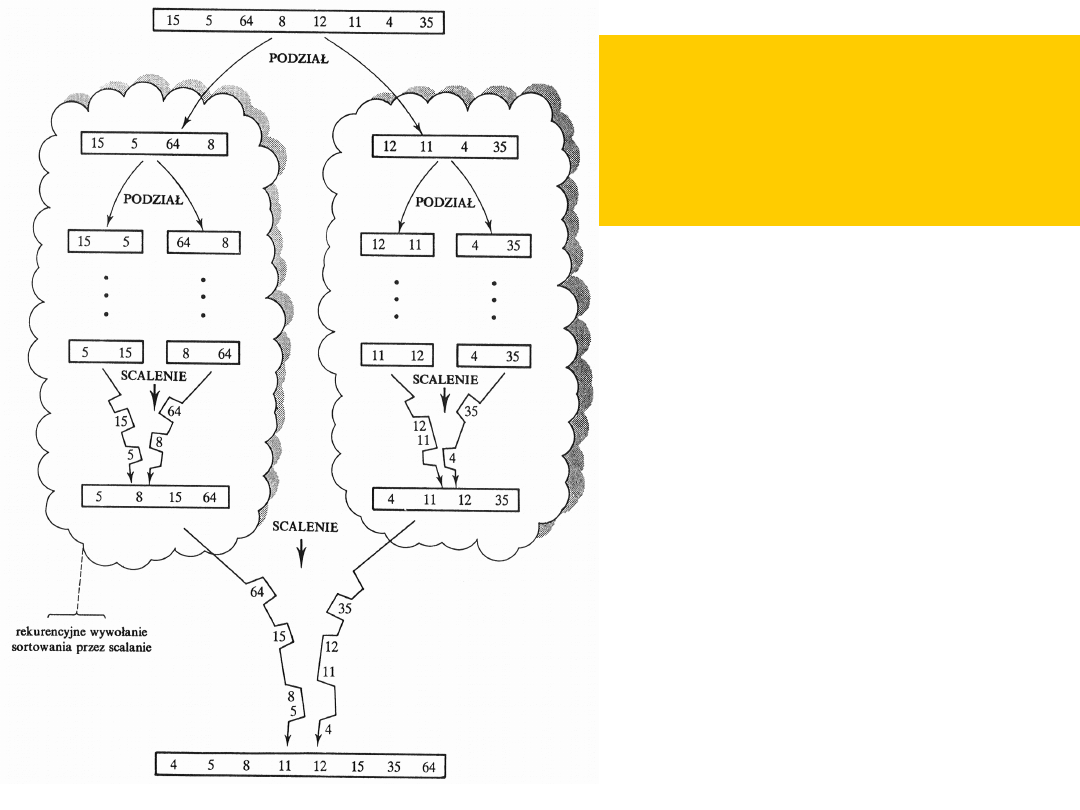
Sposób działania

algorytmu

sortowania przez

scalanie

Sortowanie przez
scalanie

jest

znacznie

lepsze

zarówno

od

sortowania
bąbelkowego, jak
i drzewiastego.

26

Zachłanne algorytmy i

budowniczowie kolei

Wiele zadań algorytmicznych wymaga dostarczenia wyniku,

który jest w jakimś sensie najlepszy z odpowiedniego zestawu

możliwości.
Rozważmy teraz sieć miast i leniwego przedsiębiorcę

budującego kolej. Przedsiębiorcy zapłacono za takie ułożenie

torów, aby z każdego miasta można było dotrzeć do każdego

innego.
W umowie nie ustalono żadnych kryteriów, takich jak

potrzeba wykonania pewnych bezpośrednich połączeń czy

największa dopuszczalna liczba miast leżących na drodze

między każdymi dwoma.
Naszego przedsiębiorcę, jako że jest leniwy, interesuje

ułożenie najtańszej (czyli najkrótszej) kombinacji odcinków

szyn.

27

Założenia

Przyjmijmy, że z przyczyn obiektywnych, takich jak
przeszkody naturalne, nie każde miasto można
połączyć

bezpośrednimi

odcinkami

szyn

ze

wszystkimi innymi i że odległości podano jedynie dla
par miast możliwych do bezpośredniego połączenia.
Przyjmijmy

dalej,

że

koszt

bezpośredniego

połączenia miasta A z miastem B jest proporcjonalny
do odległości między nimi. Co więcej, nie
dopuszczamy

skrzyżowań

i

rozjazdów

poza

miastami.

28

Grafy

Taka

sieć

nazywa

się

grafem

etykietowanym lub krócej grafem.
Grafy przypominają drzewa, tyle że drzewa
nie mogą „zrastać się” gałęziami, a więc
nie mogą zawierać cykli albo pętli,
podczas gdy grafy mogą.
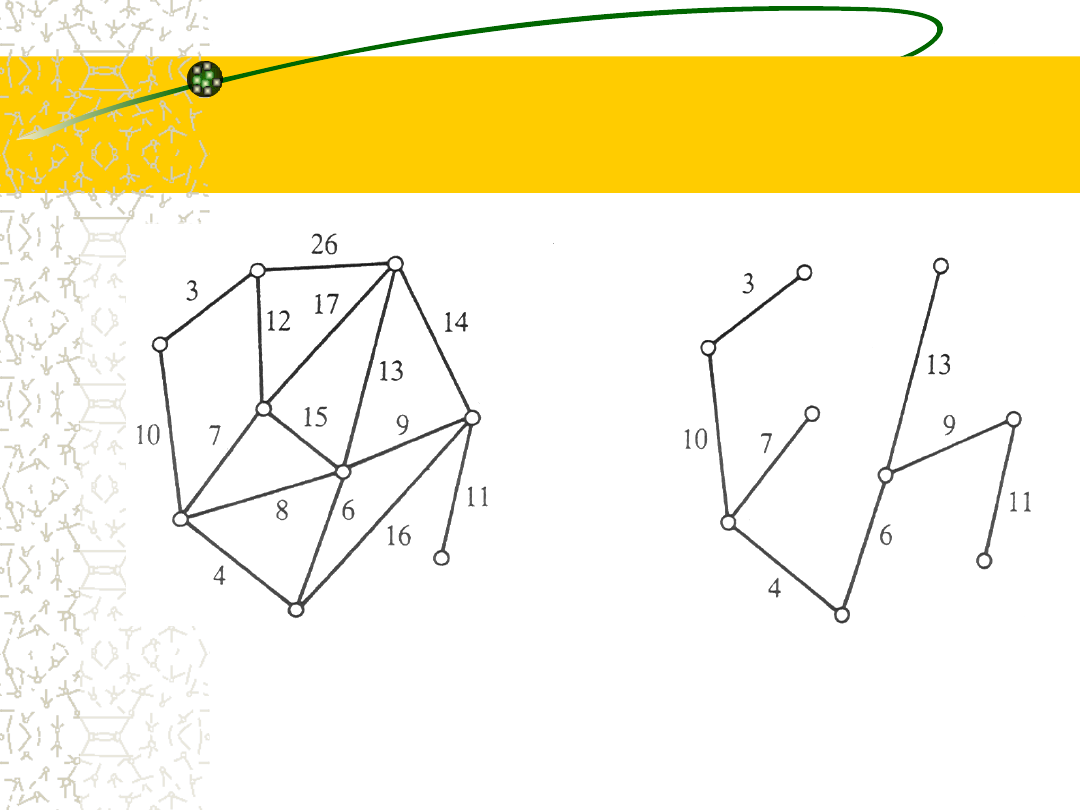
Przykład grafu miast i jego minimalnej sieci
kolejowej widzimy na rys. na następnym
slajdzie.

29

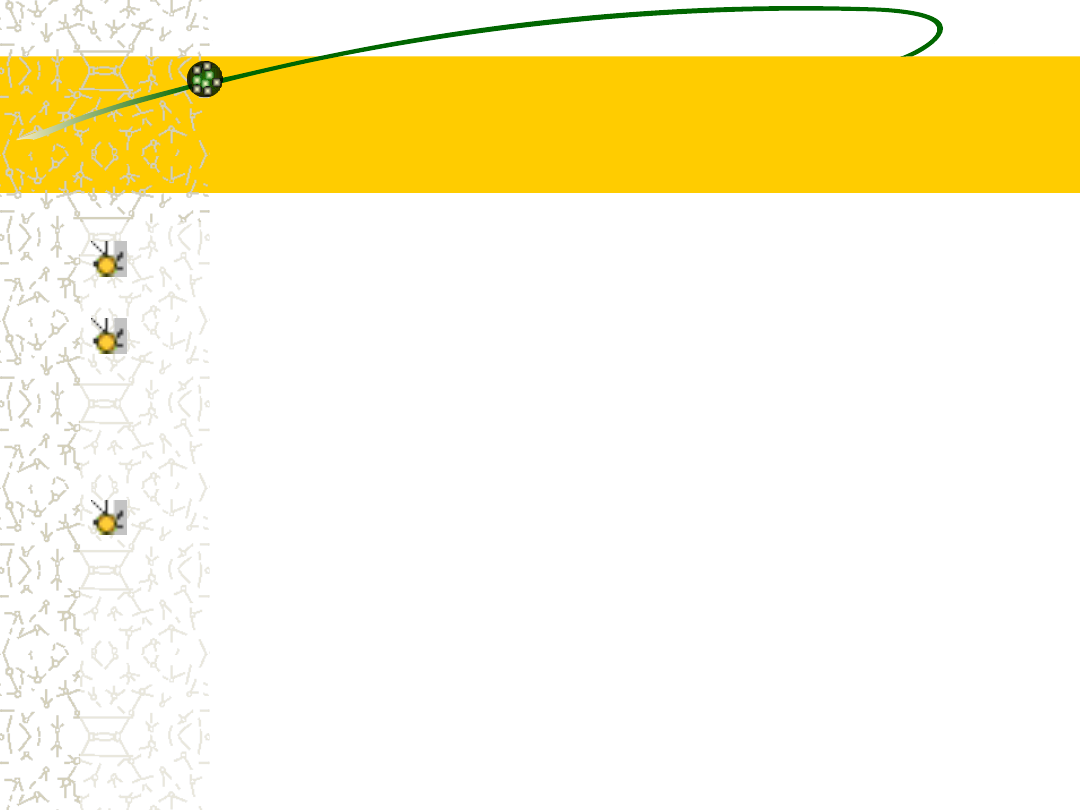
Sieć miast i jej

minimalna rozpinająca

sieć kolejowa

(Rysunek nie zachowuje proporcji) Całkowity koszt 63

30

Minimalne drzewo

rozpinające

Zauważmy, że budowniczemu zależy naprawdę na tym,

co nazywamy minimalnym drzewem rozpinającym.
To takie drzewo, na którym jest „rozpięty” graf w tym

sensie, że dociera ono do dokładnie każdego z węzłów

(w naszym przypadku miast) i które jest najtańszym z

takich drzew w tym sensie, że suma etykiet znajdujących

się przy krawędziach jest najmniejsza z możliwych.
Żądane rozwiązanie musi być oczywiście drzewem,

gdyż w przeciwnym razie musiałoby zawierać jakiś cykl,

a leniwy przedsiębiorca mógłby otrzymać tańszą sieć

kolejową,

nadal

łączącą

wszystkie

miasta,

eliminując jeden z odcinków tego cyklu.

31

Metoda zachłanna

Jest pewne algorytmiczne podejście do takich zadań,

zwane zachłanną metodą.
Zaleca ono konstruowanie minimalnego drzewa

rozpinającego krawędź po krawędzi, w drodze

wybierania jako następnej krawędzi zawsze tej, która

jest najlepsza z punktu widzenia bieżącej sytuacji.
Naprawdę oznacza to przyjęcie filozofii rodzaju

„jedzmy i pijmy dziś, bo jutro może już nas nie

będzie”.
W przypadku rozpinających sieci kolejowych można

prowadzić tą konstrukcję na przykład tak, jak

pokazano na rys.

32

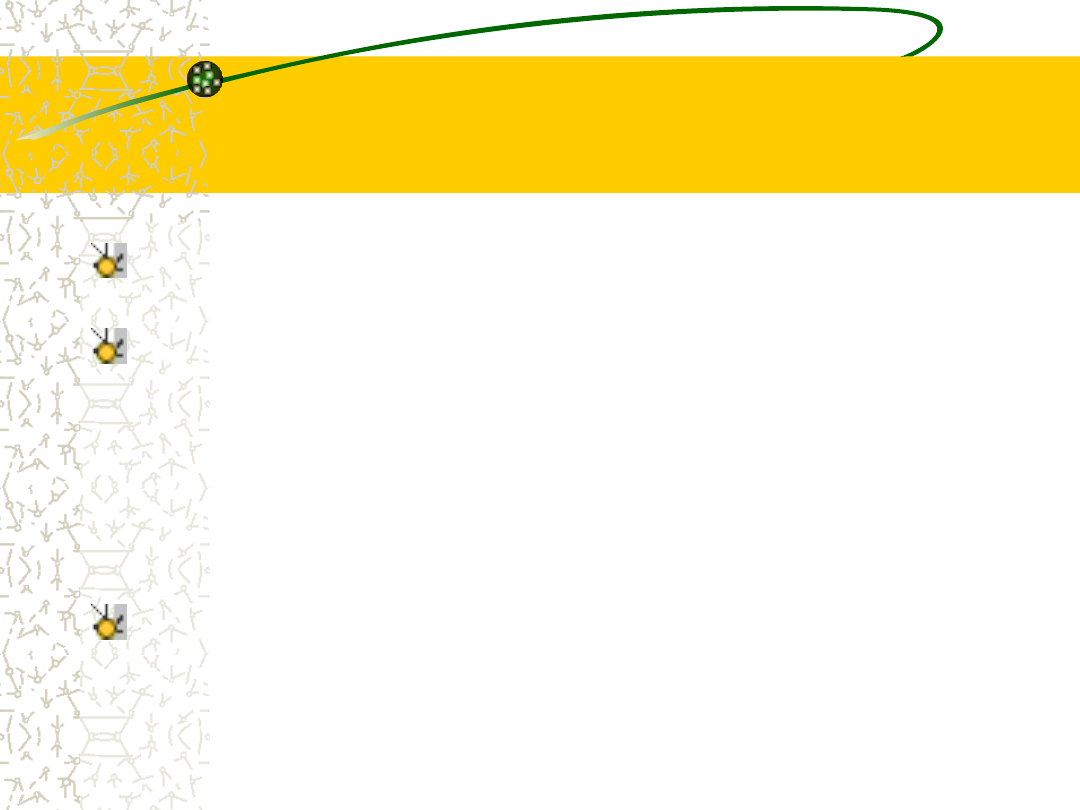
Działanie zachłannego

algorytmu znajdowania min.

drzewa rozpinającego

33

Sposób poszukiwania

minimalnego drzewa

rozpinającego

Zacznijmy

od

zdegenerowanego

drzewa

składającego się z najtańszej krawędzi grafu.
W każdym kroku rozbudowujemy skonstruowane

dotychczas drzewo, dodając do niego najtańszą z

krawędzi nie wziętych dotąd pod uwagę, które dają

nowe drzewo (w szczególności dodanie tej krawędzi

nie powinno doprowadzić do powstania cyklu; jeśli

doprowadza do tego, przechodzimy do krawędzi

następnej w porządku rosnących kosztów).
Można wykazać, że ta prosta strategia w rezultacie

rzeczywiście daje minimalne drzewo rozpinające.

34

Zachłanność nie zawsze

się opłaca

Zachłanne

algorytmy

istnieją

dla

ogromnego mnóstwa ciekawych zadań

algorytmicznych.
Zwykle można je łatwo wynaleźć i w

niektórych przypadkach bywają bardzo

intuicyjne.
Trudna część polega zwykle na pokazaniu,

że zachłanna strategia rzeczywiście działa,

a jak zobaczymy za chwilę, są sytuacje, w

których zachłanność zupełnie nie popłaca.

35

Dynamiczne planowanie

i znużeni wędrowcy

Oto zadanie podobne do znajdowania minimalnego drzewa

rozpinającego,

ale

opierające

się

zachłannym

próbom

rozwiązania.
Dotyczy ono również sieci miast, ale zamiast leniwego

budowniczego kolei mamy tu znużonego wędrowca, który musi

dostać się z jednego miasta do drugiego.
Chociaż obaj mają przed sobą zadanie do wykonania i chcą

zminimalizować jego ogólny koszt, jest między nimi zasadnicza

różnica: podczas gdy budowniczy ma połączyć siecią torów

wszystkie miasta, wędrowiec odwiedzi na ogół tylko

niektóre z nich.
Jest zatem jasne, że wędrowiec nie szuka minimalnego drzewa

rozpinającego. Szuka raczej minimalnej ścieżki, czyli najtańszej

drogi wiodącej od początkowego miasta do miasta przeznaczenia.

36

Założenia: graf jest

skierowany, spójny i

acykliczny

Aby ułatwić sobie prezentację tego zadania,

przyjmiemy, że wszystkie linie w grafie miast są

skierowane, co oznacza, że jeśli istnieje jakieś

bezpośrednie połączenie między tymi dwoma

miastami, jest to połączenie w jedną stronę.
Przyjmiemy też, że graf jest spójny, co znaczy, że z

każdego miasta można w końcu dotrzeć do każdego

innego.
Założymy dalej, że graf miast nie zawiera cykli, tak że

naprawdę znużony wędrowiec nie będzie narażony na

błąkanie się w kółko, gdyż takich kółek po prostu nie

ma. Nasz układ - to skierowany graf acykliczny.

37

Zachłanne podejście do

zadania

Mamy zatem taki graf i wędrowiec ma dotrzeć z miasta A
do B.
Zachłanne podejście do tego zadania dałoby w wyniku
następującą ścieżkę. Zaczęlibyśmy od A i dodawalibyśmy
ciągle, aż do osiągnięcia docelowego miasta B, do
bieżącej

częściowej

ścieżki

najtańszą

krawędź

wychodzącą z właśnie osiągniętego miasta i prowadzącą
do miasta jeszcze nie odwiedzonego.
Przykład zastosowania tego robiącego naturalne wrażenie
algorytmu do grafu, w którym koszt minimalnej ścieżki
między A i B wynosi 13 jednostek, pokazano na rys.
(następny slajd).

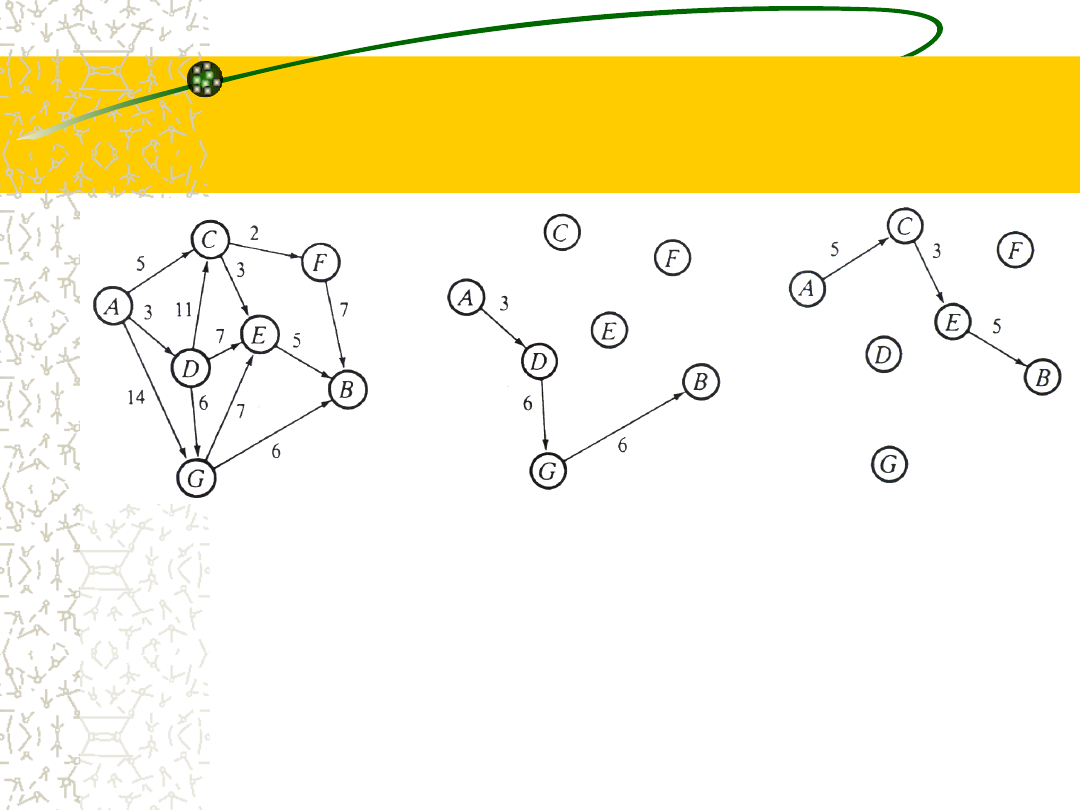
38

Algorytm musi być

bardziej wnikliwy

Nasz zachłanny algorytm znajduje ścieżkę o koszcie 15

jednostek, co jest nieco gorsze. Zachłanność w tym miejscu

nie popłaca, jako że sprytny algorytm musi być

dostatecznie wnikliwy, aby wybrać krawędź o długości 5

prowadzącą do C, a potem krawędź o długości 3 do E, mimo

że taki wybór lokalnie nie wygląda najbardziej obiecująco.

39

Planowanie dynamiczne

Inna, już nie zachłanna, metoda
algorytmiczna, zwana planowaniem
dynamicznym, sprawia, że można
dokonywać tak subtelnych wyborów.
Planowanie dynamiczne opiera się na
wysubtelnieniu

dość

zgrubnego

kryterium

używanego

przy

natychmiastowej zachłanności.

40

Idea planowania

dynamicznego

Tę metodę można opisać abstrakcyjnie w następujący

sposób.
Przypuśćmy,

że

rozwiązanie

pewnego

zadania

algorytmicznego ma składać się z optymalnego ciągu

wyborów. Jak już wykazaliśmy, całkiem możliwe, że

wybieranie z każdego lokalnego ciągu możliwości

najbardziej obiecującego wariantu nie doprowadzi do

powstania ciągu optymalnego.
Jednak często zdarza się, że można otrzymać ciąg

optymalny rozważając wszystkie kombinacje powstałe z:

a) dokonania konkretnego wyboru
b) znalezienia optymalnej części ciągu pozostałych wyborów.

41

Trzeba poszukać kilku

ścieżek i je porównać

Na przykład na rys. długość najkrótszej ścieżki wiodącej

z A do B jest najmniejszą z trzech liczb otrzymanych

przez wybranie najpierw jednego z miast C, G i D

(bezpośrednio osiągalnych z A), a potem dodanie jego

odległości od A do długości najkrótszej ścieżki

prowadzącej zeń do B.
Oznaczywszy długość najkrótszej ścieżki z X do B przez

L(X), możemy symbolicznie napisać

L(A)=minimum z 5+L(C), 14+L(G), 3+L(D)

(zob. rys.) Oznacza to, że możemy znaleźć ścieżkę

optymalną znajdując trzy „mniejsze” ścieżki optymalne,

a później wykonując kilka dodawań i porównań.

42

Ten proces można

kontynuować

L(D)=minimum z 7+L(E), 6+L(G), 11+L(C)

Kiedy już taki wywód doprowadzi do wyrażeń

zawierających L(B) (tj. minimalną odległość z B do

siebie samego), nie trzeba nam niczego więcej, gdyż

nawet całkiem wyczerpany wędrowiec wie, że L(B)=0,

na mocy faktu, że najlepszym sposobem dojścia z B

do B jest po prostu pozostanie tam, gdzie się stoi.
Te spostrzeżenia prowadzą do algorytmu planowania

dynamicznego

rozwiązującego

ogólne

zadanie

znużonego wędrowca (czasami nazywane zadaniem

znajdowania najkrótszej ścieżki).

43

Ogólne rozwiązanie

zadania poszukiwania

najkrótszej ścieżki

Jeśli miastami są C

1

, ..., C

N

, a droga ma się

rozpocząć w C

1

i skończyć w C

N

, to algorytm

wymaga obliczenia optymalnej drogi częściowej

L(C

I

), przedstawiającej najkrótszą ścieżkę z C

I

do

miasta docelowego C

N

dla każdego I między 1 a N.

Jednak L(C

I

) stanowi minimum ze wszystkich sum

postaci

odległość-z-C

I

-do-C

K

+L(C

K

)

przy czym w obliczaniu minimum uwzględnia się

wszystkie miasta C

K

, do których prowadzą

bezpośrednio krawędzie z C

I

.

44

Ogólne rozwiązanie

zadania poszukiwania

najkrótszej ścieżki

(cd.)

Ponieważ wszystkie krawędzie są jednokierunkowe,

a graf nie zawiera cykli, możemy w ten sposób

obliczyć wszystkie L(C

I

) posuwając się z B do tyłu.

Patrząc na rysunek obliczamy najpierw wprost L(F),

L(E) i L(G) i otrzymujemy odpowiednio 7, 5 i 6;

potem obliczamy L(C) jako minimum z 2+L(F) i

3+L(E) (w tym wypadku 8); potem L(D) itd., aż

wreszcie

otrzymamy

L(A).

Równocześnie

powinniśmy śledzić tak skonstruowaną ścieżkę

biegnącą do tyłu z B do A, jest bowiem ścieżką

optymalna, której szukamy.

45

Narzucająca się tu
rekurencja nie jest

optymalnym

rozwiązaniem

Pojawia się pokusa napisania rekurencyjnej procedury opartej

na obliczaniu L(C

I

) na podstawie L(C

K

) tak, jak opisano powyżej.

A jednak byłoby to błędem. Powód jest taki, że ta sama

optymalna ścieżka częściowa może być potrzebna w więcej niż

jednej „większej” ścieżce, a naiwny algorytm rekurencyjny

będzie obliczać ją wciąż na nowo.
Na rys.odległości L(E) używa się do obliczania zarówno L(C) jak

i L(D), a zatem procesor wykonujący naszkicowaną przed

chwilą procedurę obliczy tę ścieżkę dwukrotnie.
W planowaniu dynamicznym będzie właściwe iteracyjne

obliczenie wszystkich L(C

I

) w porządku wstecznym i

przechowanie ich w tablicy, tak że gdy raz już obliczy się,

powiedzmy, odległość L(E), to można jej będzie użyć powtórnie

wyszukując tę wartość w tablicy, a nie obliczając ją na nowo.

46

To nic innego jak daleko

posunięta metoda „Dziel i

zwyciężaj”

O planowaniu dynamicznym można myśleć jako o

strategii „dziel i zwyciężaj” posuniętej do

ostateczności:

wszystkie

zadania

częściowe

rozwiązuje się w kolejności wzrastania ich rozmiaru,

a wyniki przechowuje się w jakiejś strukturze

danych, tak aby ułatwić otrzymanie rozwiązań

większych zadań.
Tę metodę można stosować do wielu znacznie

bardziej

wymyślnych

zadań,

które

do

przechowywania częściowych wyników wymagają

struktur danych bardziej złożonych niż zwykłe

wektory.

47

Metody algorytmiczne

-podsumowanie

Jest niewiele powszechnie przyjętych wzorców

postępowania, na tyle ogólnych, aby można je

było nazwać metodami algorytmicznymi.
Większość lepiej znanych metod już opisaliśmy.
Mimo to, nawet bez stawiania sobie za

konkretny

cel

uzyskania

ogólnych

paradygmatów, informatycy wciąż poszukują

lepszych metod rozwiązywania coraz to

trudniejszych zadań algorytmicznych.