Sieci Bezprzewodowe

Sieci Bezprzewodowe

Wykład 3

Wykład 3

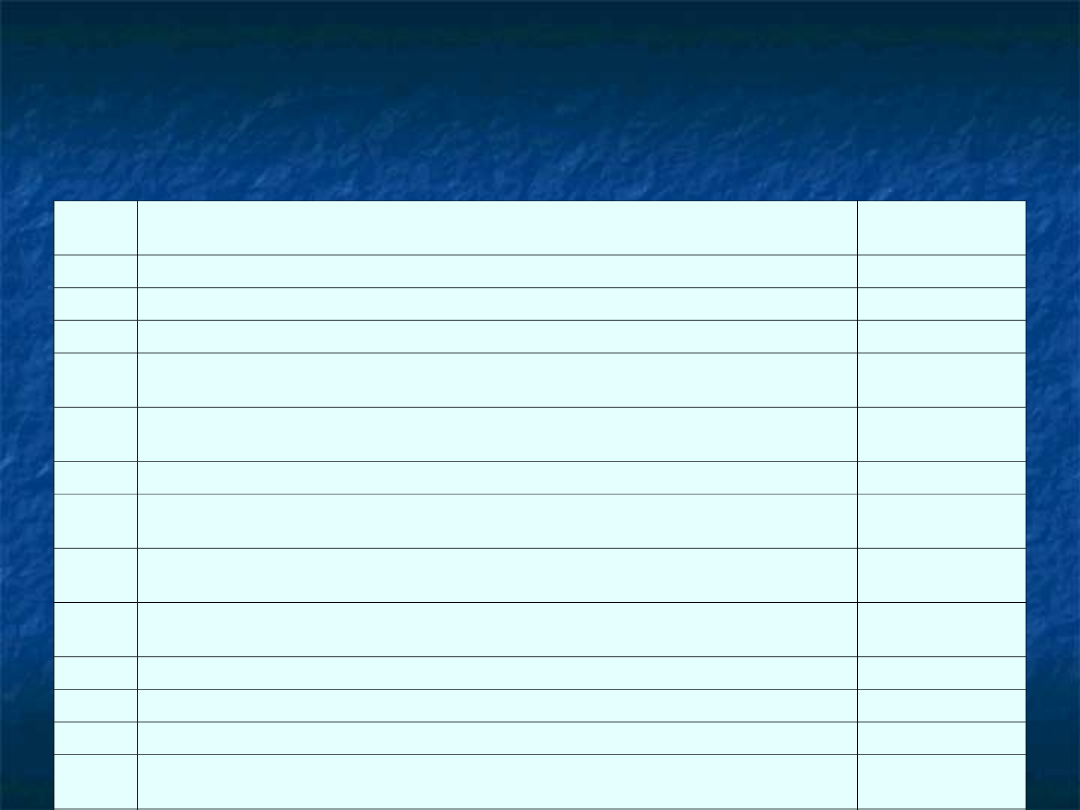
Względne szybkości wybranych

Względne szybkości wybranych

metod modulacji

metod modulacji

Typ

Metoda modulacji

Szybkość

[b/s/Hz]

AM

OOK (kluczowanie amplitudy) - detekcja koherentna

0,8

 

QAM (4-wartościowa modulacja amplitudy)

1,7

 

QPR (4-wartościowa modulacja o częściowej odpowiedzi)

2,25

FM

FSK (kluczowanie z przesuwem częstotliwości) - detekcja
niekoherentna

0,8

 

CP-FSK (kluczowanie z przesuwem częstotliwości o ciągłej fazie) -
detekcja niekoherentna

1,0

 

MSK (szybkie kluczowanie z przesuwem częstotliwości)

1,0

 

DE-MSK (szybkie kluczowanie z przesuwem częstotliwości kodowane
różnicowo)

1,9

PM

BPSK (binarne kluczowanie z przesuwem fazy) - detekcja
koherentna

0,8

 

DE-BPSK (binarne kluczowanie z przesuwem fazy kodowane
różnicowo)

0,8

 

DPSK (różnicowe kluczowanie z przesuwem fazy)

0,8

 

QPSK (4-wartościowe kluczowanie z przesuwem fazy)

1,9

 

DQPSK (różnicowe 4-wartościowe kluczowanie z przesuwem fazy)

1,8

 

8-F PSK (8-wartościowe kluczowanie z przesuwem fazy) detekcja
koherentna

2,6

 

16-F PSK (16-wartościowe kluczowanie z przesuwem fazy) detekcja
koherentna

2,9

AM/P
M

16-F APK (16-wartościowe kluczowanie z przesuwem amplitudy i
fazy)

3,1

Dwa różne rodzaje detekcji

Dwa różne rodzaje detekcji



detekcja koherentna

detekcja koherentna

, wymagająca

, wymagająca

odtworzenie sinusoidalnego sygnału

odtworzenie sinusoidalnego sygnału

odniesienia po stronie odbiorczej ,

odniesienia po stronie odbiorczej ,

zsynchronizowanego w częstotliwości i

zsynchronizowanego w częstotliwości i

fazie z odebranym sygnałem nośnym,

fazie z odebranym sygnałem nośnym,



detekcja niekoherentna

detekcja niekoherentna

, nie wymagająca

, nie wymagająca

precyzyjnego odtworzenia fali nośnej po

precyzyjnego odtworzenia fali nośnej po

stronie odbiorczej.

stronie odbiorczej.

Metody wielodostępu w

Metody wielodostępu w

systemach z widmem

systemach z widmem

rozproszonym

rozproszonym

Metody wielodostępu:

Metody wielodostępu:



wielodostęp z podziałem czasu (TDMA),

wielodostęp z podziałem czasu (TDMA),



wielodostęp z podziałem częstotliwości

wielodostęp z podziałem częstotliwości

(FDMA),

(FDMA),



wielodostęp kodowy (CDMA).

wielodostęp kodowy (CDMA).

Metody wielodostępu –

Metody wielodostępu –

TDMA

TDMA



Wielodostęp z podziałem czasu (Time

Wielodostęp z podziałem czasu (Time

Division Multiple Access).

Division Multiple Access).



każda stacja nadaje w określonej szczelinie

każda stacja nadaje w określonej szczelinie

czasowej.

czasowej.

Metody wielodostępu –

Metody wielodostępu –

FDMA

FDMA



Wielodostęp z podziałem częstotliwości

Wielodostęp z podziałem częstotliwości

(Frequency Division Multiple Access).

(Frequency Division Multiple Access).



każda stacja nadaje na swojej

każda stacja nadaje na swojej

częstotliwości.

częstotliwości.

Metody wielodostępu –

Metody wielodostępu –

FDMA

FDMA



Wielodostęp kodowy (Code Division Multiple

Wielodostęp kodowy (Code Division Multiple

Access).

Access).



Każda stacja moduluje nadawany sygnał swoim

Każda stacja moduluje nadawany sygnał swoim

kodem – rozpraszanie widma.

kodem – rozpraszanie widma.

Systemy z widmem

Systemy z widmem

rozproszonym

rozproszonym

Zalety:

Zalety:



utrudnione jest wykrywanie i rozpoznawanie takich

utrudnione jest wykrywanie i rozpoznawanie takich

sygnałów oraz przechwytywanie transmitowanej

sygnałów oraz przechwytywanie transmitowanej

informacji,

informacji,



sygnał ma wysoką odporność na zakłócenia, w tym

sygnał ma wysoką odporność na zakłócenia, w tym

na zniekształcenia spowodowane propagacją

na zniekształcenia spowodowane propagacją

wielodrogową,

wielodrogową,



możliwa jest praca we wspólnym kanale przy

możliwa jest praca we wspólnym kanale przy

niskich mocach nadajników,

niskich mocach nadajników,



pojemność systemu ograniczona jest nie liczbą

pojemność systemu ograniczona jest nie liczbą

kanałów, lecz wartością graniczną stosunku sygnału

kanałów, lecz wartością graniczną stosunku sygnału

do szumów i może być zmieniana dynamicznie.

do szumów i może być zmieniana dynamicznie.

Systemy z widmem

Systemy z widmem

rozproszonym

rozproszonym

Miarą jakości systemów z widmem rozproszonym jest zysk

Miarą jakości systemów z widmem rozproszonym jest zysk

przetwarzania (ang.

przetwarzania (ang.

processing gam

processing gam

), określany jako

), określany jako

różnica między stosunkiem sygnału do szumu na wyjściu

różnica między stosunkiem sygnału do szumu na wyjściu

i na wejściu układu. W systemie z rozpraszaniem widma

i na wejściu układu. W systemie z rozpraszaniem widma

zysk przetwarzania jest równy stosunkowi szerokości

zysk przetwarzania jest równy stosunkowi szerokości

pasma sygnału w kanale radiowym

pasma sygnału w kanale radiowym

B

B

ss

ss

[Hz] do szerokości

[Hz] do szerokości

pasma sygnału informacyjnego

pasma sygnału informacyjnego

B

B

[Hz]:

[Hz]:

Systemy z widmem

Systemy z widmem

rozproszonym

rozproszonym

Metody rozpraszania widma:

Metody rozpraszania widma:



bezpośrednie kluczowanie sygnału

bezpośrednie kluczowanie sygnału

pseudolosowym przebiegiem

pseudolosowym przebiegiem

szerokopasmowym (DS, ang.

szerokopasmowym (DS, ang.

direct

direct

sequence

sequence

),

),



przeskoki częstotliwości nośnej (FH,

przeskoki częstotliwości nośnej (FH,

ang.

ang.

frequency hoping

frequency hoping

),

),



przeskoki w czasie (TH, ang.

przeskoki w czasie (TH, ang.

time hoping

time hoping

),

),



szerokopasmowa, liniowa modulacja

szerokopasmowa, liniowa modulacja

częstotliwości (LFM, ang.

częstotliwości (LFM, ang.

linear frequency

linear frequency

modulation

modulation

), zwana także metodą

), zwana także metodą

chirp

chirp

.

.

Rozpraszanie widma metodą

Rozpraszanie widma metodą

kluczowania bezpośredniego

kluczowania bezpośredniego



Sygnał danych jest sumowany modulo 2

Sygnał danych jest sumowany modulo 2

(XOR)

(XOR)

z ciągiem pseudolosowym, a następnie

z ciągiem pseudolosowym, a następnie

poddawany modulacji.

poddawany modulacji.



Czas trwania bitu ciągu pseudolosowego jest

Czas trwania bitu ciągu pseudolosowego jest

krótszy niż czas trwania bitu danych.

krótszy niż czas trwania bitu danych.



Odtworzenie informacji w odbiorniku wymaga

Odtworzenie informacji w odbiorniku wymaga

synchronizacji ciągu pseudolosowego.

synchronizacji ciągu pseudolosowego.

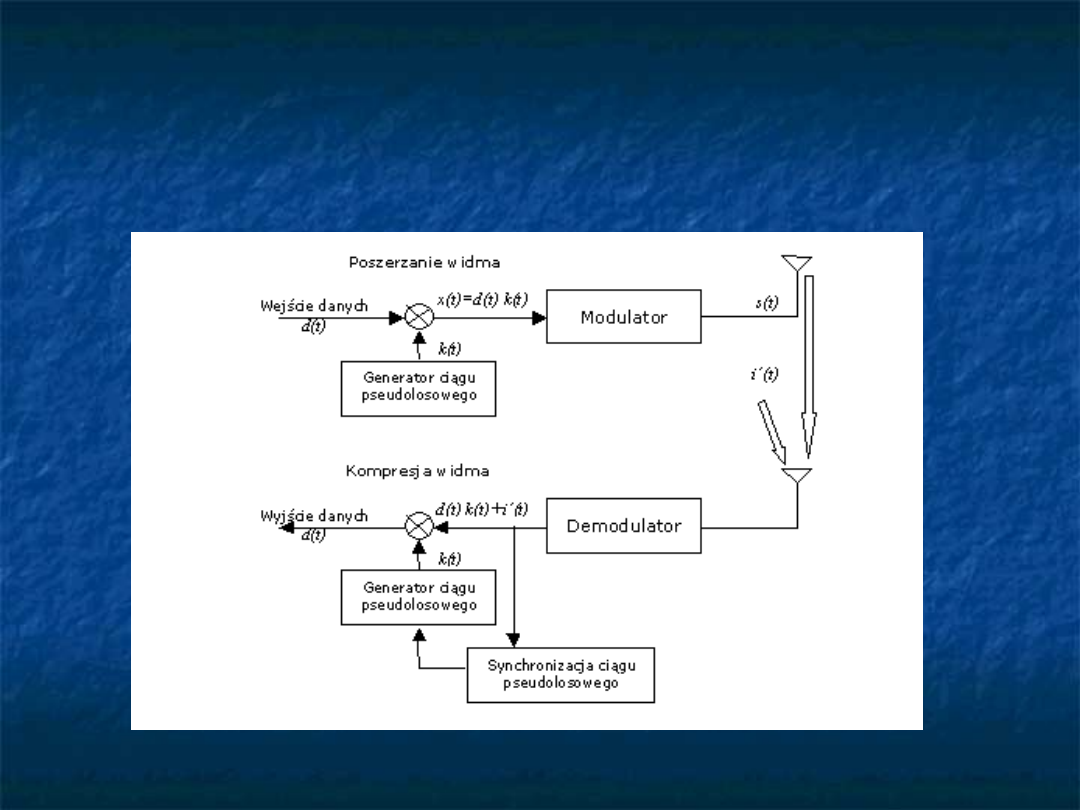
Rozpraszanie widma metodą

Rozpraszanie widma metodą

kluczowania bezpośredniego

kluczowania bezpośredniego

Rozpraszanie widma metodą

Rozpraszanie widma metodą

przeskoków częstotliwości

przeskoków częstotliwości



Pseudolosowy wybór spośród możliwych

Pseudolosowy wybór spośród możliwych

częstotliwości nośnych.

częstotliwości nośnych.

•

Metoda szybkich przeskoków – zmiana

Metoda szybkich przeskoków – zmiana

częstotliwości następuje wielokrotnie

częstotliwości następuje wielokrotnie

podczas trwania bitu informacyjnego.

podczas trwania bitu informacyjnego.

•

Metoda wolnych przeskoków - zmiana

Metoda wolnych przeskoków - zmiana

częstotliwości następuje raz na wiele bitów

częstotliwości następuje raz na wiele bitów

informacyjnych.

informacyjnych.

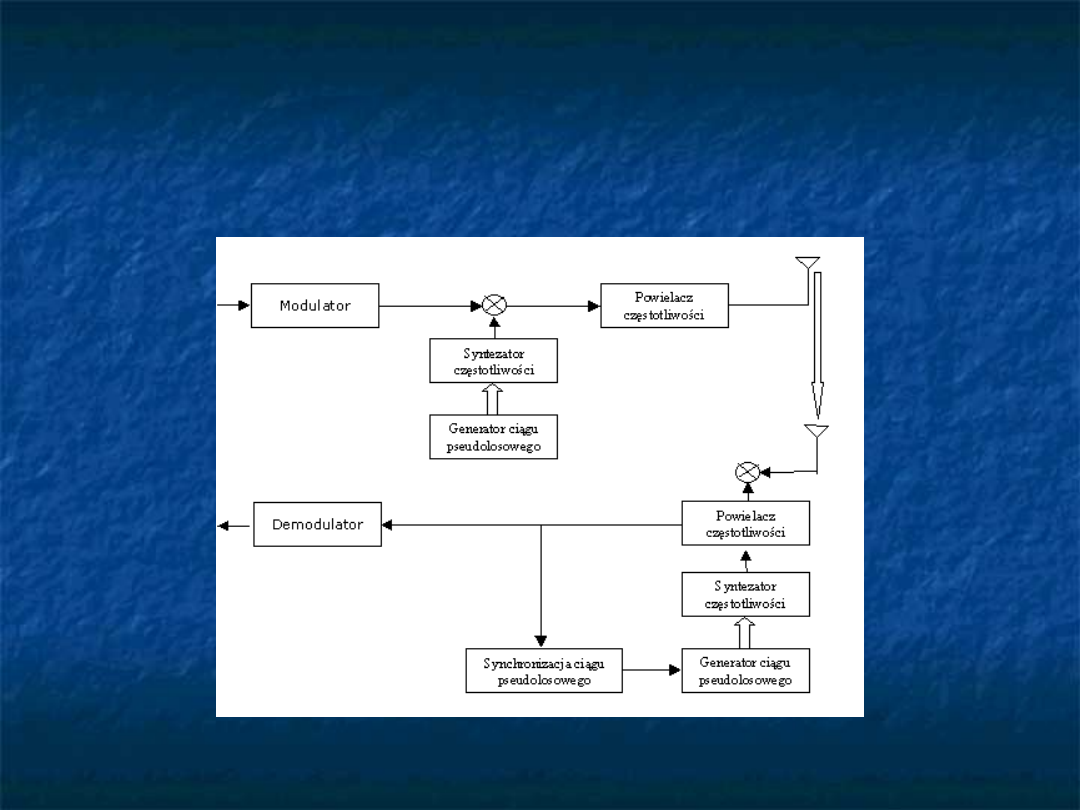
Rozpraszanie widma metodą

Rozpraszanie widma metodą

przeskoków częstotliwości

przeskoków częstotliwości

Rozpraszanie widma metodą

Rozpraszanie widma metodą

przeskoków w czasie

przeskoków w czasie



Sygnały z poszerzonym widmem uzyskiwane

Sygnały z poszerzonym widmem uzyskiwane

metodą przeskoków w czasie otrzymujemy

metodą przeskoków w czasie otrzymujemy

poprzez przesyłanie zmodulowanego ciągu

poprzez przesyłanie zmodulowanego ciągu

danych w wybranych losowo momentach czasu

danych w wybranych losowo momentach czasu



Warunkiem poprawnego przesłania danych jest

Warunkiem poprawnego przesłania danych jest

dokładne zsynchronizowanie generatora ciągu

dokładne zsynchronizowanie generatora ciągu

pseudolosowego w nadajniku i odbiorniku.

pseudolosowego w nadajniku i odbiorniku.

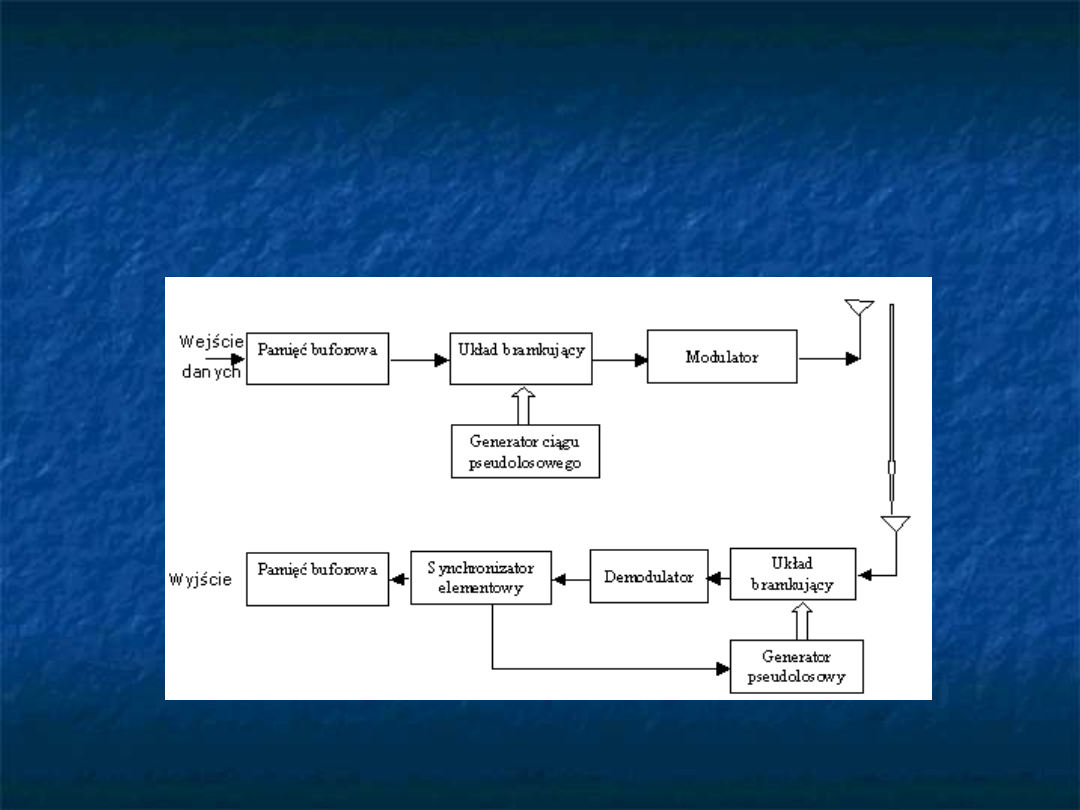
Rozpraszanie widma metodą

Rozpraszanie widma metodą

przeskoków w czasie

przeskoków w czasie

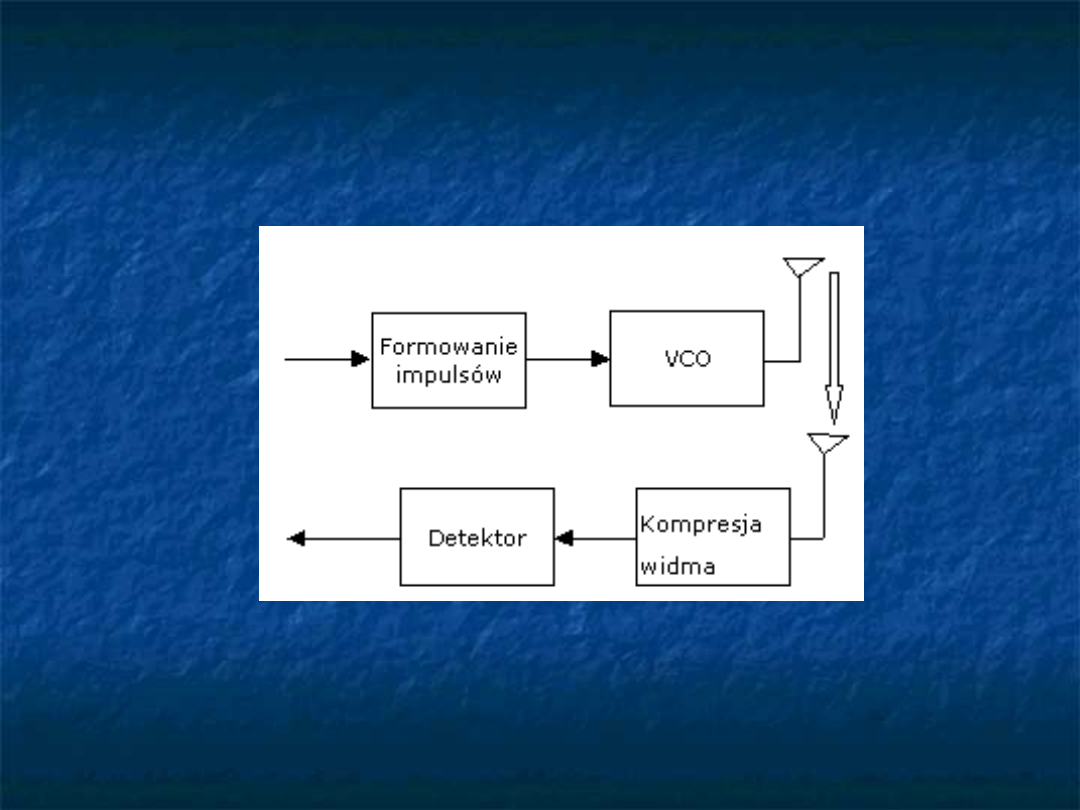
Rozpraszanie widma metodą

Rozpraszanie widma metodą

chirp

chirp



Metoda

Metoda

chirp

chirp

, zwana także szerokopasmową lub

, zwana także szerokopasmową lub

impulsową modulacją częstotliwości, nie wykorzystuje

impulsową modulacją częstotliwości, nie wykorzystuje

ciągów pseudolosowych.

ciągów pseudolosowych.



Na wyjściu układu pojawia się sygnał sinusoidalny o

Na wyjściu układu pojawia się sygnał sinusoidalny o

stałej amplitudzie. Częstotliwość tego sygnału wynosi

stałej amplitudzie. Częstotliwość tego sygnału wynosi

f

f

o

o

dla bitu 0 a narasta liniowo od

dla bitu 0 a narasta liniowo od

f

f

o

o

do f

do f

o

o

+Δf dla bitu 1.

+Δf dla bitu 1.



Ze względu na dużą szerokość pasma, metoda może

Ze względu na dużą szerokość pasma, metoda może

być zaliczona do metod rozpraszania widma.

być zaliczona do metod rozpraszania widma.

Ponieważ nie wykorzystuje ciągów pseudolosowych,

Ponieważ nie wykorzystuje ciągów pseudolosowych,

nie jest możliwe stosowanie metody wielodostępu

nie jest możliwe stosowanie metody wielodostępu

kodowego (CDMA).

kodowego (CDMA).

Rozpraszanie widma metodą

Rozpraszanie widma metodą

chirp

chirp

Dobór częstotliwości nośnej i

Dobór częstotliwości nośnej i

szerokości pasma

szerokości pasma



Mając daną żądaną szybkość transmisji

Mając daną żądaną szybkość transmisji

R

R

[b/s] oraz względną szybkość wybranej

[b/s] oraz względną szybkość wybranej

metody modulacji

metody modulacji

V

V

m

m

[b/s/Hz], można

[b/s/Hz], można

wyznaczyć częstotliwość nośną/[Hz]

wyznaczyć częstotliwość nośną/[Hz]

zgodnie zależnością:

zgodnie zależnością:

m

V

R

f[Hz]

Dobór częstotliwości nośnej i

Dobór częstotliwości nośnej i

szerokości pasma

szerokości pasma



szerokość pasma

szerokość pasma

w

w

[Hz] uzależniona jest

[Hz] uzależniona jest

od zakładanej szybkości transmisji, i

od zakładanej szybkości transmisji, i

zgodnie z twierdzeniem Nyquista,

zgodnie z twierdzeniem Nyquista,

określona jest zależnością:

określona jest zależnością:

2

R

w[Hz]

Dobór częstotliwości nośnej i

Dobór częstotliwości nośnej i

szerokości pasma

szerokości pasma



Szerokość pasma wyliczona według wzoru

Szerokość pasma wyliczona według wzoru

(wyrażona w [Hz]) teoretycznie wystarcza

(wyrażona w [Hz]) teoretycznie wystarcza

do przesłania

do przesłania

R

R

bitów na sekundę. Jest ona

bitów na sekundę. Jest ona

zwana szerokością Nyquista. W praktyce

zwana szerokością Nyquista. W praktyce

jednak, ze względu na obecność szumów,

jednak, ze względu na obecność szumów,

liczba bitów, jaką można przesłać w

liczba bitów, jaką można przesłać w

jednostce czasu, wynosi:

jednostce czasu, wynosi:



















1

log

]

/

[

2

N

S

w

s

b

R

prakt

Kodowanie korekcyjne

Kodowanie korekcyjne



Kodowanie korekcyjne lub kodowanie

Kodowanie korekcyjne lub kodowanie

korygujące (ang. ECC -

korygujące (ang. ECC -

error correction

error correction

coding

coding

, FEC -

, FEC -

forward error correction

forward error correction

) –

) –

technika dodawania bitów nadmiarowych

technika dodawania bitów nadmiarowych

do informacji transmitowanej w postaci

do informacji transmitowanej w postaci

cyfrowej, która umożliwia całkowitą lub

cyfrowej, która umożliwia całkowitą lub

częściową detekcję i korekcję błędów

częściową detekcję i korekcję błędów

powstałych w wyniku zakłóceń

powstałych w wyniku zakłóceń

Cykliczny kod nadmiarowy

Cykliczny kod nadmiarowy



Cykliczny kod nadmiarowy

Cykliczny kod nadmiarowy

, inaczej:

, inaczej:

cykliczna kontrola nadmiarowa (ang.

cykliczna kontrola nadmiarowa (ang.

Cyclic Redundancy Check), CRC

Cyclic Redundancy Check), CRC

– jest to

– jest to

system sum kontrolnych wykorzystywany

system sum kontrolnych wykorzystywany

do wykrywania błędów pojawiających się

do wykrywania błędów pojawiających się

podczas przesyłania danych cyfrowych

podczas przesyłania danych cyfrowych

Cykliczny kod nadmiarowy

Cykliczny kod nadmiarowy



n

n

-bitowy cykliczny kod nadmiarowy (

-bitowy cykliczny kod nadmiarowy (

n

n

-bitowy CRC)

-bitowy CRC)

definiuje się jako resztę z dzielenia ciągu danych

definiuje się jako resztę z dzielenia ciągu danych

przez (

przez (

n

n

+1)-bitowy dzielnik CRC, zwany również

+1)-bitowy dzielnik CRC, zwany również

wielomianem CRC.

wielomianem CRC.



w rzeczywistych zastosowaniach wielomiany

w rzeczywistych zastosowaniach wielomiany

definiuje standard. Na przykład w Ethernecie mamy

definiuje standard. Na przykład w Ethernecie mamy

32-bitowa sumę (CRC-32), której wielomian wynosi:

32-bitowa sumę (CRC-32), której wielomian wynosi:

G

G

(

(

x

x

) =

) =

=x

=x

32

32

+

+

x

x

26

26

+

+

x

x

23

23

+

+

x

x

22

22

+

+

x

x

16

16

+

+

x

x

12

12

+

+

x

x

11

11

+

+

x

x

10

10

+

+

x

x

8

8

+

+

x

x

7

7

+

+

x

x

5

5

+

+

x

x

4

4

+

+

x

x

2

2

+

+

x

x

+1

+1

Cykliczny kod nadmiarowy

Cykliczny kod nadmiarowy



Po stronie odbiorczej wykonywane jest

Po stronie odbiorczej wykonywane jest

sprawdzenie poprawności otrzymanych

sprawdzenie poprawności otrzymanych

danych, przy wykorzystaniu, utworzonego

danych, przy wykorzystaniu, utworzonego

po stronie nadawczej, kodu nadmiarowego

po stronie nadawczej, kodu nadmiarowego

CRC. Jeżeli w przesłanych danych nie ma

CRC. Jeżeli w przesłanych danych nie ma

przekłamań, to po wykonaniu powyższej

przekłamań, to po wykonaniu powyższej

procedury reszta z dzielenia przez dany

procedury reszta z dzielenia przez dany

dzielnik CRC wynosi 0

dzielnik CRC wynosi 0

Kody wykrywania i korekcji

Kody wykrywania i korekcji

błędów

błędów

Niech wektor jednorzędowy X zawiera k bitów

Niech wektor jednorzędowy X zawiera k bitów

informacyjnych do zakodowania (X=X

informacyjnych do zakodowania (X=X

1

1

, X

, X

2

2

...

...

X

X

k

k

)

)

a słowo C (także wektor jednorzędowy) zawiera

a słowo C (także wektor jednorzędowy) zawiera

n bitów (C

n bitów (C

1

1

, C

, C

2

2

... C

... C

n

n

) i jest słowem kodowym

) i jest słowem kodowym

przy czym n>k

przy czym n>k

Możemy zapisać:

Możemy zapisać:







k

j

ij

j

i

g

x

c

1

Kody wykrywania i korekcji

Kody wykrywania i korekcji

błędów

błędów

Macierzowo zapisujemy to jako

Macierzowo zapisujemy to jako

Gdzie

Gdzie

G

G

jest macierzą współczynników g

jest macierzą współczynników g

ij

ij

posiadającą k wierszy i n kolumn

posiadającą k wierszy i n kolumn

G

X

C





Kody wykrywania i korekcji

Kody wykrywania i korekcji

błędów

błędów

To znaczy

To znaczy



 





























kn

k

k

n

n

n

n

g

g

g

g

g

g

g

g

g

X

X

X

C

C

C

...

...

...

...

...

2

1

2

22

21

1

12

11

2

1

2

1

Przykład kod (6,3)

Przykład kod (6,3)

Chcemy wytworzyć wszystkie słowa kodowe tzw.

Chcemy wytworzyć wszystkie słowa kodowe tzw.

kodu (6,3) Macierz G ma w tym wypadku postać

kodu (6,3) Macierz G ma w tym wypadku postać























1

0

1

1

0

0

1

1

0

0

1

0

0

1

1

0

0

1

G

Przykład kod (6,3)

Przykład kod (6,3)

0

0

0

1

1

1

1

0

1

0

1

1

1

1

0

1

0

1

0

1

1

0

0

1

0

1

1

1

1

0

1

1

0

0

1

0

1

0

1

1

0

0

0

0

0

0

0

0

6

5

4

3

2

1

C

C

C

C

C

C

kontrolne

bity

,

,

ne

informacyj

bity

,

,

6

5

4

3

2

1





C

C

C

C

C

C

3

2

6

2

1

5

3

1

4

C

C

C

C

C

C

C

C

C













Cechy kodu

Cechy kodu

•

Ten typ kodu jest

Ten typ kodu jest

kodem blokowym

kodem blokowym

-

-

informacja X jest zawsze zamieniana na

informacja X jest zawsze zamieniana na

słowo C określone zależnością i zawsze

słowo C określone zależnością i zawsze

takie samo i tej samej długości

takie samo i tej samej długości

•

Jeżeli macierz generacyjna posiada pewne

Jeżeli macierz generacyjna posiada pewne

właściwości, że w wektorach kodu blok X

właściwości, że w wektorach kodu blok X

jest nienaruszony, a uzupełniony o bity

jest nienaruszony, a uzupełniony o bity

parzystości to jest to tzw.

parzystości to jest to tzw.

kod

kod

systematyczny

systematyczny

Konstrukcja kodu - macierz

Konstrukcja kodu - macierz

G

G

Z konstrukcji macierzy generacyjnej

Z konstrukcji macierzy generacyjnej

wynika, że pierwsze k kolumn tej macierzy

wynika, że pierwsze k kolumn tej macierzy

formuje bity informacyjne w kodzie

formuje bity informacyjne w kodzie

systematycznym natomiast pozostałe n-k

systematycznym natomiast pozostałe n-k

kolumn generuje bity parzystości

kolumn generuje bity parzystości





P

I

K

:



G

Konstrukcja kodu - macierz

Konstrukcja kodu - macierz

G

G

k

n

k

n

k































































 





 



G

Konstrukcja kodu - macierz

Konstrukcja kodu - macierz

H

H



Kod można zdefiniować również w inny

Kod można zdefiniować również w inny

sposób za pomocą macierzy H

sposób za pomocą macierzy H



Jeżeli c jest słowem kodowym (wektor

Jeżeli c jest słowem kodowym (wektor

rzędowy to jego wektor kolumnowy

rzędowy to jego wektor kolumnowy

nazywamy c

nazywamy c

T

T

0





T

c

H

Konstrukcja kodu - macierz

Konstrukcja kodu - macierz

H

H























































































0

0

0

...

...

...

2

1

)

(

2

)

(

1

)

(

2

22

21

1

12

11





n

n

k

n

k

n

k

n

n

n

C

C

C

h

h

h

h

h

h

h

h

h

Konstrukcja kodu - macierz

Konstrukcja kodu - macierz

H

H

Jak widać macierz H na n kolumn i (n-k) wierszy

Jak widać macierz H na n kolumn i (n-k) wierszy

Macierze G i H są współzależne i macierz H można

Macierze G i H są współzależne i macierz H można

zbudować znając macierz G. Macierz H ma mniej

zbudować znając macierz G. Macierz H ma mniej

elementów (zakładając że liczba bitów parzystości

elementów (zakładając że liczba bitów parzystości

jest mniejsza niż informacji)

jest mniejsza niż informacji)

0

1







j

n

j

ij

c

h

Kod Hamminga (7, 4)

Kod Hamminga (7, 4)



Bity zabezpieczające są generowane

Bity zabezpieczające są generowane

na podstawie bitów informacyjnych

na podstawie bitów informacyjnych

według następującego algorytmu:

według następującego algorytmu:

c5 = x1

c5 = x1





x2

x2





x4

x4

c6 = x1

c6 = x1





x3

x3





x4

x4

c7 = x2

c7 = x2





x3

x3





x4

x4

Kod Hamminga (7, 4)

Kod Hamminga (7, 4)

Bity

Bity

informacyj

informacyj

ne

ne

x1, x2, x3, x4

x1, x2, x3, x4

Bity

Bity

zabezpieczają

zabezpieczają

ce

ce

c5, c6, c7

c5, c6, c7

Bity

Bity

informacyjne

informacyjne

x1, x2, x3, x4

x1, x2, x3, x4

Bity

Bity

zabezpieczają

zabezpieczają

ce

ce

c5, c6, c7

c5, c6, c7

0000

0000

000

000

1000

1000

110

110

0001

0001

111

111

1001

1001

001

001

0010

0010

011

011

1010

1010

101

101

0011

0011

100

100

1011

1011

010

010

0100

0100

101

101

1100

1100

011

011

0101

0101

010

010

1101

1101

100

100

0110

0110

110

110

1110

1110

000

000

0111

0111

001

001

1111

1111

111

111

Kod Hamminga (7, 4)

Kod Hamminga (7, 4)



























1

1

0

1

0

0

0

0

1

1

0

1

0

0

1

1

1

0

0

1

0

1

0

1

0

0

0

1

G

Kod Hamminga (7, 4)

Kod Hamminga (7, 4)























1

0

0

1

0

1

1

0

1

0

1

1

1

0

0

0

1

0

1

1

1

H

Dystans Hamminga

Dystans Hamminga

Dla kodów blokowych miarą dystansu jest

Dla kodów blokowych miarą dystansu jest

wprost

wprost

liczba pozycji na których dwa słowa się

liczba pozycji na których dwa słowa się

różnią

różnią

różnią się one na trzech pozycjach - dyst=3

różnią się one na trzech pozycjach - dyst=3

10001

11010





















n

j

j

j

d

1

)

,

(









Po stronie odbiorczej

Po stronie odbiorczej

Załóżmy że słowo kodowe zostało zakłócone

Załóżmy że słowo kodowe zostało zakłócone

Dekoder wykonuje operacje na słowie r

Dekoder wykonuje operacje na słowie r

e

c

r





)

...

(

2

1

n

e

e

e

e









1

0

i

e

- brak błędu

- brak błędu

- błąd na tej pozycji

- błąd na tej pozycji

T

T

T

T

T

T

T

s

He

He

Hc

e

c

H

Hr













)

(

Efektywność kodu

Efektywność kodu

W kategorii kodów blokowych najlepsze i

W kategorii kodów blokowych najlepsze i

najczęściej używane są te dla których związek

najczęściej używane są te dla których związek

między n i k jest określony zależnością

między n i k jest określony zależnością

i są to kody:

i są to kody:

(n, k) = (3, 1), (7, 4), (15, 11), (31, 26), (63,

(n, k) = (3, 1), (7, 4), (15, 11), (31, 26), (63,

57)

57)

1

2







n

k

n

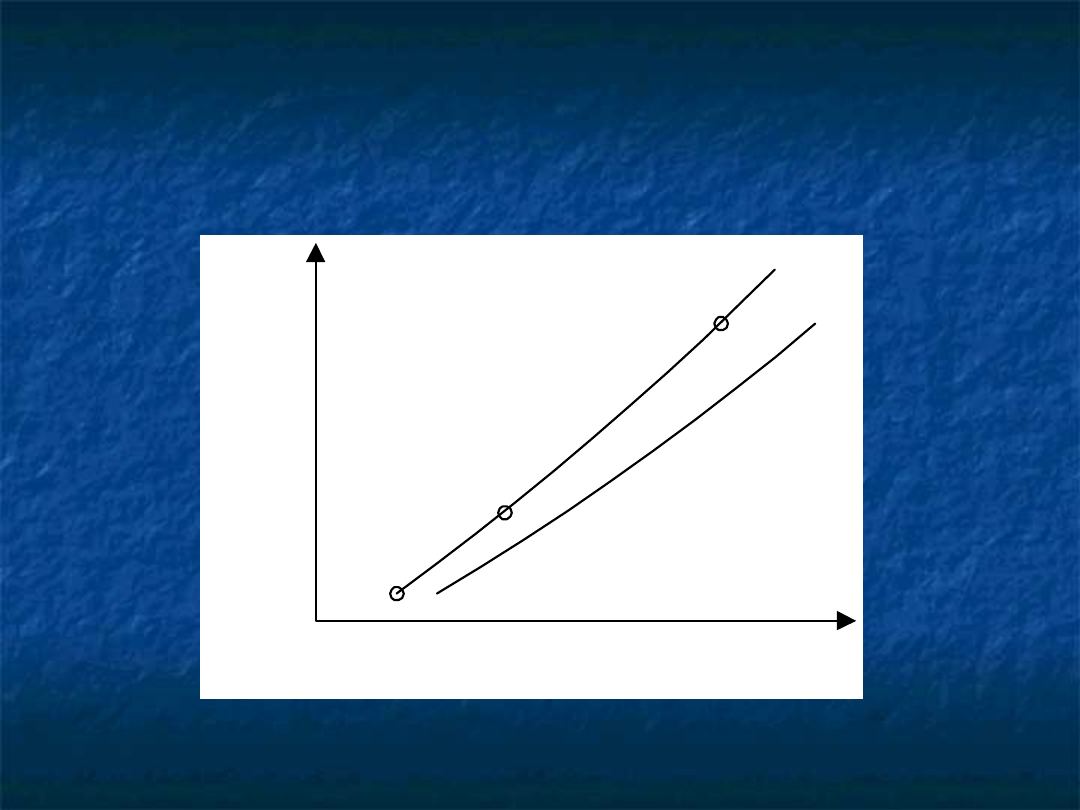
Granica Hamminga dla

Granica Hamminga dla

odpowiedniego t

odpowiedniego t

2

4

6

8

10

12

licz

ba

bitó

w in

for

ma

cyjn

ych

długość słowa kodowego

2

4

6

8

10

12

14

16

t=1

(7,4)

(15,11)

(3,1)

t=2