1

Empiryczne metody

badania efektywności

rynków finansowych

Dobromił Serwa

akson.sgh.waw.pl/~dserwa/ef1.ht

m

2

• Testy „prognozowalności”

• Testy przyczynowości

• Dodatek: testy dla rynku walutowego

3

Literatura

• J. Campbell, A. Lo, C. MacKinlay, The

Econometrics of Financial Markets,
Princeton University Press 1997.

4

Literatura

• E. Syczewska, Ekonometryczne modele

kursów walutowych, SGH 2007.

• M. Rubaszek, D. Serwa, (red. nauk.) W.

Marcinkowska-Lewandowska, Analiza

kursu walutowego, C.H.Beck 2009.

• M. Osińska, Ekonometria finansowa,

PWE 2006.

5

„Fair game” i martyngały

• Proces stochastyczny spełniający:

lub inaczej

• Wada: nie uwzględnia ryzyka

t

t

t

t

t

P

P

P

P

P

E









,...]

,

,

|

[

2

1

1

0

,...]

,

,

|

[

2

1

1











t

t

t

t

t

P

P

P

P

P

E

6

Modele stóp zwrotu

• Model błądzenia losowego (1):

lub unikając ujemnych cen:

t

t

t

P

P











 1

)

,

0

(

~

2





IID

t

t

t

t

p

p











 1

)

,

0

(

~

2





N

IID

t

7

Modele stóp zwrotu

• Model błądzenia losowego (2):

– Usunięcie założenia o stałym rozkładzie

składnika losowego

• Model błądzenia losowego (3)

– Usunięcie założenia o niezależności

składnika losowego.

– Założenie o braku korelacji między

składnikami losowymi, … ale np.

0

)

,

(

2

1

2





t

t

Cov





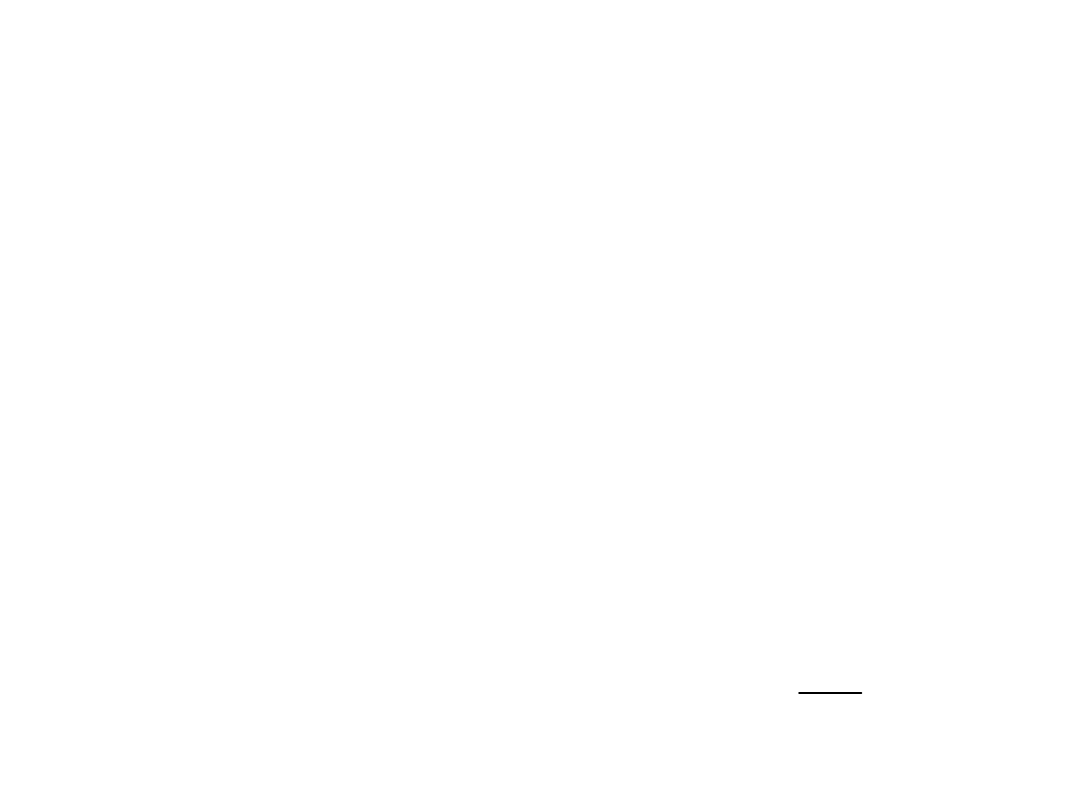
8

Testy modeli błądzenia

losowego

• Testy modelu (1)
• Sekwencje i zmiany trendu (

Cowles, Jones

1937

):

























0

0

0

1

1

1

t

t

t

t

t

t

t

p

p

r

li

jeś

p

p

r

li

jeś

I







n

t

t

s

Y

N

1

)

1

)(

1

(

1

1













t

t

t

t

t

I

I

I

I

Y

s

r

N

n

N





1

?





r

s

N

N

CJ

9

Testy modeli błądzenia

losowego

• … po uwzględnieniu „dryfu” cen:









-π

I

t

1

bienstwem

prawdopodo

z

0

bienstwem

prawdopodo

z

1

















s

s

t

Y









-

1

bienstwem

prawdopodo

z

0

)

1

(

bienstwem

prawdopodo

z

1

2

2

1

)

1

(

2

)

1

(

2

2



















CJ



























)

0

Pr(

t

r



























4

2

3

3

)

1

(

)

)

1

(

(

2

)

1

(

,

1

~

s

s

s

s

s

s

a

n

N

CJ

















10

Testy modelu błądzenia

losowego

• Testy serii (

Mood

1940

): ...1000011110000…

• Prostsza wersja: test Walda-

Wolfowitza

– kiedy





2

2

2

)

1

(

3

)

1

(

,

0

~

)

1

(

)

(

i

i

i

i

a

i

i

i

serie

i

N

n

n

i

N

x





























Asymptotycznie:
K ma rozkład
normalny

)

,

0

(

~

2



N

r

t

11

Testy modeli błądzenia

losowego

• Testy modelu (2)
• „filter rules” (algorytmy handlu)

– filtr k% - kupuj, gdy cena wzrośnie k% i

sprzedaj kiedy spadnie k%

– uwzględnij koszty transakcyjne
– porównaj całkowity zwrot z tej strategii

ze zwrotem ze strategii „kupuj i trzymaj”

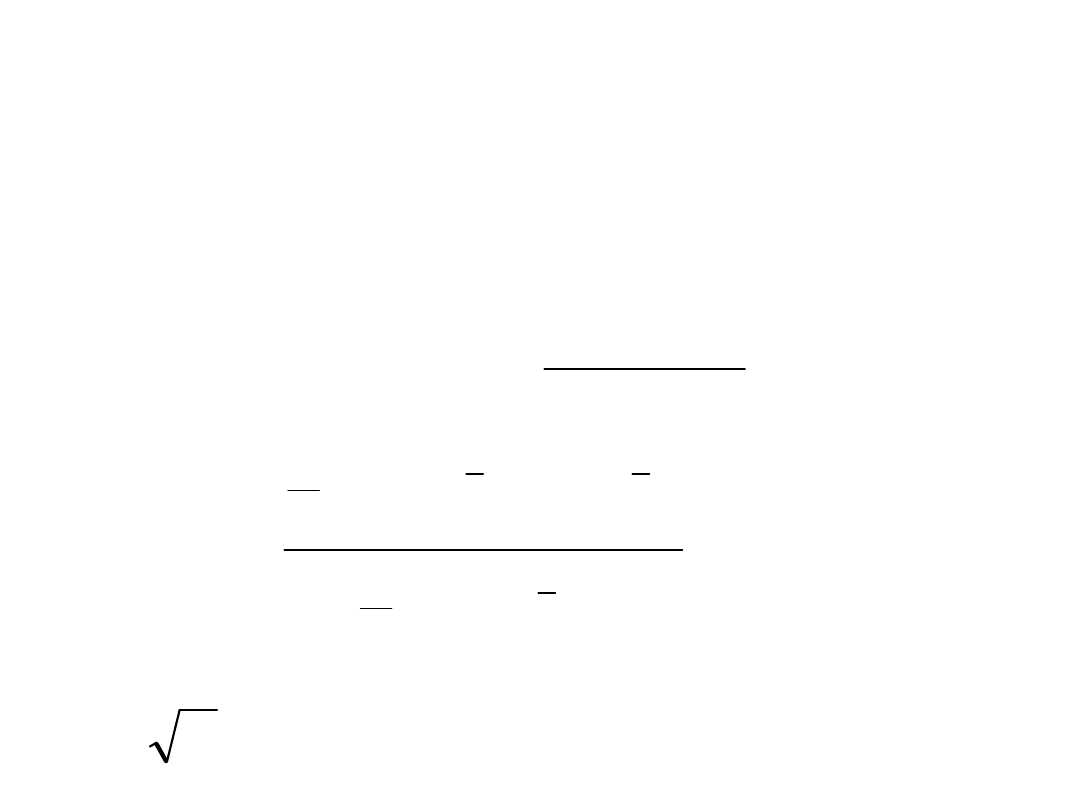
12

Testy modeli błądzenia

losowego

• Testy modelu (3)
• Współczynniki korelacji

)

(

)

,

(

)

,

(

)

(

t

k

t

t

k

t

t

r

Var

r

r

Cov

r

r

Corr

k











)

1

,

0

(

~

)

(

ˆ

N

k

T

a























T

t

T

t

k

T

t

T

k

t

T

t

r

r

T

r

r

r

r

T

k

1

2

1

)

(

1

)

)(

(

1

)

(

ˆ



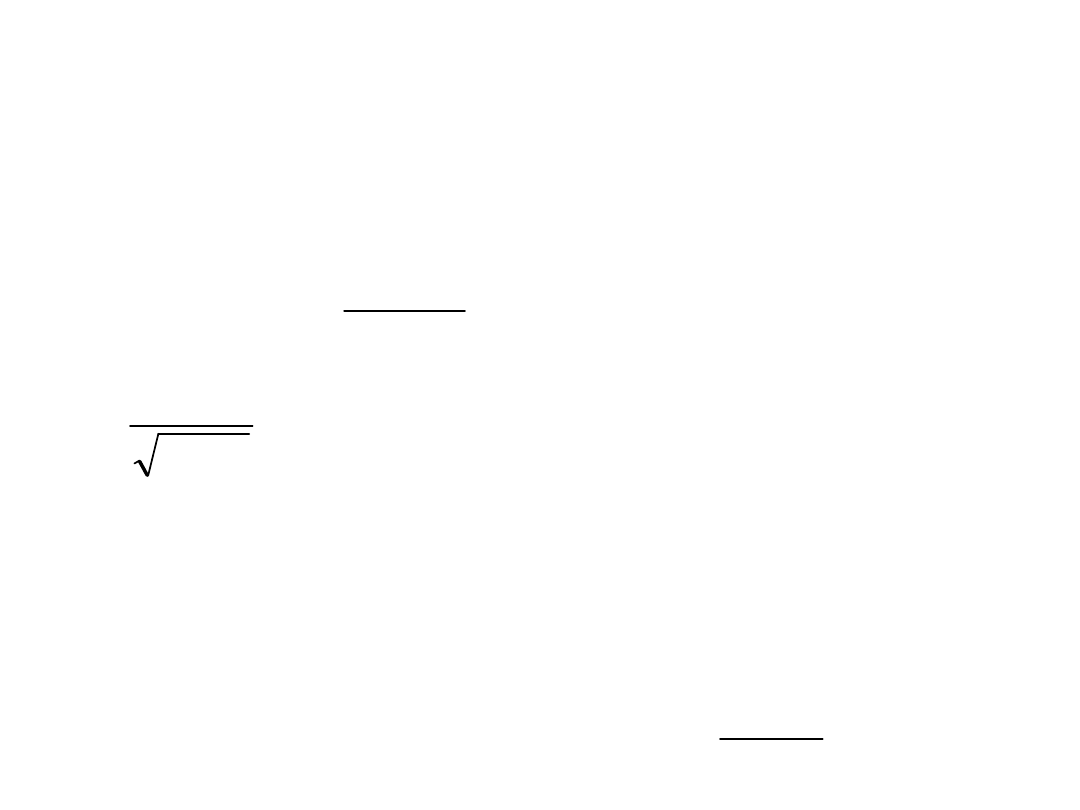
13

Testy modeli błądzenia

losowego

• W małych próbach

• Testy dla wielu wsp. korelacji na raz (

Box, Pierce

1970

)

lub w małej próbie (

Ljung, Box 1978

)

))

(

ˆ

1

(

)

1

(

)

(

ˆ

)

(

~

2

2

k

T

k

T

k

k

















)

1

,

0

(

~

)

(

~

N

k

k

T

T

a





)

(

~

)

(

ˆ

2

1

2

m

k

T

Q

a

m

k

m











)

(

~

)

(

ˆ

)

2

(

2

1

2

m

k

T

k

T

T

Q

a

m

k

m

















14

Testy modeli błądzenia

losowego

• Ilorazy wariancji

czyli dla (1) , bo wszystkie korel.=0

1

1

....

)

(















k

t

t

t

t

r

r

r

k

r

)

1

(

1

]

[

2

]

,

[

2

]

[

2

]

[

2

)]

2

(

[

)

2

(

1























t

t

t

t

t

t

r

Var

r

r

Cov

r

Var

r

Var

r

Var

VR





























1

1

)

(

1

2

1

]

[

)]

(

[

)

(

q

k

t

t

k

q

k

r

Var

q

q

r

Var

q

VR



1

)

( 

q

VR

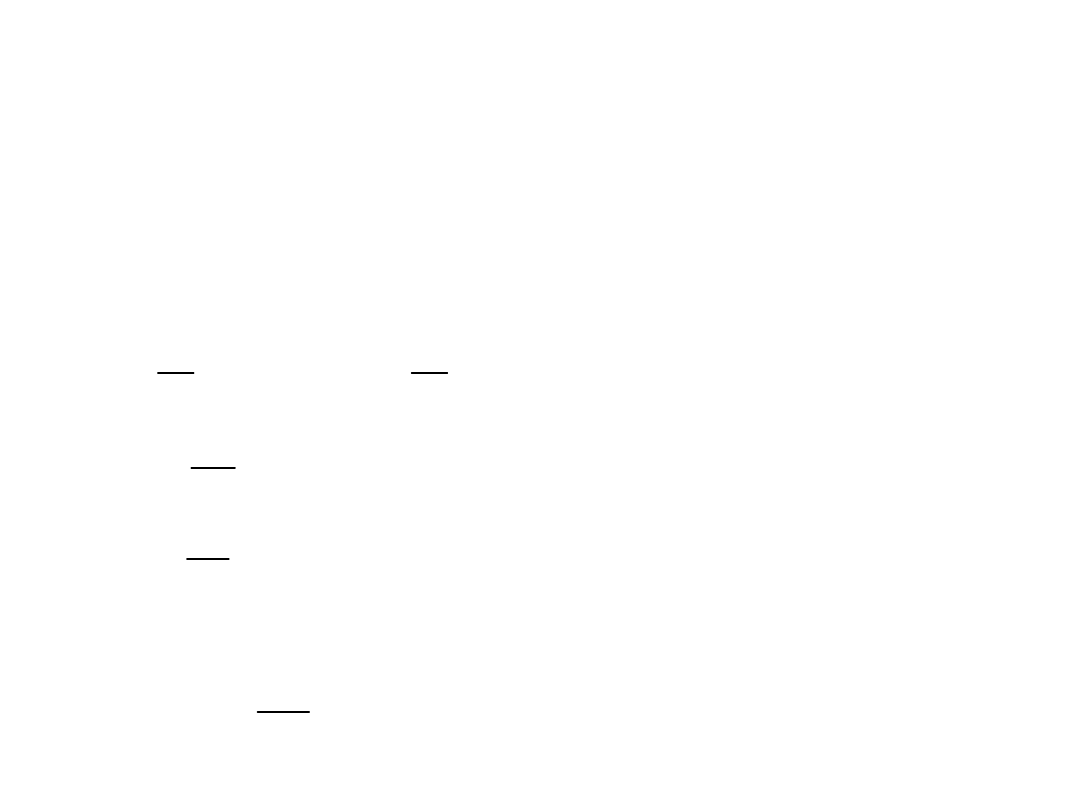
15

Testy modeli błądzenia

losowego

• Testy ilorazu i różnicy wariancji

– dla 2n+1 obserwacji mamy

zdefiniowane:















n

k

n

k

k

p

p

n

p

p

n

2

1

0

2

1

)

(

2

1

)

(

2

1

ˆ















n

k

k

k

a

p

p

n

2

1

2

1

2

)

ˆ

(

2

1

ˆ

















n

k

k

k

b

p

p

n

1

2

2

2

2

2

)

ˆ

2

(

2

1

ˆ





2

2

ˆ

ˆ

)

2

(

ˆ

a

b

R

V







2

2

ˆ

ˆ

)

2

(

ˆ

a

b

D

V









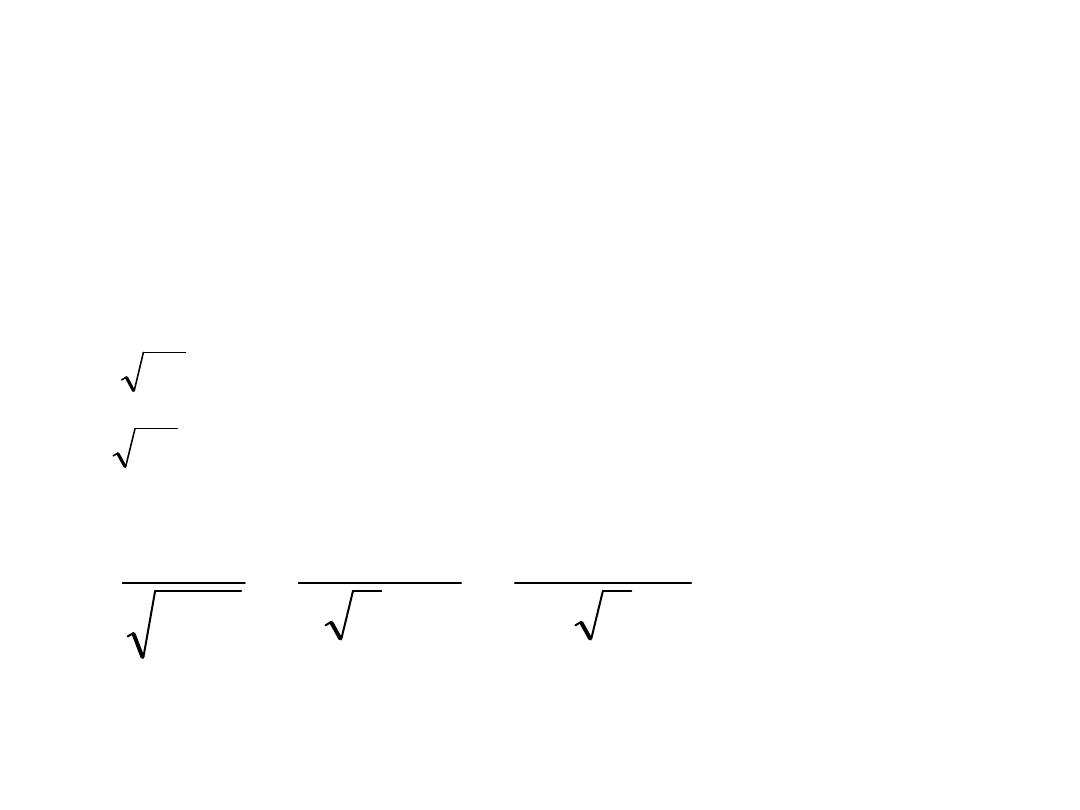
16

Testy modeli błądzenia

losowego

• c.d.

(H0: VR-1=0, VD=0)

)

2

,

0

(

~

)

2

(

ˆ

2

4



N

D

V

n

a

)

2

,

0

(

~

)

1

)

2

(

ˆ

(

2

N

R

V

n

a



)

1

,

0

(

~

2

1

)

2

(

ˆ

ˆ

2

ˆ

ˆ

ˆ

2

)

2

(

ˆ

2

2

2

4

N

R

V

D

V

a

a

a

b

a

















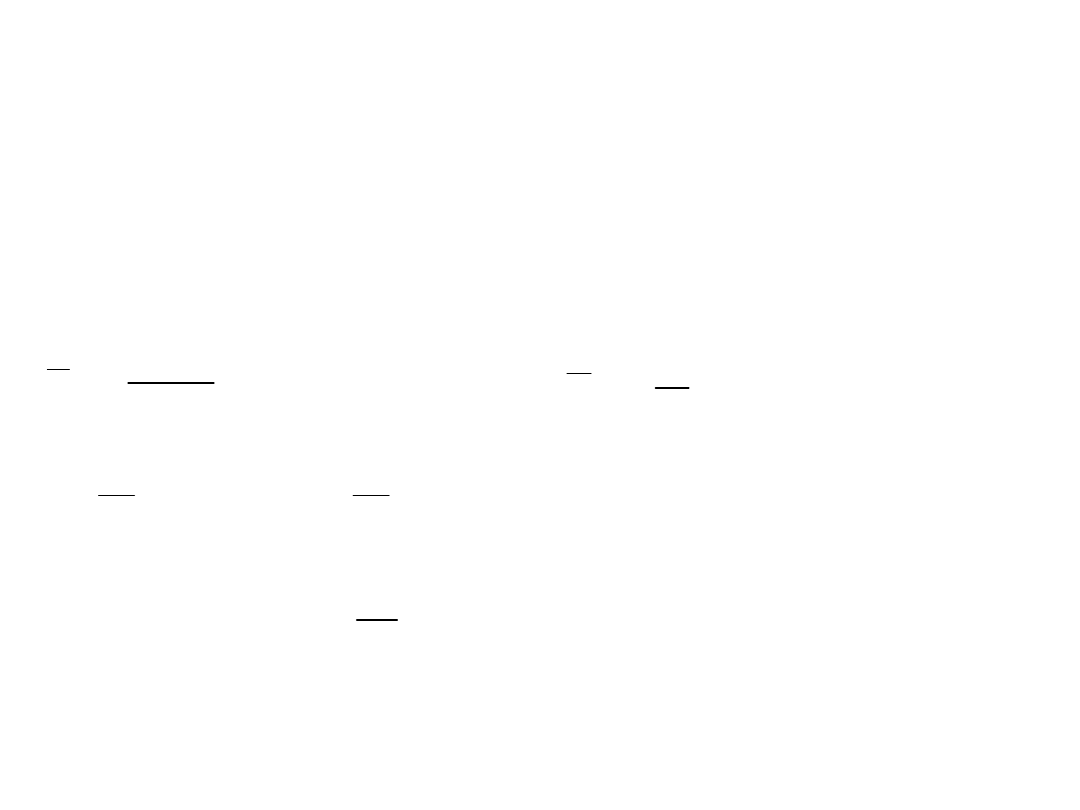
17

Testy modeli błądzenia

losowego

• Uogólnienie dla zwrotów

wielookresowych

– dla qn+1 obserwacji















qn

k

k

k

a

p

p

qn

1

2

1

2

)

ˆ

(

1

1

















nq

q

k

q

k

k

c

q

p

p

m

2

2

)

ˆ

(

1



















qn

k

qn

k

k

p

p

qn

p

p

qn

1

0

1

)

(

1

)

(

1

ˆ























nq

q

q

nq

q

m

1

)

1

(

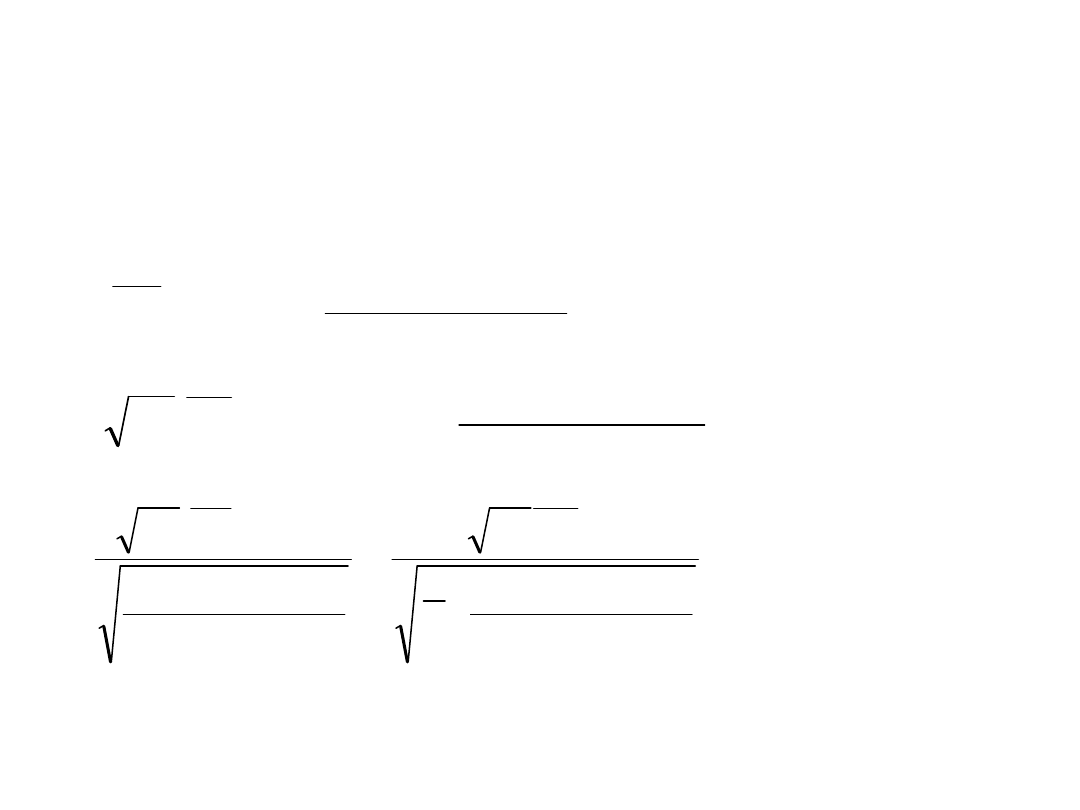
18

Testy modeli błądzenia

losowego

• c.d. testy (H0: VR-1=0, VD=0)

)

3

)

1

)(

1

2

(

2

,

0

(

~

)

(

4



q

q

q

N

q

VD

a









)

3

)

1

)(

1

2

(

2

,

0

(

~

1

)

(

q

q

q

N

q

VR

nq

a











)

1

,

0

(

~

3

)

1

)(

1

2

(

2

)

(

3

)

1

)(

1

2

(

2

1

)

(

4

N

q

q

q

q

VD

nq

q

q

q

q

VR

nq

a

a















19

Testy modeli błądzenia

losowego

• Testy dla długookresowych stóp

zwrotu (duże q)

• Problem: słaba moc testu

• Inne rozwiązanie: Hurst-Mandelbrot

rescaled range statistic



































2

2

2

1

2

3

3

4

,

0

~

1

)

(

q

q

q

n

N

q

VR

a

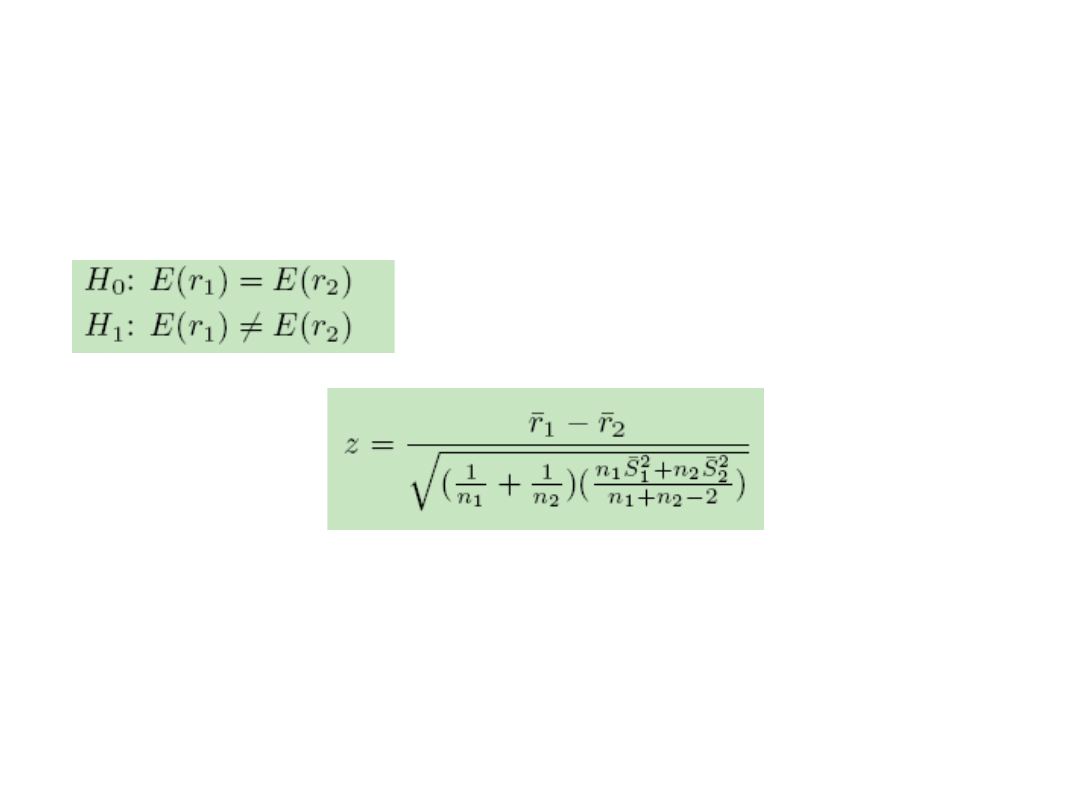
20

Efekty sezonowe

• Testy na równość średnich w próbach

– statystyka ma rozkład t(n1+n2-2)

21

Efekty sezonowe

• Modele regresji ze zmiennymi

sezonowymi

• Przykład: model jednoczynnikowy

rynkowy

model





t

t

d

r



t

M

t

t

t

r

d

r



















0

:

0





H

22

Testowanie

przyczynowości

23

Literatura

• M. Osińska (2006) Ekonometria

finansowa, PWE

• Maddala (2008) Ekonometria, PWN
• Podręcznik SGH do ekonometrii

Dodatkowo:

Cheung, Y. and L. K. Ng, 1996, A causality-in-

variance test and its application to financial

market prices, Journal of Econometrics 72, 33-48.

24

Co to jest przyczynowość?

• Zdarzenie B zależy od zdarzenia A

• Zdarzenie A miało miejsce wcześniej

niż zdarzenie B

• Zdarzenia A i B następują zaraz po

sobie

25

Przyczynowość w ekonomii

• Problem czy zmienna X ma wpływ na

zmienną Y, czy na odwrót?

• Czy dynamika kredytu zależy od

wzrostu PKB, czy też jest na odwrót?

• Czy stopy zwrotu na giełdzie w USA

zależą od stóp zwrotu na giełdzie w
Japonii?

26

Przyczynowość w ekonomii

• Przyczynowość w sensie Grangera:

– Kiedy przy pomocy zmiennej X jesteśmy

w stanie dokładniej/lepiej prognozować
wartości zmiennej Y

27

Rodzaje przyczynowości

w sensie Grangera

• Przyczynowość „w średniej” / „w

równaniu regresji” (causality in mean)
– dotyczy średniej wartości zmiennej Y

• Przyczynowość „w wariancji”

(causality in variance) - dotyczy
wariancji wartości zmiennej Y

• Przyczynowość „w rozkładzie”

(causality in distribution, in quantiles)

28

Przyczynowość w sensie

Grangera

• Przyczynowość w równaniu regresji

(causality-in-mean)

X  Y

)

...,

,

,

...,

,

,

|

(

)

...,

,

,

|

(

3

2

1

3

2

1

3

2

1





















t

t

t

t

t

t

t

t

t

t

t

x

x

x

y

y

y

y

E

y

y

y

y

E

29

Przyczynowość w modelu

regresji

• Modele autoregresyjne z rozkładem

opóźnień (autoregressive distributed
lag)





















P

i

t

i

t

i

Q

i

i

t

i

t

x

y

y

1

1









30

Przyczynowość w modelu

regresji

• Testowanie przyczynowości w modelu

ADL

• H0: parametry przy X-ach są równe

zero, czyli historyczne wartości X nie
wpływają na aktualne wartości Y

• H1: przynajmniej jeden parametr

przy X-ach jest różny od zera

31

Testowanie

• Statystyki do testowania przyczynowości

– statystyka t-Studenta
– statysyka F
– statystyka Walda
– statystyki LM, LR

• Ustawiamy restrykcje zerowe na

parametry przy opóźnionych zmiennych
X

32

Przykład (1)

Model 1: Estymacja KMNK z wykorzystaniem 199 obserwacji 1951:2-2000:4

Zmienna zależna: inf

Zmienna Współczynnik Błąd stand. Statystyka t Wartość p

const 0,208988 0,322158 0,649 0,51731

tbilrate_1 1,27788 0,229507 5,568 <0,00001 ***

tbilrate_2 -1,21589 0,354614 -3,429 0,00074 ***

tbilrate_3 0,763303 0,361774 2,110 0,03618 **

tbilrate_4 -0,660217 0,231385 -2,853 0,00481 ***

inf_1 0,151030 0,0710895 2,125 0,03492 **

inf_2 0,124406 0,0702716 1,770 0,07827 *

inf_3 0,186683 0,0703746 2,653 0,00866 ***

inf_4 0,226679 0,0693899 3,267 0,00129 ***

Przykładowe obliczenia w programie GRETL

33

Przykład (2)

Porównanie Modelu 1 z Modelem 2:

Hipoteza zerowa: parametry regresji dla wskazanych zmiennych są równe zero

tbilrate_1

tbilrate_2

tbilrate_3

tbilrate_4

Statystyka testu: F(4, 190) = 8,81846, z wartością p = 1,49553e-006

Test F (test pominiętych
zmiennych)

Test Walda (test pominiętych
zmiennych)

Hipoteza zerowa: parametry regresji dla wskazanych zmiennych są równe zero

tbilrate_1

tbilrate_2

tbilrate_3

tbilrate_4

Asymptotyczna statystyka testu:

Chi-kwadrat(4) = 35,2738, z wartością p = 4,08094e-007

34

Przykład (3)

• Model dla Y

• Model dla X

• Standaryzowane składniki losowe z

dwóch różnych równań regresji:

t

n

i

i

t

i

t

X

b

b

X















1

0

t

m

i

i

t

i

t

Y

Y



















1

0

t

z

1





t

z

2





35

Przykład (3a)

• Model objaśniający zmienną X

• Model objaśniający zmienną Y

Model 3: Estymacja KMNK z wykorzystaniem 200 obserwacji 1951:1-2000:4

Zmienna zależna: tbilrate

Zmienna Współczynnik Błąd stand. Statystyka t Wartość p

const 0,242474 0,102633 2,363 0,01914 **

tbilrate_1 1,30871 0,0691445 18,927 <0,00001 ***

tbilrate_2 -0,677465 0,108669 -6,234 <0,00001 ***

tbilrate_3 0,584943 0,108680 5,382 <0,00001 ***

tbilrate_4 -0,258889 0,0688070 -3,763 0,00022 ***

Model 4: Estymacja KMNK z wykorzystaniem 199 obserwacji 1951:2-2000:4

Zmienna zależna: inf

Zmienna Współczynnik Błąd stand. Statystyka t Wartość p

const 0,518416 0,270086 1,919 0,05640 *

inf_1 0,285613 0,0698639 4,088 0,00006 ***

inf_2 0,123775 0,0706470 1,752 0,08135 *

inf_3 0,251685 0,0703273 3,579 0,00044 ***

inf_4 0,182468 0,0692514 2,635 0,00910 ***

36

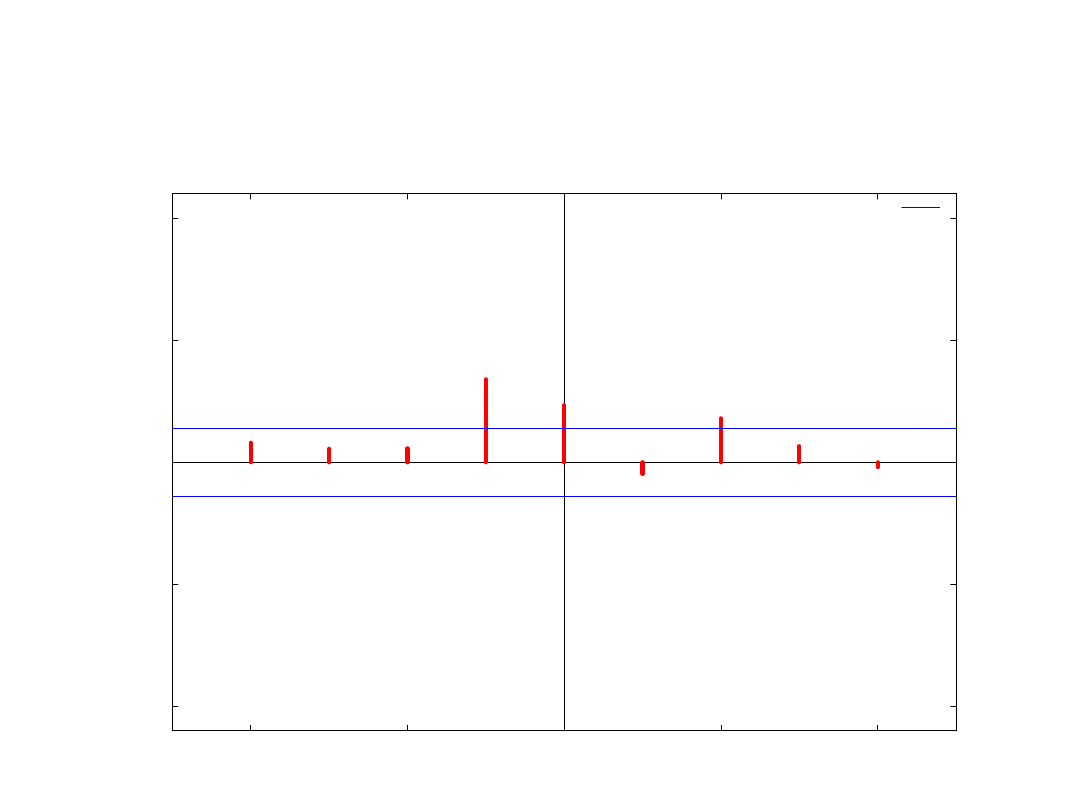
Przykład (3b)

-1

-0.5

0

0.5

1

-4

-2

0

2

4

o

p

�

n

ie

n

ia

K

o

re

lo

g

ra

m

p

o

m

i�

d

zy

zm

. u

h

a

t3

i o

p

�

n

ie

n

ia

m

i zm

. u

h

a

t4

+- 1,96/T^0,5

37

Przykład (3d)

• Testowanie przyczynowości w

równaniu średniej z opóźnieniami
od j do k:

2

1

2

~

)

(

)

,

(











j

k

k

j

i

i

r

T

k

j

S







38

Interpretacja ekonomiczna

• Zmiany rynkowych stóp procentowych

wpływają z opóźnieniem na zmiany
inflacji

• …ale istnieje też zależność odwrotna

(patrz: korelogram)

• Istnieje też zależność „natychmiastowa”,

kierunek oddziaływania nie jest znany

39

Przyczynowość w wariancji

• Czy zmienność (volatility) zmiennej X

pozwala lepiej prognozować
zmienność zmiennej Y (np. wariancję
zmian kursu walutowego)?

• causality in variance

)

...,

,

,

...,

,

,

|

(

)

...,

,

,

|

(

2

3

2

2

2

1

2

3

2

2

2

1

2

2

3

2

2

2

1

2





















t

t

t

t

t

t

t

t

t

t

t

x

x

x

y

y

y

y

E

y

y

y

y

E

40

Testowanie przyczynowości w

wariancji

• Wykorzystaj model GARCH lub

MGARCH

• Test Cheunga i Ng (1996):

wykorzystaj wystandaryzowane
reszty (i podniesione do kwadratu) z
dwóch wcześniejszych regresji

2

1t

z

U 

2

2t

z

V 

41

Przyczynowość w wariancji

• Statystyka testu do testowania

przyczynowości w wariancji z
opóźnieniami od j do k

2

1

2

~

)

(

)

,

(











j

k

k

j

i

UV

UV

i

r

T

k

j

S



42

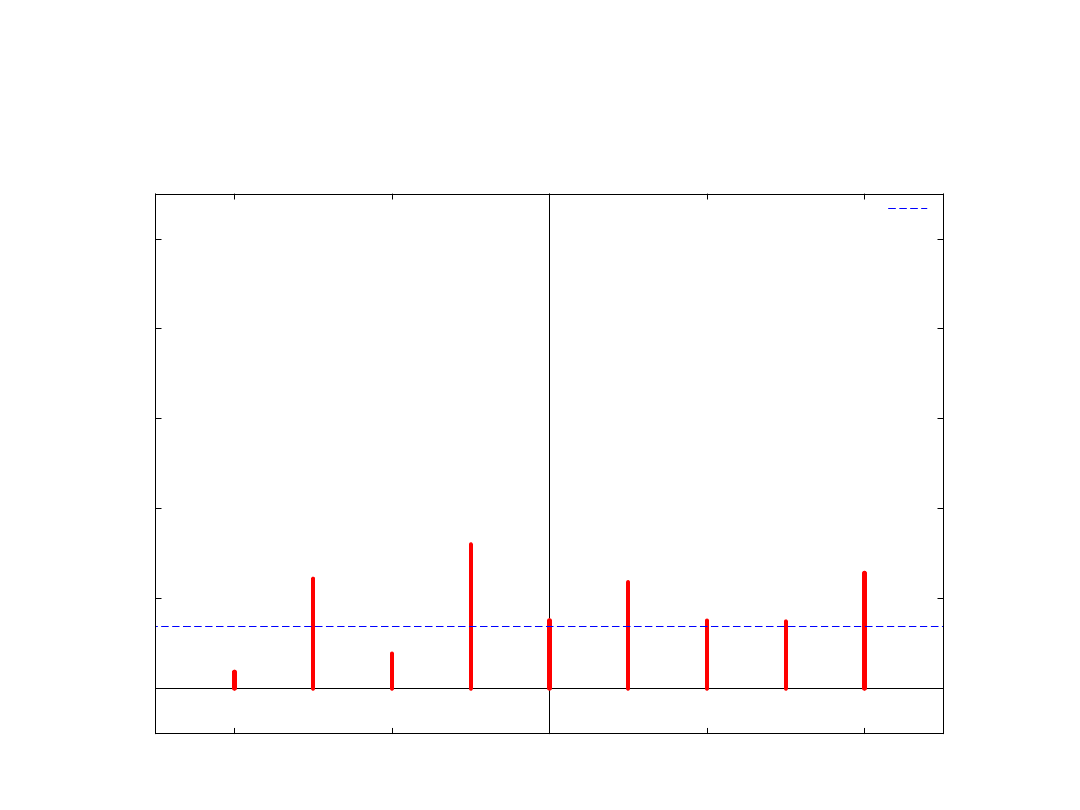
Przykład (4)

0

0.2

0.4

0.6

0.8

1

-4

-2

0

2

4

o

p

�

n

ie

n

ia

K

o

re

lo

g

ra

m

p

o

m

i�

d

zy

zm

. u

sq

4

i o

p

�

n

ie

n

ia

m

i zm

. u

sq

3

1,96/T^0,5

43

Interpretacja ekonomiczna

• Przyczynowość w wariancji na rynkach

finansowych interpretowana jest
często jako przepływ informacji /
newsów / turbulencji między rynkami /
instrumentami

• Zmienność rynkowych stóp zwrotu

(zaburzenia na rynku) wpływa z
opóźnieniem na zmienność inflacji

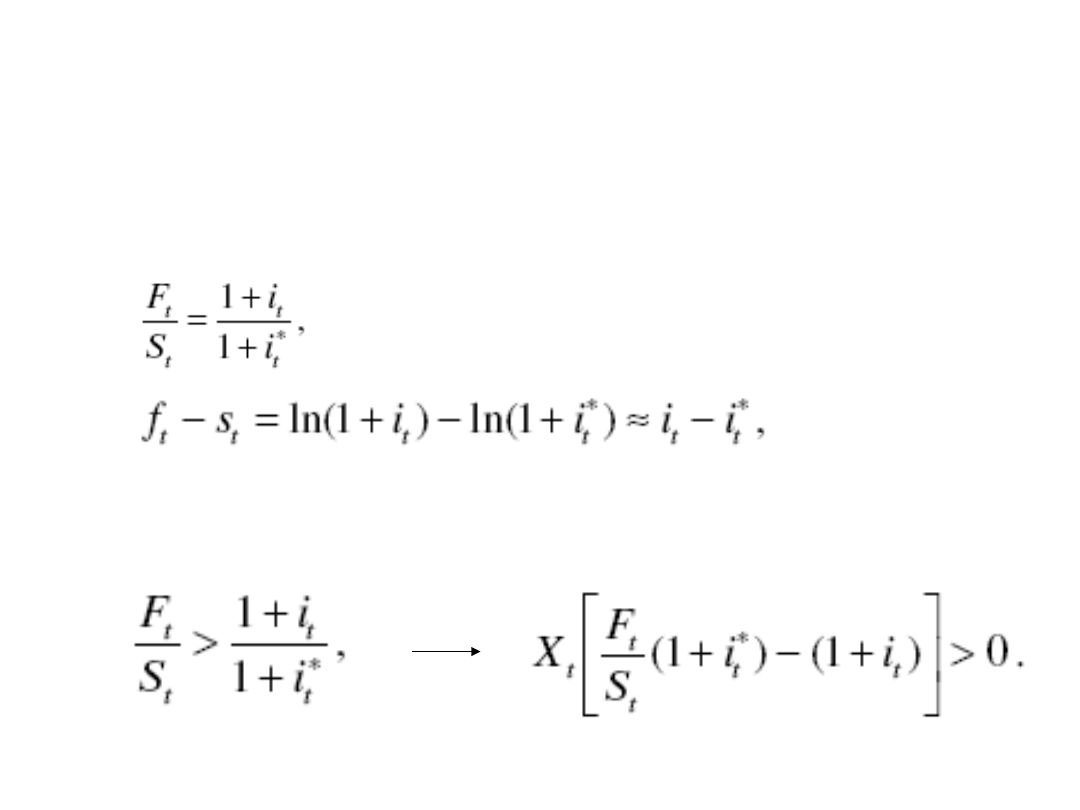
44

Kursy walutowe

• CIP – covered interest rate parity

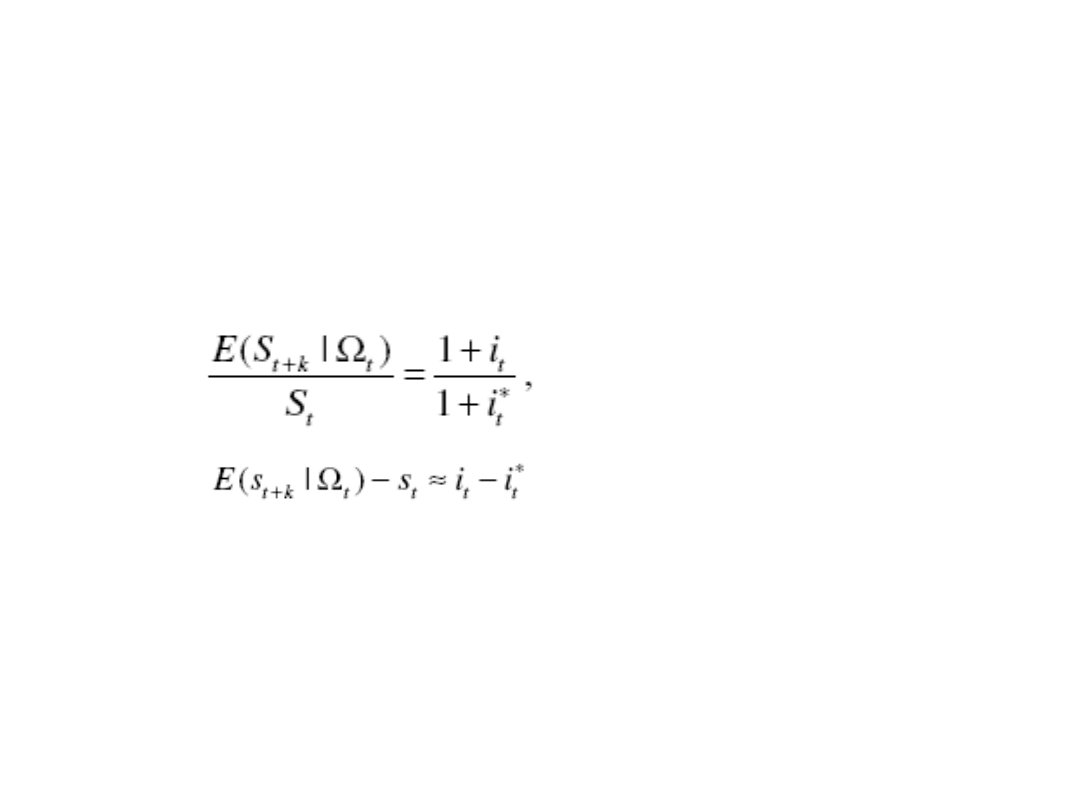
45

Kursy walutowe

• UIP – uncovered interest rate parity

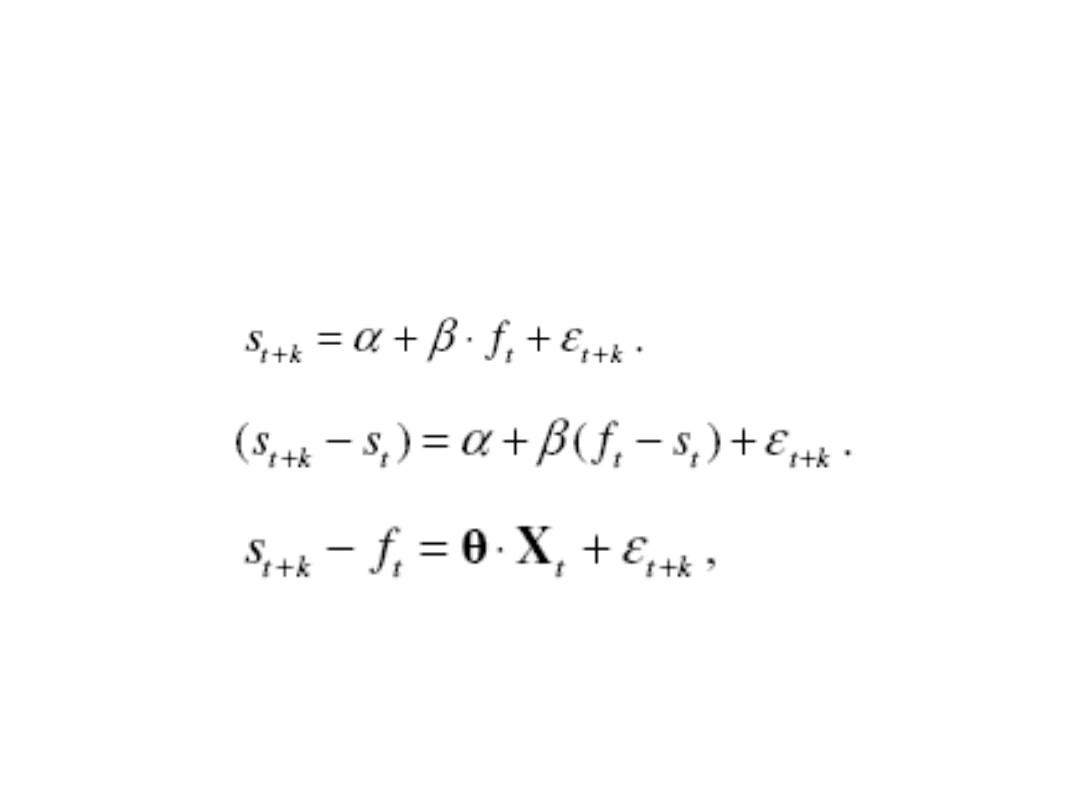
46

Testy UIP

• Czy inwestorzy neutralni wobec

ryzyka?

47

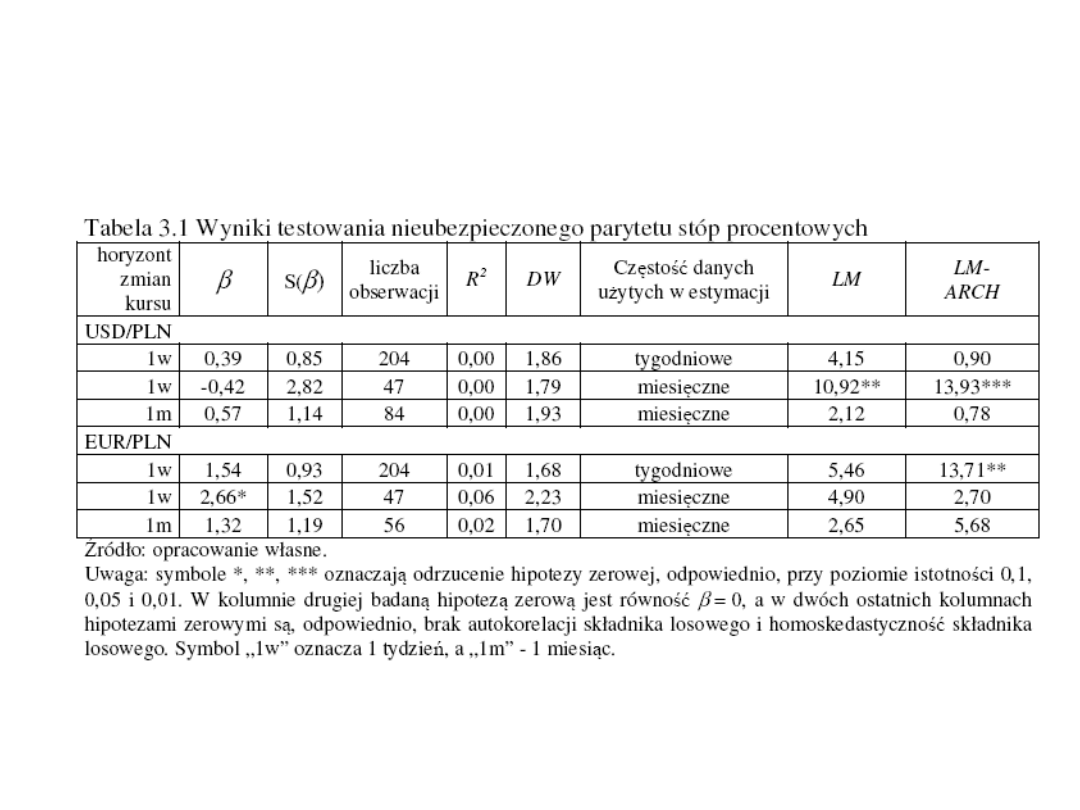
Wyniki dla Polski

48

Metody modelowania premii za

ryzyko

• Modele GARCH-M
• Modele przestrzeni stanów
• Zmienne mierzące ryzyko