WYTRZYMAŁOŚĆ MATERIAŁÓW 

prowadzący

prof. dr hab. inż.  Kazimierz WÓJS

Wykład 11

Opracował

 Andrzej Sitka

ŚCINANIE CZYSTE I 

ŚCINANIE CZYSTE I 

TECHNICZNE

TECHNICZNE

 

 

 

 

Naprężenie ścinające

Naprężenie ścinające

 

 

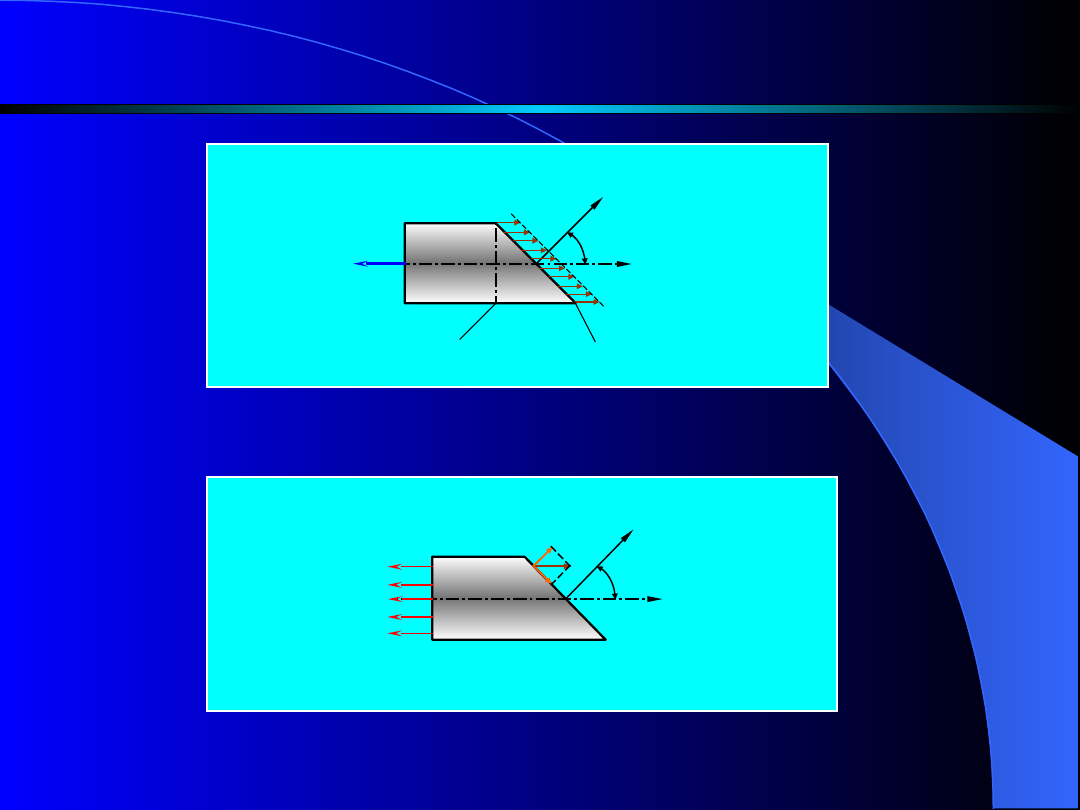
Z  analizy  naprężeń  występujących  w 

różnych przekrojach pręta rozciąganego można 
stwierdzić,  że  w  przekroju  nachylonym  pod 
kątem 



  oprócz  naprężeń  normalnych   

występują  także  naprężenia  styczne  czyli 
ścinające : 









2

sin

2

1



 (1)

 

 

 



p

n

x

kierunek 

normalnej

 

zewnętrznej

P

a
)

A

przekrój 
poprzeczny

przekrój ukośny



p

n

x











b
)

Rozkład naprężeń

Rozkład naprężeń

 

 

Rys.1. Rozkład naprężeń w pręcie rozciąganym

 

 

Rozkład naprężeń 

Rozkład naprężeń 

ścinających

ścinających

 

 

W  każdym  przekroju  pręta  rozciąganego  występują 
naprężenia 

tnące, 

z 

wyjątkiem 

przekrojów 

poprzecznych (



 = 0  i  



 = 



).

W  przypadku  dwukierunkowego  rozciągania  w  każdym 
przekroju  (oprócz  przekrojów  głównych)  występują 
naprężenia tnące, określone wzorem: 

 (2)

 















2

sin

2

1

2

1





 

 

Ścinanie czyste

Ścinanie czyste

 

 

 

Stan 

naprężenia 

w 

takich 

przekrojach,  w  których  występują 
tylko 

naprężenia 

styczne, 

nazywamy czystym ścinaniem. 

 

 

Ścinanie czyste

Ścinanie czyste

 

 

Stan  czystego  ścinania  trudno  jest 

wytworzyć  przez  bezpośrednie  obciążenie 
ciała 

samymi 

naprężeniami 

tnącymi, 

natomiast 

efekt 

taki 

można 

uzyskać 

wywołując  np.  rozciąganie  i  ściskanie  takimi 
samymi,  co  do  wartości  bezwzględnej 
naprężeniami  ,  działającymi  w  dwóch 
wzajemnie prostopadłych kierunkach (rys.2)

 

 

Ścinanie czyste

Ścinanie czyste

 

 

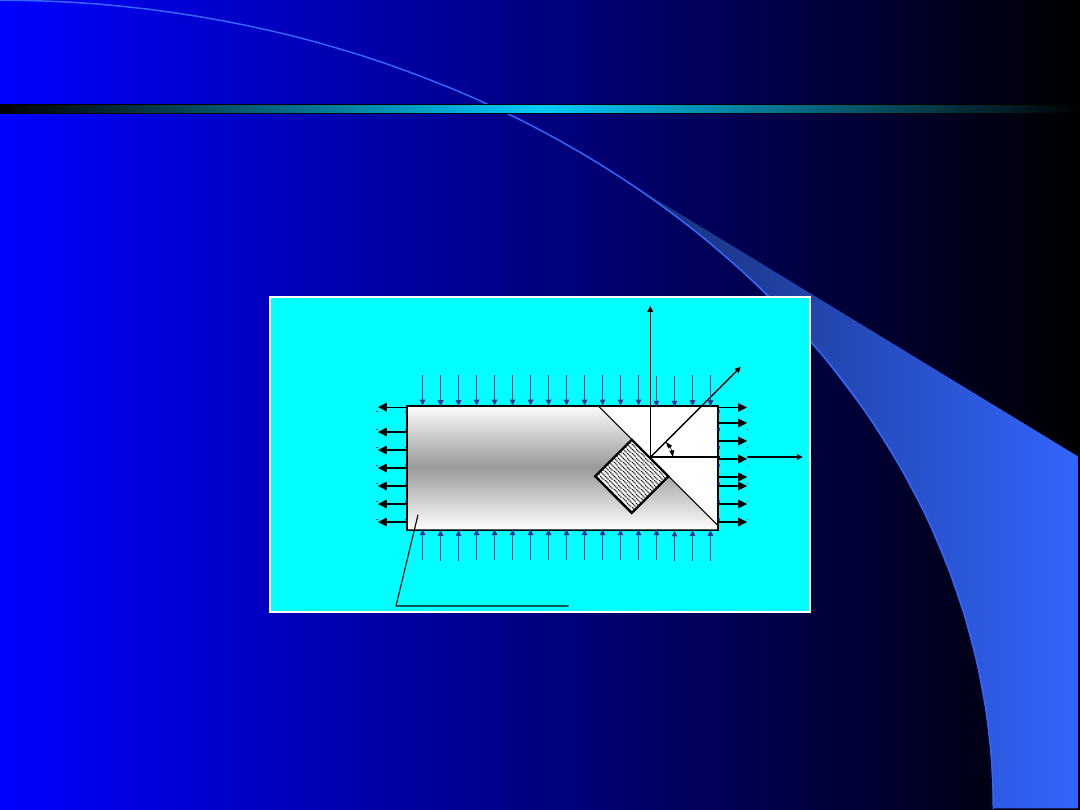
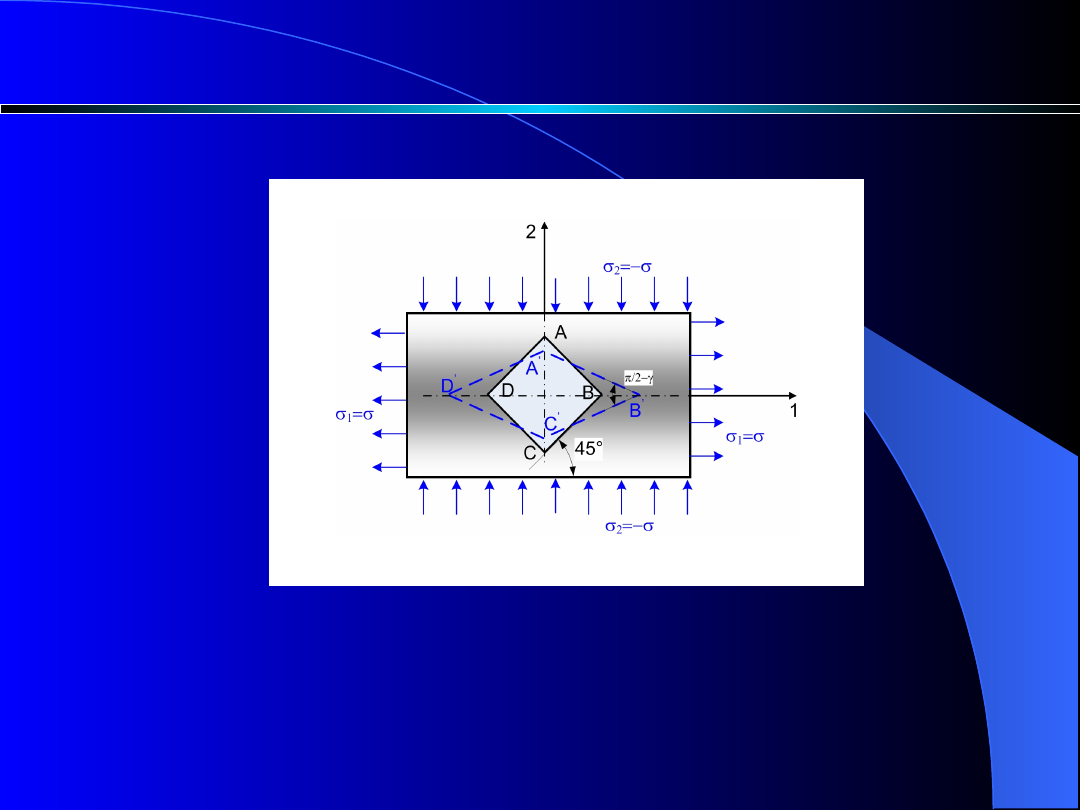
Z  badanego  ciała  wydzielmy  element  ABCD 
(rys.2)  obrócony  względem  osi  1  i  2  o  kąt 
45. 

D

C

A

B



1

=



2



1

n



1

=





2

=-



2

=-

Rys. 2. Obciążenie prostopadłościanu w 

przypadku czystego ścinania 

 

 

Ścinanie czyste

Ścinanie czyste

 

 

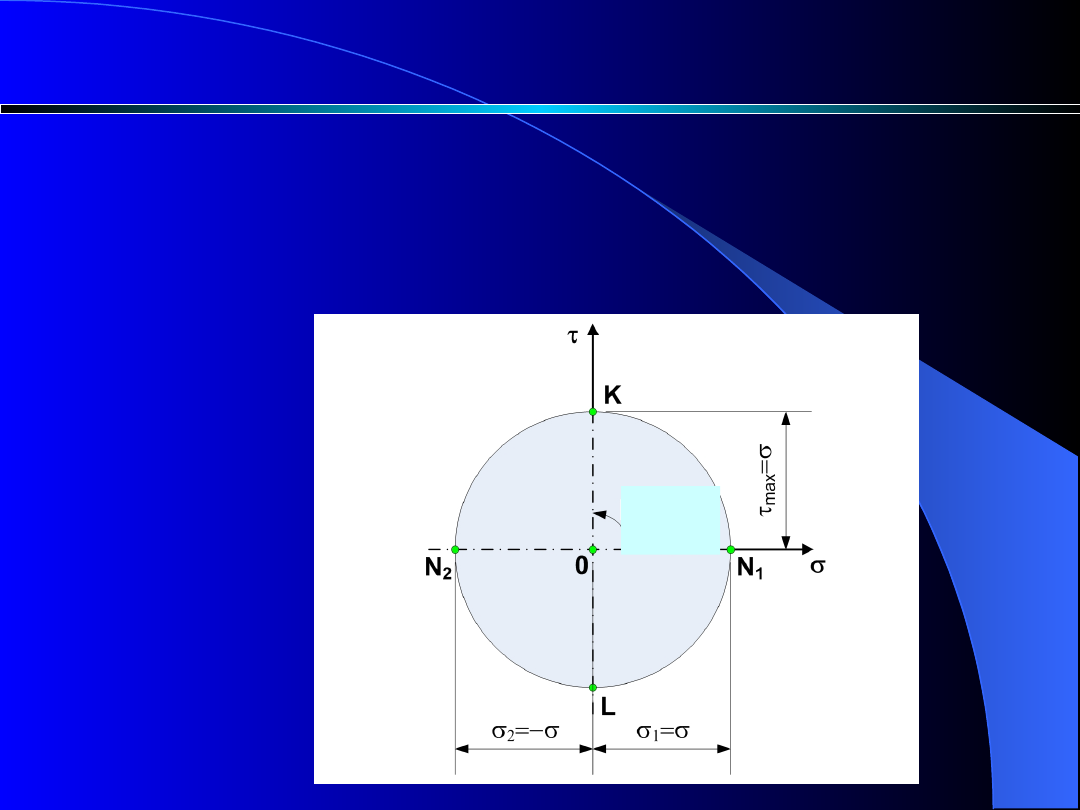
Koło  Mohra  dla  takiego  układu,  tj.  dla  

1

=  oraz 



2

=-,  przedstawia  się  jako  okrąg  o  promieniu  , 

zakreślony  z  początku  0  układu  współrzędnych  ,   
(rys.3). 

Rys. 3. Koło Mohra 

2

2

 

 

Ścinanie czyste

Ścinanie czyste

 

 

Jeżeli  rozpatrywany  element  przetniemy  w  myśli 

przekrojem  A-B  (rys.2)  określonym  normalną  nachyloną  do  osi 
głównej 

1

 pod kątem  = /4 to naprężenie normalne dla 

1

= 

oraz 

2

=- będzie równe zeru: 

 

0

2

2

2

2

4

sin

4

cos

2

2

2

2

2

1

4





















































 
(3
)

 

natomiast  naprężenia  styczne  na  podstawie  wzoru  (2) 
wyniesie:

 

 
(4)

 





 









































1

2

4

2

sin

2

1

2

1

4

 

 

Ścinanie czyste

Ścinanie czyste

 

 

Przekrojowi A-B nachylonemu do kierunku 1 pod kątem 



 = 



/4  odpowiada  na  kole  Mohra  punkt  K,  którego 

współrzędnymi są 



 = 0  oraz 



 =



  (rys.3). 

D

C

A

B

2

/4

1

n







  

Rys. 4

 

 

Prawo Hooke’a przy 

Prawo Hooke’a przy 

ś

ś

cinaniu

cinaniu

 

 

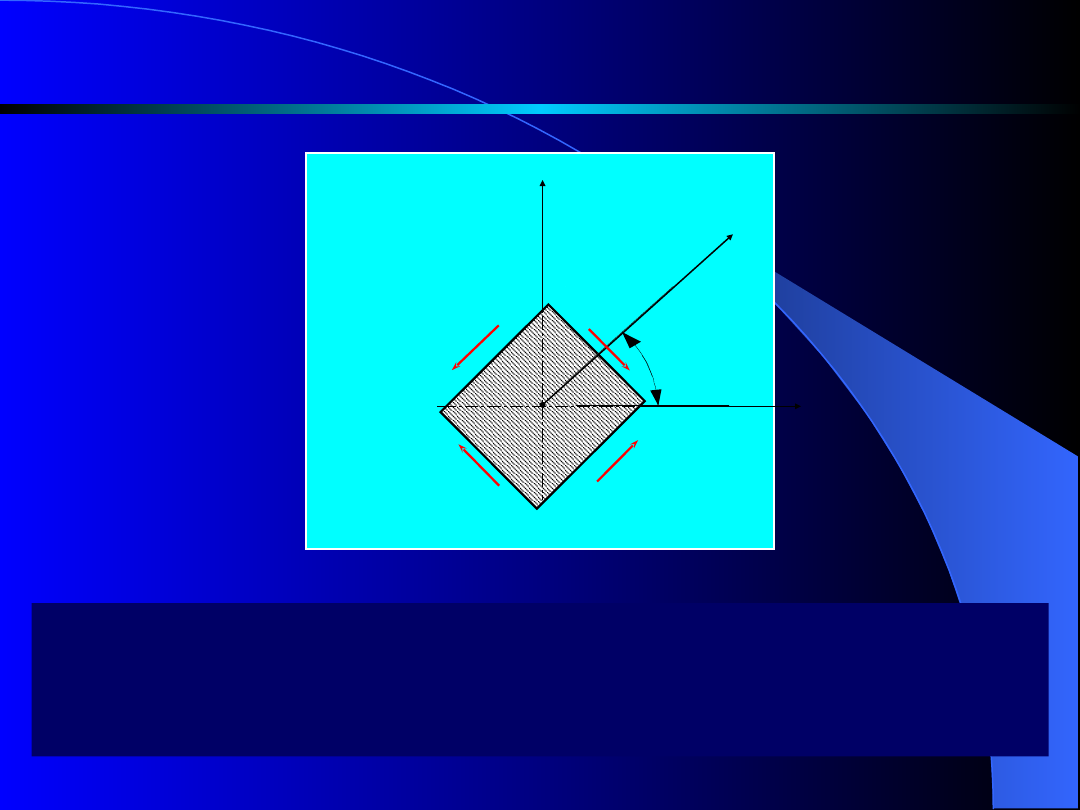
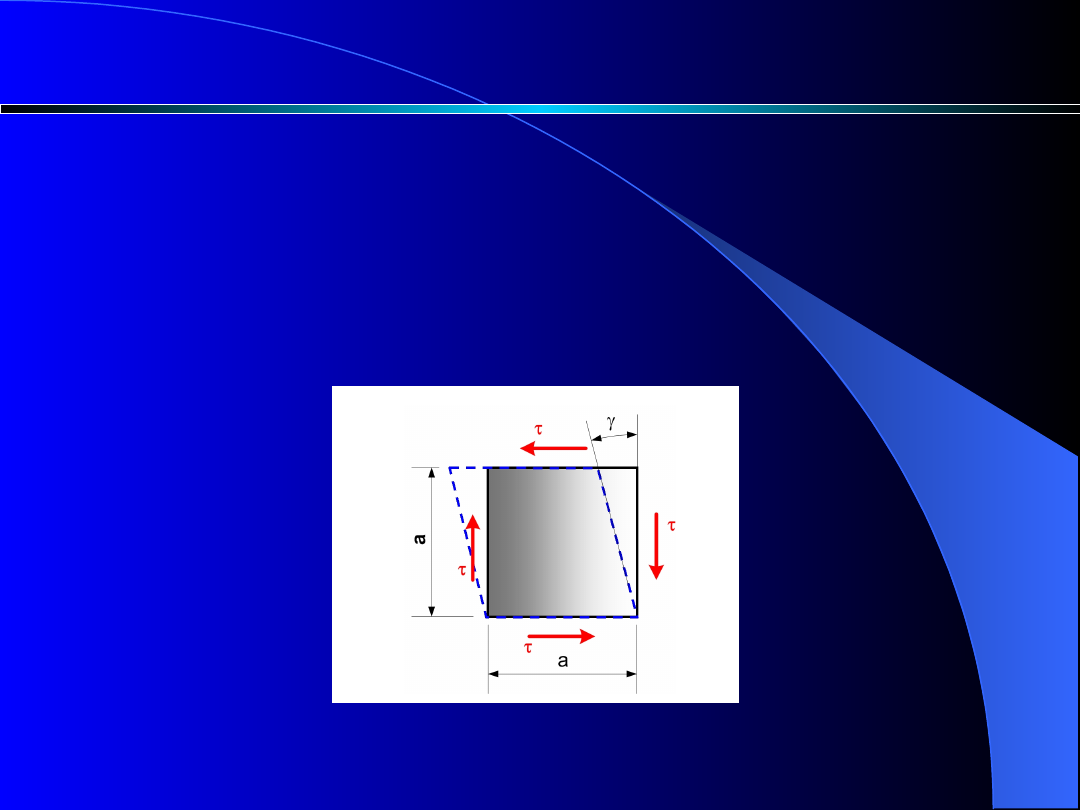
Prostopadłościan  poddany  czystemu  ścinaniu  (rys.  5)  pod 
wpływem  działania  naprężeń  tnących 



  zmieni  swój  kształt  z 

prostokątnego na rombowy. 

Ściany  nadal  pozostaną  płaskie  a  kąty  proste  ulegną 
odkształceniu o  



. 

Rys. 5. Zmiany kształtu prostopadłościanu pod wpływem naprężeń 

stycznych 

 

 

Prawo Hooke’a przy 

Prawo Hooke’a przy 

ś

ś

cinaniu

cinaniu

 

 

Dla  każdego  materiału  podlegającego  prawu 
Hooke’a  kąt    jest  wprost  proporcjonalny  do 
naprężeń tnących : 

G







 (5)

 

Jest  to 

prawo  Hooke’a  przy 

ścinaniu.

 

 

 

Prawo Hooke’a przy 

Prawo Hooke’a przy 

ś

ś

cinaniu

cinaniu

 

 

Żadna  ze  ścian  lub  krawędzi  nie  jest  ani 
rozciągana,  ani  ściskana  to  nie  ma  powodu 
przypuszczać, 

aby 

miały 

one 

ulec 

wydłużeniu lub skróceniu.

 

Objętość 

prostopadłościanu 

poddanemu 

czystemu 

ścinaniu 

pozostaje 

niezmieniona, 

następuje 

jedynie 

zmiana 

postaci 

(prostopadłościan zmienił się w równoległościan, 
a kwadrat w romb (rys.5)). 

 

 

Prawo Hooke’a przy 

Prawo Hooke’a przy 

ś

ś

cinaniu

cinaniu

 

 

   

są to odkształcenia postaciowe

       

  -  kąt  odkształcenia 

postaciowego,

        stała  materiałowa  G  – 

moduł 

sprężystości 

poprzecznej

 

(Kirchhoffa). 

 

 

MATERIAŁ

   

G 10 

- 5  

MPa 

Stal

0,81

Żeliwo

0,38

Miedź

0,45

Mosiądz 

0,32

Brąz

0,37

Aluminium

0,27

Dural

0,27

Szkło

0,22

Drewno jodłowe

0,006

Guma

0,22

Moduł Kirchoffa

Moduł Kirchoffa

 

 

 

 

Zależność między modułem 

Zależność między modułem 

sprężystości

sprężystości

postaciowej G a modułem Younga E 

postaciowej G a modułem Younga E 

Rys. 6. Odkształcenia prostopadłościanu w stanie czystego

 

ścinania

 

 

Zależność między modułem 

Zależność między modułem 

sprężystości

sprężystości

postaciowej G a modułem Younga E 

postaciowej G a modułem Younga E 

Wzdłuż  osi  1  działa  naprężenie  rozciągające 



1

=



,  a 

wzdłuż  osi  2  naprężenie  ściskające 



2

=-



,  które  co  do 

wartości  bezwzględnej  są  sobie  równe.  Odkształcenia 
względne mają postać: 

 

w  kierunku 
1 

 





































1

2

1

1

E

E

E

E

E

 (7)

 

w 

kierunku 

2: 

 (8)

 

 







































1

1

2

2

E

E

E

E

E

 

 

Zależność między modułem 

Zależność między modułem 

sprężystości

sprężystości

postaciowej G a modułem Younga E 

postaciowej G a modułem Younga E 

Wydłużenia względne mają te same wartości bezwzględne, 
więc:

 























1

2

1

E

 (9)

 

gdzie 



  - 

współczynnik  Poissona

  (proporcjonalności);  stała 

równa  stosunkowi  względnego  zwężenia  poprzecznego  pręta 
rozciąganego  do  jego  wydłużenia  względnego  w  kierunku 
rozciągania 

5,

0

0 





 

 

Współczynnik Poissona

Stal – 0,3

Żeliwo – 0,3

Miedź – 0,3

Aluminium 0,37

Szkło – 0,25

Guma – 0,49

Drewno – 0,045 – 0.065

Wartości współczynnika Poissona dla różnych 
materiałów

 

 

Zależność między modułem 

Zależność między modułem 

sprężystości

sprężystości

postaciowej G a modułem Younga E 

postaciowej G a modułem Younga E 

 

 

 

Zależność  między  modułem  Younga  E  a  modułem 
Kirchhoffa G











1

2

E

G

 

 

Ś

Ś

cinanie techniczne

cinanie techniczne

W  praktyce  realizacja  czystego  ścinania  jest 
niemożliwa  (między  siłami  tnącymi  występuje 
zawsze  jakaś  skończona  odległość  –  zakłócenie 
momentem gnącym).

Podczas  ścinania  technicznego  obok  naprężeń 
stycznych 



  występują  również  naprężenia 

normalne 



, jednak naprężenia tnące są znacznie 

większe od naprężeń normalnych. 

 

 

Ś

Ś

cinanie techniczne

cinanie techniczne

W 

przypadkach 

takich 

należy 

sprawdzić 

kryterium, 

czy 

naprężenia 

tnące 



 

nie 

przekraczają  wartości  naprężeń  dopuszczalnych 
na ścinanie 



dop.

 

 
(22)

 

gdzie:



dop 

– naprężenia dopuszczalne na ścinanie,

T – siła tnąca,

A – przekrój poddany ścinaniu. 

dop

A

T









 

 

Ś

Ś

cinanie techniczne

cinanie techniczne

 

 

Przypadki ścinania technicznego:

   nitów i sworzni,

   spoin,

   klinów. 

 

 

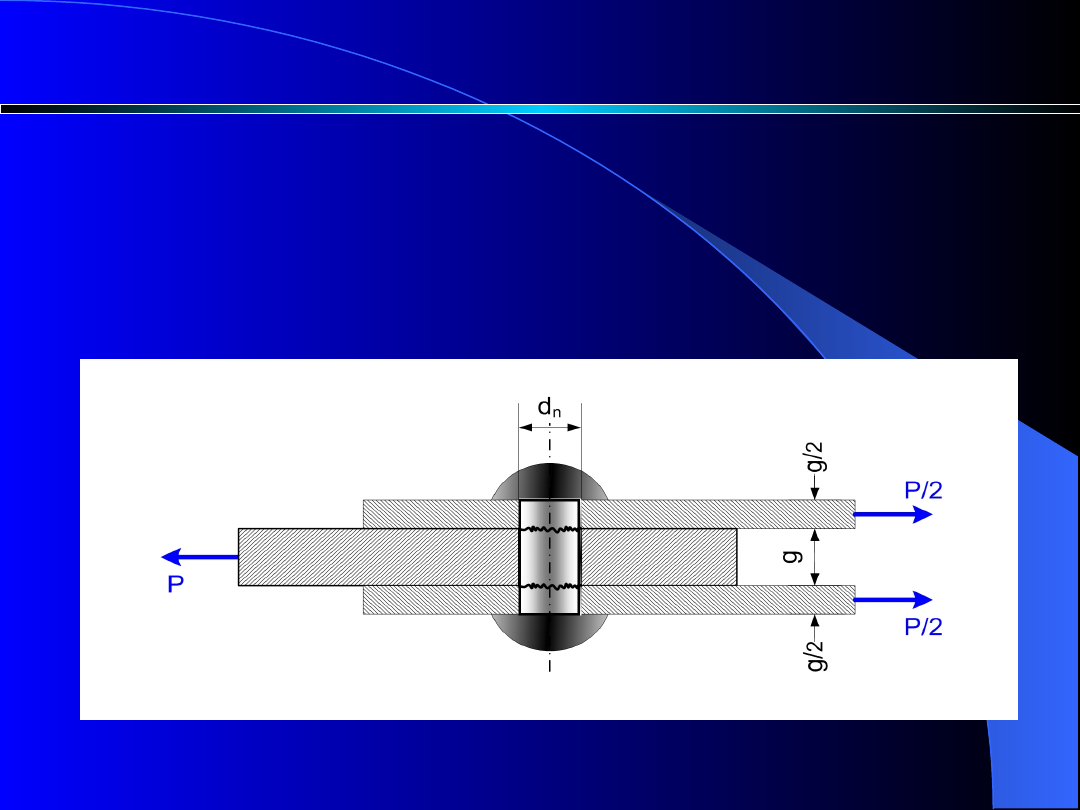
Poł

Poł

ą

ą

czenia nitowe 

czenia nitowe 

Nity  i  sworznie  są  narażone  na  ścinanie  w 
płaszczyznach  styku  blach  łączonych,  które 
wywierają 

też 

nacisk 

na 

półwalcową 

powierzchnię nita lub sworznia. 

Rys. 8. Połączenie nitowe

 

 

 

Połączenia nitowe 

Połączenia nitowe 

 

Całkowity przekrój poprzeczny nitów poddanych 

ścinaniu wynosi: 

 
(23)

 

m

n

d

A

n

4

2





gdzie:

n – liczba nitów,

m – liczba przekrojów ścinanych w nicie,

d

n

 – średnica nita.

 

 

Po  podstawieniu  wzoru  (23)  do  warunku 
wytrzymałości 

na 

ścinanie 

(22) 

i 

uwzględnieniu, że T=P otrzymamy: 

 
(24)

 

dop

n

m

n

d

P











2

4

Poł

Poł

ą

ą

czenia nitowe 

czenia nitowe 

 

 

Połączenia nitowe oblicza się także ze względu 
na docisk powierzchniowy 



d

: 

 
(25)

 

dop

d

n

d

d

g

P

A

P











gdzie:
g – grubość blachy naciskającej na nit,



d dop

 – naprężenie dopuszczalne na docisk. 

Poł

Poł

ą

ą

czenia nitowe

czenia nitowe

 

 

Podobnie  oblicza  się  naprężenia  tnące  oraz 
naprężenia na docisk w sworzniach. 

 

 

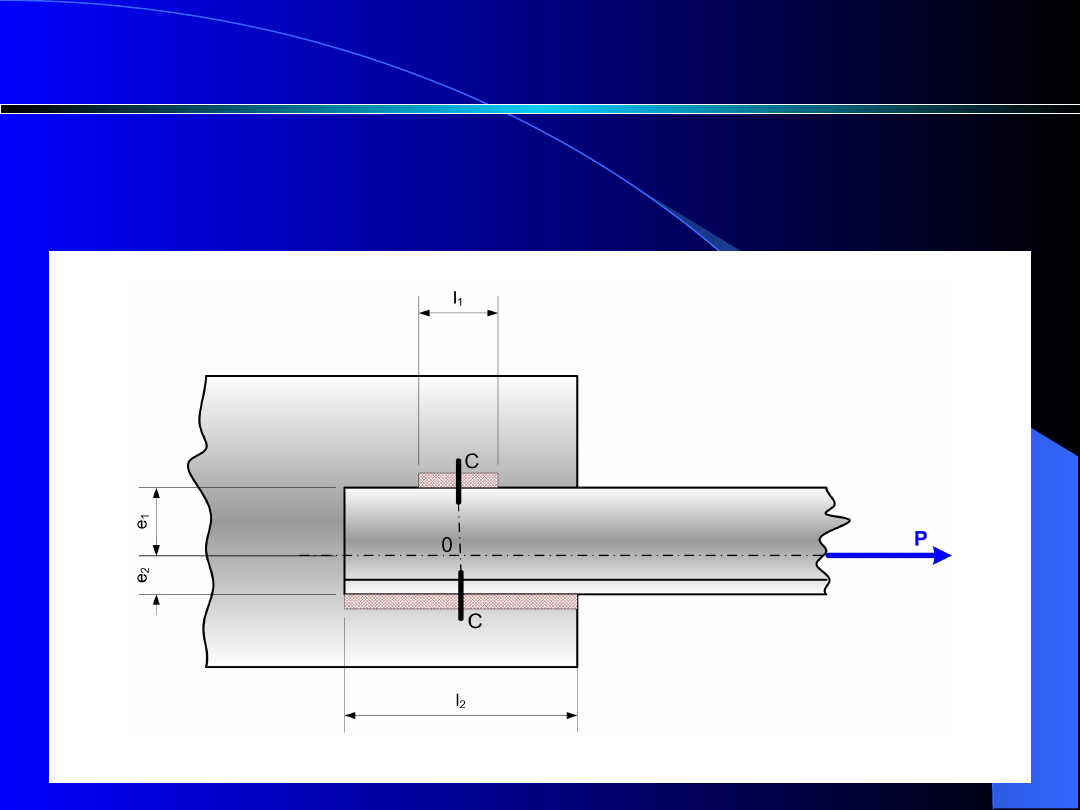
Kątownik przyspawano z dwóch stron spoinami o 
  długościach  l

1

  i  l

2  .

  Obliczyć  połączenie  dla 

obciążenia P. 

Obliczenia spoin 

Obliczenia spoin 

Rys. 9

 

 

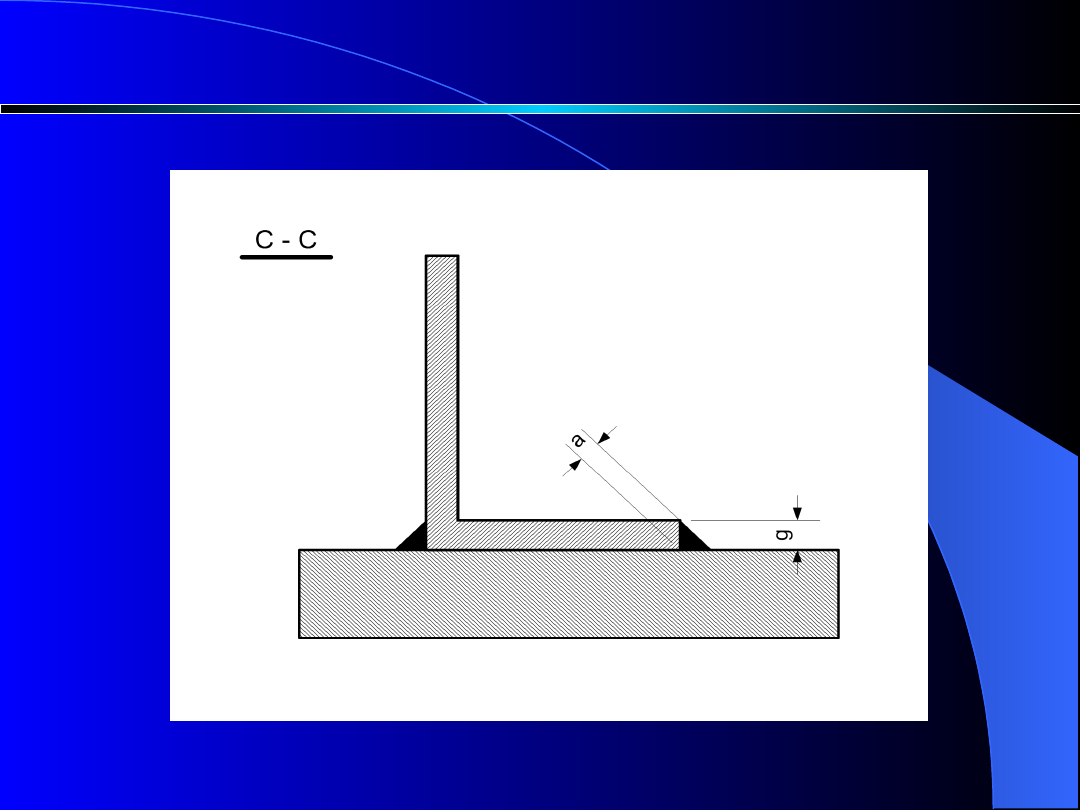
Obliczenia spoin 

Obliczenia spoin 

Rys. 10. Przekrój poprzeczny C-C połączenia spawanego 

 

 

Największe  naprężenia  ścinające  wystąpią  w 
przekroju spoiny o szerokości „a”.

Pole niebezpiecznego przekroju spoiny wynosi: 

Obliczenia spoin 

Obliczenia spoin 

 
(26)

 





g

l

l

a

l

l

A

2

2

)

(

2

1

2

1









 

 

Różne  długości  spoin  po  obydwu  stronach 
kątownika wynikają z położenia siły P  (rys. 9). 

Siły tnące w obu spoinach wynoszą:

Obliczenia spoin 

Obliczenia spoin 

 
(27)

 

dop

l

a

T



1

1



dop

l

a

T



2

2



 
(28)

 

 

 

Obliczenia spoin 

Obliczenia spoin 

 
(29)

 

 
(30)

 

0

2

2

1

1

2

2

1

1

0













e

l

a

e

l

a

e

T

e

T

M

dop

dop





Po  podzieleniu  równania  (29)  przez    a



dop 

 

otrzymamy: 

1

2

2

1

e

e

l

l



Odpowiednie długości spoin po obydwu stronach 
kątownika wyznacza się z warunku równowagi 
momentów sił tnących. 

Względem biegu O równanie ma postać:

 

 

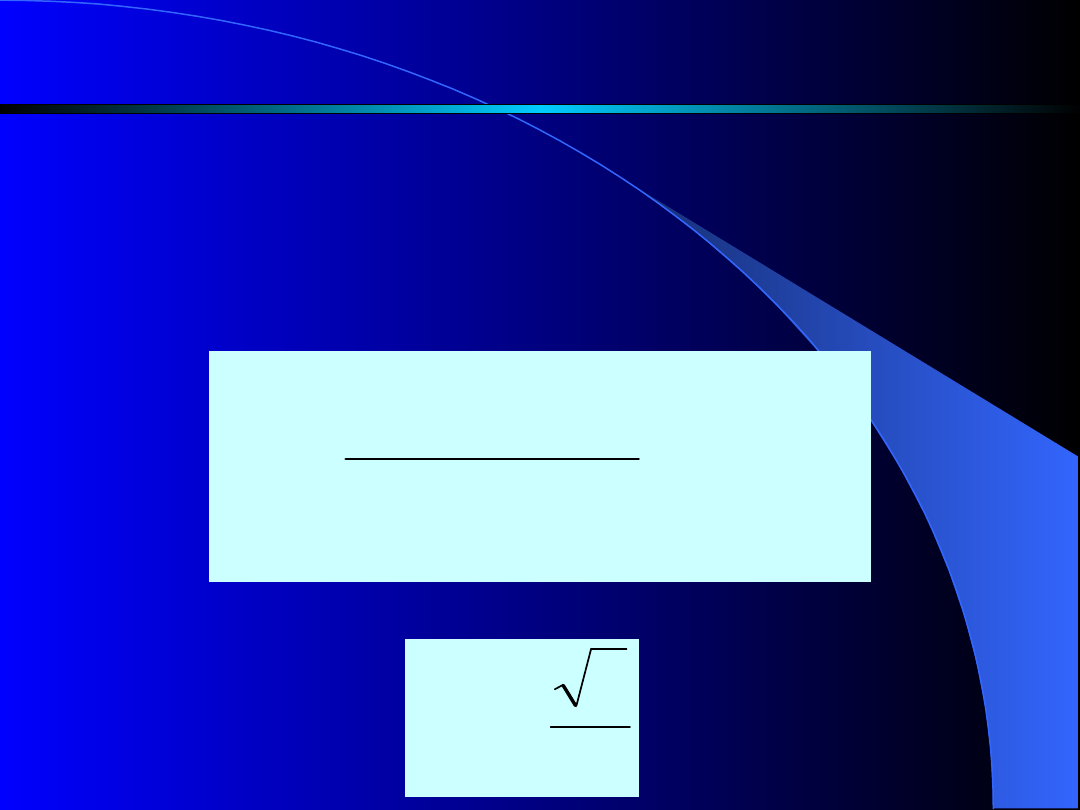
Warunek  wytrzymałości  spoiny  na  ścianie 
otrzymamy  podstawiając  wzór  (26)  do  warunku 
(22) i uwzględniając, że T

1

+T

2

=P: 

Obliczenia spoin 

Obliczenia spoin 

 
(31)

 





dop

a

l

l

P











2

1

2

2

g

a 

 

 

Obliczenia  klina  o  długości 

l

,  wysokości 

b

  i 

szerokości 

a

  w  połączeniu  korby  z  wałem 

(rys.11). 

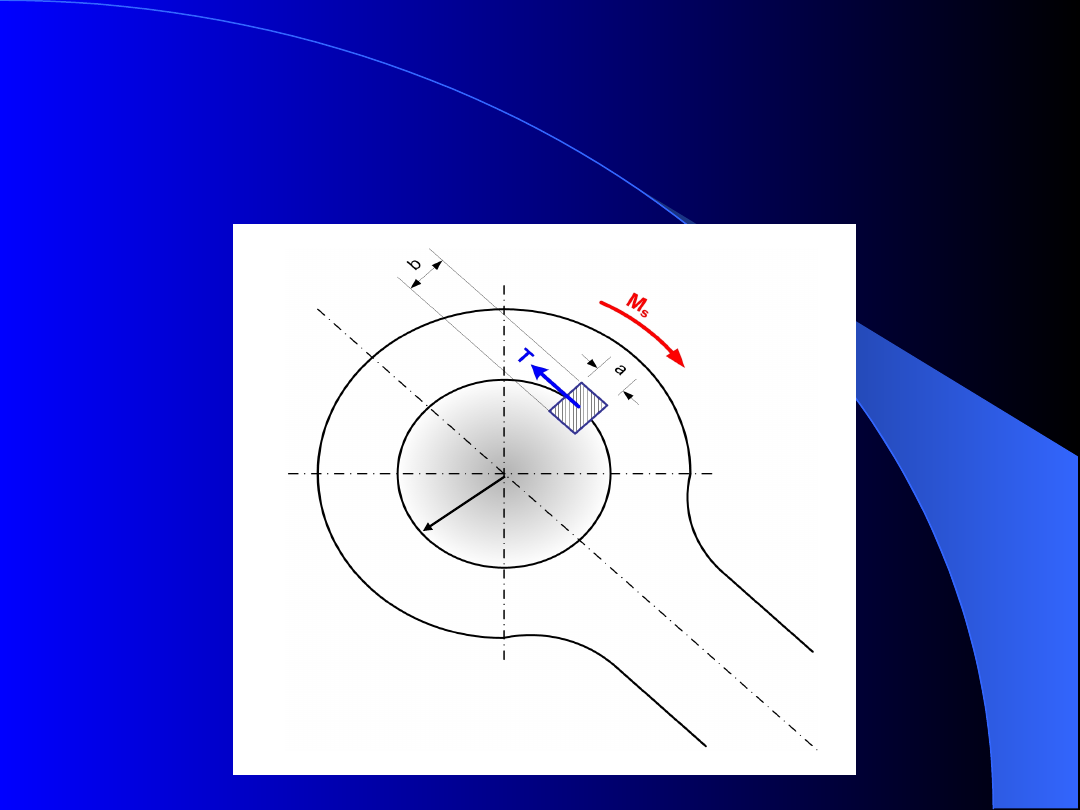
Obliczenia klinów 

Obliczenia klinów 

Rys. 11. Połączenie 
klinowe

r

 

 

Klin,  który  umożliwia  obrót  wału  wskutek 
przyłożenia  do  korby  momentu  M

s

,  jest  ścinany 

w przekroju A: 

Obliczenia klinów 

Obliczenia klinów 

l

a

A

 
(32)

 

Wartość  siły  tnącej  w  klinie  otrzymamy  z  równania 
równowagi momentów  względem środka skręcenia 0: 

0

0









r

T

M

M

s

 
(33)

 

 

 

więc 

Obliczenia klinów 

Obliczenia klinów 

 
(34)

 

Warunek 

wytrzymałości 

klina 

otrzymamy 

podstawiając (32) i (34) do równania (22): 

 
(35)

 

r

M

T

s



dop

s

l

a

r

M

A

T











 

 

Docisk powierzchniowy na styku klina z korbą 
i  wałkiem  obliczymy  w  przybliżeniu  z 
zależności: 

Obliczenia klinów 

Obliczenia klinów 

 
(36)

 

jeżeli  płaszczyzna  ścinania  leży  w  połowie  jego 
wysokości b.

dop

d

d

l

b

T









2