Podstawy statystyki

Semestr letni 2014

Mgr Paweł J.

Mazurkiewicz

Podstawowe informacje

(o mnie)

Doktorant kolegium MISDoMP

- etologia i psychologia behawioralna owadów

społecznych

Kontakt:

[e-mail]

[e-mail]

(po wcześniejszym umówieniu)

Instytut Biologii Doświadczalnej PAN

Pasteura 3/5

Pok. 629

Wydział Psychologii: wtorek 12-14, sala do ustalenia

Organizacja pracy

Dwa kolokwia 45 minutowe

Pytania otwarte (na zrozumienie)

Proste obliczenia

Używanie i rozumienie tablic z, t, chi^2 itp.

Można mieć notatki

Wysyłam większość prezentacji na maila

Czasami wysyłam zadania do zrobienia

Podstawy statystyki

Cecha
Stan
Populacja
Próba
Próba reprezentatywna

Skale pomiarowe

Na jakiej skali zapisać możemy następujące

dane:

Wyniki pomiaru inteligencji,

płeć,

temperaturę,

wiek,

stopnie wojskowe

oceny szkolne

ciśnienie atmosferyczne

nazwy miejscowości

Skale pomiarowe

Skala nominalna

– wartości na tej skali nie mają oczywistego

uporządkowania.

- wśród skal nominalnych wyróżnia się

czasem skale dychotomiczne przyjmujące

tylko dwie wartości, np. odpowiedź na pytania

tak/nie.

Przykłady:

-Płeć

-Rasa psa

-Pogoda

Skale pomiarowe

Skala porządkowa

-wartości mają jasno określony porządek, ale

nie są dane odległości między nimi

-relacje porządku ( < > ≤ ≥) i równości

Przykłady:

-stopnie wojskowe

-wykształcenie

Skale pomiarowe

Skala interwałowa (przedziałowa)

– różnice pomiędzy wartościami mają

sensowną interpretację, ale ich iloraz nie.

- nie ma zera bezwzględnego

Przykłady:

- wyniki większości testów psychologicznych

(np. test IQ Wechslera)

-oceny szkolne

-Temperatura na skali Celsjusza

Skale pomiarowe

Skala ilorazowa (stosunkowa)

– nie tylko różnice, ale także ilorazy wielkości

mają interpretację.

Przykłady:

-masa

- temperatura na skali Kelvina

Porządkowanie wyników

Rozkład empiryczny (tj. uzyskane wyniki)

możemy ukazać na szereg różnych

sposobów:

- W szeregu (rozdzielczym)

- W tabeli frekwencji

- Wykresy

-> histogram

-> dystrybuał (frekwencja skumulowana)

-> wykres skrzynkowy

Zmienna ciągła

Gdy mamy zmienną ciągłą – należy uwzględnić granice

dokładne

przedziałów. Np. gdy zapisujemy wyniki z dokładnością do

1 cm, to

16 cm przy zastosowaniu dokładniejszego pomiaru mieści

się w

Granicach 15,5 – 16, 5.

Liczebność skumulowana – dodanie od dołu liczebności.

Pozwala

powiedzieć w jakiej liczbie przypadków wyniki są niższe lub

wyższe od określonej wartości.

Skumulowane procenty liczebności – otrzymuje się poprzez

podzielenie liczebności skumulowanej przez całkowita

liczbę

przypadków. I w ten sposób można powiedzieć jaki jest

procent

wyników większych niż bądź mniejszych niż jakaś wartość.

Porządkowanie wyników

0, 0, 1, 1, 0, 1, 2, 4, 1, 0, 2, 1, 0, 1, 2, 1, 2, 2, 1,

5

Porządkowanie wyników

0, 0, 1, 1, 0, 1, 2, 4, 1, 0, 2, 1, 0, 1, 2, 1, 2, 2, 1,

5

Wartości cechy

Liczebność

Częstość

Wartości cechy

Liczebność

Częstość

0

5

0,25

1

8

0,40

2

5

0,25

4

1

0,05

5

1

0,05

Porządkowanie wyników

0, 0, 1, 1, 0, 1, 2, 4, 1, 0, 2, 1, 0, 1, 2, 1, 2, 2, 1,

5

Porządkowanie wyników

0, 0, 1, 1, 0, 1, 2, 4, 1, 0, 2, 1, 0, 1, 2, 1, 2, 2, 1,

5

Wartości cechy Liczebność skumulowana

Częstość

skumul.

0

5

0,25

1

13

0,65

2

18

0,90

4

19

0,95

5

20

1,00

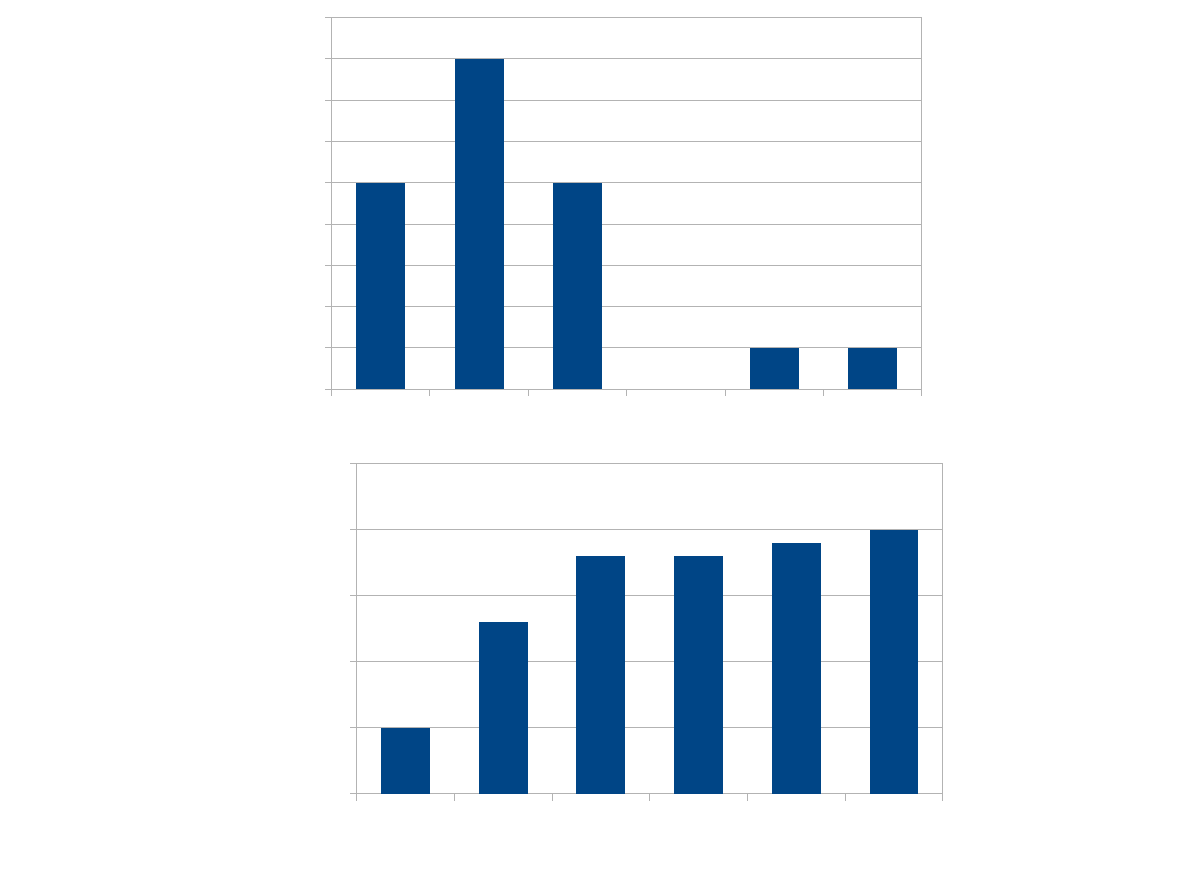
0

1

2

3

4

5

0

1

2

3

4

5

6

7

8

9

Punktacja

Fr

e

kw

e

n

cj

a

0

1

2

3

4

5

0

5

10

15

20

25

Punktacja

Fr

e

kw

e

n

cj

a

s

ku

m

u

lo

w

a

n

a

Stwórzcie własny

histogram

Dane:

0

-> 1os.

1 -> 2os.

2

-> 5os.

3

-> 12os.

4

-> 10os.

5

-> 19os.

6

-> 27os.

7

-> 13os.

8

-> 6os.

9

-> 4os.

10

-> 1os.

11

-> 1os.

Miary tendencji centralnej

Średnia

- suma uzyskanych wyników przez ich

liczbę (n)

Mediana

- wartość środkowa

- jeśli n nieparzyste, to jest to obserwacja

(n+1)/2

- jeśli n parzyste, to jest to średnia

arytmetyczna pomiędzy obserwacjami n/2 i

(n+1)/2

Modalna

- najczęściej osiągana wartość

Obliczcie średnią, medianę i

modalną

0, 0, 1, 1, 0, 1, 2, 4, 1, 0, 2, 1, 0, 1, 2, 1, 2, 2, 1,

5

Dane:

0

-> 1os.

1 -> 2os.

2

-> 5os.

3

-> 12os.

4

-> 10os.

5

-> 19os.

6

-> 27os.

7

-> 13os.

8

-> 6os.

9

-> 4os.

10

-> 1os.

11

-> 1os

Obliczcie średnią,

medianę i modalną

Miary tendencji centralnej

Populacja
μ - wartosc oczekiwana.
M - modalna.
Me - mediana.

Próba
X - srednia
arytmetyczna.
m - modalna.
me - mediana.

Odchylenie od średniej:

- różnica miedzy pewnym wynikiem a średnią.

- suma odchyleń równa się 0.

2

Suma kwadratów odchyleń od średniej

arytmetycznej jest mniejsza niż suma

kwadratów odchyleń od dowolnej innej

wartości.

Właściwości średniej

arytmetycznej

Średnia stanowi tzw. środek ciężkości

Właściwości mediany

Odcina 50% obserwacji po lewej i po prawej

stronie rozkładu

Odpowiada na pytanie: 50% próbki ma

wyniki niższe bądź równe danemu

Jest stosunkowo mniej podatna na wartości

odstające

Używana jest przede wszystkim przy

testach nieparametrycznych –

dedykowanych dla skali porządkowej,

bądź w przypadkach, gdy nie są spełnione

założenia testów parametrycznych

A co, jeśli zechcemy pokategoryzować

wyniki na cztery grupy?

W przedziałach klasowych większych niż 1

bierze się pod uwagę środek przedziału

Dla średniej

Przedział klasowy Liczebnosc (fi) Srodek przedziału Liczebnosc x

srodek

15–19 2 17 34
10–14 34 12 408
5–9 23 7 161
0–4 5 2 10
64 613

Średnia = ?

Dla mediany

Przedział l.osób środek przedz. Liczeb. skumul

0-2

-> 8os. 1 8

3-5

-> 41os. 4 49

6-8

-> 46os. 7 95

9-11 -> 6os. 10 101
me = Xd i + [(n/2 - fc i−1)/fi] * hi

Xd i - dokładna dolna granica przedziału, w którym jest mediana
fc i−1 - liczebnosc skumulowana klasy wczesniejszej niz

mediana

fi - liczebnosc klasy medialnej
hi - długosc przedziału klasowego

Podobnie z modalną

Przedział klasowy Liczebnosc (fi) Srodek przedziału Liczebnosc x

srodek

15–19 2 17 34
10–14 34 12 408
5–9 23 7 161
0–4 5 2 10
64 613

Modalna to ?

Przedziały klasowe

Liczebność

45 - 49

1

40 - 44

2

35 - 39

3

30 - 34

6

25 - 29

8

20 - 24

17

15 - 19

26

10 - 14

11

5 - 9

2

0 - 4

0

Oblicz średnią, medianę i modalną dla rozkładu

liczebności zmiennej skokowej

me = X

d i

+ [(n/2 - f

c i−1

)/f

i

] * h

i

Średnia – dobra dla zmiennych

przedziałowych i stosunkowych

Mediana – przedziałowych

Modalna – nominalnych

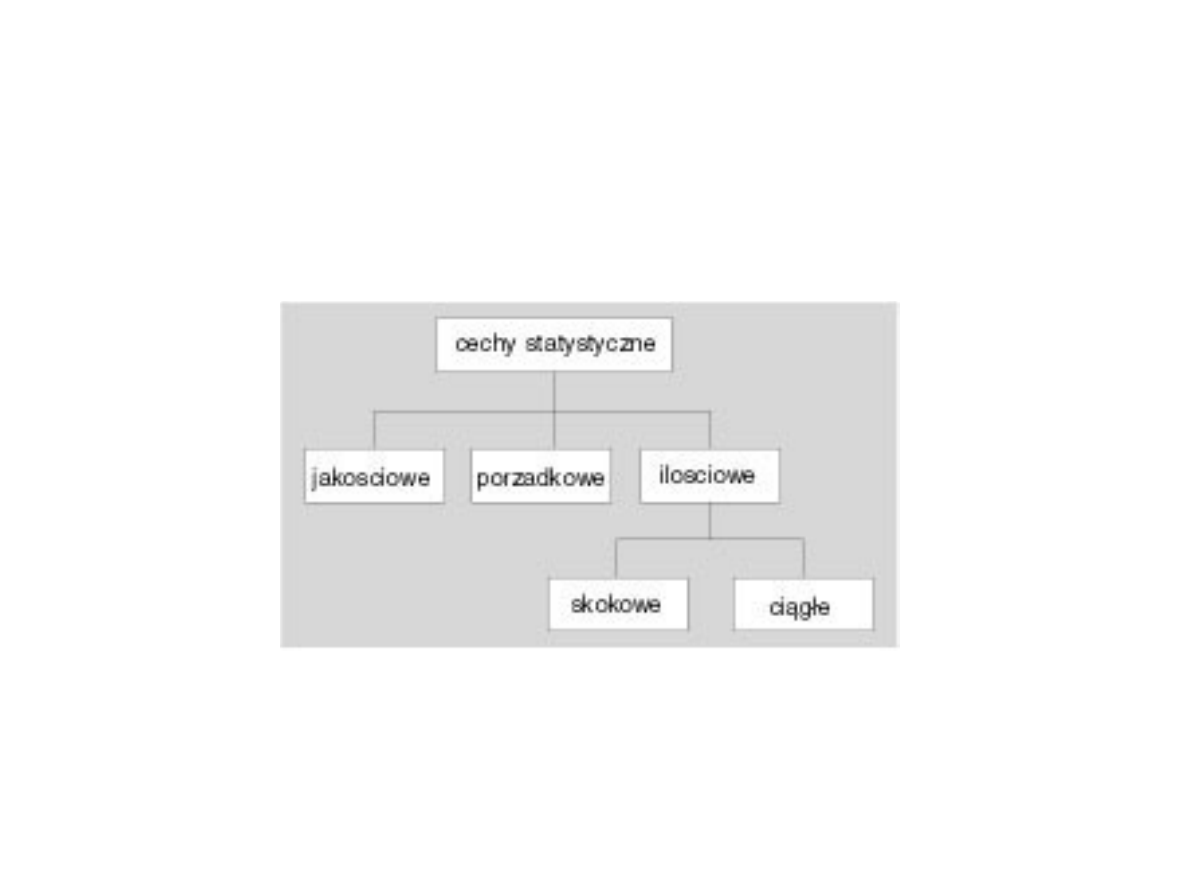
Podsumowanie

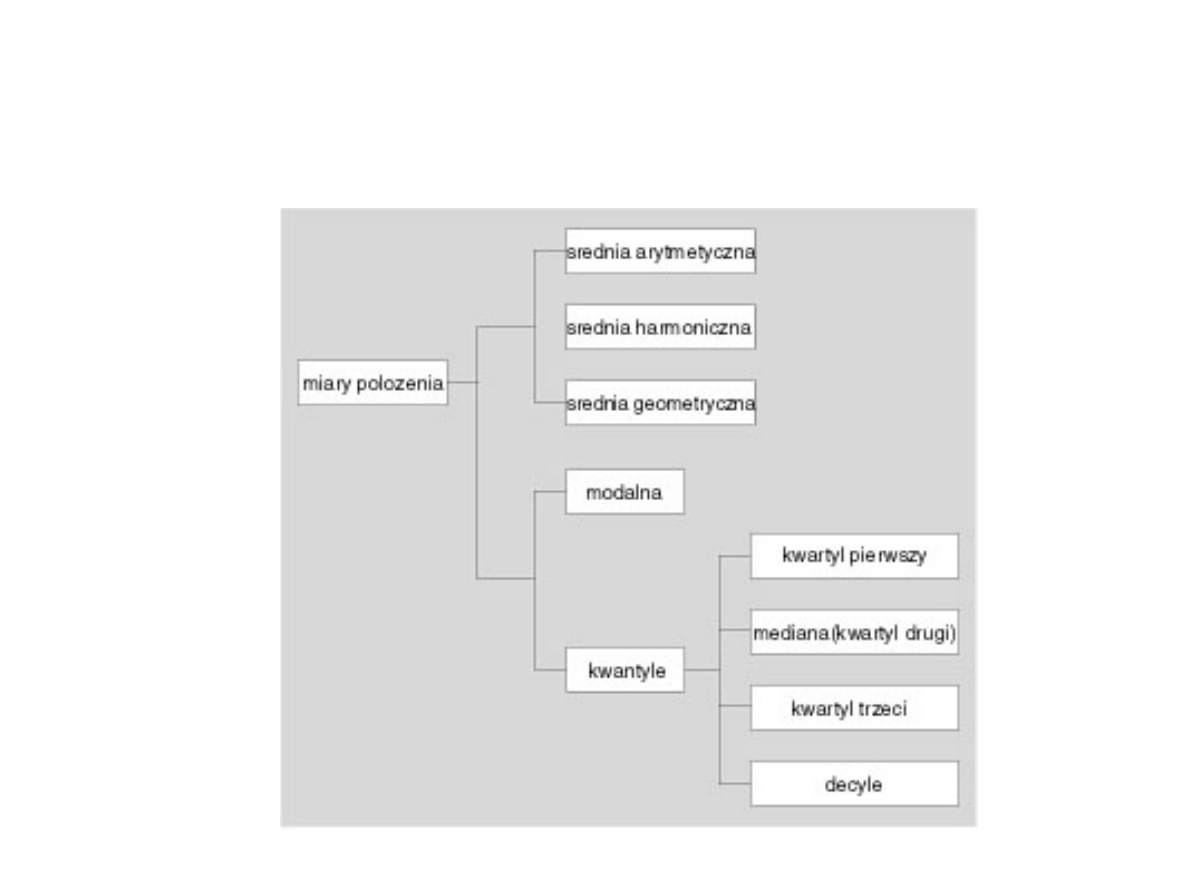
Podsumowanie

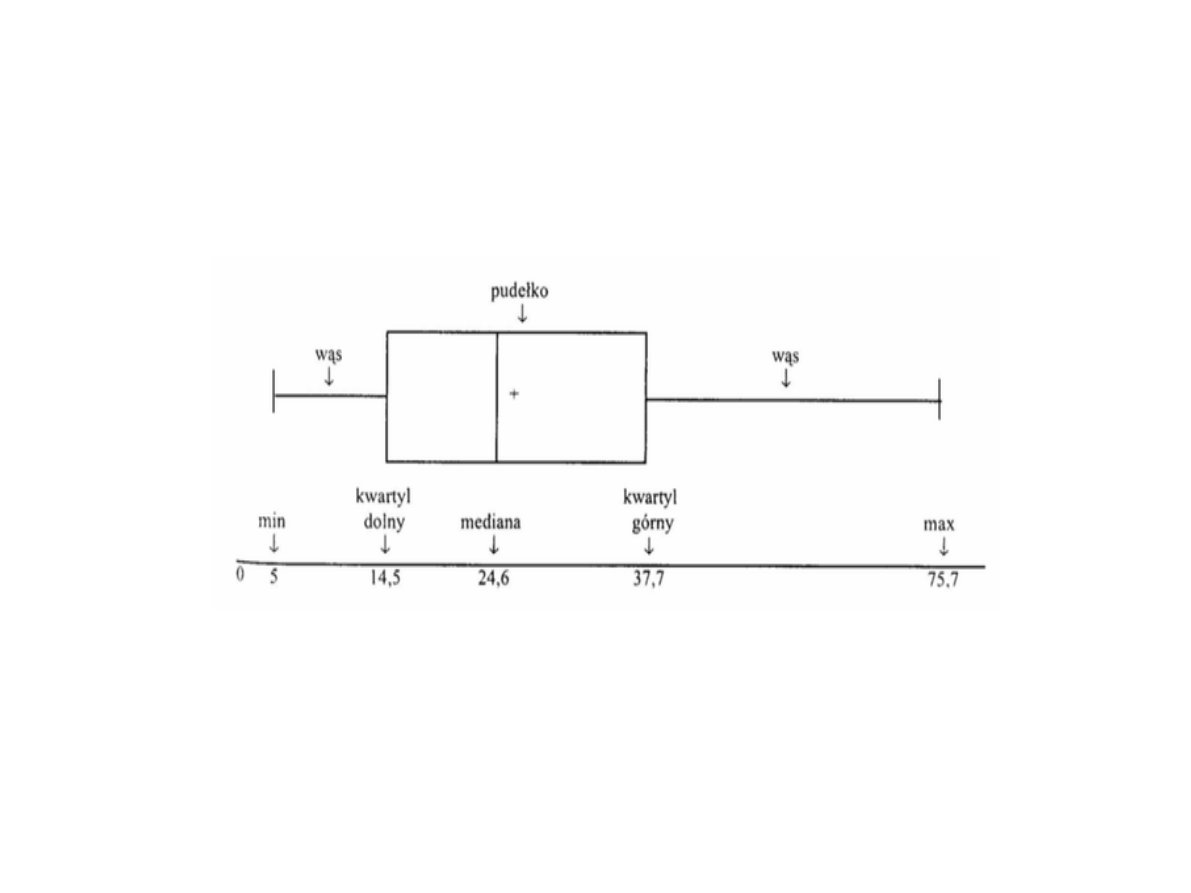
Inne miary położenia

Kwantyl rzędu p – w rozkładzie danych zmiennej

losowej to taka liczba, że z

prawdopodobieństwem p wartości zmiennej będą

mniejsze bądź równe tej liczbie.

Kwantyl rzędu 1/2 to inaczej mediana

Kwantyle rzędu 1/4, 2/4, 3/4 są inaczej nazywane

kwartylami.

Kwantyle rzędu 1/5, 2/5, 3/5, 4/5 to inaczej

kwintyle.

Kwantyle rzędu 1/10, 2/10,..., 9/10 to inaczej

decyle.

Kwantyle rzędu 1/100, 2/100,..., 99/100 to inaczej

percentyle.

Percentyl jest wielkością, poniżej której padają

wartości zadanego procentu próbek

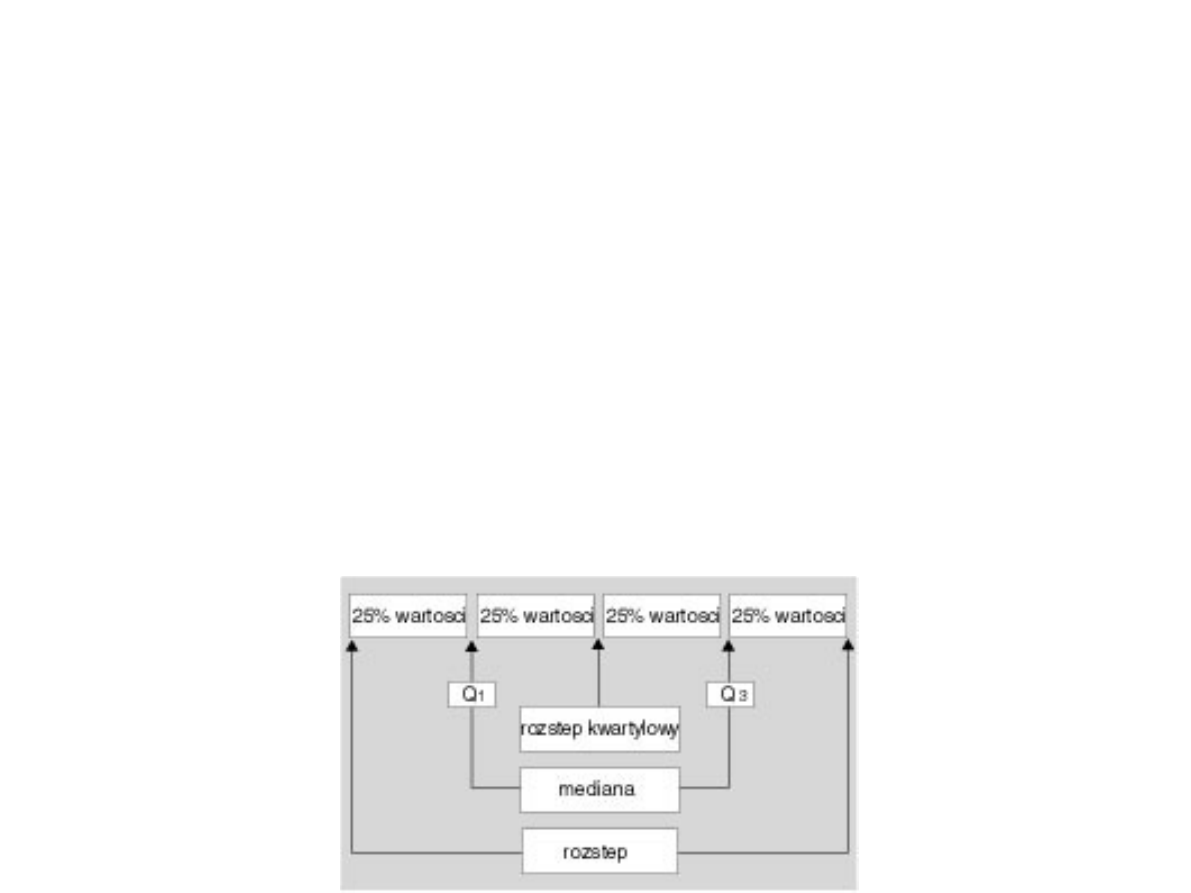
Kwartyl - jest jedną z miar położenia obserwacji

pierwszy kwartyl (notacja: Q1) = kwantyl

rzędu 1/4 = pierwszy kwartyl = dolny kwartyl =

25% obserwacji jest położonych poniżej = 25.

procent

drugi kwartyl (notacja: Q2) = mediana =

kwantyl rzędu 1/2 = dzieli zbiór obserwacji na

połowę = 50. procent

trzeci kwartyl (notacja: Q3) = górny kwartyl =

kwantyl rzędu 3/4 = dzieli zbiór obserwacji na

dwie część odpowiednio po 75% położonych

poniżej tego kwartyla i 25% położonych powyżej

= 75. procent

Miary rozproszenia

w dwu grupach chorych zmierzono skurczowe

ciśnienie tętnicze i otrzymano następujące

wyniki (w mm Hg):

-

grupa I: 145, 125, 130, 155, 140, 150, 135

- grupa II: 115, 150, 100, 180, 140, 165, 130.

Po wykonaniu obliczeń okazuje się, że średnia

i mediana są takie same w obu grupach

i wynoszą 140 mm Hg.

Trzeba więc lepiej opisać nasze grupy.

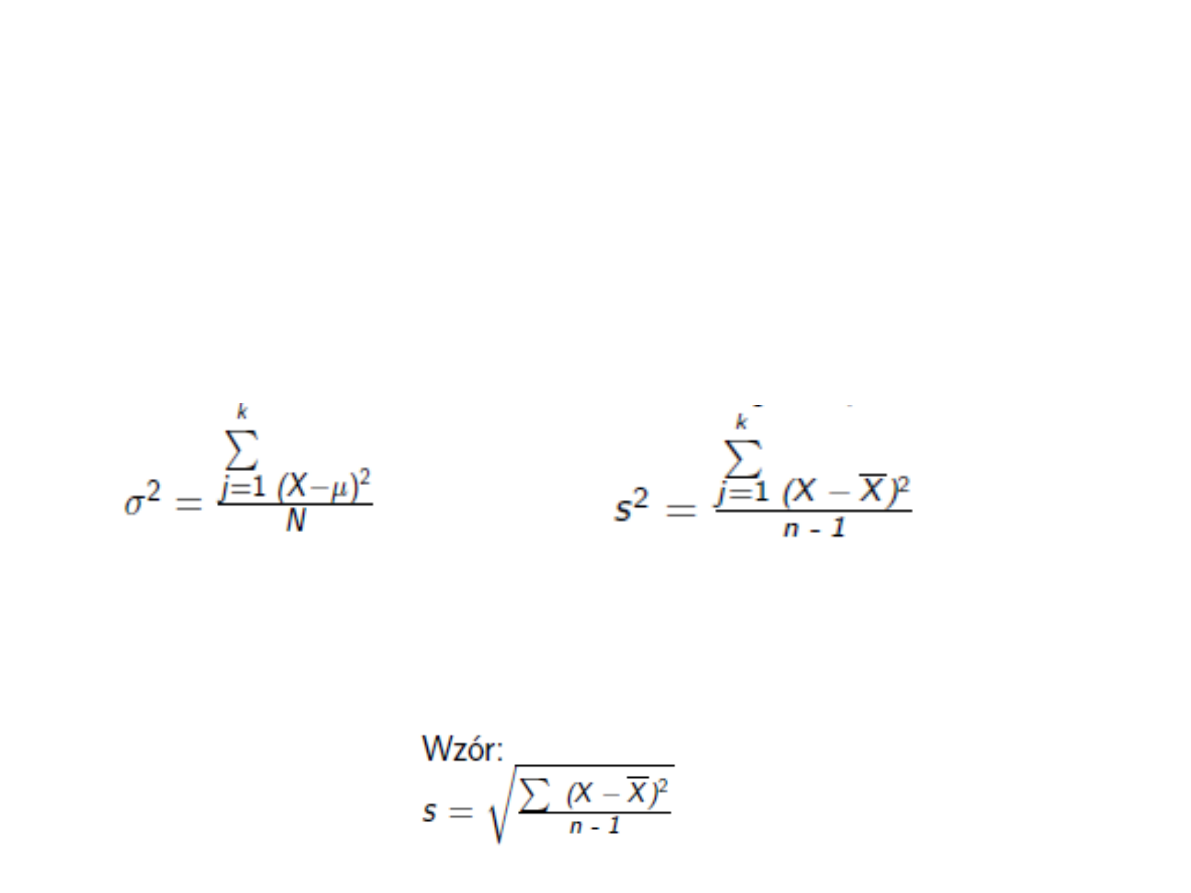
Miary rozproszenia

Rozstęp – szerokość przedziału wyników

Wariancja – średni kwadrat odchyleń od średniej

Odchylenie standardowe – pierwiastek z wariancji

Wariancja

Wariancją zmiennej X nazywamy średnią

arytmetyczną kwadratów odchyleń poszczególnych

wartości zmiennej od średniej arytmetycznej całej

zbiorowości.

Pamiętajmy: im większa wariancja, tym bardziej

rozproszone są wyniki naszych pomiarów.

Podzielmy całą zbiorowość według pewnych kryteriów

na k grup. Wówczas wariancja dla całej zbiorowości

(wariancja ogólna) równa się sumie dwóch

składników: średniej arytmetycznej

wewnątrzgrupowych wariancji wartości zmiennej

(wariancja wewnątrzgrupowa) oraz wariancji średnich

grupowych wartości tej zmiennej (wariancja

międzygrupowa). Spostrzeżenie to jest podstawą tzw.

analizy wariancji, często okrelanej skrótem ANOVA

(Analysis of Variance).

Odchylenie standardowe

Gdy chcemy uzyskać miarę zróżnicowania

o jednostce zgodnej z jednostką zmiennej,

obliczamy pierwiastek kwadratowy

z wariancji, czyli tzw. odchylenie

standardowe (standard deviation - SD).

Odchylenie standardowe jest obok średniej

najczęciej stosowanym parametrem

statystycznym, który ma następujące

podstawowe własności:

1. Odchylenie standardowe oblicza się ze

wszystkich wyników. Im zbiorowość jest

bardziej zróżnicowana, tym odchylenie

standardowe jest większe. W 

przedstawionych powyżej dwu grupach

chorych odchylenia standardowe

wynoszą: w  pierwszej - 10,8, a w drugiej -

27,83. Widać więc, że pomiary w drugiej

grupie są bardziej rozproszone niż

w pierwszej.

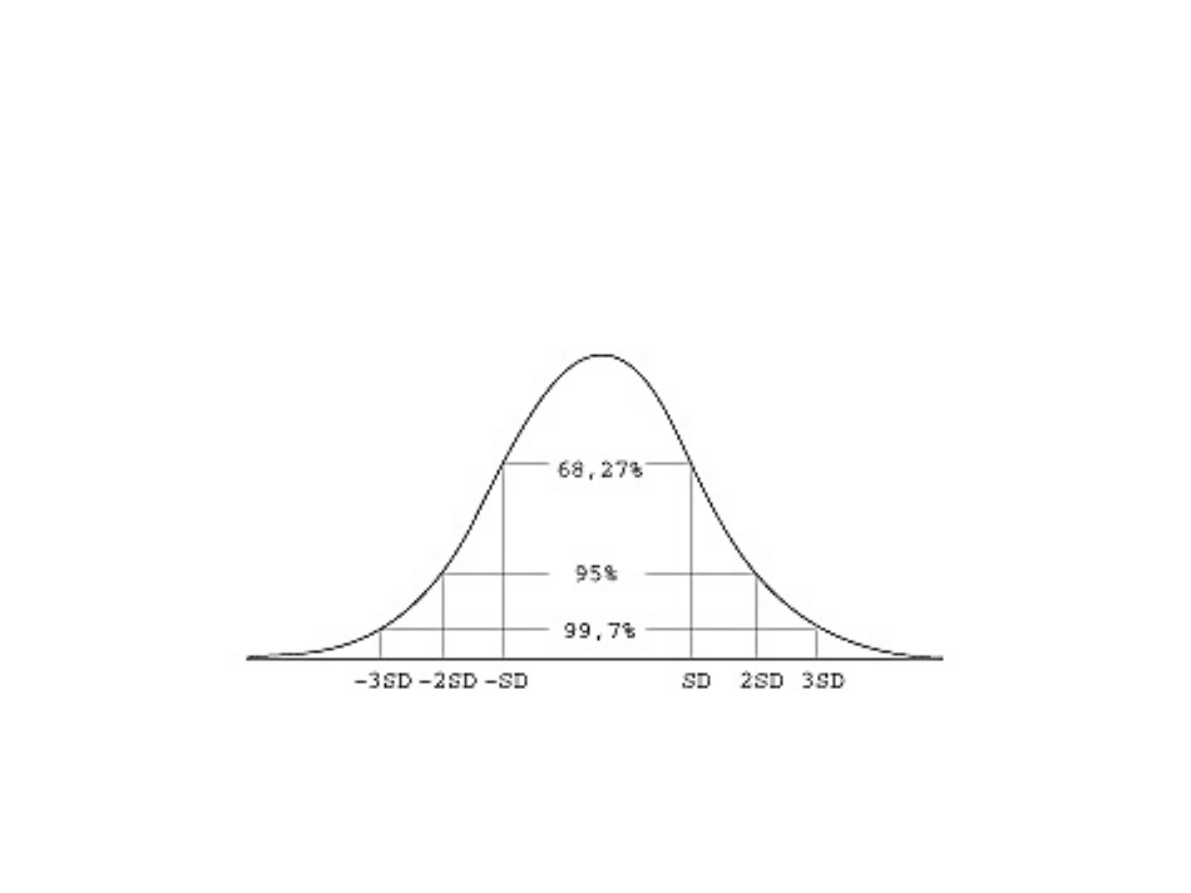
2. Odchylenie standardowe spełnia regułę

trzech sigm (rys. 1), według której

w przypadku rozkładu normalnego lub

zbliżonego do normalnego blisko 31,73%

wszystkich wyników różni się od średniej

arytmetycznej o więcej niż +/- SD;

tylko 5% obserwacji wykracza poza

przedział ( - 2SD, + 2SD);

tylko 0,3% wszystkich obserwacji

wykracza poza przedział ( - 3SD, + 3SD).

Reguła 3 sigm

Zważono 10 losowo wybranych

myszy otrzymując dane

(w gramach):

14, 20, 24, 19, 18, 21, 22, 25, 20,

17,

Ile wynosi odchylenie

standardowe?

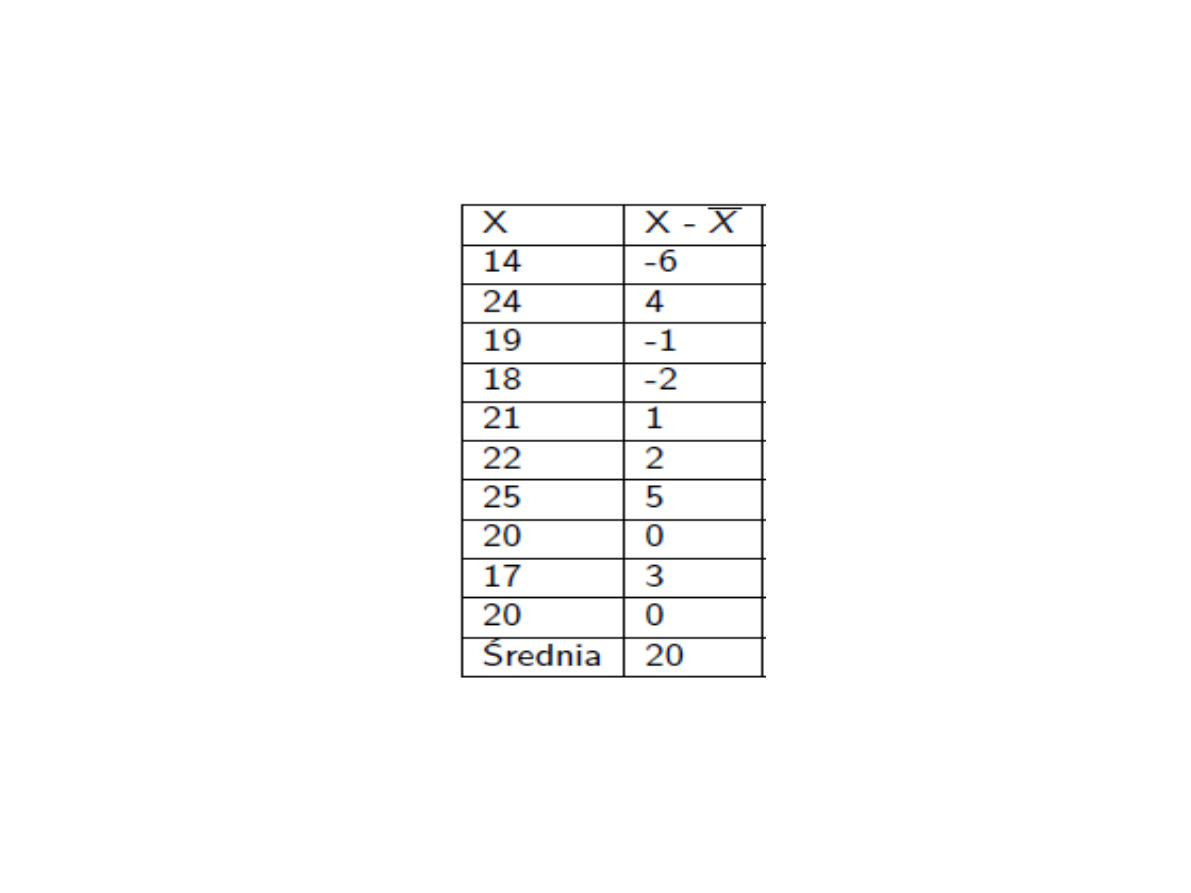
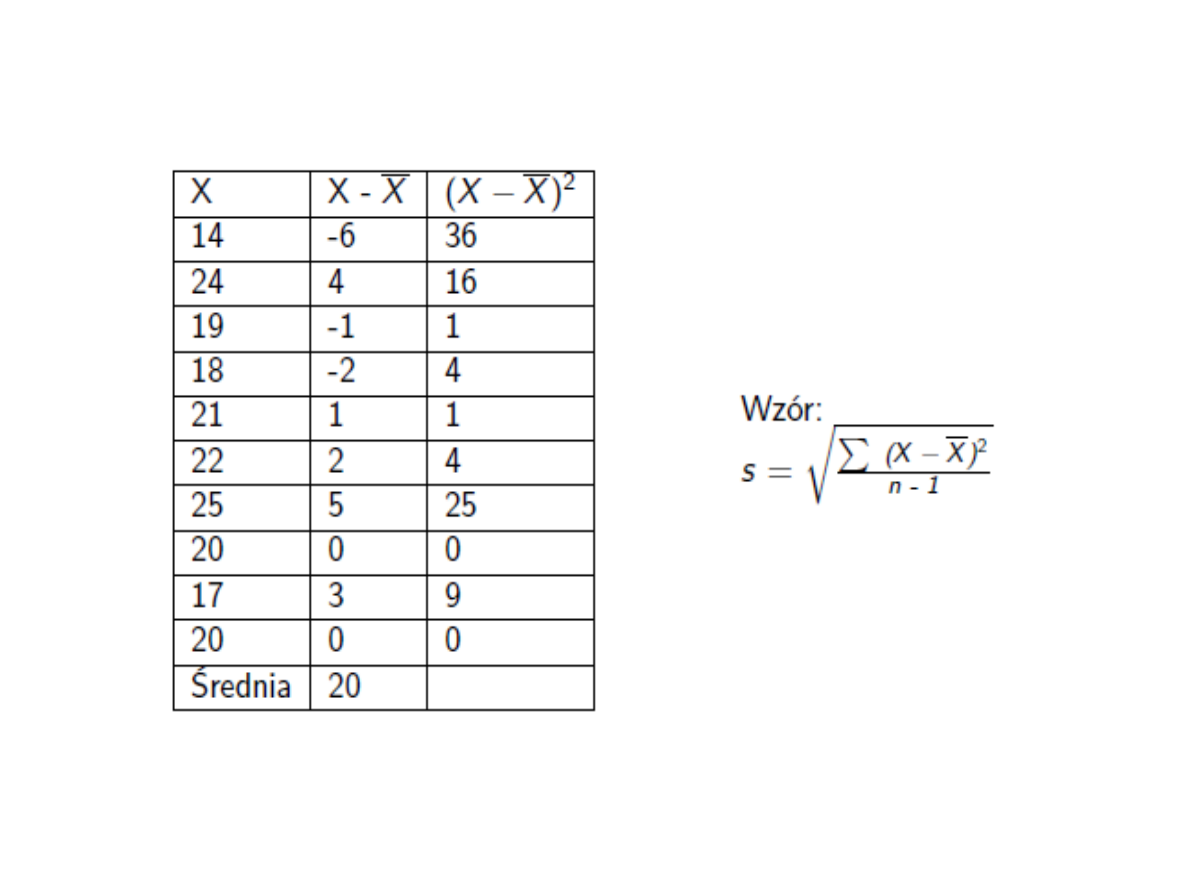
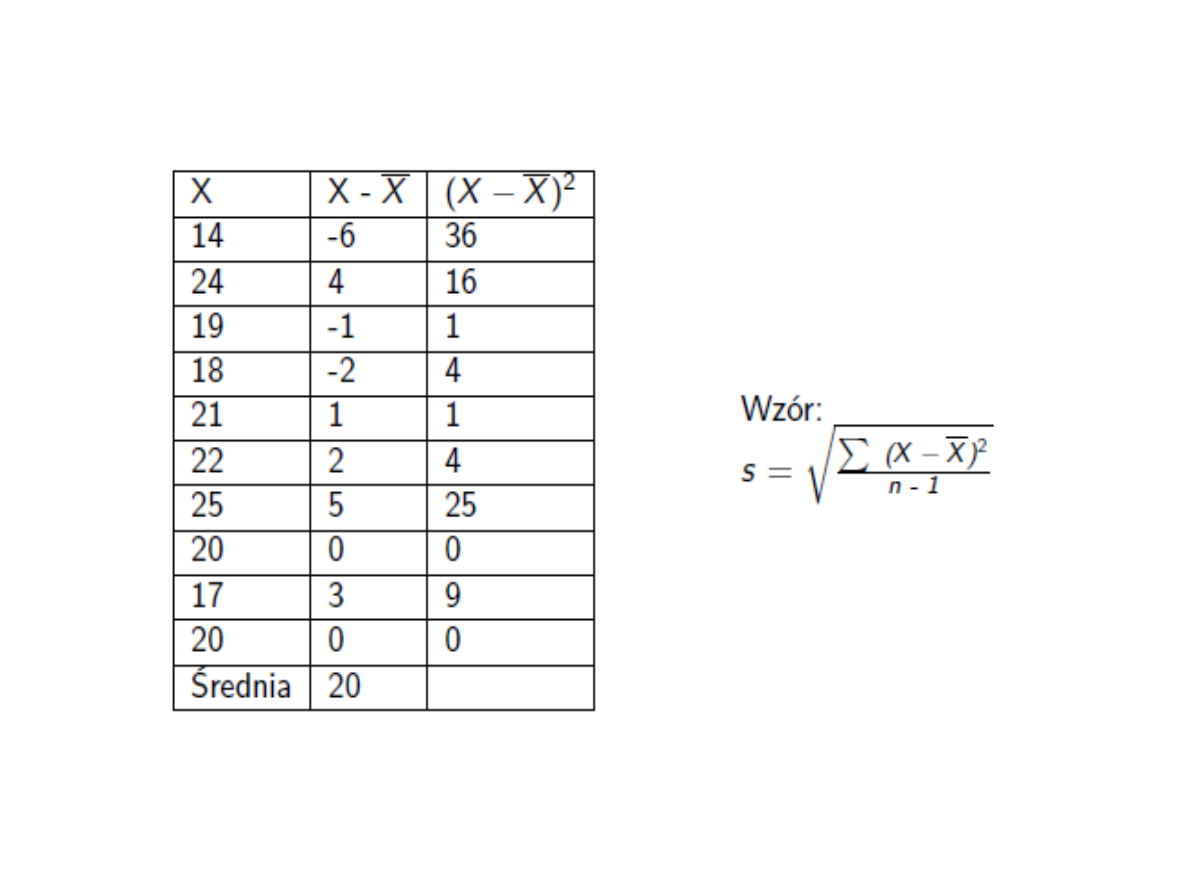
= 3,26

Odchylenie standardowe mówi, jak szeroko

wartości jakiejś wielkości są rozrzucone wokół jej

średniej.

Im mniejsza wartość odchylenia tym obserwacje

są bardziej skupione wokół średniej

Podaj:

średnią,

medianę,

modalną,

wariancję,

odchylenie standardowe

Własności wariancji

D^2 – wariancja

X, Y – zmienne badane

a, c – wartość stała

Własności wariancji

1. Wariancja ze stałej jest zerowa

2. Gdy przeskalujemy zmienną, to wariancja też

się zmieni, i to z kwadratem.

3. Dodanie stałej nie wpływa na zmienność

4. Wariancja dwóch niezależnych od siebie

zmiennych to suma wariancji tych zmiennych

Wypiszcie własności średniej.

Miary badające kształt rozkładu

Czas reakcji

Grupa 1

Grupa 2

Grupa 3

10-20

10

5

10

20-30

20

35

25

30-40

40

25

25

40-50

20

25

35

50-60

10

10

5

Średnia arytmetyczna i wariancja są jednakowe dla wszystkich grup

i wynoszą odpowiednio  = 35, s2 = 120.

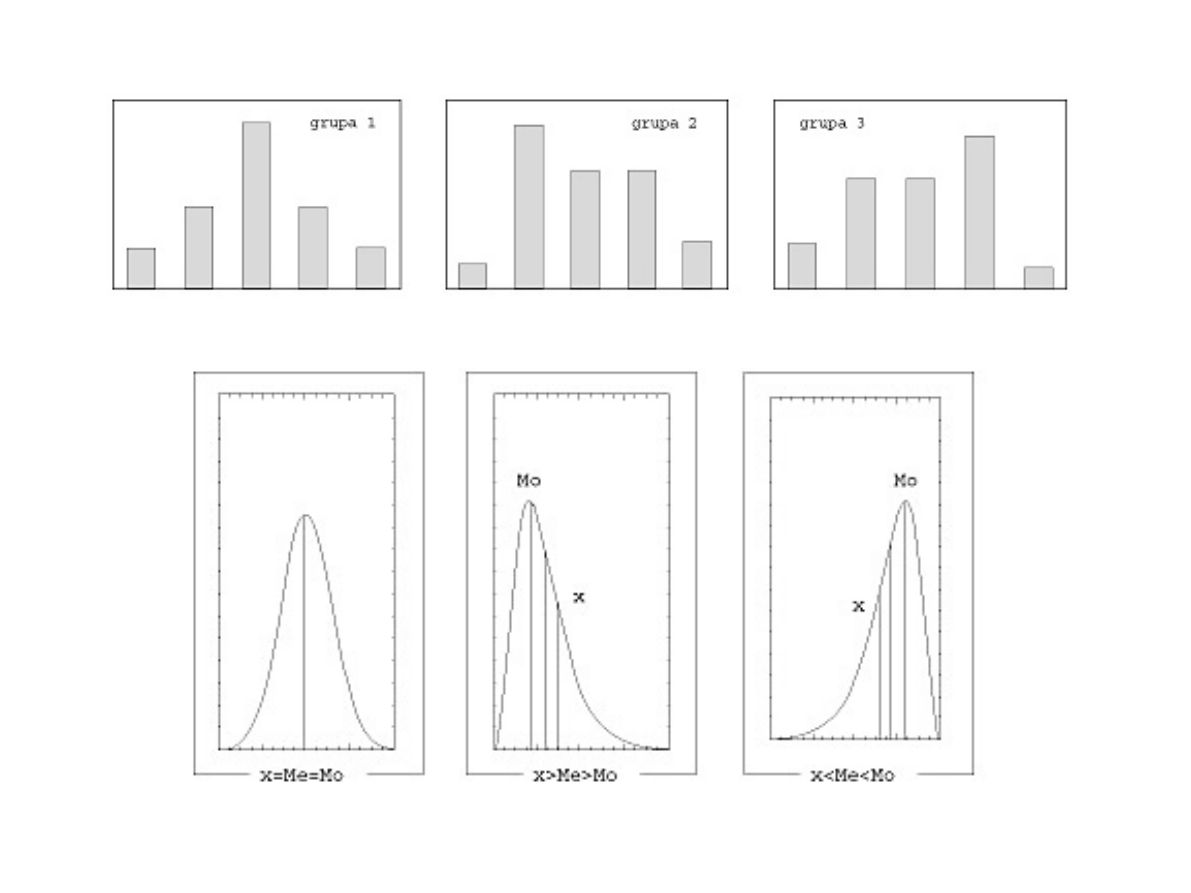
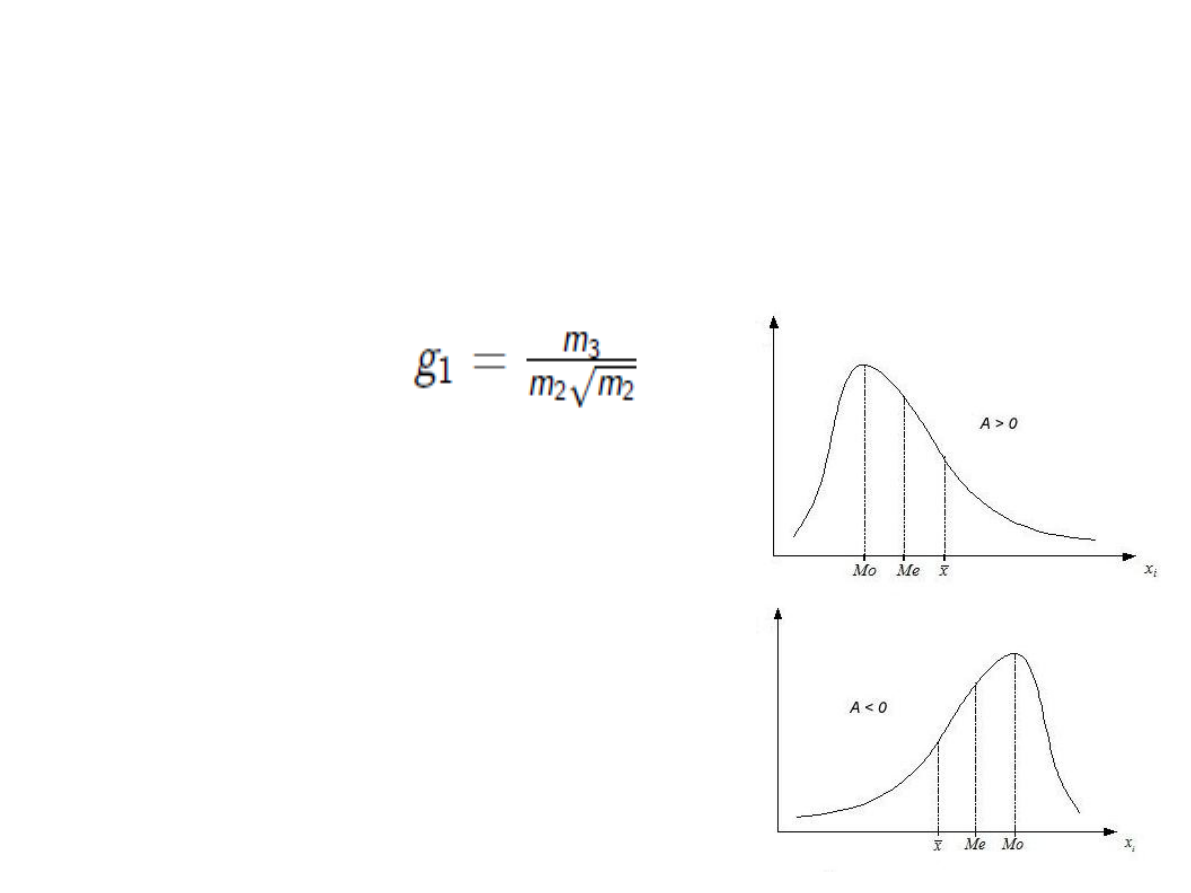
Miary badające kształt rozkładu

Skośność – wskaźnik asymetrii rozkładu

wokół średniej.

A = 0 => rozkład jest symetryczny

A < 0 => rozkład skośny ujemnie.

A > 0 => rozkład skośny dodatnio

Inne wzory do sprawdzenia

na wikipedii

Czy dają taki sam wynik?

Skośność

  średnia = Me = Mo - rozkład symetryczny

średnia    > Me > Mo - rozkład o asymetrii prawostronnej

średnia    < Me < Mo - rozkład o asymetrii lewostronnej

Do określania kierunku i siły asymetrii wprowadzono

współczynnik asymetrii (skośność [skewness], symbol -

As). Współczynnik ten jest cennym narzędziem analizy

statystycznej.

Współczynnik asymetrii równy zeru wskazuje na symetrię

rozkładu zmiennej, wartość dodatnia oznacza asymetrię

prawostronną (rozkład ma dłuższy prawy "ogon"), a wartość

ujemna - asymetrię lewostronną (rozkład ma dłuższy lewy

"ogon").

W naszym przykładzie As dla grupy 1. wynosi 0 (rozkład

symetryczny), dla grupy 2. - 0,2317 (asymetria prawostronna),

a dla grupy 3. - -0,2317 (asymetria lewostronna).

Podaj przykład cechy dla której korzystna

jest asymetria

a) prawostronna,

b) lewostronna.

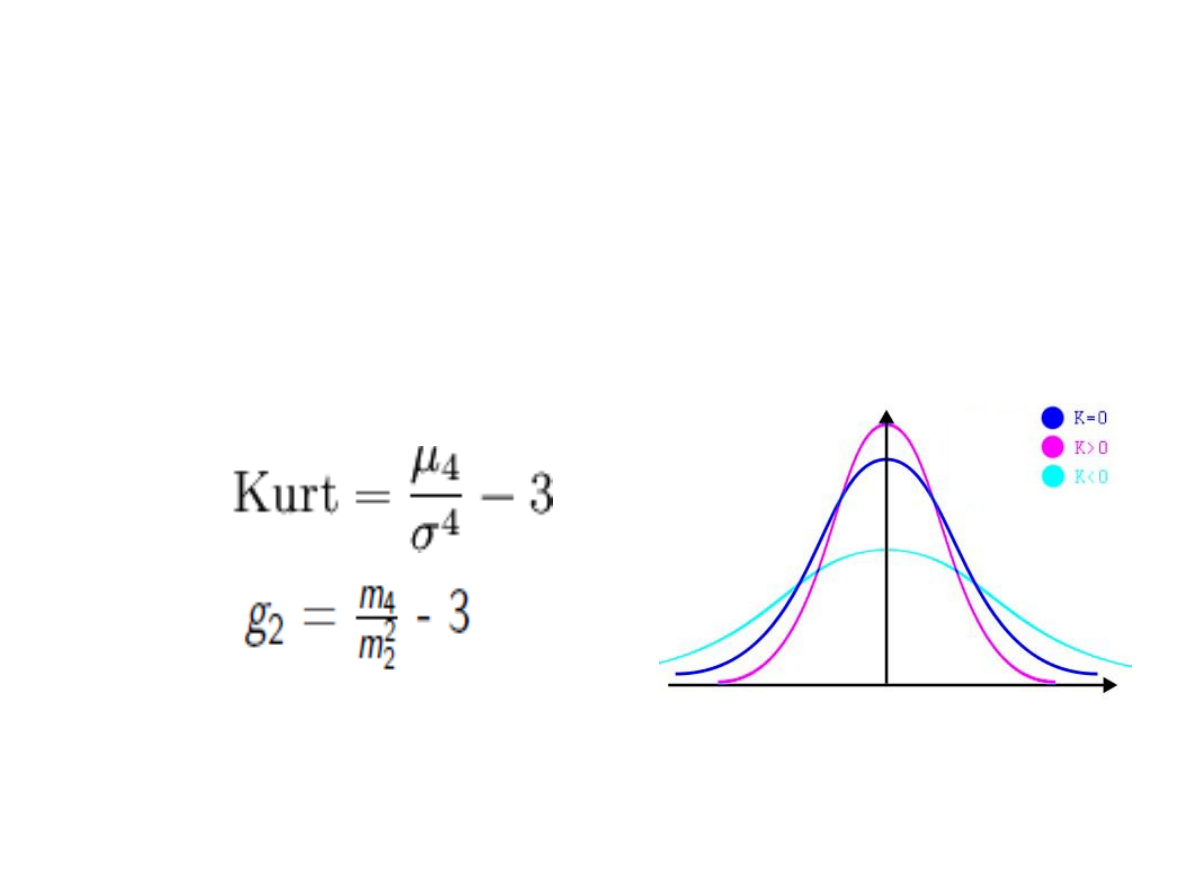
Miary badające kształt rozkładu

Kurtoza – wskaźnik informujący, czy rozkład

jest leptokurtyczny (smukły) czy

platokurtyczny (spłaszczony)

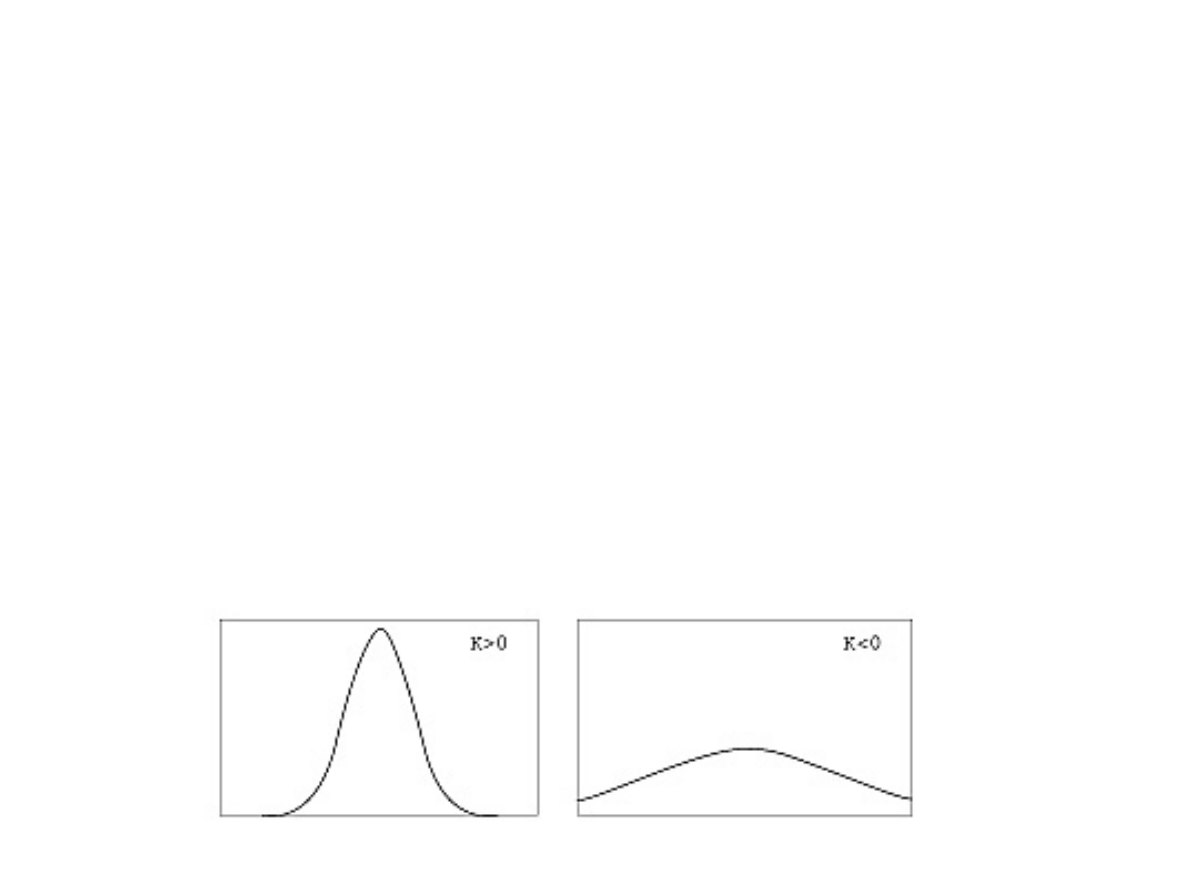
Kurtoza

Im większa jest wartość K, tym bardziej

wysmukła krzywa liczebności, a zatem

większa koncentracja wartości zmiennej

wokół średniej. Jeżeli K <0, to rozkład jest

bardziej spłaszczony od normalnego,

a jeżeli K >0 - bardziej wysmukły.

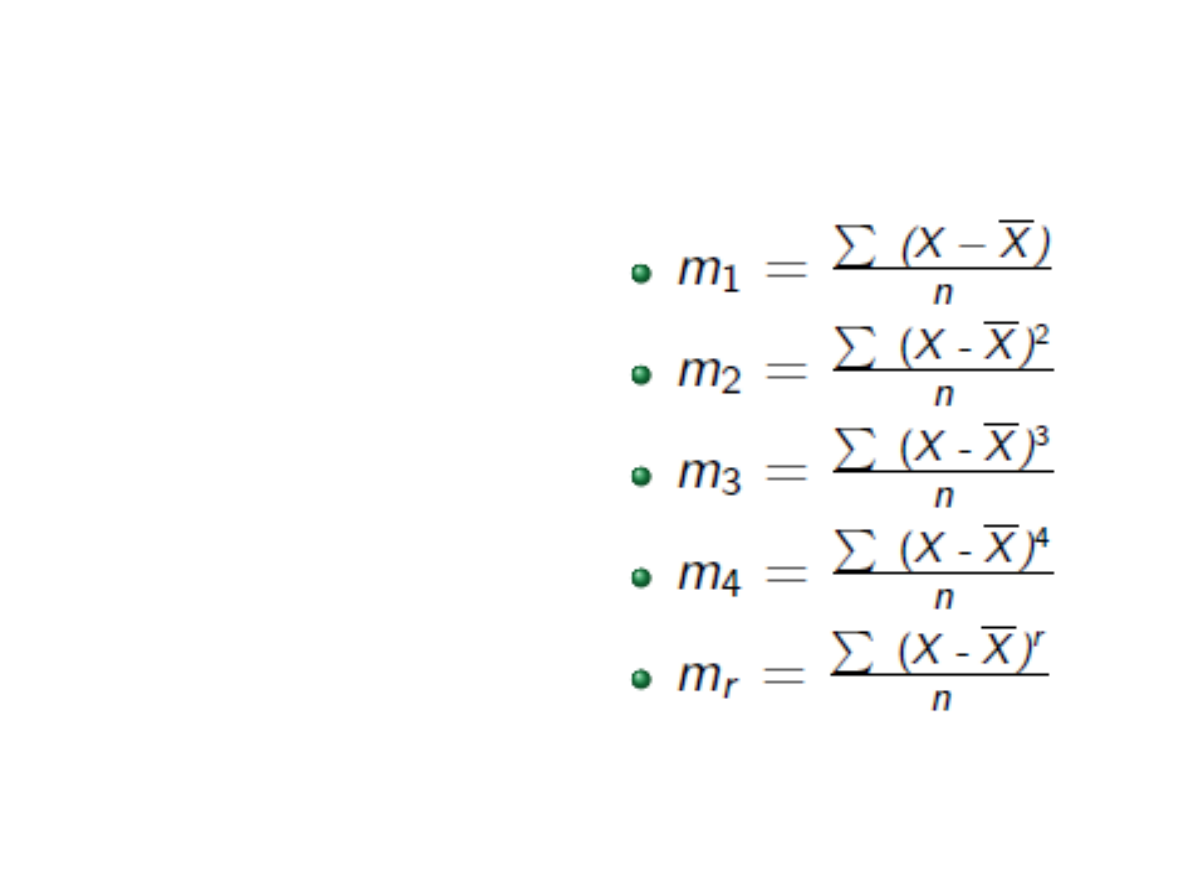
Momenty centralne

suma potęg odchyleń

wartości cechy

statystycznej od wartości

średniej arytmetycznej,

podzielona przez n, gdzie

n – liczba obserwacji:

ZADANIE

W grupie 10 studentów badano wyniki z egzaminu ze

statystyki.

Otrzymano następujące dane:

3, 4, 3, 5, 4, 3, 3, 2, 2, 4

Dla powyższych danych:

a) zbuduj szereg rozdzielczy punktowy,

b) wykonaj histogram

c) wyznacz średnią z próby, medianę i dominantę,

d) wyznacz wariancję, odchylenie standardowe

e) określ, jaki jest rozkład (skośność i kurtoza)

f) wyznacz współczynnik asymetrii (skośność)

g) wyznacz kurtozę.

Badano liczbę błędów w maszynopisie 30

maszynistek. Otrzymano następujące dane

2 3 0 1 1 5 3 2 5 6

0 1 2 4 3 4 2 4 3 0

1 2 0 2 3 2 4 5 2 2

a) Dokonaj prezentacji tych danych w szeregu

rozdzielczym punktowym.

b) Oblicz charakterystyki położenia: średnią

arytmetyczną, kwartyle, dominantę.

c) Oblicz charakterystyki rozproszenia:

wariancję, odchylenie standardowe,

d) wyznacz współczynnik asymetrii.

Rozkład prawdopodobieństwa

uzyskania danego wyniku

Do tej pory mówiąc o naszych danych,

używaliśmy słów: "grupy" lub "zbiory" liczb.

Często dla opisania zbioru liczb używa się

określenia "rozkład". Oznacza ono to samo co

"grupa", ale niesie też sugestię, że liczby

układają się w jakiś konkretny wzór.

Rozkłady lub grupy liczb najczęściej

przedstawia się w postaci szeregu

rozdzielczego lub graficznie

w postaci histogramu. 

Jeszcze lepsze przybliżenie rzeczywistości

otrzymujemy, wykreślając krzywą łączącą

środki górnych boków w histogramie – jest to

wykres gęstości rozkładu

Obok rozkładów otrzymanych dla danych z grupy próbnej

matematycy dali nam doskonałe narzędzie – rozkłady

zmiennych losowych. Zmienną losową nazywamy funkcję,

która każdemu zdarzeniu elementarnemu

przyporządkowuje liczbę rzeczywistą z określonym

prawdopodobieństwem. Jej wartości nie możemy więc z gry

przewidzieć, gdyż zależy ona od przyczyn losowych.

Jeżeli zbiór wartości zmiennej losowej jest zbiorem

przeliczalnym (lub skończonym), wówczas zmienną losową

nazywamy dyskretną. Jeżeli natomiast zmienna losowa

przyjmuje wartości z pewnego przedziału liczbowego, to

nazywamy ją zmienną losową ciągłą.

Z rozkładem zmiennej losowej są związane pewne

charakteryzujące go wielkości liczbowe. Charakterystyki te

nazywamy parametrami rozkładu zmiennej losowej. Do

najważniejszych parametrów zmiennych losowych należą:

wartość oczekiwana i wariancja zmiennej losowej. Wartość

oczekiwana – E(X) = m – jest to wartość, wokół której

skupiają się wartości zmiennej losowej przy wielokrotnym

powtarzaniu eksperymentu. Wariancja zmiennej

losowej to miara rozproszenia wartości zmiennej wokół

wartości średniej, którą obliczamy według wzoru V(X)

= E(X – E(X))2.

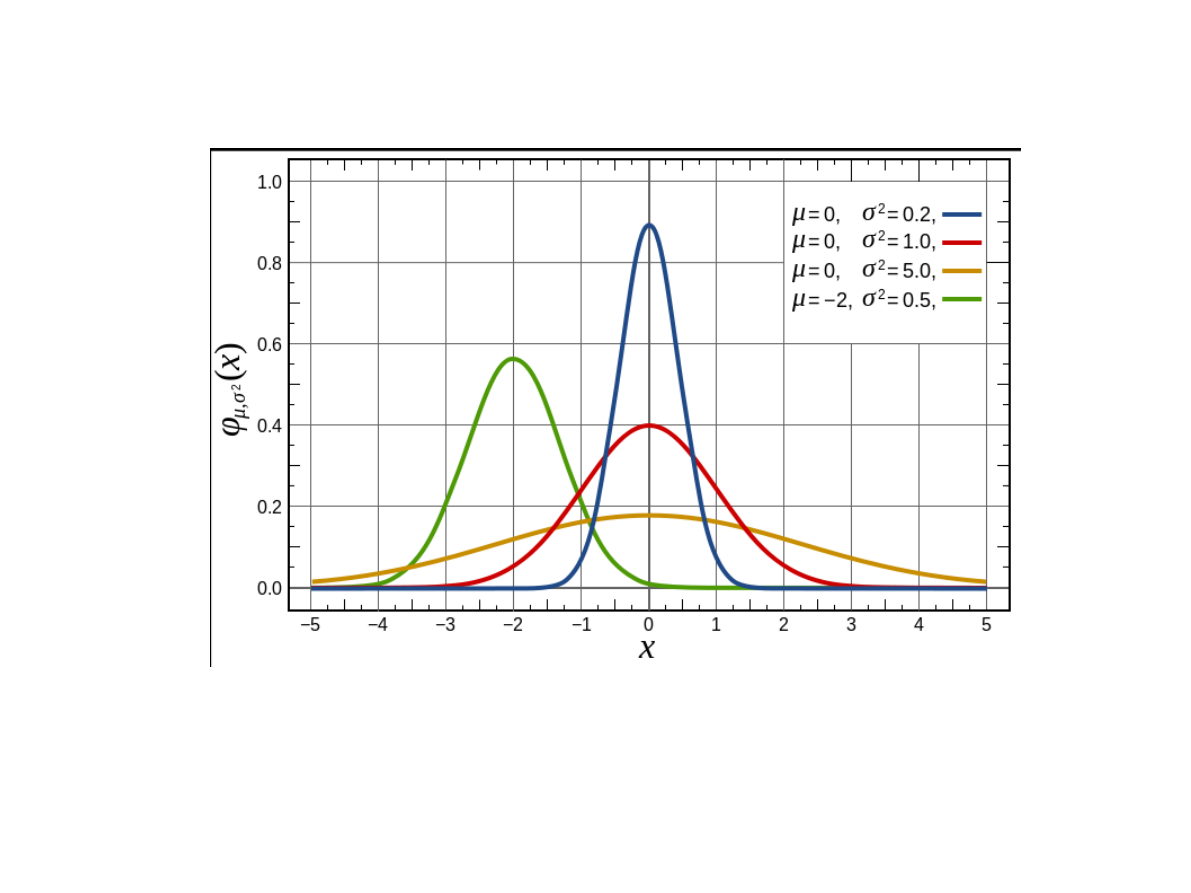
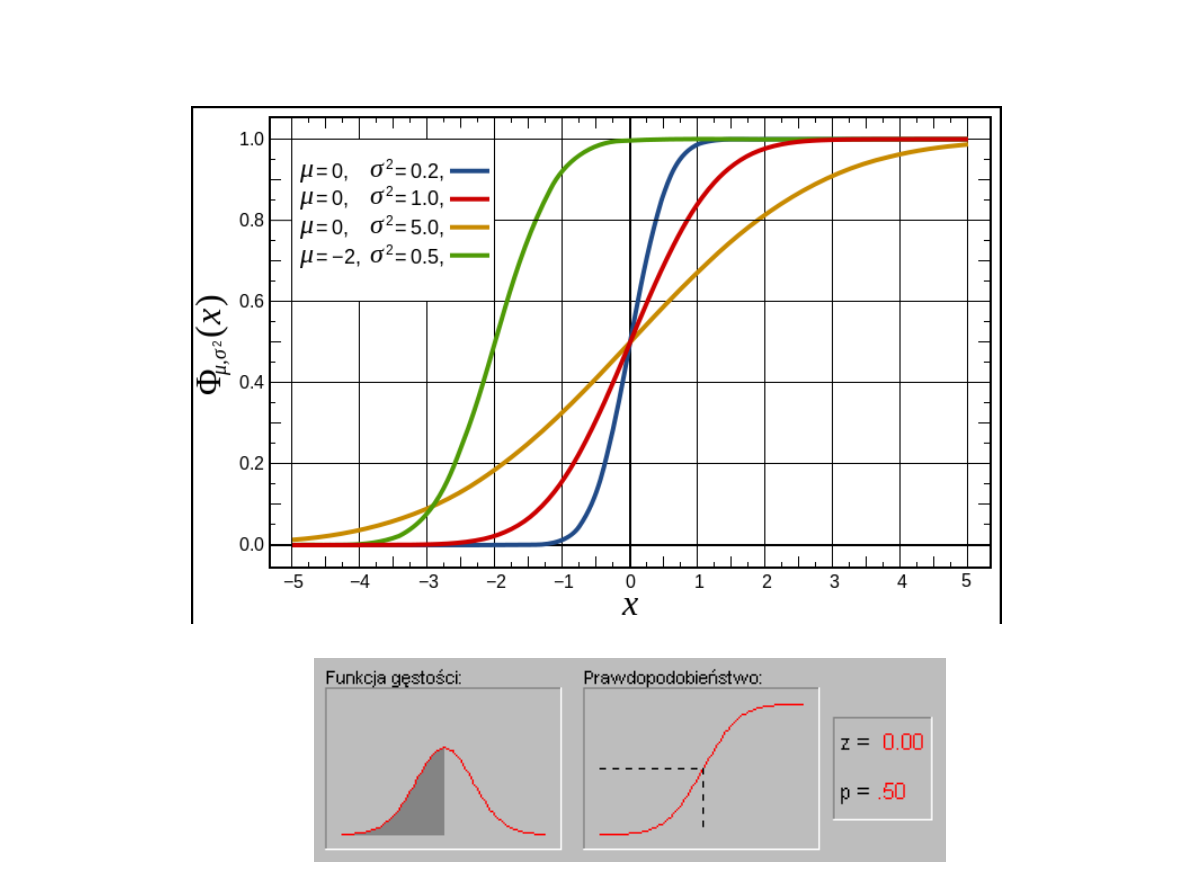
W wielkim skrócie:

opisuje on sytuacje, gdzie większość przypadków jest

bliska średniemu wynikowi, a im dany wynik bardziej

odchyla się od średniej tym jest mniej reprezentowany.

Najwięcej jest przypadków blisko przeciętnej. Im dalej

oddalamy się od średniego wyniku, tym przypadków jest

mniej. Można to z łatwością odnieść do rzeczywistych

sytuacji.

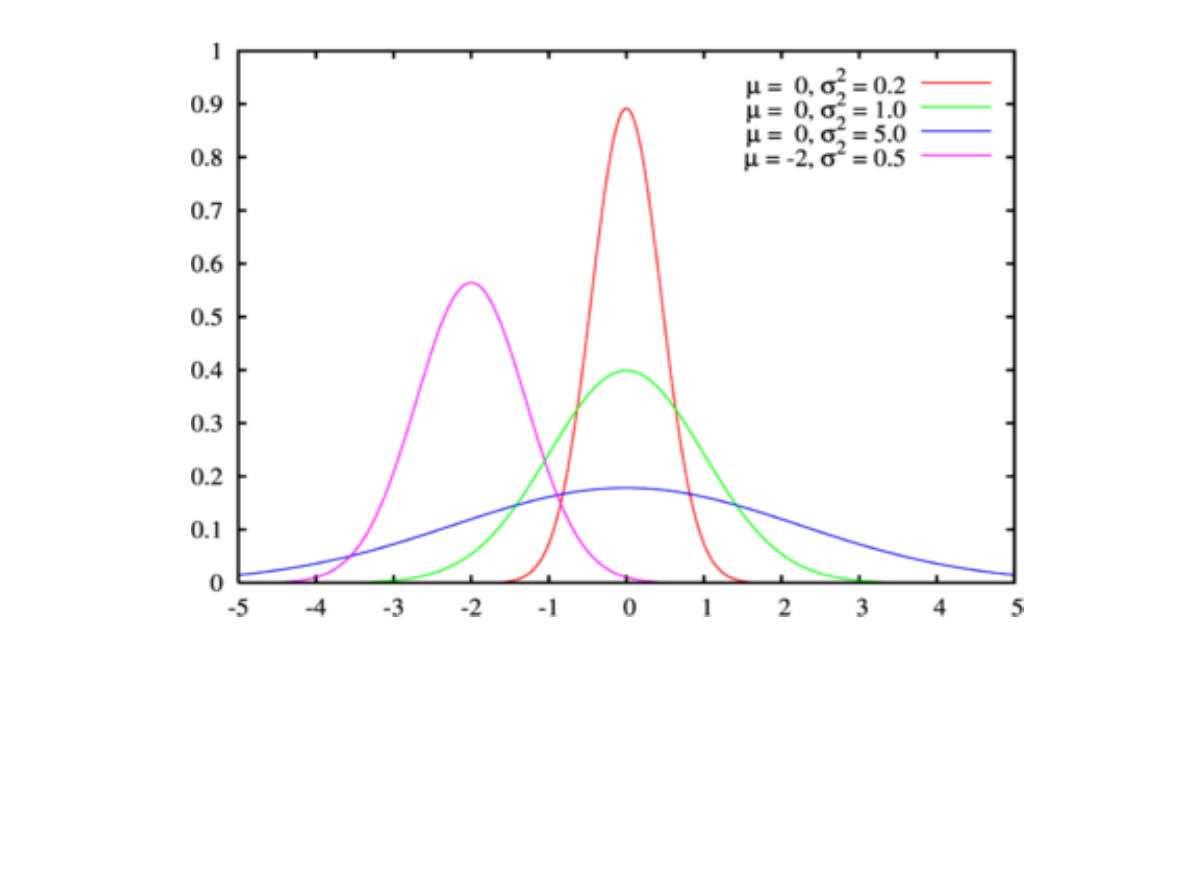
Rozkład normalny

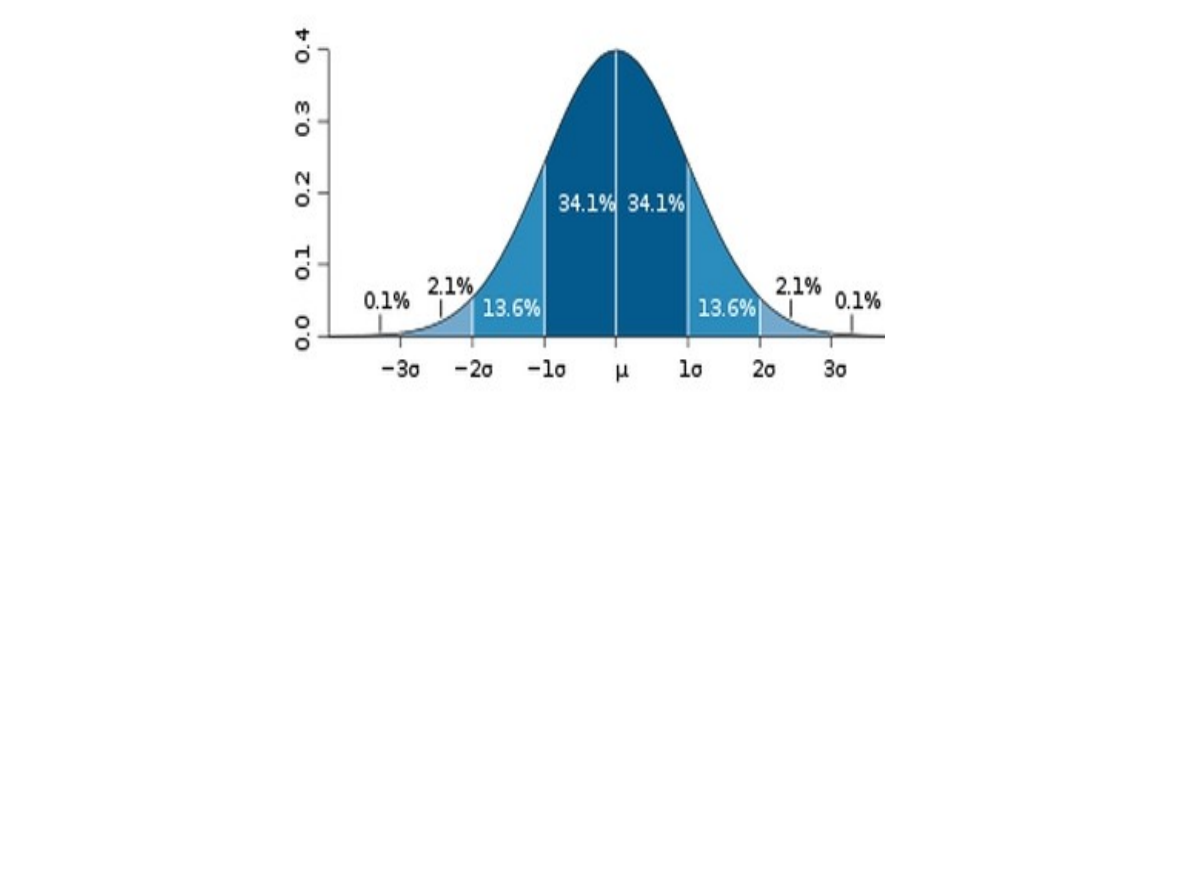
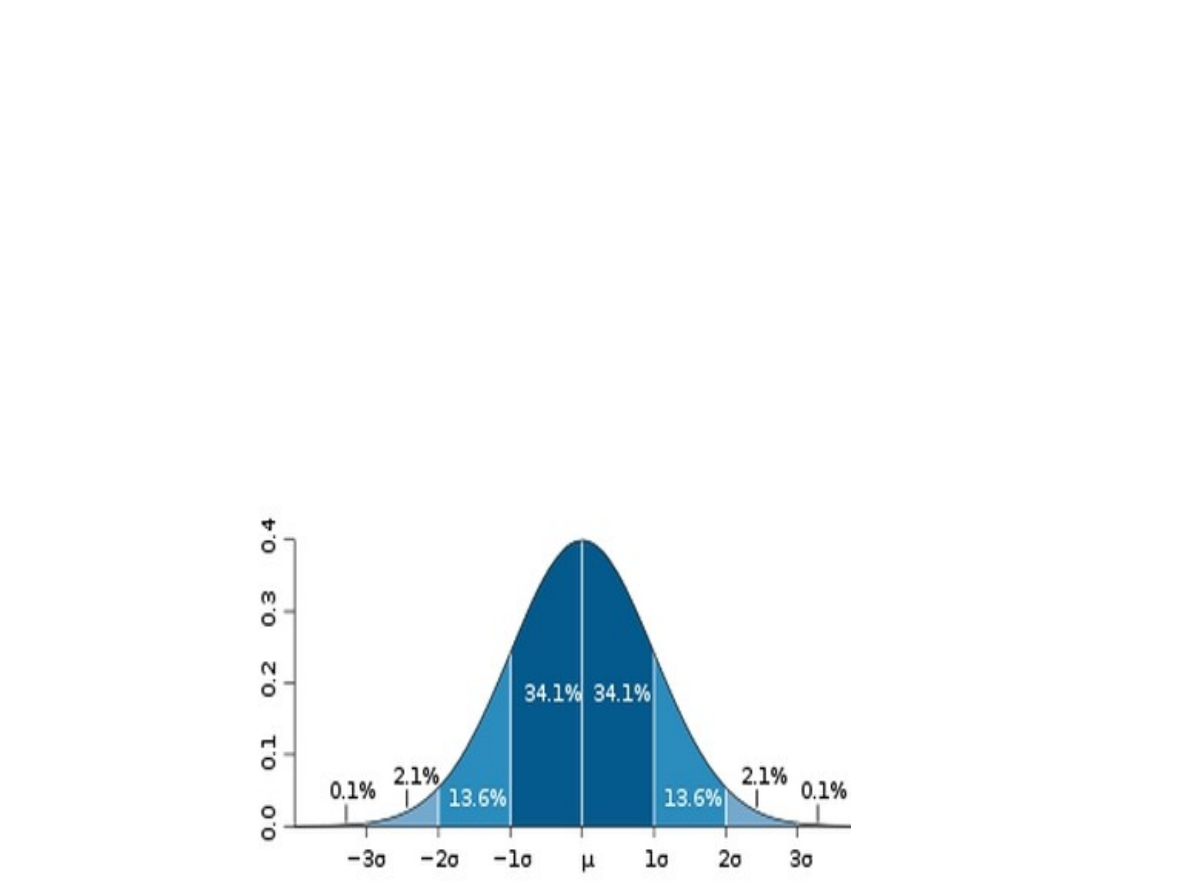
μ - oznacza wartość średnią, przeciętną – w

populacji;

σ - oznacza odchylenie standardowe.

Jak można zauważyć, około 68% obserwacji

znajduje się blisko średniej, w odległości jednego

odchylenia standardowego od średniej. Wraz z

odsuwaniem się od średniej krzywa Gaussa opada.

W odległości dwóch odchyleń standardowych

znajduje się aż 95% obserwacji. Wartości skrajne

(na krańcach krzywej Gaussa) reprezentowane są

przez znikomy procent obserwacji.

Wyniki pod krzywa normalna zapisuje się w

jednostkach

odchylenia standardowego - są to bowiem wyniki

uniwersalne

W tym celu używa się tzw. wyniki standardowe,

które mają

średnią 0 i odchylenie standardowe 1.

Powierzchnia pod krzywa traktowana jest jako 1.

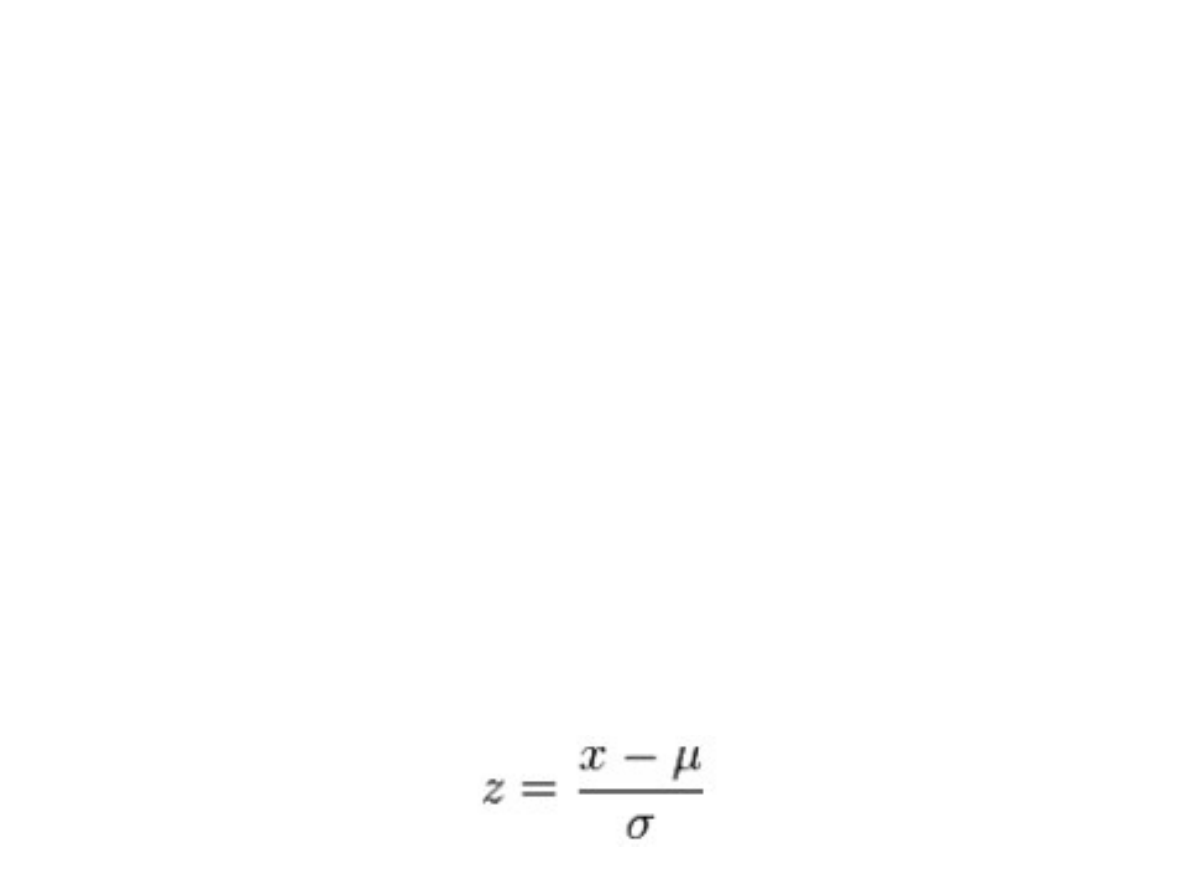
Standaryzacja

Jest to przełożenie danych na język statystyczny.

Statystyka posiada "własny język". Ten język to

odległość o ilość odchyleń standardowych danego

wyniku od średniej dla danej zmiennej.

Innymi słowy, standaryzując wyniki "tłumaczymy"

różne zmienne na jeden wspólny język.

Poprzez standaryzację możemy określić, na ile dany

wynik, dana obserwacja jest odstająca od średniego

wyniku.

Standaryzując wyniki stosujemy wzór:

x - oznacza wartość danej obserwacji

μ - oznacza wartość oczekiwaną danej zmiennej, a w

praktyce (dla naszej próby badanej, jeżeli nie znamy

prawdziwej, teoretycznej średniej w populacji)

średnią dla naszego pomiaru

σ - oznacza wartość odchylenia standardowego w

populacji, a w praktyce (dla naszej próby badanej,

jeżeli nie znamy prawdziwego, teoretycznego

odchylenia standardowego w populacji) odchylenie

standardowe z naszego pomiaru

Przekształcając każdy uzyskany w pomiarze wynik

poprzez zastosowanie wzoru standaryzacji,

uzyskujemy znormalizowaną miarę, gdzie

wartość oczekiwana (średnia) wynosi 0, a

wariancja równa jest 1.

Dzięki temu, możemy określić na ile dany wynik

(x) jest odległy od średniej wartości, w języku

statystycznym. Z = 1 oznacza, że dany wynik jest

wyższy od średniej o 1 odchylenie standardowe. Z

= -0,5 oznacza, że dany wynik jest niższy od

średniej o 0,5 odchylenia standardowego.

W ten sposób możemy przekształcić dwie różne

zmienne (o nieporównywalnych miarach, np: wiek

i wzrost) w jedną porównywalną miarę

statystyczną.

Standaryzacja zmiennych pomocna jest do

określania przypadków odstających. Przyjęto, że

wyniki poniżej -3Z lub powyżej 3Z są wynikami

odstającymi.

Zamien na wyniki standardowe następujące wyniki surowe:

4, 8, 8, 9, 16, 20

Jaki jest całkowity obszar pod krzywa normalna poniżej z = 1?

Jaki jest całkowity obszar pod krzywa normalna poniżej z =

1,96?

Jaki jest całkowity obszar pod krzywa normalna powyzej z = 1?

WAŻNE PODSUMOWANIE

Średnią, odchylenie standardowe itp.

Obliczamy dla zmiennych na skali

ILOŚCIOWEJ:

-> ilorazowej
-> przedziałowej

Dla zmiennych na skali porządkowej

możemy obliczyć medianę i modalną.

Dla zmiennych na skali nominalnej możemy

obliczyć JEDYNIE modalną!

Kilka słów o planowaniu badań

1. CO BADAMY

2. KOGO BADAMY

3. JAK BADAMY

Punkt 1.

Postawienie hipotez badawczych.

H0
H1
-> kierunkowa
-> bezkierunkowa

CO BADAMY

Niezależnymi nazywamy te spośród zmiennych,

których wartość możemy zmieniać (zmienne

manipulowane), np.:

-> muzyka, przy jakiej wykonywane jest badanie

-> naświetlenie pokoju eksperymentalnego

-> poziom trudności zadania

Zmienne zależne są jedynie mierzone lub

rejestrowane. Będą (mogą być) zależne od

manipulacji lub innych warunków eksperymentu,

np.:

-> poziom lęku

-> poziom inteligencji

-> ciśnienie tętnicze

-> zadowolenie

Zmienne

Nieco w opozycji do natury tego rozróżnienia

terminy te bywają również używane w

badaniach gdzie nie manipuluje się

dosłownie zmiennymi niezależnymi, lecz

jedynie przypisuje obiekty do pewnych

grup eksperymentalnych na podstawie

posiadanych przez nie cech.

Jeśli na przykład w pewnym eksperymencie

mężczyźni porównywani są z kobietami pod

względem liczby białych komórek krwi, to

Płeć może być nazwana zmienną niezależną,

a liczba białych ciałek zmienną zależną.

Zmienne zakłócające

Wszystkie zmienne, których nie

kontrolujemy w pełni, a mogą mieć wpływ

na wyniki eksperymentu:

-> chwilowy humor osoby badanej
-> historie osobiste o.b.
-> cechy psychologiczne o.b., których nie

bierzemy akurat pod uwagę

-> zmęczenie eksperymentatora

KOGO BADAMY

Dobieramy grupę z populacji (jednej bądź

wielu), na które chcemy transponować

wnioski z naszych badań.

Staramy się, by próba była losowa i

możliwie jak największa.

W przypadku, gdy wiemy, że próba może

źle odwzorowywać reprezentowaną

populację, robimy dobór kontrolowany.

WARIANTY BADAWCZE

1. GRUPY ZALEŻNE

2. GRUPY NIEZALEŻNE

1. PORÓWNYWANIE GRUP

EKSPERYMENTALNCYH

2. GRUPA(Y) EKSPERYMENTALNE I KONTROLNA

3. BADANIA KORELACYJNE

Grupy (badane) zależne

I porównujemy:

wyniki danej cechy przed i po szoku elektrycznym

Grupy (badane) niezależne

Grupa badana i kontrolna

NIC

Coś

nieszkodliwe

go

Badania korelacyjne

Ekstrawersja Poziom lęku

Czy poziom ekstrawersji jest powiązany

(skorelowany) z poziomem lęku?

JAK BADAMY?

W badaniach eksperymentalnych badacz

manipuluje niektórymi zmiennymi, a następnie

mierzy wpływ tych manipulacji na inne

zmienne; badacz może na przykład sztucznie

zwiększyć ciśnienie krwi i następnie rejestrować

poziom cholesterolu.

JAK BADAMY?

W badaniu korelacyjnym badacz nie

wpływa na żadną ze zmiennych,

rejestrując je jedynie i obserwując relacje

(korelacje) między pewnymi podzbiorami

zmiennych, na przykład między

ciśnieniem krwi i poziomem cholesterolu.

W trakcie analizy danych będących

wynikiem badania eksperymentalnego

zdarza się również obliczać korelacje

między zmiennymi, w szczególności

pomiędzy tymi, którymi manipulujemy a

tymi, na które ta manipulacja wpłynęła.

Dane pochodzące z badania eksperymentalnego

dostarczają jednak najczęściej informacji lepszej

jakościowo niż dane z badań korelacyjnych.

W szczególności pamiętać należy, że jedynie badania

typu eksperymentalnego mogą efektywnie

dowieść relacji przyczynowej między zmiennymi.

Jeśli na przykład stwierdzimy, że ilekroć zmieniamy

wartość zmiennej A, to zmienia się wartość zmiennej B,

wówczas możemy wysnuć wniosek, że zmienna A

wpływa na zmienną B.

Dane z badań korelacyjnych mogą być jedynie

interpretowane w sposób przyczynowy w świetle

pewnych teorii, lecz nigdy nie pozwalają na

ostateczne udowodnienie istnienia związku

przyczynowego

CECHY RELACJI MIĘDZY

ZMIENNYMI

Siła ("wielkość") zależności (relacji)

Jeśli w mierzonej próbie każdy mężczyzna

posiada większy nos niż jakakolwiek kobieta,

to możemy powiedzieć, iż siła relacji pomiędzy

dwiema zmiennymi (Płeć i długość nosa) jest

duża w mierzonej próbie. Innymi słowy można

przewidzieć jedną zmienną na podstawie

pomiaru drugiej (przynajmniej w obrębie

naszej próbki).

CECHY RELACJI MIĘDZY

ZMIENNYMI

Wiarygodność ("prawdziwość") -

dotyczy reprezentatywności wyniku

uzyskanego na podstawie pobranej próbki

w odniesieniu do całej badanej populacji.

Informuje jakie jest prawdopodobieństwo

tego, że analogiczna relacja zostałaby

zmierzona, gdyby eksperyment powtórzyć

na innych próbkach pobranych z tej samej

populacji.

Pamiętajmy, że badacz nigdy nie

ogranicza swoich zainteresowań do

mierzonej próbki, lecz faktycznie

próbka potrzebna mu jest jedynie do

tego, aby dostarczyć mu informacji o

całej badanej populacji. Wiarygodność

relacji zmierzonej w próbie może być

wyrażona ilościowo w postaci konkretnej

liczby (poziomem istotności)

Poziom istotności statystycznej

Na przykład poziom-p równy 0,05 (tzn. 1/20)

oznacza, że istnieje 5% szansa, iż odkryta w

próbce relacja jest dziełem przypadku.

Inaczej mówiąc, zakładając, że w populacji relacja

taka nie zachodzi, a my będziemy powtarzać

doświadczenie jedno po drugim w długim ciągu,

to możemy oczekiwać, że w przybliżeniu w co

dwudziestym eksperymencie zmierzona relacja

będzie równie silna lub mocniejsza niż ta, która

została zmierzona aktualnie.

Statystyczną istotnością wyniku nazywamy miarę

stopnia, do jakiego jest on prawdziwy (w sensie jego

reprezentatywności dla całej badanej populacji).

Im wyższy poziom istotności, tym mniej możemy być

pewni, że relacja obserwowana w próbce jest

wiarygodnym wskaźnikiem relacji pomiędzy mierzonymi

wielkościami w całej interesującej nas populacji.

Dokładnie rzecz biorąc, poziom istotności

odpowiada prawdopodobieństwu popełnienia

błędu polegającego na tym, że przyjmujemy

uzyskany rezultat jako prawdziwy, tj.

reprezentatywny dla populacji.

Jeżeli założymy, że w populacji generalnej pomiędzy

interesującymi nas zmiennymi nie ma żadnej zależności, to

najbardziej prawdopodobnym wynikiem badania

statystycznego w próbce będzie również brak takiej

zależności.

Łatwo na tej podstawie wysnuć wniosek, że im silniejsza

relacja między zmiennymi została zmierzona w próbce, tym

mniej prawdopodobnym jest brak takiej relacji w populacji

generalnej.

Siła i istotność relacji między zmiennymi są ze sobą

związane i można wyliczyć istotność na podstawie wartości

siły relacji i na odwrót. Stwierdzenie to jest jednak

prawdziwe tylko w odniesieniu do próbki o stałej wielkości.

Relacja (zależność) o określonej sile może się bowiem

okazać albo bardzo istotna, albo kompletnie nieistotna w

zależności od wielkości próbki.

Dlaczego?

Dlaczego silniejsze relacje między zmiennymi są bardziej

istotne?

Jeśli mamy do czynienia z małą liczbą obserwacji,

wówczas istnieje też mała liczba wszystkich możliwych

kombinacji różnych wartości poszczególnych zmiennych,

a co za tym idzie, prawdopodobieństwo tego, że przez

przypadek zdarzy się w pomiarze kombinacja wskazująca

na silną zależność jest relatywnie duże.

Rozważmy następujący przykład. Jeśli interesują nas dwie

zmienne (Płeć - mężczyzna/kobieta i poziom białych

krwinek (LBC) - wysoki/niski) oraz mamy do dyspozycji

tylko cztery obiekty w naszej próbce (dwie kobiety i

dwóch mężczyzn), wówczas prawdopodobieństwo tego,

że z powodów czysto losowych stwierdzimy 100% relację

między zmiennymi wynosi 1/8. Szansa, iż obie kobiety

mają niską LBC, a obydwaj mężczyźni wysoką LBC (lub

na odwrót), równa jest jednej ósmej (2/16).

Rozpiszmy to sobie.

Wielkość próby

Zastanówmy się teraz, jaka byłaby szansa w próbce

liczącej 100 obiektów. Rachunek wskazuje, że szansa ta

wynosi wówczas praktycznie zero. Jest tylko jedna na

2^99, że wszyscy mężczyźni będą mieli inny wynik niż

wszystkie kobiety.

Przeanalizujmy bardziej ogólny przykład.

Wyobraźmy sobie teoretyczną populację, w której

średnia wartość LBC u mężczyzn i kobiet jest dokładnie

taka sama. Jest oczywiste, że jeśli zaczniemy

przeprowadzać sekwencyjnie eksperyment polegający

na losowaniu par próbek o ustalonej wielkości (próbka

mężczyzn i próbka kobiet) i obliczaniu różnicy średnich

wartości LBC w każdej parze próbek, to większość

wyników będzie bliska wartości 0. Jednakże od czasu do

czasu wylosowana para próbek da wynik, który będzie

się znacznie różnił od zera. Jak często można się

spodziewać takiego wyniku? Otóż im mniejsza jest

liczność próbki, tym częstość takiego błędnego rezultatu

będzie większa, wskazując tym samym na istnienie

zależności, która faktycznie w populacji generalnej nie

występuje.

Rejestrujemy liczbę urodzin dziewczynek i

chłopców w dwóch szpitalach. W jednym z

nich rodzi się dziennie 120 dzieci, w drugim

12. Średnio w każdym ze szpitali rodzi się

tyle samo chłopców co dziewczynek

(stosunek liczby urodzeń jest 50/50). Jednego

dnia wszakże w jednym ze szpitali urodziło

się dwa razy tyle dziewczynek co chłopców.

W którym ze szpitali to się zdarzyło?

Przede wszystkim istotność zależy od liczności próbki.

Na podstawie bardzo licznej próbki nawet bardzo słaba

zależność może być uznana za istotną, podczas gdy małe

próbki nie pozwalają na ocenę wiarygodności nawet bardzo

silnych zależności.

Widać potrzebę posiadania funkcji, która wyrażałaby związek

pomiędzy siłą a istotnością relacji pomiędzy zmiennymi w

zależności od liczności próbki.

Funkcja taka odpowiadałaby na pytanie: jak dalece

prawdopodobne jest uzyskanie obserwowanej (lub większej)

siły zależności w próbce określonej wielkości, przy założeniu,

że zależność ta nie istnieje w ogóle w populacji generalnej?

Jak oblicza się poziom istotności

statystycznej.

Innymi słowy, funkcja ta podaje wartości poziomu

istotności (p), który informuje nas o

prawdopodobieństwie błędu polegającego na

odrzuceniu hipotezy, że zależność, którą badamy, nie

występuje w populacji generalnej.

Ta hipoteza (brak zależności w populacji generalnej)

nazywana jest w statystyce hipotezą zerową.

Byłoby stanem idealnym, gdyby omawiana funkcja

była funkcją liniową i na przykład posiadała jedynie

różne współczynniki kierunkowe dla różnych wartości

wielkości próbki. Niestety jej postać jest bardziej

złożona i różna w różnych przypadkach. Na szczęście

jednak w większości przypadków znamy jej kształt i

możemy go użyć do obliczania poziomów istotności

dla różnych liczności próbek. Większość tych funkcji

jest związana z ogólnym typem funkcji zwanej

normalną.