T12. Kinematyka bryły



Stopnie swobody bryły sztywnej.



Opis ruchu bryły sztywnej.



Ruch płaski bryły sztywnej.



Mechanizmy płaskie.

0

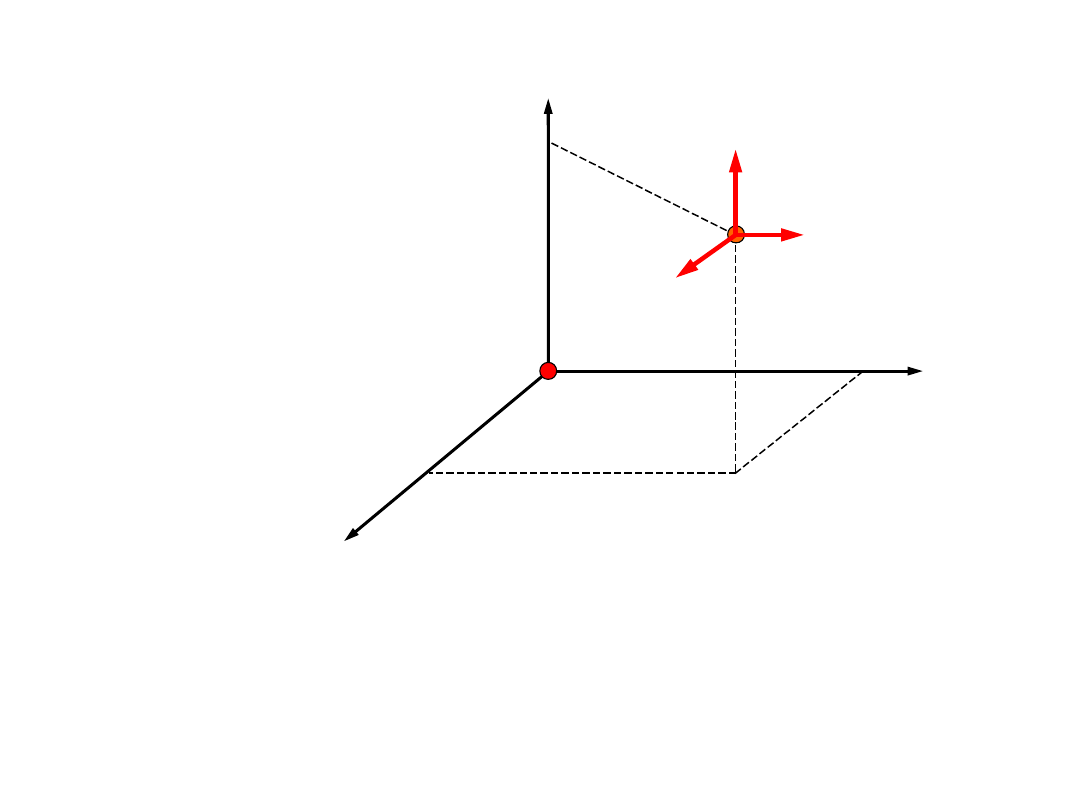
Punkt materialny może przemieszczać się w
trzech kierunkach przestrzeni. Dowolny ruch
punktu materialnego możemy przedstawić jako
złożenie trzech ruchów wzdłuż osi układu
współrzędnych. Mówimy, że punkt materialny
posiada trzy

stopnie swobody

.

( )

y t

( )

x t

( )

z t

x

y

z

Stopnie swobody bryły sztywnej

0

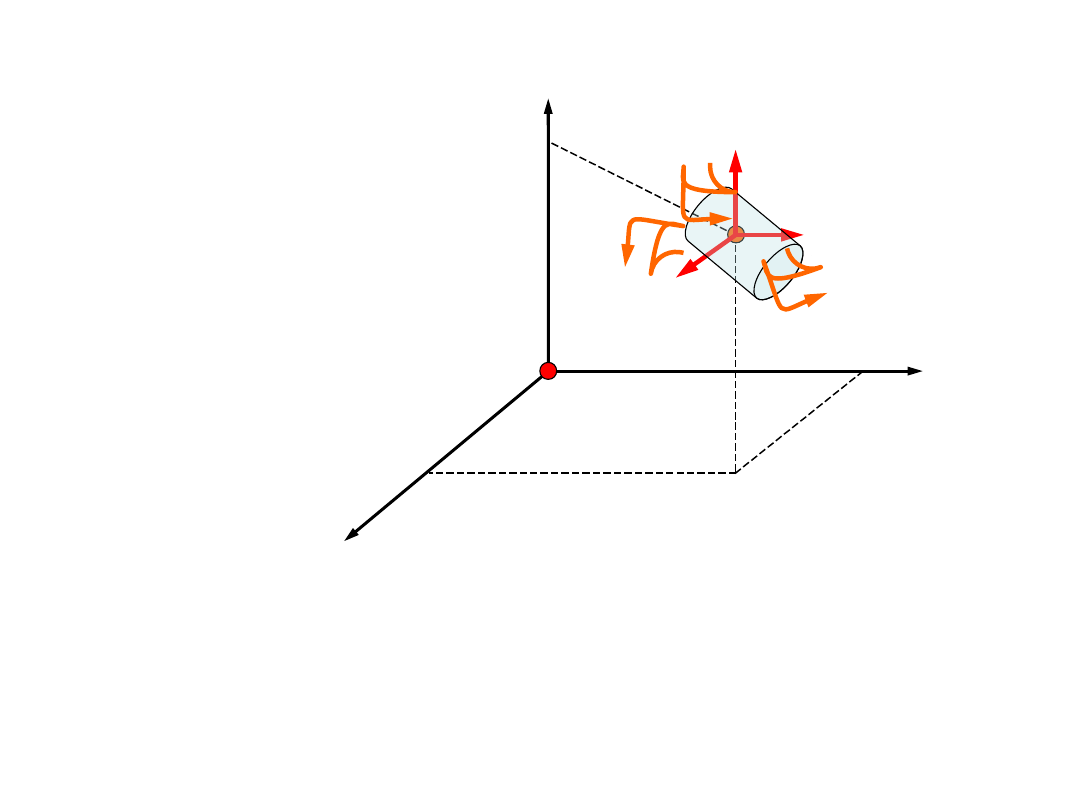
Bryła sztywna, oprócz ruchu w trzech
kierunkach przestrzeni, może także obracać się
wokół trzech osi. Dlatego posiada dodatkowe
trzy stopnie swobody. W sumie, ma

sześć stopni

swobody

– trzy

translacyjne

i trzy

rotacyjne.

( )

y t

( )

x t

( )

z t

x

y

z

Stopnie swobody bryły sztywnej

0

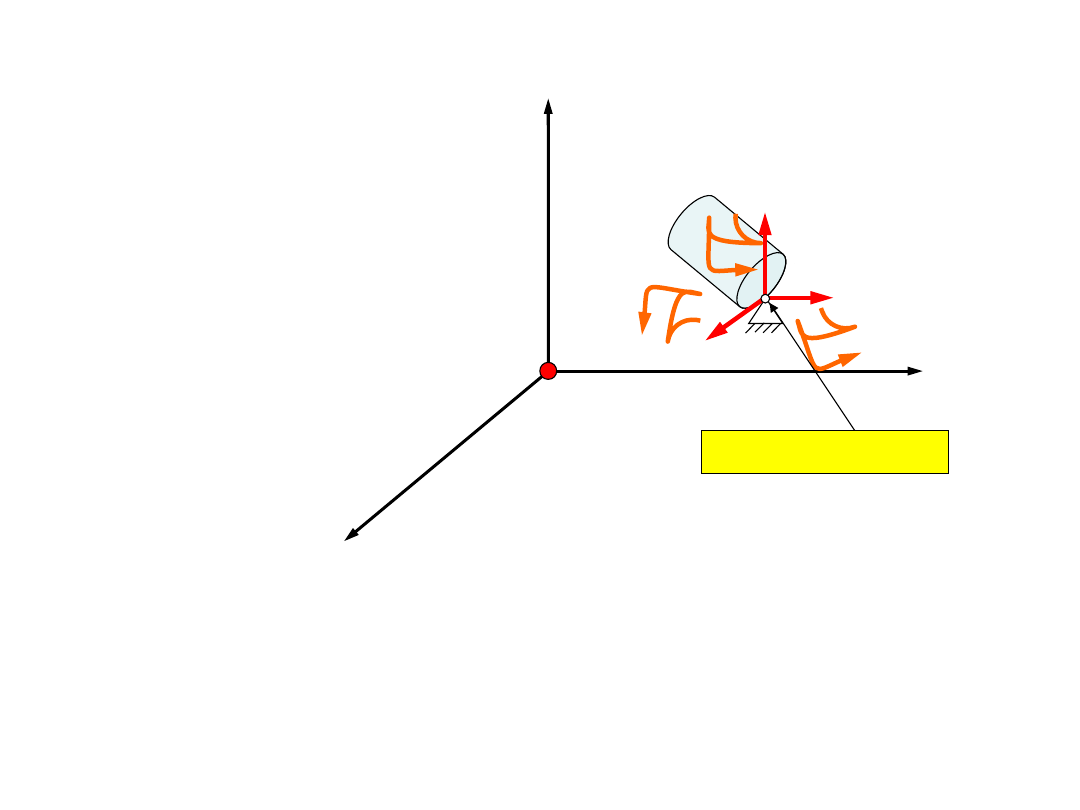
Jeżeli na bryłę sztywną nałożymy więzy w
postaci przegubu kulowego, będzie mogła
jedynie obracać się wokół trzech osi. Liczba
stopni swobody zostanie ograniczona do trzech.

x

y

z

przegub kulowy

Stopnie swobody bryły sztywnej

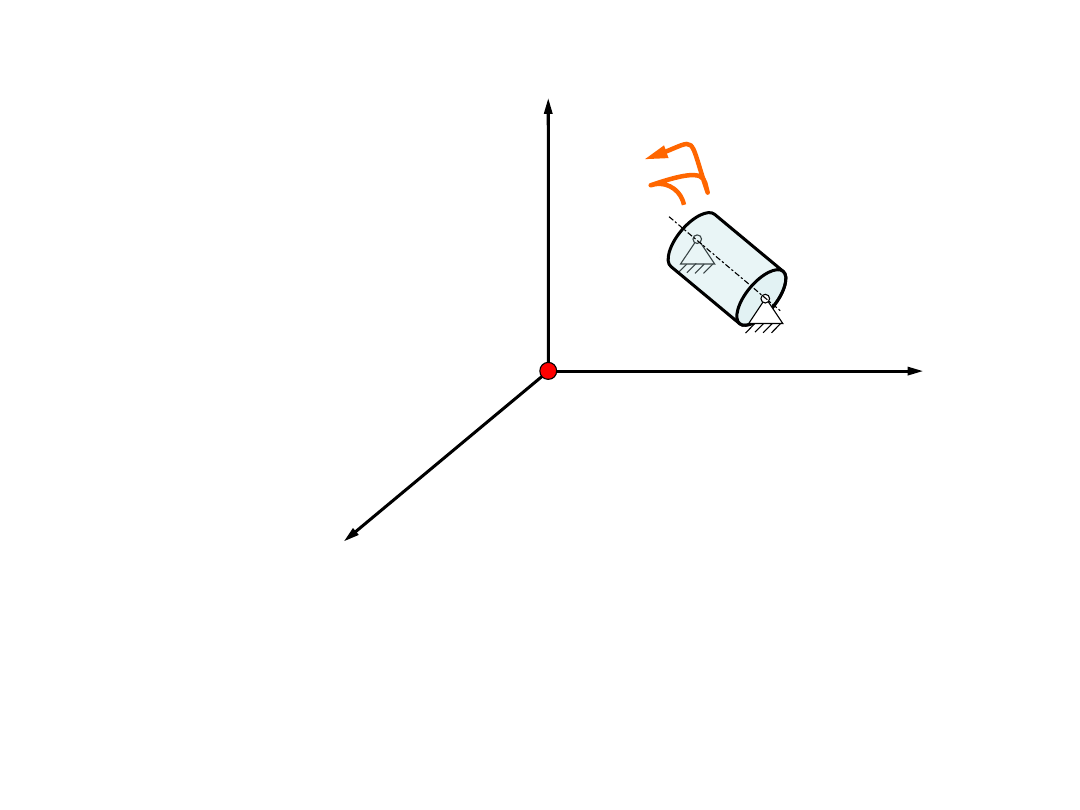
Stopnie swobody bryły sztywnej

0

Jeżeli na bryłę sztywną nałożymy więzy, które
ustalą położenie w przestrzeni dwóch punktów
bryły, możliwy jest wówczas jedynie ruch wokół
jednej osi. Liczba stopni swobody została
zredukowana do jednego.

x

y

z

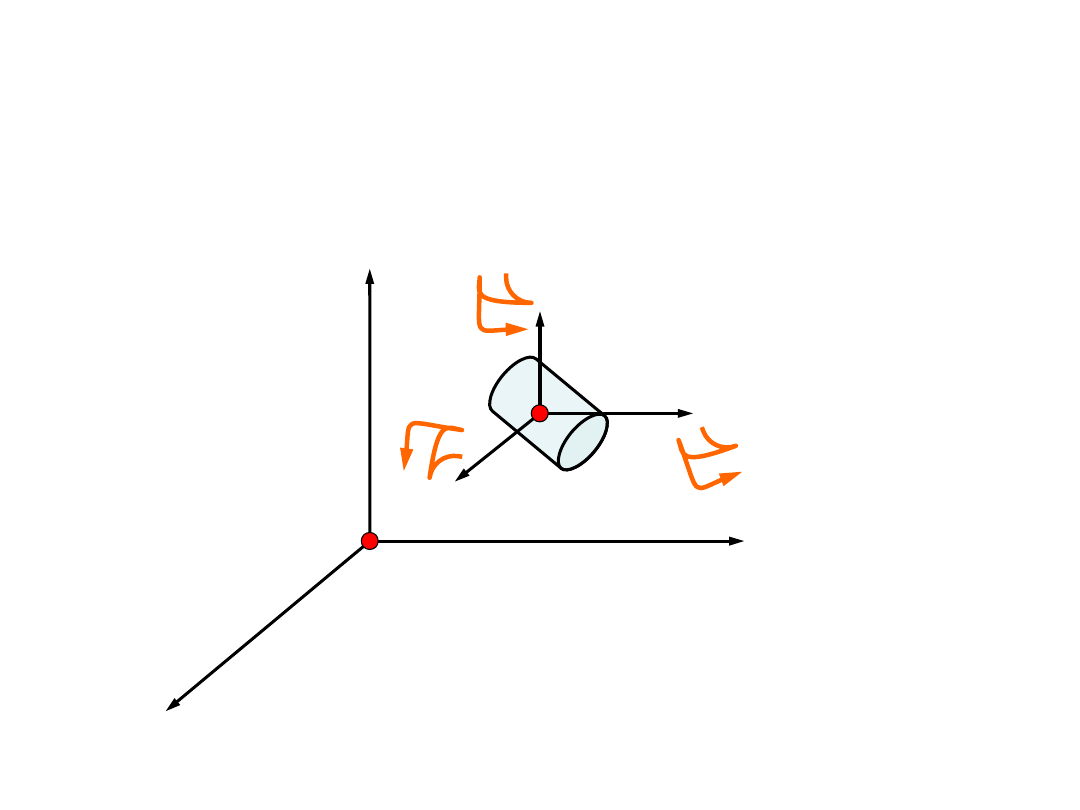
Opis ruchu bryły
sztywnej

0

Problem

Jak opisać matematycznie ruch bryły sztywnej ?

x

y

z

x

1

y

1

z

1

0

1

Układ współrzędnych x

1

, y

1

, z

1

jest

związany z wybranym punktem
bryły 0

1

. Punkt ten nazywamy

biegunem

.

Opis ruchu bryły
sztywnej

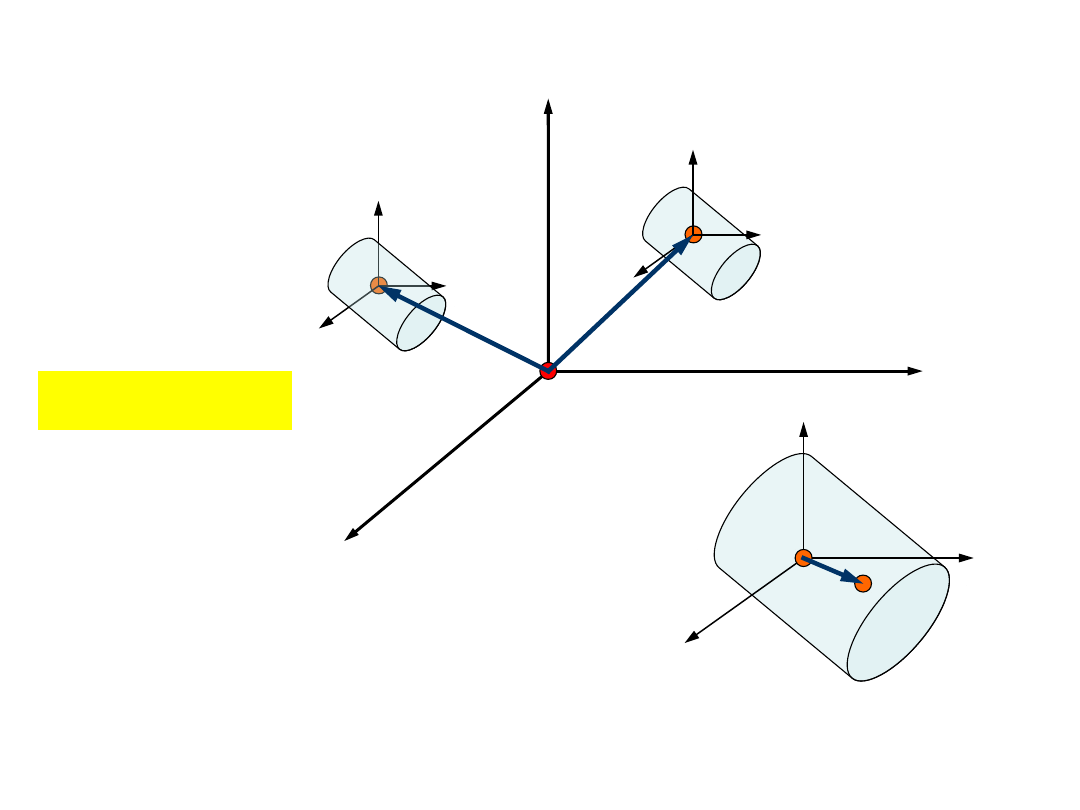
Wniosek

Ruch bryły sztywnej możemy opisywać jako
złożenie ruchu wybranego punktu bryły 0

1

i

obrotu bryły wokół osi układu współrzędnych
związanego z punktem 0

1

.

Jeżeli bryła nie obraca się względem osi układu
współrzędnych związanego z punktem 0

1

, ruch

bryły nazywamy

ruchem postępowym

.

Jeżeli wybrany punkt bryły 0

1

nie porusza się

względem układu odniesienia, zaś bryła obraca
się względem osi układu współrzędnych
związanego z punktem 0

1

, ruch bryły nazywamy

ruchem obrotowym

.

Dowolny ruch bryły sztywnej można opisywać,
jako złożenie ruchu postępowego i ruchu
obrotowego.

0

( )

r t

r

x

y

z

Opis ruchu bryły
sztywnej

(0)

r

r

0

1

0

1

Ruch postępowy

1

r

r

x

1

y

1

z

1

A

Położenie punktu A w układzie
ruchomym opisuje niezmienny w
czasie promień wodzący . Położenie
w chwili czasu t punktu A opisuje
suma

wektorowa

promienia

wodzącego i wektora

.

1

r

r

( )

r t

r

1

r

r

1

( )

( )

A

r t

r t

r

=

+

r

r

r

0

1

Opis ruchu bryły
sztywnej

Zagadnienie opisu ruchu postępowego bryły
sztywnej sprowadza się do rozwiązania równań
ruchu punktu materialnego 0

1

oraz do czysto

geometrycznego opisu położenia punktów
bryły sztywnej względem punktu 0

1

Opis ruchu bryły
sztywnej

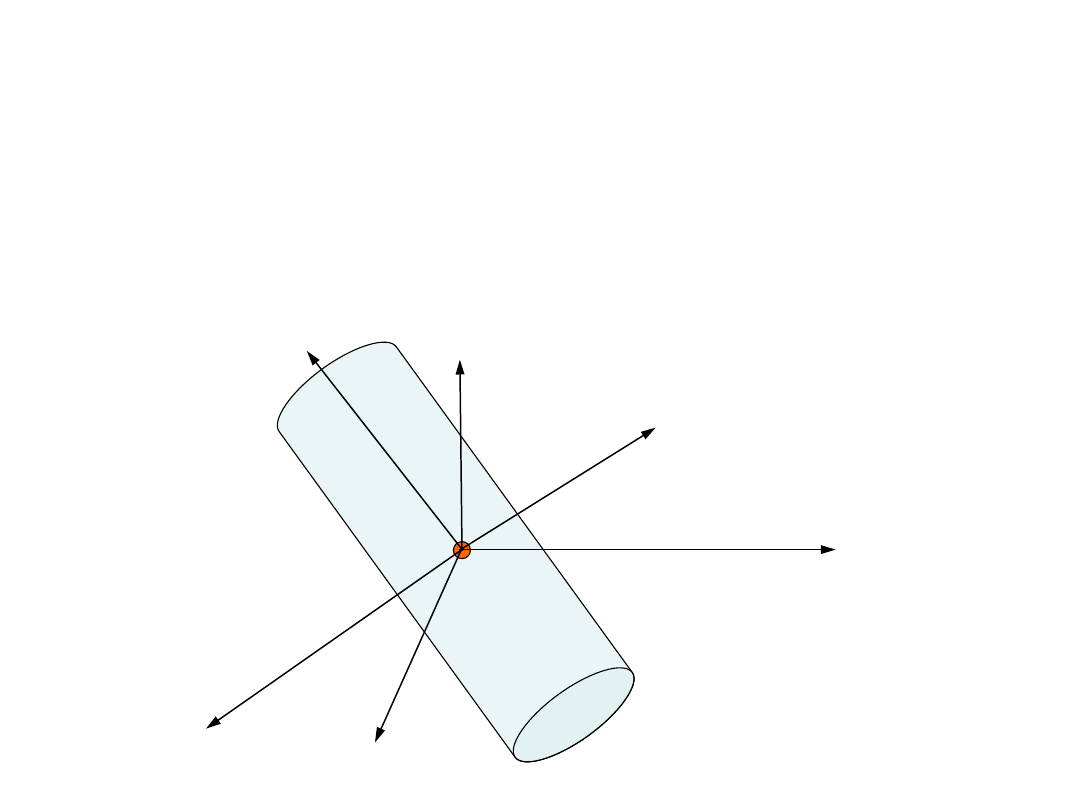
Dla

uproszczenia

sposobu

wyznaczania

położenia punktów bryły sztywnej w układzie
związanym z punktem 0

1

, celowe jest czasami

wprowadzenie

dodatkowego

układu

współrzędnych, dopasowanego do kształtu
bryły.

y

1

0

1

x

1

z

1

x

h

V

Opis ruchu bryły
sztywnej

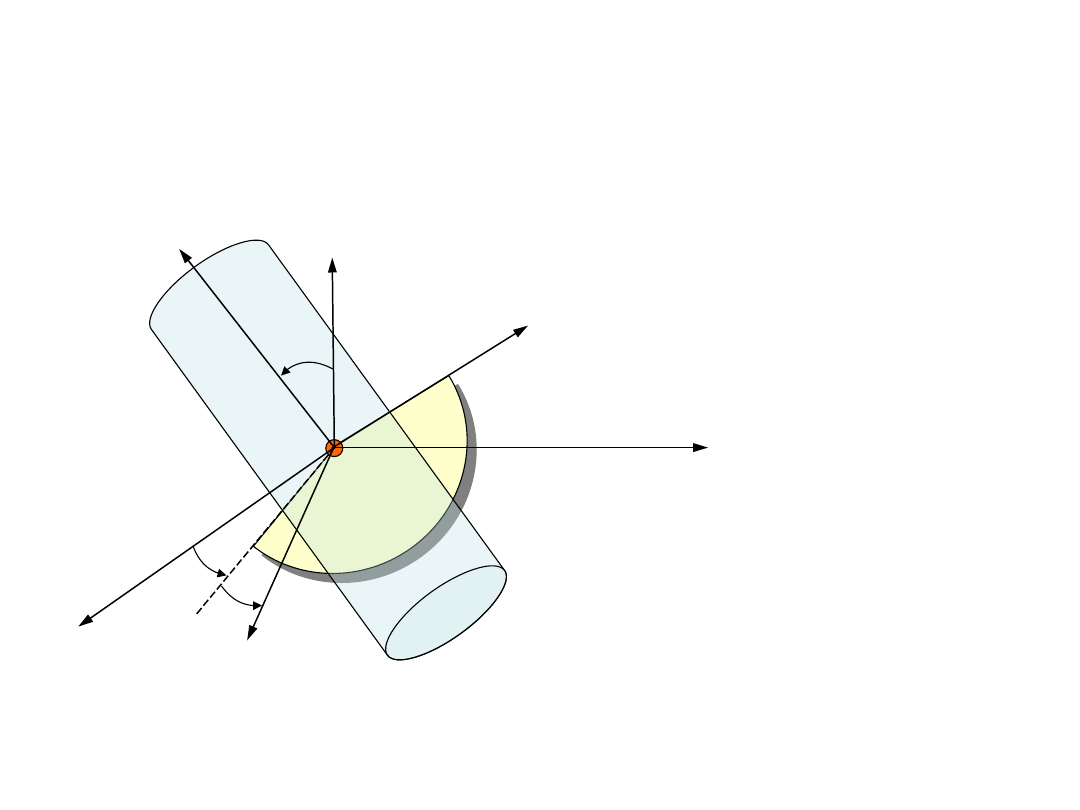
Kąty Eulera

:

 - kąt nutacji
– kąt precesji
 – kąt obrotu

własnego

y

1

0

1

x

1

z

1

x

h

V

N

y

j

J

Znając współrzędne 

danego punktu bryły oraz kąty
Eulera, możemy wyznaczyć
wartości współrzędnych x

1

, y

1

,

z

1

określające

położenie

punktu względem punktu 0

1

.

Linia 0

1

N stanowi ślad

przecięcia płaszczyzny x

1

y

1

przez płaszczyznę 

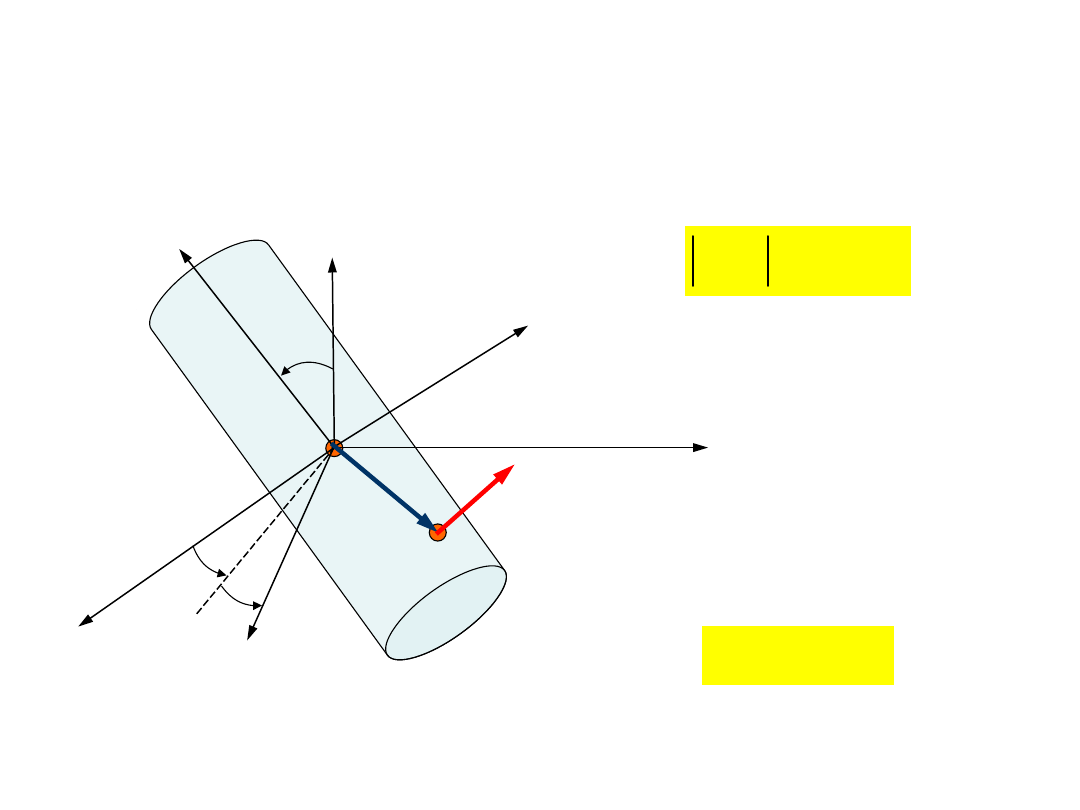
Opis ruchu bryły
sztywnej

y

1

0

1

x

1

z

1

x

h

V

N

y

j

J

Ruch
obrotowy

A

1

( )

r t

r

Ponieważ odległość punktów A i 0

1

jest stała, punkt A porusza się po
powierzchni kuli o promieniu:

( )

u t

r

1

( )

r t

const

=

r

Dla każdego położenia punktu
A punkt 0

1

stanowi środek

krzywizny toru punktu A.
Zatem:

1

( )

( )

t

r t

r

=

r

r

Ruch punktów bryły sztywnej w ruchu
obrotowym jest

ruchem kulistym

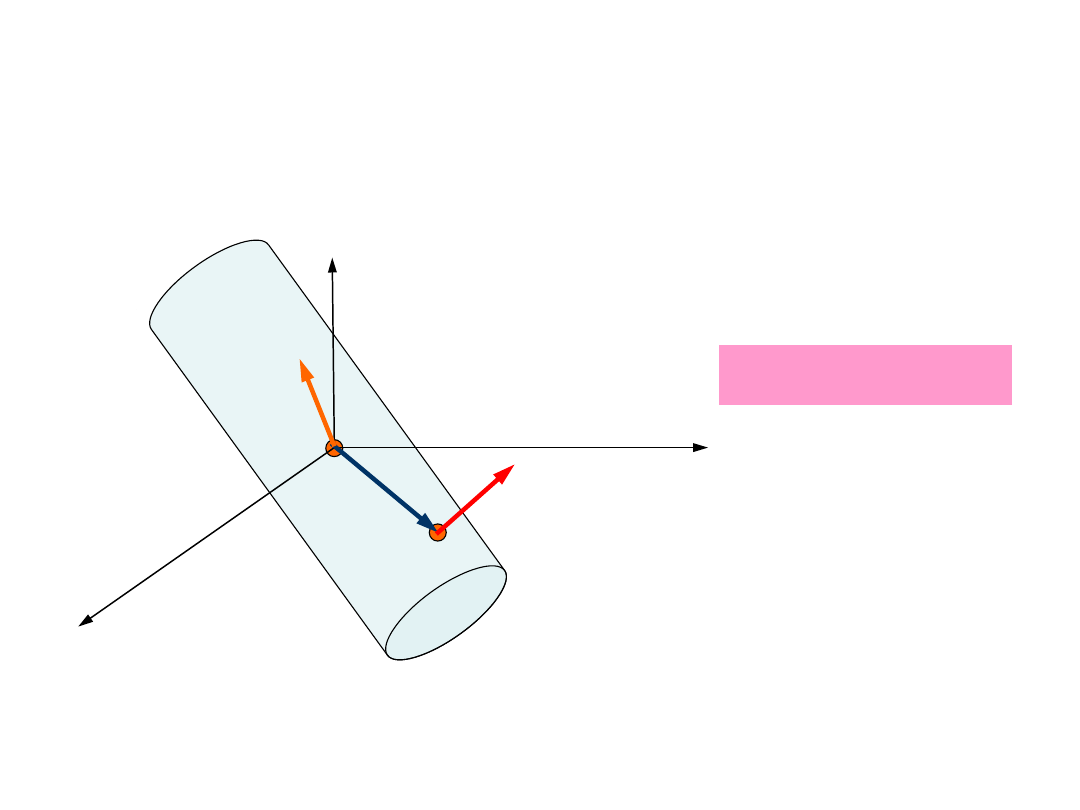
Opis ruchu bryły
sztywnej

y

1

0

1

x

1

z

1

A

1

( )

r t

r

( )

u t

r

( )

t

w

r

1

( )

( )

( )

u t

t r t

w

=

�

r

r

r

Ruch
obrotowy

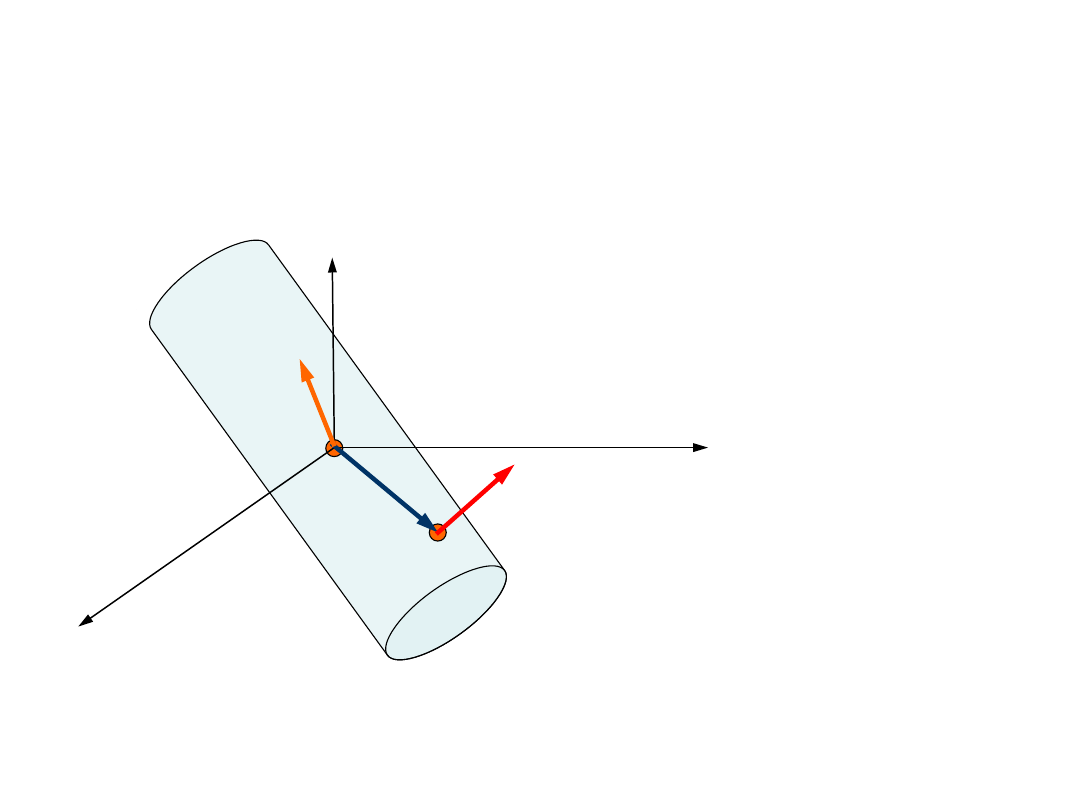
Opis ruchu bryły
sztywnej

y

1

0

1

x

1

z

1

Ruch
obrotowy

A

1

( )

r t

r

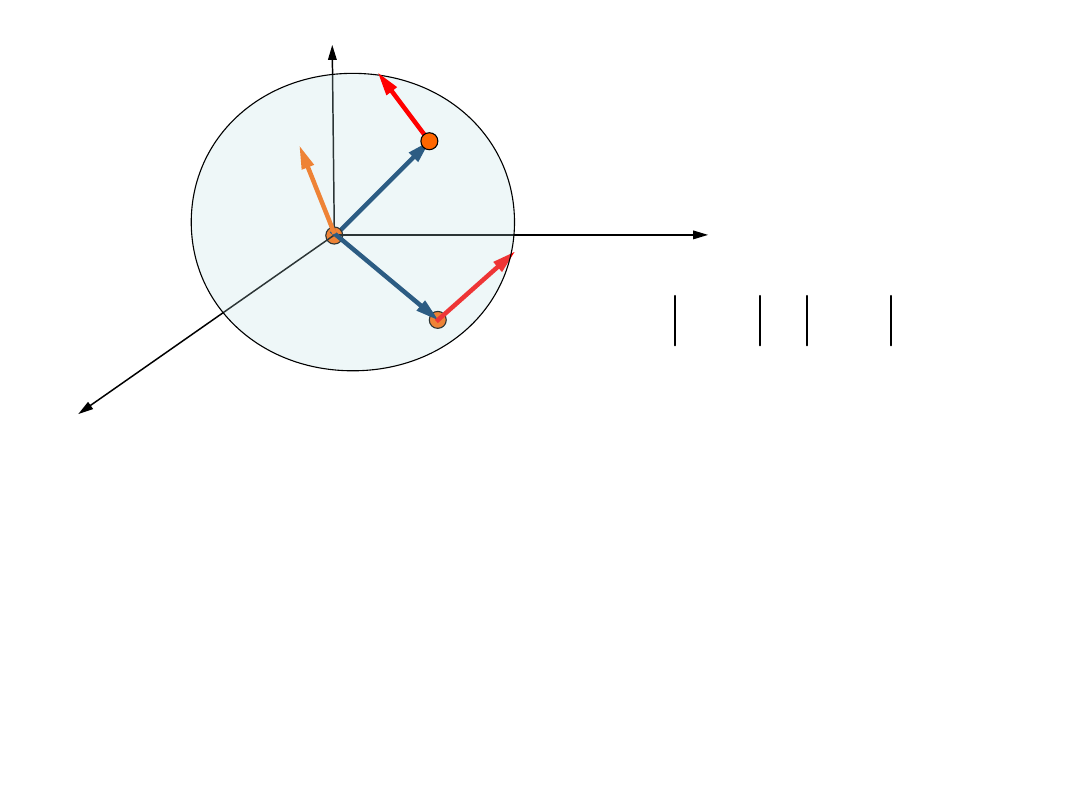
Punkty materialne leżące na linii 0

1

A

nie zmieniają swojego wzajemnego
położenia. Zatem punkty te poruszają
się z tą samą prędkością kątową co
punkt A.

( )

u t

r

( )

t

w

r

( )

B

r t

r

Opis ruchu bryły
sztywnej

y

1

0

1

x

1

z

1

A

( )

A

r t

r

Rozpatrzmy ruch punktów materialnych A i B, równo odległych
od punktu 0

1

. Ich położenia w kolejnych chwilach czasu leżą na

tej samej kuli. Ponieważ kąt pomiędzy promieniami wodzącymi
nie może się zmienić, punkty muszą poruszać się z tą samą
prędkością kątową.

( )

u t

r

( )

t

w

r

B

Wniosek:

W ruchu obrotowym bryły sztywnej, wszystkie punkty bryły
poruszają się z tą samą prędkością kątową.

i

A

B

r r

r r

( )

( )

A

B

r t

r t

=

r

r

Opis ruchu bryły
sztywnej

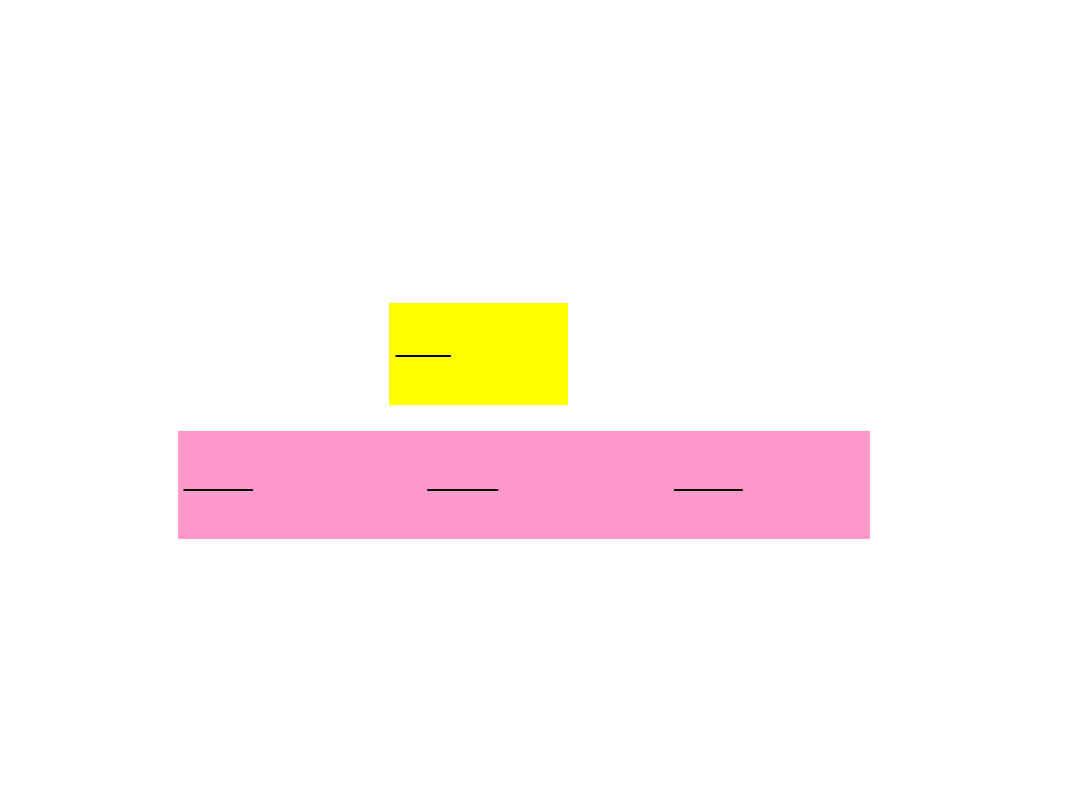
Wniosek:

Wszystkie punkty bryły sztywnej obracają się w danym momencie
czasu wokół tej samej

chwilowej osi obrotu

, której kierunek

wyznacza wektor prędkości kątowej. Zmiany położenia chwilowej
osi obrotu określa wektor przyspieszenia kątowego.

( )

d

t

dt

w

e

=

r

r

( )

( )

( )

,

,

y

x

z

x

y

z

d

d

d

t

t

t

dt

dt

dt

w

w

w

e

e

e

=

=

=

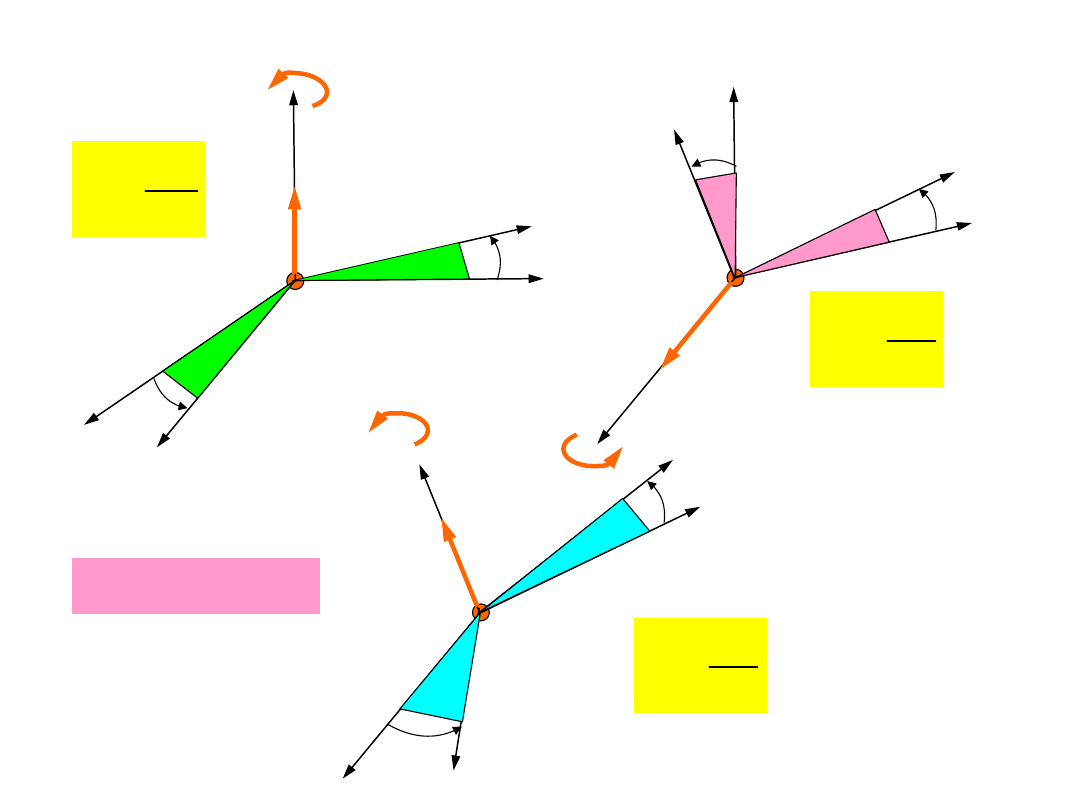
Opis ruchu bryły
sztywnej

y

1

0

1

x

1

z

1

h�

y

y

x�

1

w

1

d

dt

y

w =

0

1

h�

J

x�

h�

�

J

V

z

1

2

w

2

d

dt

J

w =

0

1

h

j

x�

h�

�

J

V

x

j

3

d

dt

j

w =

3

w

1

2

3

w w w w

= + +

r

r

r

r

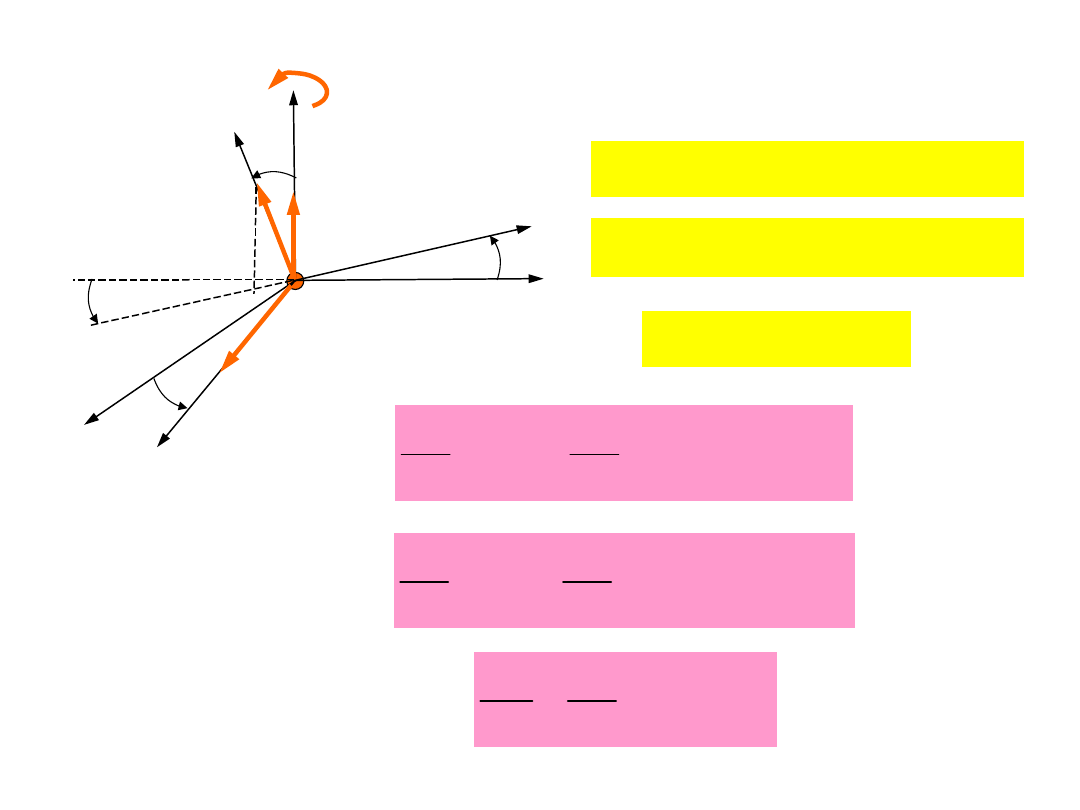
Opis ruchu bryły
sztywnej

y

1

0

1

x

1

z

1

y

x�

1

w

2

w

V

3

w

h�

y

2

3

cos

sin sin

x

w w

y w

J

y

=

+

2

3

sin

sin cos

y

w w

y w

J

y

=

-

1

3

cos

z

w w w

J

= +

cos

sin sin

x

d

d

dt

dt

J

j

y

J

y

w

+

=

J

sin

sin cos

y

d

d

dt

dt

J

j

y

J

y

w

-

=

cos

z

d

d

dt

dt

y

j

J

w

+

=

y

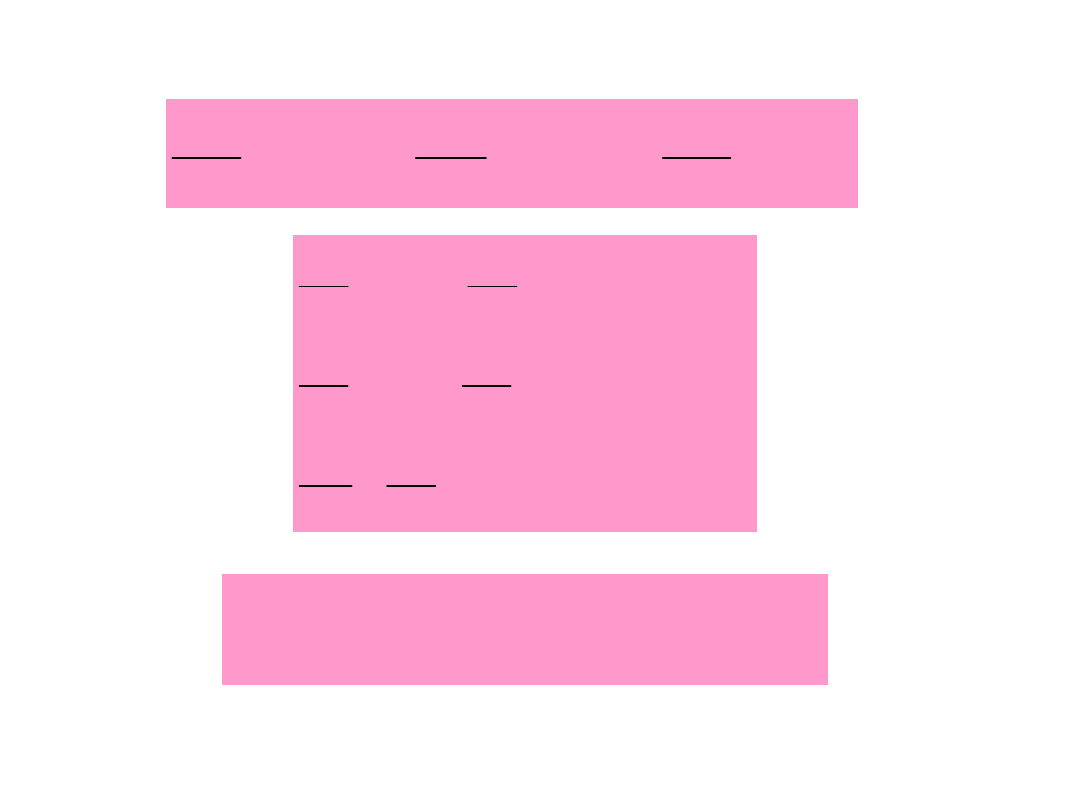
Opis ruchu bryły
sztywnej

cos

sin sin

sin

sin cos

cos

x

y

z

d

d

dt

dt

d

d

dt

dt

d

d

dt

dt

J

j

y

J

y

w

J

j

y

J

y

w

y

j

J

w

+

=

-

=

+

=

( )

( )

( )

,

,

y

x

z

x

y

z

d

d

d

t

t

t

dt

dt

dt

w

w

w

e

e

e

=

=

=

0

0

0

0

0

0

(0)

,

(0)

,

(0)

(0)

,

(0)

,

(0)

x

x

y

y

z

z

w

w

w

w

w

w

y

y

J

J

j

j

=

=

=

=

=

=

Ruch płaski bryły
sztywnej

Ruchem płaskim

bryły sztywnej nazywamy ruch, w

którym wszystkie punkty bryły sztywnej wykonują
ruch płaski

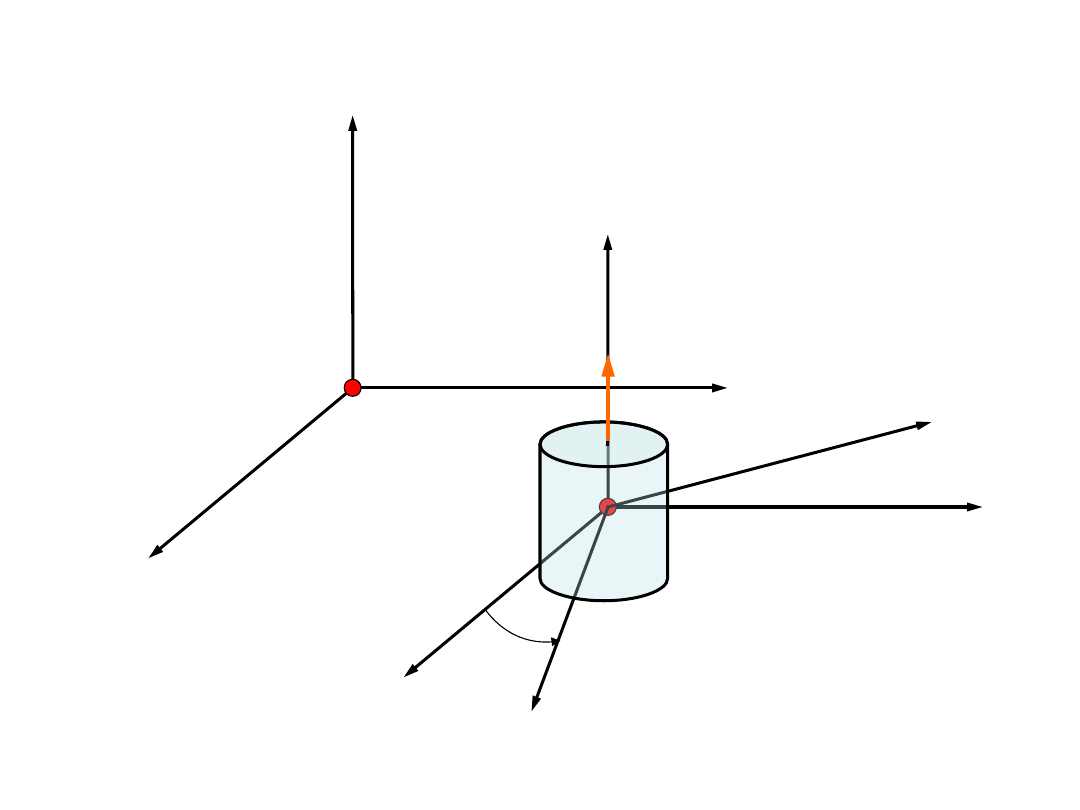
Ruch płaski bryły
sztywnej

0

x

y

z

0

1

x

1

y

1

z

1

w

h

x

j

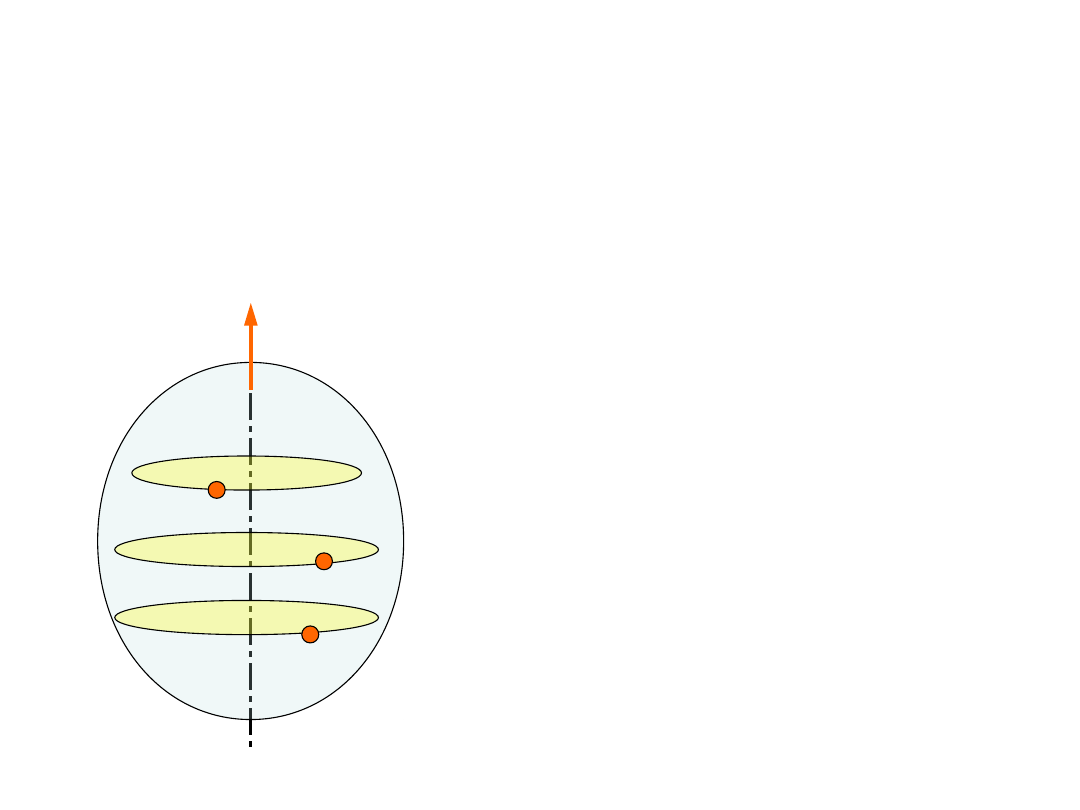
Ruch płaski bryły
sztywnej

1. Początek ruchomego układu współrzędnych 0

1

porusza się ruchem płaskim.

2. Wektor prędkości kątowej jest prostopadły do

płaszczyzny ruchu punktu 0

1

.

w

W płaskim ruchu obrotowym
punkty bryły poruszają się po
współosiowych okręgach

Ruch płaski bryły
sztywnej

0

1

0

1

( , , )

( )

( , , )

( , , )

( )

( , , )

x

t

x t

x

t

y

t

y t

y

t

x h

x h

x h

x h

=

+

=

+

1

1

( , , )

cos ( )

sin ( )

( , , )

sin ( )

cos ( )

x

t

t

t

y

t

t

t

x h

x

j

h

j

x h

x

j

h

j

=

-

=

+

0

0

0

0

0

0

0

0

( ),

( )

( ),

( ),

( ),

( )

y

x

x

x

x

y

d

d

t

t

dt

dt

du

dx

dy

du

u t

u t

a t

a t

dt

dt

dt

dt

j

w

w

e

=

=

=

=

=

=

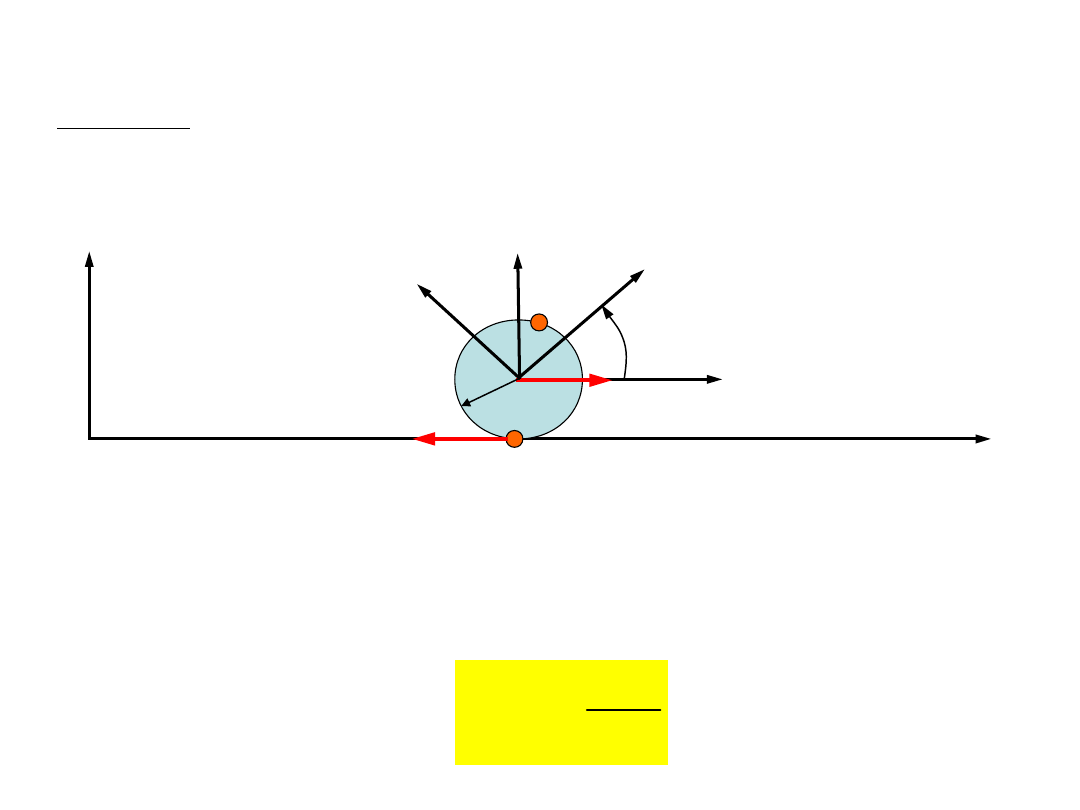
Ruch płaski bryły
sztywnej

Zadanie:

Samochód porusza się ruchem prostoliniowym, jednostajnie
przyspieszonym. Opisać ruch punktu na obwodzie koła
samochodu.

x

y

x

1

y

1

0

( )

u t

h

x

A

B

1

0

( )

( )

u t

u t

=-

Jeżeli koło ma dobrą przyczepność do podłoża, punkt B koła
ma w chwili czasu t w układzie nieruchomym prędkość równą
0. Dlatego w układzie ruchomym jego prędkość będzie równa
– u

0

(t).

0

r

0

0

( )

( )

u t

t

r

w

=-

j

Prędkość

kątowa

koła będzie równa:

Punkt A ma w układzie współrzędnych związanym z kołem
ustalone współrzędne



.

Ruch płaski bryły
sztywnej

1

1

( , , )

cos ( )

sin ( )

( , , )

sin ( )

cos ( )

x

t

t

t

y

t

t

t

x h

x

j

h

j

x h

x

j

h

j

=

-

=

+

0

1

0

1

( , , )

( )

( , , )

( , , )

( )

( , , )

x

t

x t

x

t

y

t

y t

y

t

x h

x h

x h

x h

=

+

=

+

0

0

0

0

0

0

0

0

( )

( )

( )

1

( )

u t

d

t

dt

r

u t

du

a

d

d

t

dt

dt

r

r dt

r

j

w

w

e

=

=-

�

�

=

=

-

=-

=-

�

�

�

�

Ruch płaski bryły
sztywnej

0

0

0

0

0

0

0

0

0

( )

(0)

(0) 0

(0) 0

( )

t

t

a

a t

d

d

d

t

d

r

r

a t

u

t

r

w

t

t

w

w

t

w

w

�

�

= -

�

-

=-

�

�

�

�

= �

=

=-

�

�

2

0

0

0

0

0

0

2

0

0

( )

(0)

2

(0) 0

( )

2

t

t

a

a t

d

d

d

t

d

r

r

a t

t

r

t

j

t

t

j

j

t

j

j

�

�

= -

�

-

=-

�

�

�

�

=

=-

�

�

Ruch płaski bryły
sztywnej

0

0

0

0

0

0

0

0

0

0

( ),

( )

(0)

(0) 0

( )

t

t

dx

du

u t

a

dt

dt

du

d

ad

u t u

at

d

u

u t

at

t

t

t

=

=

=

�

-

=

=

=

�

�

2

0

1

0

0

2

0

0

2

1

0

0

2

( )

(0)

(0) 0

( )

t

t

dx

d

a d

x t

x

at

d

x

x t

at

t

t t

t

=

�

-

=

=

=

�

�

Ruch płaski bryły
sztywnej

2

2

2

0

0

1

2

0

0

2

2

0

0

0

0

0

( , , )

cos

sin

2

2

( , , )

sin

cos

2

2

a t

a t

x

t

at

r

r

a t

a t

y

t

r

r

r

x h

x

h

x h

x

h

�

�

�

�

=

+

-

-

-

�

�

�

�

�

�

�

�

�

�

�

�

= +

-

+

-

�

�

�

�

�

�

�

�

Mechanizmy
płaskie

Mechanizmem

nazywamy

zespół

elementów

konstrukcyjnych połączonych ze sobą w taki
sposób, aby ruch jednego elementu wywoływał
określony ruch pozostałych elementów. Elementy
wchodzące w skład mechanizmu nazywamy

członami

lub

ogniwami mechanizmu

.

W każdym mechanizmie można wyodrębnić:

człon czynny

(napędzający),

człony bierne

(napędzane),

ostoję

(podstawę, człon nieruchomy)

Mechanizmem płaskim

nazywamy mechanizm,

którego wszystkie człony wykonują ruch płaski.

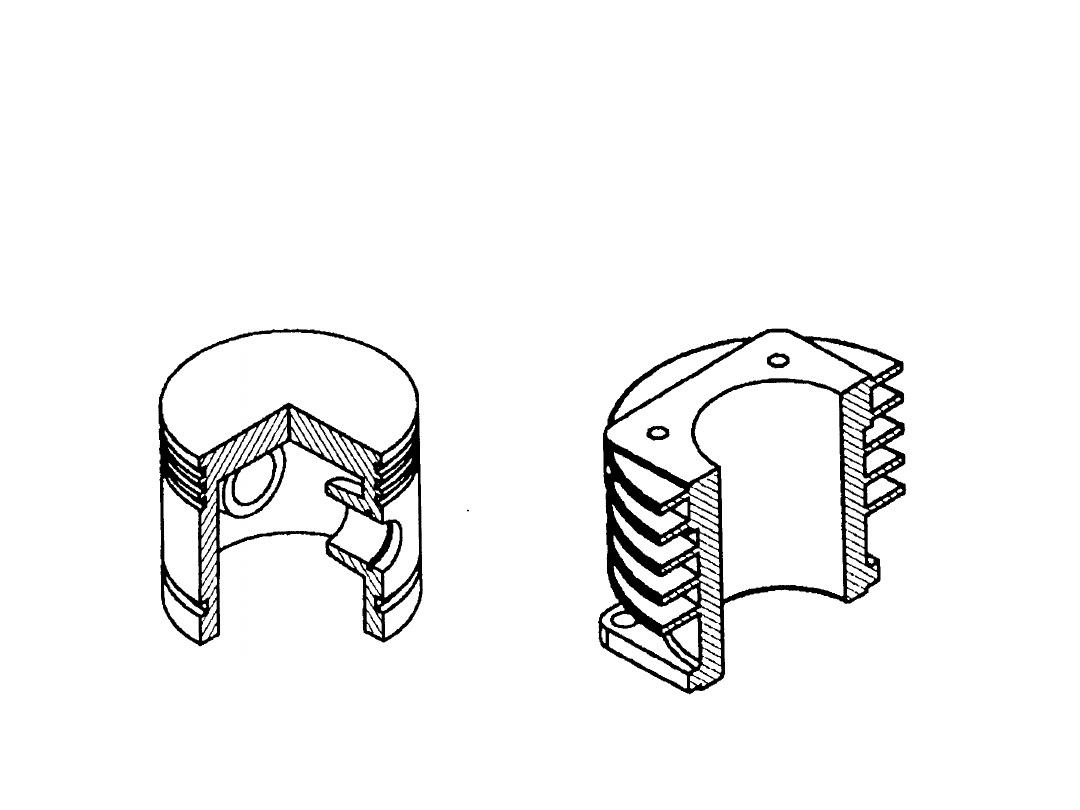
Mechanizmy
płaskie

Dwa człony połączone węzłem tworzą

parę

kinematyczną

.

Człony mechanizmów łączą się w

węzłach

. Dwa

człony tworzą węzeł, jeżeli mają co najmniej jeden
punkt wspólny i mogą się względem siebie
poruszać.

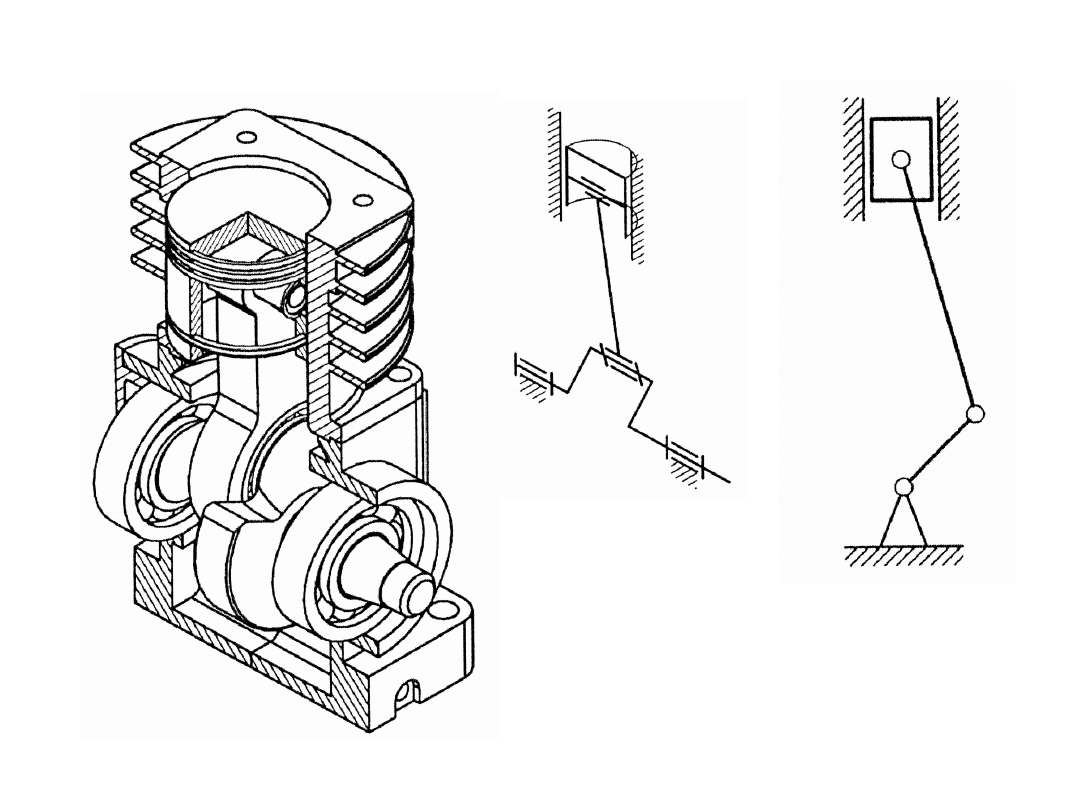
Para: tłok (człon czynny) – cylinder (człon
nieruchomy)

Mechanizmy
płaskie

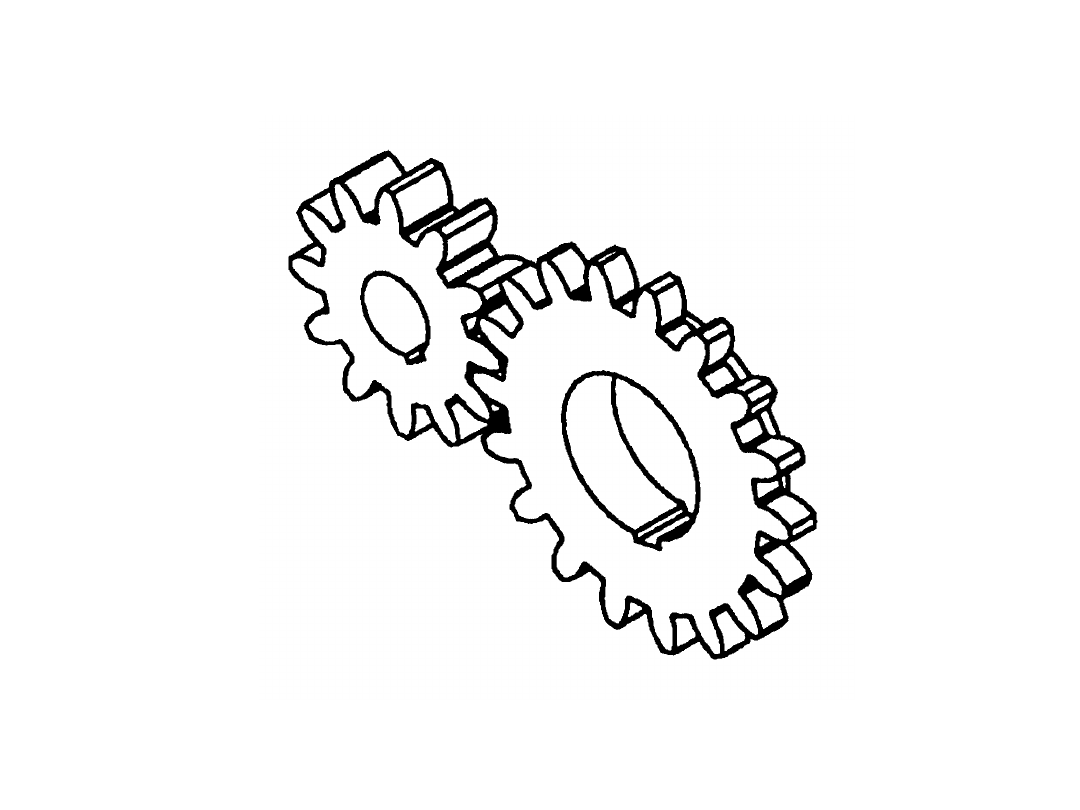
Para: koło zębate (człon czynny) – koło zębate (człon
bierny)

Mechanizmy
płaskie

Para: podstawa (człon nieruchomy) – dźwignia (człon
bierny)

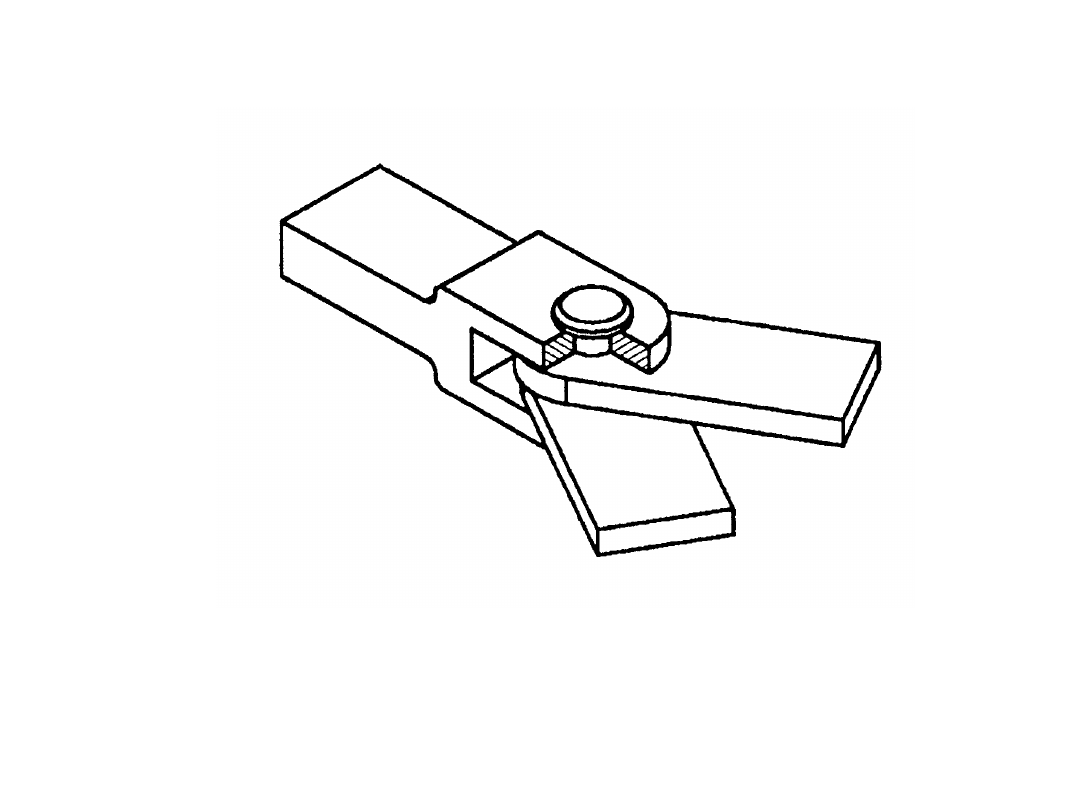
Mechanizmy
płaskie

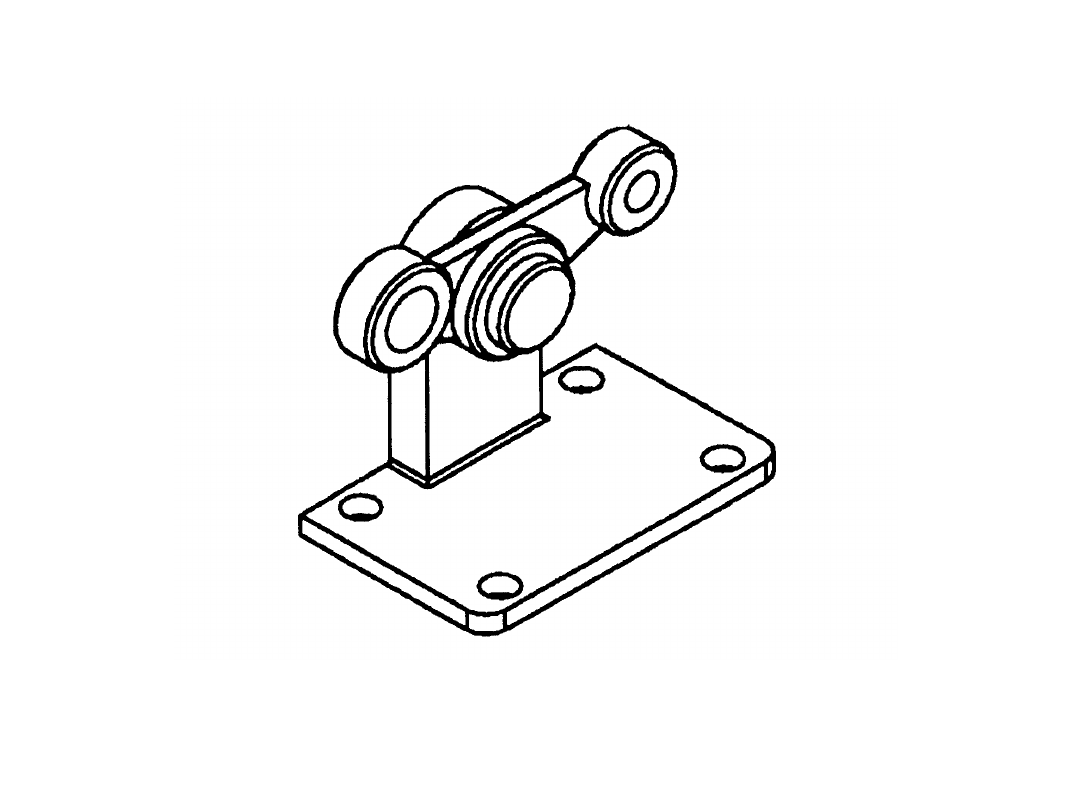
Para wielokrotna (połączenie sworzniowe): podstawa
(człon nieruchomy) – pręty (człony bierne)

Mechanizmy
płaskie

Schemat kinematyczny

(przestrzenny i płaski)

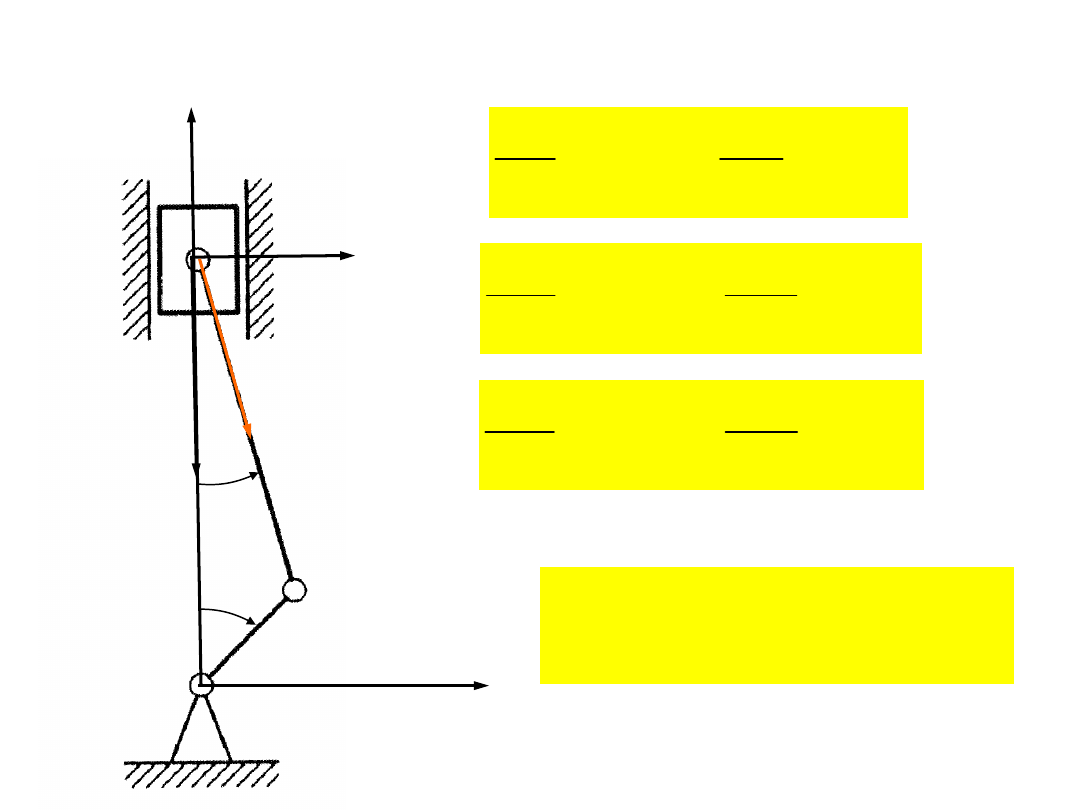
Mechanizmy
płaskie

x

y

y

1

x

1

B

A

C

A

j

C

j

( ),

( )

A

A

A

A

dx

du

u t

a t

dt

dt

=

=

( ),

( )

A

A

A

A

d

d

t

t

dt

dt

j

w

w

e

=

=

( ),

( )

C

C

C

C

d

d

t

t

dt

dt

j

w

w

e

=

=

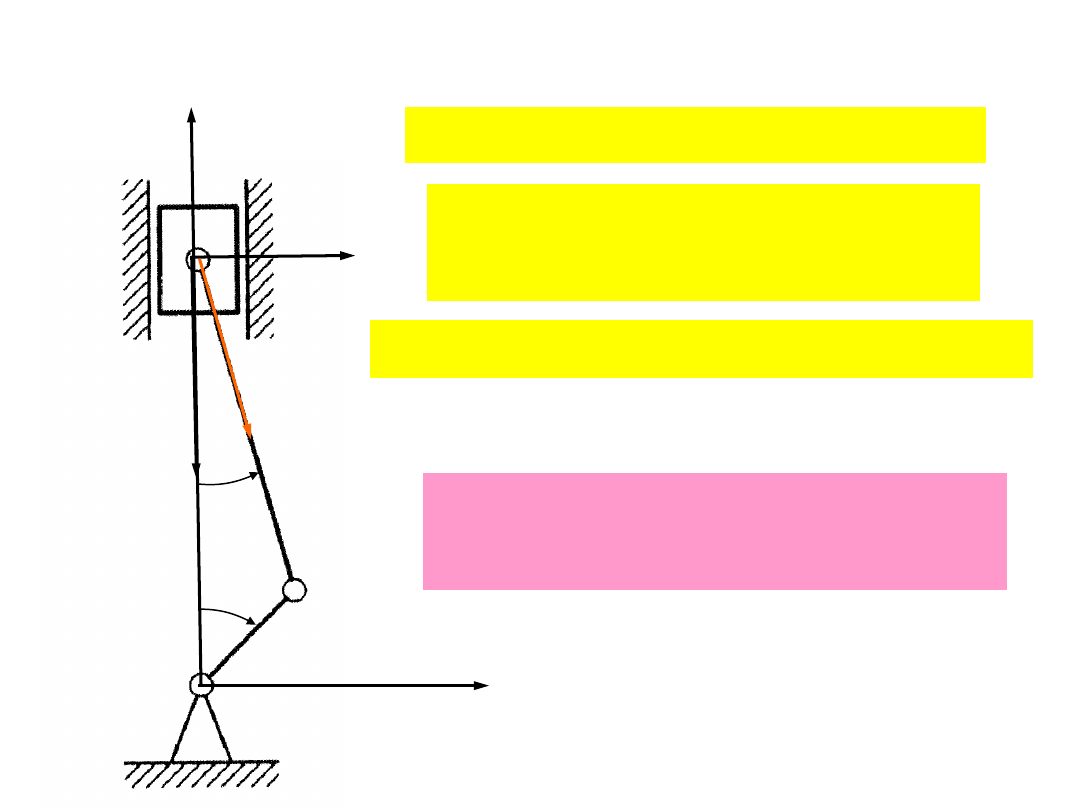
Niewiadome funkcje:

( ), ( ), ( ),

( ), ( ),

( ),

( ), ( )

A

A

A

A

A

C

C

C

x t u t

t

t

t

t

t

t

j

w

e

j

w

e

x

Mechanizmy
płaskie

x

y

y

1

x

1

B

A

C

A

j

C

j

1

1

( )

( )

( ),

( )

( )

B

A

B

B

B

x t

x t

x t

y t

y t

=

-

=

x

1

1

( )

cos ( )

cos ( ),

( )

sin ( )

B

B

A

AB

A

B

AB

A

x t

t

l

t

y t

l

t

x

j

j

j

=

=

=

( )

cos ( ),

( )

sin ( )

B

BC

C

B

BC

C

x t

l

t

y t

l

t

j

j

=

=

( )

cos ( )

cos ( ),

sin ( )

sin ( )

A

AB

A

BC

C

AB

A

BC

C

x t l

t

l

t

l

t

l

t

j

j

j

j

-

=

=

Związki kinematycznej
zgodności:

Mechanizmy
płaskie

[

]

[

]

( )

cos ( )

cos ( )

A

AB

A

BC

C

d

d

x t l

t

l

t

dt

dt

j

j

-

=

sin ( )

sin ( )

C

A

A

AB

A

BC

C

d

dx

d

l

t

l

t

dt

dt

dt

j

j

j

j

+

=-

( )

( )sin ( )

( )sin ( )

A

AB A

A

BC C

C

u t l

t

t

l

t

t

w

j

w

j

+

=-

[

]

[

]

sin ( )

sin ( )

AB

A

BC

C

d

d

l

t

l

t

dt

dt

j

j

=

( )cos ( )

( )cos ( )

AB A

A

BC C

C

l

t

t

l

t

t

w

j

w

j

=