Programowanie liniowe

dr inż. Jarosław Prońko

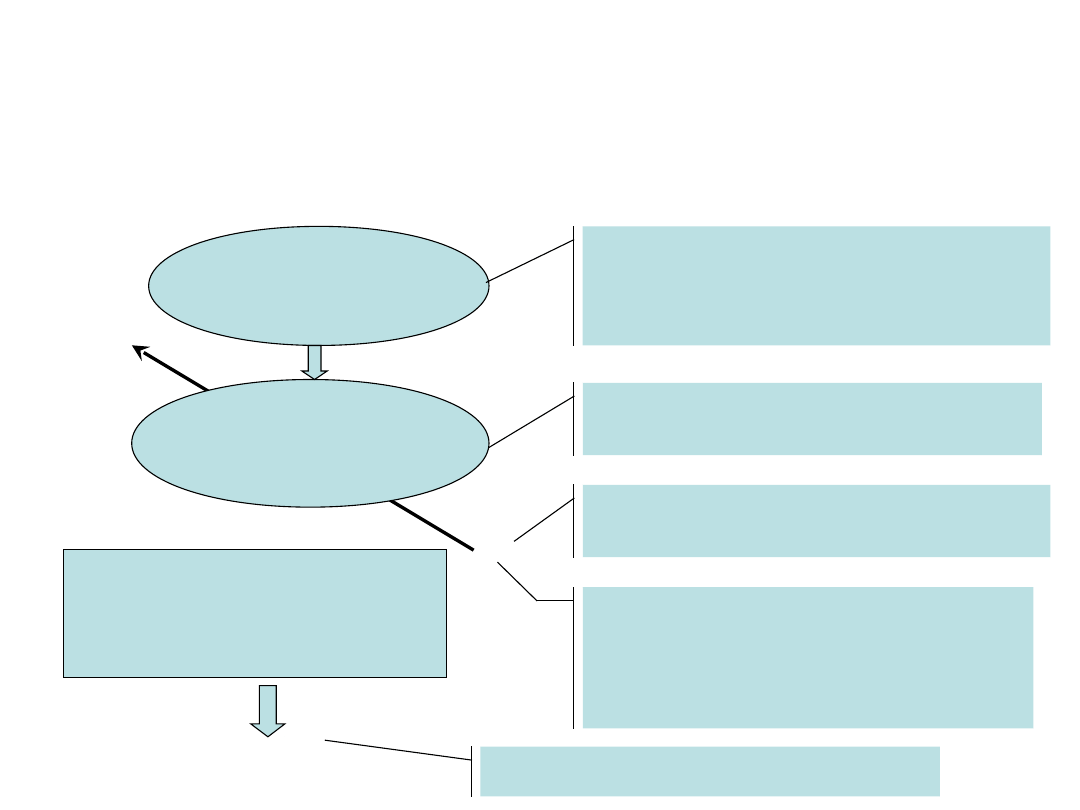
Proces podejmowania

decyzji

Fragment Rzeczywistości

Sytuacja decyzyjna

Coś co zmusza nas do działania

– podjęcia decyzji

Model rzeczywistości

Myślowa reprezentacja

rzeczywistości – problem

decyzyjny

X

Zmienna decyzyjna

Coś co możemy zmieniać?

Na zmienne nałożone są

ograniczenia?

np.: ilość pieniędzy, czasu

którym dysponujemy

Algorytm

Sposób wyszukiwania

Rozwiązań spełniających

ograniczenia i kryteria wyboru

X

1

Rozwiązanie - decyzja

Model rzeczywistości

programowanie matematyczne





max

min

,

,

,

2

1





n

x

x

x

f



Modelem rzeczywistości w programowaniu matematycznym jest funkcja celu,
która łączy zmienne decyzyjne x

i

z celem jaki zamierzamy osiągnąć.

Przy nałożonych na zmienne decyzyjne ograniczeniach, które najczęściej
zapisujemy w postaci:













i

n

i

i

n

i

i

n

i

b

x

x

x

h

b

x

x

x

h

b

x

x

x

h







,

,

,

,

,

,

,

,

,

2

1

2

1

2

1







.

,

,

1

,

,

1

,

,

,

2

,

1

u

p

i

p

r

i

r

i

















Oraz ograniczeń logicznych

 



i

d

.

,

,

1

r

u

i







Które najczęściej przyjmują postać żądania nieujemności zmiennych decyzyjnych,
lub aby były one całkowitoliczbowe.

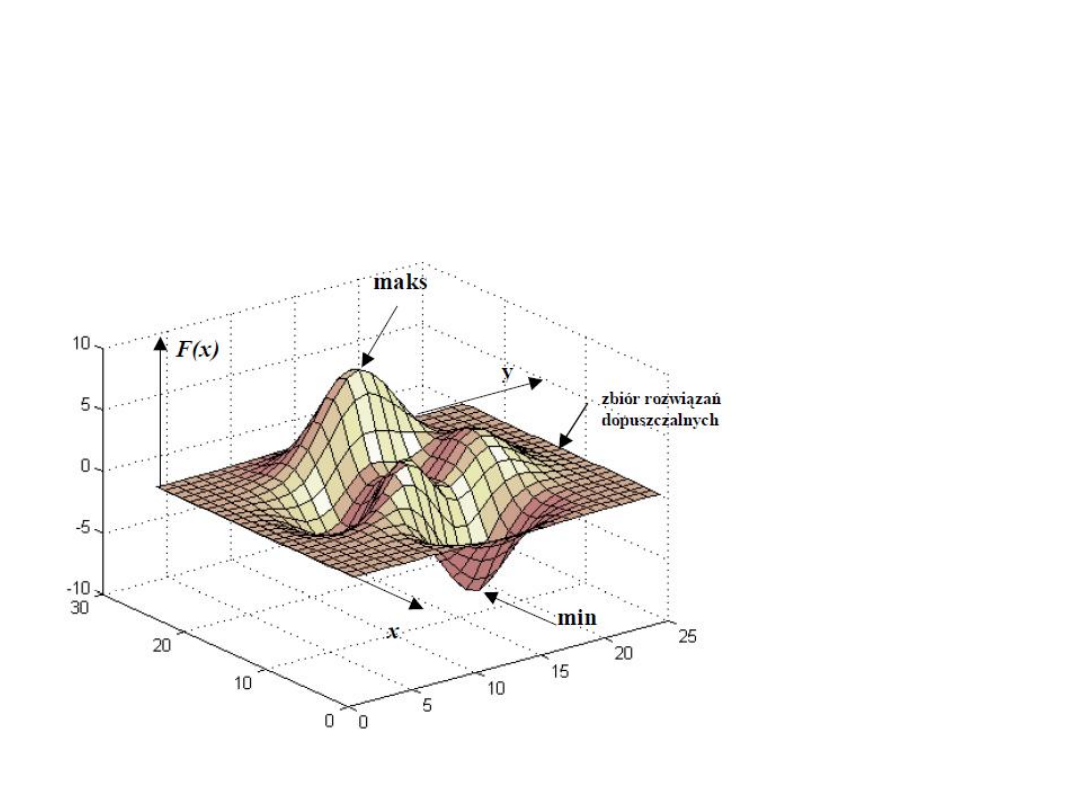
Programowanie matematyczne dla

dwóch zmiennych

x, y – zmienne decyzyjne
F(x,y) – funkcja celu
X

0

Y

0

– zbiór rozwiązań dopuszczalnych

 





Y

Y

y

X

X

x

y

x

F









0

0

,

min

Standardowe zadanie

optymalizacji

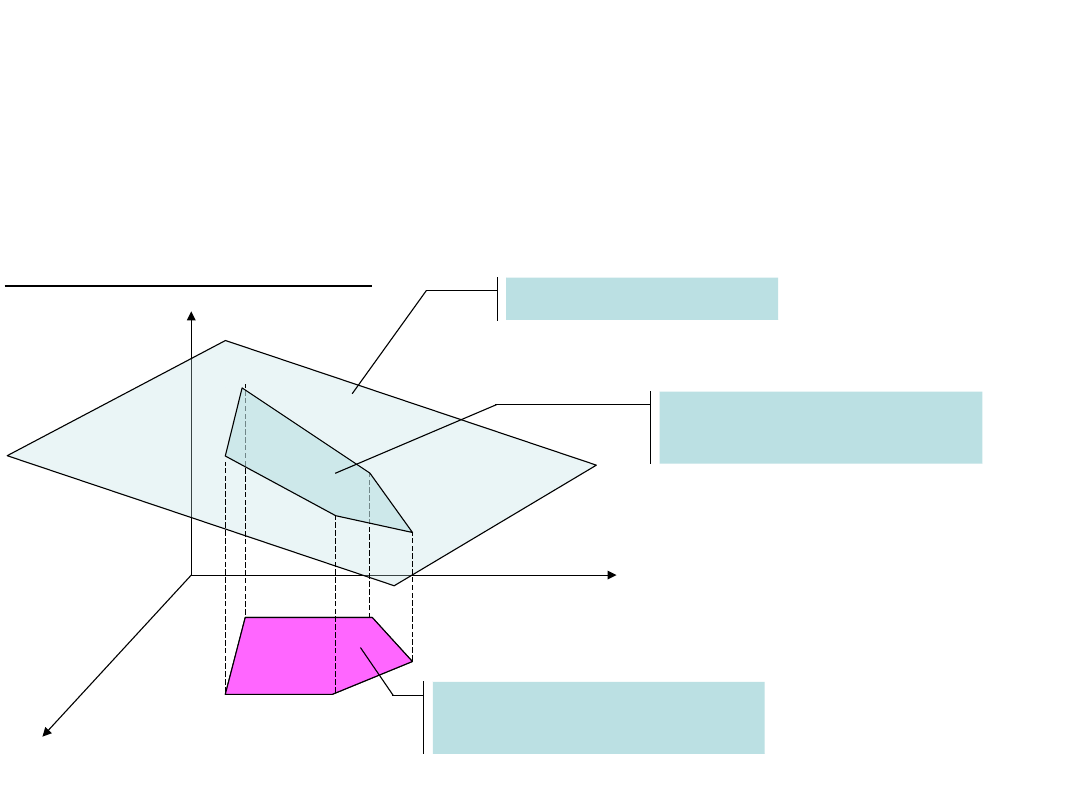
Programowanie liniowe

Jeżeli wszystkie funkcje programowania matematycznego przyjmą postać
funkcji liniowych to takie zadanie optymalizacji nazywamy
programowaniem liniowym

x

y

F(x,y)

Funkcja celu

Ograniczenia

zmiennych

decyzyjnych

Obszar poszukiwania

ekstremum funkcji

celu

2

2

1

1

min

x

c

x

c

z









0

,

2

1

5

2

52

1

51

4

2

42

1

41

3

2

32

1

31

2

2

22

1

21

1

2

12

1

11











































x

x

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

Programowanie liniowe

dwie zmienne decyzyjne

min

)

,

(

2

2

1

1

2

1











x

c

x

c

x

x

f







































0

,

2

1

3

2

32

1

31

2

2

22

1

21

1

2

12

1

11

x

x

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

x

1

x

2

1

2

12

1

11

b

x

a

x

a

































12

1

12

1

2

1

2

12

1

,

0

0

a

b

A

a

b

x

b

x

a

x















12

1

,

0

a

b

A















,

0

,

11

1

a

b

B

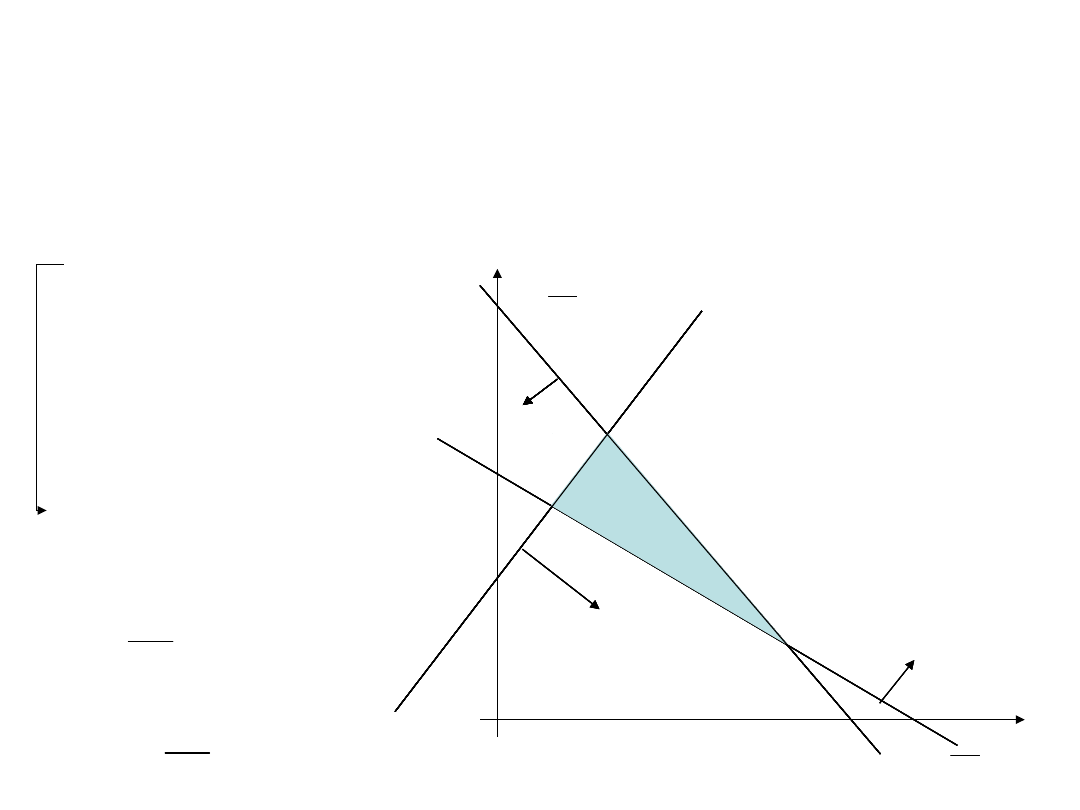
Programowanie liniowe

dwie zmienne decyzyjne

min

)

,

(

2

2

1

1

2

1











x

c

x

c

x

x

f







































0

,

2

1

3

2

32

1

31

2

2

22

1

21

1

2

12

1

11

x

x

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

x

2

1

2

12

1

11

b

x

a

x

a

































12

1

12

1

2

1

2

12

1

,

0

0

a

b

A

a

b

x

b

x

a

x

e

f

d

x

1















12

1

,

0

a

b

A















,

0

,

11

1

a

b

B

d















,

0

,

11

1

a

b

B















,

0

,

11

1

a

b

B















,

0

,

11

1

a

b

B

d















,

0

,

11

1

a

b

B

d















,

0

,

11

1

a

b

B

d















,

0

,

11

1

a

b

B

d















,

0

,

11

1

a

b

B















12

1

,

0

a

b

A

d















,

0

,

11

1

a

b

B

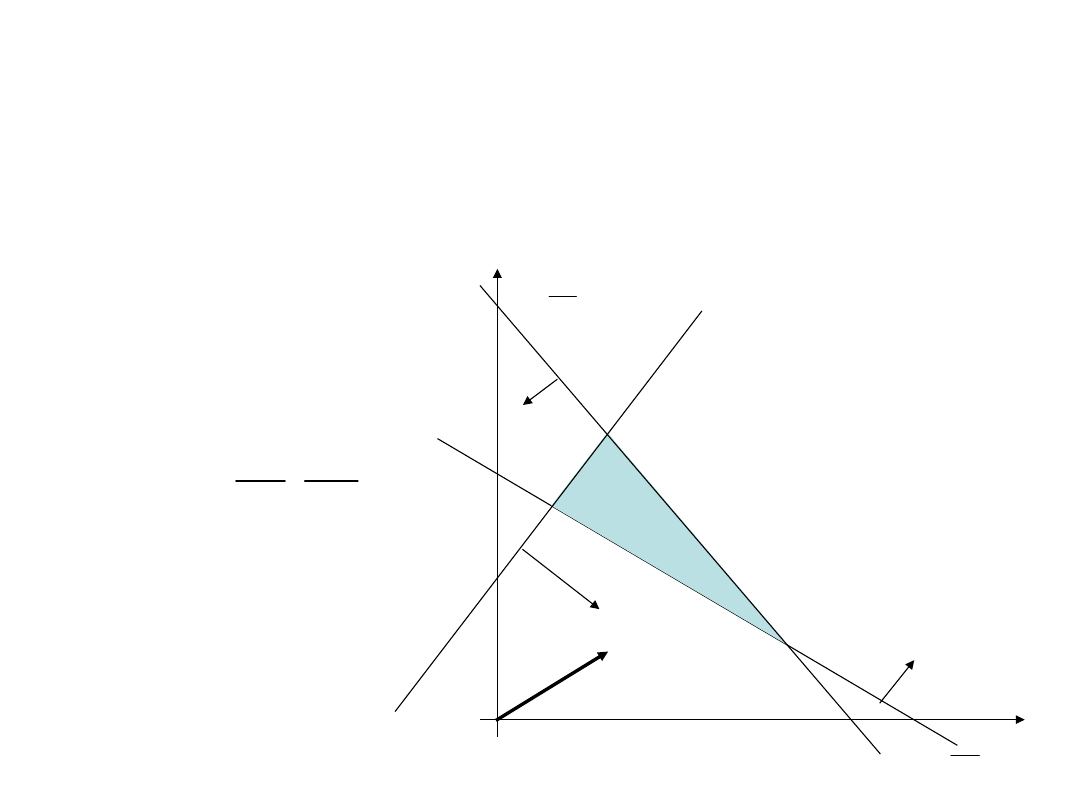
Programowanie liniowe

dwie zmienne decyzyjne

min

)

,

(

2

2

1

1

2

1











x

c

x

c

x

x

f







































0

,

2

1

3

2

32

1

31

2

2

22

1

21

1

2

12

1

11

x

x

b

x

a

x

a

b

x

a

x

a

b

x

a

x

a

x

1

x

2

Gradient – operator różniczkowy,
Przyporządkowujący polu skalarnemu,
Pole wektorowe, wskazujące kierunek
największego wzrostu funkcji
w danym punkcie

























2

1

2

1

,

)

,

(

x

f

x

f

x

x

f





2

1

2

1

,

)

,

(

c

c

x

x

f





f

















12

1

,

0

a

b

A

d















,

0

,

11

1

a

b

B

e

f

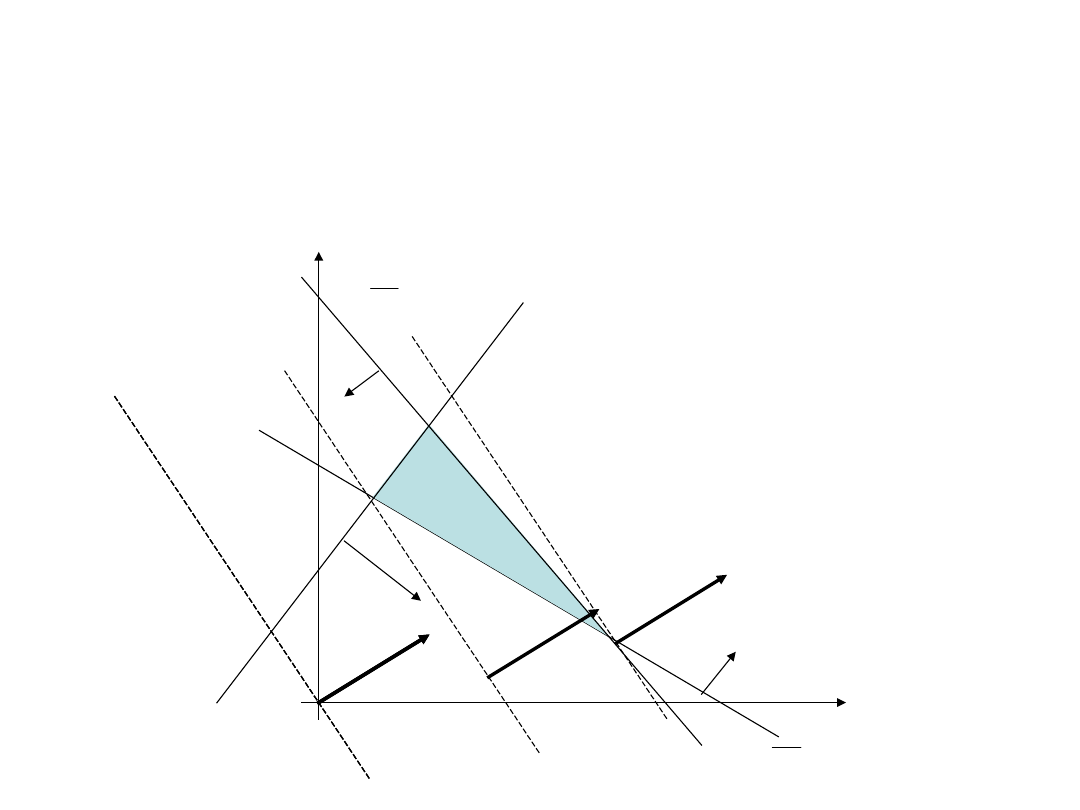
Programowanie liniowe

dwie zmienne decyzyjne

x

1

x

2

f

f



f



min

max















12

1

,

0

a

b

A

d















,

0

,

11

1

a

b

B

f



e

f



























3

2

32

1

31

2

2

22

1

21

min

b

x

a

x

a

b

x

a

x

a

f

e

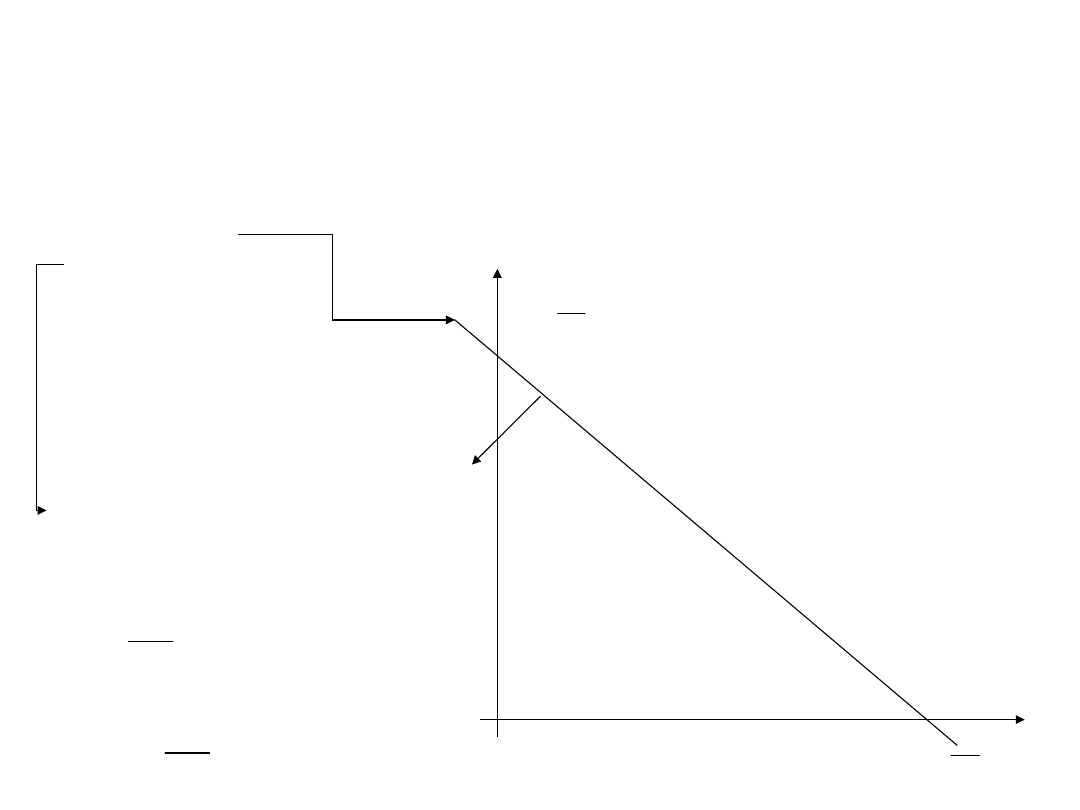
Metoda graficzna

Algorytm metody graficznej

• Na płaszczyźnie zmiennych decyzyjnych rysujemy

obszar ograniczeń.

• Wyznaczamy gradient funkcji celu.
• Rysujemy gradient i prostą prostopadłą do niego - l.
• Przesuwamy prostą l w kierunku wskazanym przez

gradient.

• Funkcja celu ma najmniejszą wartość w pierwszym

punkcie, napotkanym przez prostą l, w obszarze

ograniczeń.

• Funkcja celu ma największą wartość w ostatnim

punkcie, napotkanym przez prostą l, w obszarze

ograniczeń.

Metoda graficzna

• Pozwala rozwiązać programowanie liniowe dla 2

zmiennych decyzyjnych.

• Wskazuje, ze rozwiązanie programowania liniowego

znajduje się w wierzchołkach obszaru ograniczeń.

• lub ewentualnie na jednym z jego brzegów, jeżeli

jest on prostopadły do gradientu funkcji celu.

• Rozwiązując zadanie programowani liniowego dla

większej liczby zmiennych decyzyjnych należałoby:

– wyznaczyć wierzchołki obszaru ograniczeń – rozwiązać

układ równań opisujących ograniczenia,

– Obliczyć wartość funkcji celu w wyznaczonych punktach,
– Wybrać największą lub najmniejszą.

Uogólniona postać programowania liniowego

Podstawowe twierdzenia

1. Zadanie, w którym maksymalizuje się funkcję celu można zawsze zastąpić

zadaniem, w którym minimalizuje się funkcję przeciwną, przy tych
samych ograniczeniach

f

f









max

min

2. Prawdziwe są następujące zależności:





























0

,

,

,

,

,

,

1

1

2

1

2

1

n

i

n

n

i

i

n

i

x

b

x

x

x

x

h

b

x

x

x

h

































0

,

,

,

,

,

,

1

1

2

1

2

1

n

i

n

n

i

i

n

i

x

b

x

x

x

x

h

b

x

x

x

h





Uogólniona postać programowania liniowego

Podstawowe twierdzenia

3. Jeżeli warunki logiczne dotyczą nieujemności wszystkich zmiennych

decyzyjnych to nazywamy je kompletnymi.

4. Jeżeli na którąś ze zmiennych decyzyjnych nie nałożony warunku nieujemności

to możemy to zrobić poprzez zastąpienie jej dwoma zmiennymi nieujemnymi

0

0

2

1

2

1









k

k

k

k

k

x

x

x

x

x

Uwzględniając powyższe zależności każdą postać zadania programowania
liniowego możemy sprowadzić do postaci standardowej, w której:

1. Minimalizujemy funkcję celu
2. Warunki ograniczające podane są w postaci układu równań o nieujemnych

wyrazach wolnych.

3. Wszystkie zmienne decyzyjne są nieujemne.

Standardowa postać zadania

programowania liniowego

Wyznaczyć:

n

n

x

c

x

c

x

c

z

















2

2

1

1

min

Przy warunkach:

0

2

2

1

1

2

2

2

22

1

21

1

1

2

12

1

11













































i

m

n

mn

m

m

n

n

n

n

x

b

x

c

x

c

x

a

b

x

c

x

c

x

a

b

x

c

x

c

x

a































Standardowa postać zadania

programowania liniowego

w postaci wektorowej

Znaleźć taki nieujemny wektor:

Którego współrzędne spełniają równanie wektorowe:



























n

x

x

x

X



2

1

B

X

A

















































































m

n

mn

m

m

n

n

b

b

b

x

x

x

a

a

a

a

a

a

a

a

a



















2

1

2

1

2

1

2

22

21

1

12

11

A iloczyn CX osiąga wartość najmniejszą



































n

n

x

x

x

c

c

c

X

C





2

1

2

1

Metoda Simpleks



































































































































0

0

0

0

2

1

2

1

2

1

2

1

2

22

21

1

12

11

n

n

n

mn

m

m

n

n

b

b

b

z

x

x

x

c

c

c

a

a

a

a

a

a

a

a

a























Algorytm simpleks:

1. Konstruujemy dopuszczalne rozwiązanie wstępne – sprowadzenie

układu do postaci bazowej (macierz rozszerzona), przy czym wartość z
zawsze musi być wartością bazową.

2. Sprawdzenie spełnienia kryterium minimalności – wszystkie, wartości

w ostatnim wierszu macierzy są nie dodatnie.

3. Jeżeli nie to konstruujemy następny rozwiązanie dopuszczalne

i sprawdzamy kryterium.

Przykład