Histogram

Histogram

Bibliografia:



A. Hamrol „Zarządzanie jakością z 

przykładami”



A. Hamrol, W. Mantura „Zarządzanie 

jakością. Teoria i praktyka”



Dennis Lock „Podstawy zarządzania 

projektami”



R. Wolniak, B. Skotnicka „Metody i 

narzędzia zarządzania jakością”

Histogram jest rodzajem diagramu 
słupkowego, stosowanego w statystyce do 
graficznego przedstawiania częstości 
występowania realizacji zmiennej losowej 
w określonym przedziale. W analizie 
danych histogram służy do wizualnej 
zmienności, np. wyników procesu, stanów 
określonej cechy wyrobu.

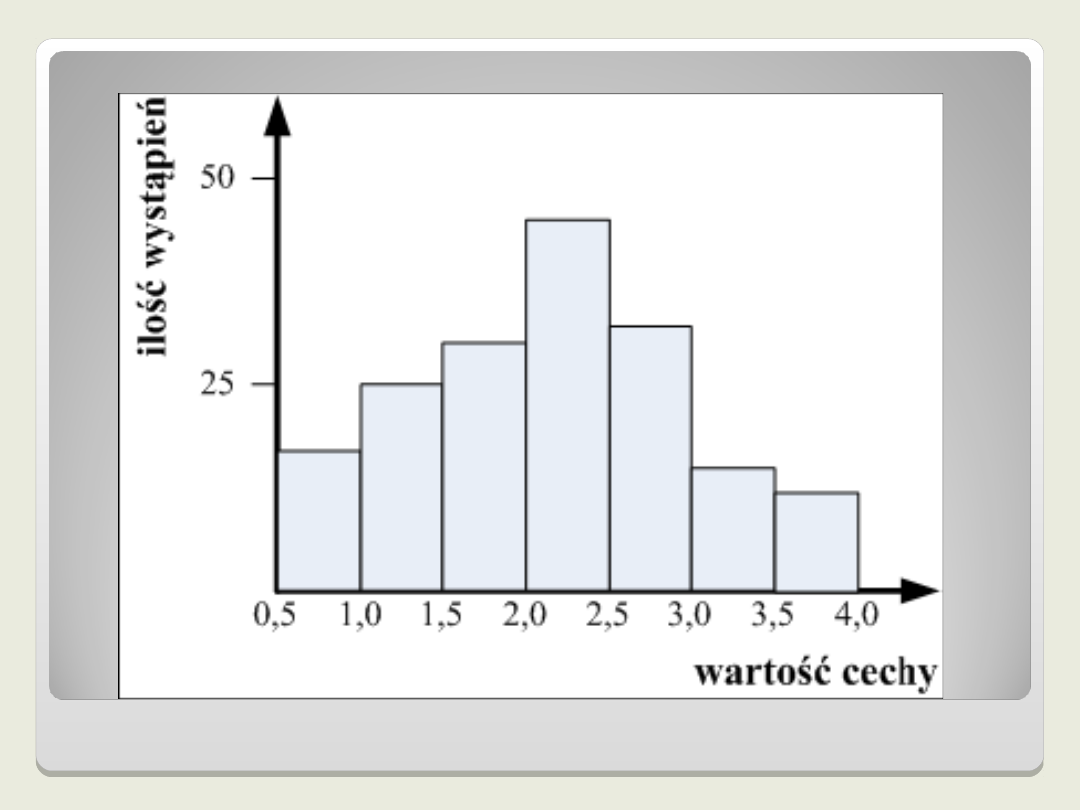
Jego kształt zależy od liczby przyjętych 
przedziałów, dlatego jej wyborowi 
należy poświęcić szczególną uwagę. 
Jako zalecane liczby przedziałów 
histogramu można przyjąć:

Liczebność 

próbki

n

Liczba 

przedziałów

k

30-50

51-100

101-200
201-500

6-10
7-11

8-12
9-15



szerokość przedziałów powinna być 

„naturalna” (np. co 0,02 mm a nie co 
0,0167)



klasy muszą się wykluczać! (np.:  1,25 < x 

 1,30 albo 1,25  x < 1,30)



można podać granice tolerancji



unikać przedziałów pustych

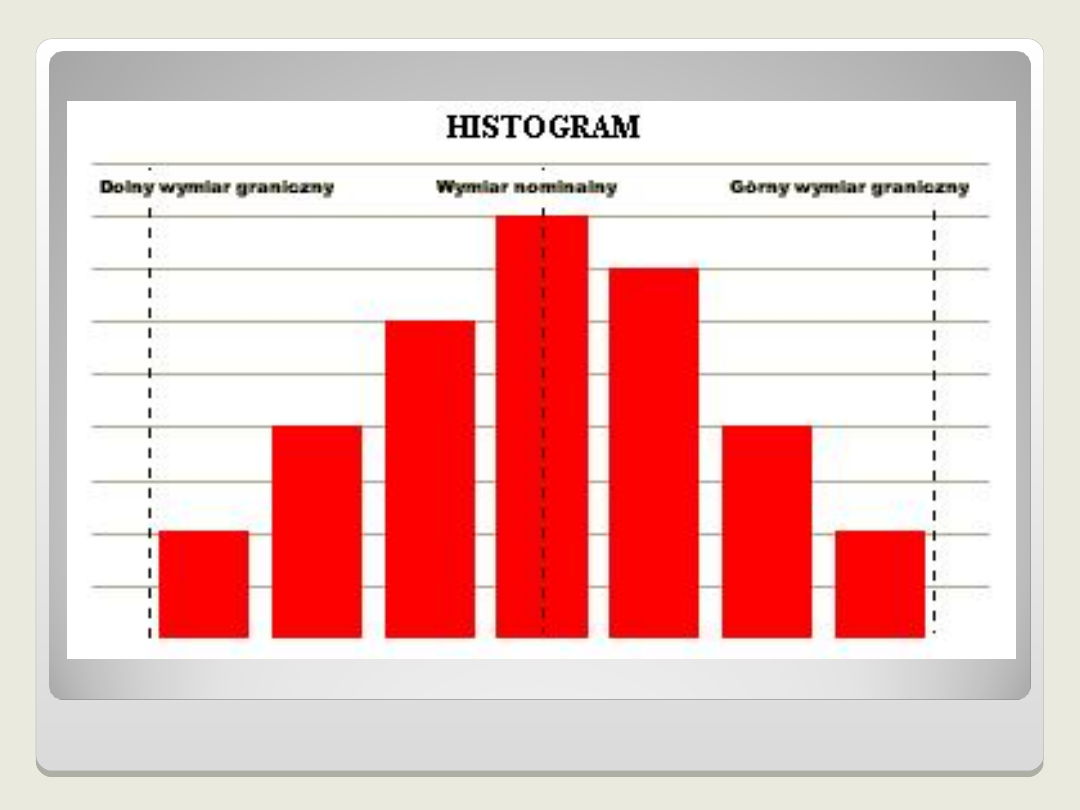
Histogram zbudowany jest z ciągu 

prostokątów o równych podstawach 

odpowiadających przedziałom 

określonych podczas grupowania danych i 

określania liczb klas. Wysokość 

prostokątów uwarunkowana jest wartością 

danych w określonym przedziale. Tak więc 

analizując wysokości poszczególnych 

prostokątów uzyskuje się obraz rozkładu 

wartości danych. 

Przykłady histogramów

Przykłady histogramów

Przy sporządzaniu histogramu zaleca się

kroki:

1.

Zebrać dane

2.

Ustalić rozstęp wartości

3.

Ustalić liczbę przedziałów

4.

Podzielić rozstęp przez liczbę przedziałów- 
uzyskamy szerokość przedziałów

5.

Poprzez dodawanie do najniższej liczby wartości 
szerokości przedziałów uzyskamy przedziały

6.

Następnie należy przyporządkować dane do 
przedziałów

7.

Na wykresie zaznaczyć ilość danych 
przypadających na dany przedział

Użyteczność histogramu

Użyteczność histogramu



prezentuje dane w postaci rysunkowej, co 

ułatwia sformułowanie odpowiednich 

wniosków



pozwala zaobserwować zmienność 

analizowanych danych (zmienność zjawiska), 

co stanowi pierwszy krok do zapanowania 

nad tą zmiennością



pozwala dostrzec pewien sposób 

uporządkowania problemu (można wyłonić 

prawidłowości w rozłożeniu wyników)



pozwala przeanalizować dane o procesie 

bazując na faktach, a nie na intuicji

Przykład

Przykład 2