
Psychometria, metoda
testów
Psychometria, metoda
testów
Rzetelność testu psychologicznego
wykład 5

Próba klasyfikacji błędów
pomiaru
Próba klasyfikacji błędów
pomiaru
błąd systematyczny, w rozumieniu klasycznej
teorii testów, nie wiąże się z nierzetelnością
testu, świadczy raczej o „inwalidacji” narzędzia
błąd losowy powoduje obniżenie rzetelności
pomiaru testem, może być konsekwencją:
–
konstrukcji testu,
–
sytuacji testowania,
–
złej oceny wyników.

Podstawy teorii
rzetelności (1)
Podstawy teorii
rzetelności (1)
Twierdzenie 1:
Wynik otrzymany w rezultacie pomiaru testem składa się z
wyniku prawdziwego i błędu pomiaru.
Założenia:
1.
Wartość oczekiwana błędu pomiaru
(średnia) jest równa zeru.
2.
Wynik prawdziwy jest nieskorelowany
z błędem pomiaru.
3.
Błędy pomiarów są nieskorelowane.
X
X
X
e
t
x
0
Μ
e
0
2
1
r
e
e
0
r
te

Podstawy teorii
rzetelności (2)
Podstawy teorii
rzetelności (2)
Twierdzenie 2:
Średnia wyników otrzymanych w rezultacie pomiaru testem jest
sumą średniej wyników prawdziwych i średniej błędów pomiaru
(równej zeru).
Twierdzenie 3:
Zmienność wyników otrzymanych jest sumą wariancji wyników
prawdziwych i wariancji błędu.
t
e
t
x
M
M
M
M
2
2
2
e
t
x
s
s
s

Idea testu równoległego
Idea testu równoległego
Dwa testy są testami równoległymi, jeżeli spełnione
są cztery warunki:
1.
Średnia wyników otrzymanych w teście A równa się
średniej wyników otrzymanych w teście B.
2.
Odchylenie standardowe
wyników otrzymanych
w teście A równa się odchyleniu standardowemu
wyników
otrzymanych w teście B.
3.
Interkorelacje w teście A są takie same jak
interkorelacje w teście B.
4.
Test A (wyniki otrzymane) koreluje
z zewnętrznym kryterium tak samo jak test B.
M
M
a
b
s
s
a
b
r
r
iaja
ibjb
r
r
aZ
bZ
Podstawy teorii
rzetelności (3)
Podstawy teorii
rzetelności (3)
Kolejne założenia:
1. Można oczekiwać, że wyniki otrzymane i prawdziwe
będą skorelowane. Korelację taką nazywamy
wskaźnikiem rzetelności.
2. Można wykazać, że korelacja między dwoma testami
równoległymi równa jest współczynnikowi rzetelności -
kwadratowi wskaźnika rzetelności, stosunkowi wariancji
wyników prawdziwych do wyników otrzymanych.
Każdy współczynnik rzetelności można interpretować
jako odsetek wariancji wyników otrzymanych
„determinowanych” przez wariancję wyników
prawdziwych.
r
r
xt
tt

Podstawy teorii
rzetelności (4)
Podstawy teorii
rzetelności (4)
Twierdzenie 4:
Rzetelność pomiaru to stosunek wariancji
wyników
prawdziwych
do wariancji wyników
otrzymanych.
Twierdzenie 5:
Standardowy błąd pomiaru jest odchyleniem standardowym
rozkładu błędów pomiaru wokół wyniku otrzymanego.
2
2
2
2
2
x
e
x
x
t
s
s
s
s
s
tt
r
SEM s
s
r
e
x
tt
(
)
1

Interpretacja wartości współczynników
rzetelności
Interpretacja wartości współczynników
rzetelności
r
tt
> 0,90
– bardzo rzetelny pomiar, test może być
stosowany zarówno w badaniach naukowych, jak i do
formułowania diagnoz indywidualnych
0,90 > r
tt
> 0,80
– rzetelny pomiar, test może być
stosowany w badaniach naukowych, jak i do diagnoz
indywidualnych, które będą mniej precyzyjne
0,80 > r
tt
> 0,70
– przeciętna rzetelność, test
powinien być stosowany jedynie w badaniach naukowych
0,70 > r
tt
> 0,60
– niska rzetelność, test może być
stosowany warunkowo w badaniach naukowych
0,60 > r
tt
> 0,50
– wątpliwa rzetelność pomiaru,
test bezużyteczny

Formuła obliczania przedziału
ufności
dla wyniku otrzymanego
Formuła obliczania przedziału
ufności
dla wyniku otrzymanego
Przedział ufności dla wyniku otrzymanego pozwala na
określenie granic, w których - z przyjętym
prawdopodobieństwem - znajduje się wynik prawdziwy
osoby badanej; przedział ten budujemy według formuły:
stała z
/2
przyjmuje następujące wartości:
0,15 0,10 0,05 0,01
z
/2
1,44 1,64 1,96 2,58
X
X
z SEM X
z SEM
t
x
x
/
/
;
2
2
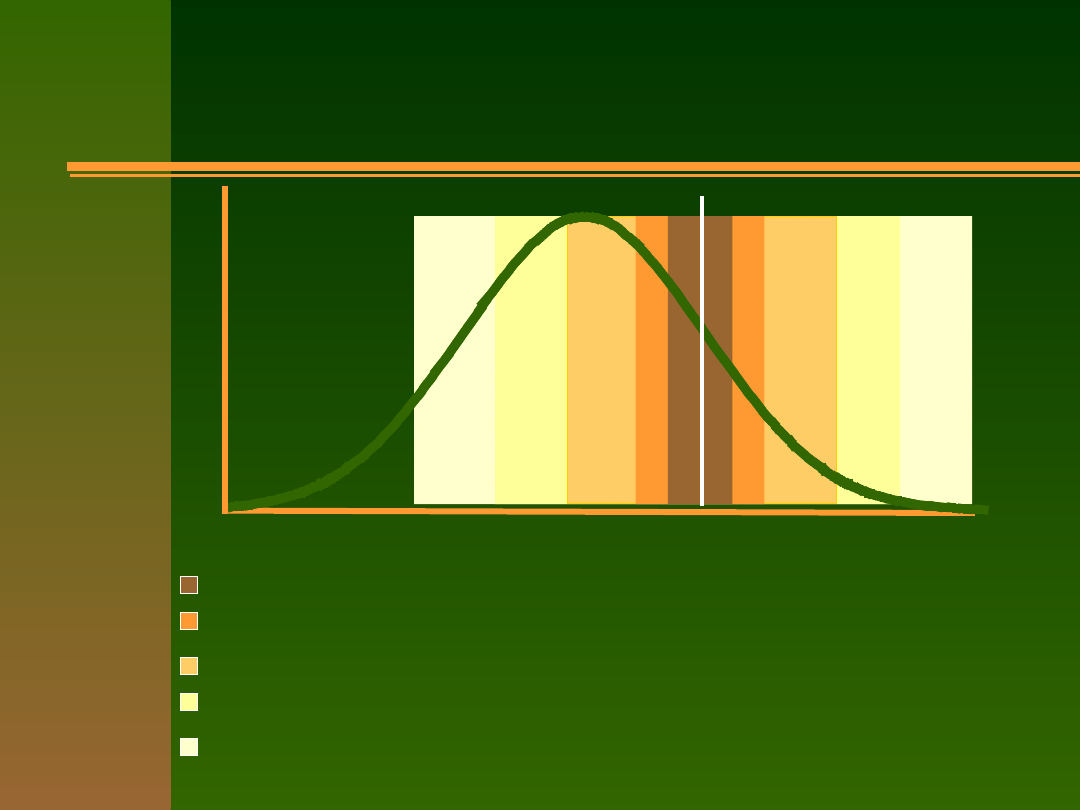
Przykład: SEM a r
tt
i
Przykład: SEM a r
tt
i
wysoka rzetelność i niski standard wnioskowania
wysoka rzetelność i wysoki standard wnioskowania
niska rzetelność i niski standard wnioskowania
niska rzetelność i wysoki standard wnioskowania
bardzo niska rzetelność i wysoki standard
wnioskowania

SEM a SEE
SEM a SEE
Lord i Novick zaproponowali inne niż Gulliksen
rozumienie standardowego błędu pomiaru -
standardowy błąd estymacji wyniku otrzymanego,
który jest charakter zależy od wyniku
prawdziwego.
Błąd ten ma rozkład symetryczny wokół wyniku
prawdziwego
i niesymetryczny wokół wyniku otrzymanego
(ściśle - jest symetryczny dla wyników średnich i
skośny dla wyników skrajnych).
W praktyce jednak, bardziej „zachowawcze” jest
stosowanie SEM, a różnica jest subtelna, wynika to
z następującej relacji:
SEE SEM r
tt
Standardowy błąd różnicy między dwoma
wynikami
Standardowy błąd różnicy między dwoma
wynikami
Oceniając istotność różnicy między dwoma
wynikami posługujemy się wzorem:
Gdy obliczamy różnicę między wynikami
dwóch testów, przyjmuje on postać:
Gdy obliczamy różnicę między wynikami
dwóch osób badanych tym samym testem:
SEM
SEM
SEM
X Y
X
Y
(
)
2
2
SEM
S
r
S
r
X Y
X
xx
Y
yy
2
2
1
1
(
)
(
)
SEM
S
r
X Y
X
tt
2 1
(
)

Psychometria, metoda
testów
Psychometria, metoda
testów
Metody szacowania rzetelności
wykład 6

Metody szacowania
rzetelności
Metody szacowania
rzetelności
dwukrotne badanie tym samym testem
porównanie form równoległych testu
porównanie części (np. połówek) testu
– oparte na analizie właściwości statystycznych
pozycji testowych
– oparte na analizie związków itemów z ogólnym
wynikiem testu
badanie stopnia zgodności sędziów
kompetentnych oceniających odpowiedzi testowe

Dwukrotne badanie tym samym
testem
Dwukrotne badanie tym samym
testem
–
metoda estymacji stabilności bezwzględnej testu
odwołuje się do dwukrotnego pomiaru tym samym
testem tej samej grupy osób badanych, między
pomiarami mija jakiś czas (inna nazwa – badanie
stałości);
metoda ta jest wrażliwa na przypadkowe zmiany
dotyczące osoby badanej i warunków badania
–
metoda estymacji wiarygodności testu, podobnie jak
wyżej jest to dwukrotne badanie tej samej grupy,
jednak między pomiarami nie ma przerwy – badanie
drugie następuje zaraz po zakończeniu pierwszego;
metoda pozwala ocenić chwilowe – nie trwające dłużej
niż samo badanie – i związane z osobą badaną
czynniki zakłócające pomiar np. zmęczenie, lub
fluktuacje uwagi
Porównanie form
równoległych testu
Porównanie form
równoległych testu
–
metoda ta – podobnie jak omówione wcześniej –
odwołuje się do dwukrotnego badania grupy osób
badanych, jednak w miejsce dwukrotnego użycia tego
samego testu używane są dwie wersje równoległe
–
w przypadku dokonania pomiarów bez przerwy
czasowej metoda nazywana jest estymacją
równoważności międzytestowej; pozwala określić
związek między błędem pomiaru a różnicami wersji,
zatem ocenić związek rzetelności i specyficznych treści
pytań
–
współczynnik stabilności względnej uzyskujemy
dokonując pomiarów wersjami równoległymi z
odstępstwem czasu; uzyskana informacja o źródle
błędu dotyczy zarówno zmienności intraindywidualnej,
jak i treści pytań

Porównanie części (np. połówek)
testu
Porównanie części (np. połówek)
testu
–
metoda połówkowa pozwala określić współczynnik
równoważności międzypołówkowej; odwołuje się do
jednokrotnego pomiaru jednym testem; de facto
postępowanie takie przypomina – omówiony
wcześniej – współczynnik równoważności
międzytestowej
–
test może być podzielony na połowy: losowo,
lub z uwzględnieniem statystyk opisujący
poszczególne pytania, albo po prostu na pytania o
numerach parzystych vs. pytania o numerach
nieparzystych
–
ocenianym źródłem błędu są różnice między
połówkami dotyczące specyficznych treści pytań

Metody oparte na analizie
właściwości statystycznych pozycji
testowych
Metody oparte na analizie
właściwości statystycznych pozycji
testowych
–
estymacja zgodności wewnętrznej opiera się na
jednokrotnym badaniu, w ogólnym rozumieniu
współczynniki tego rodzaju są średnią wszystkich
możliwych współczynników równoważności
międzypołówkowej odwołujących się do różnych
„przepołowień”
–
metody tego typu odwołują się do tzw. wzorów KR
20
i KR
21
opracowanych przez Kuderę i Richardson, oraz
formuły obliczania przedstawionej przez Cronbacha
–
współczynniki tego typu maksymalizują się dla skal
jednorodnych czynnikowo (homogenicznych), w
których poszczególne pozycje są względem siebie
równoległe; źródłem błędu jest zatem
heterogeniczność pytań i ich treści

Metody oparte na analizie związków
itemów z ogólnym wynikiem testu
Metody oparte na analizie związków
itemów z ogólnym wynikiem testu
–
metody tego typu pozwalają na określenie
rzetelności
w oparciu o jednokrotne badanie
–
w sensie operacyjnym obliczane wskaźniki są
pochodnymi mocy dyskryminacyjnych – korelacji
między pozycjami
a wynikami ogólnymi w skali
–
w celu obliczenia tak budowanych współczynników
rzetelności stosuje się wzory zaproponowane przez
Spearmana-Browna lub Gulliksena
–
źródłem błędu jest dobór treści itemów

Ocena stopnia zgodności sędziów
kompetentnych
Ocena stopnia zgodności sędziów
kompetentnych
–
metoda stosowana niezbyt często, zazwyczaj w
przypadku narzędzi, gdzie odpowiedzi osoby
badanej podlegają „swobodnej ocenie” diagnosty
–
w celu oceny zgodności kilku zestawów ocen
tego samego materiału, dokonanych przez kilku
niezależnie pracujących diagnostów – sędziów
kompetentnych oblicza się np. współczynnik
zgodności sędziów W-Kendalla.
–
źródłem wariancji błędu mogą być niedostatki
pracy diagnostów lub niedostatki klucza według
którego dokonywane są oceny

Czynniki wpływające na rzetelność
pomiaru
Czynniki wpływające na rzetelność
pomiaru
długość testu
jakość pytań
homogeniczność wymiaru
(jednorodność grupy pytań)
zakres mierzonej cechy
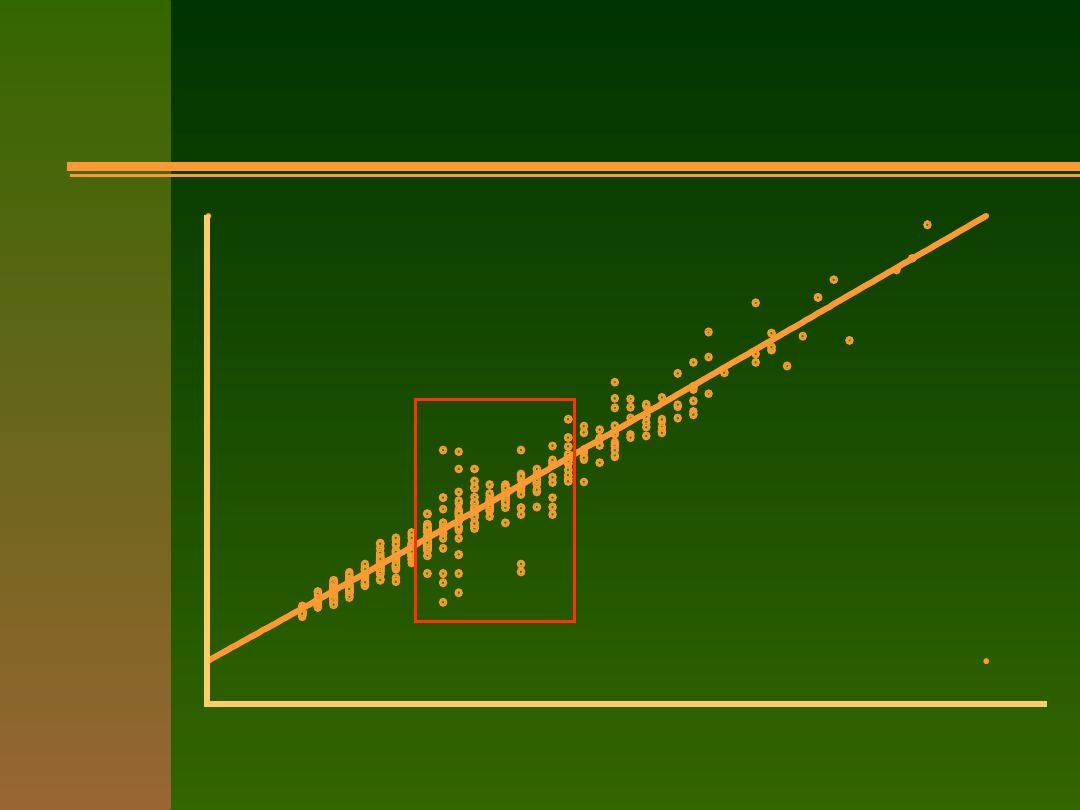
Przykład - rzetelność a zakres
pomiaru
Przykład - rzetelność a zakres
pomiaru

Przykład - analiza
rzetelności (1)
Przykład - analiza
rzetelności (1)
R E L I A B I L I T Y A N A L Y S I S
I t em- t ot al St at i st i cs
Scal e Scal e Correct ed
Mean Vari ance I t em- Al pha
i f I t em i f I t em Tot al i f I t em
Del et ed Del et ed Correl at i on Del et ed
VAR00010 83, 8901 43, 9211 - , 4012 , 4356
VAR00011 82, 8571 40, 1016 - , 0256 , 3810
VAR00012 82, 4945 39, 0305 , 0746 , 3642
VAR00014 82, 4835 35, 8747 , 3365 , 3108
VAR00015 82, 9011 35, 5790 , 3510 , 3062
VAR00030 82, 5385 35, 3402 , 4069 , 2982
VAR00032 82, 5934 34, 3995 , 5299 , 2762
Rel i abi l i t y Coeff i ci ent s
N of Cases = 91, 0 N of I t ems = 35
Al pha = , 3704

Przykład - analiza
rzetelności (2)
Przykład - analiza
rzetelności (2)
Rel i abi l i t y Coeff i ci ent s
N of I t ems = 20
Al pha = , 8390
N of I t ems = 18
Al pha = , 8277
N of I t ems = 16
Al pha = , 8371
N of I t ems = 14
Al pha = , 8423
N of I t ems = 12
Al pha = , 8357

Wzory „prorocze” Spearmana i
Browna
Wzory „prorocze” Spearmana i
Browna
Pozwalają na określenie rzetelności testu n-krotnie
wydłużonego
n - wielkość przedłużenia testu, r
tt
- rzetelność testu przed
przedłużeniem,
r
tt
n
- rzetelność testu po n-krotnym przedłużeniu
Powyższy wzór można przekształcić, aby określał krotność
przedłużenia
r
tt
n
- pożądana rzetelność testu po n-krotnym wydłużeniu, r
tt
- pierwotna
rzetelność testu
r
nr
n
r
tt
tt
tt
n
1
1
(
)
n
r
r
r
r
tt
tt
tt
tt
n
n
(
)
(
)
1
1
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
Wyszukiwarka
Podobne podstrony:
Rzetelnosc testu
Rzetelność testu
18 Badanie słuchu fonemowego z uzyciem testu sylab nagłosowychid 17648 ppt
opracowanie testu
Odpowiedzi do testu 1 poziom podstawowy id 332449
odpowiedzi do testu id 332437 Nieznany
klucz do testu II Stopień
WYKŁAD 4 Rzetelska spolki, skany szkoła, studia (pyt. o hasło)
Rozwiazanie Testu SP, ^ Turystyka i Rekreacja GWSH Katowice, 3 semestr, podstawy przedsiebiorcz
więcej podobnych podstron