
Informatyka
Informatyka
Projekt
Projekt
Dr hab. inż. Zbigniew Fąfara
Dr hab. inż. Zbigniew Fąfara
Paw. A1, parter, pok. 21
Paw. A1, parter, pok. 21

Literatura
Literatura
Dowolny podręcznik opisujący
Dowolny podręcznik opisujący
komputerową edycję tekstów za
komputerową edycję tekstów za
pomocą MS Word
pomocą MS Word
Dowolny podręcznik opisujący
Dowolny podręcznik opisujący
wykorzystanie na poziomie
wykorzystanie na poziomie
podstawowym arkusz kalkulacyjny
podstawowym arkusz kalkulacyjny
MS Excel
MS Excel

Część 1.
Część 1.
Komputerowa edycja
Komputerowa edycja
tekstów
tekstów
MS Word
MS Word

Edycja tekstów
Edycja tekstów
Podczas komputerowej edycji teksów komputer ma nam
Podczas komputerowej edycji teksów komputer ma nam
pomóc automatycznie formatując tekst, a nie
pomóc automatycznie formatując tekst, a nie
utrudnić pracę. Dlatego wprowadzając tekst należy
utrudnić pracę. Dlatego wprowadzając tekst należy
przestrzegać następujących zasad:
przestrzegać następujących zasad:
Użytkownik dzieli wprowadzany tekst na akapity
Użytkownik dzieli wprowadzany tekst na akapity
(fragmenty wyrażające jakąś myśl, oznaczające
(fragmenty wyrażające jakąś myśl, oznaczające
zamkniętą całość).
zamkniętą całość).
W przypadku krótkich akapitów, mieszczących się w
W przypadku krótkich akapitów, mieszczących się w
jednej linii, podział na akapity jest równoznaczny z
jednej linii, podział na akapity jest równoznaczny z
podziałem na wiersze.
podziałem na wiersze.
W przypadku dłuższych akapitów obejmujących
W przypadku dłuższych akapitów obejmujących
więcej niż jeden wiersz, podział na wiersze jest
więcej niż jeden wiersz, podział na wiersze jest
robiony automatycznie przez komputer. Człowiek
robiony automatycznie przez komputer. Człowiek
wprowadza jedynie tekst w całym akapicie (w jednym
wprowadza jedynie tekst w całym akapicie (w jednym
wierszu).
wierszu).

Edycja tekstów
Edycja tekstów
Znakiem końca akapitu jest znak generowany po
Znakiem końca akapitu jest znak generowany po
wciśnięciu klawisza [ENTER].
wciśnięciu klawisza [ENTER].
Akapit to fragment tekstu pomiędzy dwoma
Akapit to fragment tekstu pomiędzy dwoma
kolejnymi znakami końca akapitu.
kolejnymi znakami końca akapitu.
Nowy akapit zawsze zaczyna się w nowej linii.
Nowy akapit zawsze zaczyna się w nowej linii.
Wciśnięcie klawisza [ENTER] powoduje przejście do
Wciśnięcie klawisza [ENTER] powoduje przejście do
nowej linii, ale należy go używać tylko wtedy, gdy
nowej linii, ale należy go używać tylko wtedy, gdy
zaczynamy nowy akapit.
zaczynamy nowy akapit.
Znaki interpunkcyjne, jak: . , : ; ! ? itp. wprowadzamy
Znaki interpunkcyjne, jak: . , : ; ! ? itp. wprowadzamy
zawsze łącząc je ze słowem poprzedzającym (bez
zawsze łącząc je ze słowem poprzedzającym (bez
odstępu), a następnie wstawiamy odstęp [SPACJA] –
odstępu), a następnie wstawiamy odstęp [SPACJA] –
dzięki temu komputer nie będzie odrywał
dzięki temu komputer nie będzie odrywał
pojedynczych znaków interpunkcyjnych i zaczynał od
pojedynczych znaków interpunkcyjnych i zaczynał od
nich nowej linii.
nich nowej linii.

Edycja tekstów
Edycja tekstów
Przed nawiasem otwierającym i po nawiasie
Przed nawiasem otwierającym i po nawiasie
zamykającym wstawiamy odstęp [SPACJA].
zamykającym wstawiamy odstęp [SPACJA].
Wewnątrz nawiasu pierwsze słowo łączymy z
Wewnątrz nawiasu pierwsze słowo łączymy z
nawiasem otwierającym (bez odstępu), a ostatnie
nawiasem otwierającym (bez odstępu), a ostatnie
słowo z nawiasem zamykającym – dzięki temu
słowo z nawiasem zamykającym – dzięki temu
komputer nie będzie na końcu linii pozostawiał
komputer nie będzie na końcu linii pozostawiał
samego nawiasu otwierającego, oraz nowej linii nie
samego nawiasu otwierającego, oraz nowej linii nie
będzie zaczynał od samego nawiasu zamykającego.
będzie zaczynał od samego nawiasu zamykającego.
Podane zasady należy bezwzględnie przestrzegać – w
Podane zasady należy bezwzględnie przestrzegać – w
przeciwnym razie w tekście pojawią się błędy
przeciwnym razie w tekście pojawią się błędy
edycyjne.
edycyjne.
Po wprowadzeniu tekstu należy poprawić ewentualne
Po wprowadzeniu tekstu należy poprawić ewentualne
błędy literowe (sygnalizowane standardowo
błędy literowe (sygnalizowane standardowo
czerwonym podkreśleniem), oraz błędy gramatyczne
czerwonym podkreśleniem), oraz błędy gramatyczne
(sygnalizowane zielonym podkreśleniem).
(sygnalizowane zielonym podkreśleniem).

Edycja tekstów
Edycja tekstów
Nie wszystkie fragmenty tekstu podkreślane na czerwono
Nie wszystkie fragmenty tekstu podkreślane na czerwono
lub zielono muszą zawierać błędy. Nie wszystkie słowa
lub zielono muszą zawierać błędy. Nie wszystkie słowa
występują w słowniku ortograficznym edytora tekstu
występują w słowniku ortograficznym edytora tekstu
dla danego języka (nie ma np. nazw własnych). Takie
dla danego języka (nie ma np. nazw własnych). Takie
słowa należy pozostawić nie zmienione. Uzupełniać
słowa należy pozostawić nie zmienione. Uzupełniać
własne słowniki należy rozważnie!
własne słowniki należy rozważnie!
Po wprowadzeniu tekstu i poprawieniu błędów można
Po wprowadzeniu tekstu i poprawieniu błędów można
przystąpić do jego składania (formatowania), czyli
przystąpić do jego składania (formatowania), czyli
nadawania właściwego wyglądu.
nadawania właściwego wyglądu.
Formatowanie tekstu obejmuje:
Formatowanie tekstu obejmuje:
Formatowanie czcionek (liter, znaków) – wymaga to
Formatowanie czcionek (liter, znaków) – wymaga to
zaznaczenia odpowiedniego fragmentu tekstu i zmiany:
zaznaczenia odpowiedniego fragmentu tekstu i zmiany:
–
wielkości czcionki,
wielkości czcionki,
–
stylu czcionki,
stylu czcionki,
–
kroju czcionki
kroju czcionki

Edycja tekstów
Edycja tekstów
Wielkość czcionki ustalana jest w tzw. punktach
Wielkość czcionki ustalana jest w tzw. punktach
drukarskich. Standardowo pisze się czcionką o
drukarskich. Standardowo pisze się czcionką o
wielkości 10 lub 12 punktów. Wielkość 72 punktów
wielkości 10 lub 12 punktów. Wielkość 72 punktów
odpowiada w rzeczywistości czcionce o wysokości 1
odpowiada w rzeczywistości czcionce o wysokości 1
cala, ok. 2,5 cm (duża litera, np. A). Narzędzie do
cala, ok. 2,5 cm (duża litera, np. A). Narzędzie do
zmiany wielkości znajduje się na standardowym pasku
zmiany wielkości znajduje się na standardowym pasku
narzędziowym.
narzędziowym.
Styl czcionki to pogrubienie (Bold), pochylenie (Italic),
Styl czcionki to pogrubienie (Bold), pochylenie (Italic),
podkreślenie (Underline) i inne opcje dostępne w menu
podkreślenie (Underline) i inne opcje dostępne w menu
Format/Narzędzia_gł
Format/Narzędzia_gł
Czcionka. Style można łączyć.
Czcionka. Style można łączyć.
Krój czcionki to jej kształt – wybór z użyciem narzędzia
Krój czcionki to jej kształt – wybór z użyciem narzędzia
na standardowym pasku narzędzi. Wyróżnia się
na standardowym pasku narzędzi. Wyróżnia się
czcionki:
czcionki:
–
Nieproporcjonalne, czyli szerokość każdego znaku jest
Nieproporcjonalne, czyli szerokość każdego znaku jest
jednakowa, znaki ułożone są jakby w kolumnach tabeli, tekst
jednakowa, znaki ułożone są jakby w kolumnach tabeli, tekst
nieładnie wygląda, ponieważ zmienne są odstępy między
nieładnie wygląda, ponieważ zmienne są odstępy między
literami (przykład czcionki COURIER).
literami (przykład czcionki COURIER).

Edycja tekstów
Edycja tekstów
–
Proporcjonalne, gdzie szerokość znaku zależy od tego, jaki
Proporcjonalne, gdzie szerokość znaku zależy od tego, jaki
to znak. Takie czcionki należy wybierać, tekst ładnie
to znak. Takie czcionki należy wybierać, tekst ładnie
wygląda, stałe są odstępy między literami. Przykład: TIMES
wygląda, stałe są odstępy między literami. Przykład: TIMES
NEW ROMAN, ARIAL.
NEW ROMAN, ARIAL.
–
Z wersalikami (ozdobnikami), stanowiącymi podkreślenia
Z wersalikami (ozdobnikami), stanowiącymi podkreślenia
znaków. Przykład TIMES NEW ROMAN. Kiedyś takiej czcionki
znaków. Przykład TIMES NEW ROMAN. Kiedyś takiej czcionki
zalecano używać w dokumentach urzędowych. Podkreślenia
zalecano używać w dokumentach urzędowych. Podkreślenia
nieco zmniejszają znaki.
nieco zmniejszają znaki.
–
Bez wersalików (ozdobników). Przykład ARIAL. Kiedyś takiej
Bez wersalików (ozdobników). Przykład ARIAL. Kiedyś takiej
czcionki zalecano używać w dokumentach prywatnych.
czcionki zalecano używać w dokumentach prywatnych.
Znaki bez wersalików są nieco większe od znaków z
Znaki bez wersalików są nieco większe od znaków z
wersalikami przy identycznej liczbie punktów (np. ARIAL 10
wersalikami przy identycznej liczbie punktów (np. ARIAL 10
pkt = TIMES NEW ROMAN 12 pkt).
pkt = TIMES NEW ROMAN 12 pkt).
Formatowanie akapitu (informacja przechowywana
Formatowanie akapitu (informacja przechowywana
w znaku końca akapitu) – wystarczy być w akapicie,
w znaku końca akapitu) – wystarczy być w akapicie,
nie ma potrzeby go zaznaczać. Formatowanie to
nie ma potrzeby go zaznaczać. Formatowanie to
obejmuje:
obejmuje:

Edycja tekstów
Edycja tekstów
–
Ustalenie wcięć tekstu od prawej i lewej (liczonych od
Ustalenie wcięć tekstu od prawej i lewej (liczonych od
marginesów strony). Najprościej zrobić to za pomocą linijki:
marginesów strony). Najprościej zrobić to za pomocą linijki:
lewy górny trójkąt – wcięcie pierwszego wiersza akapitu od
lewy górny trójkąt – wcięcie pierwszego wiersza akapitu od
lewej, lewy dolny trójkąt – wcięcie pozostałych wierszy
lewej, lewy dolny trójkąt – wcięcie pozostałych wierszy
akapitu od lewej poza pierwszym, lewy dolny kwadrat –
akapitu od lewej poza pierwszym, lewy dolny kwadrat –
wcięcie wszystkich wierszy akapitu od lewej, prawy dolny
wcięcie wszystkich wierszy akapitu od lewej, prawy dolny
trójkąt – wcięcie wszystkich wierszy akapitu od prawej.
trójkąt – wcięcie wszystkich wierszy akapitu od prawej.
Można tez użyć menu: Format/Narzędzia_główne
Można tez użyć menu: Format/Narzędzia_główne
Akapit.
Akapit.
–
Ustalenie sposobu wyrównywania tekstu (za pomocą paska
Ustalenie sposobu wyrównywania tekstu (za pomocą paska
narzędziowego lub menu
narzędziowego lub menu
Format/Narzędzia_główne
Format/Narzędzia_główne
Akapit): wyrównanie do lewego
Akapit): wyrównanie do lewego
marginesu, wyrównanie do prawego marginesu, ustawienie
marginesu, wyrównanie do prawego marginesu, ustawienie
na środku, wyjustowanie (wyrównanie do obu marginesów)
na środku, wyjustowanie (wyrównanie do obu marginesów)
– komputer zwiększa odstępy między słowami.
– komputer zwiększa odstępy między słowami.
–
Ustalenie odstępów między wierszami
Ustalenie odstępów między wierszami
(Format/Narzędzia_główne
(Format/Narzędzia_główne
Akapit), standardowo 1 wiersz
Akapit), standardowo 1 wiersz
odstępu, 1,5 wiersza i 2 wiersze.
odstępu, 1,5 wiersza i 2 wiersze.

Edycja tekstów
Edycja tekstów
–
Ustalenie dodatkowych odstępów między akapitami
Ustalenie dodatkowych odstępów między akapitami
(Format/Narzędzia_główne
(Format/Narzędzia_główne
Akapit), przed akapitem i/lub po
Akapit), przed akapitem i/lub po
akapicie.
akapicie.
Formatowanie strony – zmiana w dowolnym miejscu
Formatowanie strony – zmiana w dowolnym miejscu
dokumentu powoduje automatyczną zmianę całego
dokumentu powoduje automatyczną zmianę całego
dokumentu (Plik/Układ_strony
dokumentu (Plik/Układ_strony
Ustawienia_strony) .
Ustawienia_strony) .
Formatowanie to obejmuje:
Formatowanie to obejmuje:
–
Ustalenie marginesów strony: prawy, lewy, dolny, górny.
Ustalenie marginesów strony: prawy, lewy, dolny, górny.
Standardowo są przyjmowane marginesy o szerokości 1 cala
Standardowo są przyjmowane marginesy o szerokości 1 cala
(ok. 2,5 cm). Ustalając marginesy należy zadbać, by
(ok. 2,5 cm). Ustalając marginesy należy zadbać, by
ewentualne nagłówki i stopki zmieściły się oraz trzeba wziąć
ewentualne nagłówki i stopki zmieściły się oraz trzeba wziąć
pod uwagę możliwości drukarki – marginesy drukowania).
pod uwagę możliwości drukarki – marginesy drukowania).
–
Ustalenie orientacji papieru: pionowa lub pozioma.
Ustalenie orientacji papieru: pionowa lub pozioma.
–
Ustalenie wielkości papieru: standardowo format A4.
Ustalenie wielkości papieru: standardowo format A4.
–
Dodanie nagłówków i stopek (Widok
Dodanie nagłówków i stopek (Widok
Nagłówek/Stopka).
Nagłówek/Stopka).
Standardowo dodaje się numerację stron. Można ustalić, by
Standardowo dodaje się numerację stron. Można ustalić, by
nagłówki/stopki nie pojawiały się na pierwszej stronie oraz
nagłówki/stopki nie pojawiały się na pierwszej stronie oraz
były inne na stronach parzystych, inne na stronach
były inne na stronach parzystych, inne na stronach
nieparzystych.
nieparzystych.

Edycja tekstów
Edycja tekstów
–
Ustalenie liczby kolumn, w której będzie się pojawiał tekst
Ustalenie liczby kolumn, w której będzie się pojawiał tekst
(standardowo jest jedna kolumna):
(standardowo jest jedna kolumna):
Format/Układ_strony
Format/Układ_strony
Kolumny.
Kolumny.
W przypadku, gdy chcemy, by część dokumentu
W przypadku, gdy chcemy, by część dokumentu
posiadała inne ustawienia strony, niż pozostała (np.
posiadała inne ustawienia strony, niż pozostała (np.
w dokumencie o pionowej orientacji stron wstawienie
w dokumencie o pionowej orientacji stron wstawienie
strony poziomej) należy dokument podzielić na
strony poziomej) należy dokument podzielić na
sekcje (Wstawianie/Układ_strony
sekcje (Wstawianie/Układ_strony
Znak_podziału).
Znak_podziału).
Można utworzyć nową sekcję w obrębie jednej strony
Można utworzyć nową sekcję w obrębie jednej strony
(podział ciągły) – dwie lub więcej sekcji na jednej
(podział ciągły) – dwie lub więcej sekcji na jednej
stronie, lub utworzyć nową sekcję zaczynającą się od
stronie, lub utworzyć nową sekcję zaczynającą się od
nowej strony (nowa strona). Dodatkowo nowa sekcja
nowej strony (nowa strona). Dodatkowo nowa sekcja
może się zaczynać na stronie parzystej lub
może się zaczynać na stronie parzystej lub
nieparzystej. W obrębie każdej sekcji można
nieparzystej. W obrębie każdej sekcji można
ustawiać dowolne parametry strony, niezależnie od
ustawiać dowolne parametry strony, niezależnie od
reszty dokumentu (za wyjątkiem dwóch sekcji na tej
reszty dokumentu (za wyjątkiem dwóch sekcji na tej
samej stronie).
samej stronie).

Edycja tekstów
Edycja tekstów
Łamanie (kończenie) strony, kolumny sekcji
Łamanie (kończenie) strony, kolumny sekcji
można robić wstawiając odpowiedni znak końca:
można robić wstawiając odpowiedni znak końca:
Wstawianie/Układ_strony
Wstawianie/Układ_strony
Znak_podziału. Jest on
Znak_podziału. Jest on
wyświetlany jako pojedyncza lub podwójna linia w
wyświetlany jako pojedyncza lub podwójna linia w
poprzek strony (znaki te nie są drukowane).
poprzek strony (znaki te nie są drukowane).
Wstawianie do dokumentu równań matematycznych
Wstawianie do dokumentu równań matematycznych
należy robić za pomocą polecenia:
należy robić za pomocą polecenia:
Wstawianie
Wstawianie
Obiekt
Obiekt
Microsoft_Equation_3.0.
Microsoft_Equation_3.0.
Wówczas wejdziemy do wygodnego edytora
Wówczas wejdziemy do wygodnego edytora
równań. Tworzenie równania jako tekst zasadniczy
równań. Tworzenie równania jako tekst zasadniczy
ma sens tylko w przypadku bardzo prostych
ma sens tylko w przypadku bardzo prostych
równań matematycznych, chociaż nawet wtedy
równań matematycznych, chociaż nawet wtedy
nie jest zalecane.
nie jest zalecane.

Edycja tekstów
Edycja tekstów
Dodatkowe zagadnienia wymagane na ćwiczeniach:
Dodatkowe zagadnienia wymagane na ćwiczeniach:
Tworzenie tabeli – scalanie komórek, orientacja
Tworzenie tabeli – scalanie komórek, orientacja
tekstu, ukrywanie krawędzi
tekstu, ukrywanie krawędzi
Tworzenie list wypunktowanych, numerowanych,
Tworzenie list wypunktowanych, numerowanych,
wielopoziomowych konspektów numerowanych
wielopoziomowych konspektów numerowanych
Korespondencja seryjna – tworzenie kopert i
Korespondencja seryjna – tworzenie kopert i
listów korespondencji seryjnej
listów korespondencji seryjnej
Tworzenie dokumentów obejmujących wiele sekcji
Tworzenie dokumentów obejmujących wiele sekcji
Automatyczne tworzenie spisu treści
Automatyczne tworzenie spisu treści

Edycja tekstów
Edycja tekstów
W ramach edycji tekstów należy wykonać
W ramach edycji tekstów należy wykonać
samodzielnie przygotowane ćwiczenia wraz z
samodzielnie przygotowane ćwiczenia wraz z
opisem. Pliki ćwiczeń można pobrać z serwera w
opisem. Pliki ćwiczeń można pobrać z serwera w
laboratorium komputerowym wydziału w
laboratorium komputerowym wydziału w
lokalizacji:
lokalizacji:
G:\wspolne\Fąfara\IT-EdycjaTekstów
G:\wspolne\Fąfara\IT-EdycjaTekstów
Umiejętność komputerowej edycji tekstów zostanie
Umiejętność komputerowej edycji tekstów zostanie
sprawdzona indywidualnie, w czasie kolokwium.
sprawdzona indywidualnie, w czasie kolokwium.

Koniec części 1
Koniec części 1

Część 2.
Część 2.
Komputerowy arkusz
Komputerowy arkusz
kalkulacyjny
kalkulacyjny
MS Excel
MS Excel

Arkusz kalkulacyjny
Arkusz kalkulacyjny
Przykładem bardzo popularnego arkusza kalkulacyjnego
Przykładem bardzo popularnego arkusza kalkulacyjnego
jest program MS Excel.
jest program MS Excel.
Okno programu ma postać tabeli z numerowanymi
Okno programu ma postać tabeli z numerowanymi
kolumnami (duże lub małe litery alfabetu
kolumnami (duże lub małe litery alfabetu
angielskiego, później ich kombinacje dwuliterowe,
angielskiego, później ich kombinacje dwuliterowe,
trzyliterowe itd.) i numerowanymi wierszami (liczby
trzyliterowe itd.) i numerowanymi wierszami (liczby
od 1 do wyczerpania). Każda komórka w tabeli ma
od 1 do wyczerpania). Każda komórka w tabeli ma
więc swój unikalny adres (najpierw podajemy numer
więc swój unikalny adres (najpierw podajemy numer
kolumny, potem wiersza). W opracowywanych
kolumny, potem wiersza). W opracowywanych
wyrażeniach (tzw. formułach) odwołujemy się do
wyrażeniach (tzw. formułach) odwołujemy się do
wartości liczbowych poprzez adres komórki, w której
wartości liczbowych poprzez adres komórki, w której
się znajdują (inaczej, niż w matematyce, gdzie
się znajdują (inaczej, niż w matematyce, gdzie
podajemy nazwę zmiennej). Pisanie formuły musimy
podajemy nazwę zmiennej). Pisanie formuły musimy
zacząć od znaku „=„.
zacząć od znaku „=„.

Arkusz kalkulacyjny
Arkusz kalkulacyjny
Jeżeli w jakiejś komórce mamy zapisaną formułę z
Jeżeli w jakiejś komórce mamy zapisaną formułę z
odwołaniami do innych komórek, to przy
odwołaniami do innych komórek, to przy
kopiowaniu lub przenoszeniu (przesuwaniu) formuły
kopiowaniu lub przenoszeniu (przesuwaniu) formuły
do innej komórki adresy odwołań do komórek
do innej komórki adresy odwołań do komórek
zostaną uaktualnione o tzw. wektor translacji (każdy
zostaną uaktualnione o tzw. wektor translacji (każdy
numer kolumny zostanie zwiększony/zmniejszony o
numer kolumny zostanie zwiększony/zmniejszony o
liczbę kolumn, o jaką się przesuwany; każdy numer
liczbę kolumn, o jaką się przesuwany; każdy numer
wiersza zostanie zwiększony/zmniejszony o liczbę
wiersza zostanie zwiększony/zmniejszony o liczbę
wierszy, o którą się przesuwany). Uwagi te dotyczą
wierszy, o którą się przesuwany). Uwagi te dotyczą
tylko tzw. adresów względnych. Zawsze można
tylko tzw. adresów względnych. Zawsze można
zapisać adres odwołania do wartości liczbowej w
zapisać adres odwołania do wartości liczbowej w
komórce tak, by nie ulegał on zmianie przy operacji
komórce tak, by nie ulegał on zmianie przy operacji
kopiowania lub przenoszenia.
kopiowania lub przenoszenia.
Arkusz kalkulacyjny
Arkusz kalkulacyjny
A
B
C
D
E
F
1
2
=A2+B1
3
4
5
?
6
7
8
9
10

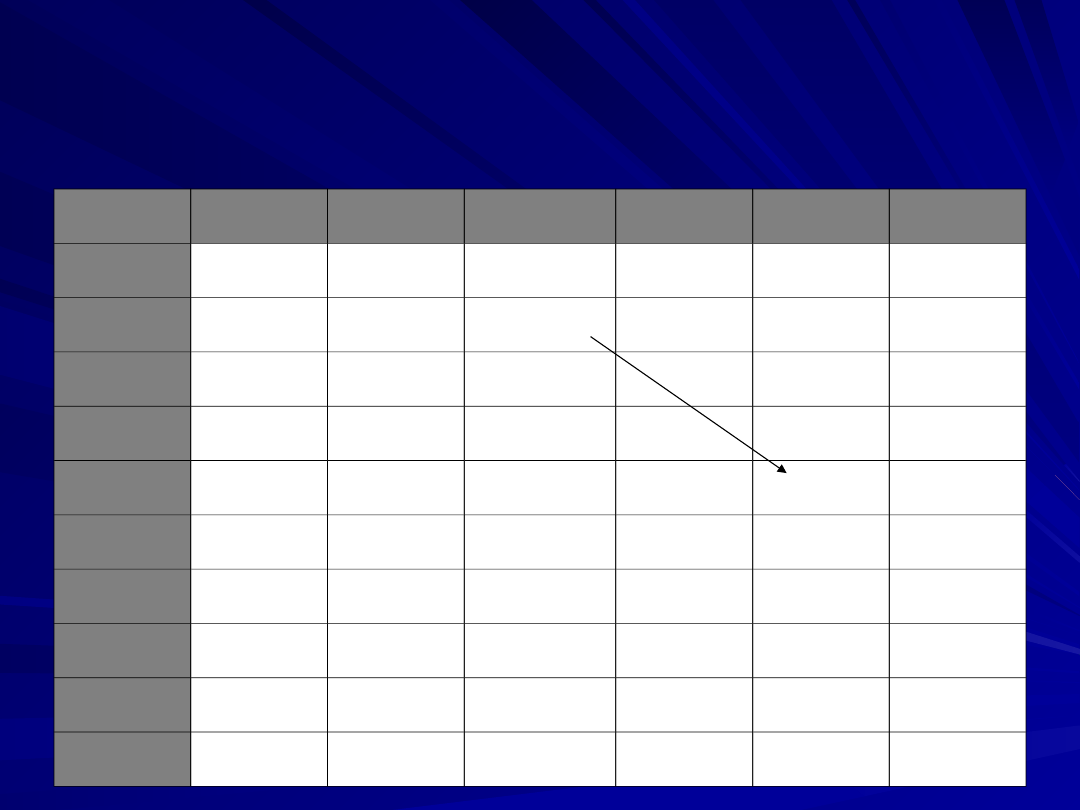
Arkusz kalkulacyjny
Arkusz kalkulacyjny
Ćwiczenie: co będzie wpisane w komórce E5, jeżeli w
Ćwiczenie: co będzie wpisane w komórce E5, jeżeli w
komórce C2 wpiszemy „=A2+B1”?
komórce C2 wpiszemy „=A2+B1”?
=B5+C4
=B5+C4
=C5+D4
=C5+D4
=B2+C1
=B2+C1
Ile wynosi wektor translacji:
Ile wynosi wektor translacji:
[+2 kolumny, +3 wiersze]
[+2 kolumny, +3 wiersze]
[+2 kolumny, +2 wiersze]
[+2 kolumny, +2 wiersze]
[+1 kolumna, +2 wiersze]
[+1 kolumna, +2 wiersze]
Jak należy zapisać formułę, by adresy się nie zmieniały:
Jak należy zapisać formułę, by adresy się nie zmieniały:
=$A2+$B1
=$A2+$B1
=$A$2+$B$1
=$A$2+$B$1
=A$2+B$1
=A$2+B$1

Arkusz kalkulacyjny
Arkusz kalkulacyjny
Rodzaje adresów:
Rodzaje adresów:
Adres względny: A2 (uaktualniany przy kopiowaniu
Adres względny: A2 (uaktualniany przy kopiowaniu
lub przenoszeniu)
lub przenoszeniu)
Adres bezwzględny: $A$2 (żadna jego część nie
Adres bezwzględny: $A$2 (żadna jego część nie
ulega zmianie przy kopiowaniu lub przenoszeniu
ulega zmianie przy kopiowaniu lub przenoszeniu
do dowolnej komórki)
do dowolnej komórki)
Adres mieszany: $A2 (nie ulega zmianie numer
Adres mieszany: $A2 (nie ulega zmianie numer
kolumny, cały adres nie będzie się zmieniał przy
kolumny, cały adres nie będzie się zmieniał przy
kopiowaniu lub przenoszeniu do innej komórki w
kopiowaniu lub przenoszeniu do innej komórki w
obrębie tego samego wiersza)
obrębie tego samego wiersza)
Adres mieszany: A$2 (nie ulega zmianie numer
Adres mieszany: A$2 (nie ulega zmianie numer
wiersza, cały adres nie będzie się zmieniał przy
wiersza, cały adres nie będzie się zmieniał przy
kopiowaniu lub przenoszeniu do innej komórki w
kopiowaniu lub przenoszeniu do innej komórki w
obrębie tej samej kolumny)
obrębie tej samej kolumny)

Arkusz kalkulacyjny
Arkusz kalkulacyjny
Dodatkowe zagadnienia wymagane na ćwiczeniach:
Dodatkowe zagadnienia wymagane na ćwiczeniach:
Porządkowanie i filtrowanie (Autofiltr) danych w
Porządkowanie i filtrowanie (Autofiltr) danych w
tabelach
tabelach
Tworzenie arkuszy wykorzystujących adresowanie
Tworzenie arkuszy wykorzystujących adresowanie
względne i bezwzględne, adresy zakresów komórek
względne i bezwzględne, adresy zakresów komórek
Robienie podsumowań (SUMA) i podsumowań
Robienie podsumowań (SUMA) i podsumowań
warunkowych (SUMA.JEŻELI)
warunkowych (SUMA.JEŻELI)
Wykorzystanie tzw. formuły tablicowej
Wykorzystanie tzw. formuły tablicowej
Wstawianie do arkusza wykresów:
Wstawianie do arkusza wykresów:
–
Wykresy kołowe
Wykresy kołowe
–
Wykresy kolumnowe
Wykresy kolumnowe
–
Wykresy liniowe (etykiety osi odciętych to wartości zmiennej x)
Wykresy liniowe (etykiety osi odciętych to wartości zmiennej x)

Arkusz kalkulacyjny
Arkusz kalkulacyjny
Robienie jednowymiarowych podsumowań – suma
Robienie jednowymiarowych podsumowań – suma
częściowa (pośrednia)
częściowa (pośrednia)
Robienie dwuwymiarowych podsumowań (tabela
Robienie dwuwymiarowych podsumowań (tabela
przestawna)
przestawna)
Formuła tablicowa – sposób na automatyczne dokonanie
Formuła tablicowa – sposób na automatyczne dokonanie
obliczeń w szeregu komórek za pomocą jednej
obliczeń w szeregu komórek za pomocą jednej
formuły, bez możliwości zmiany zawartości
formuły, bez możliwości zmiany zawartości
pojedynczej komórki:
pojedynczej komórki:
Krok 1 – zaznaczenie obszaru, w którym maja się
Krok 1 – zaznaczenie obszaru, w którym maja się
pojawić obliczone wartości
pojawić obliczone wartości
Krok 2 – wpisanie formuły z użyciem zakresów
Krok 2 – wpisanie formuły z użyciem zakresów
Krok 3 – wciśnięcie [ CTRL]-[SHIFT]-[ENTER]
Krok 3 – wciśnięcie [ CTRL]-[SHIFT]-[ENTER]

Arkusz kalkulacyjny
Arkusz kalkulacyjny
W ramach arkusza kalkulacyjnego należy wykonać
W ramach arkusza kalkulacyjnego należy wykonać
samodzielnie przygotowane ćwiczenia wraz z
samodzielnie przygotowane ćwiczenia wraz z
opisem. Pliki ćwiczeń można pobrać z serwera w
opisem. Pliki ćwiczeń można pobrać z serwera w
laboratorium komputerowym wydziału w
laboratorium komputerowym wydziału w
lokalizacji:
lokalizacji:
G:\wspolne\Fąfara\IT-Arkusz Kalkulacyjny
G:\wspolne\Fąfara\IT-Arkusz Kalkulacyjny
Umiejętność obsługi arkusza kalkulacyjnego
Umiejętność obsługi arkusza kalkulacyjnego
zostanie sprawdzona indywidualnie, w czasie
zostanie sprawdzona indywidualnie, w czasie
kolokwium.
kolokwium.

Koniec części 2
Koniec części 2

Część 3.
Część 3.
Komputerowy arkusz
Komputerowy arkusz
kalkulacyjny – ćwiczenia
kalkulacyjny – ćwiczenia
zaawansowane
zaawansowane
MS Excel
MS Excel

Instrukcje warunkowe
Instrukcje warunkowe
Projekt: Spadek
Projekt: Spadek
ciśnienia
ciśnienia

Instrukcje warunkowe
Instrukcje warunkowe
Podstawową konstrukcją przy programowaniu obliczeń
Podstawową konstrukcją przy programowaniu obliczeń
są instrukcje warunkowe, które pozwalają wybrać
są instrukcje warunkowe, które pozwalają wybrać
drogę dalszych obliczeń w zależności od wartości
drogę dalszych obliczeń w zależności od wartości
logicznej warunku. Typowa instrukcja warunkową
logicznej warunku. Typowa instrukcja warunkową
jest:
jest:
JEŻELI(Argument1;Argument2;Argument3)
JEŻELI(Argument1;Argument2;Argument3)
Argument1 – wyrażenie logiczne o wartości PRAWDA
Argument1 – wyrażenie logiczne o wartości PRAWDA
lub FAŁSZ
lub FAŁSZ
Argument2 – wartość lub wyrażenie zwracające
Argument2 – wartość lub wyrażenie zwracające
wartość przyjmowaną gdy PRAWDA
wartość przyjmowaną gdy PRAWDA
Argument3 – wartość lub wyrażenie zwracające
Argument3 – wartość lub wyrażenie zwracające
wartość przyjmowaną gdy FAŁSZ
wartość przyjmowaną gdy FAŁSZ

Instrukcje warunkowe
Instrukcje warunkowe
Wyrażenie logiczne może być dowolnym wyrażeniem
Wyrażenie logiczne może być dowolnym wyrażeniem
przyjmującym wartości logiczne. Wyrażenie to może
przyjmującym wartości logiczne. Wyrażenie to może
zawierać odwołania do komórek, operatory logiczne
zawierać odwołania do komórek, operatory logiczne
(<, <=, >, >=, =) oraz funkcje logiczne (ORAZ, LUB,
(<, <=, >, >=, =) oraz funkcje logiczne (ORAZ, LUB,
NIE).
NIE).
Jedno polecenie JEŻELI pozwala oprogramować dwie
Jedno polecenie JEŻELI pozwala oprogramować dwie
alternatywne drogi prowadzenia obliczeń. Chcąc
alternatywne drogi prowadzenia obliczeń. Chcąc
opisać więcej dróg można zagnieżdżać funkcję JEŻELI:
opisać więcej dróg można zagnieżdżać funkcję JEŻELI:
2 zagnieżdżone funkcje JEŻELI – 3 drogi
2 zagnieżdżone funkcje JEŻELI – 3 drogi
3 zagnieżdżone funkcje JEŻELI – 4 drogi
3 zagnieżdżone funkcje JEŻELI – 4 drogi
4 zagnieżdżone funkcje JEŻELI – 5 dróg
4 zagnieżdżone funkcje JEŻELI – 5 dróg
Itd.
Itd.

Instrukcje warunkowe
Instrukcje warunkowe
Funkcja ORAZ sprawdza, czy wszystkie warunki
Funkcja ORAZ sprawdza, czy wszystkie warunki
mają wartość logiczną PRAWDA. Gdy tak zwraca
mają wartość logiczną PRAWDA. Gdy tak zwraca
wartość logiczną PRAWDA, w przeciwnym razie
wartość logiczną PRAWDA, w przeciwnym razie
FAŁSZ (jest to koniunkcja warunków):
FAŁSZ (jest to koniunkcja warunków):
ORAZ(Warunek1;Warunek2;…;Warunekn)
ORAZ(Warunek1;Warunek2;…;Warunekn)
Funkcja LUB sprawdza, czy którykolwiek warunek
Funkcja LUB sprawdza, czy którykolwiek warunek
ma wartość logiczną PRAWDA. Gdy tak zwraca
ma wartość logiczną PRAWDA. Gdy tak zwraca
wartość logiczną PRAWDA, w przeciwnym razie
wartość logiczną PRAWDA, w przeciwnym razie
FAŁSZ (jest to alternatywa warunków):
FAŁSZ (jest to alternatywa warunków):
LUB(Warunek1;Warunek2;…;Warunekn)
LUB(Warunek1;Warunek2;…;Warunekn)
Funkcja NIE zamienia wartość logiczną warunku na
Funkcja NIE zamienia wartość logiczną warunku na
przeciwną
przeciwną
NIE(Warunek)
NIE(Warunek)

Instrukcje warunkowe
Instrukcje warunkowe
Przygotować arkusz kalkulacyjny obliczający straty
Przygotować arkusz kalkulacyjny obliczający straty
ciśnienia cieczy w rurociągu (spadek hydrauliczny)
ciśnienia cieczy w rurociągu (spadek hydrauliczny)
na skutek sił tarcia wewnętrznego dla przepływu
na skutek sił tarcia wewnętrznego dla przepływu
izotermicznego. Niezbędne rozważania
izotermicznego. Niezbędne rozważania
teoretyczne, równania i dane do obliczeń można
teoretyczne, równania i dane do obliczeń można
znaleźć w plikach MS Word:
znaleźć w plikach MS Word:
Ćwiczenie MS Excel – straty ciśnienia 1
Ćwiczenie MS Excel – straty ciśnienia 1
Ćwiczenie MS Excel – straty ciśnienia 2
Ćwiczenie MS Excel – straty ciśnienia 2
W pierwszym przypadku przepływ ropy odbywa się w
W pierwszym przypadku przepływ ropy odbywa się w
rurach gładkich, w drugim w rurach chropowatych.
rurach gładkich, w drugim w rurach chropowatych.
Straty ciśnienia określamy w prostoliniowych,
Straty ciśnienia określamy w prostoliniowych,
poziomych odcinkach rurociągu.
poziomych odcinkach rurociągu.

Instrukcje warunkowe
Instrukcje warunkowe
Arkusz kalkulacyjny powinien określać wartość liczby
Arkusz kalkulacyjny powinien określać wartość liczby
Reynoldsa i na jej podstawie wybierać zależność do
Reynoldsa i na jej podstawie wybierać zależność do
określenia współczynnika oporu i ostatecznie strat
określenia współczynnika oporu i ostatecznie strat
ciśnienia w rurociągu. Do obliczenia współczynnika
ciśnienia w rurociągu. Do obliczenia współczynnika
oporu należy wykorzystać zagnieżdżoną funkcję
oporu należy wykorzystać zagnieżdżoną funkcję
logiczną JEŻELI(warunek logiczny; wartość gdy
logiczną JEŻELI(warunek logiczny; wartość gdy
prawda; wartość gdy falsz) i ewentualnie funkcje
prawda; wartość gdy falsz) i ewentualnie funkcje
ORAZ i LUB.
ORAZ i LUB.
Dla przepływu w rurach gładkich mamy trzy możliwości,
Dla przepływu w rurach gładkich mamy trzy możliwości,
dlatego należy jedną z wartości funkcji JEŻELI zastąpić
dlatego należy jedną z wartości funkcji JEŻELI zastąpić
kolejną funkcją JEŻELI.
kolejną funkcją JEŻELI.
Dla przepływu w rurach chropowatych mamy cztery
Dla przepływu w rurach chropowatych mamy cztery
możliwości, ale jeden warunek na sposób obliczenia
możliwości, ale jeden warunek na sposób obliczenia
współczynnika oporu wymaga jego znajomości.
współczynnika oporu wymaga jego znajomości.
Dlatego należy dwukrotnie liczyć współczynnik oporu.
Dlatego należy dwukrotnie liczyć współczynnik oporu.

Instrukcje warunkowe
Instrukcje warunkowe
Każda osoba ma przygotować skoroszyt MS Excel z
Każda osoba ma przygotować skoroszyt MS Excel z
dwoma arkuszami obliczającymi straty ciśnienia dla rur
dwoma arkuszami obliczającymi straty ciśnienia dla rur
gładkich (pierwszy arkusz) i rur chropowatych (drugi
gładkich (pierwszy arkusz) i rur chropowatych (drugi
arkusz). W obliczeniach należy wykorzystać swoje dane
arkusz). W obliczeniach należy wykorzystać swoje dane
wejściowe przygotowane przez prowadzącego.
wejściowe przygotowane przez prowadzącego.
Arkusze należy wysłać prowadzącemu na adres e-mail:
Arkusze należy wysłać prowadzącemu na adres e-mail:
(plik MS Excel ma stanowić
(plik MS Excel ma stanowić
załącznik do wiadomości, wiadomość ma zawierać tytuł
załącznik do wiadomości, wiadomość ma zawierać tytuł
i treść z podaniem imienia i nazwiska wysyłającego).
i treść z podaniem imienia i nazwiska wysyłającego).
Powtórzymy te same obliczenia wykorzystując
Powtórzymy te same obliczenia wykorzystując
podprogram VBA.
podprogram VBA.

Regresja
Regresja
Projekt: Optymalizacja
Projekt: Optymalizacja

Regresja
Regresja
Często w zagadnieniach, które chcemy rozwiązać
Często w zagadnieniach, które chcemy rozwiązać
dysponujemy pewną liczbą punktów pomiarowych,
dysponujemy pewną liczbą punktów pomiarowych,
ale brakuje nam zależności matematycznej, która
ale brakuje nam zależności matematycznej, która
pozwoliłaby na ocenę zmiennej zależnej (y) w
pozwoliłaby na ocenę zmiennej zależnej (y) w
oparciu o znane wartości zmiennej niezależnej (x).
oparciu o znane wartości zmiennej niezależnej (x).
Wspomnianą zależność można wówczas dopasować
Wspomnianą zależność można wówczas dopasować
metodami regresyjnymi. W tym celu należy:
metodami regresyjnymi. W tym celu należy:
1.
1.
Wprowadzić znane wartości (x,y) do tabeli.
Wprowadzić znane wartości (x,y) do tabeli.
2.
2.
Zrobić wykres „liniowy” y=f(x) – należy zrobić
Zrobić wykres „liniowy” y=f(x) – należy zrobić
wykres liniowy wartości y, a następnie ustawić
wykres liniowy wartości y, a następnie ustawić
współrzędne osi kategorii X jako wartości x
współrzędne osi kategorii X jako wartości x
(standardowo MS Excel na osi poziomej będzie
(standardowo MS Excel na osi poziomej będzie
umieszczał numery kolejne punktów)
umieszczał numery kolejne punktów)

Regresja
Regresja
3.
3.
Dodać linię trendu wybierając właściwą funkcję
Dodać linię trendu wybierając właściwą funkcję
oddającą charakter zależności. Należy samemu
oddającą charakter zależności. Należy samemu
zadecydować, jaki model regresyjny wybrać,
zadecydować, jaki model regresyjny wybrać,
ewentualnie wybierać kolejno różne modele i
ewentualnie wybierać kolejno różne modele i
porównać jakość dopasowania. Do wyboru mamy:
porównać jakość dopasowania. Do wyboru mamy:
1.
1.
Model liniowy
Model liniowy
2.
2.
Model potęgowy
Model potęgowy
3.
3.
Model wykładniczy
Model wykładniczy
4.
4.
Model logarytmiczny
Model logarytmiczny
5.
5.
Model wielomianowy
Model wielomianowy
Linię trendu wstawiamy np. klikając prawym
Linię trendu wstawiamy np. klikając prawym
przyciskiem myszy na linii punktów i wybierając
przyciskiem myszy na linii punktów i wybierając
polecenie „Dodaj linie trendu”
polecenie „Dodaj linie trendu”

Regresja
Regresja
6
6
5
5
4
4
3
3
2
2
1
0
)
ln(
x
a
x
a
x
a
x
a
x
a
x
a
a
y
b
x
a
y
e
c
y
x
a
y
b
x
a
y
x
b
b

Regresja
Regresja
4.
4.
W przypadku wątpliwości, jaki model wybrać można
W przypadku wątpliwości, jaki model wybrać można
dopasować linie trendu dla różnych modeli. W celu
dopasować linie trendu dla różnych modeli. W celu
sprawdzenia jakości dopasowania każdego z nich
sprawdzenia jakości dopasowania każdego z nich
można ustawić wyświetlanie współczynnika
można ustawić wyświetlanie współczynnika
determinacji (R
determinacji (R
2
2
) – im wyższa wartość współczynnika
) – im wyższa wartość współczynnika
determinacji, tym dopasowanie lepsze.
determinacji, tym dopasowanie lepsze.
Współczynnik determinacji wyświetlamy klikając
Współczynnik determinacji wyświetlamy klikając
prawym przyciskiem na linii trendu (lub dwa razy
prawym przyciskiem na linii trendu (lub dwa razy
klik na linii trendu), wybieramy polecenie „Formatuj
klik na linii trendu), wybieramy polecenie „Formatuj
linię trendu” i ustawiamy „Wyświetl wartości R-
linię trendu” i ustawiamy „Wyświetl wartości R-
kwadrat na wykresie” w zakładce „Opcje”.
kwadrat na wykresie” w zakładce „Opcje”.
5.
5.
Istnieją jeszcze inne możliwości statystycznej oceny
Istnieją jeszcze inne możliwości statystycznej oceny
jakości dopasowania linii trendu, ale tutaj je
jakości dopasowania linii trendu, ale tutaj je
pominiemy (będą omówione na przedmiocie
pominiemy (będą omówione na przedmiocie
Statystyka).
Statystyka).

Regresja
Regresja
6.
6.
Znalezienie równania linii trendu – wydać
Znalezienie równania linii trendu – wydać
polecenie „Formatuj linię trendu” (patrz punkty
polecenie „Formatuj linię trendu” (patrz punkty
poprzednie) i ustawić opcję „Wyświetl równanie
poprzednie) i ustawić opcję „Wyświetl równanie
na wykresie”
na wykresie”
7.
7.
Odpisujemy tak otrzymane równanie regresji i
Odpisujemy tak otrzymane równanie regresji i
wykorzystujemy w dalszych obliczeniach.
wykorzystujemy w dalszych obliczeniach.

Solver
Solver
Inną metodę dopasowania krzywej do punktów
Inną metodę dopasowania krzywej do punktów
pomiarowych oferuje dodatek Solver. W tym
pomiarowych oferuje dodatek Solver. W tym
przypadku można dopasować krzywą dowolnej
przypadku można dopasować krzywą dowolnej
postaci, nie ograniczając się do ustalonych z góry
postaci, nie ograniczając się do ustalonych z góry
modeli. Konieczna jest tylko umiejętność zapisania
modeli. Konieczna jest tylko umiejętność zapisania
postaci szukanego modelu.
postaci szukanego modelu.
Dodatek Solver można znaleźć w Narzędzia/Solver.
Dodatek Solver można znaleźć w Narzędzia/Solver.
Jeżeli nie będzie tam widoczny należy dodać Solver
Jeżeli nie będzie tam widoczny należy dodać Solver
do narzędzi. W tym celu należy wybrać
do narzędzi. W tym celu należy wybrać
Narzędzia/Dodatki i zaznaczyć opcję Solver. Od
Narzędzia/Dodatki i zaznaczyć opcję Solver. Od
tego momentu będzie już widoczny w Narzędziach.
tego momentu będzie już widoczny w Narzędziach.
W celu wykorzystania dodatku Solver należy
W celu wykorzystania dodatku Solver należy
odpowiednio przygotować arkusz programu Excel:
odpowiednio przygotować arkusz programu Excel:
1.
1.
Kopiujemy dane (x,y), do których chcemy
Kopiujemy dane (x,y), do których chcemy
dopasować krzywą w wolne miejsce arkusza, jako
dopasować krzywą w wolne miejsce arkusza, jako
tabelę.
tabelę.

Solver
Solver
2.
2.
Mamy tabelę zawierającą dwie pierwsze kolumny z
Mamy tabelę zawierającą dwie pierwsze kolumny z
wartościami x i y. Trzecią kolumną będzie
wartościami x i y. Trzecią kolumną będzie
y_obliczone na podstawie zaproponowanej postaci
y_obliczone na podstawie zaproponowanej postaci
modelu.
modelu.
3.
3.
Musimy zadać wartości początkowe współczynników
Musimy zadać wartości początkowe współczynników
modelu gdzieś z boku na wolnym polu. Solver
modelu gdzieś z boku na wolnym polu. Solver
będzie je zmieniał w celu uzyskania najlepszego
będzie je zmieniał w celu uzyskania najlepszego
dopasowania. Generalnie rozwiązanie nie powinno
dopasowania. Generalnie rozwiązanie nie powinno
zależeć od zadanych wartości początkowych.
zależeć od zadanych wartości początkowych.
4.
4.
Obliczamy trzecią kolumnę tabeli na podstawie
Obliczamy trzecią kolumnę tabeli na podstawie
proponowanego modelu z odwołaniami do wartości
proponowanego modelu z odwołaniami do wartości
początkowych współczynników modelu.
początkowych współczynników modelu.
5.
5.
Najprościej optymalizację wykonać minimalizując
Najprościej optymalizację wykonać minimalizując
sumę kwadratów różnic y – y_obliczone.
sumę kwadratów różnic y – y_obliczone.

Solver
Solver
6.
6.
Tworzymy czwartą kolumnę tabeli z wartościami
Tworzymy czwartą kolumnę tabeli z wartościami
różnic.
różnic.
7.
7.
W komórce poniżej ostatniej wartości czwartej
W komórce poniżej ostatniej wartości czwartej
kolumny znajdujemy sumę kwadratów przy
kolumny znajdujemy sumę kwadratów przy
pomocy funkcji standardowej MS Excel:
pomocy funkcji standardowej MS Excel:
SUMA.KWADRATÓW(zakres komórek)
SUMA.KWADRATÓW(zakres komórek)
8.
8.
Uruchamiamy dodatek Solver. W oknie Solver-
Uruchamiamy dodatek Solver. W oknie Solver-
Parametry ustawiamy:
Parametry ustawiamy:
1.
1.
Komórka celu – adres komórki z sumą kwadratów różnic
Komórka celu – adres komórki z sumą kwadratów różnic
2.
2.
Równa – Min (minimum sumy kwadratów reszt)
Równa – Min (minimum sumy kwadratów reszt)
3.
3.
Komórki zmieniane – adresy wartości współczynników
Komórki zmieniane – adresy wartości współczynników
4.
4.
Warunki ograniczające – ewentualnie
Warunki ograniczające – ewentualnie

Solver
Solver
9.
9.
Naciskamy przycisk ROZWIĄŻ – Solver w drodze
Naciskamy przycisk ROZWIĄŻ – Solver w drodze
kolejnych iteracji dopasuje wartości współczynników
kolejnych iteracji dopasuje wartości współczynników
modelu w celu osiągnięcia najlepszego rozwiązania
modelu w celu osiągnięcia najlepszego rozwiązania
10.
10.
W oknie dodatku Solver możemy też wybrać
W oknie dodatku Solver możemy też wybrać
wcześniej przycisk OPCJE i zmienić jego ustawienia:
wcześniej przycisk OPCJE i zmienić jego ustawienia:
1.
1.
Narzucić model liniowy rozwiązania
Narzucić model liniowy rozwiązania
2.
2.
Zmienić dokładność obliczeń i ich tolerancję
Zmienić dokładność obliczeń i ich tolerancję
3.
3.
Zmienić maksymalny czas obliczeń
Zmienić maksymalny czas obliczeń
4.
4.
Zmienić maksymalną liczbę iteracji
Zmienić maksymalną liczbę iteracji
5.
5.
Zmienić inne ustawienia
Zmienić inne ustawienia
W celu sprawdzenia jakości dopasowania dodamy obok
W celu sprawdzenia jakości dopasowania dodamy obok
w wolnym polu wartość współczynnika korelacji
w wolnym polu wartość współczynnika korelacji
(Funkcja Statystyczna WSP.KORELACJI) i
(Funkcja Statystyczna WSP.KORELACJI) i
współczynnika determinacji (Funkcja Statystyczna
współczynnika determinacji (Funkcja Statystyczna
R.KWADRAT).
R.KWADRAT).

Solver
Solver
Argumentami tych funkcji statystycznych mają być:
Argumentami tych funkcji statystycznych mają być:
y i y_obliczone.
y i y_obliczone.
Należy powtórzyć w osobnym arkuszu tego samego
Należy powtórzyć w osobnym arkuszu tego samego
skoroszytu procedurę dopasowania krzywych
skoroszytu procedurę dopasowania krzywych
regresji do dostarczonych danych z
regresji do dostarczonych danych z
wykorzystaniem dodatku Solver i porównać
wykorzystaniem dodatku Solver i porównać
uzyskane wyniki.
uzyskane wyniki.

Funkcja złożona
Funkcja złożona
Projekt: Optymalizacja
Projekt: Optymalizacja

Funkcja złożona
Funkcja złożona
Omówioną poprzednio metodą dopasowujemy równania
Omówioną poprzednio metodą dopasowujemy równania
regresji:
regresji:
y = f1(x)
y = f1(x)
y = f2(x)
y = f2(x)
dla dwóch niezależnych populacji danych (x,y).
dla dwóch niezależnych populacji danych (x,y).
Interesująca nas funkcja będzie sumą znalezionych
Interesująca nas funkcja będzie sumą znalezionych
funkcji. Będziemy szukać ekstremum
funkcji. Będziemy szukać ekstremum
(minimum/maksimum) sumy funkcji: f = f1 + f2.
(minimum/maksimum) sumy funkcji: f = f1 + f2.
W tym celu tworzymy tabelę o czterech kolumnach:
W tym celu tworzymy tabelę o czterech kolumnach:
Kolumna 1 – wartości x
Kolumna 1 – wartości x
Kolumna 2 – y = f1(x) liczone według równania regresji
Kolumna 2 – y = f1(x) liczone według równania regresji
Kolumna 3 – y = f2(x) liczone według równania regresji
Kolumna 3 – y = f2(x) liczone według równania regresji
Kolumna 4 – suma f1(x) + f2(x)
Kolumna 4 – suma f1(x) + f2(x)

Badanie przebiegu
Badanie przebiegu
funkcji
funkcji
Projekt: Optymalizacja
Projekt: Optymalizacja

Optymalizacja
Optymalizacja
Optymalizacja polega na takim doborze wartości
Optymalizacja polega na takim doborze wartości
parametrów, by uzyskane rozwiązanie było
parametrów, by uzyskane rozwiązanie było
najkorzystniejsze z jakiegoś powodu. Rozwiązanie
najkorzystniejsze z jakiegoś powodu. Rozwiązanie
zagadnienia optymalizacyjnego zwykle polega na
zagadnienia optymalizacyjnego zwykle polega na
zdefiniowaniu tzw. funkcji celu i znalezieniu wartości
zdefiniowaniu tzw. funkcji celu i znalezieniu wartości
jej parametrów tak, by:
jej parametrów tak, by:
Wartość funkcji celu osiągała lokalne ekstremum
Wartość funkcji celu osiągała lokalne ekstremum
(minimum lub maksimum)
(minimum lub maksimum)
Wartość funkcji celu mieściła się w pewnym przedziale
Wartość funkcji celu mieściła się w pewnym przedziale
Zagadnienie optymalizacji zostanie omówione na
Zagadnienie optymalizacji zostanie omówione na
najprostszym z możliwych przykładów – funkcja celu
najprostszym z możliwych przykładów – funkcja celu
jest funkcją jednej zmiennej. Poszukujemy wartości
jest funkcją jednej zmiennej. Poszukujemy wartości
argumentu, dla którego funkcja celu osiąga minimum.
argumentu, dla którego funkcja celu osiąga minimum.

Optymalizacja
Optymalizacja
Poszukujemy takiej średnicy rurociągu transportującego
Poszukujemy takiej średnicy rurociągu transportującego
ropę naftową, by koszty budowy i eksploatacji rurociągu
ropę naftową, by koszty budowy i eksploatacji rurociągu
były najmniejsze. Całkowite koszty rurociągu obejmują:
były najmniejsze. Całkowite koszty rurociągu obejmują:
Koszty budowy rurociągu rosnące wraz ze wzrostem
Koszty budowy rurociągu rosnące wraz ze wzrostem
średnicy rurociągu (rośnie ilość materiałów)
średnicy rurociągu (rośnie ilość materiałów)
Koszty eksploatacji rurociągu malejące wraz ze
Koszty eksploatacji rurociągu malejące wraz ze
wzrostem średnicy rurociągu (maleją opory ruchu
wzrostem średnicy rurociągu (maleją opory ruchu
cieczy)
cieczy)
Funkcja celu będąca suma powyższych kosztów posiada
Funkcja celu będąca suma powyższych kosztów posiada
minimum dla warunków najbardziej optymalnych.
minimum dla warunków najbardziej optymalnych.
Ograniczeniem jest minimalna średnica rurociągu
Ograniczeniem jest minimalna średnica rurociągu
wynikająca z założonego minimalnego wydatku
wynikająca z założonego minimalnego wydatku
objętościowego oraz maksymalnej prędkości tłoczenia
objętościowego oraz maksymalnej prędkości tłoczenia
ropy.
ropy.
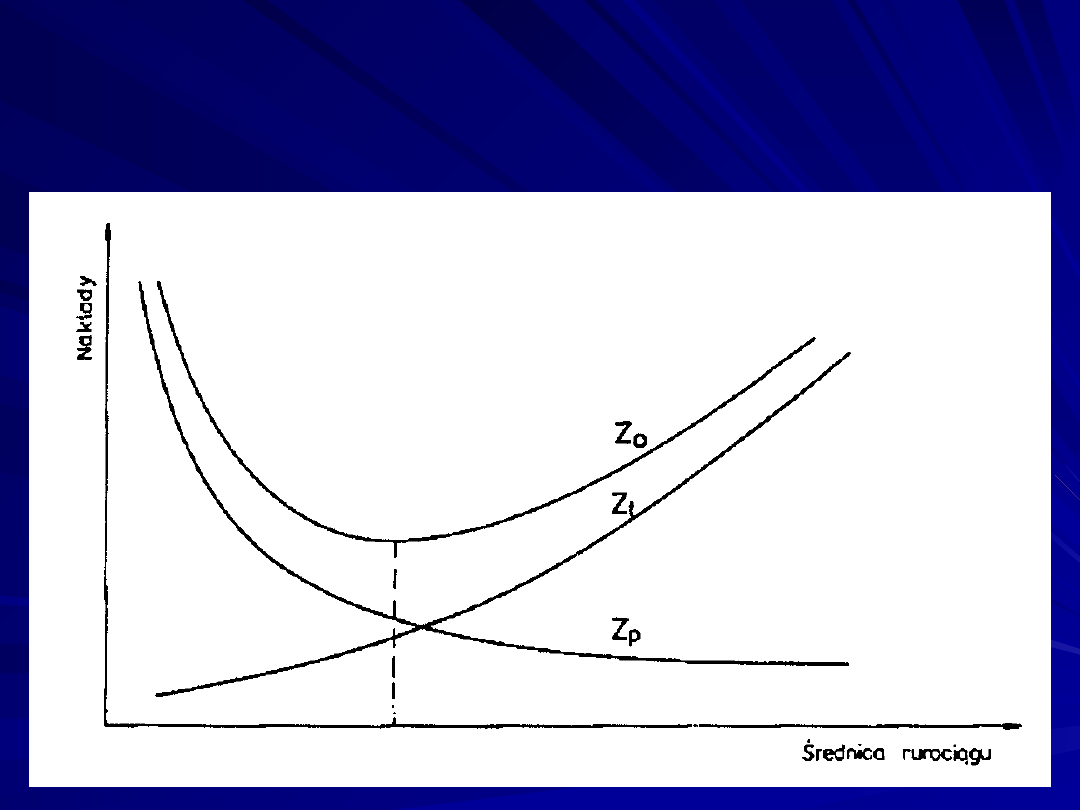
Rys. Nakłady na budowę rurociągu (rury i stacja
Rys. Nakłady na budowę rurociągu (rury i stacja
pomp). Dobór średnicy rurociągu ekonomicznie
pomp). Dobór średnicy rurociągu ekonomicznie
uzasadnionej.
uzasadnionej.

Optymalizacja
Optymalizacja
Znajdowanie wartości minimalnej funkcji celu F = f1 + f2:
Znajdowanie wartości minimalnej funkcji celu F = f1 + f2:
Najprostsza metoda polegać będzie na wygenerowaniu
Najprostsza metoda polegać będzie na wygenerowaniu
dyskretnych wartości funkcji celu (dla ciągu wartości
dyskretnych wartości funkcji celu (dla ciągu wartości
średnic wewnętrznych rur), co już zostało zrobione i
średnic wewnętrznych rur), co już zostało zrobione i
odszukaniu wartości najmniejszej (dodatkowo należy
odszukaniu wartości najmniejszej (dodatkowo należy
sprawdzić warunek ograniczający). W poszukiwaniu
sprawdzić warunek ograniczający). W poszukiwaniu
minimum można sobie też pomóc standardową funkcją:
minimum można sobie też pomóc standardową funkcją:
MIN(zakres komórek), która zwraca najmniejsza wartość
MIN(zakres komórek), która zwraca najmniejsza wartość
w zbiorze. Dla wartości minimalnej funkcji celu
w zbiorze. Dla wartości minimalnej funkcji celu
odczytujemy wartość argumentu – średnicy rurociągu.
odczytujemy wartość argumentu – średnicy rurociągu.
Nieco dokładniejsze rozwiązanie dostaniemy robiąc
Nieco dokładniejsze rozwiązanie dostaniemy robiąc
liniowy wykres funkcji celu i odczytując z niego wartość
liniowy wykres funkcji celu i odczytując z niego wartość
argumentu dla minimum funkcji.
argumentu dla minimum funkcji.

Optymalizacja
Optymalizacja
Najdokładniejsze rozwiązanie dostaniemy
Najdokładniejsze rozwiązanie dostaniemy
korzystając z dodatku Solver:
korzystając z dodatku Solver:
1.
1.
W dowolnej komórce arkusza wpisujemy
W dowolnej komórce arkusza wpisujemy
początkową wartość średnicy rur,
początkową wartość średnicy rur,
wykorzystywaną w obliczeniach
wykorzystywaną w obliczeniach
2.
2.
W innej komórce wprowadzamy warunek
W innej komórce wprowadzamy warunek
ograniczający – minimalną dopuszczalną
ograniczający – minimalną dopuszczalną
średnicę rurociągu
średnicę rurociągu
3.
3.
W jeszcze innej komórce wpisujemy formułę
W jeszcze innej komórce wpisujemy formułę
na obliczanie wartości funkcji (suma równań
na obliczanie wartości funkcji (suma równań
dopasowanych poprzednio), gdzie
dopasowanych poprzednio), gdzie
argumentem jest adres komórki z wartością
argumentem jest adres komórki z wartością
średnicy podana w punkcie 1
średnicy podana w punkcie 1
4.
4.
Uruchamiamy dodatek Solver
Uruchamiamy dodatek Solver

Optymalizacja
Optymalizacja
W oknie dodatku Solver wprowadzamy:
W oknie dodatku Solver wprowadzamy:
Komórka celu – komórka z wartością funkcji celu
Komórka celu – komórka z wartością funkcji celu
Równa – Min (minimum funkcji celu)
Równa – Min (minimum funkcji celu)
Komórki zmieniane – komórka z wartością
Komórki zmieniane – komórka z wartością
początkową średnicy rurociągu
początkową średnicy rurociągu
Warunki ograniczające – komórka z wartością
Warunki ograniczające – komórka z wartością
średnicy ma być nie mniejsza od wartości
średnicy ma być nie mniejsza od wartości
minimalnej
minimalnej
Rozwiąż – uruchamiamy obliczenia
Rozwiąż – uruchamiamy obliczenia
Szukana optymalna wartość średnicy rurociągu
Szukana optymalna wartość średnicy rurociągu
zastąpi jej początkową wartość.
zastąpi jej początkową wartość.

Całkowanie
Całkowanie
numeryczne
numeryczne
Projekt
Projekt

Całkowanie numeryczne
Całkowanie numeryczne
Do znajdowania całek oznaczonych opracowano
Do znajdowania całek oznaczonych opracowano
wiele metod numerycznych. Najprostszą z nich
wiele metod numerycznych. Najprostszą z nich
jest metoda trapezów (chociaż nie jest
jest metoda trapezów (chociaż nie jest
najdokładniejsza). Do zastosowania tej metody w
najdokładniejsza). Do zastosowania tej metody w
MS Excel musimy dysponować ciągiem wartości
MS Excel musimy dysponować ciągiem wartości
(x,y), gdzie wartości x muszą się zmieniać o stały
(x,y), gdzie wartości x muszą się zmieniać o stały
krok (jeżeli dysponujemy równaniem y = f(x)
krok (jeżeli dysponujemy równaniem y = f(x)
zawsze można wygenerować taki ciąg wartości).
zawsze można wygenerować taki ciąg wartości).
Jeżeli s jest krokiem, o jaki zmieniają się wartości x,
Jeżeli s jest krokiem, o jaki zmieniają się wartości x,
to skrajne trapezy odpowiadające pierwszemu i
to skrajne trapezy odpowiadające pierwszemu i
ostatniemu punktowi mają połowę szerokości s
ostatniemu punktowi mają połowę szerokości s
(skrajnym trapezom przyporządkowujemy
(skrajnym trapezom przyporządkowujemy
współczynnik 0,5, natomiast pozostałym 1).
współczynnik 0,5, natomiast pozostałym 1).
Wysokość każdego trapezu odpowiada wartości y.
Wysokość każdego trapezu odpowiada wartości y.

Całkowanie numeryczne
Całkowanie numeryczne
W celu określenia całki oznaczonej funkcji metodą
W celu określenia całki oznaczonej funkcji metodą
numeryczna trapezów należy:
numeryczna trapezów należy:
Utworzyć tabelę z kolumną x (wartości z określonym
Utworzyć tabelę z kolumną x (wartości z określonym
krokiem od dolnej do górnej granicy całkowania) i
krokiem od dolnej do górnej granicy całkowania) i
odpowiadającymi im wartościami y. W trzeciej
odpowiadającymi im wartościami y. W trzeciej
kolumnie podajemy wartości współczynników: skrajne
kolumnie podajemy wartości współczynników: skrajne
równe 0,5, pozostałe równe 1.
równe 0,5, pozostałe równe 1.
W dowolnej pustej komórce podajemy krok całkowania
W dowolnej pustej komórce podajemy krok całkowania
(różnica pomiędzy kolejnymi wartościami x).
(różnica pomiędzy kolejnymi wartościami x).
W innej pustej komórce wpisujemy formułę do
W innej pustej komórce wpisujemy formułę do
wyliczenia całki:
wyliczenia całki:
s*SUMA.ILOCZYNÓW(zakres_y;zakres_współcz)
s*SUMA.ILOCZYNÓW(zakres_y;zakres_współcz)
MS Excel w tej komórce poda wartość całki
MS Excel w tej komórce poda wartość całki

Całkowanie numeryczne
Całkowanie numeryczne
Dokładniejsza metodą całkowania jest metoda
Dokładniejsza metodą całkowania jest metoda
Simpsona (górna krawędź figury nie jest linią
Simpsona (górna krawędź figury nie jest linią
prostą, jak w metodzie trapezów, ale krzywą
prostą, jak w metodzie trapezów, ale krzywą
drugiego rzędu). Współczynniki tym razem są
drugiego rzędu). Współczynniki tym razem są
następujące:
następujące:
Pierwszy i ostatni zawsze równy 1
Pierwszy i ostatni zawsze równy 1
Drugi i przedostatni zawsze równe 4
Drugi i przedostatni zawsze równe 4
Pozostałe zmieniają się regularnie: 2,4,2,4,2 …
Pozostałe zmieniają się regularnie: 2,4,2,4,2 …
Wzór ogólny na wartość całki oznaczonej jest
Wzór ogólny na wartość całki oznaczonej jest
następujący:
następujący:
(s/3)*SUMA.ILOCZYNÓW(zakres_y;zakres_współcz)
(s/3)*SUMA.ILOCZYNÓW(zakres_y;zakres_współcz)

Całkowanie numeryczne
Całkowanie numeryczne
W ćwiczeniu należy obliczyć zadane przez
W ćwiczeniu należy obliczyć zadane przez
prowadzącego całki oznaczone metodą trapezów i
prowadzącego całki oznaczone metodą trapezów i
metodą Simpsona dobierając trzy różne
metodą Simpsona dobierając trzy różne
szerokości kroku całkowania.
szerokości kroku całkowania.

Koniec części 3
Koniec części 3
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
- Slide 53
- Slide 54
- Slide 55
- Slide 56
- Slide 57
- Slide 58
- Slide 59
- Slide 60
Wyszukiwarka
Podobne podstrony:
Konspekt projektu I część 2013
Informacje uzupełniające Projektowanie elementów oporowych przenoszących siłę poziomą w stopach słup
KSPD projekt część opisowa
Pytania kontrolne z Informatyki INiG 13 Fąfara
informacje do projektu
Zestaw D Zarządznie?nymi infomacyjnymi?zy?nych Systemy informatyczne Zarządznie Projektami (2)
Informatyczne Podstawy Projektowania sprawozdanie
KSPD Projekt Część opisowa i rysunkowa
informacje do projektu MJSSF5RGNVGADFO6P5FI53XZQJPKQ5HSFLCTVVA
SN024a Informacje uzupelniajace Projekt wstepny zakladkowego styku srubowego trzonu slupa
PROJEKT czesc opisowa
Projekt czesc 1
TI sprawozdanie cw 2, studia, sem 5, Lab. Technologia informacyjna w elektroenergetyce, projekt
więcej podobnych podstron