
Identyfikacja nadmiaru w
Identyfikacja nadmiaru w
trakcie dodawania i
trakcie dodawania i
odejmowania (1)
odejmowania (1)
algorytmy dodawania i odejmowania liczb
kodowanych w systemie U2 są takie same jak dla
liczb bez znaku (tj. liczb kodowanych w
naturalnym kodzie binarnym)
z tego powodu rozkaz dodawania ADD może
służyć zarówno do dodawania liczb bez znaku, jak
i do dodawania liczb ze znakiem w kodzie U2;
również rozkaz odejmowania SUB może
wykonywać działania na obu typach liczb
jednak dla obu typów inaczej określone są
warunki powstania nadmiaru – ilustruje to
przykład

Identyfikacja nadmiaru w
Identyfikacja nadmiaru w
trakcie dodawania i
trakcie dodawania i
odejmowania (2)
odejmowania (2)
za pomocą rozkazu ADD zostały dodane dwie
liczby binarne — liczba podana w nawiasie
wpisywana jest do znacznika CF i stanowi wartość
przeniesienia, które wystąpiło w trakcie
dodawania najstarszych bitów obu liczb
0 0 1 1 1 0 0 1
0 0 1 1 1 0 0 1
1 1 1 1 1 1 1 1
1 1 1 1 1 1 1 1
---------------
---------------
(1)
(1)
0 0 1 1 1 0 0 0
0 0 1 1 1 0 0 0

Identyfikacja nadmiaru w
Identyfikacja nadmiaru w
trakcie dodawania i
trakcie dodawania i
odejmowania (3)
odejmowania (3)
czy uzyskany wynik dodawania jest poprawny?
czy uzyskany wynik dodawania jest poprawny?
udzielenie odpowiedzi na to pytanie jest możliwe
udzielenie odpowiedzi na to pytanie jest możliwe
tylko wówczas, gdy znamy typy dodawanych liczb
tylko wówczas, gdy znamy typy dodawanych liczb
jeśli przyjąć, że sumowanie wykonywane na
jeśli przyjąć, że sumowanie wykonywane na
liczbach w kodzie U2, tzn. wykonano obliczenie
liczbach w kodzie U2, tzn. wykonano obliczenie
57+(–1)=56, to wynik jest poprawny
57+(–1)=56, to wynik jest poprawny
jeśli jednak sumowane liczby interpretowano jako
jeśli jednak sumowane liczby interpretowano jako
liczby bez znaku, tzn. wykonano dodawanie
liczby bez znaku, tzn. wykonano dodawanie
57+255=312, to wynik (=56) jest niepoprawny —
57+255=312, to wynik (=56) jest niepoprawny —
w tym przypadku uzyskany wynik (312) nie mógł
w tym przypadku uzyskany wynik (312) nie mógł
być zapisany na 8 bitach, wskutek czego
być zapisany na 8 bitach, wskutek czego
wystąpiło przepełnienie
wystąpiło przepełnienie

Identyfikacja nadmiaru w
Identyfikacja nadmiaru w
trakcie dodawania i
trakcie dodawania i
odejmowania (4)
odejmowania (4)
w przypadku dodawania liczb bez znaku
w przypadku dodawania liczb bez znaku
ustawienie znacznika CF w stan 1 oznacza
ustawienie znacznika CF w stan 1 oznacza
wystąpienie przeniesienia, co w podanym
wystąpienie przeniesienia, co w podanym
przykładzie interpretujemy jako nadmiar, a co z
przykładzie interpretujemy jako nadmiar, a co z
tym idzie niepoprawny wynik dodawania
tym idzie niepoprawny wynik dodawania
przeniesienie to nie ma jednak wpływu na
przeniesienie to nie ma jednak wpływu na
poprawność wyniku, jeśli liczby interpretowane są
poprawność wyniku, jeśli liczby interpretowane są
jako liczby ze znakiem w kodzie U2
jako liczby ze znakiem w kodzie U2
na podstawie analizy podanego przykładu można
na podstawie analizy podanego przykładu można
stwierdzić, że identyfikacja nadmiaru powinna być
stwierdzić, że identyfikacja nadmiaru powinna być
prowadzona oddzielnie dla liczb ze znakiem (w
prowadzona oddzielnie dla liczb ze znakiem (w
kodzie U2) i dla liczb bez znaku
kodzie U2) i dla liczb bez znaku

Znaczniki CF i OF (1)
Znaczniki CF i OF (1)
w trakcie wykonywania rozkazu dodawania ADD procesor
w trakcie wykonywania rozkazu dodawania ADD procesor
nie posiada żadnych informacji czy dodawane liczby
nie posiada żadnych informacji czy dodawane liczby
zakodowane są jako liczby bez znaku czy też jako liczby
zakodowane są jako liczby bez znaku czy też jako liczby
w kodzie U2 — informacje takie posiada jedynie autor
w kodzie U2 — informacje takie posiada jedynie autor
programu (czy kompilatora, który wytworzył te rozkazy)
programu (czy kompilatora, który wytworzył te rozkazy)
w tej sytuacji procesor udziela informacji o nadmiarze za
w tej sytuacji procesor udziela informacji o nadmiarze za
pomocą dwóch znaczników:
pomocą dwóch znaczników:
•
CF (ang. carry flag) — dla przypadku, gdy dodawano liczby bez
CF (ang. carry flag) — dla przypadku, gdy dodawano liczby bez
znaku
znaku
•
OF (ang. overflow flag) — dla przypadku, gdy dodawano liczby w
OF (ang. overflow flag) — dla przypadku, gdy dodawano liczby w
kodzie U2
kodzie U2

Znaczniki CF i OF (2)
Znaczniki CF i OF (2)
w dalszej kolejności, w zależności od typu
w dalszej kolejności, w zależności od typu
dodawanych liczb programista testuje znacznik
dodawanych liczb programista testuje znacznik
CF albo OF (do testowania można zastosować
CF albo OF (do testowania można zastosować
rozkazy jc, jnc albo jo, jno)
rozkazy jc, jnc albo jo, jno)
procesor ustawia znacznik CF na podstawie
procesor ustawia znacznik CF na podstawie
wartości przeniesienia, które powstaje przy
wartości przeniesienia, które powstaje przy
dodawaniu najstarszych bitów obu liczb
dodawaniu najstarszych bitów obu liczb
procesor ustawia znacznik OF na podstawie
procesor ustawia znacznik OF na podstawie
wartości wyrażenia p
wartości wyrażenia p
n
n
p
p
n–1
n–1
, gdzie p
, gdzie p
n–1
n–1
i p
i p
n
n
oznaczają przeniesienia występujące podczas
oznaczają przeniesienia występujące podczas
dodawania dwóch najbardziej znaczących bitów
dodawania dwóch najbardziej znaczących bitów

Nadmiar przy operacjach
Nadmiar przy operacjach
mnożenia i dzielenia (1)
mnożenia i dzielenia (1)
w typowych operacjach mnożenia (np. MUL,
w typowych operacjach mnożenia (np. MUL,
IMUL), mnożna i mnożnik zajmują jednakową
IMUL), mnożna i mnożnik zajmują jednakową
liczbę bitów, a iloczyn umieszczany jest w
liczbę bitów, a iloczyn umieszczany jest w
rejestrze dwukrotnie dłuższym (zazwyczaj
rejestrze dwukrotnie dłuższym (zazwyczaj
stanowiącym złożenie dwóch rejestrów, np.
stanowiącym złożenie dwóch rejestrów, np.
EDX:EAX) — w tej sytuacji nadmiar nigdy nie
EDX:EAX) — w tej sytuacji nadmiar nigdy nie
wystąpi
wystąpi
w typowych operacjach dzielenia (np. DIV, IDIV)
w typowych operacjach dzielenia (np. DIV, IDIV)
dzielna jest dwukrotnie dłuższa od dzielnika, a
dzielna jest dwukrotnie dłuższa od dzielnika, a
iloraz i reszta umieszczane w rejestrach tych
iloraz i reszta umieszczane w rejestrach tych
samych długości co dzielnik
samych długości co dzielnik

Nadmiar przy operacjach
Nadmiar przy operacjach
mnożenia i dzielenia (2)
mnożenia i dzielenia (2)
błędne argumenty dzielenia mogą łatwo
błędne argumenty dzielenia mogą łatwo
doprowadzić do powstania nadmiaru, który w
doprowadzić do powstania nadmiaru, który w
przypadku rozkazu dzielenia prowadzi do
przypadku rozkazu dzielenia prowadzi do
wygenerowania
wygenerowania
wyjątku procesora
wyjątku procesora
, co powoduje
, co powoduje
przekazanie sterowania do systemu operacyjnego
przekazanie sterowania do systemu operacyjnego
i zakończenie wykonywania programu
i zakończenie wykonywania programu
wyjątki procesora omawiane będą w dalszej
wyjątki procesora omawiane będą w dalszej
części wykładu
części wykładu
podany niżej fragment programu wykonuje
podany niżej fragment programu wykonuje
dzielenie 256/1, co przy nieodpowiednio
dzielenie 256/1, co przy nieodpowiednio
dobranych długościach rejestrów prowadzi do
dobranych długościach rejestrów prowadzi do
wyjątku procesora (i zakończenia programu)
wyjątku procesora (i zakończenia programu)

Nadmiar przy operacjach
Nadmiar przy operacjach
mnożenia i dzielenia (3)
mnożenia i dzielenia (3)
mov
mov
ax, 256
ax, 256
mov
mov
bh, 1
bh, 1
div
div
bh
bh
; wyjątek procesora !!!
; wyjątek procesora !!!
Podany rozkaz dzielenia DIV dzieli liczbę zawartą
Podany rozkaz dzielenia DIV dzieli liczbę zawartą
w 16-bitowym rejestrze AX przez liczbę
w 16-bitowym rejestrze AX przez liczbę
umieszczoną w 8-bitowym rejestrze BH
umieszczoną w 8-bitowym rejestrze BH
Reszta z dzielenia wpisywana jest do rejestru AH,
Reszta z dzielenia wpisywana jest do rejestru AH,
a iloraz (tu: 256) do 8-bitowego rejestru AL —
a iloraz (tu: 256) do 8-bitowego rejestru AL —
ponieważ w rejestrze AL może być zapisana co
ponieważ w rejestrze AL może być zapisana co
najwyżej liczba 255, więc powstaje nadmiar, a
najwyżej liczba 255, więc powstaje nadmiar, a
ślad za tym generowany jest wyjątek procesora
ślad za tym generowany jest wyjątek procesora

Operacje bitowe (1)
Operacje bitowe (1)
lista rozkazów procesora zawiera zazwyczaj
lista rozkazów procesora zawiera zazwyczaj
obszerną grupę rozkazów wykonujących działania
obszerną grupę rozkazów wykonujących działania
na pojedynczych bitach, w szczególności możliwe
na pojedynczych bitach, w szczególności możliwe
jest wykonanie różnych operacji logicznych:
jest wykonanie różnych operacji logicznych:
negacji, sumy, iloczynu, sumy modulo dwa
negacji, sumy, iloczynu, sumy modulo dwa
omawiana grupa rozkazów jest szczególnie
omawiana grupa rozkazów jest szczególnie
rozbudowana w procesorach przeznaczonych do
rozbudowana w procesorach przeznaczonych do
zastosowań w systemach sterowania
zastosowań w systemach sterowania

Operacje bitowe (2)
Operacje bitowe (2)
w architekturze IA–32 dostępne są m.in. poniższe
w architekturze IA–32 dostępne są m.in. poniższe
rozkazy wykonujące działania na wybranym bicie,
rozkazy wykonujące działania na wybranym bicie,
przy czym przed wykonaniem operacji zawartość
przy czym przed wykonaniem operacji zawartość
bitu jest kopiowana do znacznika CF
bitu jest kopiowana do znacznika CF
BT
bit nie ulega zmianie
BTS
wpisanie 1 do bitu
BTR
wpisanie 0 do bitu
BTC
zanegowanie zawartości bitu

Operacje bitowe (3)
Operacje bitowe (3)
każdy ww. rozkaz ma dwa operandy:
•
pierwszy operand określa rejestr lub komórkę
pamięci zawierającą modyfikowany bit
•
drugi operand wskazuje numer bitu, na którym
ma być wykonana operacja
przykład: rozkaz
btc edi, 29
powoduje
zanegowanie bitu nr 29 w rejestrze EDI

Operacje bitowe (4)
Operacje bitowe (4)
bitowe
operacje
logiczne
są
zazwyczaj
wykonywane jednocześnie na grupach bitach
umieszczonych w rejestrach lub w komórkach
pamięci
rozkaz NOT jest jednoargumentowy — następuje
zanegowanie wszystkich bitów
rozkazy AND, OR, XOR wykonują operacje
logiczne na odpowiadających sobie bitach obu
operandów — rezultat wpisywany jest do
operandu docelowego
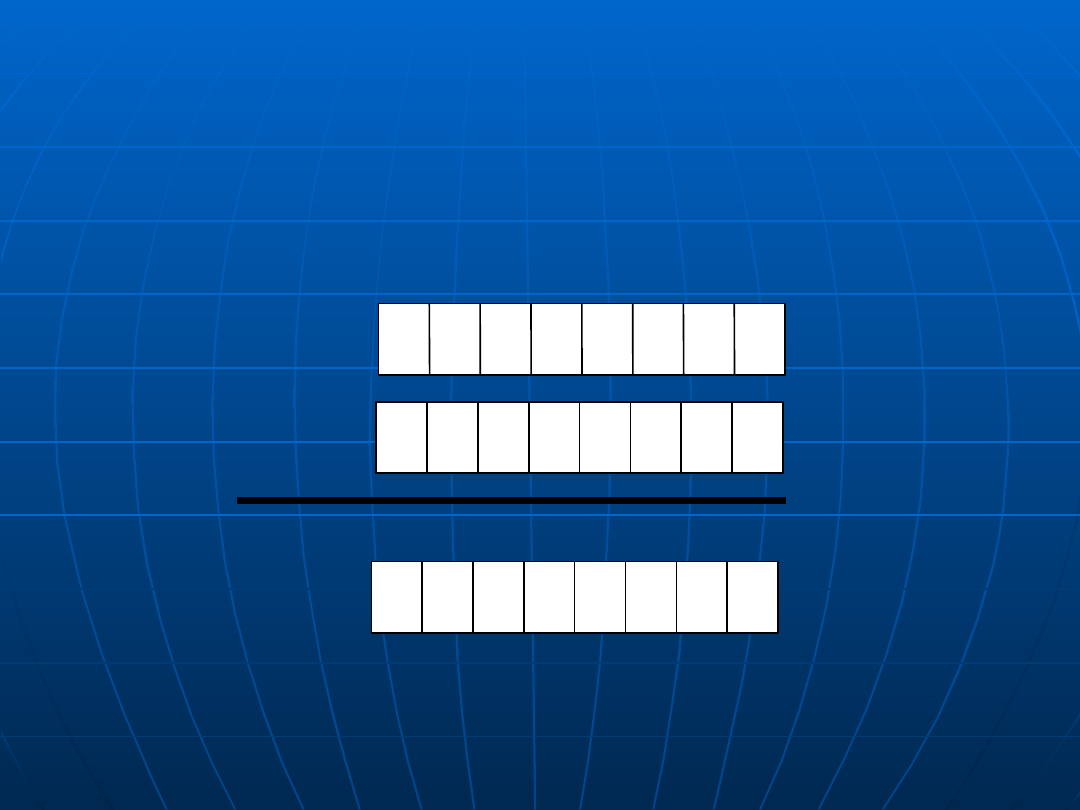
Operacje bitowe (5)
Operacje bitowe (5)
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
suma logiczna
1 0 1 0 0 1 1 1
0 1 1 1 0 1 0 1
1 1 1 1 0 1 1 1
rejestr AH
rejestr BL
rozkazu OR AH, BL
zawartość AH
po wykonaniu
bitowa
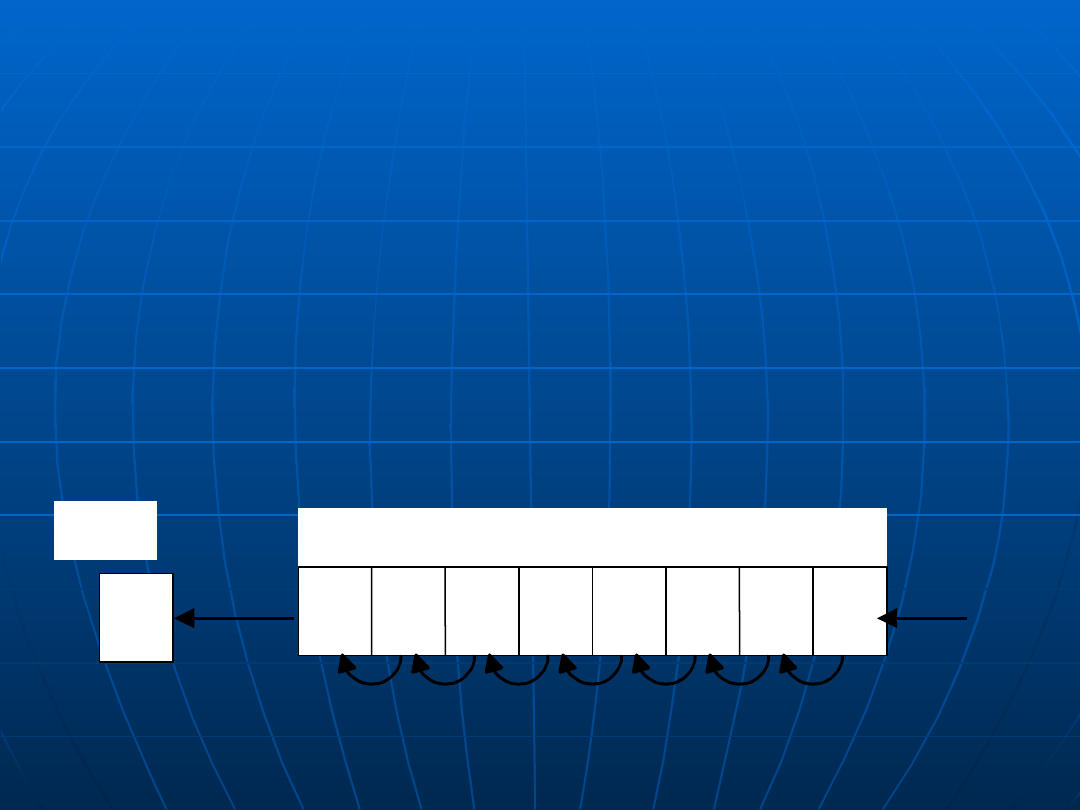
Przesunięcia logiczne
Przesunięcia logiczne
zawartość rejestru lub komórki pamięci traktowana jako
ciąg bitów może być przesunięta w lewo lub prawo o
podaną liczbę pozycji
jeśli w trakcie przesuwania bity wychodzące z rejestru
(lub z komórki pamięci) są tracone, to mówimy wówczas
o przesunięciu logicznym (np. w IA–32 rozkazy SHL, SHR)
7 6 5 4 3 2 1 0
CF
0
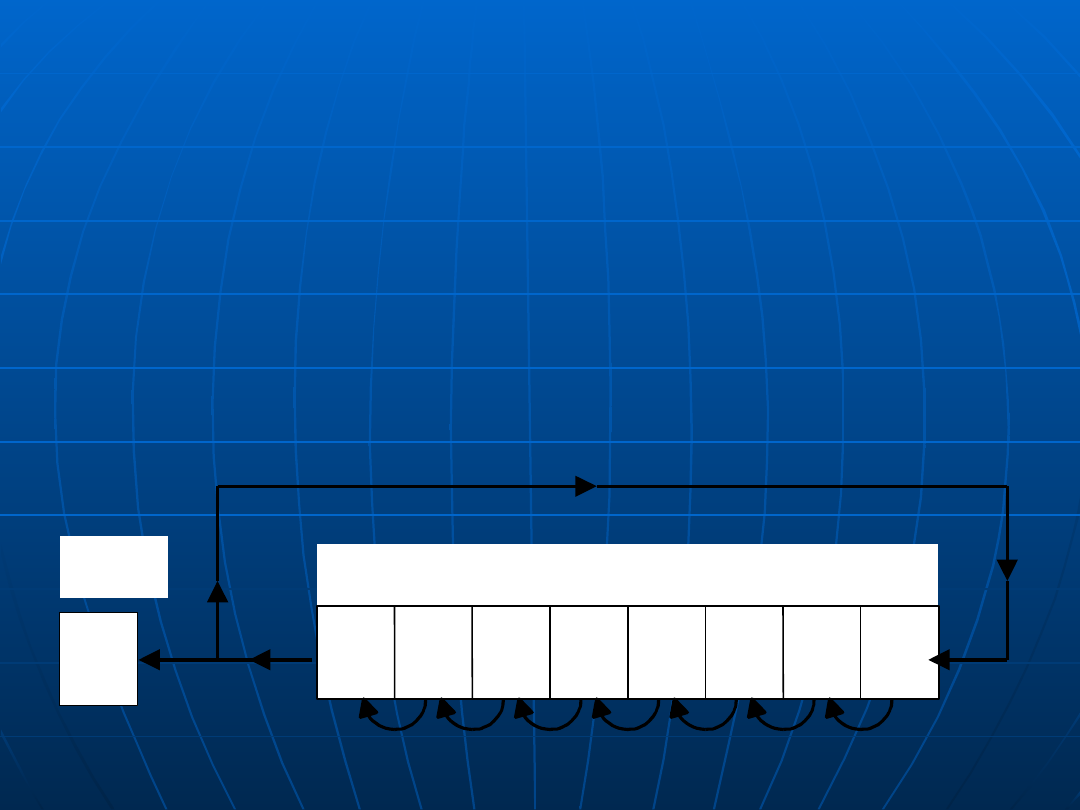
Przesunięcia cykliczne (1)
Przesunięcia cykliczne (1)
jeśli bity wychodzące są zawracane i wprowadzane
z drugiej strony rejestru, to mówimy o przesunięciu
cyklicznym, nazywanym także obrotem (np. w IA–
32 rozkazy ROL, ROR)
7 6 5 4 3 2 1 0
CF

Przesunięcia cykliczne (2)
Przesunięcia cykliczne (2)
dostępne są także odmiany przesunięć cyklicznych: RCL i RCR
dostępne są także odmiany przesunięć cyklicznych: RCL i RCR
— w rozkazach tych przyjmuje się, że na czas ich wykonywania
— w rozkazach tych przyjmuje się, że na czas ich wykonywania
znacznik CF staje się 9-, 17- lub 33-bitem rejestru — poniższy
znacznik CF staje się 9-, 17- lub 33-bitem rejestru — poniższy
rysunek ilustruje przesunięcie w lewo (RCL)
rysunek ilustruje przesunięcie w lewo (RCL)
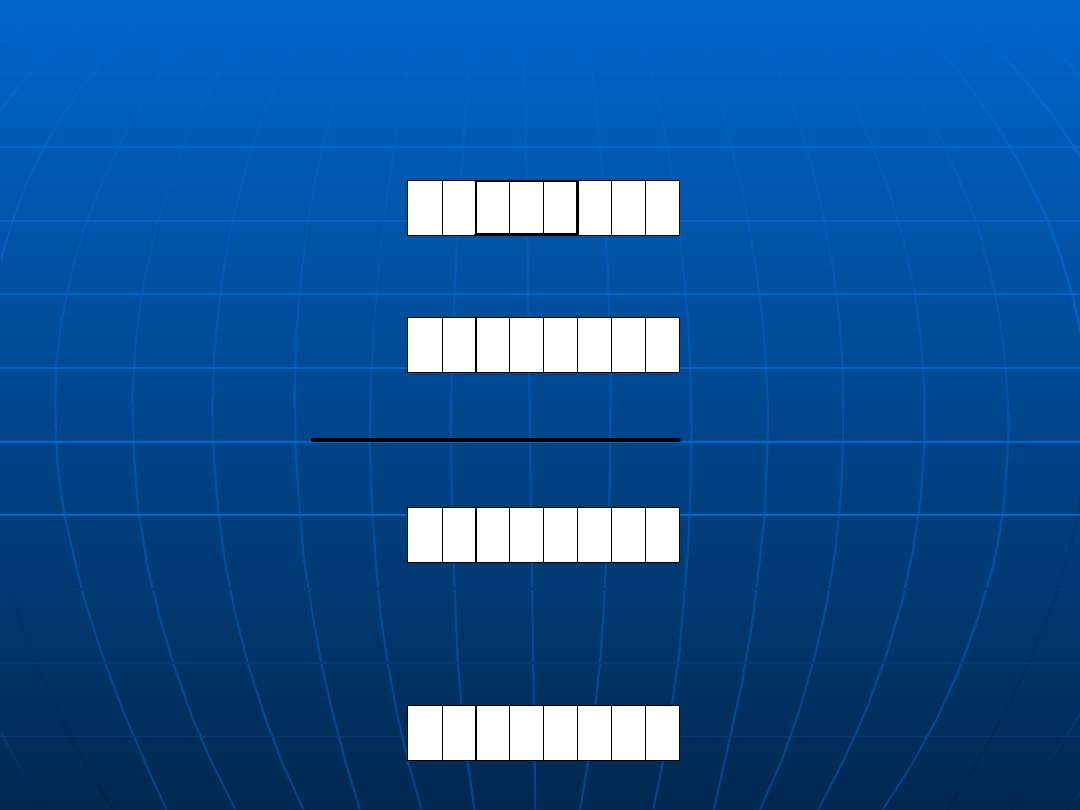
Wyodrębnianie pól bitowych
0
1
2
3
4
5
6
7
0
1
2
3
4
5
6
7
1 0 1 0 0 1 1 1
0 0 1 1 1 0 0 0
rejestr AH
rejestr BL
0
1
2
3
4
5
6
7
iloczyn logiczny
0 0 1 0 0 0 0 0
rozkazu and ah, bl
zawartość AH
po wykonaniu
bitowy
na bitach 5-3
umieszczona jest
"maska" bitowa
liczba 3-bitowa
0
1
2
3
4
5
6
7
logiczne w prawo
0 0 0 0 0 1 0 0
rozkazu shr ah, 3
zawartość AH
po wykonaniu
przesunięcie
o 3 pozycje

Przesunięcia arytmetyczne
Przesunięcia arytmetyczne
(1)
(1)
rozkazy przesunięć w mogą być zastosowane do
rozkazy przesunięć w mogą być zastosowane do
mnożenia i dzielenia przez 2, 4, 8, ... (ogólnie:
mnożenia i dzielenia przez 2, 4, 8, ... (ogólnie:
przez 2
przez 2
k
k
) — w przypadku dzielenia pozwala to
) — w przypadku dzielenia pozwala to
znaczne skrócenie czasu operacji (np. 10 razy)
znaczne skrócenie czasu operacji (np. 10 razy)
ze względu na specyfikę kodowania liczb ze
ze względu na specyfikę kodowania liczb ze
znakiem w systemie U2 w architekturze IA–32
znakiem w systemie U2 w architekturze IA–32
wprowadzono rozkazy przesunięć
wprowadzono rozkazy przesunięć
arytmetycznych, (np. SAL, SAR), które są bardzo
arytmetycznych, (np. SAL, SAR), które są bardzo
podobne lub identyczne do przesunięć bitowych
podobne lub identyczne do przesunięć bitowych

Przesunięcia arytmetyczne
Przesunięcia arytmetyczne
(2)
(2)
przykład realizacji mnożenia przez 2 za pomocą
przykład realizacji mnożenia przez 2 za pomocą
rozkazu przesunięcia arytmetycznego w lewo o
rozkazu przesunięcia arytmetycznego w lewo o
jedną pozycję (
jedną pozycję (
SAL BH, 1
SAL BH, 1
)
)
znacznik CF sygnalizuje nadmiar w trakcie działań
znacznik CF sygnalizuje nadmiar w trakcie działań
na liczbach bez znaku, a znacznik OF — na
na liczbach bez znaku, a znacznik OF — na
liczbach ze znakiem
liczbach ze znakiem
Zawartość rejestru BH
Rozkaz
przed wykonaniem
rozkazu
po wykonaniu rozkazu
11111111 (–1)
11111110 (–2) OF=0, CF=1
11000000 (–64)
10000000 (–128) OF=0, CF=1
00111111 (+63)
01111110 (+126) OF=0, CF=0
SAL BH, 1
10111111 (–65)
01111110 (+126) OF=1,CF=1

Kodowanie liczb mieszanych
Kodowanie liczb mieszanych
opisy rozkazów arytmetycznych wykonywanych
przez procesor podawane są zazwyczaj przy
założeniu, że operacje wykonywane są na
liczbach całkowitych
działania mogą być wykonywane także na
liczbach ułamkowych i mieszanych — wymaga to
przekształcenia algorytmu w taki sposób, by
operacje na ułamkach zostały zastąpione przez
operacje na liczbach całkowitych

Przykład kodowania liczby
Przykład kodowania liczby
mieszanej
mieszanej
0
1
2
3
4
5
6
7
8
9
11
12
13
14
15
10
bit znaku
2
–2
2
–3
2
–4
2
–5
3
2
2
2
1
2
0
2
–1
2
6
2
5
2
4
2
2
9
2
8
2
7
0
0 0 0
0 0
0
0
0
0
1
1
1 1
1
1
5625
.
549
0625
.
0
5
.
0
1
4
32
512
2
2
2
2
2
2
4
1
0
2
5
9

Formaty liczb mieszanych
Formaty liczb mieszanych
nie ma standardowych formatów liczb
nie ma standardowych formatów liczb
mieszanych — przypisanie wag poszczególnym
mieszanych — przypisanie wag poszczególnym
bitom, a więc ustalenie położenia kropki
bitom, a więc ustalenie położenia kropki
rozdzielającej część całkowitą i ułamkową liczby
rozdzielającej część całkowitą i ułamkową liczby
zależy od decyzji programisty
zależy od decyzji programisty
ustalenie formatu wynika z zakresu zmienności
ustalenie formatu wynika z zakresu zmienności
danych i wyników pośrednich, jak również z
danych i wyników pośrednich, jak również z
wymagań dotyczących dokładności obliczeń
wymagań dotyczących dokładności obliczeń
dość często spotyka się format
dość często spotyka się format
śródprzecinkowy
śródprzecinkowy
,
,
w którym połowa bitów ma przypisane wagi o
w którym połowa bitów ma przypisane wagi o
wartościach całkowitych, a pozostałe – ułamkowe
wartościach całkowitych, a pozostałe – ułamkowe

Ułamki dziesiętne a ułamki
Ułamki dziesiętne a ułamki
binarne (1)
binarne (1)
zazwyczaj dane przekazywane są do programu w
postaci liczb dziesiętnych
reprezentacja binarna części całkowitej liczby jest
zawsze dokładna
reprezentacja ułamka dziesiętnego w postaci
binarnej stanowi na ogół przybliżenie — tylko
niektóre liczby, jak np. 0.625 (tj. 0.5 + 0.125)
mają dokładną reprezentację binarną

Ułamki dziesiętne a ułamki
Ułamki dziesiętne a ułamki
binarne (2)
binarne (2)
rozwinięcie binarne liczby 0.3 ma postać
0.010 011
001 100 110 011 001 100 110 011 001 100 ... = 0.0(1001)
w poniższym programie
int i; float a =
0, b = 0; for (i=0; i < 100; i++)
{
a = a + 0.3; b = b + 0.25;
}
printf("\na = %f b = %f", a, b);
zostały wyświetlone wyniki
a = 29.999971 b =
25.000000

Obliczenia na liczbach bardzo
Obliczenia na liczbach bardzo
dużych
dużych
i bardzo małych (1)
i bardzo małych (1)
przykład: obliczenie stałej czasowej obwodu RC
wartość R (=
4 700 000)
4 700 000) w postaci 24-bitowej
liczby binarnej:
R=01000111 10110111 01100000
wartość pojemności C (= 0.000 000 000 068) w
postaci binarnej ma rozwinięcie nieskończone
okresowe
6
12
6
10
6
.
319
10
68
10
7
.
4
RC
pF
68
=
C
,
M
4.7
=
R

Obliczenia na liczbach bardzo
Obliczenia na liczbach bardzo
dużych
dużych
i bardzo małych (2)
i bardzo małych (2)
przyjmujemy, że część ułamkowa liczby będzie
zajmowała 40 bitów
trzy najbliższe 40-bitowe liczby binarne do
wartości 0.000 000 000 068 mają postać:
0.00000000 00000000 00000000 00000000 01001010
(= 0.
000 000 000 067 302 607 931 196 689 605 712 890 625)
000 000 000 067 302 607 931 196 689 605 712 890 625)
0.00000000 00000000 00000000 00000000 01001011
(= 0.
000 000 000 068 212 102 632 969 617 843 627 929 687 5
000 000 000 068 212 102 632 969 617 843 627 929 687 5)
0.00000000 00000000 00000000 00000000 01001100
(= 0.
000 000 000 069 121 597 334 742 546 081 542 968 75
000 000 000 069 121 597 334 742 546 081 542 968 75
liczba
0.00000000 00000000 00000000 00000000 01001011
stanowi więc najlepsze przybliżenie 40-bitowe

Obliczenia na liczbach bardzo
Obliczenia na liczbach bardzo
dużych
dużych
i bardzo małych (3)
i bardzo małych (3)
zatem obliczenie wartości RC wymaga przyjęcia
formatu, w którym część całkowita liczby
zajmować będzie 24 bity, a część ułamkowa 40
bitów – łącznie 64 bity, czyli 8 bajtów
przy podanym formacie liczby R i C będą
zajmować w pamięci po 8 bajtów, przy czym w
reprezentacji binarnej liczby R część ułamkowa
będzie zawierała same zera (5 bajtów), a w
reprezentacji liczby C część całkowita liczby
będzie zawierała same zera (3 bajty), a także
początkowe 4 bajty części ułamkowej będą
wypełnione zerami

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
(1)
(1)
podany poprzednio sposób kodowania liczb jest
podany poprzednio sposób kodowania liczb jest
szczególnie nieefektywny jeśli w obliczeniach
szczególnie nieefektywny jeśli w obliczeniach
występują liczby bardzo duże i bardzo małe, co
występują liczby bardzo duże i bardzo małe, co
jest charakterystyczne dla obliczeń naukowo-
jest charakterystyczne dla obliczeń naukowo-
technicznych
technicznych
radykalną poprawę w tym zakresie przynosi
radykalną poprawę w tym zakresie przynosi
kodowanie zmiennoprzecinkowe (zmienno-
kodowanie zmiennoprzecinkowe (zmienno-
pozycyjne), w którym skupia się uwagę na cyfrach
pozycyjne), w którym skupia się uwagę na cyfrach
znaczących liczby, rejestrując jednocześnie
znaczących liczby, rejestrując jednocześnie
położenie kropki rozdzielającej część całkowitą i
położenie kropki rozdzielającej część całkowitą i
ułamkową
ułamkową

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
(2)
(2)
weźmy pod uwagę omawianą poprzednio liczbę
weźmy pod uwagę omawianą poprzednio liczbę
binarną
binarną
0.00000000 00000000 00000000 00000000 01001011
spróbujmy przesunąć kropkę w prawo, tak by
spróbujmy przesunąć kropkę w prawo, tak by
kropka znalazła się za po prawej stronie najbardziej
kropka znalazła się za po prawej stronie najbardziej
znaczącej cyfry 1 — otrzymamy:
znaczącej cyfry 1 — otrzymamy:
1.001011
w tym przypadku kropkę przesunęliśmy o 34
w tym przypadku kropkę przesunęliśmy o 34
pozycje w prawo
pozycje w prawo
późniejsze odtworzenie oryginalnej liczby będzie
późniejsze odtworzenie oryginalnej liczby będzie
możliwe, jeśli obok wartości liczby (z przesuniętą
możliwe, jeśli obok wartości liczby (z przesuniętą
kropką) zapiszemy także liczbę przesunięć (tu: 34)
kropką) zapiszemy także liczbę przesunięć (tu: 34)

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
(3)
(3)
omawiany sposób kodowania wymaga więc
omawiany sposób kodowania wymaga więc
przechowywania liczby w postaci dwóch elementów:
przechowywania liczby w postaci dwóch elementów:
mantysy
mantysy
, stanowiącej wartość liczby znormalizowaną do
, stanowiącej wartość liczby znormalizowaną do
przedziału (–2,–1> lub <1,2)
przedziału (–2,–1> lub <1,2)
wykładnika
wykładnika
, opisującego liczbę przesunięć kropki w
, opisującego liczbę przesunięć kropki w
prawo lub w lewo
prawo lub w lewo
mantysa
wykładnik

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
(4)
(4)
Powyższe wyrażenie określa wartość liczby
Powyższe wyrażenie określa wartość liczby
zmiennoprzecinkowej różnej od 0
zmiennoprzecinkowej różnej od 0
Liczba 0 kodowana jest jako wartość specjalna
Liczba 0 kodowana jest jako wartość specjalna
(pola mantysy i wykładnika wypełnione są
(pola mantysy i wykładnika wypełnione są
zerami)
zerami)
dla liczb różnych od zera wymaga się, by mantysa
dla liczb różnych od zera wymaga się, by mantysa
spełniała
spełniała
warunek normalizacji
warunek normalizacji
:
:
1
1
mantysa
mantysa
< 2
< 2
mantysa
wykladnik
2

Liczby zmiennoprzecinkowe
Liczby zmiennoprzecinkowe
(5)
(5)
tak więc liczba omawiana liczba przykładowa
tak więc liczba omawiana liczba przykładowa
0.00000000 00000000 00000000 00000000 01001011
w
postaci zmiennoprzecinkowej może być zakodowana jako
:
mantysa
wykładnik
–34 (binarnie)
1.001011

Standardy kodowania liczb
Standardy kodowania liczb
zmiennoprzecinkowych (1)
zmiennoprzecinkowych (1)
Podane zasady kodowania zostały sformalizowane
Podane zasady kodowania zostały sformalizowane
w postaci standardu znanego jako norma IEEE 754
w postaci standardu znanego jako norma IEEE 754
w standardzie zdefiniowano trzy formaty liczb
w standardzie zdefiniowano trzy formaty liczb
zmiennoprzecinkowych: 32-bitowy (float), 64-bitowy
zmiennoprzecinkowych: 32-bitowy (float), 64-bitowy
(double) i 80-bitowy; określono także reguły
(double) i 80-bitowy; określono także reguły
zaokrąglania, postępowanie w przypadków błędów
zaokrąglania, postępowanie w przypadków błędów
w obliczeniach, itd.
w obliczeniach, itd.
W formatach 32- i 64-bitowych pomija się
W formatach 32- i 64-bitowych pomija się
kodowanie części całkowitej mantysy (ale
kodowanie części całkowitej mantysy (ale
uwzględnia w obliczeniach!) – z warunku
uwzględnia w obliczeniach!) – z warunku
normalizacji wynika bowiem, że bit ten jest zawsze
normalizacji wynika bowiem, że bit ten jest zawsze
równy 1 (dla liczb różnych od 0)
równy 1 (dla liczb różnych od 0)

Standardy kodowania liczb
Standardy kodowania liczb
zmiennoprzecinkowych (2)
zmiennoprzecinkowych (2)
Znak mantysy określa skrajny bit z lewej strony
Znak mantysy określa skrajny bit z lewej strony
w standardzie nie przewidziano bitu znaku
w standardzie nie przewidziano bitu znaku
wykładnika — zamiast tego w
wykładnika — zamiast tego w
polu wykładnika
polu wykładnika
zapisuje się wartość wykładnika powiększoną o
zapisuje się wartość wykładnika powiększoną o
stałą wartość (127 dla formatu 32-bitowego, 1023
stałą wartość (127 dla formatu 32-bitowego, 1023
dla formatu 64-bitowego i 16383 dla formatu 80-
dla formatu 64-bitowego i 16383 dla formatu 80-
bitowego)
bitowego)
w rezultacie liczba zapisywana w polu wykładnika
w rezultacie liczba zapisywana w polu wykładnika
jest zawsze dodatnia i bit znaku nie jest
jest zawsze dodatnia i bit znaku nie jest
potrzebny
potrzebny
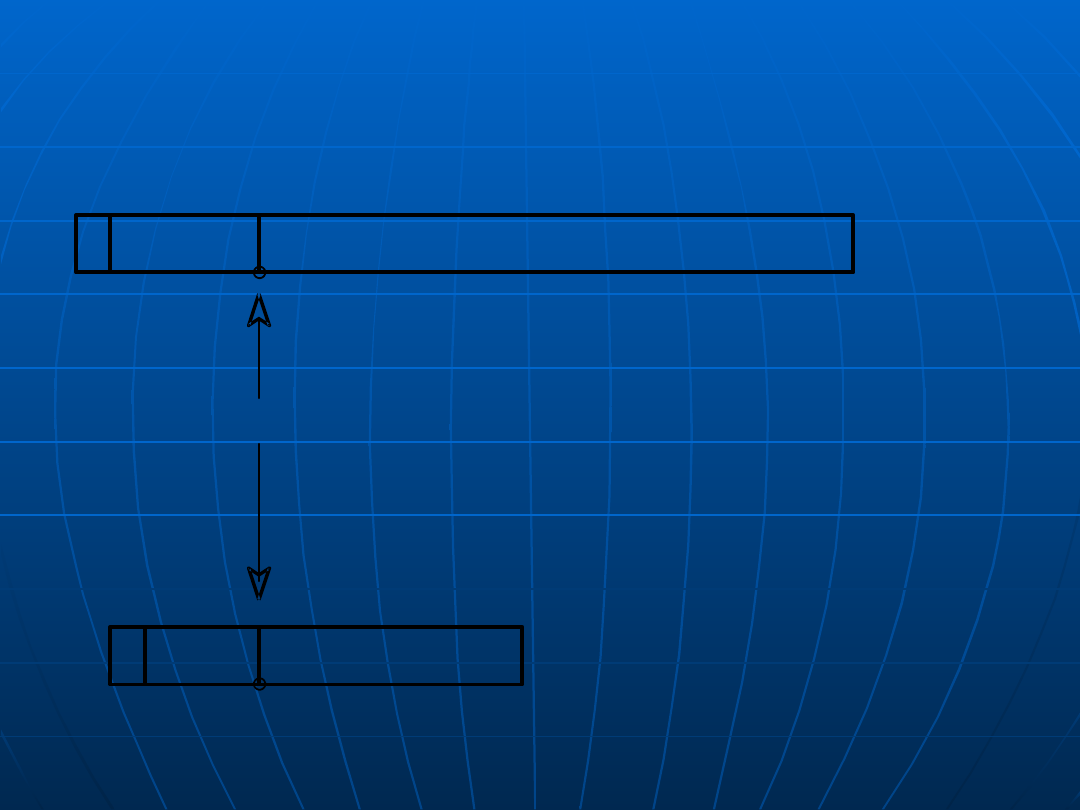
Formaty liczb
Formaty liczb
zmiennoprzecinkowych (1)
zmiennoprzecinkowych (1)
S wykładn.
mantysa
11 bitów
52 bity
umowna kropka rozdzielająca część całkowitą
i ułamkową mantysy
(w formacie 32- i 64-bitowym część całkowita
mantysy występuje w postaci niejawnej)
S
mantysa
8 bitów
23 bity
wykł.
format 32-bitowy
format
64-bitowy
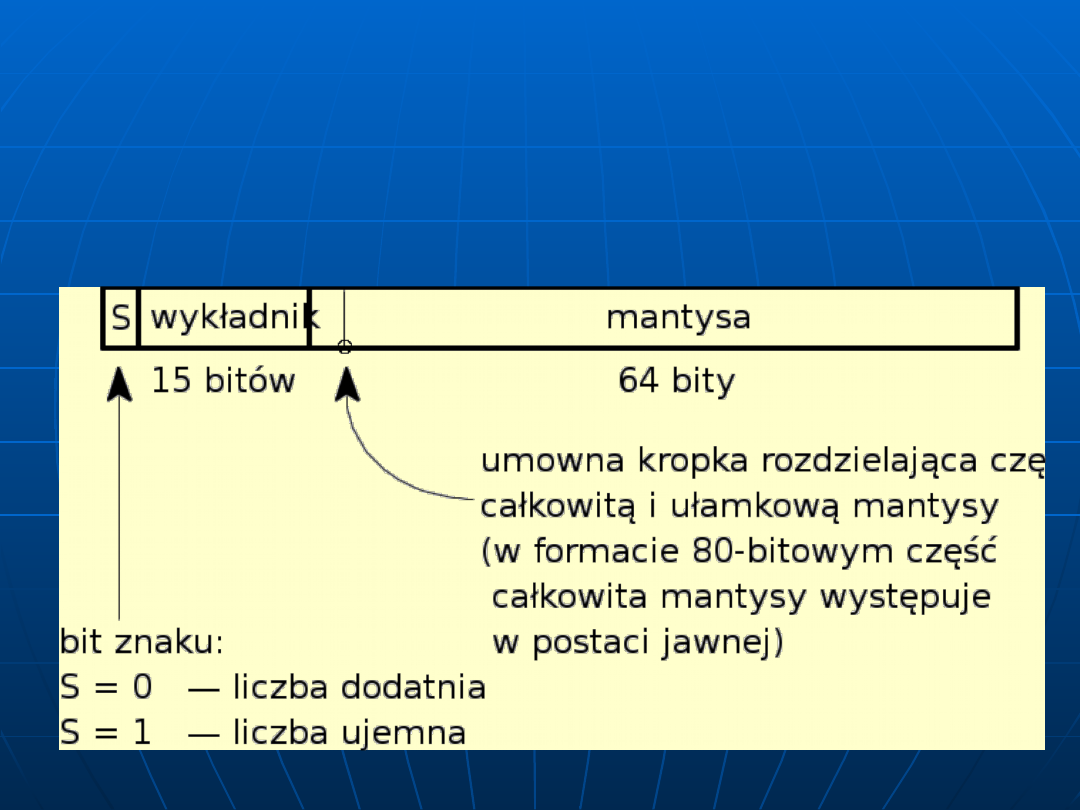
Formaty liczb
Formaty liczb
zmiennoprzecinkowych (2)
zmiennoprzecinkowych (2)
format 80-bitowy pośredni (ang. temporary real)
format 80-bitowy pośredni (ang. temporary real)

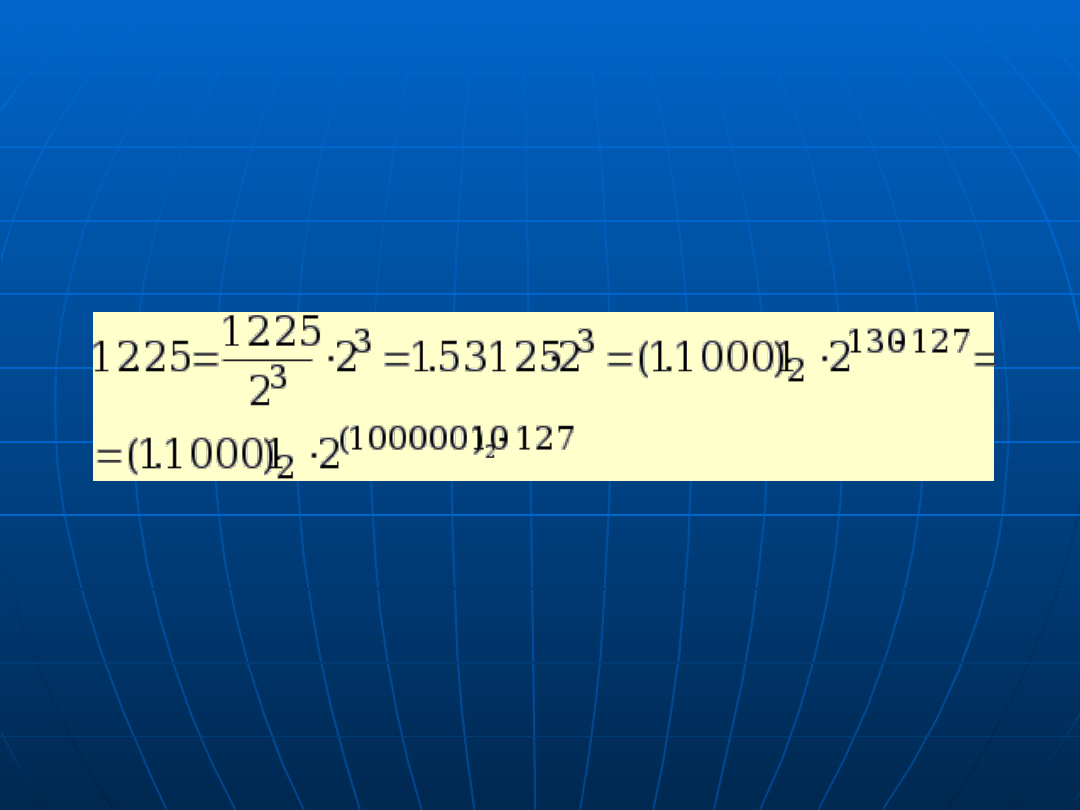
Przykład kodowania
Przykład kodowania
liczby 12.25 w formacie 32-
liczby 12.25 w formacie 32-
bitowym (1)
bitowym (1)
k
m 2
Liczbę 12.25 przedstawiamy w postaci iloczynu
Liczbę 12.25 przedstawiamy w postaci iloczynu
Wykładnik potęgi
Wykładnik potęgi
k
k
musi być tak dobrany, by
musi być tak dobrany, by
spełniony był warunek normalizacji mantysy
spełniony był warunek normalizacji mantysy
czyli
czyli
2
|
|
1
m
2
2
25
.
12
1
k
Przykład kodowania
Przykład kodowania
liczby 12.25 w formacie 32-
liczby 12.25 w formacie 32-
bitowym (2)
bitowym (2)
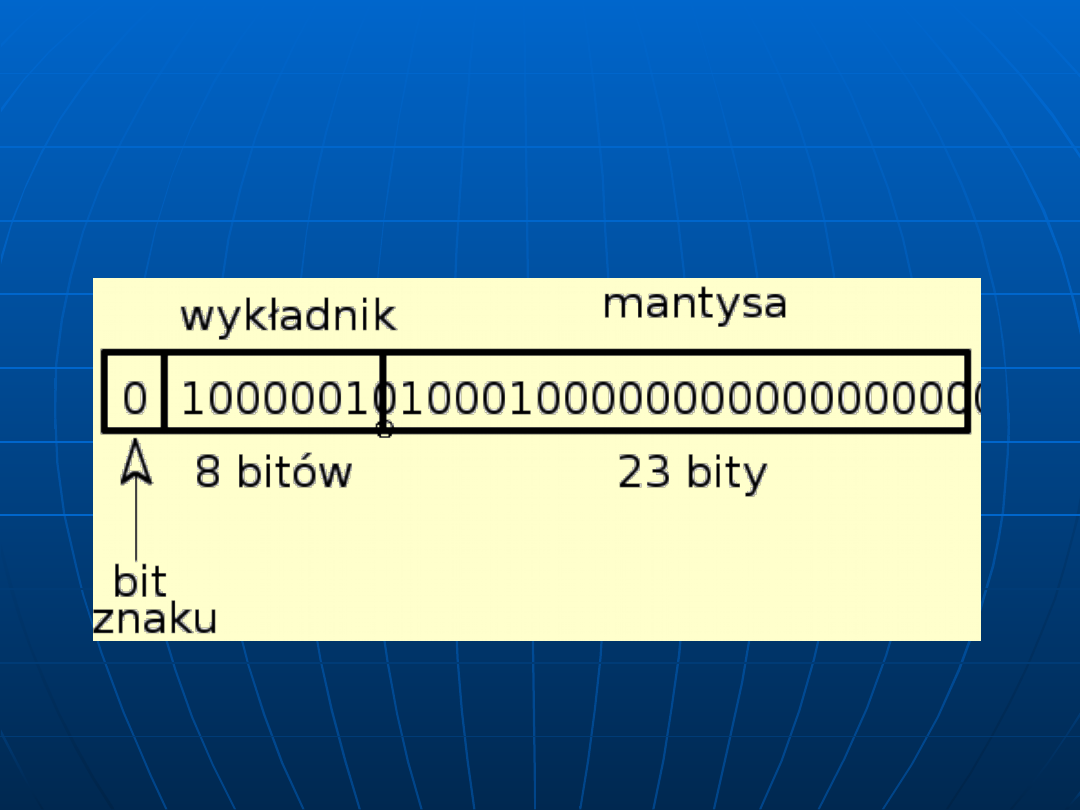
Łatwo zauważyć, że warunek normalizacji jest
Łatwo zauważyć, że warunek normalizacji jest
spełniony, gdy
spełniony, gdy
k
k
= 3. Zatem
= 3. Zatem
Ponieważ część całkowita mantysy nie jest
Ponieważ część całkowita mantysy nie jest
kodowana, więc w polu mantysy zostanie wpisana
kodowana, więc w polu mantysy zostanie wpisana
liczba (0.10001)
liczba (0.10001)
2
2
, zaś w polu wykładnika (po
, zaś w polu wykładnika (po
przesunięciu o 127) liczba (10000010)
przesunięciu o 127) liczba (10000010)
2
2
.
.
Ostatecznie otrzymamy
Ostatecznie otrzymamy
Przykład kodowania
Przykład kodowania
liczby 12.25 w formacie 32-
liczby 12.25 w formacie 32-
bitowym (3)
bitowym (3)
Przykład kodowania
Przykład kodowania
liczby 68*10
liczby 68*10
–12
–12
Poniżej podano liczbę 68*10
Poniżej podano liczbę 68*10
–12
–12
zakodowaną
zakodowaną
w formacie 32-bitowym (float)
w formacie 32-bitowym (float)
dokładna wartość zakodowanej liczby
dokładna wartość zakodowanej liczby
wynosi:
wynosi:
0.00000000006800000146300888559380837250500917434692
0.00000000006800000146300888559380837250500917434692
mantysa
wykładnik
01011101
00101011000100010011001
0
(–34+127=93)

Zakresy liczb
Zakresy liczb
zmiennoprzecinkowych (1)
zmiennoprzecinkowych (1)
w formacie 32-bitowym można kodować liczby o
wartościach do
3.37*10
38
, a w formacie 64-
bitowym nawet do
1.67*10
308
;
w przypadku bardzo dużych liczb, ze względu na
ograniczoną długość pola mantysy, podane
wartości zastępowane są przez przybliżenia;
przykład:
float a = 17000000.0, b = 16999999.0;
float a = 17000000.0, b = 16999999.0;
printf("\n%e\n", a-b );
printf("\n%e\n", a-b );
// na ekranie zostanie wyświetlona wartość 0
// na ekranie zostanie wyświetlona wartość 0

Zakresy liczb
Zakresy liczb
zmiennoprzecinkowych (2)
zmiennoprzecinkowych (2)
możliwe jest także kodowanie liczb bardzo
małych, np. w formacie 64-bitowym można
zakodować z zadowalającą dokładnością (ok. 14
cyfr dziesiętnych) liczby bliskie
2.23*10
–308
;
takie same zakresy dotyczą również liczb
ujemnych

Zasady wykonywania obliczeń
Zasady wykonywania obliczeń
przez koprocesor arytmetyczny
przez koprocesor arytmetyczny
(1)
(1)
koprocesor arytmetyczny stanowi odrębny
koprocesor arytmetyczny stanowi odrębny
procesor, współdziałający z procesorem głównym
procesor, współdziałający z procesorem głównym
i znajdujący się w tej samej obudowie
i znajdujący się w tej samej obudowie
w przeszłości koprocesor stanowił oddzielny układ
w przeszłości koprocesor stanowił oddzielny układ
scalony instalowany na płycie głównej komputera
scalony instalowany na płycie głównej komputera
liczby, na których wykonywane są obliczenia,
liczby, na których wykonywane są obliczenia,
składowane są w 8 rejestrach 80-bitowych
składowane są w 8 rejestrach 80-bitowych
tworzących
tworzących
stos rejestrów koprocesora
stos rejestrów koprocesora
arytmetycznego
arytmetycznego

Zasady wykonywania obliczeń
Zasady wykonywania obliczeń
przez koprocesor arytmetyczny
przez koprocesor arytmetyczny
(2)
(2)

Zasady wykonywania obliczeń
Zasady wykonywania obliczeń
przez koprocesor arytmetyczny
przez koprocesor arytmetyczny
(3)
(3)
z każdym rejestrem związane jest 2-bitowe
z każdym rejestrem związane jest 2-bitowe
pole
pole
stanu rejestru
stanu rejestru
(nazywane także
(nazywane także
polem znaczeń
polem znaczeń
);
);
wszystkie pola stanu tworzą 16-bitowy rejestr
wszystkie pola stanu tworzą 16-bitowy rejestr
zwany
zwany
rejestrem stanu stosu koprocesora
rejestrem stanu stosu koprocesora
;
;
interpretacja pola stanu jest następująca:
interpretacja pola stanu jest następująca:
0 – rejestr zawiera liczbę różną od zera,
0 – rejestr zawiera liczbę różną od zera,
1 – rejestr zawiera zero,
1 – rejestr zawiera zero,
2 – rejestr zawiera błędny rezultat,
2 – rejestr zawiera błędny rezultat,
3 – rejestr jest pusty;
3 – rejestr jest pusty;

Zasady wykonywania obliczeń
Zasady wykonywania obliczeń
przez koprocesor arytmetyczny
przez koprocesor arytmetyczny
(4)
(4)
rozkazy koprocesora adresują rejestry stosu nie
rozkazy koprocesora adresują rejestry stosu nie
bezpośrednio, ale względem wierzchołka stosu
bezpośrednio, ale względem wierzchołka stosu
w kodzie asemblerowym rejestr znajdujący się na
w kodzie asemblerowym rejestr znajdujący się na
wierzchołku stosu oznaczany jest ST(0) lub ST, a
wierzchołku stosu oznaczany jest ST(0) lub ST, a
dalsze ST(1), ST(2),..., ST(7)
dalsze ST(1), ST(2),..., ST(7)
ze względu na specyficzny sposób adresowania
ze względu na specyficzny sposób adresowania
koprocesor arytmetyczny zaliczany jest do
koprocesor arytmetyczny zaliczany jest do
procesorów o
procesorów o
architekturze stosowej
architekturze stosowej
mechanizmy stosu rejestrów koprocesora są
mechanizmy stosu rejestrów koprocesora są
analogiczne do mechanizmów stosu w procesorze
analogiczne do mechanizmów stosu w procesorze
(m.in. stos rośnie w kierunku malejących numerów
(m.in. stos rośnie w kierunku malejących numerów
rejestrów)
rejestrów)

Lista rozkazów koprocesora
Lista rozkazów koprocesora
arytmetycznego (1)
arytmetycznego (1)
lista rozkazów koprocesora arytmetycznego
lista rozkazów koprocesora arytmetycznego
zawiera rozkazy wykonujące działania na liczbach
zawiera rozkazy wykonujące działania na liczbach
zmiennoprzecinkowych, w tym rozkazy
zmiennoprzecinkowych, w tym rozkazy
przesłania, działania arytmetyczne, obliczanie
przesłania, działania arytmetyczne, obliczanie
pierwiastka kwadratowego, funkcji
pierwiastka kwadratowego, funkcji
trygonometrycznych (sin, cos, tg, arc tg),
trygonometrycznych (sin, cos, tg, arc tg),
wykładniczych i logarytmicznych
wykładniczych i logarytmicznych
wszystkie mnemoniki rozkazów koprocesora
wszystkie mnemoniki rozkazów koprocesora
zaczynają się od litery F (ang. float)
zaczynają się od litery F (ang. float)

Lista rozkazów koprocesora
Lista rozkazów koprocesora
arytmetycznego (2)
arytmetycznego (2)
prawie zawsze jeden z argumentów wykonywanej
prawie zawsze jeden z argumentów wykonywanej
operacji znajduje się na wierzchołku stosu ST(0),
operacji znajduje się na wierzchołku stosu ST(0),
nawet jeśli nie jest określony w postaci jawnej
nawet jeśli nie jest określony w postaci jawnej
przykładowo rozkaz mnożenia
przykładowo rozkaz mnożenia
fmul
fmul
vc
vc
powoduje pomnożenie liczby znajdującej się na
powoduje pomnożenie liczby znajdującej się na
wierzchołku stosu przez wartość zmiennej vc, a
wierzchołku stosu przez wartość zmiennej vc, a
wynik wpisywany w miejsce dotychczasowej
wynik wpisywany w miejsce dotychczasowej
wartości na wierzchołku stosu (wskaźnik stosu nie
wartości na wierzchołku stosu (wskaźnik stosu nie
zmienia się)
zmienia się)

Przykład: obliczanie wartości tg
Przykład: obliczanie wartości tg
przykładowo, do obliczenia wartości funkcji
przykładowo, do obliczenia wartości funkcji
tangens używa się rozkazu FPTAN, który oblicza
tangens używa się rozkazu FPTAN, który oblicza
wartość funkcji dla argumentu (w radianach)
wartość funkcji dla argumentu (w radianach)
podanego na wierzchołku stosu koprocesora
podanego na wierzchołku stosu koprocesora
w wyniku podaje dwie liczby — ich iloraz stanowi
w wyniku podaje dwie liczby — ich iloraz stanowi
wartość funkcji (bezpośrednio po rozkazie FPTAN
wartość funkcji (bezpośrednio po rozkazie FPTAN
należy wykonać rozkaz FDIV (bez operandów))
należy wykonać rozkaz FDIV (bez operandów))

Przykład: obliczanie wartości
Przykład: obliczanie wartości
wyróżnika trójmianu
wyróżnika trójmianu
kwadratowego (1)
kwadratowego (1)
zakładamy, że wartości współczynników trójmianu
zakładamy, że wartości współczynników trójmianu
a
a
,
,
b
b
,
,
c
c
przechowywane są w zmiennych,
przechowywane są w zmiennych,
odpowiednio
odpowiednio
va
va
,
,
vb
vb
,
,
vc
vc
va
va
dq
dq
1.0
1.0
vb
vb
dq
dq
5.5
5.5
vc
vc
dq
dq
-15.0
-15.0
liczba4
liczba4
dq
dq
4.0
4.0

Przykład: obliczanie wartości
Przykład: obliczanie wartości
wyróżnika trójmianu
wyróżnika trójmianu
kwadratowego (2)
kwadratowego (2)
finit
finit
; inicjalizacja koprocesora
; inicjalizacja koprocesora
; załadowanie wartości 'b' na wierzchołek stosu
; załadowanie wartości 'b' na wierzchołek stosu
fld
fld
vb
vb
fmul
fmul
st(0), st(0) ; obliczenie b^2
st(0), st(0) ; obliczenie b^2
; załadowanie wartości 'a' na wierzchołek stosu
; załadowanie wartości 'a' na wierzchołek stosu
fld
fld
va
va
fmul
fmul
vc
vc
; mnożenie a * c
; mnożenie a * c
fmul
fmul
liczba4
liczba4
; obliczenie 4 * (a * c)
; obliczenie 4 * (a * c)
fsubp
fsubp
st(1), st(0)
st(1), st(0)
; obliczenie pierwiastka z liczby na wierz. stosu
; obliczenie pierwiastka z liczby na wierz. stosu
fsqrt
fsqrt
Document Outline
- Slide 1
- Slide 2
- Slide 3
- Slide 4
- Slide 5
- Slide 6
- Slide 7
- Slide 8
- Slide 9
- Slide 10
- Slide 11
- Slide 12
- Slide 13
- Slide 14
- Slide 15
- Slide 16
- Slide 17
- Slide 18
- Slide 19
- Slide 20
- Slide 21
- Slide 22
- Slide 23
- Slide 24
- Slide 25
- Slide 26
- Slide 27
- Slide 28
- Slide 29
- Slide 30
- Slide 31
- Slide 32
- Slide 33
- Slide 34
- Slide 35
- Slide 36
- Slide 37
- Slide 38
- Slide 39
- Slide 40
- Slide 41
- Slide 42
- Slide 43
- Slide 44
- Slide 45
- Slide 46
- Slide 47
- Slide 48
- Slide 49
- Slide 50
- Slide 51
- Slide 52
Wyszukiwarka
Podobne podstrony:
AKO 2009 cz 4
AKO 2009 cz 3
więcej podobnych podstron