Prowadzący:
dr inż. Ryszard Klempous

Plan prezentacji:

• prezentacja grupy
• przedstawienie problemu
• możliwe sposoby rozwiązania
• omówienie wykorzystanego algorytmu

programu

• literatura
• wykres Gantt’a (przebieg pracy)
• demonstracja programu

Skład
grupy:

Lp

imię i nazwisko

nr

albumu

funkcja w

grupie

1

Grzegorz

Wrębiak

133189

szef grupy

2

Wojciech Jarosz

133097

prezentacja wyników

(marketing)

3

Artur Czupryna

133067

sekretariat

+archiwizacja

4

Sławomir

Tajnert

133174

osoba

merytoryczna

Temat seminarium:

(0-1 knapsack problem)

„Dyskretny problem plecakowy”

Tematyka problemu:

sklep

plecak

złodzieja o

wytrzymałości
W-kilogramów

3

n

4 5

1 2

p

1

w

1

p

2

w

2

p

3

w

3

p

4

w

4

p

5

w

5

p

n

w

n

p

i

= wartość przedmiotu i-tego

w

i

= masa przedmiotu i-tego

Pytanie brzmi:

Jakie przedmioty z puli n znalezionych przedmiotów powinien

zapakować złodziej do plecaka, aby zabrać najbardziej

wartościowy łup???

Przykładowe praktyczne zastosowania:

- pakowanie walizek, paczek

- załadunek statków, pociągów, samolotów

- obsługa magazynów

- itp.

Problem w ujęciu

analitycznym

Niech

w

i

będzie masą i-tego przedmiotu

p

i

wartością i-tego przedmiotu

a

W

to pojemność plecaka

Ponadto przyjmijmy, że:













zabrany

jest

nie

przedmiot

ty

i

gdy

plecaka

do

zabrany

jest

przedmiot

ty

i

gdy

x

i

,

0

,

1

Możemy zatem określić naszą funkcję celu:





n

i

i

i

x

p

1

max

przy ograniczeniu:







n

i

i

i

W

x

w

1

Jak zatem rozwiązać problem plecakowy?

1) Przegląd siłowy (

bruteforce

) - polega na sprawdzeniu

wszystkich możliwych kombinacji.

Zdecydowanie

najgorszy sposób, złożoność obliczeniowa algorytmu

Θ(2

n

)

, co znacznie zawyża czas działania dla dużych

n

.

Zapewnia

100%

skuteczność.

2) Algorytmy przybliżone (zachłanne) – ustalamy pewne

kryteria kolejności wkładania przedmiotów do plecaka.

 kryterium wartości

- maksymalizujemy wartość

plecaka wkładając jako pierwsze najbardziej
wartościowe przedmioty

 kryterium masy

- maksymalizujemy wartość

plecaka wkładając tak dużo przedmiotów jak to
możliwe

 kryterium wskaźnika wartości

- maksymalizujemy

wartość plecaka wkładając przedmioty których
stosunek

p

i

/w

i

jest jak największy

Czy ten algorytm jest optymalny?? Sprawdźmy na krótkim
przykładzie:

W = 100

i w

i

p

i

p

i

/w

i

1 100 40
0,4

2 50 35
0,7

3 45 18
0,4

4 20 4
0,2

5 10 10
1,0
6 5 2
0,4

kryterium

1

0

0

0

0

0

całkowita masa:

całkowita wartość:

0

0

1

1

1

1

100

40

80

34

0

1

0

1

1

1

85

51

0

1

1

0

0

1

100

55

rozw.

optymaln

e

wartość waga wsk.
wart

Wadą tej metody jest niepewność co do optymalności

otrzymanego upakowania, co widać na przykładzie.

3)

Programowanie dynamiczne

– rozwiązywany problem

dzielony jest na szereg prostych do rozwiązania
podproblemów, ale z uwzględnieniem dodatkowego warunku,
że wyniki każdego wcześniej rozwiązywanego podproblemu
mogą zostać wykorzystane do późniejszego rozwiązania
innych podproblemów. Technika ta często łączona jest z
metodą

backtrakingu

.

Algorytm działania programu na przykładzie:

Dane:

pojemność plecaka – 21
liczba znalezionych elementów – 4
masy elementów – v = [10, 7, 5, 5]

wartości elementów – w = [20, 15, 11, 12]

Program tworzy następującą tablicę D:

0

-1 -1 -1 -1 -1 -1

15

-1 -1

20

-1 -1 -1 -1 -1 -1

35

-1 -1 -1 -1

0

-1 -1 -1 -1

11

-1

15

-1 -1

20

-1

26

-1 -1

31

-1

35

-1 -1 -1 -1

0

-1 -1 -1 -1

12

-1

15

-1 -1

23

-1

27

-1 -1

31

-1

38

-1 -1

43

-1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

el 1 10

el 2 7
el 3 5

el 4 5

masa

0

-1 -1 -1 -1 -1 -1 -1 -1 -1

20

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

for (i=1; i<=n;i++)
for (j=0; j<=b; j++)
{
D[i][j]=D[i-1][j];
if (j>=v[i-1])
if ((D[i-1][j-v[i-1]]!=-1)&&(D[i-1][j-v[i-1]]+w[i-1]>D[i][j]))
D[i][j]=D[i-1][j-v[i-1]]+w[i-1];
}

0

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

for(j=1; j<=b; j+
+)
{
D[0][j]=-1;
}

backtracking

- odnalezienie elementów należących do optymalnego rozwiązania

43

20

-12

- 5

-11

- 5

masy elementów – v = [10, 7, 5, 5]
wartości elementów – w = [20, 15, 11, 12]

A więc optymalne elementy to: el1, el3 i el4

Ze zbudowanej tablicy łatwo odczytać że:
maksymalna wartość załadunku plecaka – 43
masa optymalnego załadunku – 20

Lecz nie widzimy bezpośrednio, które elementy należą

do optymalnego załadunku ???

0

-1 -1 -1 -1 -1 -1

15

-1 -1

20

-1 -1 -1 -1 -1 -1

35

-1 -1 -1 -1

0

-1 -1 -1 -1

11

-1

15

-1 -1

20

-1

26

-1 -1

31

-1

35

-1 -1 -1 -1

0

-1 -1 -1 -1

12

-1

15

-1 -1

23

-1

27

-1 -1

31

-1

38

-1 -1

43

-1

0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21

el 1 10

el 2 7
el 3 5

el 4 5

masa

0

-1 -1 -1 -1 -1 -1 -1 -1 -1

20

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

0

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1

-1 -1 -1 -1 -1 -1 -1 -1 -1 -1 -1

-20 = 0

-10 = 0

Literatura:

• M.M. Sysło, N. Deo i J.S. Kowalik, Discrete Optimization

Algorithms, Prentice-Hall, 1983 (polski przeklad pt. Algorytmy
optymalizacji dyskretnej, PWN, 1991).

• J. Cea, Optymalizacja: Teoria i algorytmy, PWN, Warszawa 1976.

• E. Pollak, Metody obliczeniowe optymalizacji. MIR, 1974.

• H. Kellerer, U. Pferschy, D. Pisinger , Knapsack Problems, Springer

Verlag

Strony www:

• http://pascal.lo2.opole.pl/pakowanie_plecaka.html

• http://pl.wikipedia.org/wiki/Problem_plecakowy

• http://encyklopedia.korba.pl/wiki/Problem_plecakowy

• http://www.nist.gov/dads/HTML/knapsackProblem.html

• http://www.ifors.ms.unimelb.edu.au/tutorial/knapsack

• http://www-

cse.uta.edu/~holder/courses/cse2320/lectures/l15/node3.html

• http://magma.maths.usyd.edu.au/magma/Examples/node7.html

O

p

ra

co

w

a

n

ie

p

ie

rw

sz

y

ch

sl

a

jd

ó

w

p

ro

je

k

tu

Pi

sa

n

ie

p

ro

g

ra

m

u

P

ra

ca

n

a

d

r

o

zw

ią

za

n

ie

m

a

n

a

lit

y

cz

n

y

m

,

o

k

re

śl

e

n

ie

m

o

żl

iw

y

ch

s

p

o

so

b

ó

w

ro

zw

ią

za

n

ia

.

P

rz

y

k

ła

d

y

za

st

o

so

w

a

n

ia

p

ra

k

ty

cz

n

e

g

o

O

p

ra

co

w

a

n

ie

sl

a

jd

ó

w

d

o

ty

cz

ą

cy

ch

ro

zw

ią

za

n

ia

p

ro

b

le

m

u

S

a

m

o

d

zi

e

ln

a

p

ra

ca

n

a

d

t

e

m

a

te

m

p

ro

je

k

tu

.

-n

ie

st

e

ty

b

e

z

e

fe

k

tu

I

sp

o

tk

a

n

ie

:

sp

re

cy

zo

w

a

n

ie

t

e

m

a

tu

p

ro

je

k

tu

.

C

o

p

o

w

in

n

iś

m

y

u

m

ie

śc

ić

?

R

o

zd

zi

e

le

n

ie

z

a

d

a

ń

p

o

sz

cz

e

g

ó

ln

y

m

o

so

b

o

m

.

II

I

sp

o

tk

a

n

ie

:

Z

e

b

ra

n

ie

p

rz

y

g

o

to

w

a

n

e

g

o

m

a

te

ri

a

łu

,

te

st

o

w

a

n

ie

p

ro

g

ra

m

u

,

d

y

sk

u

sj

e

o

r

ze

cz

y

w

is

ty

m

w

y

ko

rz

y

st

a

n

iu

p

ro

b

le

m

u

p

le

ca

ko

w

e

g

o

i

j

e

g

o

p

rz

y

d

a

tn

y

m

z

a

st

o

so

w

a

n

iu

.

IV

s

p

o

tk

a

n

ie

:

O

st

a

tn

ie

p

o

p

ra

w

k

i

d

o

p

ro

je

k

tu

,

p

rz

e

p

ro

w

a

d

ze

n

ie

p

ró

b

n

e

j

p

re

ze

n

ta

cj

i

In

d

y

w

id

u

a

ln

e

p

o

sz

u

k

iw

a

n

ia

l

it

e

ra

tu

ry

i

s

tr

o

n

W

W

W

.

D

o

kł

a

d

n

e

z

a

p

o

zn

a

n

ie

s

ię

z

p

ro

b

le

m

e

m

i

s

p

o

so

b

a

m

i

je

g

o

r

o

zw

ią

za

n

ia

.

II

s

p

o

tk

a

n

ie

:

b

u

rz

a

m

ó

zg

ó

w

,

w

y

m

ia

n

a

c

e

n

n

y

ch

i

n

fo

rm

a

cj

i,

o

p

ra

co

w

a

n

ie

p

la

n

u

p

ro

je

k

tu

.

O

p

ra

co

w

a

n

ie

o

st

a

tn

ic

h

sl

a

jd

ó

w

,

Po

łą

cz

e

n

ie

i

d

o

p

ra

co

w

a

n

i

e

c

a

łe

j

p

re

ze

n

ta

cj

i.

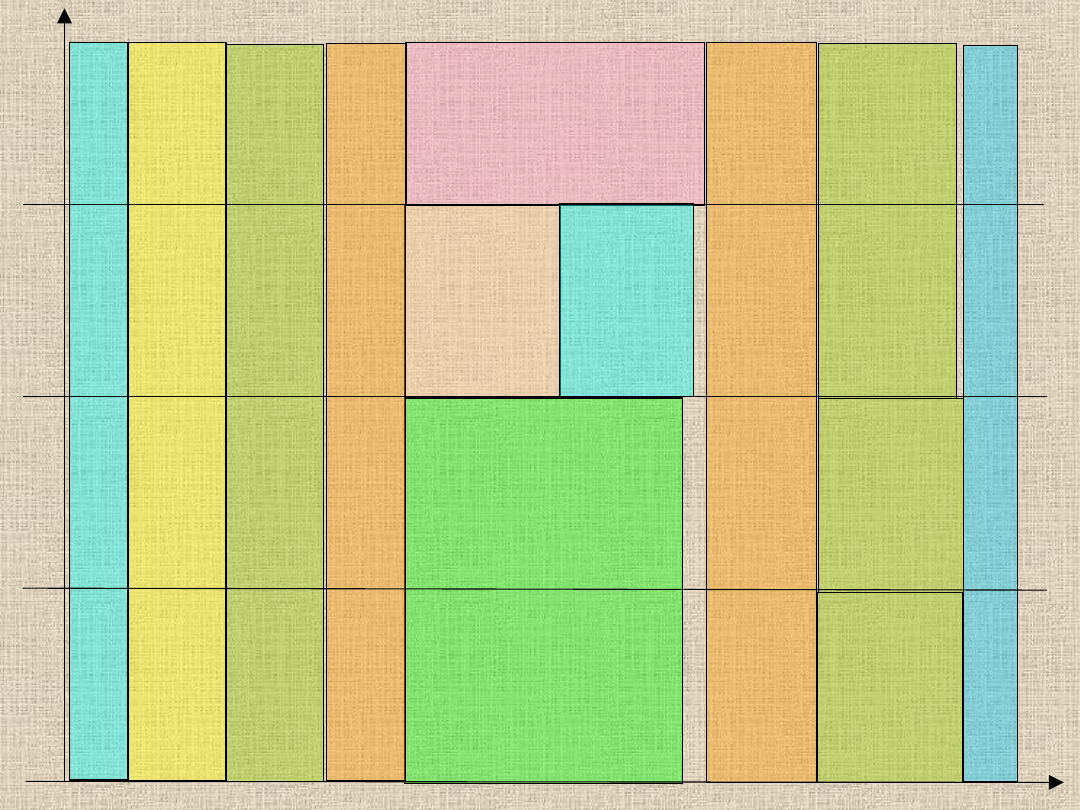
0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19
20 21godz

G

rz

e

g

o

rz

W

rę

b

ia

k

WYKRES GANTT’A

W

o

jc

ie

ch

J

a

ro

sz

S

ła

w

o

m

ir

T

a

jn

e

rt

A

rt

u

r

C

zu

p

ry

n

a