ZAAWANSOWANY MODEL

VaR

Małgorzata Murdzia

Katarzyna Jędrzejek

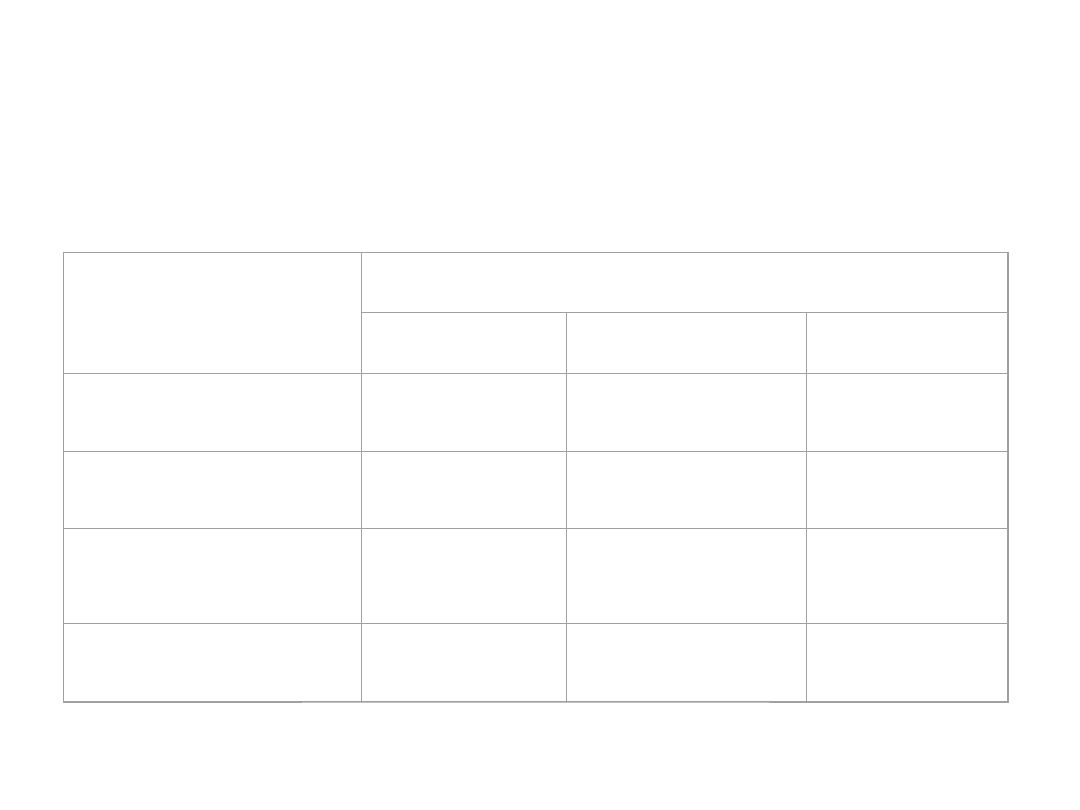
Założenia dla metod

podstawowych

Metoda VaR

Analityczna

Historyczna

Monte

Carlo

Współczynnik

ryzyka/Rozkłady

aktywa

Normalny

Brak założenia

Normalny

Rozkład P&L

Analityczny

(Normalny)

Empiryczny

(Historyczny)

Empiryczny
(Symulacja)

Wymagana macierz

kowariancji?

 

TAK

NIE

TAK

Współczynnik

ryzyka/Zwroty

aktywa

TAK

TAK

TAK

ZAŁOŻENIA ROZKŁADU

STANDARDOWEGO

• Zwroty są niezależne i o tym samym

rozkładzie normalnym

• Założenie o normalności wymaga

skośności i kurtozy równej zero (to
jest rzadki przypadek)

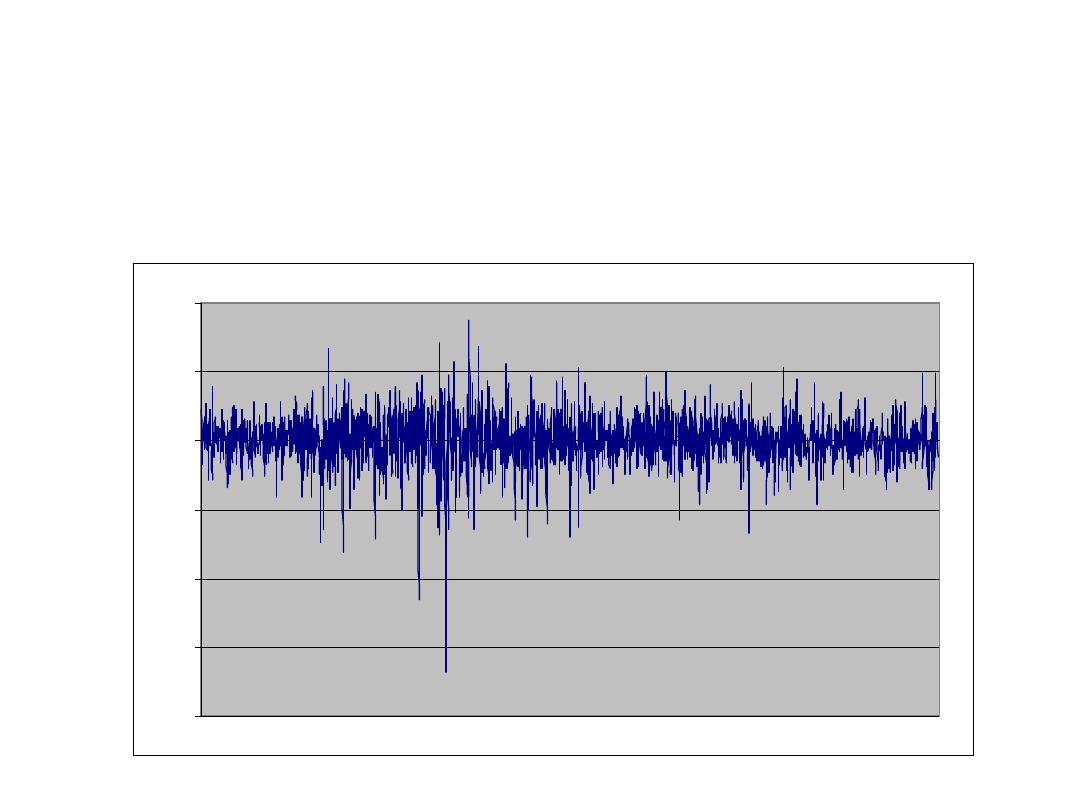
Zwroty USD/JPY od

01.01.1996 do 31.06.2004

-0,08

-0,06

-0,04

-0,02

0

0,02

0,04

0

500

1000

1500

2000

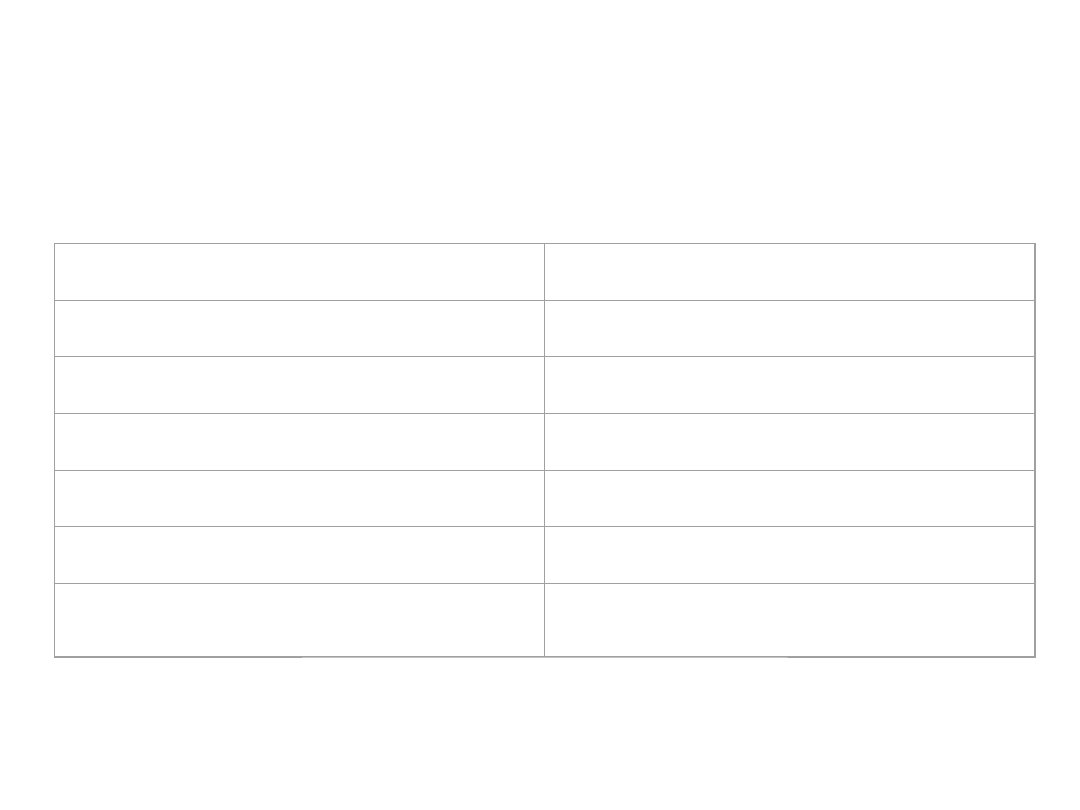
Przykład zwroty USD/JPY

Liczba obserwacji

2161

Średni zwrot

2.60047x10

-5

Odchylenie standardowe za dzień

0.718%

Zmienność

11.35%

Skośność

-0.8255

Kurtoza

6.241

Liczba obserwacji poniżej dolnej

granicy 99% przedziału ufności

48 wobec 22 oczekiwanych

 

• Średnia dziennych zwrotów jest bliska

zeru

• Ryzyko wyrażone na dwa sposoby:

odchylenie standardowe za dzień i

zmienność

• Skośność jest ujemna
• Kurtoza jest dodatnia co wskazuje na

ciężkie ogony w stosunku do rozkładu

normalnego

dzień

za

e

standardow

odchylenie

b

dni

b

z

e

standardow

odchylenie





Ujemna skośność i dodatnia kurtoza

powoduje, że prawdopodobieństwo ze
zwrotów jest lepsze od
przewidzianego przez rozkład
normalny. Wówczas wielkość VaR z
wysokim poziomem ufności obliczane
zgodnie z założeniem o normalności
będzie nieprawidłowe i w rezultacie
zapasy kapitału mogą być nie
wystarczające do zabezpieczenia.

Zgodnie z rozkładem normalnym,

dolna granica 99% przedziału ufności
zdefiniowana jest przez średnią
mniejszą od 2.33 odchylenia
standardowego. W naszym przypadku
dolna granica równa się

–2.33 x 0.00718=-0.0167

1% obserwowanych zwrotów będzie

niższy niż na wykresie. Z 2161
obserwacji tylko 22 zwrotów powinno
leżeć poniżej dolnego ogona (w
rzeczywistości jest ich 48)

• Dane finansowe naruszają

założenie o rozkładzie normalnym

• Jeżeli zwroty są identycznie

rozłożone to parametry rozkładu
(wariancja i średnia) powinny być
stałe

• Jeśli zwroty są niezależne to zwroty

z poprzedzającego dnia nie
powinny mieć wpływu na zwrot z
dnia aktualnego

• Analiza doświadczalna rynku

finansowego pokazuje że założenie
o niezależności zwrotów jest
bezpodstawne. Wysoki zwrot
prawdopodobnie następuje po
innym wysokim zwrocie. Zjawisko
to nazywa się „efektem
falowania zmienności” lub
„efektem grupowania
zmienności”

MODEL GRUPOWANIA

ZMIENNOŚCI

• Ruchoma wykładnicza średnia

ważona EWMA (exponentially
weighted moving average)

• GARCH (generalised autoagressive

conditional heteroscedasticity )
ogólny model autoregresji z
heteroskedastycznością warunkową

EMWA

Wariancja obliczana w i-tym dniu

λ - „wygładzanie stałej”
r

i-1

– zwrot z dnia i-1

Gdy λ jest dodatnia to dzisiejsza wariancja

jest dodatnio skorelowana z wczorajszą
wariancją

2

1

2

1

2

ˆ

)

1

(

ˆ











i

i

i

r









• Im wyższy parametr λ tym

wariancja ma wyższą tendencję do
utrzymywania się po wstrząsie na
rynku

• Wariancja EMWA reaguje

natychmiast na wstrząsy rynku

• Im większe 1- λ tym większa

będzie wielkość reakcji na wstrząs
zwrotu

Model zmienności GARCH opiera się na

danych statystycznych firmy, natomiast
model zmienności EMWA nie, gdyż:

• Nie ma procedury estymacji wygładzonej

stałej, wartość λ się zakłada (zazwyczaj
stosowana jest λ =0.94)

• Dla pewnego portfela obliczana wariancja

może być ujemna, gdy macierz
kowariancji jest pół określona. Dlatego
dla EMWA nie można używać różnej
wartości λ dla różnych aktywów do
wyznaczania macierzy kowariancji

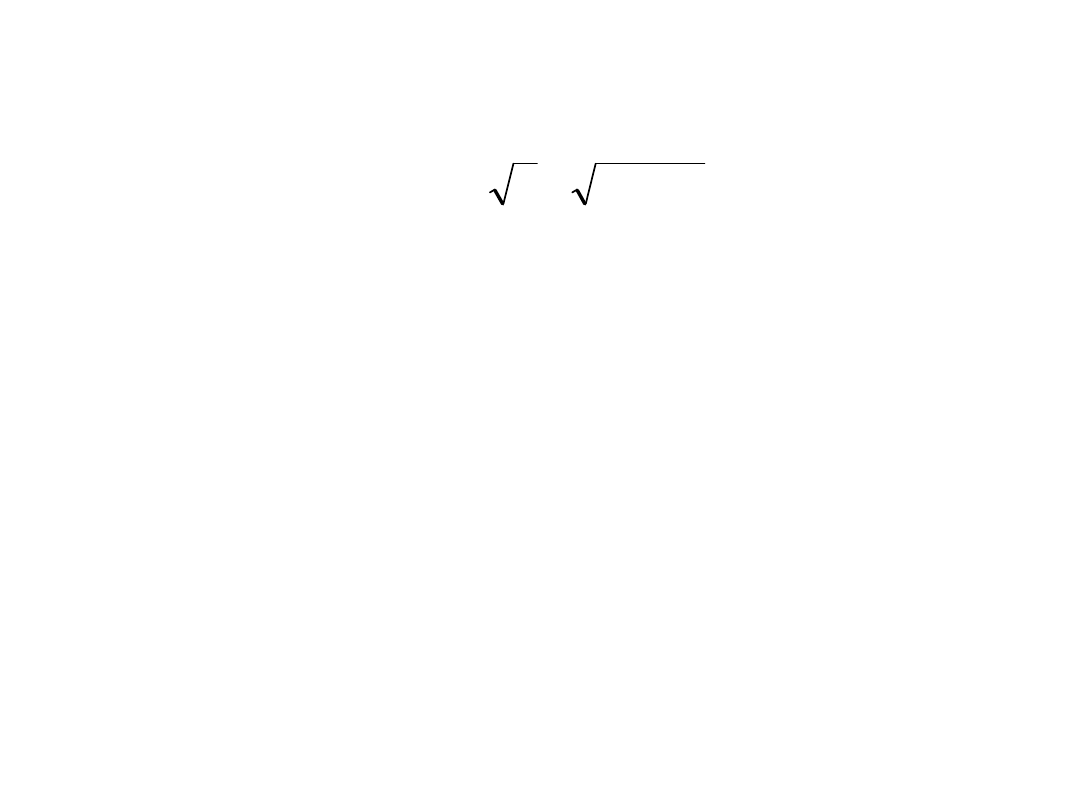
Model EMWA nie jest odpowiedni dla

estymowania ewolucji rynku dla
horyzontu czasowego dłuższego niż
kilka dni

b

b

/

250

ˆ

dni

b

horyzontu

dla

t

czasie

EMWA w

zmienno

śm

Estymowa

t







Standaryzowane zwroty

USD/JPY (02.1996-087.2004)

e

standardow

odchylenie

zwrot

wany

standaryzo

Zwrot



Liczba obserwacji

2140

Skośność

-0.1974

Kurtoza

0.2727

Liczba obserwacji poniżej

dolnej granicy 99%

przedziału ufności

29 wobec 21 oczekiwanych

Model GARCH

Równanie na warunkową średnią i

wariancję

Parametry α, β, ω są estymowane za

pomocą metody największej
wiarygodności

c- średnia

0

,

,

0

2

1

2

1

2



































i

i

i

i

i

c

r

Gdy wtedy mówi się, że

zmienność jest średnio
powracająca (mean-reverting) i
stosunek powrotu średniej jest
odwrotnie powiązany z tą sumy,
czyli wariancja będzie zwykle
bliska steady-state wariancji
definiowanej w następujący sposób

1























1

2

Przykład: model GARCH dla

USD/JPY

Obliczamy model GARCH(1,1) dla dziennych
zwrotów. Warunkowa wariancja obliczana

metodą największej wiarogodności:

Warunkowa wariancja jest stała

(współczynnik stałości=0.955710) i nie

szczególnie reagująca w porównaniu z innymi

rynkami (współczynnik reakcji =0.03684) ,

stały okres (3.78x10

-7

) jest mały

2

1

2

1

7

2

95571

.

0

03684

.

0

10

78

.

3















t

t

t







Steady-state wariancja

Zmienność = =11,24%
(wynik bliski zmienności = 11,35%)

250





5

7

2

10

07

,

5

95571

,

0

03684

,

0

1

10

78

,

3



















Grupowanie zmienności i

VaR

Wybór miary zmienności ma duży

wpływ na miarę ryzyka i
konsekwencje dla odpowiedniego
kapitału. Złe obliczenie zmienności
grupowanej może spowodować, że
instytucja finansowa weźmie zbyt
wysokie ryzyko (albo będzie trzymać
niewystarczającą ilość kapitału) w
okresie kryzysu na rynku.

Obliczanie VaR używając

EMWA

Równanie dla kowariancji między

aktywami 1 i 2 :

r

1,t-1

,r

2,t-1

zwroty z dnia wcześniejszego

dla aktywa 1 i 2

λ =0,94

1

,

12

1

,

2

1

,

1

,

12

ˆ

)

1

(

ˆ













t

t

t

t

r

r









VaR b-dni - metoda

analityczna

Z

α

- dystrybuanta

rozkładu

standardowego normalnego dla
wartości krytycznej α

P -wartość bieżąca portfela
σ -przewidywane odchylenie

standardowe z

b-dni ze zwrotów portfela







P

Z

VaR

b



,

Odchylenie standardowe

Odchylenie standardowe oblicza się używając

macierzy kowariancji zwrotów z b-dni następująco

1. Reprezentacja poziomu aktywów

w=(w

1

,..., w

n

) wektor wag portfela

V - przewidywana macierz kowariancji zwrotów

aktywa z b-dni

wektor kwoty inwestowanej w każde aktywo

Vw

w

T





,

Pw

p

gdzie

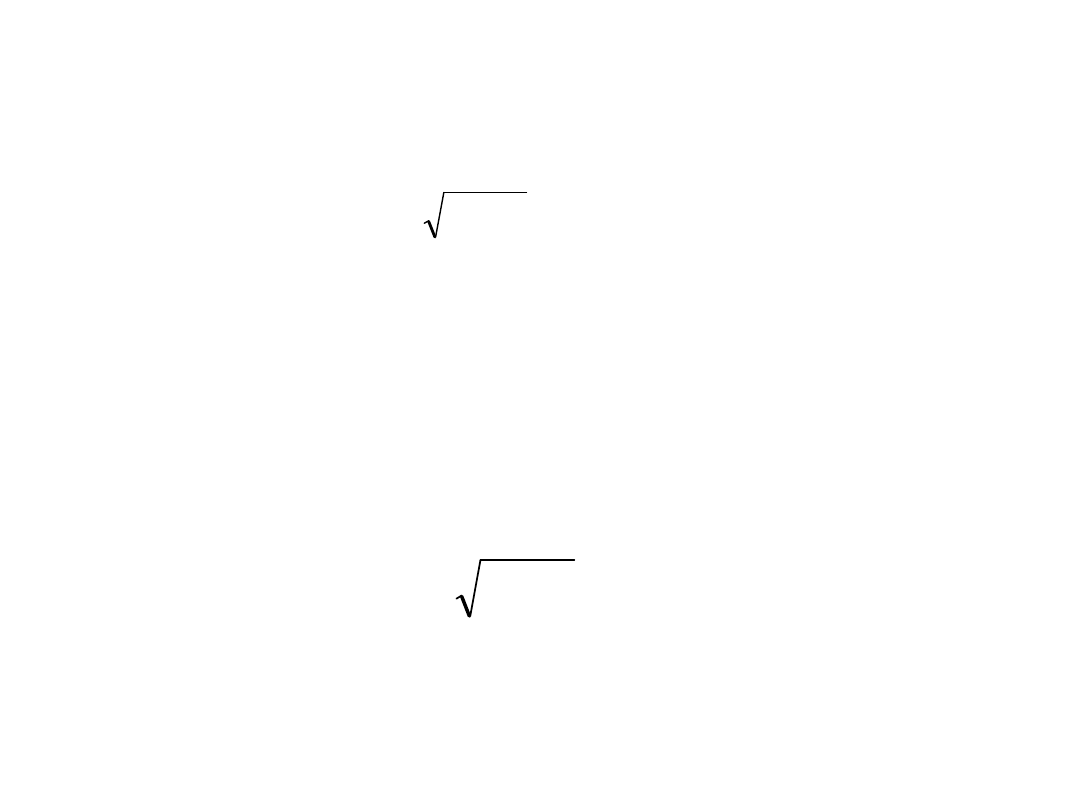
Vp

p

Z

VaR

T

b









2. Reprezentacja poziomu czynnika

ryzyka

gdzie wektor wrażliwości

portfela

V - przewidywana macierz kowariancji

zwrotów czynnika ryzyka z b-dni

gdzie
wektor wrażliwości dla

każdego czynnika ryzyka







V

T



)

,...

(

1

n









Vp

p

Z

VaR

T

b







,



P

p

Przykład

Inwestujemy 1m $ w aktywo 1 i 2m $

w aktywo 2

Obliczyć 5% 10-dniowego VaR-u.
P=(1,2)

T

zmienność

0,002

0,005,

,

01

,

0

12

2

2

2

1



























005

,

0

002

,

0

002

,

0

01

,

0

V

$

014

,

1

10

3207

,

0

VaR

dniowy

-

10

%

5

$

3207

,

0

19

,

0

645

,

1

VaR

dniowy

-

1

%

5

$

19

,

0

038

,

0

L

&

P

m

m

m

Vp

p

T



















Przewidywanie zmienności z

GARCH

Zakładamy:
Średni zwrot =0
Wariancja warunkowa dana wzorem:

Steady-state wariancja =0.0001

2

1

2

1

6

2

88

.

0

07

.

0

10

0

.

5















t

t

t







0001663

,

0

0001698

,

0

)

88

,

0

07

,

0

(

10

5

0001698

,

0

00006

,

0

88

,

0

)

04

,

0

(

07

,

0

10

5

00006

,

0

%,

4

6

2

2

2

6

2

1

2







































t

t

t

t









Przewidywane zmienności z

GARCH

ZMIENNOŚĆ Z 10 DNI=

DZIEŃ

WARIANCJA

ZMIENNOŚĆ

T+1

0,0001698

20,6%

T+2

0,0001663

20,4%

T+3

0,0001630

20,2%

T+4

0,0001598

20,0%

T+5

0,0001569

19,8%

T+6

0,0001540

19,6%

T+7

0,0001513

19,4%

T+8

0,0001487

19,3%

T+9

0,0001463

19,1%

T+10

0,0001440

19,0%

 

HORYZONT 10 DNI

0,0015601

19,7%

%

7

,

19

10

250

10

1

2









i

i



VaR z rozkładem t-Studenta

• Rozkład t-Studenta jest możliwym

kandydatem opisywania stopy zwrotu
instrumentów finansowych ze względu na
„grube ogony”. Obecnie nie jest on
najlepszym kandydatem, ponieważ
zakłada on, że stopy zwrotu są iid.
Przyjmując, że dzienne stopy zwrotu mają
rozkład t-Studenta zakładamy, że
są niezależne od wcześniejszych stóp.

VaR z rozkładem t-Studenta

• Rozkład t-Studenta pozostaje dość

popularny wśród profesionalnych
managerów ryzyka. Standardowy test
t-Studenta ma tylko jeden
parametr v , oznaczający liczbę stopni
swobody. Rozkład ten został stworzony
do pracowania z małymi próbami,
gdzie liczba stopni swobody jest o
jeden mniejsza od rozmiaru próby.

• Dla standardowego rozładu t-

Studenta zachodzi:

• Odchylenie standardowe jest równe 0
• Wariancja jest równa
• Skośność jest równa 0
• Kurtoza jest równa

2







4

)

2

(

3









• Używając VaR będziemy pracować z

dużym zbiorem danych i postaramy się

sztucznie dobrać parametr v pasujący do

kształtu ogonów rozkładu t (tj. dobrze

dopasowany do wzoru na kurtozę).

Ponieważ obserwowana wariancja nie

będzie równa będzie konieczne

oszacować wariancję. Generalnie nie

będzie konieczne oszacować średnią jako

średnią stopę zwrotu (dzienną, tygodniową

czy inną) bliską 0.

2







• Dowd w 2002 roku wyjaśnił następująco jak można

przystosować standardowy rozkład t-Studenta do

obliczenia VaR dla pojedynczego aktywu:

• Wybrać parametr stopni swobody dobrze

dopasowany do wzoru na kutrozę :

• Wariancja empiryczna powinna być bliska
• Wybrać odpowiednią wartość krytyczną z

rozkładu t dla pożądanego poziomu ufności (np.

0,01) i wybranych wcześniej stopni swobody

• Kontynuować obliczenia z VaR używając np.

metod analitycznych.

4

)

2

(

3









2







VaR z mieszanym rozkładem

normalnym

• Funkcja gęstości mieszanego rozkładu normalnego,

np. złożonego z dwóch funkcji gęstości rozkładu
normalnego

i ma funkcję

gęstości

parametr p może być rozumiany jako

prawdopodobieństwo tego, że obserwacja x wpływa
na gęstość f

1

(x). W rezultacie mamy, że raz

x ma odchylenie standardowe µ

1

i wariancję drugi

raz x ma odchylenie standardowe µ

2

i wariancję .

)

,

;

(

)

(

2

1

1

1







x

x

f



)

,

;

(

)

(

2

2

2

2







x

x

f



)

(

)

1

(

)

(

)

(

2

1

x

f

p

x

pf

x

g







2

1



2

2



• Rozważmy mieszany rozkład normalny o

zerowym odchyleniu standardowym
swoich składników, tzn. µ

1

=µ

2

=0. W tym

przypadku wariancja wynosi

• Skośność jest równa 0 zaś kurtoza

2

2

2

1

)

1

(

)

2

(





p

p

wariancja

NM







2

2

2

2

1

4

2

4

1

]

)

1

(

[

)

1

(

3

)

2

(









p

p

p

p

kurtoza

NM











• Kurtoza jest zawsze większa od 3,

więc mieszany rozkład normalny z
dwoma składnikami o zerowym
odchyleniu standardowym daje
nam funkcję gęstości, której
wykres ma wyżej wierzchołek i
grubsze ogony niż rozkład
normalny o tej samej wariancji.

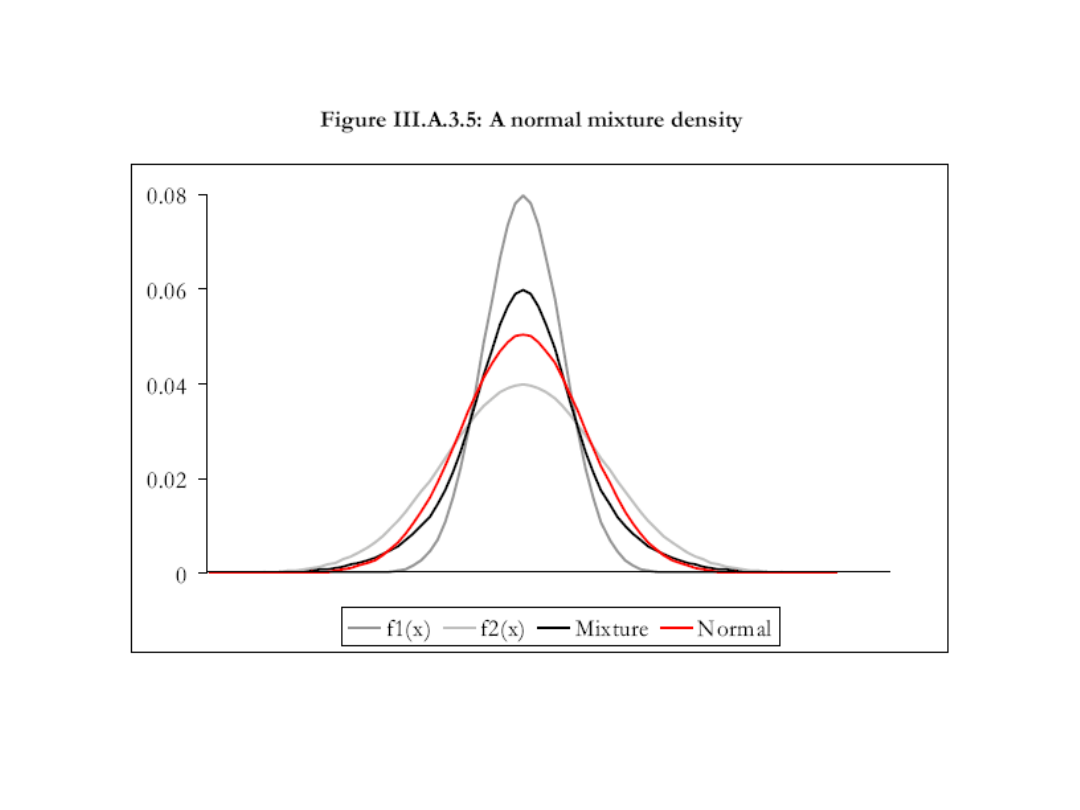
• Dla przykładu powyższy rysunek

przedstawia wykres czterech funkcji
gęstości:

 3 spośród nich to gęstości rozkładu

normalnego o zerowym odchyleniu
standardowym ze zmiennością 5%, 10%
(szare) i 7,906%(czerwony)

 Mieszany rozkład normalny (na rys. czarny),

składa się z dwóch pierwszych funkcji
gęstości z wagą prawdopodobieństwa 0.5

• Wariancja mieszanego rozkładu wynosi

0,5*5

2

+0,5*10

2

=62,5. Ponieważ

7,906

2

=62.5 to mieszany rozkład ma

taką samą zmienność jak rozkład
normalny narysowany na czerwono.
Jednakże jego kurtoza wynosi 4,87.
Innymi słowy kurtoza jest za duża o
1,87 co jest znacznie większe od 0
odpowiadającemu rozkładowi
normalnemu.

• Bardziej ogólnie: biorąc kilka składników

o różnych odchyleniach standardowych i
wariancjach do rozkładu mieszanego
możemy doprowadzić do prawie
każdego kształtu dla gęstości.
Maclachlan i Peel w 2000 roku
dostarczyli kilku interesujących
przykładowych wykresów. Parametry
funkcji gęstości mieszanego rozkładu
normalnego mogą być szacowane przy
użyciu danych historycznych.

• Nie ma wyraźnej formuły dla

oszacowania VaR zakładającego, że
stopy zwrotu portfela mają gęstość
mieszanego rozkładu normalnego. Jest
uwikłana formuła, którą w exelu
możemy rozwiązać wykorzystując np.
solver. Żeby zobaczyć jak przypuśćmy,
że mamy rozkład normalny dla
zmiennej P&L portfela liniowego.

• Wtedy analityczna formuła VaR wynika

wprost z definicji, czyli:

P(P&L<-VaR

α

)=α

• więc jeśli P&L ma rozkład normalny z

parametrami µ i σ to mamy

P(Z<[- VaR

α

-

µ]/σ= α

• Gdzie Z jest zmienną losową o

standardowym rozkładzie normalnym. Stąd

[- VaR

α

-

µ]/σ= -Z

α

α jest wartością krytyczną

Z i przekształacając otrzymujemy

analityczną formułę dla normalnego VaR:

VaR

α

=

Z

α

σ-

µ

Incremental VaR

IVar

• Incremental VaR mierzy jak każdy

składnik portfela wpływa na ryzyko

portfela.

• VaR

Incremental,A

=VaR

P+A

-VaR

P

• VaR

P+A

-ryzyko portfela zawierającego

pozycję A

• VaR

P

-ryzyko portfela nie

zawierającego pozycji A

Incremental VaR

IVar

• Innymi słowy IVar mówi nam, jaki

wkład w ryzyko (mierzone przez VaR)
portfela będzie miało dodanie jednej
pozycji. Incremental VaR zawsze
musi być rozpatrywany w kontekście
konkretnego portfela, ponieważ ta
sama pozycja będzie miała różny
Incremental VaR w różnych
portfelach.

Component VaR

CVaR

• Component VaR mówi, o ile zmieni się VaR

całego portfela, gdy usuniemy z portfela
daną pozycję. Component VaR mówi o
ryzyku pozycji obecnej a portfelu. Każdy
składnik portfela ma swój Component VaR,
a suma Component VaR wszystkich
instrumentów w portfelu daje VaR portfela:







n

i

VaR

1

i

VaR

Component