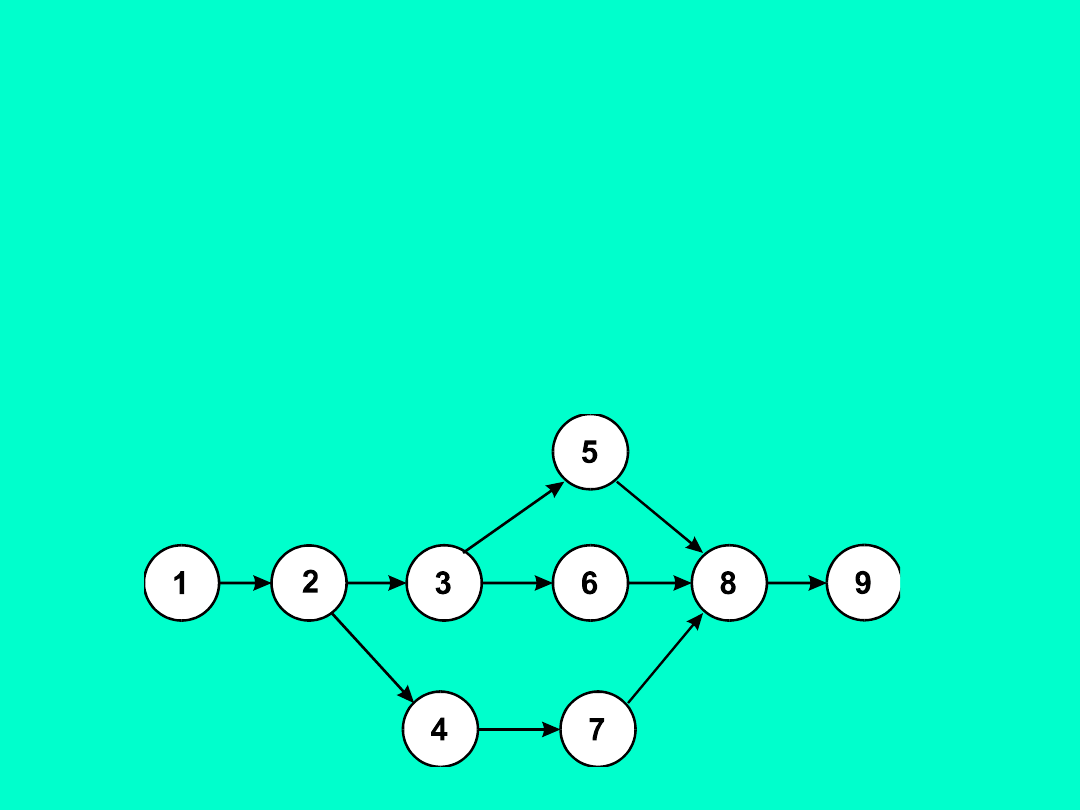
1

Metody sieciowe:

Metody sieciowe oparte są na specjalnych
wykresach

zwanych

sieciami

czynności.

Wykorzystywane są one do harmonogramowania i
kontroli złożonych przedsięwzięć gospodarczych,
technicznych i organizacyjnych.

Wykres

sieciowy

ilustruje

przebieg

całego

przedsięwzięcia bazując na dwóch zasadniczych
elementach: czynnościach i zdarzeniach

2

Zastosowanie metod sieciowych

umożliwia:

•

ustalenie programu działania (co, gdzie i w jakiej
kolejności ma być wykonane),

•

określenie terminów rozpoczęcia i ukończenia
poszczególnych czynności oraz czasu wykonania
całego programu,

•

określenie tzw. „czynności krytycznych”, tj. takich,
od których zależy termin wykonania całego
projektu,

•

przydział ograniczonych zasobów gwarantujący
wykonanie projektu,

•

bieżącą kontrolę terminów wykonania oraz
korektę harmonogramu w przypadku zagrożenia
terminu wykonania projektu.

3

Zasady wykonywania wykresu

sieciowego:

•

Zdarzenia

początkowe

nie

mają

czynności

poprzedzających.

•

Zdarzenia

końcowe

nie

mają

czynności

następujących.

•

Wykres sieciowy może mieć kilka początkowych i

kilka końcowych zdarzeń, w tym przypadku:

- zdarzenia początkowe łączy się czynnościami

pozornymi

w jedno zdarzenie początkowe,

- zdarzenia końcowe łączy się pozornymi

czynnościami w

jedno zdarzenie końcowe,

•

Nie wykonuje się wykresu sieciowego w skali

czasu.

•

Dane zdarzenie nie może nastąpić, dopóki nie

będą

zakończone

wszystkie

czynności

warunkujące zajście tego zdarzenia.

•

Żadna czynność nie może być rozpoczęta, dopóki

nie będą zakończone zdarzenia poprzedzające tę

czynność.

4

•

Pomiędzy dwoma zdarzeniami może być tylko jedna
czynność przedstawiona strzałką.

•

Strzałki przedstawiające czynności powinny być
skierowane z lewej strony do prawej.

•

Należy unikać skrzyżowań strzałek.

•

Oznaczenie zdarzeń powinno spełniać warunek, że
liczba oznaczająca zdarzenie następne jest większa
od liczby oznaczającej zdarzenie poprzedzające.

•

Wykres sieciowy nie powinien mieć zdarzeń, z
których nie wychodzi żadna czynność (wyjątek
zdarzenia końcowe) i zdarzeń, do których nie jest
doprowadzona ani jedna czynność (wyjątek zdarzenia
początkowe).

•

Wykres sieciowy nie powinien mieć obiegów
zamkniętych, tj. pętli, które łączą dwukrotnie te
same zdarzenia.

5

Elementy składowe wykresu

sieciowego:

Symbol

Nazwa

Znaczenie

Czynno

ść

Zadania występujące w projekcie,
ze

zdefiniowanym

terminem

rozpoczęcia i zakończenia. Zadanie
związane jest z upływem czasu.
Długość strzałki nie ma znaczenia.

Przykładem czynności mogą być:
obróbka części, montaż zespołu.

Czynno
ść

pozorna

Czynność pozorna nie jest związana
z upływem czasu. Łączy zdarzenia,
między którymi nie jest wymagane

wydatkowanie środków, lecz istnieje
następstwo czasowe.

Zdarze

nie

Zdarzenie

oznacza

moment

ukończenia (lub początku) jednej
lub kilku czynności.

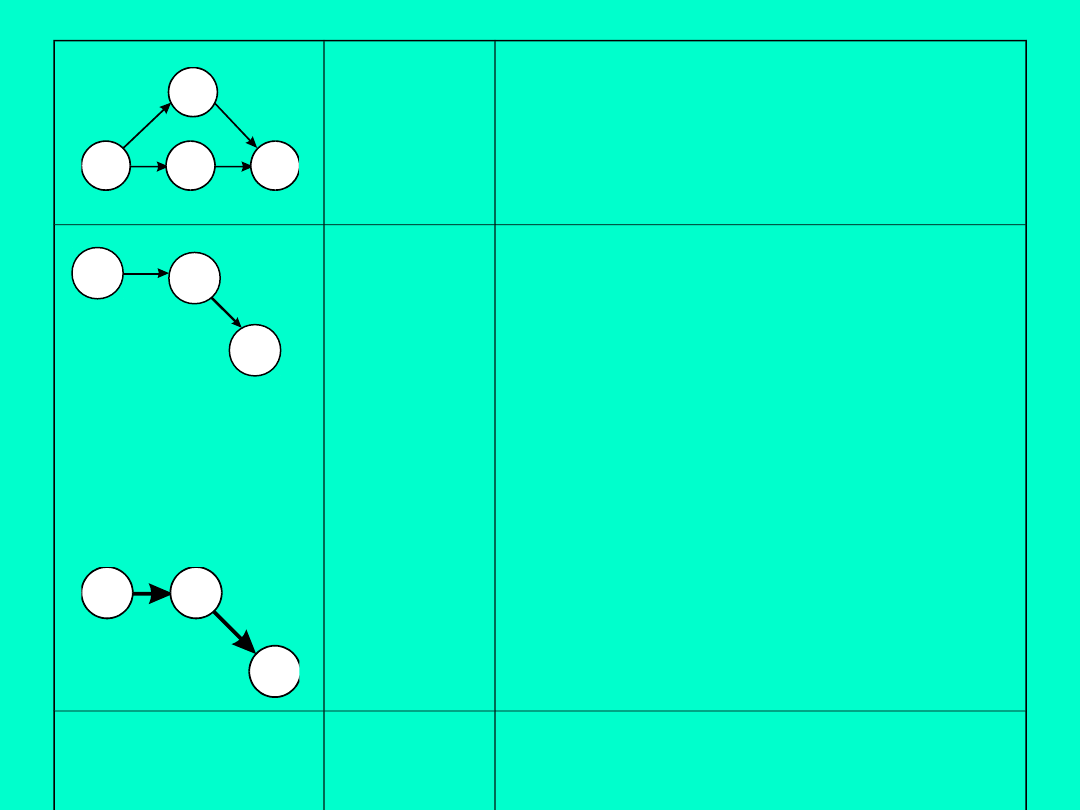
6

Sieć

Kolejność

wszystkich

czynności

projektu.

Zdarzenia

połączone

strzałkami.

Droga
(ścieżka

)

Część

projektu,

zaczynająca

się

od

pierwszej

czynności

a

kończąca się czynnością

ostatnią.

Dla

każdej

czynność określony jest

tylko

jedna

czynność

następująca po niej. Każdą

parę wierzchołków łączy
tylko

jedna

strzałka

(czynność).

Droga
(ścieżka

)
krytycz

na

Ścieżka, z której czynności
zajmą

najwięcej

czasu

(determinują czas realizacji
projektu).

7

Metoda sieciowa realizowana jest w

następujących krokach:

1. Definiowanie wszystkich czynności projektu.

2. Ustalenie następstwa czasowego czynności.

3. Wykreślenie w formie diagramu następstwa

czasowego czynności.

4. Oszacowanie czasu trwania każdej czynności.

5. Obliczenie ścieżki krytycznej.

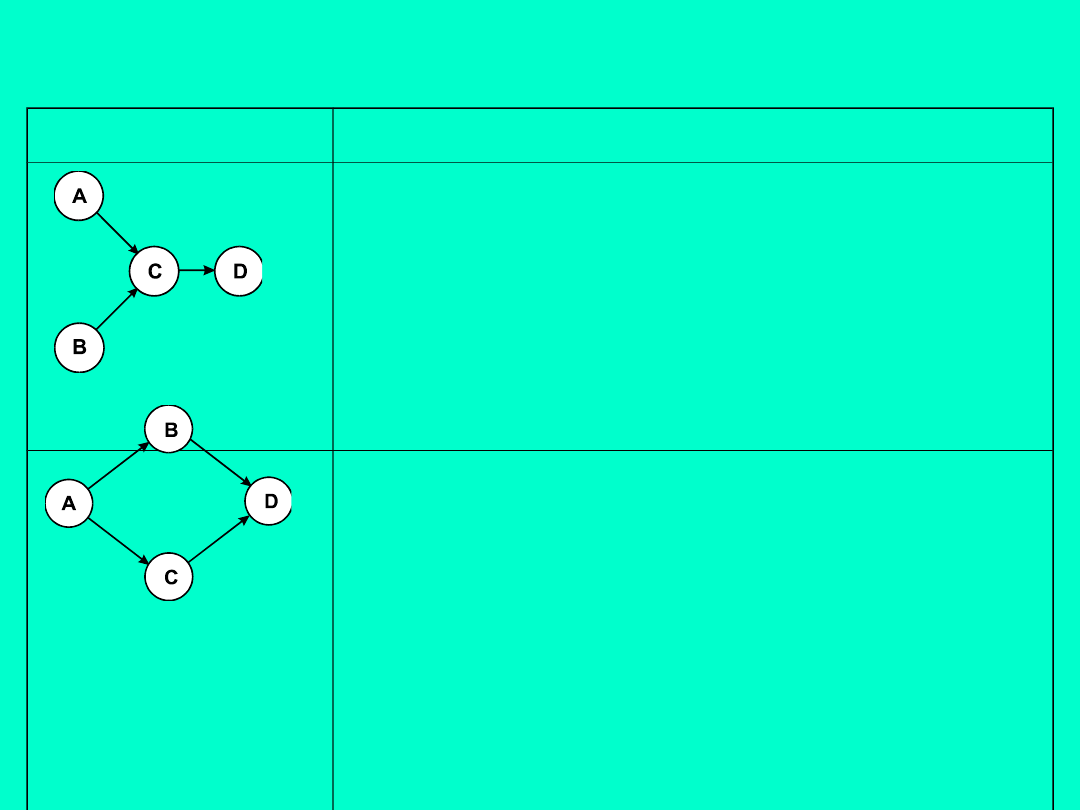
8

Przykłady prostych sieci:

Sieć

Znaczenie

Sieć reprezentuje trzy czynności AC, BC i
CD. Czynność CD nie może się rozpocząć

zanim nie zakończy się czynność AC i BC.
Czynność AC i BC mogą przebiegać
równocześnie.

Nazywa

się

je

czynnościami

równoległymi

(współbieżnymi).

Czynność BD nie może się rozpocząć
dopóki nie skończy się czynność AB.
Czynność CD nie może się rozpocząć

dopóki nie skończy się czynność AC.
Ścieżki AB-BD i AC-CD są ścieżkami
równoległymi. Czynność AC nie musi się

rozpocząć w tym samym czasie co
czynność AB. Podobnie czynność BD nie
musi się zakończyć w tym samym czasie

co czynność CD. Czynność BD może być
zakończona przed czynnością AC.

9

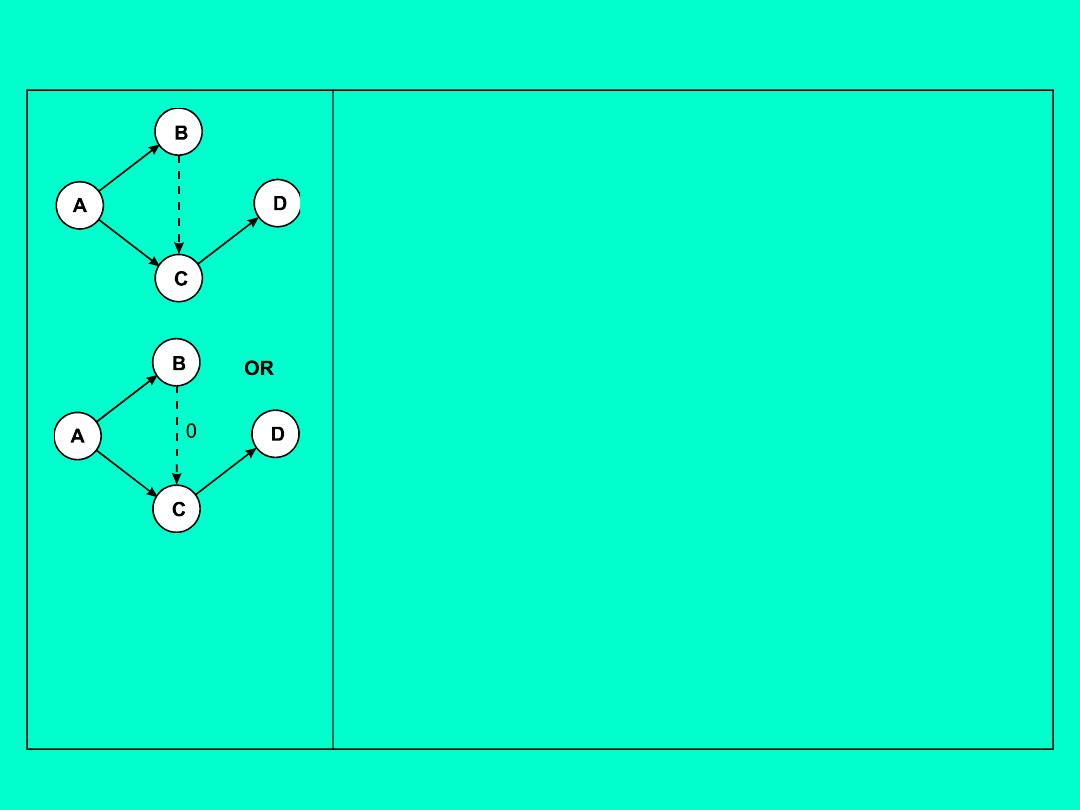
Czynność BC jest czynnością pozorną.
Używa się jej w celu uzyskania

pożądanego następstwa czasowego.
Może być symbolizowana w dwojaki

sposób, tak jak to jest przedstawione
na

schematach

obok.

Czynność

pozorna nie trwa i nie wymaga
wydatkowania

środków.

Użycie

czynności

pozornej

pozwala

na

jednoznaczną identyfikację czynności
za pomocą pary węzłów. Czynność CD

nie może się rozpocząć zanim nie
zakończą się czynności AB i AC. W

sieci są dwie ścieżki: AB-BC-CD i AC-
CD.

10

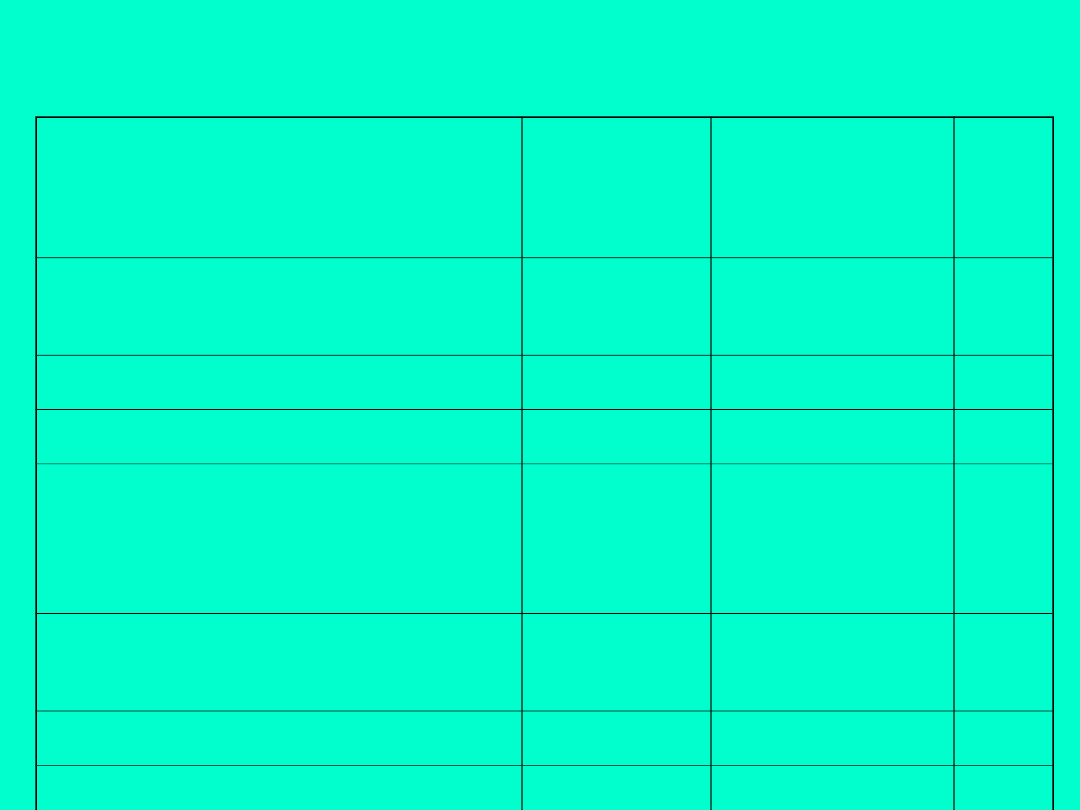
Przykładowy projekt:

Zdarzenia

Oznacze

nie

Zdarzenie

poprzedzaj

ące

Cza

s

Uzyskanie pozwolenia na
budowę

A

-

2

Wykonanie fundamentów

B

A

1

Wykonanie ścian i dachu

C

B

1

Instalacje wodno-

kanalizacyjna
i CO

D

C

2

Instalacja gazowa i

elekteryczna

E

C

5

Wykończenie

F

D, E

5

Odbiór

G

F

1

11

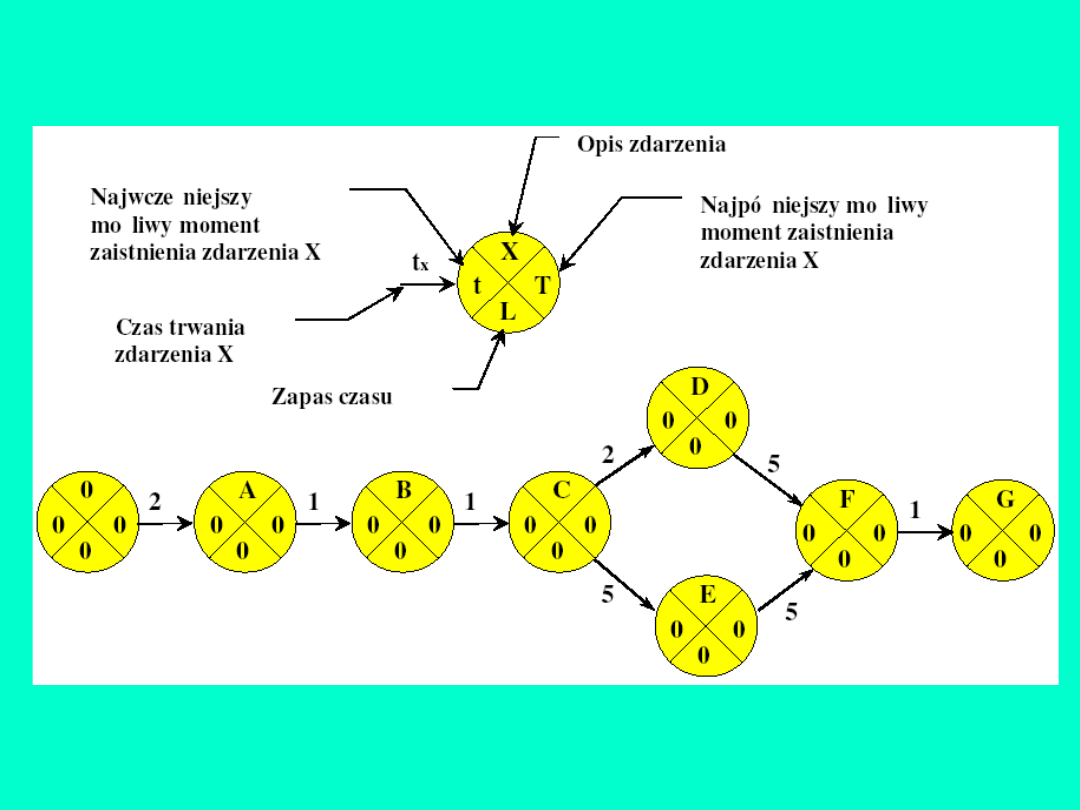
Tworzenie sieci CPM:

ś

ż

ź

ż

12

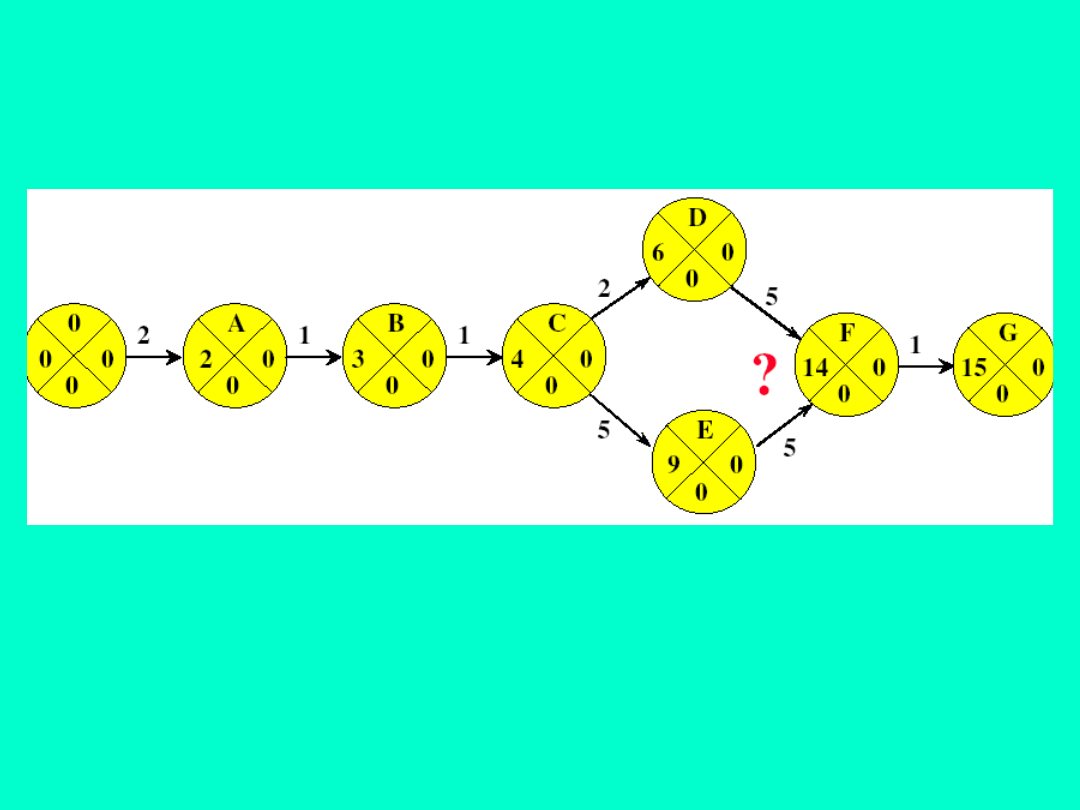
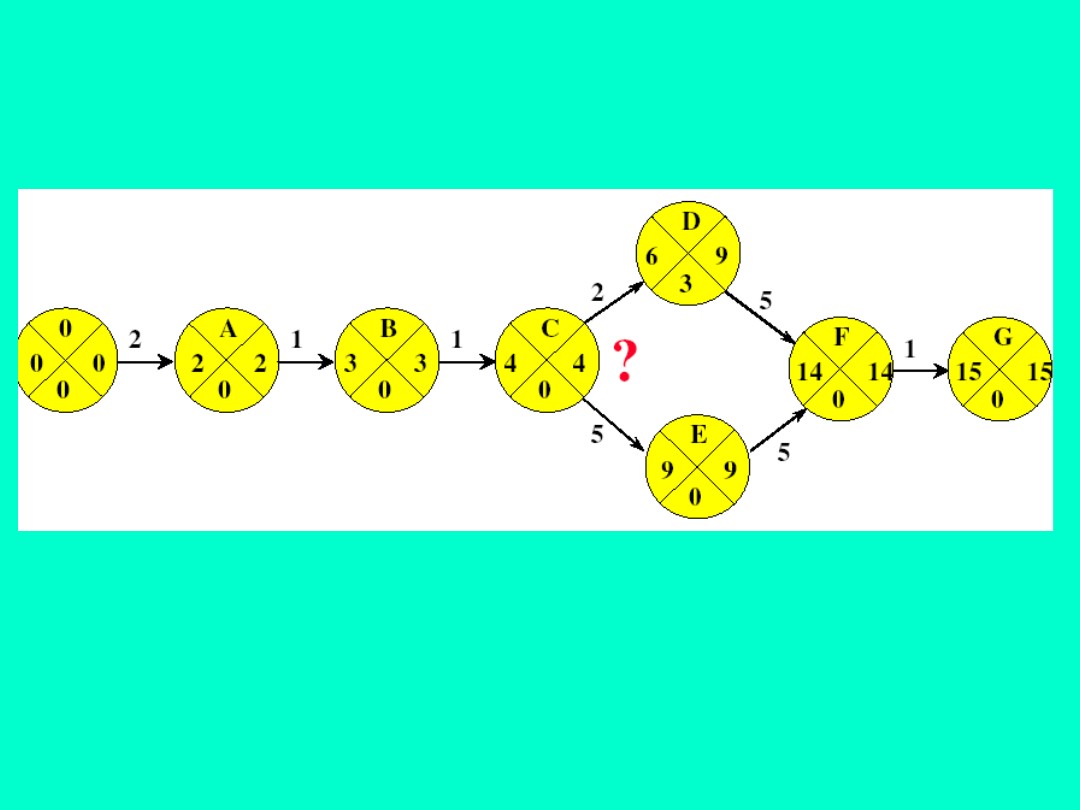
Określenie najwcześniejszych

możliwych momentów zaistnienia

zdarzeń:

t

j

= max{t

i

+ t

i-j

} => t

j

= max{6+5;9+5} = 14

13

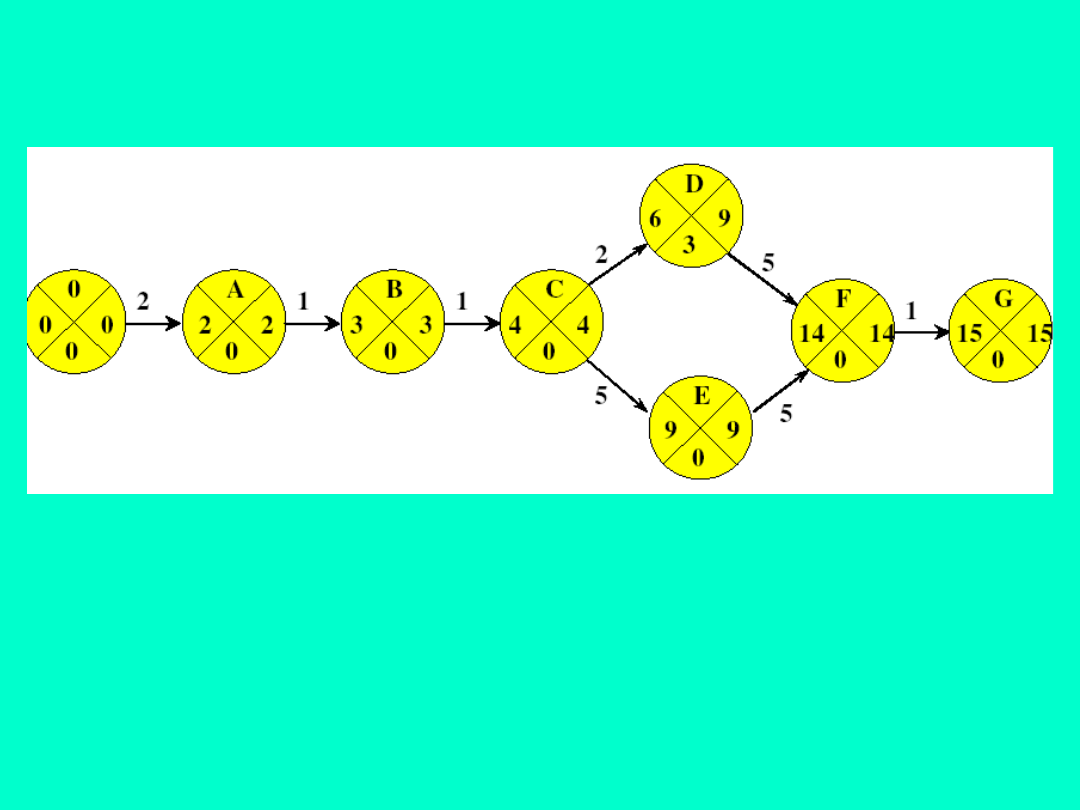
Określenie najpóźniej szych

możliwych momentów zaistnienia

zdarzeń:

t

i

= min{t

j

- t

i-j

} => t

i

= min{9-2;9-5}=4

14

Czas realizacji projektu:

Czas realizacji projektu: 2+1+1+5+5+1=15

jednostek

15

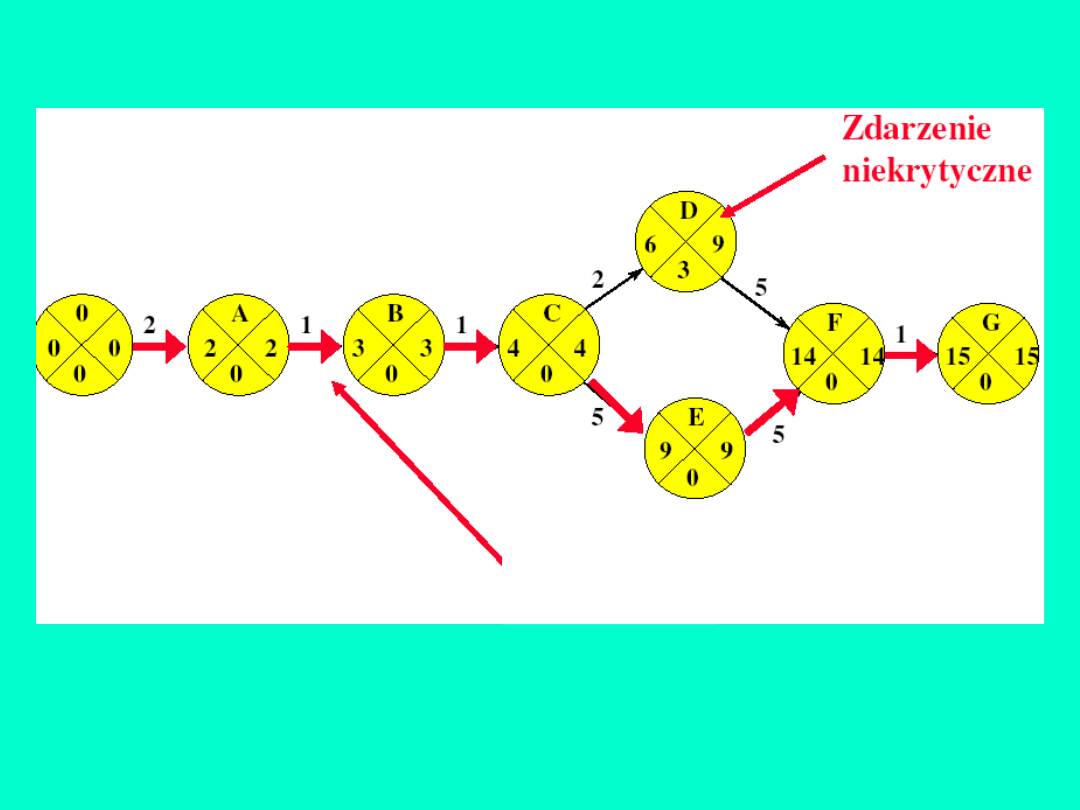
Zdarzenia niekrytyczne i ścieżka

krytyczna

Ścieżka
krytyczna

2+1+1+2+5+1=12

2+1+1+5+5+1=15