stationary gas power-

station

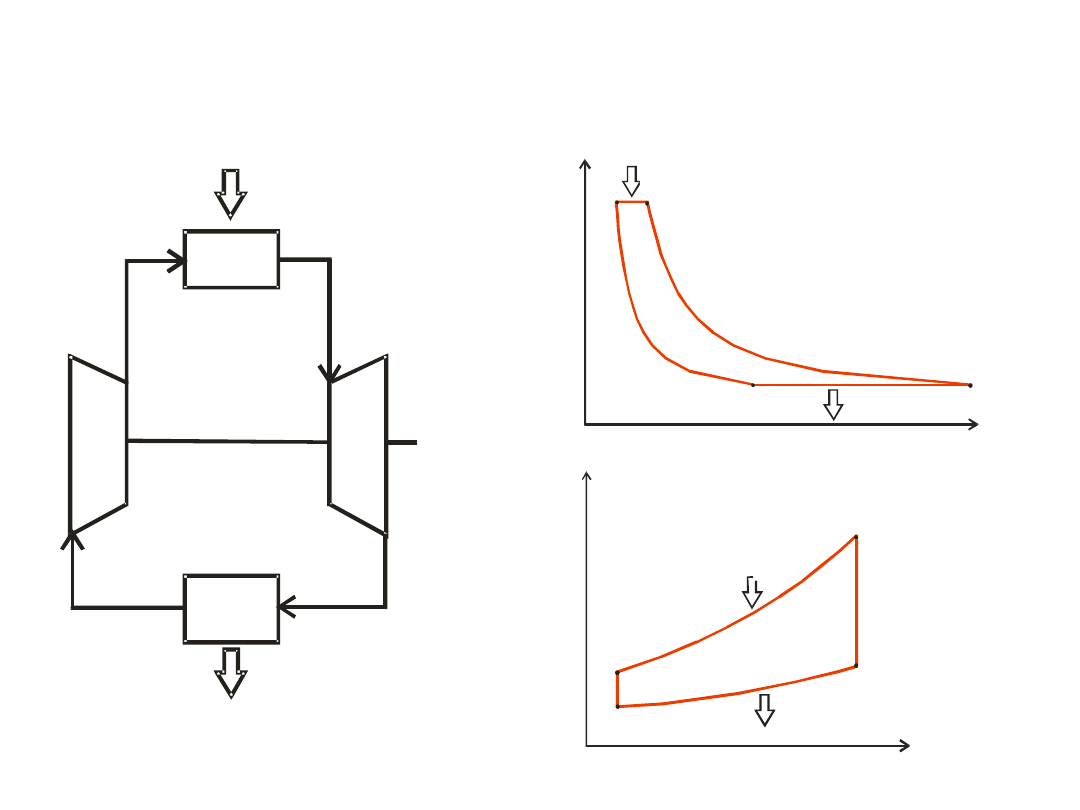
Joule cycle

Brayton-Armengaud cycle

1

2

4

3

q

o

q

d

P

m

1

2

3

4

Q

d

q

o

T

s

1

2

3

4

Q

d

q

o

P

V

closed system

q

d

q

d

Theroretical – model
case

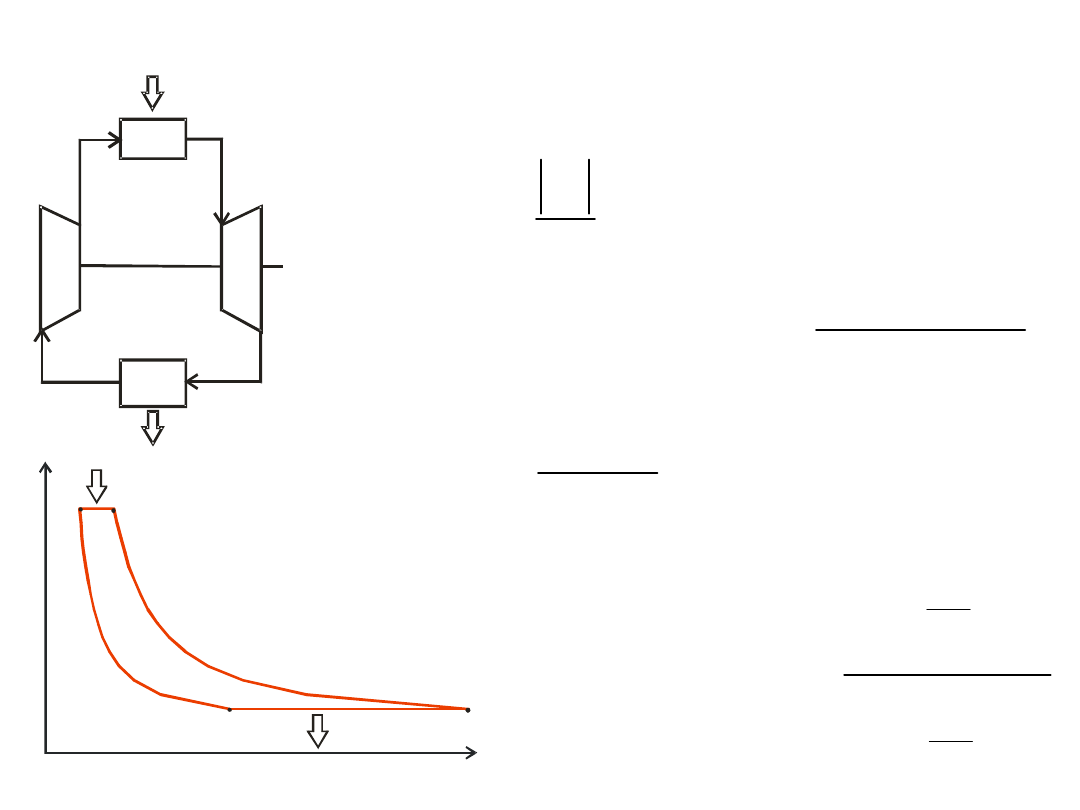
efficiency of the

cycle

1

2

4

3

q

o

q

d

P

m

d

o

t

q

q



1











2

3

1

4

1

T

T

c

T

T

c

p

p

t















2

3

1

4

1

T

T

T

T

t















































1

1

1

2

3

2

1

4

1

T

T

T

T

T

T

t



1

2

3

4

Q

d

q

o

P

V

q

d

Theroretical – model
case

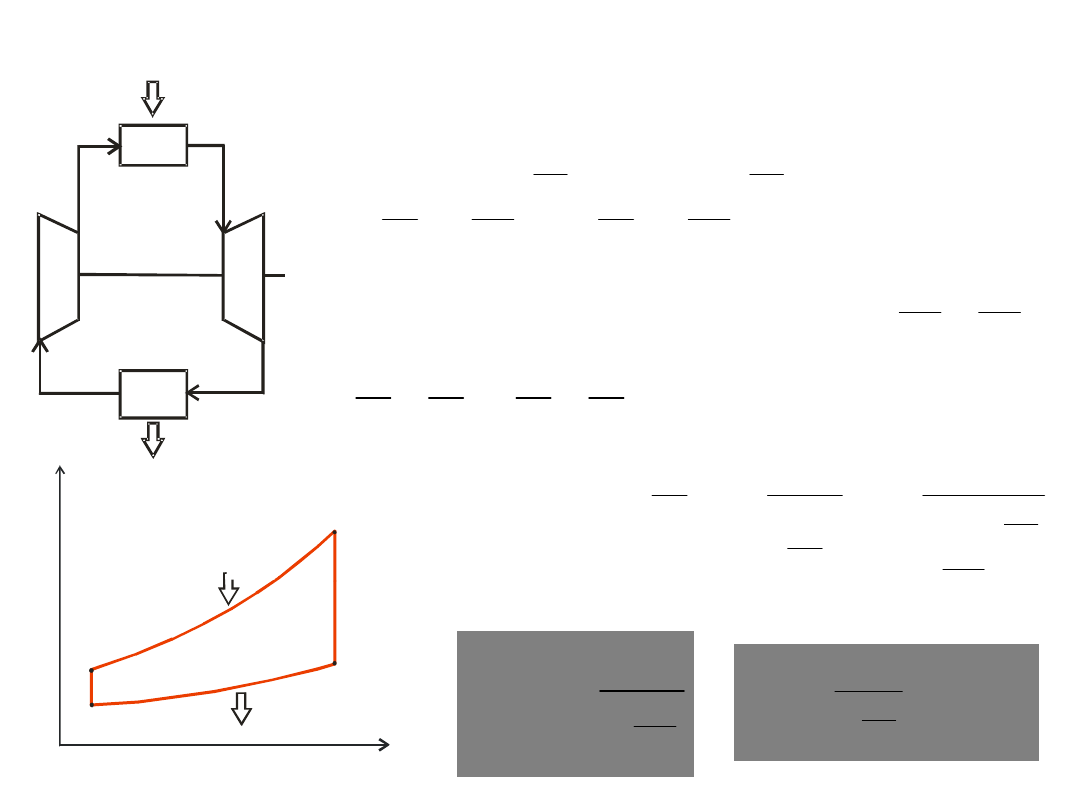
efficiency of the cycle

1

2

4

3

q

o

q

d

P

m

k

k

k

k

p

p

T

T

i

p

p

T

T

1

4

3

4

3

1

1

2

1

2

































4

3

1

2

2

3

4

1

p

p

p

p

p

p

i

p

p









2

3

1

4

4

3

1

2

T

T

T

T

T

T

T

T







k

k

t

p

p

T

T

T

T

1

1

2

1

2

2

1

1

1

1

1

1









































k

k

t

1

1

1



















t

k

k







1

1

1

2

3

4

Q

d

q

o

T

s

q

d

Theroretical – model
case

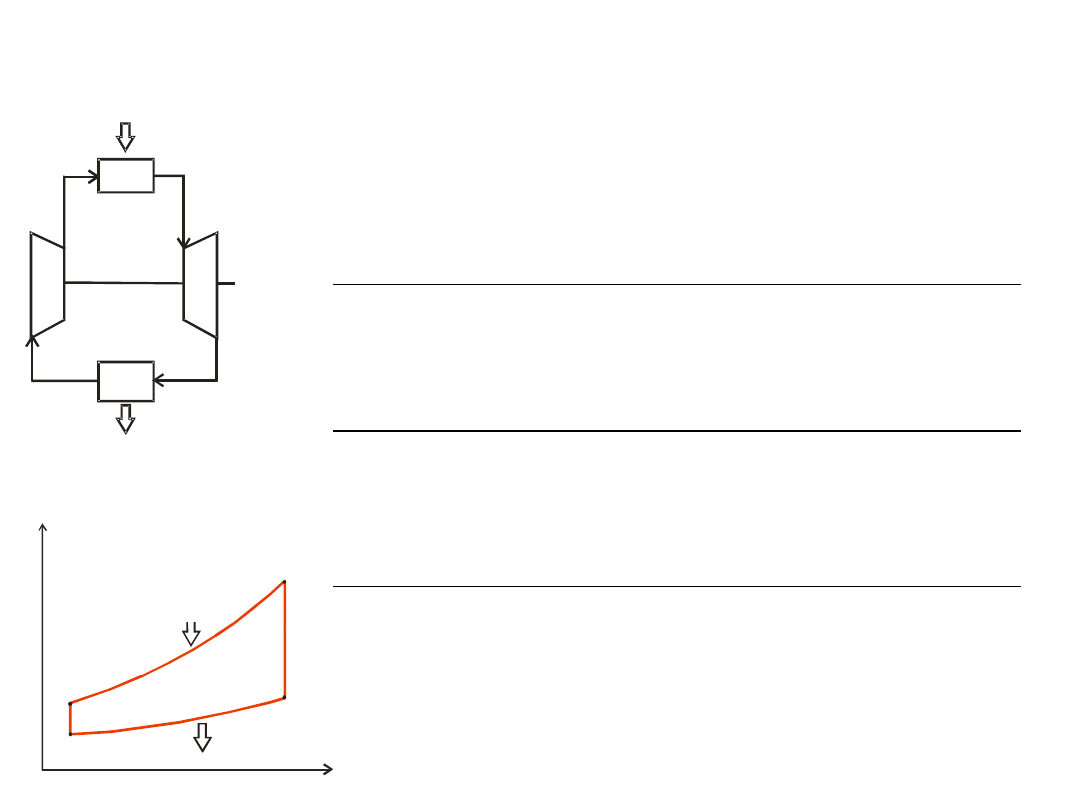
work

1

2

4

3

q

o

q

d

P

m

C

T

t

l

l

l





4

3

i

i

l

T





T

1

– minimal temperature of the cycle;

(resulted from external conditions)

T

3

=T

max

results from internal limitations (material features)

1

2

3

4

Q

d

q

o

T

s

- work at the cycle

- work of the turbine

as for an ideal gas

p

p

T

c

T

c

T

l









4

3

1

2

i

i

l

S





- work of the compressor

as for an ideal gas

p

p

C

c

T

c

T

l









1

2

summary

)

(

)

(

1

2

4

3

p

p

p

p

t

c

T

c

T

c

T

c

T

l

















q

d

Theroretical – model
case

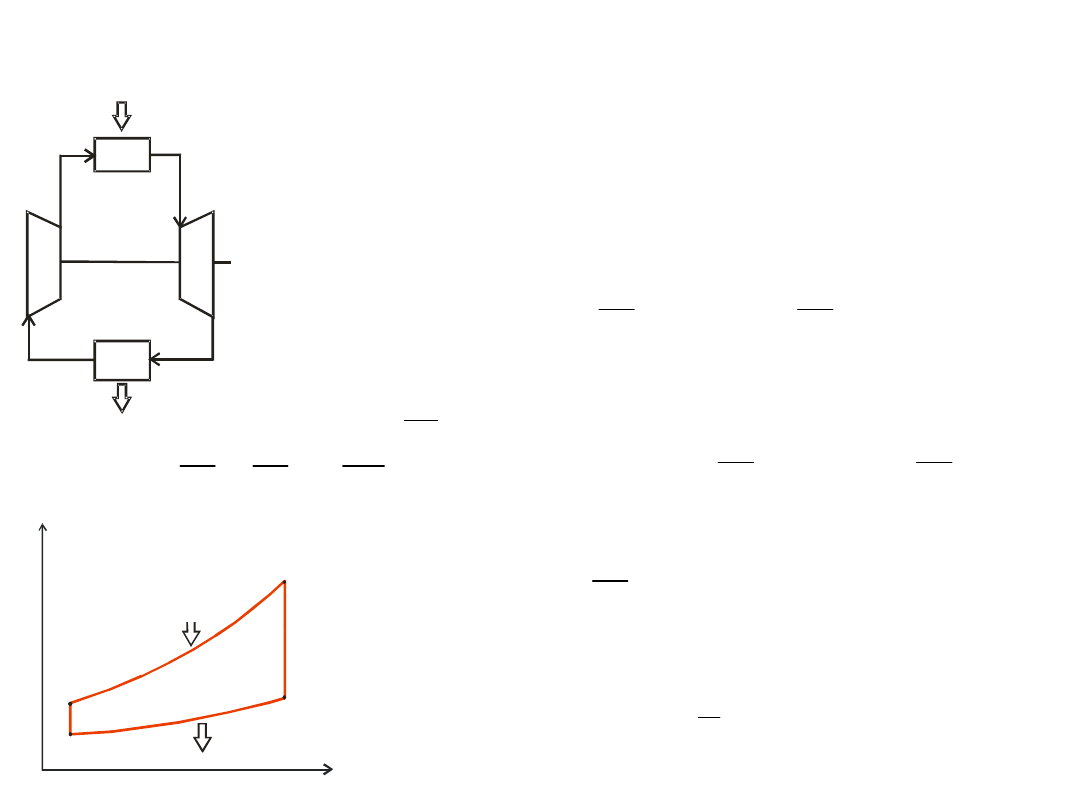
work

1

2

4

3

q

o

q

d

P

m

k

k

p

p

T

T

T

T

1

1

2

4

3

1

2



























































1

1

1

2

1

3

4

3

T

T

T

c

T

T

T

c

l

p

p

t









































1

1

1

2

1

2

1

3

T

T

T

c

T

T

T

c

l

p

p

t

:

1

2

then

T

T

if









1

1

1

1

3



















 











T

c

T

c

l

p

p

t

1

2

3

4

Q

d

q

o

T

s

)

(

)

(

1

2

4

3

p

p

p

p

t

c

T

c

T

c

T

c

T

l

















q

d

Theroretical – model
case

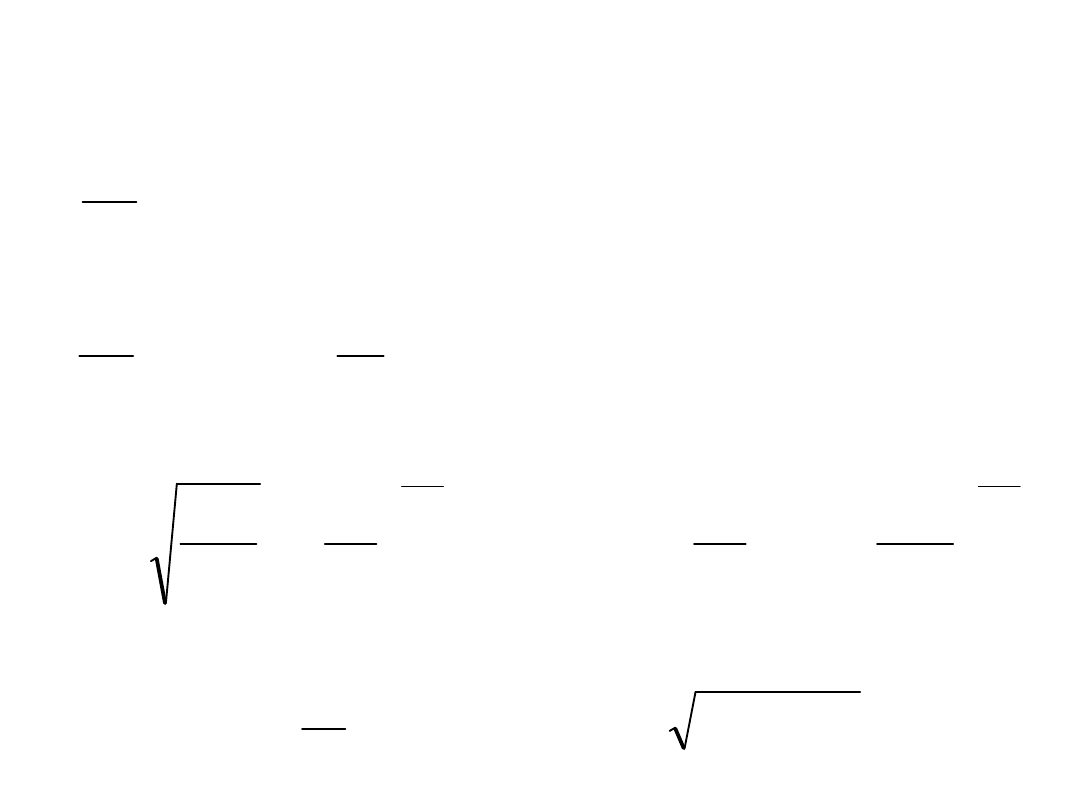
maximal work for T

max

and T

min

const. :

0





d

dl

t

0

1

1

2

max













T

c

T

c

d

dl

p

p

t





k

k

opt

opt

k

k

opt

opt

T

T

p

p

p

p

T

T





















































2

1

min

max

1

2

1

1

2

1

max



1

2

T

T





as

then

min

max

2

T

T

T

opt





Theroretical – model
case

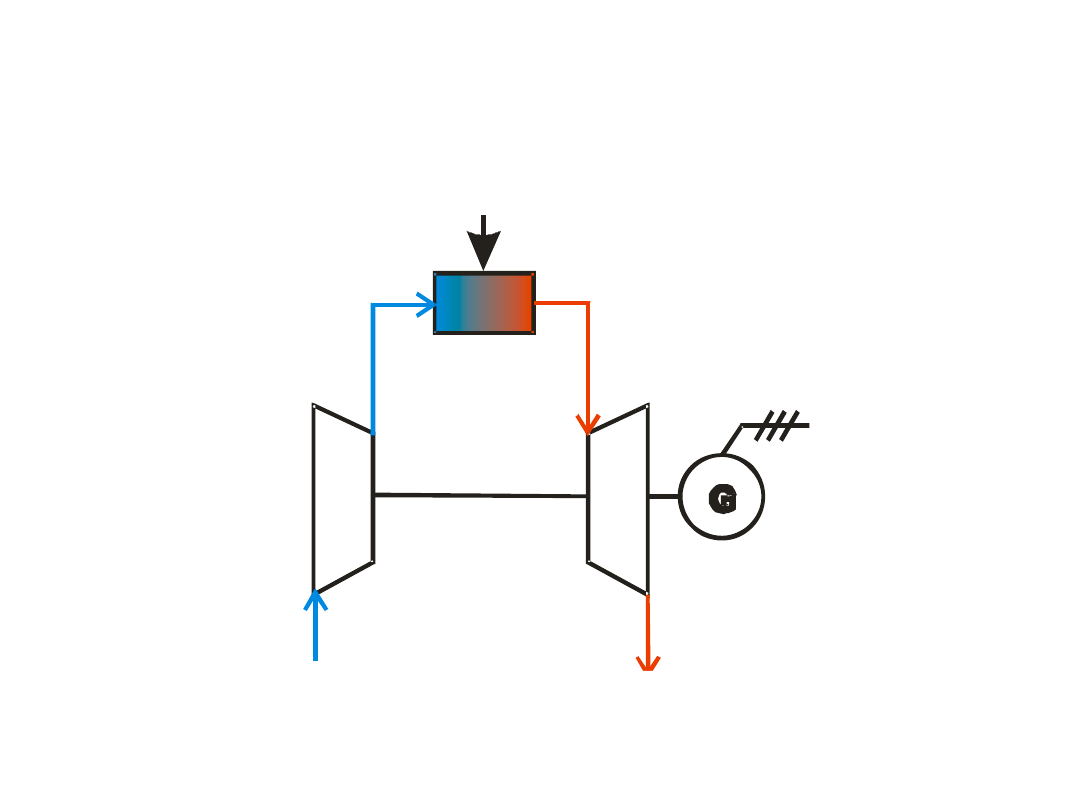
Open cycle – gas power unit

Powietrze

Spaliny

Paliwo

1

2

4

3

P

e

open cycle

fuel

air

exhaust gases

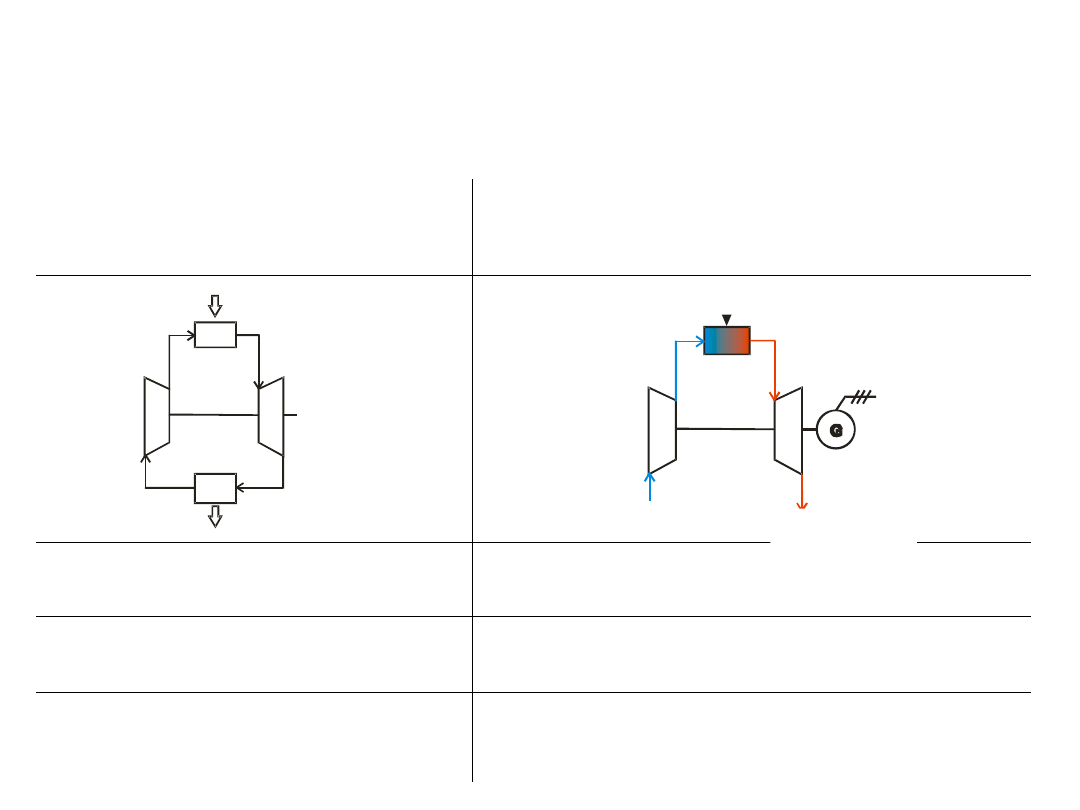
closed and open cycles

Powietrze

Spaliny

Paliwo

1

2

4

3

P

e

1

2

4

3

q

o

q

d

P

m

closed

open

m

1

=m

2

=m

3

=m

4

m

1

=m

2

≠m

3

=m

4

one agent

air/exhaust gases

possible choice of an agent
with a better k and c

p

/ρ

fuel

air

exhaust
gases

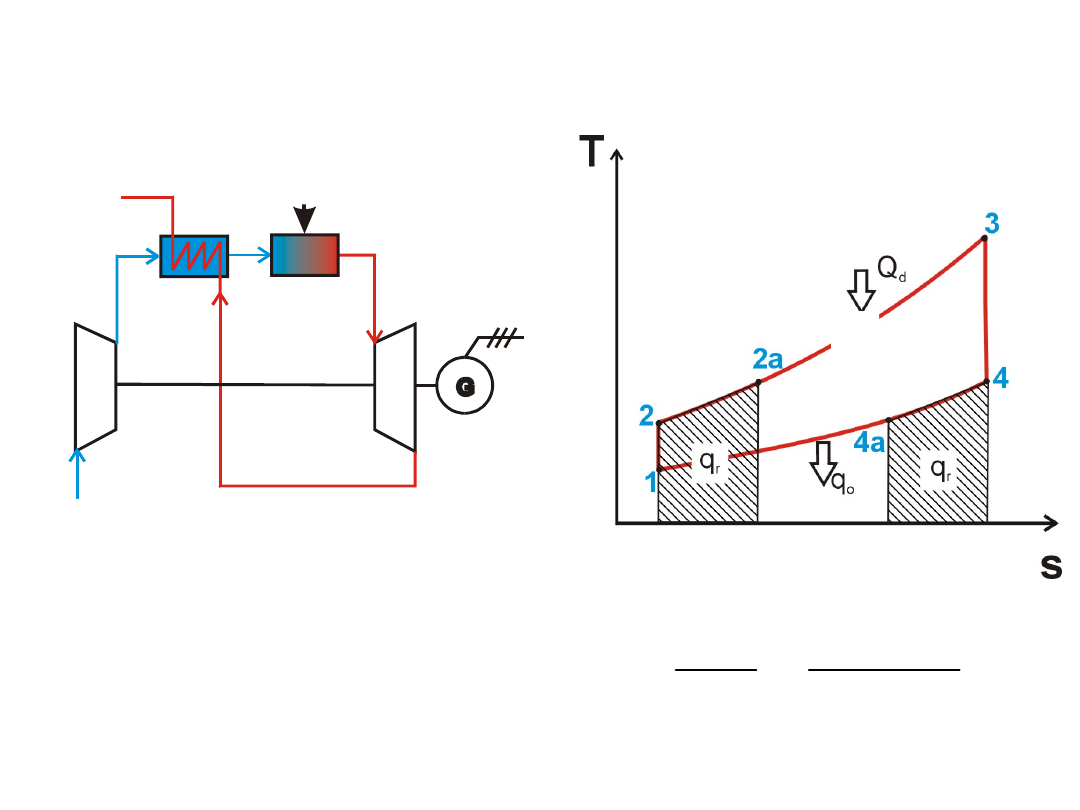
a cycle with a regeneration

system

P o w ie tr z e

S p a lin y

P a liw o

1

2 a

4 a

3

P

e

2

4

fuel

air

exhaust gases

q

d

2

4

2

2

T

T

T

T

Q

Q

a

r

r













Regeneration
factor:

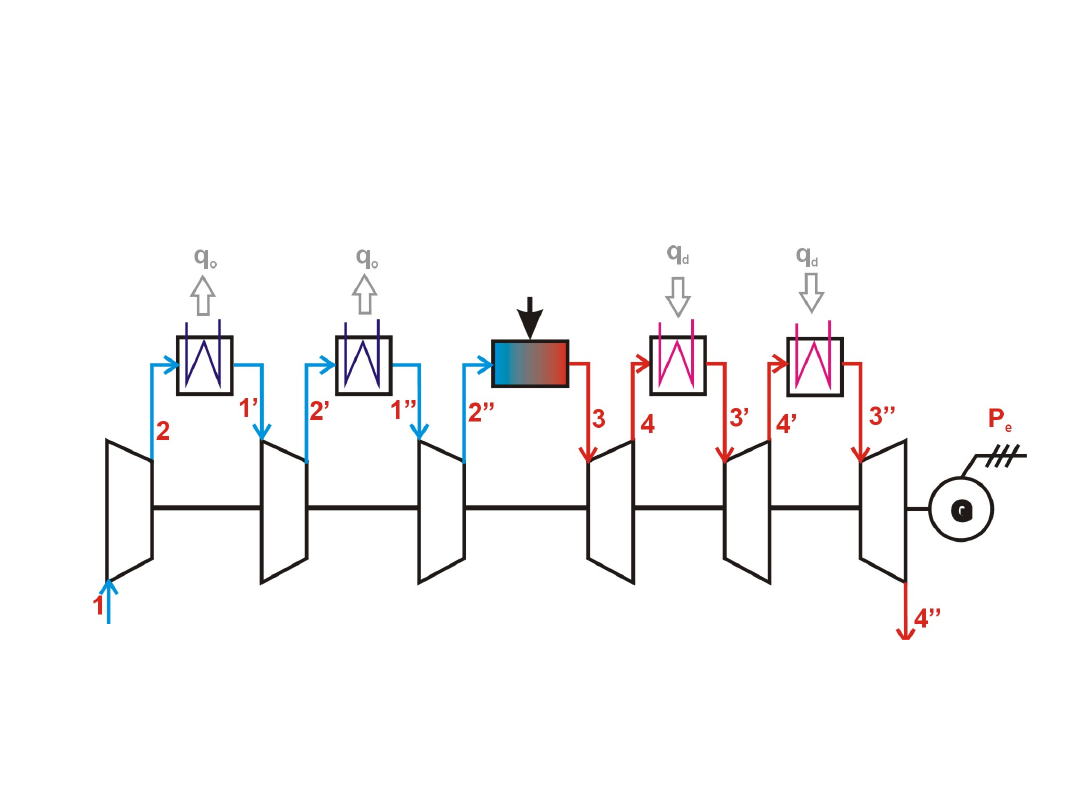
a cycle with intersectional cooling and

heating

exhaust gases

air

fuel

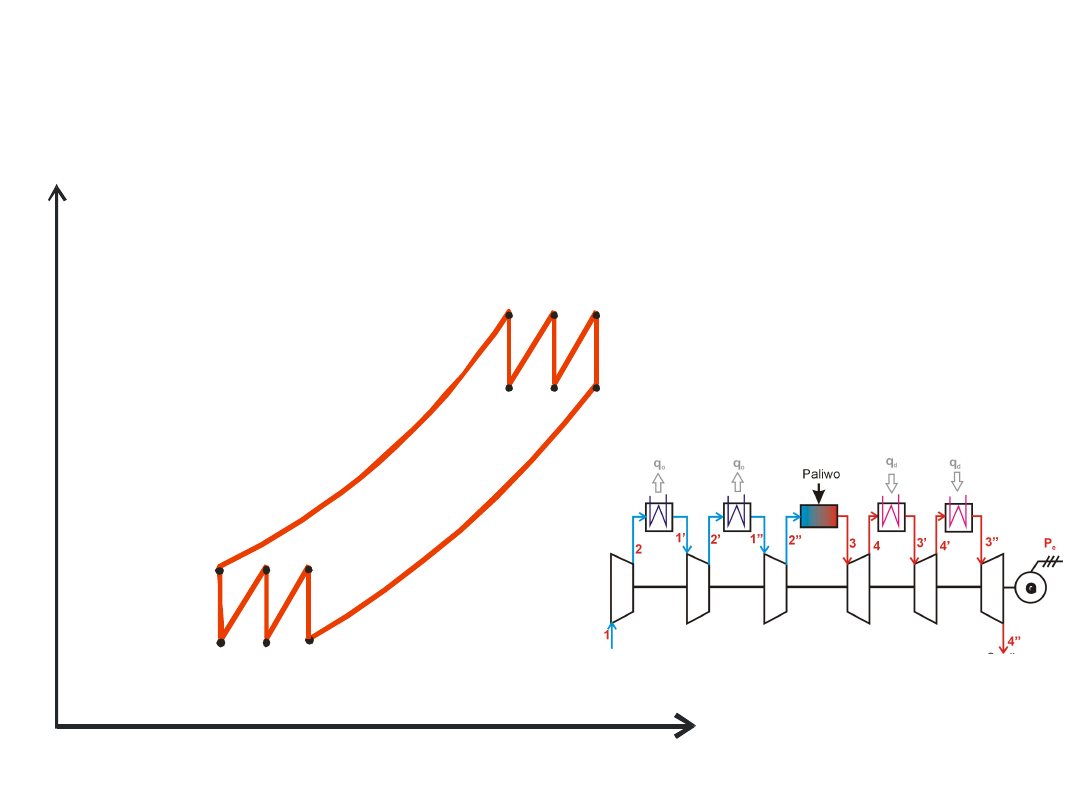
a cycle with intersectional cooling and

heating

1’

2

3’

4’

T

s

1”

1

2’

2”

3”

3

4”

4

air

exhaust
gases

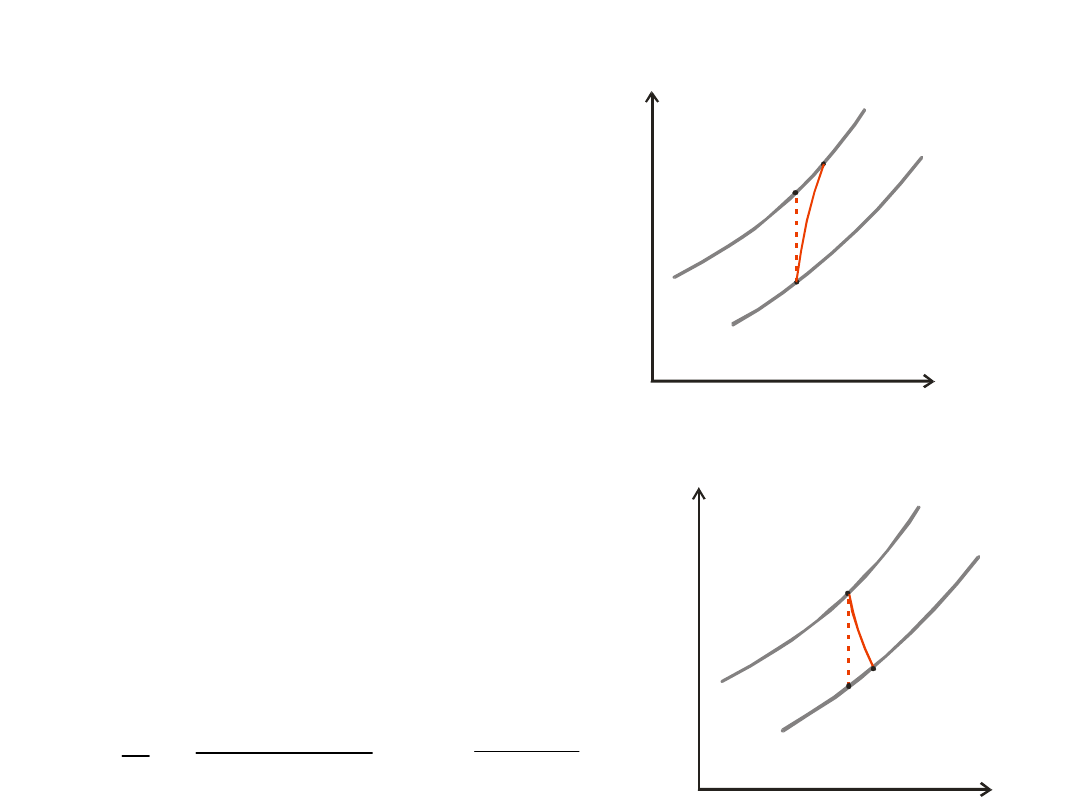
real cycles

• c

p

– changes with T

(c

p

=f(T))

• different mass flows

and different agents

• losses at the

compressor

• losses at the turbine
• losses at the

combustion
chamber

2r

T

s

1

2t

p1

p2

2r

T

s

1

2t

p1

p2

t

r

iT

l

l













t

p

r

p

T

T

c

T

T

c

2

1

2

1











t

r

T

T

T

T

2

1

2

1







compressor

turbine

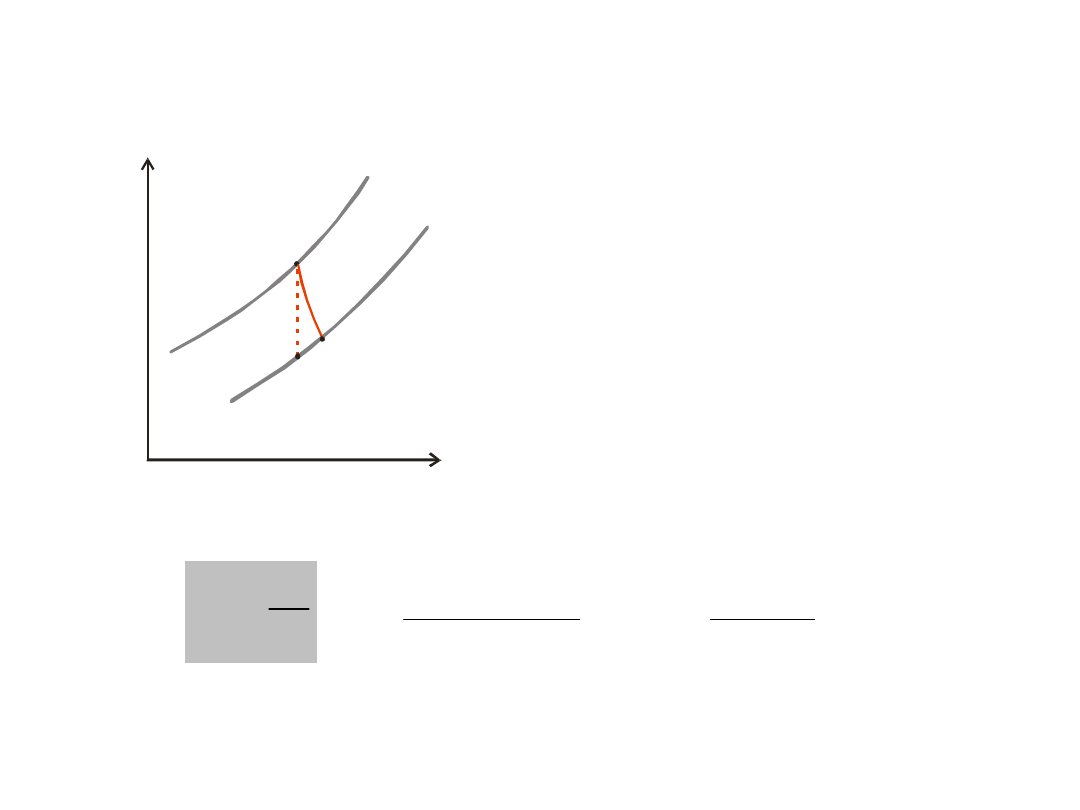
turbine – internal efficiency

2r

T

s

1

2t

p1

p2

tT

rT

iT

l

l













t

p

r

p

T

T

c

T

T

c

2

1

2

1











t

r

T

T

T

T

2

1

2

1







turbine

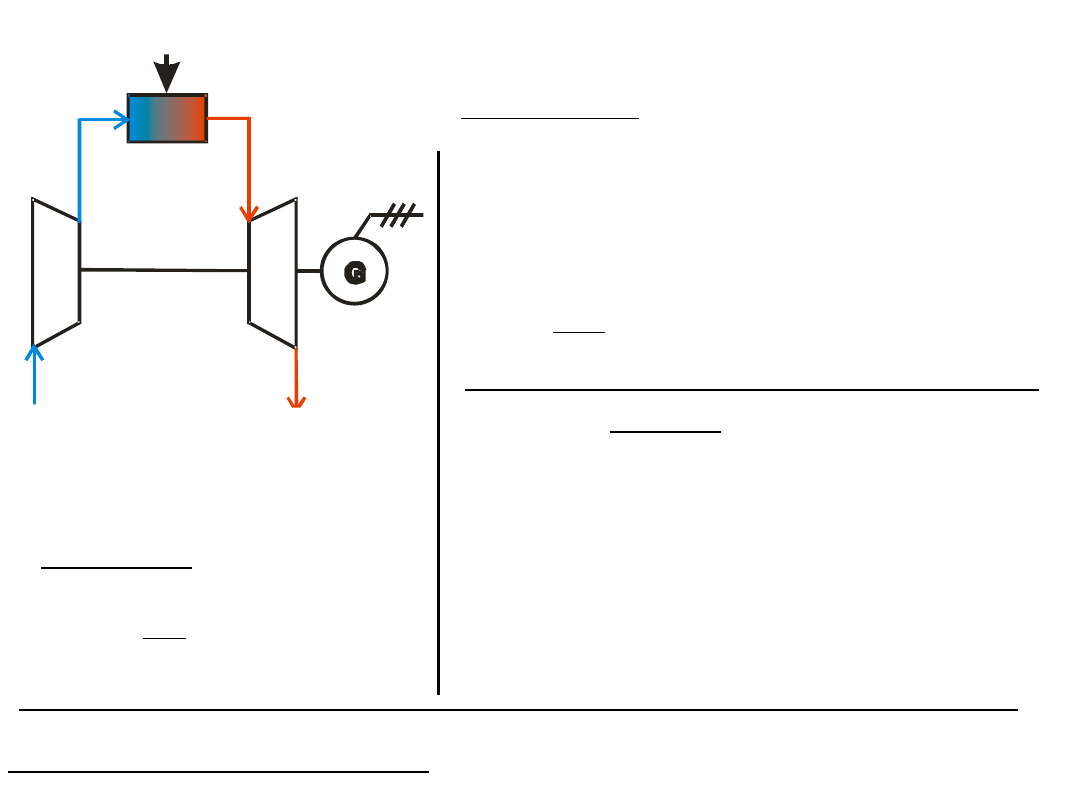
balances

Powietrze

Spaliny

Paliwo

1

2

4

3

P

e

compressor





1

2

_

T

T

c

l

air

p

iC











1

2

T

T

c

m

m

l

P

pp

p

p

is

iC

















turbine





4

3

_

T

T

c

l

eg

p

iT











4

3

T

T

c

m

m

l

P

ps

s

s

iT

iT

















ms

is

mC

P

P





mT

iT

mT

P

P







power balance at the shaft:

G

el

mG

P

P





generator

mG

mC

mT

P

P

P





fuel

air

exhaust gases

CC

C

T

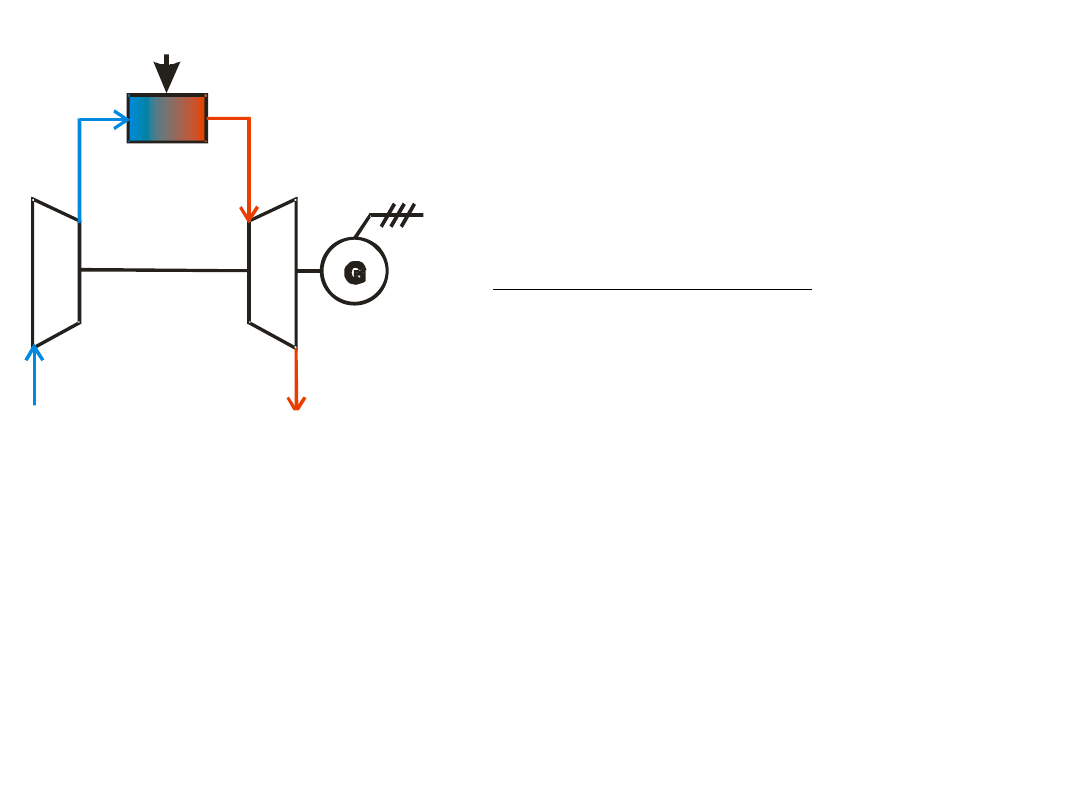
balances

Powietrze

Spaliny

Paliwo

1

2

4

3

P

e

combustion chamber

gases

exhaust

fuel

air

m

m

m

_











3

_

_

_

2

_

T

c

m

m

HCV

T

c

m

g

ex

p

gases

exhaust

CC

fuel

air

p

air

























mass balance

energy balance

fuel

air

exhaust gases

C

T

CC

mechanical output

mC

iC

mT

iT

mC

iC

mT

iT

eC

eT

e

P

P

P

P

P

P

P

P

P



























)

(

)

(

mC

iC

tC

air

mT

iT

tT

eg

mC

iC

air

mT

iT

eg

e

l

m

l

m

l

m

l

m

P













































mC

iC

t

air

p

air

mT

iT

t

eg

p

fuel

air

e

T

T

c

m

T

T

c

m

m

P

































)

(

)

(

)

(

1

2

_

4

3

_







mechanical
output

mC

iC

t

air

p

air

mT

iT

t

eg

p

fuel

air

e

T

T

c

m

T

T

c

m

m

P

































)

(

)

(

)

(

1

2

_

4

3

_







mC

iC

k

k

air

p

air

mT

iT

k

k

eg

p

fuel

air

e

air

air

eg

eg

p

p

T

c

m

p

p

T

c

m

m

P



































































































































1

1

)

(

1

1

2

min

_

1

3

4

max

_







eg

air

eg

p

air

p

eg

air

k

k

c

c

m

m

g

simplifyin







;

;

:

_

_























































 













1

1

1

min

max













mC

iC

mT

iT

p

e

T

T

c

m

P



























k

k

p

p

noting

p

p

p

p

and

1

1

2

4

3

1

2

:

;

:

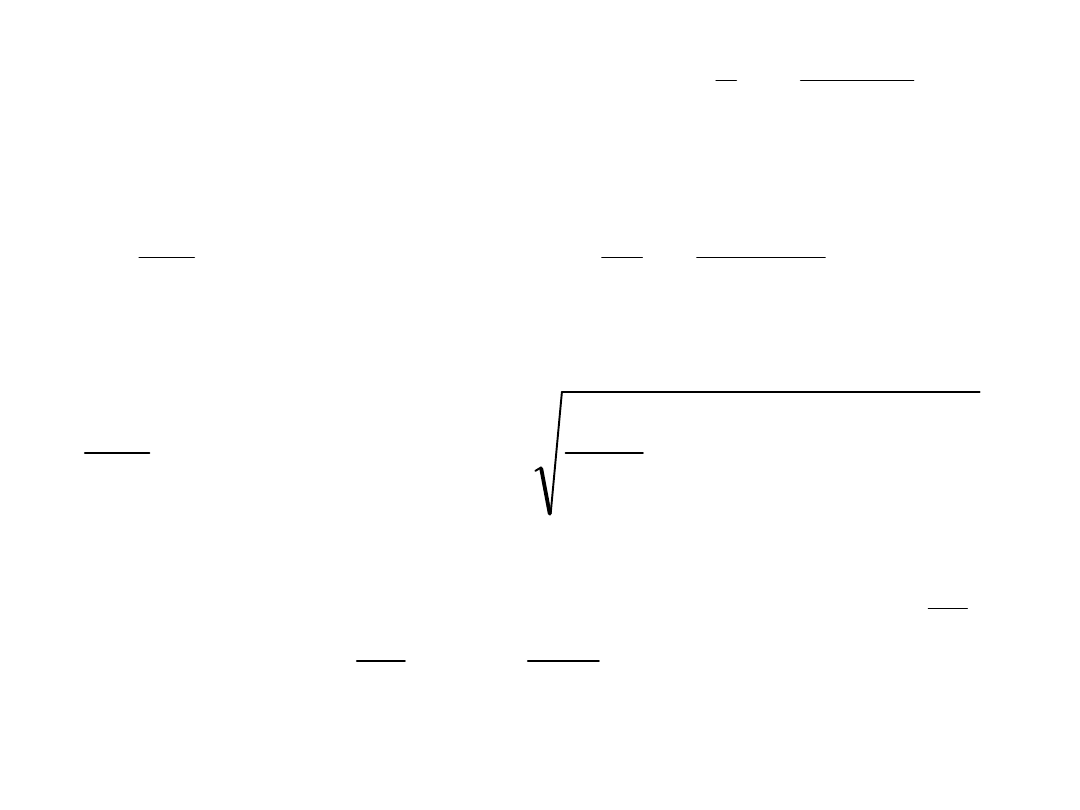
mechanical
output



















































 













1

1

1

min

max













mC

iC

mT

iT

p

e

T

T

c

m

P



















































mC

iC

mT

iT

p

e

T

T

c

m

P













min

2

max

1



mC

iC

mT

iT

e

T

T

if

P





























min

max

:

0

k

k

mC

iC

mT

iT

opt

opt

T

T

p

p

so









































2

1

min

max

1

2

:











internal work

heat delivered



th

=













r

p

r

p

r

p

d

i

th

T

T

c

T

T

c

T

T

c

Q

P

2

3

1

2

4

3

















 



power output

heat delivered (in time)



o

=

thermal efficiency

overall efficiency

HCV

m

P

Q

P

P

fuel

e

d

mC

mT

o















overall efficiency





CC

r

air

p

air

eg

p

eg

mC

iC

t

air

p

air

mT

iT

t

eg

p

fuel

air

fuel

e

o

T

c

m

T

c

m

T

T

c

m

T

T

c

m

m

HCV

m

P













2

_

3

_

1

2

_

4

3

_

)

(

)

(

)

(

















































CC

iC

k

k

air

p

air

eg

p

fuel

air

mC

iC

k

k

air

p

air

mT

iT

k

k

eg

p

fuel

air

o

air

air

air

air

eg

eg

T

c

m

T

c

m

m

T

c

m

T

c

m

m





































































































































)

1

(

1

)

(

)

1

(

)

1

1

(

)

(

1

min

_

max

_

1

min

_

1

max

_











































































iC

k

k

iC

t

r

air

p

air

air

p

p

T

T

T

T

T

const

c

if





1

1

.

1

1

2

1

1

2

1

2

_

overall efficiency























 







































iC

CC

mC

iC

mT

iT

o

T

T

T

T





















)

1

(

1

)

1

(

)

1

1

(

min

max

min

max

eg

air

eg

p

air

p

eg

air

k

k

c

c

m

m

g

simplifyin







;

;

:

_

_























k

k

p

p

noting

1

1

2

:

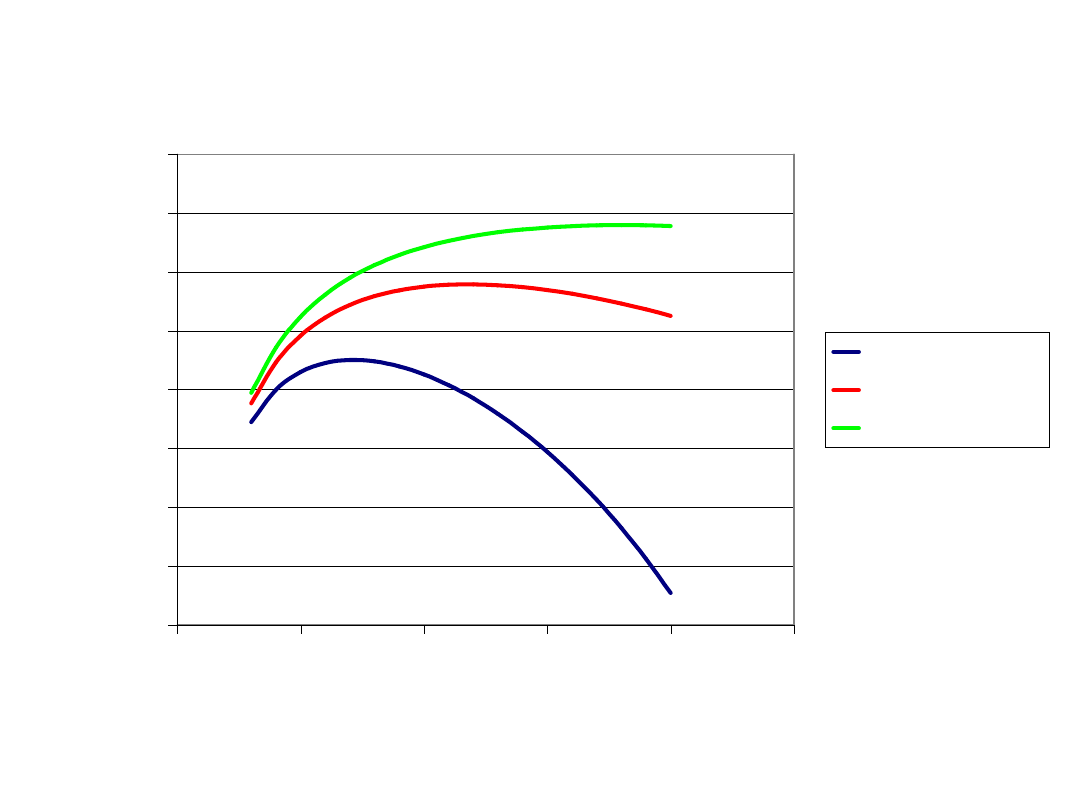
overall efficiency changes

0

0,05

0,1

0,15

0,2

0,25

0,3

0,35

0,4

0

5

10

15

20

25

spręż pi

sp

ra

w

n

o

ść

t

u

rb

o

ze

sp

o

łu

Tmax=900 k
Tmax=1100 k
Tmax=1300 k

compression

o

v

e

ra

ll

e

ffi

ci

e

n

cy

for assumed
values of inner
and
mechanical
efficiencies

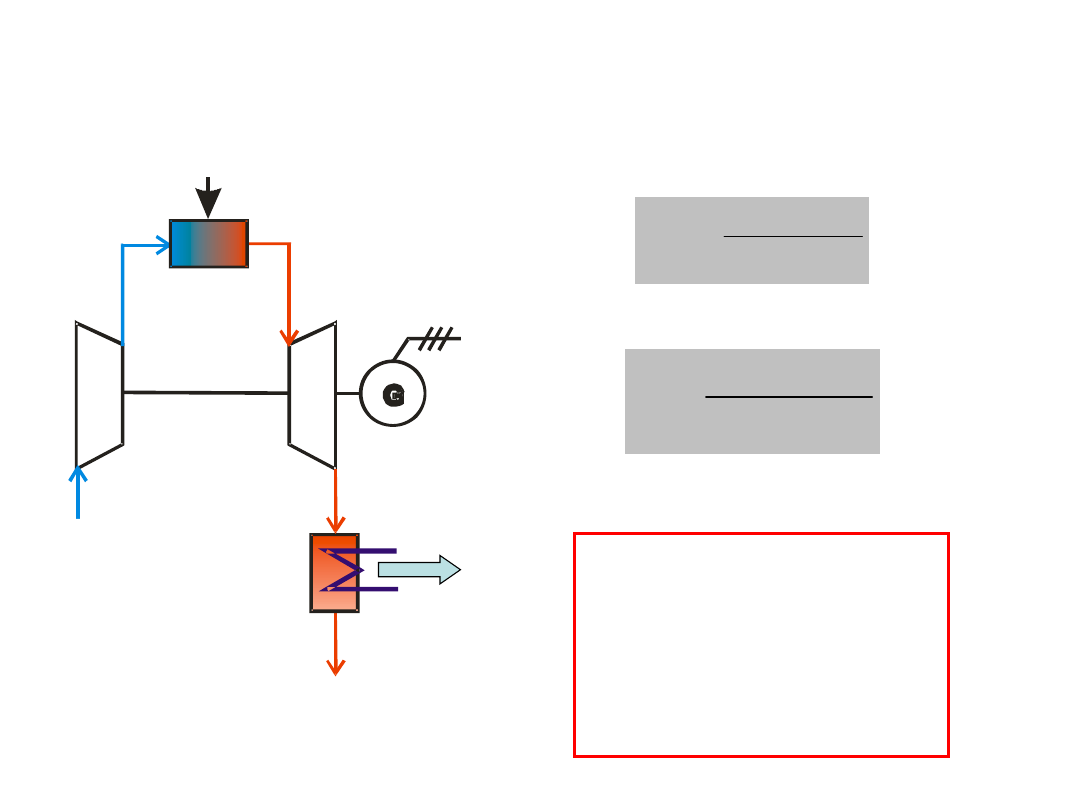
Recovery of exhaust gases enthalpy

– combined heat and power generation with a

gas cycle

Powietrze

Spaliny

Paliwo

1

2

5

3

P

e

4

Q

u

HCV

m

Q

P

fuel

u

el

CHP











HCV

m

P

fuel

el

el









air

exhaust
gas

fuel

T

C

CC

Remark:

It is also in practice to
relate overall efficiencies
of power units or CHP
plants based on gas
cycles to LCV

Exercise 1

A simple stationary gas system consists with an one-section roto-dynamic compressor,
a combustion chamber, a gas turbine, and an electricity generator. The compressor
sucks 150 kg/s of an ambient air (t

a

=10°C, p

a

=997 hPa) and compresses it to p

2

=1.3

MPa. The internal polytrophic efficiency of the compressor is η

ipC

=0.88. Mechanical

losses at the compressor are estimated on about 35 kW. The compressed air flows into
the combustion chamber. The combustion chamber is supplied with natural gas of
LCV=37.26 MJ/m3, HCV=41.26 MJ/m3, and density ρ=0.784 kg/m3 (all those
parameters are given for standard conditions: 0.1013 MPa, 0°C). The actual pressure of
the gas is 1.3 MPa and temperature 20°C. It can be assumed that an overall efficiency
of the combustion chamber is η

CC

=0.98. One can assume also that the combustion

process is isobaric. Exhaust gases generated at the combustion chamber have a
temperature t

3

=1300 °C and supply the gas turbine where expand up to p

4

=1.02 bar.

The exhaust gases leave the gas turbine with a temperature t4=570°C. The gas turbine
drives the compressor and the generator. A mechanical efficiency of the turbine is
η

mT

=0.993 and an overall efficiency of the generator is η

G

=0.98.

Accept: c

pair

=1.004 kJ/kgK, c

pex.g.

=1.04 kJ/kgK, k

air

=1.4, k

ex.g

=1.39

Calculate:

1.

internal adiabatic efficiency of the compressor,

2.

mechanical power driving the compressor and mechanical efficiency of the compressor,

3.

fuel consumption at the combustion chamber

4.

electricity output form the generator

5.

overall efficiency of the power plant

Exercise 2

A gas cycle power plant consists with an one-section roto-dynamic

compressor, a combustion chamber, a gas turbine, an electricity

generator, and a recuperator. The compressor sucks an ambient air

(t

a

=0°C, p

a

=1 bar hPa) and compresses it to p

2

=0.7 MPa. The internal

adiabatic efficiency of the compressor is η

ipC

=0.85 and a mechanical

efficiency is η

mC

=0.994. The compressed air flows into the iso-baric

recuperator, and is heated by a exhaust gases flowing form the turbine,

up to 530°C. The superheated and compressed air supplies the

combustion chamber where a fuel oil (HCV-46 MJ/kg) is combusted (also

an iso-baric process). An overall efficiency of the combustion chamber is

η

CC

=0.98. Exhaust gases temperature behind the combustion chamber is

t

3

=1100 °C. The exhaust gases expand at the turbine up to p

4

=1 bar with

an internal efficiency of the process η

iT

=0,89. The gas turbine drives the

compressor and the generator. A mechanical efficiency of the turbine is

η

mT

=0.992 and an overall efficiency of the generator is η

G

=0.975.

Electricity output of the power unit is 40 MWe.
Accept: c

pair

=1.004 kJ/kgK, c

pex.g.

=1.04 kJ/kgK, k

air

=1.4, k

ex.g

=1.39

Calculate:

1.

fuel consumption at the combustion chamber

2.

overall efficiency of the power plant

3.

regeneration factor

4.

outlet temperature of the exhaust gases