Metody podejmowania

decyzji

Plan zajęć z grupą 23AAA 1-2

Semestr letni 2008

1. Metody badań naukowych: W
2. Metody oceny prawdopodobieństwa

zdarzeń: W i Z

3. Podejmowanie decyzji w warunkach

niepewności:

W i Z
4. Podejmowanie decyzji na podstawie

drzewa decyzyjnego: W i Z.

2. Metody oceny prawdopodobieństwa

zdarzeń

Prawdopodobieństwo realizacji projektu

Prawdopodobieństwo zdarzenia w
doświadczeniu określane jest wg relacji

gdzie: LZS – liczba zdarzeń sprzyjających,
LWZ – liczba wszystkich zdarzeń.
Na przykład prawdopodobieństwo, że wypadnie

parzysta liczba oczek w kostce do gry wynosi:

LWZ

LZS

p 

– liczba sprzyjających zdarzeń: ścianki z

liczbami 2, 4, 6, razem LZS = 3,
– liczba wszystkich zdarzeń: LWZ = 6,
– prawdopodobieństwo: p = 3 / 6 =0,5.
Ten sposób postępowania nie zawsze jest

możliwy, dlatego często korzysta się z

metody czynnikowo-punktowej oceny

prawdopodobieństwa. Zilustrujemy to na

przykładzie oceny ryzyka realizacji

przedsięwzięcia (projektu). Załóżmy, że

zostały określone potencjalne czynniki

ryzyka (tablica 1.). Załóżmy również, że

wybierzemy 10 czynników ryzyka z tablicy

1 i że będą one punktowane w skali 3

punktowej. Wynik takich ocen zawiera

tablica 2.

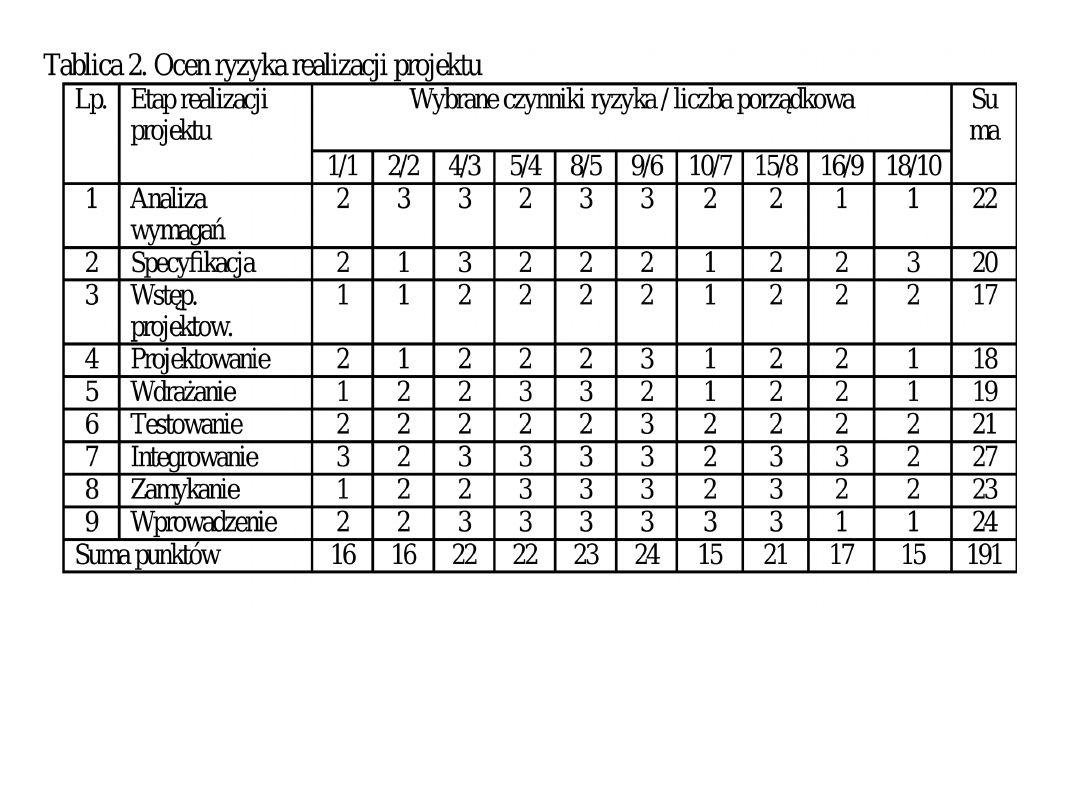
Maksymalna liczba punktów wynosi: LWZ =

10 ∙ 9 ∙ 3 =270,

Liczba punktów pozytywnych wynosi: LZS =

191,

Ryzyko realizacji projektu wynosi: p = 191 /

270 = 0,71.

Ocena prawdopodobieństwa zaistnienia

określonych dopełniających się

sytuacji np. siły, słabości
Niech ocena prawdopodobieństwa będzie

taka jak w tablicy 3.

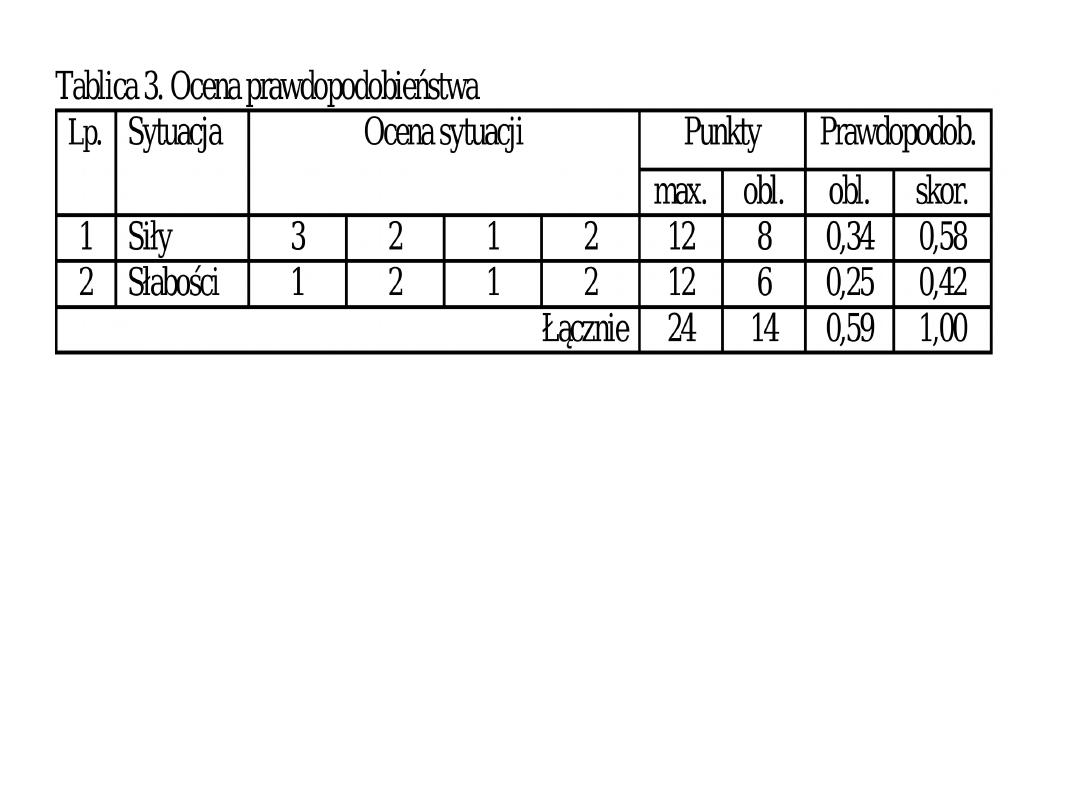
Ponieważ analizowane sytuacje się

dopełniają, suma ich prawdopodobieństw
musi wynosić 1, dlatego obliczone
prawdopodobieństwa muszą być
odpowiednio skorygowane wg relacji:

gdzie: psi – prawdopodobieństwo

skorygowane,

pci – prawdopodobieństwo obliczone.
Na przykład w tablicy 3 mamy:





pci

pci

psi

58

,

0

59

,

0

34

,

0

1





ps

42

,

0

59

,

0

25

,

0

2





ps

3. Podejmowanie decyzji w warunkach

niepewności

Cechą charakterystyczną podejmowanych

decyzji w warunkach niepewności jest to,

że mamy do czynienia:
- z różnymi wyborami,
- z niepewnością.

Optymalna decyzja wymaga spełnienia

następujących postulatów:
- najkorzystniejszy wybór,
- najpewniejszy wybór.

Decyzje podejmowane w warunkach

niepewności dzieli się na decyzje przy:

- znanych prawdopodobieństwach zaistnienia

określonych sytuacji,
- nieznanych prawdopodobieństwach

zaistnienia określonych sytuacji.

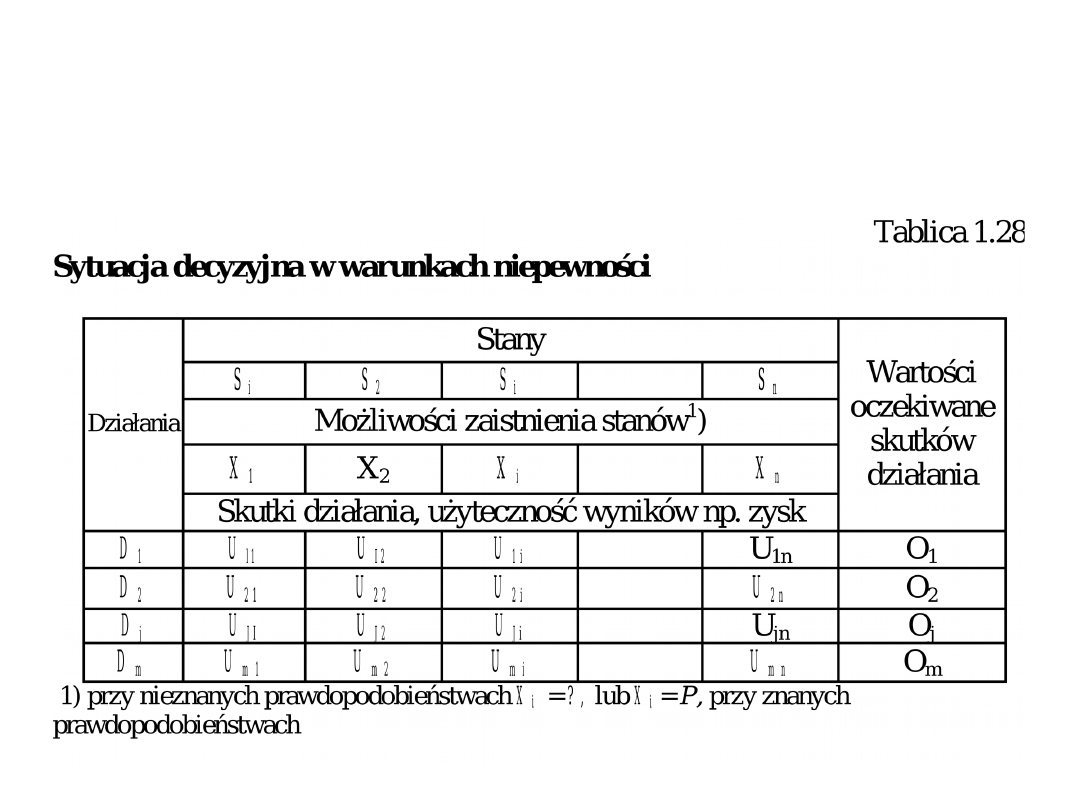
Sytuację decyzyjną w warunkach niepewności

można scharakteryzować tak, jak w tablicy

1.28.

Z podanych wielkości wynika, że każdemu

działaniu Dj przy każdym stanie Si należy

przyporządkować odpowiednie miary

użyteczności wyników działań Uji.

Mogą nimi być: subiektywnie odczuwane korzyści

lub straty przypisywane wynikom działań przy

każdym stanie lub mogą to być zyski (straty).

Ponadto, przy znanych

prawdopodobieństwach każdemu stanowi
należy przypisać odpowiednie wielkości
prawdopodobieństw.

Sposób ustalania wartości oczekiwanej skutków

działania (użyteczności wyników) jest różnie

określany w różnych regułach decyzyjnych.

Jest on cechą charakterystyczną tych reguł.

Ponieważ sposobów działania jest wiele (co

najmniej dwa), dlatego zachodzi potrzeba

określenia kryteriów, według których można

wybrać działanie optymalne.

Przyjmuje się, że działanie optymalne to takie,

dla którego wartość oczekiwana skutków

działania jest maksymalna, to znaczy jest

ustalana zgodnie z relacją

DO = max {O1, O2, ....,Om}
gdzie: DO - decyzja optymalna,
Oj - wartość oczekiwana skutków

działania.

Decyzje przy znanych

prawdopodobieństwach

Jeżeli znane są prawdopodobieństwa pojawienia

się analizowanych stanów, to przy

podejmowaniu decyzji bierze się pod uwagę:
- użyteczność wyników działania,
- prawdopodobieństwo ich otrzymania.

Decyzja optymalna określona jest relacją:
D = max {(∑Uji pi)}
dla: i = 1,2 , ... , n oraz j = 1,2, ... , m.
Oznacza to, że należy podjąć to działanie, dla

którego wartość oczekiwana skutków

działania jest maksymalna.

2) Ocena użyteczności cząstkowych w

punktach

Kryteria oceny użyteczności:

przyjemne spędzenie wakacji  4 punkty,
dobre spędzenie wakacji  3 punkty,
przeciętne spędzenie wakacji  2 punkty,
złe spędzenie wakacji  1 punkt,

Uwzględniając te założenia, otrzymamy

użyteczności stanów pogodowych

zestawione w tablicy 1.30.

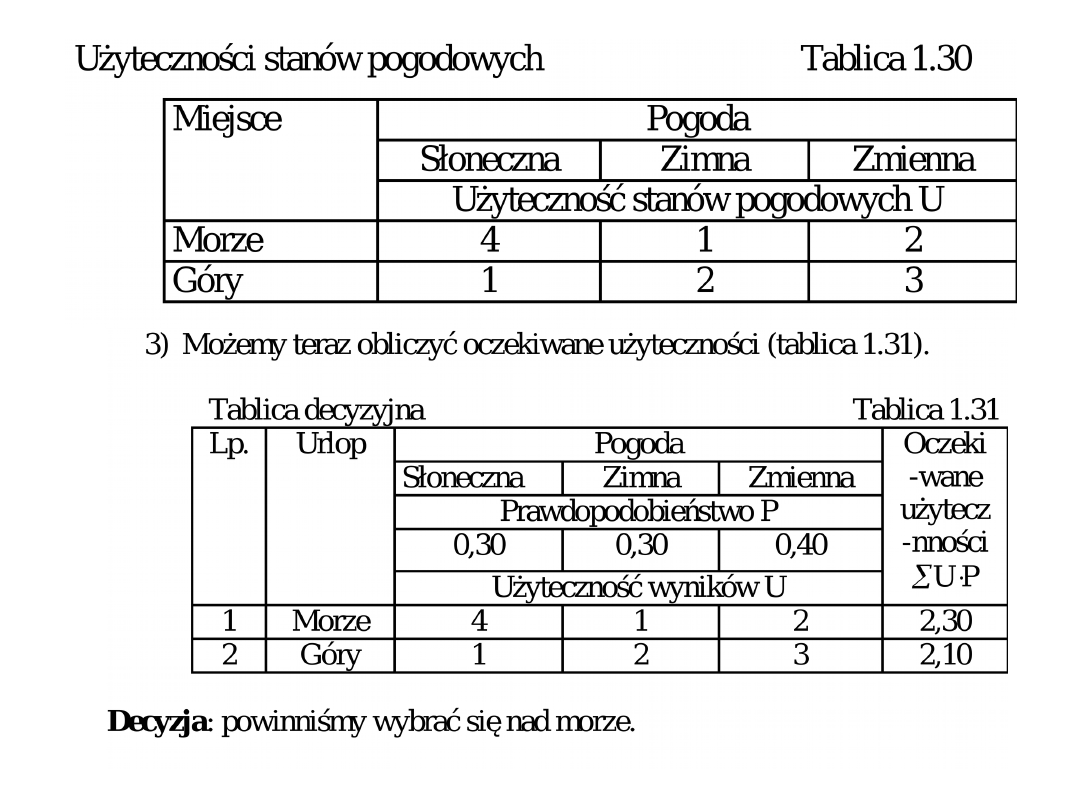
Przykład 2
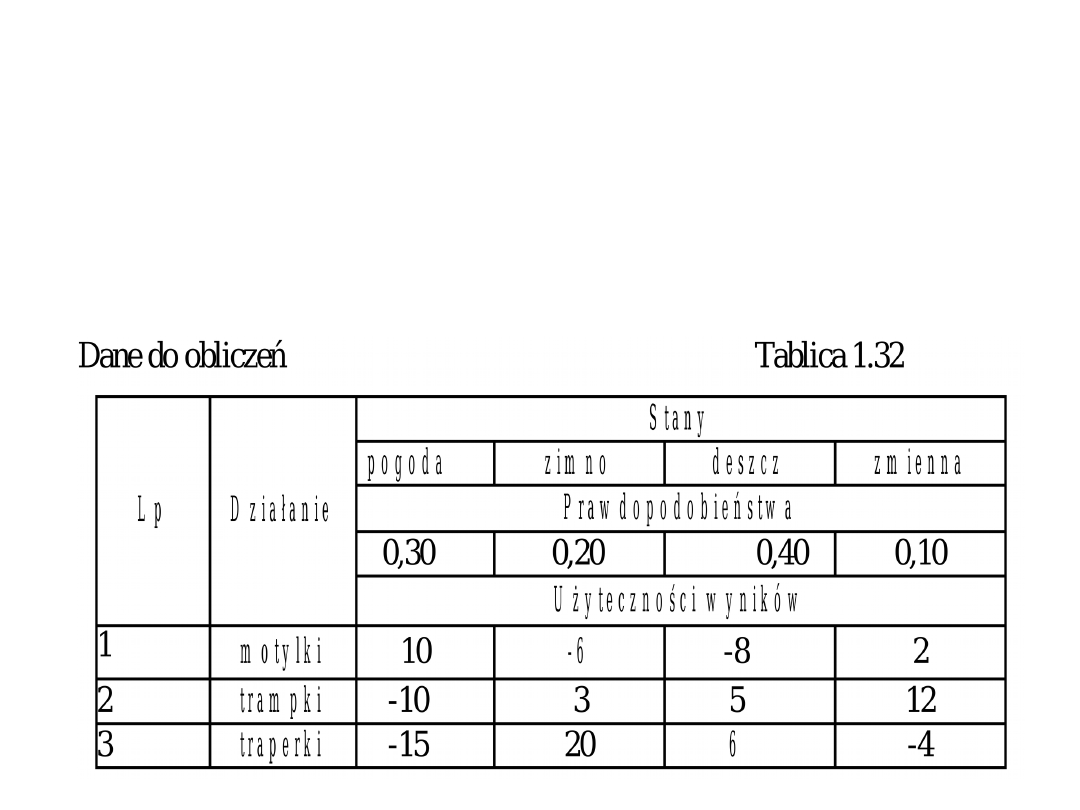
Rozważmy problem wyboru rodzaju

produkcji; możemy produkować jeden z
wyrobów: motylki, trampki lub traperki.
Dane dotyczące tych wyrobów zawiera
tablica 1.32.

Obliczenia:
- działanie l. lOxO,3-6xO,2-8x0,4+2xO,1 = -1,2
- działanie 2. -10 x 0,33 + 3 x 0,2 + 5 x 0,4 + 12

x 0,1 = 0,8

- działanie 3. -15xO,3+20xO,2+6xO,4-4xO,1 =

1,5

Wynik: DO = max {-1,2; 0,8; 1,5} = 1,5 → poz. 3.
Decyzja: produkować traperki.

Decyzje przy nieznanych

prawdopodobieństwach

Przy nieznanych prawdopodobieństwach

stosowane są następujące reguły decyzyjne:

- maksimaksu (skrajnego optymizmu),
- minimaksu (skrajnego pesymizmu,

asekuranctwa),
- optymizmu i pesymizmu,
- równej szansy.

W konkretnej sytuacji decyzyjnej stosuje się

jedną wybraną regułę decyzyjną.

REGUŁA SKRAJNEGO OPTYMIZMU

(MAKSIMAKSU). Reguła ta zaleca brać pod

uwagę najlepsze wyniki działania, stąd

nazwa skrajny optymizm. Decyzja

optymalna określona jest relacją

DO = max {max {Uji}} dla: j = l, 2, ...

, m oraz i = l, 2, ... , n.

Przykład
Dla danych z tablicy 1.32 mamy:
Obliczenia:

- działanie l. max { 10, -6, -8, 2} = 10,
- działanie 2. max{-l0, 3, 5, 12} = 12,
- działanie 3. max{-15, 20, 6, -4} = 20.

Wynik: DO = max {l0, 12, 20} = 20 → poz. 3.
Decyzja: produkować traperki.
REGUŁA SKRAJNEGO ASEKURANCTWA

(MINIMAKSU). Reguła ta zaleca brać pod

uwagę najgorsze wyniki działania. Decyzja

optymalna określona jest relacją

dla: j = 1, 2, ... , m oraz i = 1,2, ... , n.
Przykład
Dla danych z tablicy 1.32 mamy:
Obliczenia:

- działanie l. min { 10, -6, -8, 2} = -8,
- działanie 2. min {-lO, 3, 5, 12} = -10,
- działanie 3. min{-15, 20, 6, -4} = -15.

Wynik: DO = max{-8, -10, -15} = -8 → poz. 1.
Decyzja: produkować motylki.

REGUŁA OPTYMIZMU I PESYMIZMU. Reguła

ta zaleca brać pod uwagę zarówno najlepsze,
jak i najgorsze wyniki działania oraz wskaźnik
optymizmu W. Przy W = O reguła zamienia
się w regułę minimaksu, zaś przy W = l w
regułę maksimaksu. Decyzja optymalna
określona jest relacją

DO = max {[max {Uji} W + min {Uji} (1 -

W)]}

dla: j = 1, 2, ... , m oraz i = 1,2, ... , n.
Przykład
Dla danych z tablicy 1.32 oraz przy założeniu

wskaźnika optymizmu W = 0,5 mamy:

Obliczenia:

- działanie l. 10 x 0,5 + (-8) x 0,5 = l,
- działanie 2. 12 x 0,5 + (-10) x 0,5 = 1,
- działanie 3. 20x0,5+(-15)x0,5 = 2,5.

Wynik: DO = max{l, 1, 2,5} = 2,5 → poz.3.
Decyzja: produkować traperki.
REGUŁA RÓWNEJ SZANSY (LAPLACE' A).

W regule tej przyjęto założenie, że skoro

nieznane są prawdopodobieństwa, to

rozsądnie jest przyjąć, iż wszystkie stany

mają jednakowe szanse pojawienia się.

Decyzja optymalna określona jest relacją

DO = max {∑Uji}

Dla: j = 1,2, ... , m oraz i = 1,2, ... , n.
Przykład
Dla danych z tablicy 1.32 mamy:
Obliczenia:

- działanie 1. 10 - 6 - 8 + 2 = -2,
- działanie 2. -10 + 3 + 5 + 12 = 10,
- działanie 3. -15+20+6-4 = 7.

Wynik: DO = max{-2, 10, 7} = 10 → poz. 2.
Decyzja: produkować trampki.

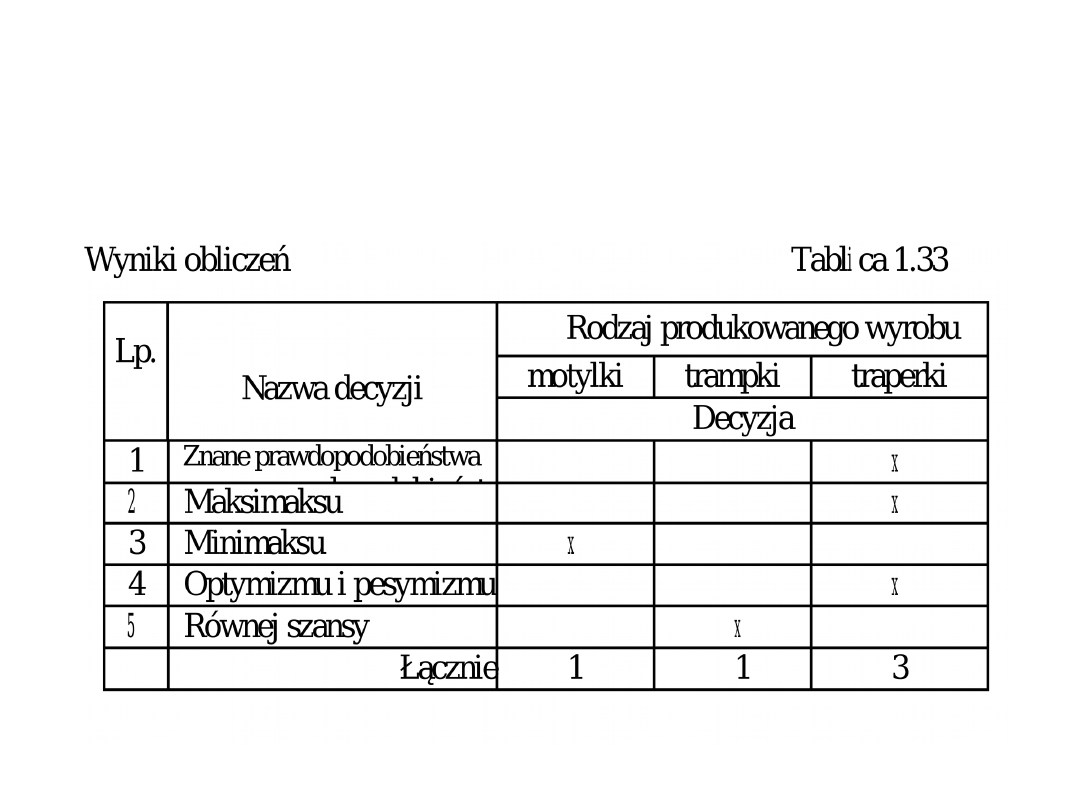
PORÓWNANIE DECYZJI. Rozważane reguły

decyzyjne prowadziły do decyzji
zestawionych w tablicy 1.33.

4. Podejmowanie decyzji na podstawie

drzewa decyzyjnego

W drzewie decyzyjnym najczęściej określa się

cztery obszary:

1. Definicja decyzji: trzeba określić czego

decyzja ma dotyczyć, np. budować nową

fabrykę, czy modernizować dotychczasową?

2. Węzeł decyzyjny: najpierw podane są

alternatywy decyzji: budowa nowej fabryki,

modernizacja fabryki (idąc od lewej do prawej)

i koszt ich realizacji: 120, 50, później wartość

podjętej decyzji (idąc od prawej do lewej).

3. Węzeł szans: podane są wartości ścieżek: 200

i 90 oraz 120 i 60 i ich prawdopodobieństwa:

65% i 35% (dla każdej alternatywy suma

prawdopodobieństw wynosi 1).

4. Wartość netto ścieżki: podane są

prawdopodobieństwa i wartości netto dla

każdej alternatywy (wartość minus koszt),

odpowiednio: 200 – 120 =80 i 90 – 120 = –

30 oraz

120– 50 = 70 =70 i 60 – 50 = 10.
Mając te dane, można obliczyć wartość decyzji

dla każdej alternatywy:

WA = (W1 – K) ∙ P1 + (W2 – K) ∙ P2

gdzie: W1 – wartość pierwszej ścieżki przy

danej alternatywie,
W2 – wartość drugiej ścieżki przy

danej alternatywie,

K – koszt danej alternatywy,

P1, P2 – prawdopodobieństwa

analizowanych ścieżek, P1 + P2 = 1.

Dla naszego przypadku:
WA1 = 80 ∙ 0,65 – 30 ∙ 0,35 = 41,5
WA2 = 70 ∙ 0,65 + 10 ∙ 0,35 = 49
Wartość decyzji końcowej wynosi:
W = max [WA1, WA2] = max[41,5;49] =

49, a więc modernizacja fabryki.

5. Wybraną alternatywę odpowiednio

zaznaczamy oraz dopisujemy w

odpowiednich miejscach: prawda – fałsz.

6. Przykład analizy zawiera schemat.