1

Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera

Zmienne losowe mogą mieć inne rozkłady niż normalne.
Zastępuje się je wtedy zastępczymi rozkładami normalnymi

zastępczymi rozkładami normalnymi

.

Rozkład miennej losowej X o parametrach 

X

i 

X

opisany jest dystrybuantą F

X

(x) oraz funkcją

gęstości prawdopodobieństwa f

X

(x).

Parametry zastępczego rozkładu normalnego

zastępczego rozkładu normalnego

, 

X

e

i 

X

e

wyznacza się zakładając, że:

1.wartości dystrybuant obu rozkładów (rzeczywistego i

zastępczego)
są sobie równe w punkcie projektowym x

*

.

2.wartości funkcji gęstości prawdopodobieństwa obu

rozkładów
są sobie równe w punkcie projektowym x

*

.

2

 























e

X

e

X

*

*

X

x

x

F

 

























e

X

e

X

*

e

X

*

X

x

1

x

f

Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera





)

x

(

F

x

*

X

1

e

X

*

e

X























)

x

(

F

)

x

(

f

1

x

)

x

(

f

1

*

X

1

*

X

e

X

e

X

*

*

X

e

X

































Po odpowiednich przekształceniach:

 

 























dz

z

P

f

Prawdopdobieństwo awarii:

3

1. Dana jest funkcja stanu granicznego:

g = R – Q

2. Przyjmujemy pierwsze przybliżenie R

*

, między 

R

i 

Q

.

R

*

= Q

*

.

3. Przybliżamy rozkłady R i Q zastępczymi rozkładami

normalnymi, tak aby:

f

R

e

(R

*

) = f

R

(R

*

)

f

Q

e

(Q

*

) = f

Q

(Q

*

)

F

R

e

(R

*

) = F

R

(R

*

)

F

Q

e

(Q

*

) = F

Q

(Q

*

)

Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera

-

-

dwie zmienne nieskorelowane R i Q

dwie zmienne nieskorelowane R i Q

4





)

R

(

F

R

*

R

1

e

R

*

e

R























)

R

(

F

)

R

(

f

1

*

R

1

*

R

e

R



















)

Q

(

F

)

Q

(

f

1

*

Q

1

*

Q

e
Q















)

Q

(

F

Q

*

Q

1

e
Q

*

e
Q















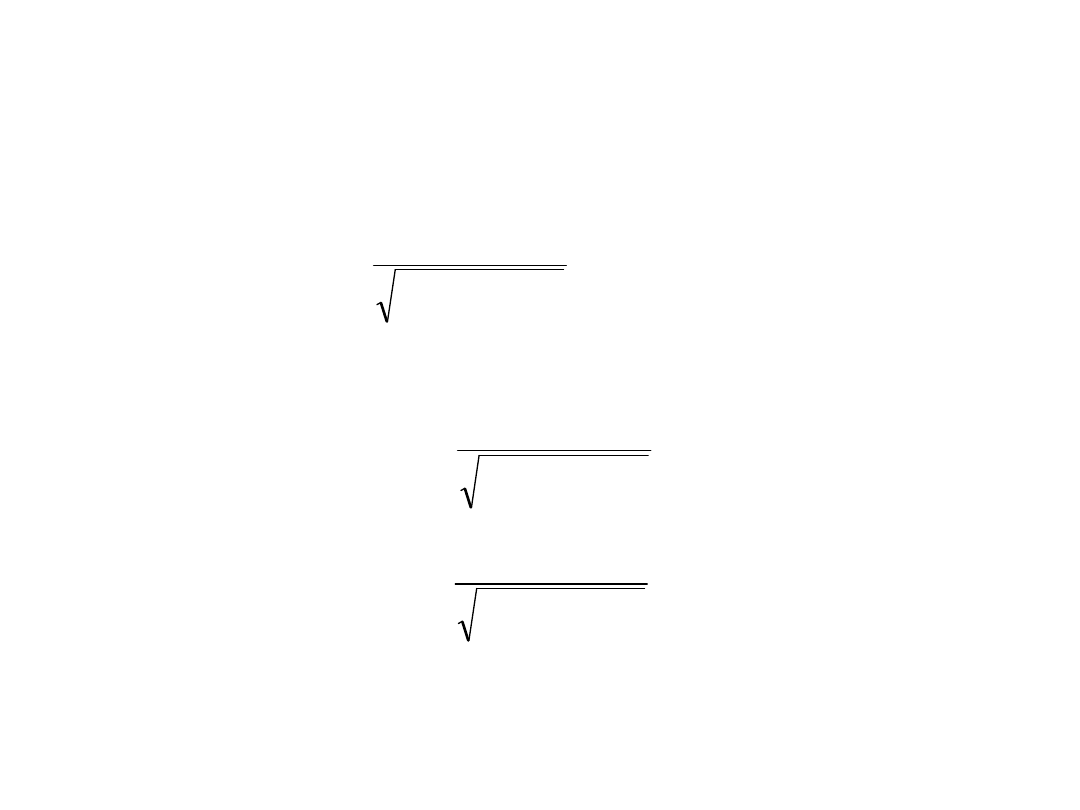
4. Obliczamy parametry zastępczych rozkładów normalnych:

Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera

-

-

dwie zmienne nieskorelowane R i Q

dwie zmienne nieskorelowane R i Q

5

5. Obliczamy  na podstawie parametrów

zastępczych rozkładów normalnych:

6. Obliczamy współrzędne nowego punktu projektowego:

7. Powtarzamy obliczenia począwszy od kroku 2

aż do uzyskania zbieżności wyników.

   

2

e
Q

2

e

R

e
Q

e

R

















 

   

2

e
Q

2

e

R

2

e

R

e

R

*

R

















 

   

2

e
Q

2

e

R

2

e
Q

e
Q

*

Q

















Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera

-

-

dwie zmienne nieskorelowane R i Q

dwie zmienne nieskorelowane R i Q

6

0.0000

0.0025

0.0050

0.0075

0.0100

0.0125

0

50

100

150

200

250

300

 

x

f

e

X

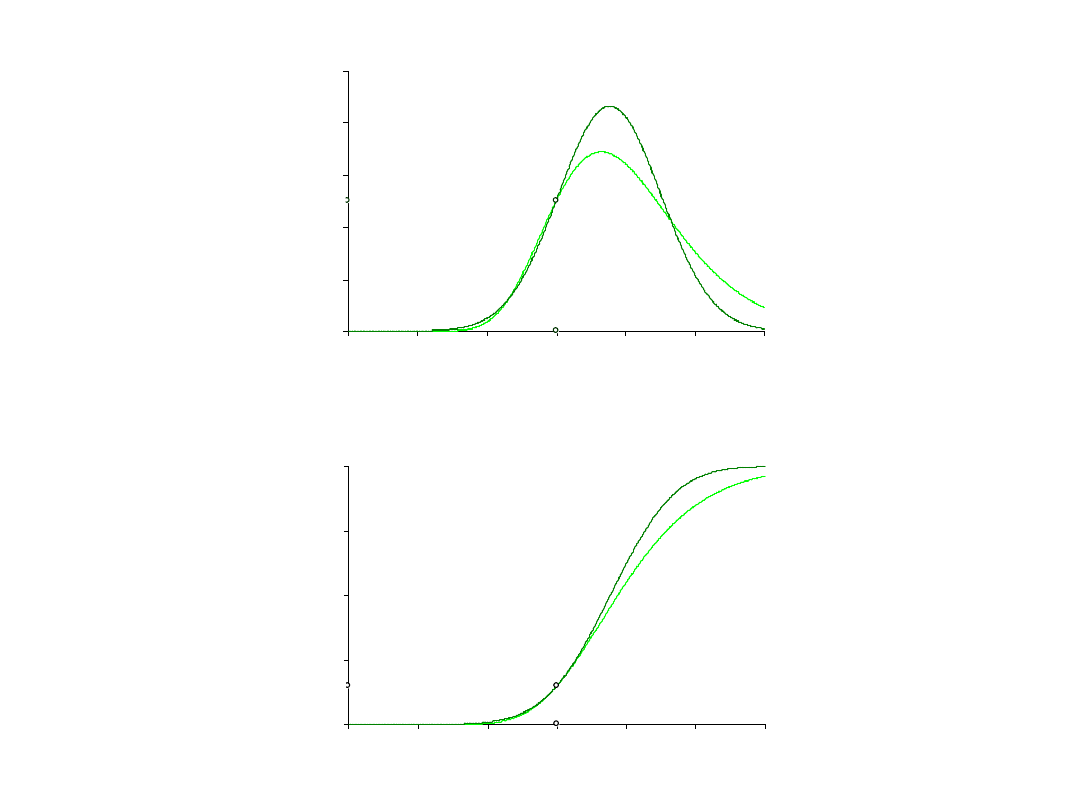
funkcja gęstości

prawdopodobieństwa

zastępczego rozkładu

normalnego

funkcja gęstości

prawdopodobieństwa

zmiennej X

 

x

f

X

 

 

*

X

*

e

X

x

f

x

f



x

*

e
X



0.0000

0.2500

0.5000

0.7500

1.0000

0

50

100

150

200

250

300

 

x

F

e

X

dystrybuanta

zastępczego rozkładu

normalnego

dystrybuanta

zmiennej X

 

x

F

X

 

 

*

X

*

e

X

x

F

x

F



x

*

e
X



7

Przykład 7

Przykład 7

Dana jest funkcja stanu granicznego:

Nośność R i obciążenie Q są zmiennymi losowymi nieskorelowanymi
o następujących rozkładach:

R – logarytmiczno-normalnym



R

= 200 kNm 

R

= 20 kNm

Q – ekstremalnym typu I



Q

= 100 kNm 

Q

= 12 kNm

Wyznaczyć wskaźnik niezawodności stosując metodę analityczną Rackwitza-Fiesslera.

Q

R

)

Q

,

R

(

g





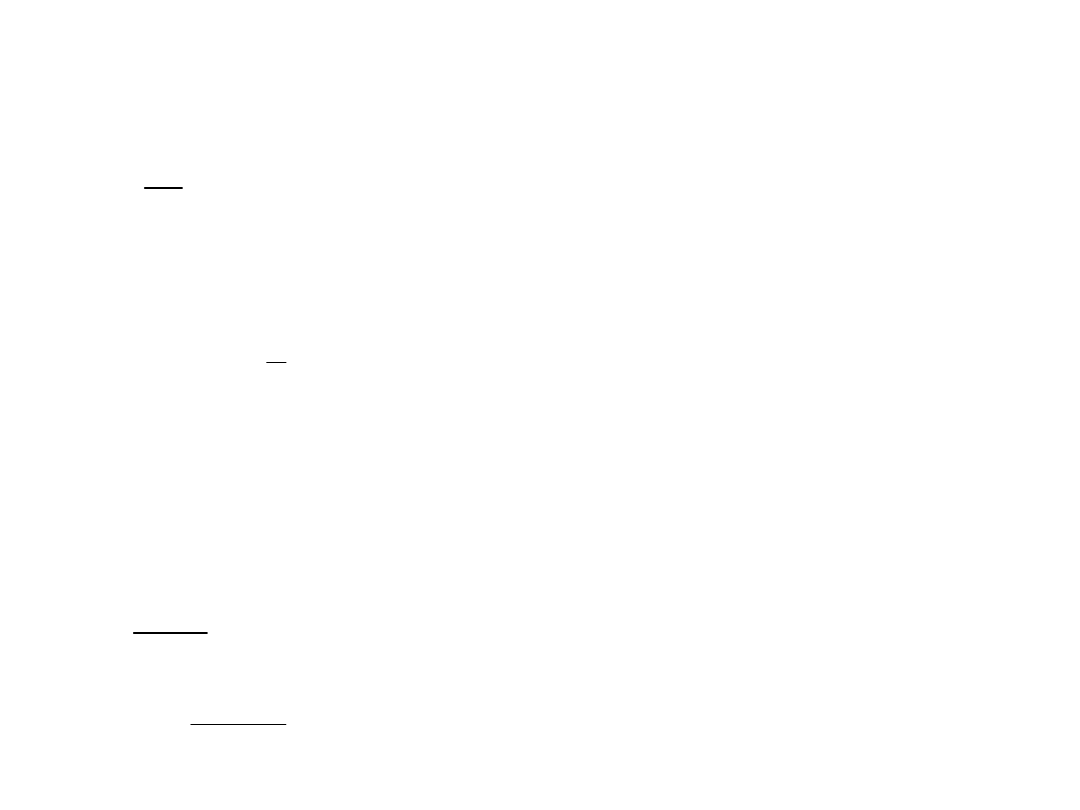
8

Przykład 7

Przykład 7

Wyznaczamy parametry rozkładu logarytmiczno-normalnego zmiennej R:

Wyznaczamy parametry rozkładu ekstremalnego typu I zmiennej Q:

10

,

0

V

R

R

R













009950

,

0

V

1

ln

2

R

2

R

ln









 

293

,

5

2

1

ln

2

R

ln

R

R

ln













099751

,

0

R

ln





107

,

0

282

,

1

Q









597

,

94

5772

,

0

u

Q











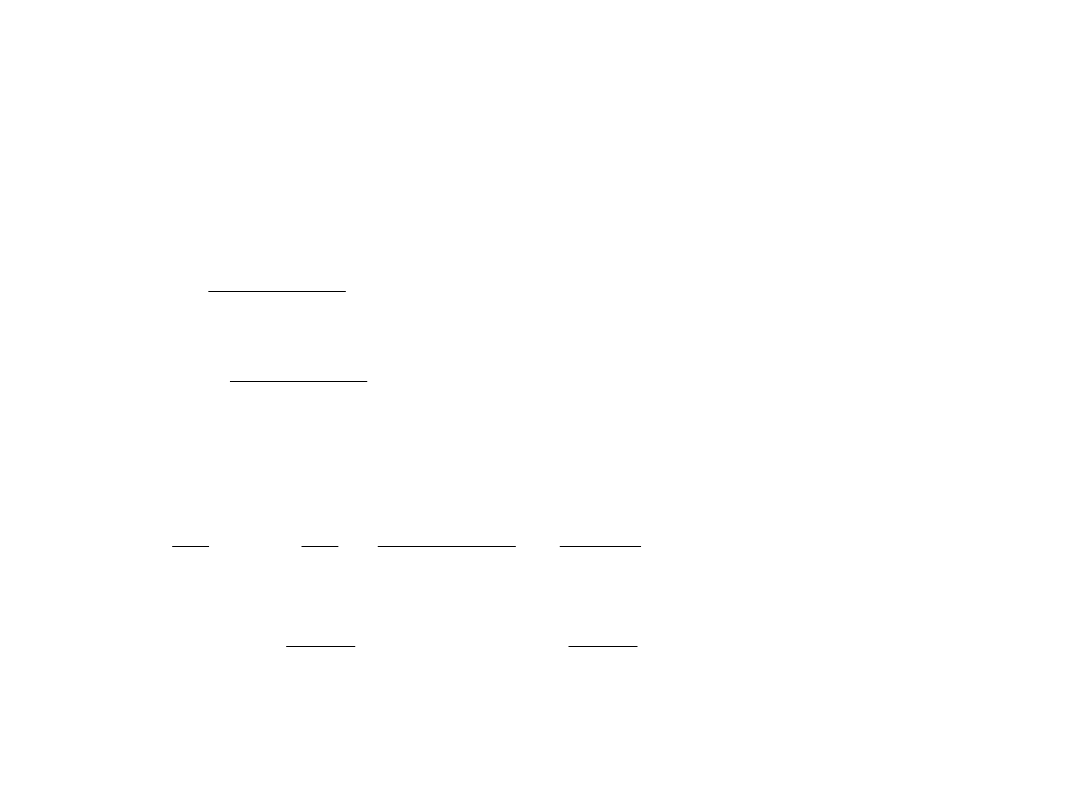
9

Przykład 7

Przykład 7

Przyjmujemy pierwsze przybliżenie współrzędnych punktu projektowego:

R

*

= Q

*

= 150 kNm

Obliczamy parametry zastępczego rozkładu normalnego zmiennej R:

 





 

834

,

2

z

R

ln

R

F

R

ln

R

ln

*

*

R

1



















 

 

 

 

z

R

1

R

ln

dR

d

R

F

dR

d

R

f

R

ln

R

ln

R

ln

*

*

*

R

































 









 

z

R

F

*

R

1











 

 









 

 

963

,

14

R

R

f

z

R

F

R

f

1

R

ln

*

*

R

*

R

1

*

R

e

R





















 





406

,

192

z

*

R

R

F

R

e

R

*

R

1

e

R

*

e

R

























 

 























R

ln

R

ln

*

*

R

R

ln

R

F

10

Przykład 7

Przykład 7

Obliczamy parametry zastępczego rozkładu normalnego zmiennej Q:

 













997

,

0

u

Q

exp

exp

Q

F

*

*

Q













 





784

,

2

Q

F

*

Q

1







 





















00286

,

0

u

Q

exp

exp

u

Q

exp

Q

f

*

*

*

Q

























 









008277

,

0

Q

F

*

Q

1









 

 









898

,

28

Q

F

Q

f

1

*

Q

1

*

R

e
Q













 





548

,

69

Q

F

Q

*

Q

1

e
Q

*

e
Q















11

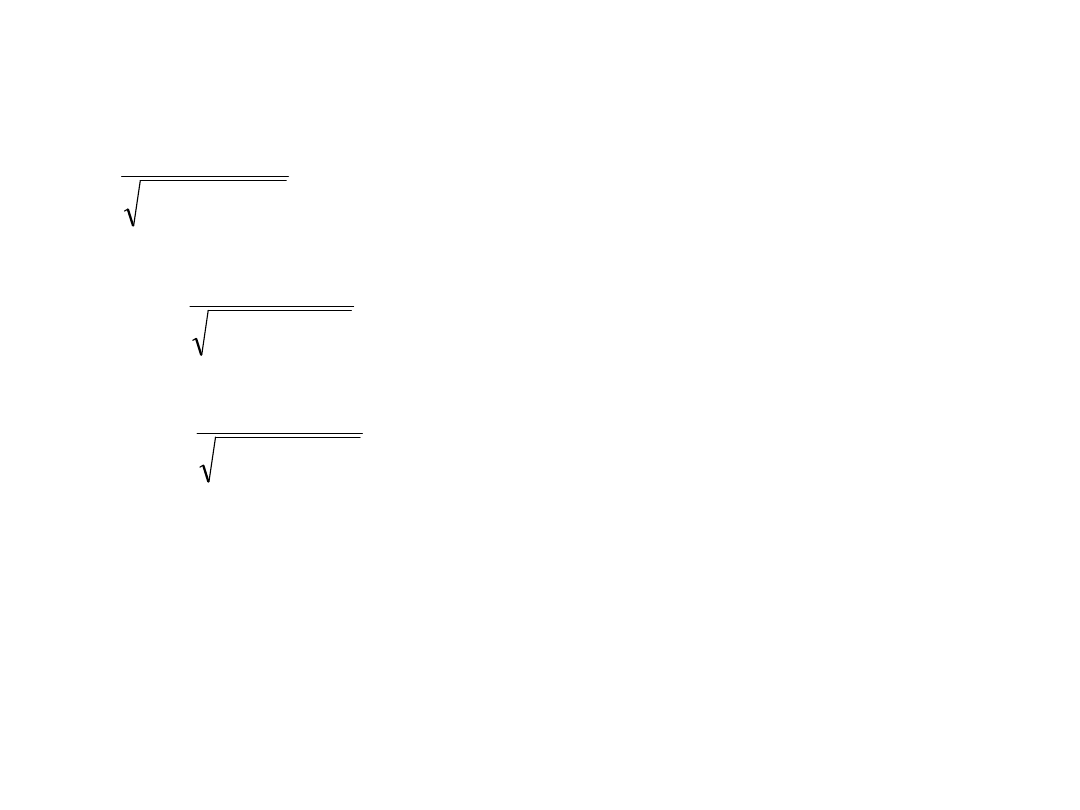
Przykład 7

Przykład 7

Obliczamy wskaźnik niezawodności i współrzędne nowego punktu projektowego:

   

775

,

3

2

e
Q

2

e

R

e
Q

e

R



















 

   

432

,

166

R

2

e
Q

2

e

R

2

e

R

e

R

*



















 

   

432

,

166

Q

2

e
Q

2

e

R

2

e
Q

e
Q

*



















Przyjmujemy nowe przybliżenie współrzędnych punktu projektowego:

R

*

= Q

*

= 166,432 kNm

12

Przykład 7

Przykład 7

e
R



e
Q



e
Q



e

R



R

*

= Q

*



R

*

= Q

*

Iteracja 1

150,00

0

14,963 192,40

6

28,898 69,548

3,775 166,43

2

Iteracja 2

166,43

2

16,602 196,18

3

33,460 55,640

3,763 168,41

8

Iteracja 3

168,41

8

16,800 196,52

6

33,976 53,915

3,763 168,50

8

Powtarzamy kolejne etapy iteracji aż do uzyskania zbieżności wyników:

Przyjmujemy ostatecznie:  = 3,76

13

Stosuje się ją w przypadku dowolnych rozkładów zmiennych losowych,

gdy ich dystrybuanty wykreślone są na arkuszu probabilistycznym.

Każda zmienna losowa o innym rozkładzie niż normalny zastępowana

jest
rozkładem normalnym, reprezentowanym na arkuszu
probabilistycznym
przez linię prostą:

• Z warunku F

X

e

(x

*

) = F

X

(x

*

) wynika, że prosta reprezentująca

dystrybuantę zastępczego rozkładu normalnego F

X

e

musi przecinać

dystrybuantę rozkładu oryginalnego F

X

w punkcie projektowym x

*

.

• Z warunku f

X

e

(x

*

) = f

X

(x

*

) oraz z faktu, że funkcja gęstości

prawdopodobieństwa jest styczną do dystrybuanty
(jako jej pierwsza pochodna) wynika, że prosta reprezentująca
dystrybuantę zastępczego rozkładu normalnego F

X

e

musi być

styczna do dystrybuanty rozkładu oryginalnego w punkcie
projektowym x

*

.

Parametry zastępczego rozkładu normalnego - wartość średnia

i odchylenie standardowe - mogą być odczytane z wykresu.

Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera

-

-

procedura graficzna

procedura graficzna

14

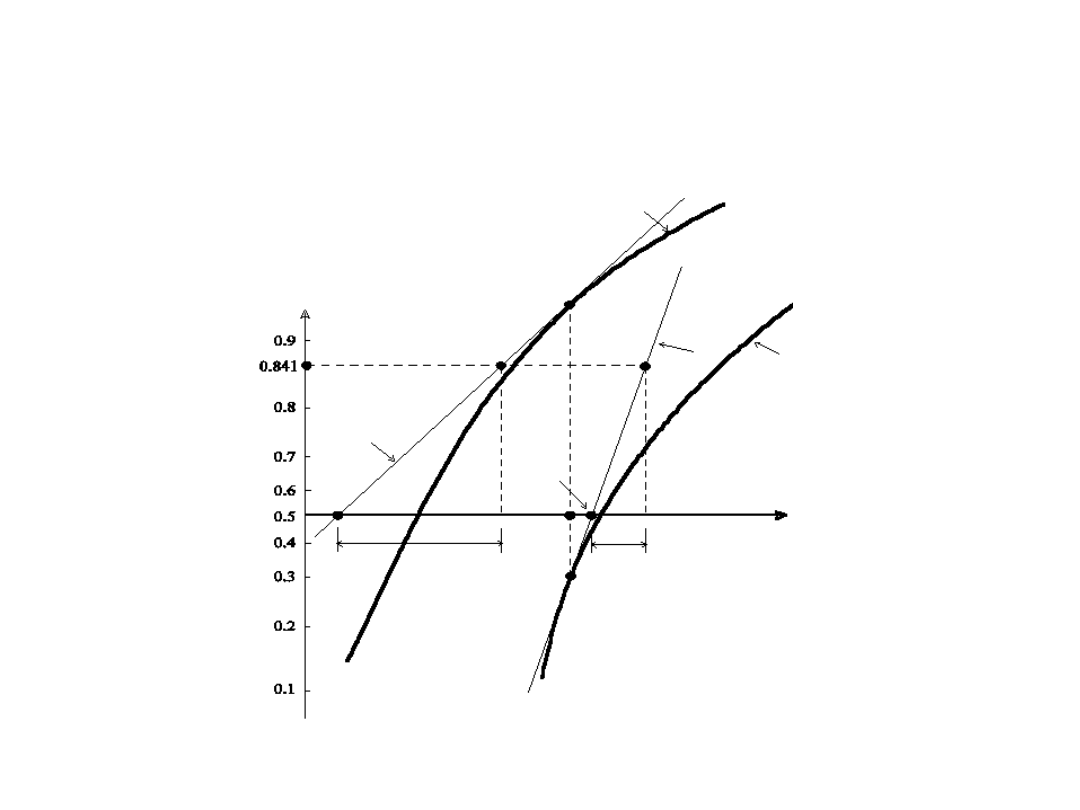
Ilustracja graficzna procedury Rackwitza-Fiesslera

R, Q

F

R

F

Q

F

Q

e

F

R

e

styczna do F

R

w punkcie r*

Q

*

= R

*



R

e



Q

e



R

e



Q

e

styczna do F

Q

w punkcie q*

Metoda Rackwitza-Fiesslera

Metoda Rackwitza-Fiesslera

-

-

procedura graficzna

procedura graficzna

15

Przykład 8

Przykład 8

Dana jest funkcja stanu granicznego:

g(R, Q) = R - Q

R - nośność
Q - obciążenie

Dystrybuanty zmiennych R i Q wykreślono

na arkuszu probabilistycznym rozkładu normalnego.

Wyznaczyć wskaźnik niezawodności.

16

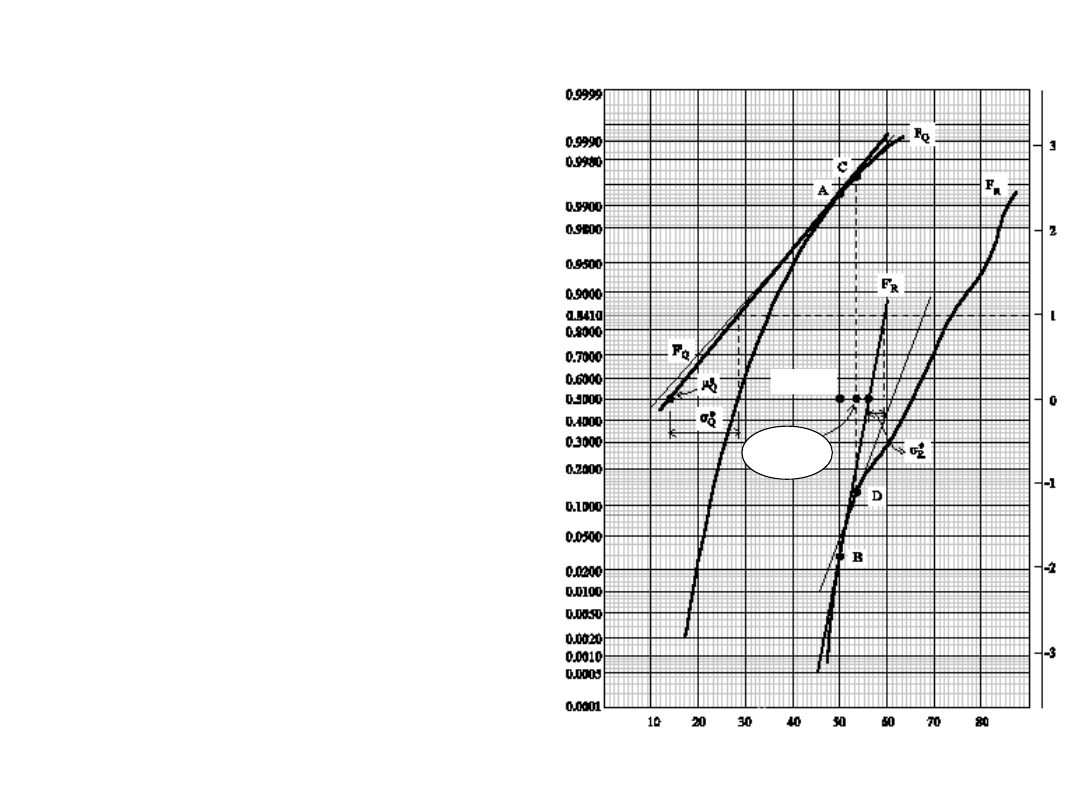
1. Przyjmujemy wartość

początkową
współrzędnej punktu
projektowego,
na przykład R* = 50
Zaznaczamy na wykresach F

Q

i

F

R

punkty A i B.

2. Prowadzimy styczne do F

Q

i F

R

w punktach A i B.

3. Z wykresu odczytujemy:

56

e

R





14

e
Q





5

,

3

e

R





5

,

14

e
Q





Przykład 8

Przykład 8

nowy punkt

projektowy

R

*

=Q

*

17

4. Obliczamy .

5. Wyznaczamy nowy

punkt projektowy.

Z równania g = 0 wynika: Q

*

= R

*

   

  



82

,

2

6

,

14

5

,

3

14

56

2

2

2

e
Q

2

e

R

e
Q

e

R

























 

   

  



  



7

,

53

6

,

14

5

,

3

82

,

2

5

,

3

56

R

2

2

2

2

e
Q

2

e

R

2

e

R

e

R

*

























nowy punkt

projektowy

R

*

=Q

*

Przykład 8

Przykład 8

18

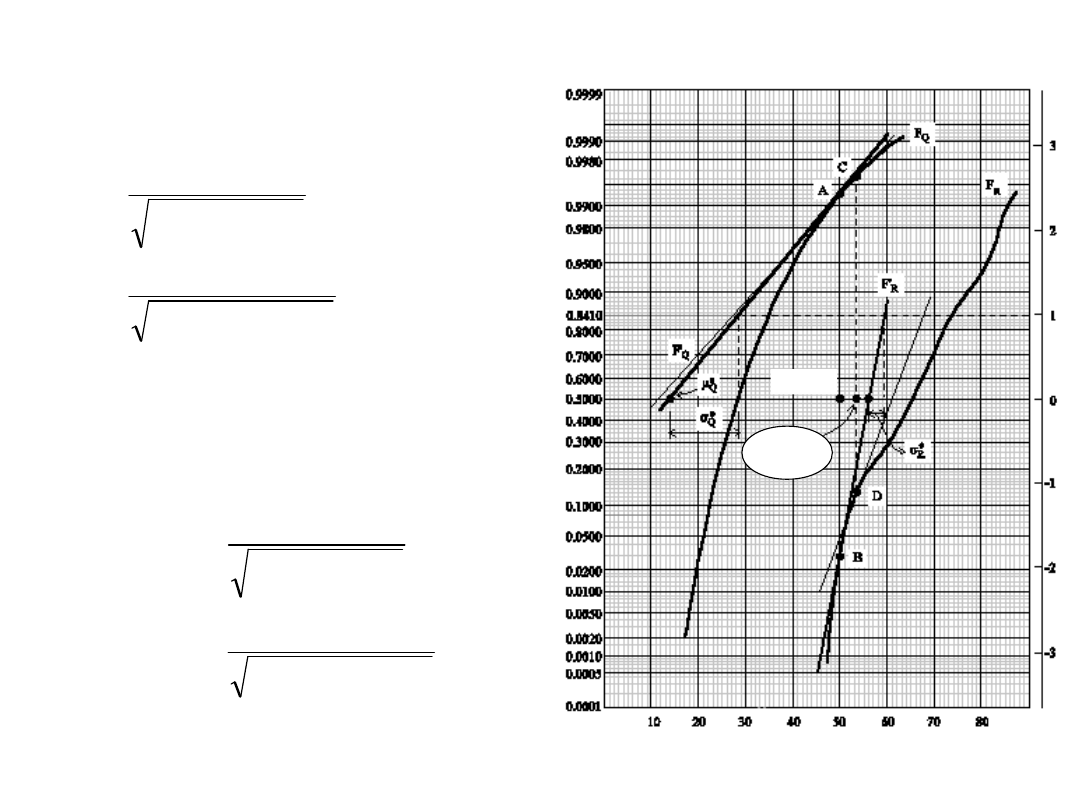
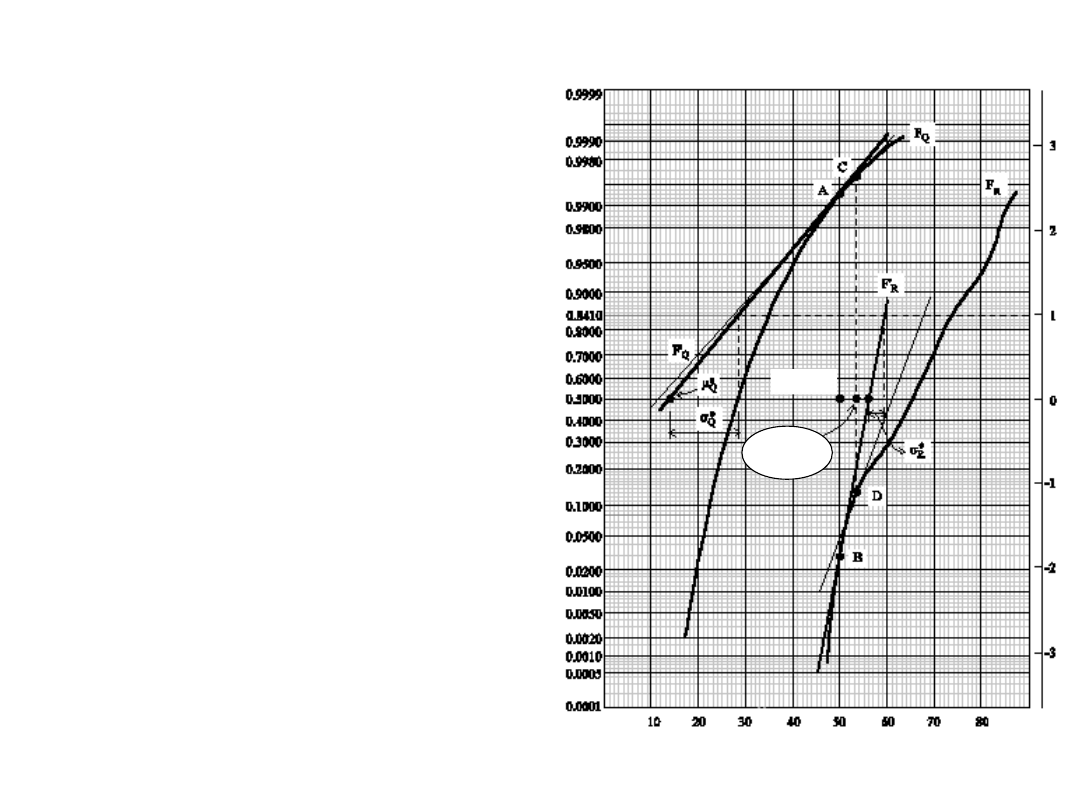
6. Prowadzimy styczne do F

Q

i F

R

w punktach C i D odpowiadających
nowemu punktowi projektowemu.

7. Z wykresu odczytujemy :

8. Obliczamy nowy  i współrzędne

nowego punktu projektowego.

9. Powtarzamy iteracje, aż do uzyskania

zbieżności wyników.

61

e

R





5

,

11

e
Q





5

,

6

e

R





5

,

15

e
Q





94

,

2





6

,

53

Q

R

*

*





nowy punkt

projektowy

R

*

=Q

*

Przykład 8

Przykład 8