ZASADA ZACHOWANIA PĘDU
1. Zasada zachowania pędu dla pojedynczego ciała; popęd
siły
2. Zasada zachowania pędu dla układu ciał
3. Zderzenia
4. Środek masy i jego własności
5. Napęd rakietowy
ZASADA ZACHOWANIA PĘDU
1. Zasada zachowania pędu dla pojedynczego ciała; popęd
siły
2. Zasada zachowania pędu dla układu ciał
3. Zderzenia
4. Środek masy i jego własności
5. Napęd rakietowy
ZASADA ZACHOWANIA PĘDU
POPĘD SIŁY
Jeśli siła działa w czasie dt, to znaczy to, że pęd ciała się zmienia
dp=Fdt
A jeśli siła działa dłużej, to zmiana pędu wynosi:
2
1
t
t
dt
F
p
Popęd siły
Jeśli na ciało działają siły, to ciało zmienia swój pęd z szybkością
proporcjonalną do siły wypadkowej (wektorowej sumy sił).
t
p
d
F
F
wyp
i
i
d
PRZYPOMNIENIE: I zasada dynamiki
jeśli na ciało nie działa żadna siła, to jego pęd jest zachowany:
p
przed
=p
po
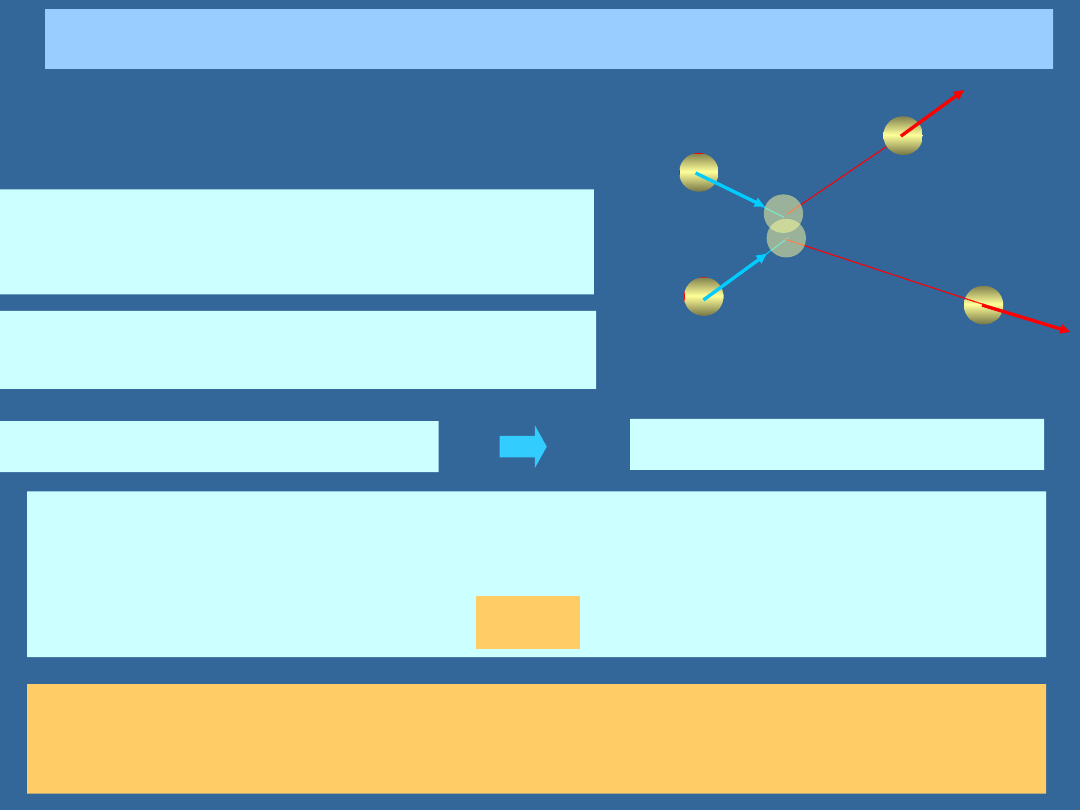
ZACHOWANIE PĘDU UKŁADU DWÓCH CZĄSTEK
zderzenie 2 swobodnych kul
Skutkiem działania siły jest nadanie ciału
przyśpieszenia: F
12
=m
2
V
2
/t i F
21
=m
1
V
1
/t
m
1
m
2
V
1p
V
2p
V
1k
V
2k
Jeśli na układ nie działają siły zewnętrzne, to całkowity pęd
układu
p=m
i
V
i
jest stały
układ odizolowany kulek: nic za wyjątkiem samych
kulek na te kulki nie działa
F
12
: siła działająca na kulę 2 pochodząca od
kuli 1,
F
21
: siła działająca na kulę 1 pochodząca od
kuli 2
F
12
=-F
21
F
12
+F
21
=0
F
12
+F
21
=0 m
2
V
2
/t
+m
1
V
1
/t=0.
m
2
V
2
+m
1
V
1
=0.
V jest różnicą między prędkością początkową i końcową: V
k
-V
p
, czyli:
m
2
(V
2k
-V
2p
)= -m
1
(V
1k
-V
1p
)
m
2
V
2k
+m
1
V
1k
= m
1
V
1p
+ m
2
V
2p
m
i
V
i
-pęd układu kulek
.
k
p
p
p
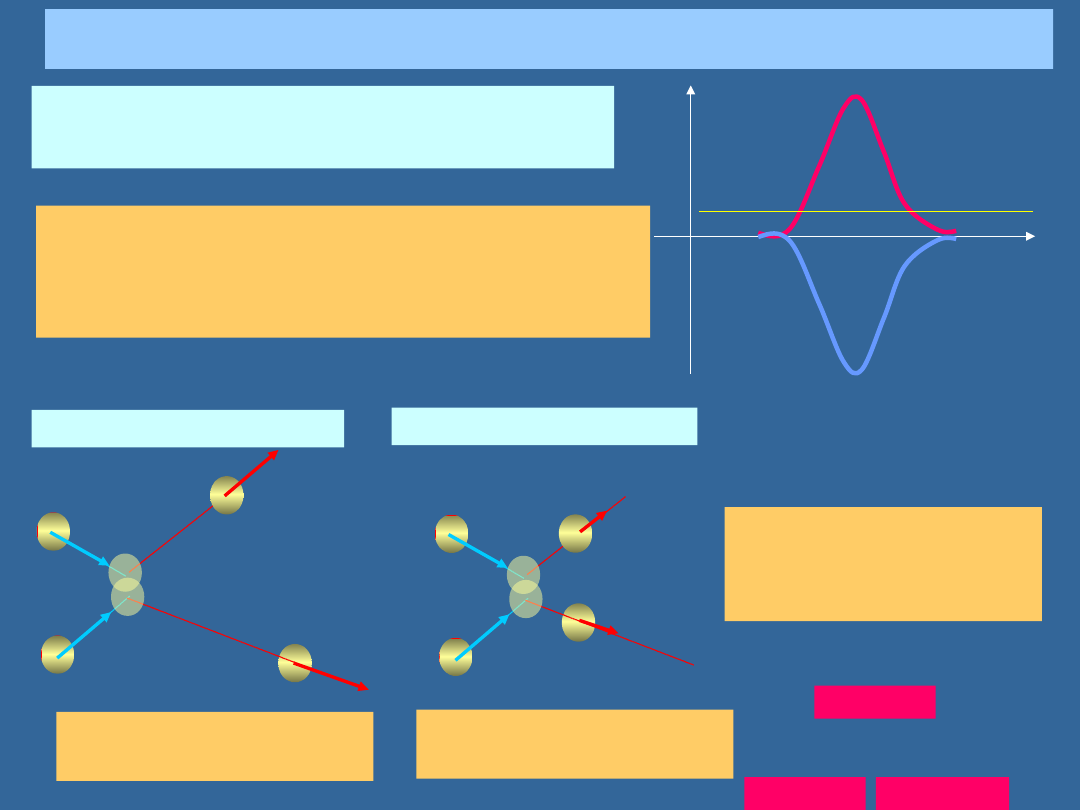
ZDERZENIA
Popęd siły w czasie zderzenia jest dużo
większy niż skutek działania jakichkolwiek
innych sił.
W zderzeniu całkowity pęd układu tuż przed
zderzeniem jest równy całkowitemu pędowi tuż
po zderzeniu
p
przed
=p
po
F
12
F
21
F
czas
inne
siły
m
1
m
2
V
1p
V
2p
V
1k
V
2k
Zderzenia elastyczne
p
przed
=p
po
E
Kprzed
= E
Kpo
Zderzenia
nieelastyczne
m
1
m
2
V
1p
V
2p
V
1k
V
2k
p
przed
=p
po
W każdym zderzeniu,
nawet nieelastycznym,
pęd jest zachowany
m
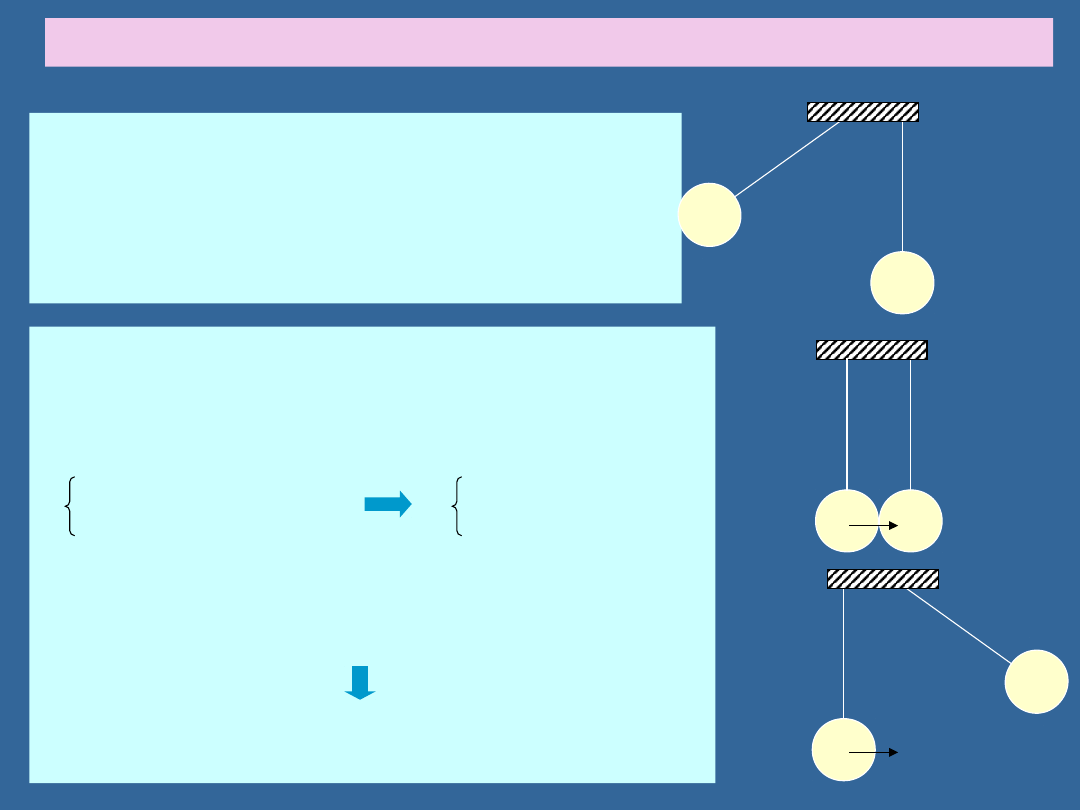
ZASADA ZACHOWANIA PĘDU: PRZYKŁAD
Wiemy, ze gdy jedna kula uderza w 3 stojące, to
kule uderzająca i najdalsza od uderzenia zamieniają
się miejscami. Ten sam przypadek mamy, jeśli
zderzają się 2 kule (jedna stojąca nieruchomo): ta
która stała porusza się teraz z identyczną
prędkością jak pierwsza, a ta pierwsza stoi.
Dlaczego tak jest?
Ponieważ zderzenie jest elastyczne, to zachowany jest
zarówno pęd jak i energia kinetyczna:
P
przed
=p
po
E
Kprzed
=E
Kpo
mV+0=mV
1
+mV
2
V=V
1
+V
2
V
1
=V-
V
2
mV
2
/2=mV
1
2
/2+ mV
2
2
/2
V
2
= V
1
2
+ V
2
2
V
2
= (V-V
2
)
2
+ V
2
2
V
2
= V
2
-2VV
2
2
+ 2V
2
2
0= V
2
(V
2
-V)
V
2
=0 lub V
2
= V
V
V
1
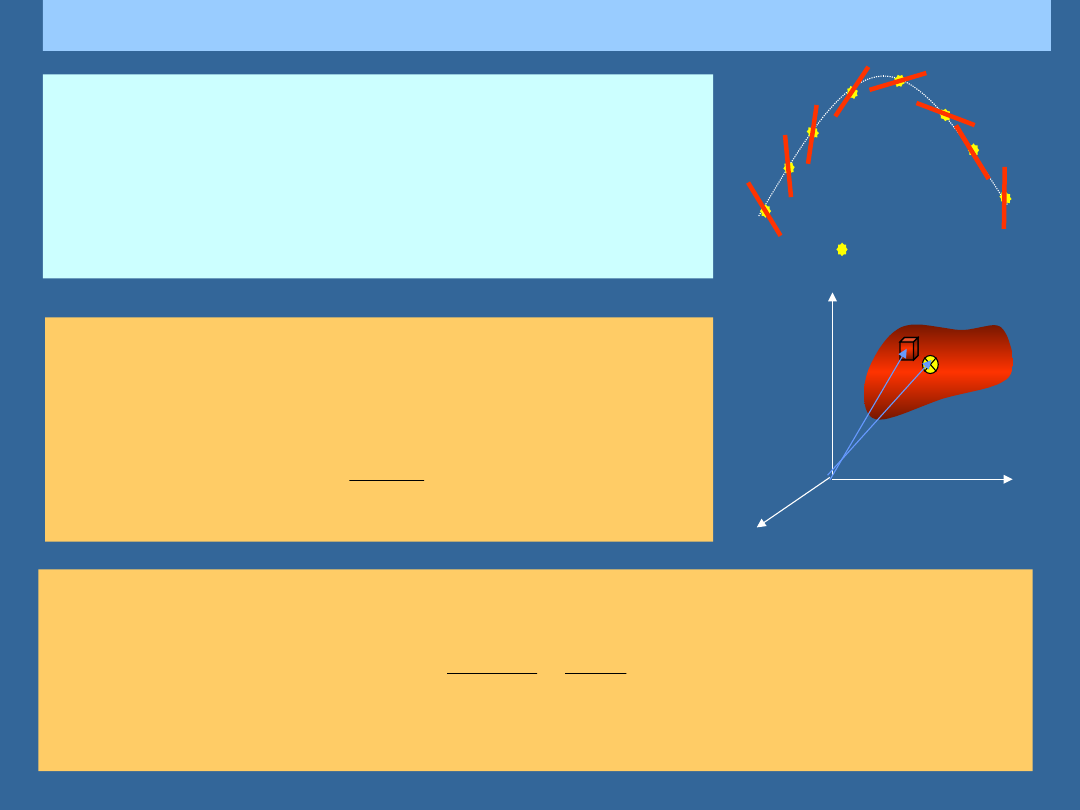
ŚRODEK MASY
Jeśli bryła jest zbiorem mas m
i
to współrzędna środek
masy układu N punktów materialnych o masach m
i
położonych w punktach o wektorach r
i
, jest punktem
którego położenie opisane jest wektorem :
i
i
i
i
i
sm
m
m
r
R
m
i
R
sm
r
i
x
y
z
Jeśli zbiór punktów stanowi bryłę to współrzędna środka masy takiej bryły ma
postać
M
dm
r
m
m
r
R
i
i
i
i
i
sm
środek
masy
Jeśli rzucimy do góry kijem, to jego ruch jest bardzo
skomplikowany. Jednak dla kogoś patrzącego z oddali
i widzącego tylko zarys wydaje się, że jest to prosty
rzut ukośny punktu. Czy istnieje zatem punkt kija,
który mimo skomplikowanego ruchu całości porusza
się prosto, tak jak w rzucie ukośnym?
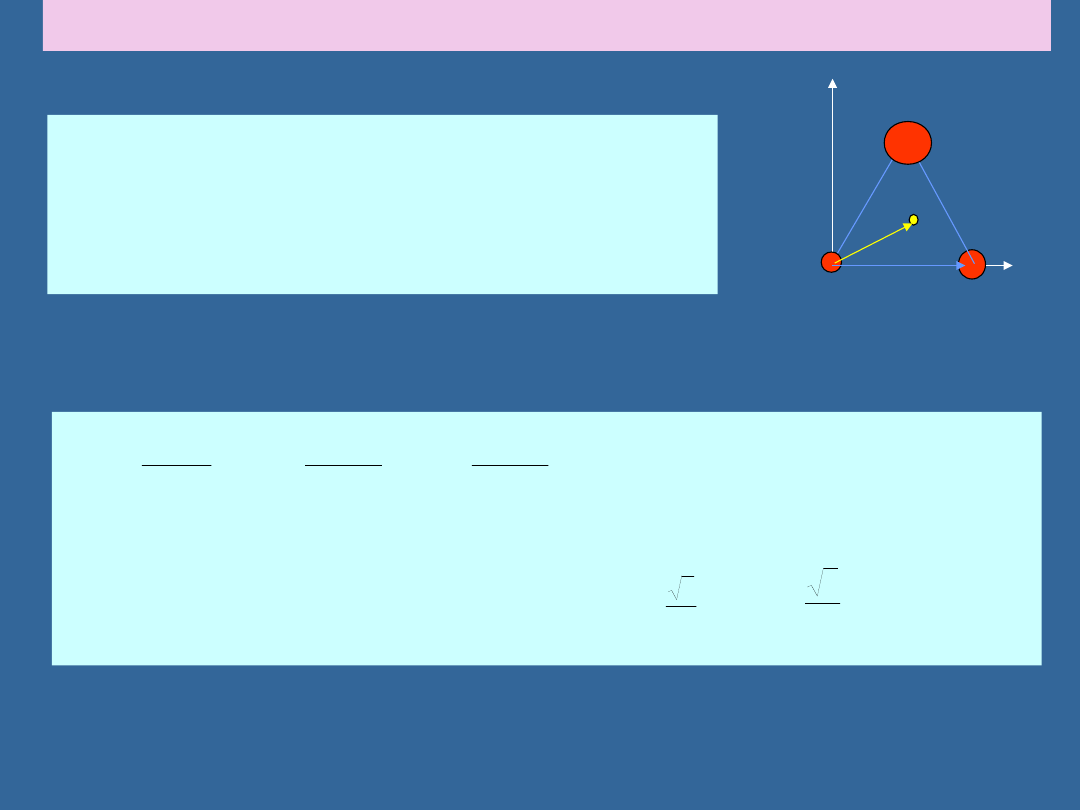
ZNAJDOWANIE ŚRODKA MASY: PRZYKŁAD
Znaleźć środek masy układu trzech cząstek o masach
m
1
= 1kg, m
2
= 2kg i m
3
= 3kg, umieszczonych w
rogach równobocznego trójkąta o boku 1m.
Ponieważ wynik nie zależy od wyboru układu
odniesienia to możemy przyjąć układ tak jak na
rysunku.
m
2
r
3
y
x
m
1
m
3
r
2
x
śrm
= (m
1
x
1
+ m
2
x
2
+ m
3
x
3
)/M = (1kg·0m + 2kg·1m + 3kg·0.5m)/6kg = 7/12m
y
śrm
= (m
1
y
1
+ m
2
y
2
+ m
3
y
3
)/M = (1kg·0m + 2kg·0m+3kg· m)/6kg = m
i
i
i
i
i
sm
i
i
i
i
i
sm
i
i
i
i
i
sm
m
m
y
y
,
m
m
x
x
m
m
r
R
2
3
4
3
R
sm
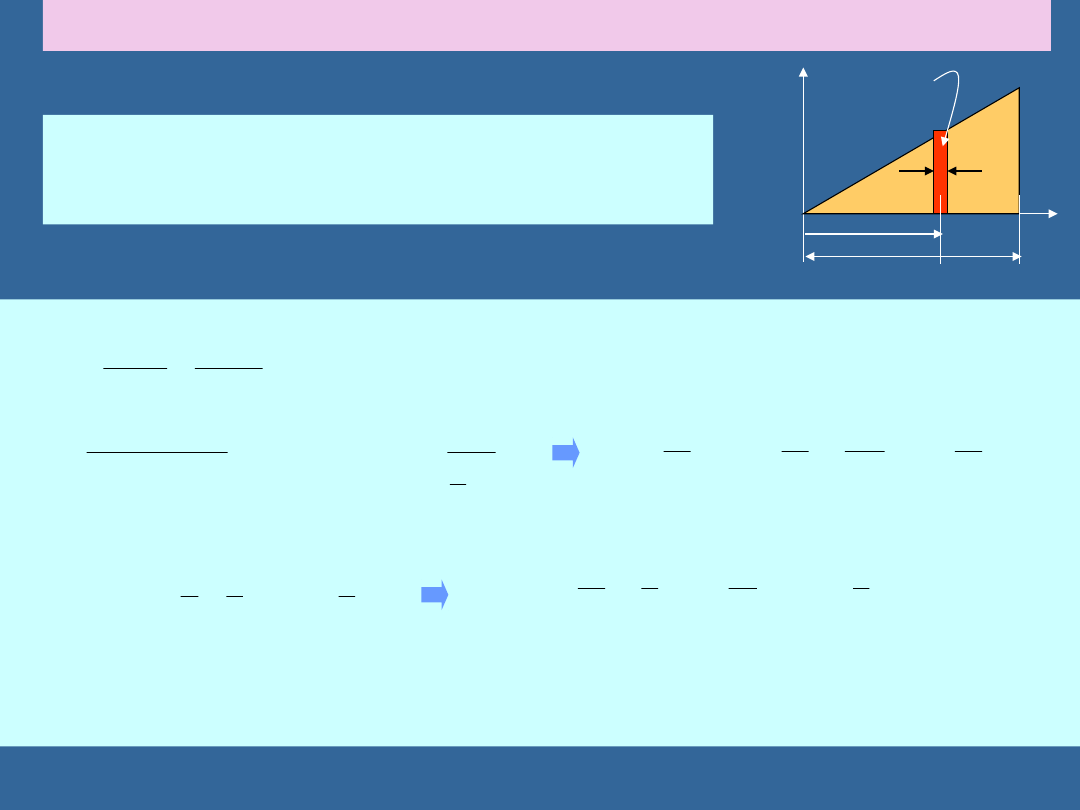
ZNAJDOWANIE ŚRODKA MASY: PRZYKŁAD
Znaleźć środek masy płyty w formie trójkąta
prostokątnego o masie M i podanych wymiarach
zakładając, że masa w płycie jest rozłożona
jednorodnie
x
dm’
y
dx
x
c
a
b
y
gdzie dm’ jest masą paska o grubości dx i rozciągającego się na
całą
szerokość trójkąta w kierunku y
Musimy teraz wyrazić wysokość paska y poprzez jego położenie x
Takie same obliczenia prowadzą do wyniku na y
sm
=b/3
M
'
xdm
M
xdm
x
sm
ydx
ab
2
1
M
dS
paska
.
pow
ia
powierzchn
masa
'
dm
a
0
a
0
sm
xydx
ab
2
ydx
ab
M
2
x
M
1
xdm
M
1
x
a
b
x
y
a
b
x
y
a
3
2
dx
x
a
2
xdx
a
b
x
ab
2
x
a
0
2
2
a
0
sm
WŁASNOŚCI ŚRODKA MASY
Ponieważ
więc
Pęd środka
masy
M
m
r
R
i
i
i
sm
M
m
V
V
dt
R
d
i
i
i
sm
sm
Całkowity pęd układu cząstek jest równy pędowi cząstki o masie równej całkowitej
masie cząstek M pomnożonej przez prędkość środka masy układu
i
i
i
sm
m
V
V
M
środek masy ciała porusza się tak, jak cząstka o masie M do
której przyłożone są wszystkie siły zewnętrzne działające na
układ cząstek
Ma
sm
=m
i
*a
i
ale
m
i
*a
i
=F
ij
Przyśpieszenie środka masy
i
i
i
sm
m
V
V
M
m
i
m
j
F
ji
F
ij
F
ij
+ F
ji
=0
dla każdej pary sił wewnętrznych: F
ij
=-F
ji
.
z
sm
F
a
M
w sumie zostaną tylko siły
zewnętrzne
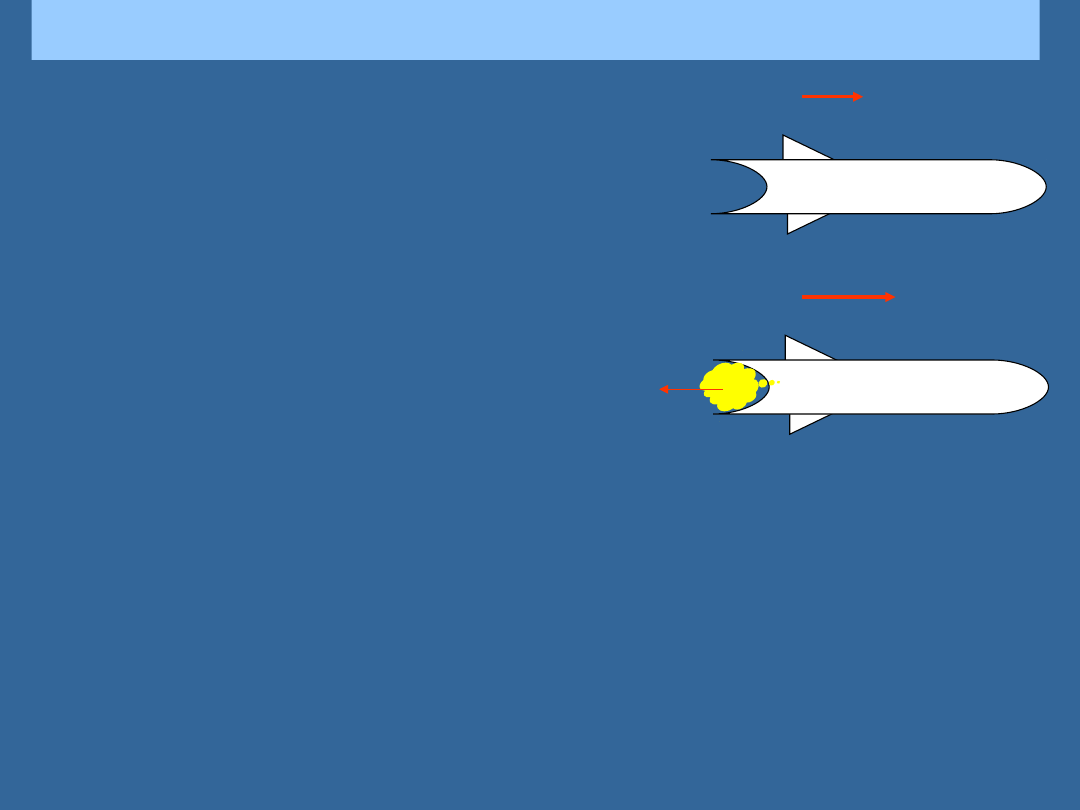
NAPĘD RAKIETOWY
V
m+m
p
i
=(m+m)V
m
V+ V
m
V- V
w
V
w
-prędkość gazów
względem rakiety
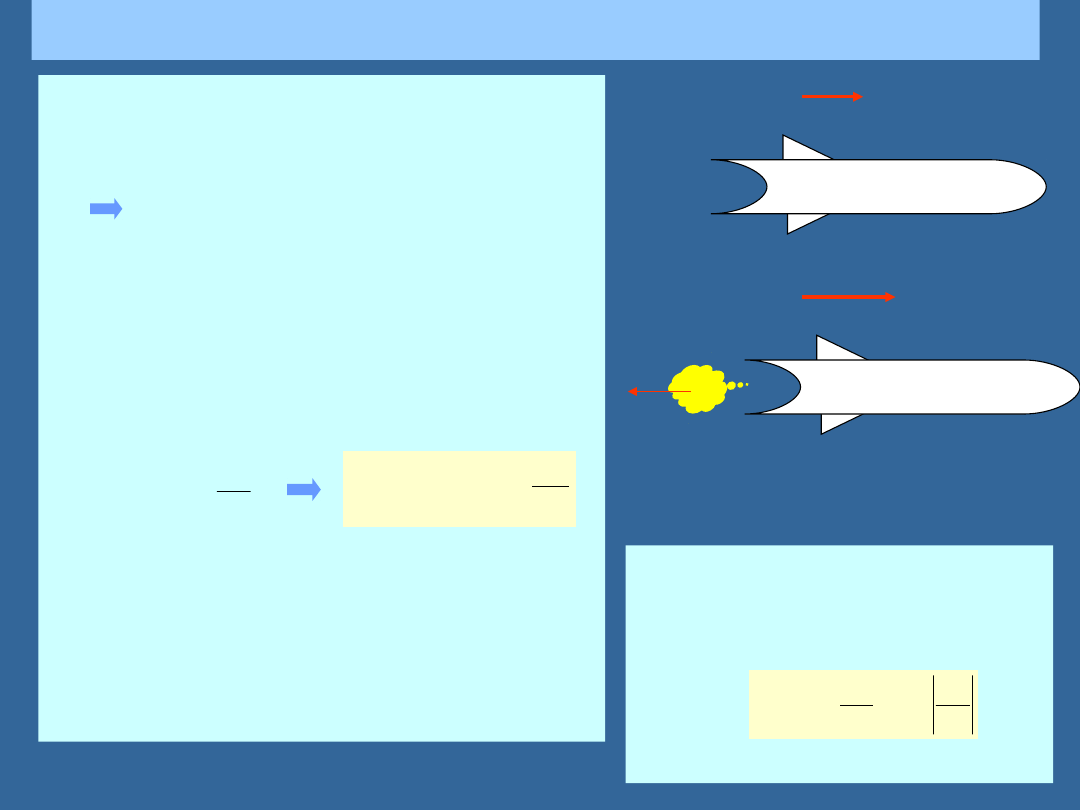
NAPĘD RAKIETOWY
m+m
p
i
=(m+m)V
m
V+ V
m
V- V
w
V
w
-prędkość gazów
względem rakiety
Ciąg rakiety: siła wywierana na
rakietę przez wyrzucone gazy.
Ponieważ mdV=-V
W
dm, to
dt
dm
V
dt
dV
m
ciag
W
Pęd rakiety zmienia się jeśli część gazu z
dużą prędkością zostaje wyrzucona wstecz.
Całkowity pęd rakiety i wyrzuconych gazów
nie zmienia się.
(m+m)V= m(V+V)+ m(V-V
W
)
mV= V
W
m
ale:
Vdv , m -dm
(m to masa gazów, a dm to masa-ujemna-
o jaką zmniejszy się masa rakiety)
mdV=-V
W
dm
rozdzielając zmienne i całkując dostajemy:
m
i
-początkowa masa rakiety i paliwa
m
f
-końcowa masa rakiety i paliwa
Wnioski:
-jak najwyższa prędkość wyrzutu gazów
-jak największa ilość paliwa
f
i
f
i
m
m
W
V
V
m
dm
V
dV
f
i
W
i
f
m
m
ln
V
V
V
V