
Automatyka i regulacja
automatyczna
Wykład 11
Modele dyskretne obiektów
regulacji

2
Modele dyskretne obiektu inercyjnego I
rzędu
)
(
)
(
0
t
u
k
t
y
dt
dy
T
p
p
p
p
p
T
T
a
n
u
k
n
y
n
y
n
y
a
nT
u
k
nT
y
nT
y
T
T
)
(
)
(
)]
1
(
)
(
[
)
(
)
(
)
(
0
0
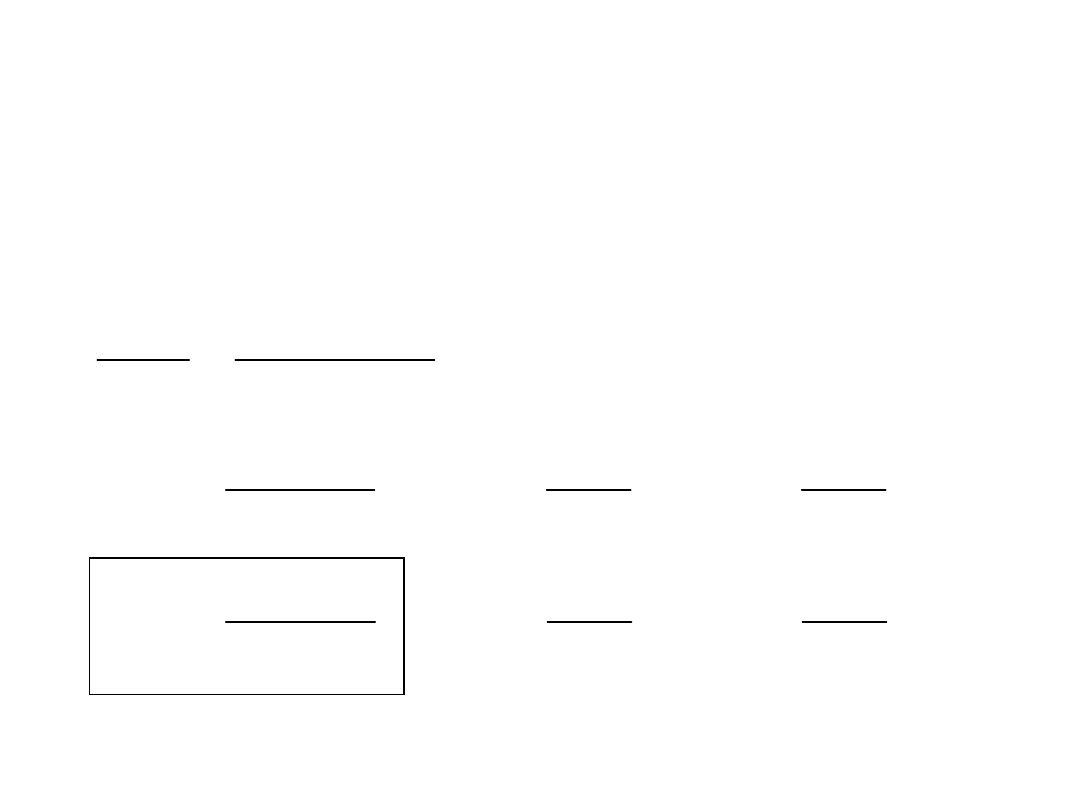
Dyskretne równanie wejścia - wyjścia
Transformata Z
0
)
(
)
(
n
n
p
def
z
nT
u
z
U
3
0
)
1
(
)
(
)}
1
(
{
1
y
z
Y
z
n
y
Z
1
1
1
)
(
1
1
1
)
(
1
)
(
)
(
)
(
)
(
)
(
)
1
(
)
(
)
(
)]
(
)
(
[
1
0
0
1
1
0
1
0
0
1
1
0
1
0
0
1
0
1
a
a
a
a
k
b
z
a
b
z
G
a
a
a
a
k
b
z
a
b
z
G
az
a
k
z
U
z
Y
z
U
k
z
Y
az
z
Y
a
z
U
k
z
Y
z
Y
z
z
Y
a
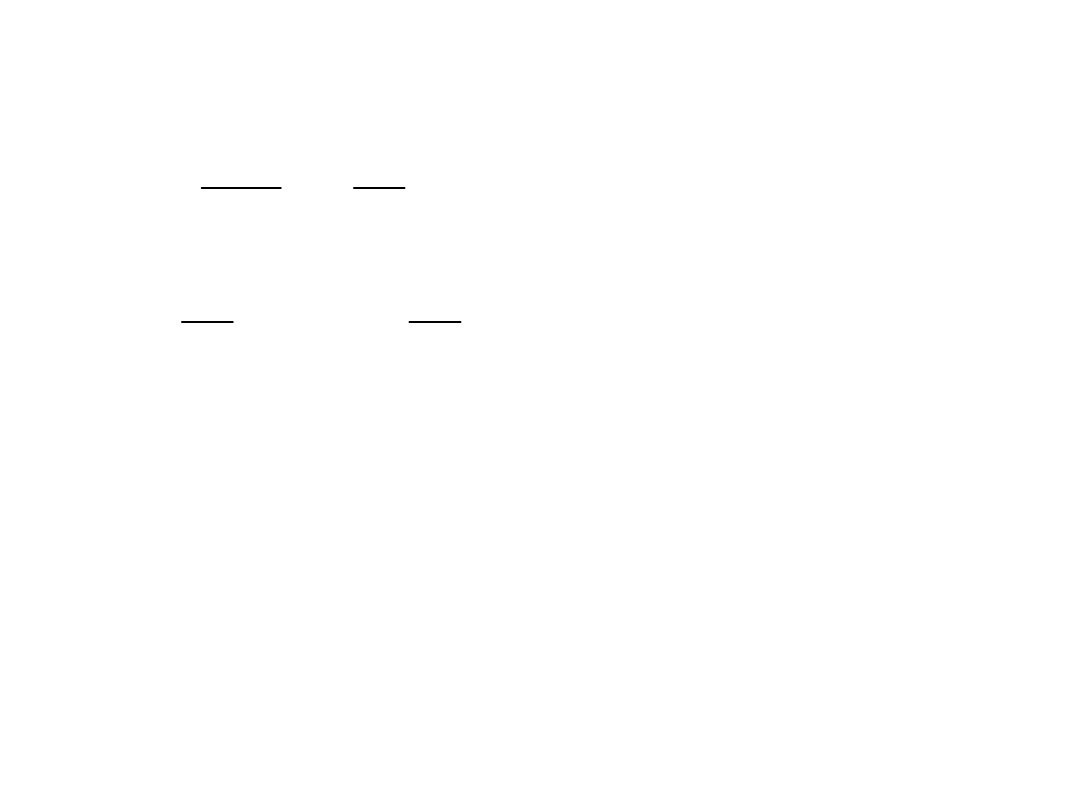
4
Modele dyskretne obiektu II
rzędu
)
(
)
(
0
2
2
t
u
k
t
cy
dt
dy
b
dt
y
d
a
)
2
(
)
1
(
2
)
(
)
(
)]
2
(
)
1
(
[
)
1
(
)
(
)
(
)
1
(
)
(
)
(
)
(
)
(
2
2
2
2
2
n
y
n
y
n
y
n
y
n
y
n
y
n
y
n
y
n
y
n
y
n
y
n
y
n
y
t
y
d
)
(
)
(
)
(
0
2
n
u
k
n
cy
y
T
b
n
y
T
a
p
p
5
)
(
)
2
(
)
1
(
)
(
0
2
1
n
u
b
n
y
a
n
y
a
n
y
2
2
1
1
0
2
2
1
1
0
0
2
2
1
1
1
)
(
1
)
(
)
(
)
(
)
(
)
(
)
(
z
a
z
a
b
z
G
z
a
z
a
b
z
U
z
Y
z
U
b
z
Y
z
a
z
Y
z
a
z
Y
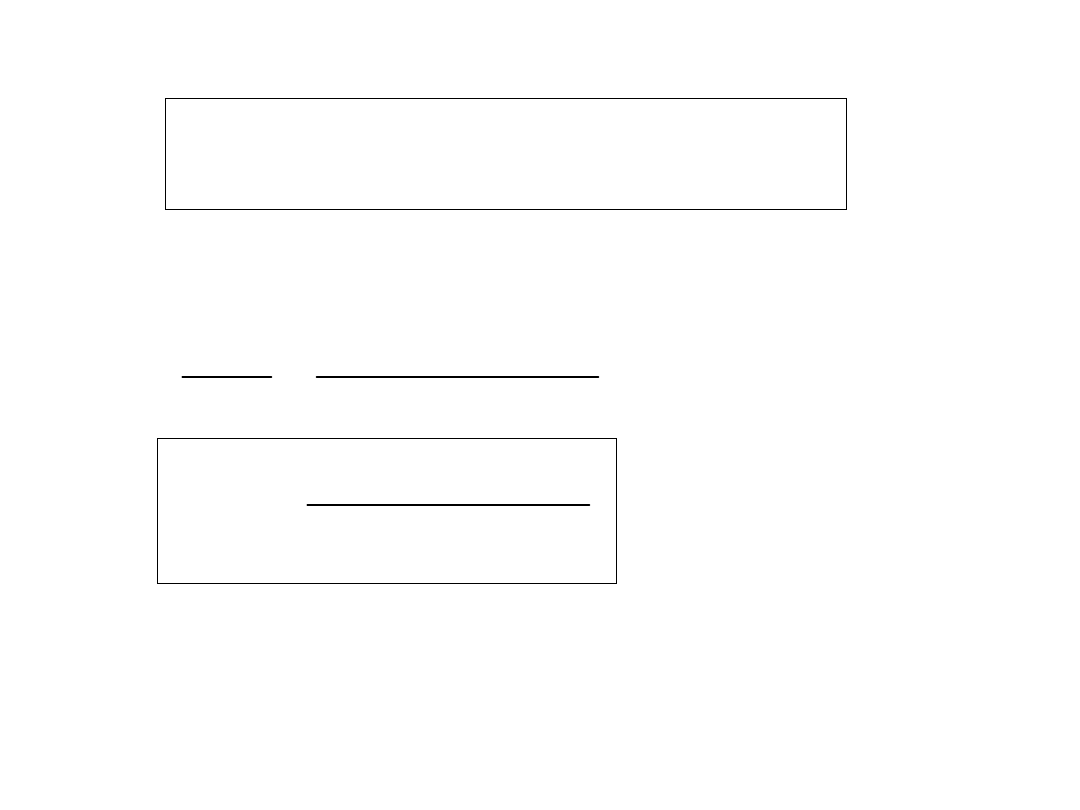
Transmitancja
dyskretna

6
Modele dyskretne obiektu k-tego
rzędu
)
(
)
(
)
1
(
...
)
1
(
)
(
0
1
1
n
u
b
k
n
y
a
k
n
y
a
n
y
a
n
y
k
k
Dyskretne równanie wejścia –
wyjścia:
Transmitancja
dyskretna:
k
k
z
a
z
a
z
a
b
z
G
2
2
1
1
0
1
)
(

7
)
(
)
1
(
...
)
1
(
)
(
)
(
)
1
(
...
)
1
(
)
(
1
1
0
1
1
l
n
u
b
l
n
u
b
n
u
b
n
u
b
k
n
y
a
k
n
y
a
n
y
a
n
y
l
l
k
k
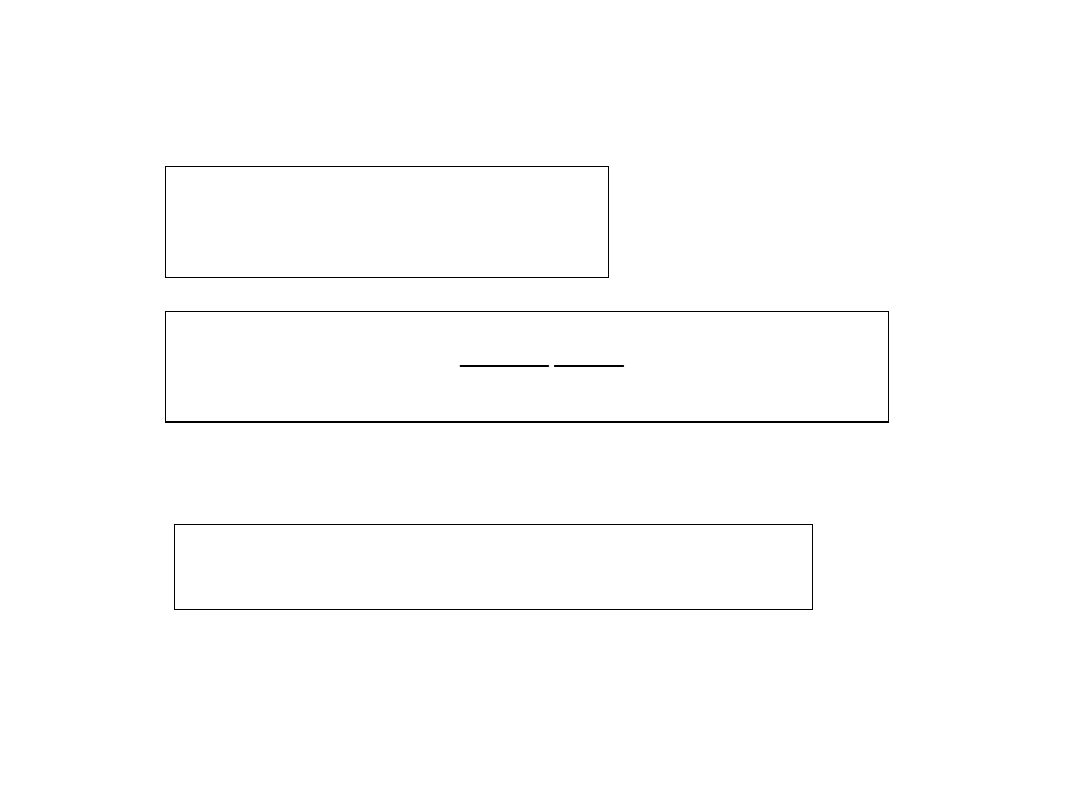
W ogólnym przypadku:
k
k
l
l
z
a
z
a
z
a
z
b
z
b
z
b
b
z
G
2
2
1
1
2
2
1
1
0
1
)
(
8
)
(
)
(
)
(
z
U
z
G
z
Y
0
)
(
]
)
[(
)
(
i
p
p
p
iT
u
T
i
n
g
nT
y
i
z
z
n
p
i
z
z
Y
res
nT
y
]
)
(
[
)
(
1
]
)
)(
(
[
)!
1
(
1
lim
]
)
(
[
1
1
1
1
n
p
i
p
p
z
z
z
z
n
z
z
z
z
Y
dz
d
p
z
z
Y
res
i
i
]
)
)(
(
[
lim
]
)
(
[
1
1
n
i
z
z
z
z
n
z
z
z
z
Y
z
z
Y
res
i
i
Dla p = 1 (p – krotność bieguna funkcji
Y(z) )

9
)
1
(
)
1
(
)
(
)
1
(
)
2
(
)
(
)
1
(
)
1
(
)
(
)
(
)
(
1
2
3
1
2
1
n
x
k
n
y
n
x
n
x
n
y
n
x
n
x
n
y
n
x
n
y
n
x
k
k
Dyskretne równania stanu i równanie wyjścia
)
(
)
(
)
1
(
...
)
1
(
)
(
0
1
1
n
u
b
n
y
a
n
y
a
k
n
y
a
k
n
y
k
k
)
(
)
(
)
(
...
)
(
)
1
(
0
1
2
1
1
n
u
b
n
x
a
n
x
a
n
x
a
n
x
k
k
k
k
)
(
)
(
...
)
(
)
(
)
1
(
0
1
2
1
1
n
u
b
n
x
a
n
x
a
n
x
a
n
x
k
k
k
k
)
(
)
(
)
1
(
...
)
1
(
)
(
0
1
1
n
u
b
k
n
y
a
k
n
y
a
n
y
a
n
y
k
k
10
)
(
)
(
...
)
(
)
(
)
1
(
)
(
)
1
(
)
(
)
1
(
)
(
)
1
(
0
1
2
1
1
1
3
2
2
1
n
u
b
n
x
a
n
x
a
n
x
a
n
x
n
x
n
x
n
x
n
x
n
x
n
x
k
k
k
k
k
k
)
(
)
(
1
n
x
n
y
- dyskretne równanie
wyjścia
Dyskretne równania stanu
)
(
)
(
)
1
(
n
Bu
n
x
A
n
x
)
(
)
(
n
x
C
n
y
Zapis wektorowo-
macierzowy
dysketnych równań
stanu
i równania wyjścia

11
1
2
2
1
1
0
0
0
0
0
0
1
0
0
0
0
0
1
0
a
a
a
a
a
A
k
k
k
)
(
)
(
)
(
)
(
)
(
1
2
1
n
x
n
x
n
x
n
x
n
x
k
k
0
0
0
0
b
B
0
0
0
1
C

12
)
(
)
(
)
(
z
BU
z
X
A
z
X
z
)
(
)
(
)
1
(
n
Bu
n
x
A
n
x
)
(
)
(
n
x
C
n
y
Wyznaczanie transmitancji dyskretnej na
podstawie równań stanu i równania wyjścia
)
(
)
(
z
X
C
z
Y
)
(
)
(
)
(
1
z
BU
A
zI
z
X
)
(
)
(
)
(
1
z
BU
A
zI
C
z
Y
B
A
zI
C
z
U
z
Y
1
)
(
)
(
)
(
B
A
zI
C
z
G
1
)
(
)
(
Document Outline
Wyszukiwarka
Podobne podstrony:
Automatyczna regulacja zasięgu reflektorów przegląd podzespołów
Instalowanie urządzeń automatyki i obsługa prostych układów automatycznej regulacji
Automatyka (wyk 11 12) ppt [try Nieznany
DOBÓR NASTAW REGULATORÓW W MODELOWYM UKŁADZIE AUTOMATYCZNEJ REGULACJI, SGGW Technika Rolnicza i Leśn
Laboratorium automatyki Regulacja impulsowa
Komputer w układzie automatycznej regulacji (2)
Podstawy automatyki (w 3) regula id 366722
16 Podstawy automatyki regulatory optymalne
Podstawy automatyki i regulacji cd
10 Automatyka i regulacja automatyczna test
1. Zadania i metody automatycznej regulacji, pytania egzamin inżynierski AiR ARS
Automatyka i regulacja automatyczna
Czujnik poziomu zawieszenia w samochodach z automatyczną regulacją zasięgu reflektorów przód
Automatyka Układ automatycznej regulacji w silnikach prądu stałego
automatyka regulator pid nr 1
sprawko automatyka no 11
Automatyka Regulacja Temperatury
więcej podobnych podstron