BADANIE ZGODNOŚCI ROZKŁADU
EMPIRYCZNEGO Z TEORETYCZNYM
TEST CHI-KWADRAT
Kolejnym badaniem wyników pomiaru
chronometrażowego czasu wykonywania danej
czynności jest sprawdzenie czy rozrzut czasów
ma charakter rozkładu normalnego. Do analizy
tej stosuje się tzw.
test chi-kwadrat. Analizuje
on różnice pomiędzy liczebnością teoretyczną
wyników w danej klasie wartości (przedziale
wartości) a liczbą wyników uzyskanych z
pomiarów, które przypadają do danej klasy.
W celu przeanalizowania tych różnic
musimy „zbudować” dwa rozkłady:
-
pierwszy
–
empiryczny,
reprezentujący wyniki
uzyskane z
przeprowadzonego pomiaru,
- drugi – teoretyczny, będący obrazem
teoretycznego
rozkładu normalnego.
Zastosowanie testów zgodności jest
poprawne, gdy: - liczebność próby
N
jest stosunkowo duża,
- liczba przedziałów klasowych
r
powinna być
dostatecznie liczna - przyjmuje
się, że
r
≥ 5,
- liczebności teoretyczne w
poszczególnych
przedziałach klasowych nie
mogą być zbyt małe;
zazwyczaj przyjmuje się
np
I
≥ 5,
gdzie i = 1,2,…r.
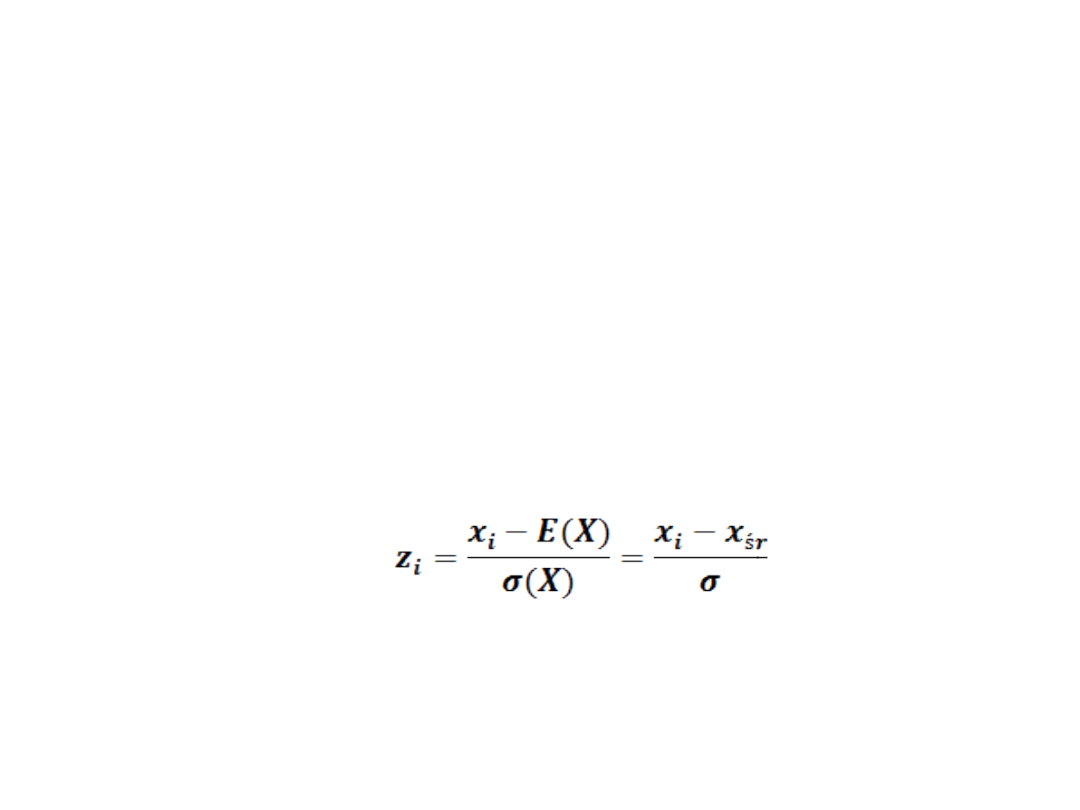
- oba rozkłady muszą być ze sobą
porównywalne
co uzyskuje się poprzez
zestandaryzowanie
rozkładu empirycznego.
Rozkład zestandaryzowany to taki, w
którym wartość
oczekiwana E(x) = 0, a odchylenie
standardowe σ = 1;
co zapisujemy N(0;1).
W celu standaryzacji, po
obliczeniu
wartości
oczekiwanej
i
odchylenia
standardowego
badanego
rozkładu, obliczamy poniższą statystykę
dla zmiennej standaryzowanej Z:
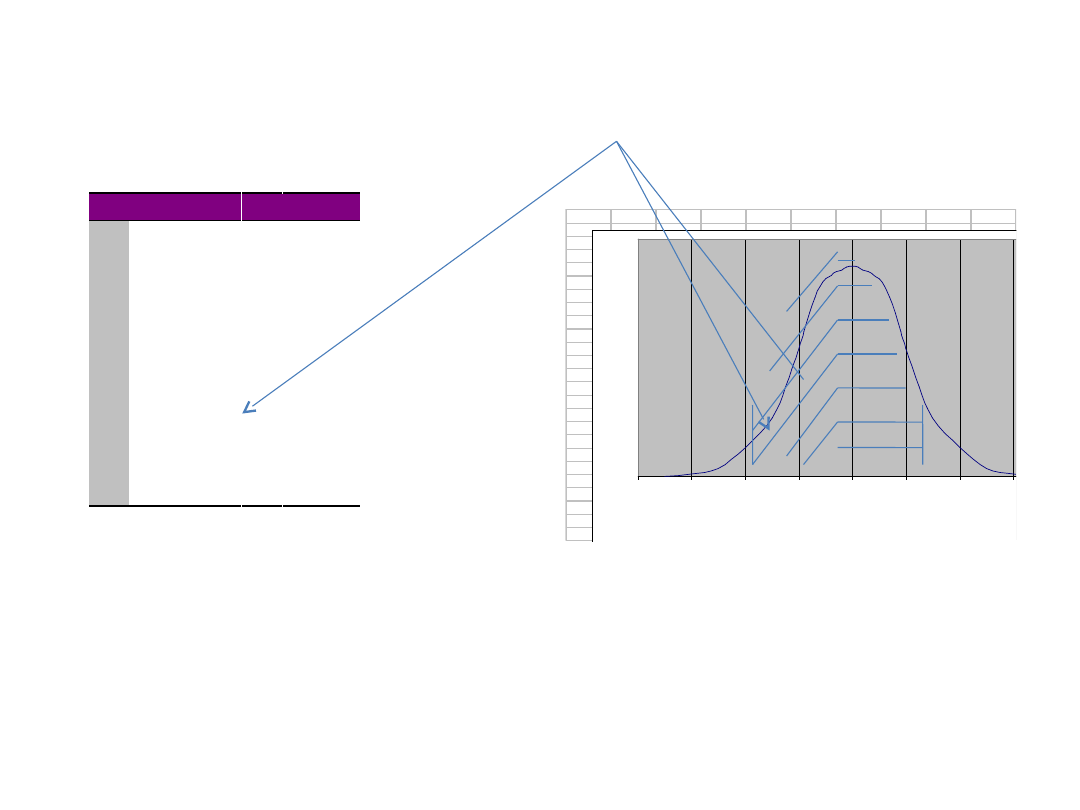
Dla zestandaryzowanej funkcji
opracowano
różne rodzaje tablic, w tym
tablicę dystrybuanty (zawiera
skumulowaną wartość liczności zdarzeń od
-∞ do miejsca z
i
na osi Z).
Z
0,00
0,01 ... 0,09
0,0
0,1
...
0,5
0,6
...
1,0
1,5
2,0
3,0
4,0
0,0000
0,0398
...
0,1915
0,2257
...
0,3413
0,4332
0,4772
0,49865
0,4999683
... ... ...
0
0,1
0,2
0,3
0,4
0,5
0,6
0,7
0,8
0,9
1
0
0,2
0,4
0,6
0,8
1
1,2
Serie1
-4
-3
-2
-1
0
1
2
3
4
Zmienna standaryzowana Z
F
u
n
kc
ja
g
ęs
to
śc
i
f(
X
)
Ponieważ tablice dystrybuanty zawierają
skumulowane liczności od z=0 do miejsca
z
i
, to w przedziale od -1 do -2 będziemy
mieli liczność równą 0,4772 − 0,3413 =
0,1359, co oznacza, że w tym przedziale
znajduje się 13,59% całej liczności
wyników. W przedziale od -1,5 do +1,5
będzie dwa razy 0,4332, tj. 86,64%
wszystkich liczności.
F
*
(
Z)
Tablica dystrybuanty
Dla mało licznej próby, gęstości
wyznacza się z tablicy Studenta
uwzględniającej przyjęty poziom
istotności oraz określoną liczbę stopni
swobody.
KONIEC
BADANIE ROZKŁADU ZMIENNOŚCI
ZMIENNEJ LOSOWEJ
PRZYKŁAD
Zbadano 200 osób pod względem
czasu wykonania pewnego zadania. Na
poziomie istotności α = 0,05 należy
zweryfikować hipotezę, że rozkład
czasu wykonania zadania jest
rozkładem normalnym (Gaussa).
Czas
[min]
71,0 –
71,4
71,4 –
71,8
71,8 –
72,2
72,2 –
72,6
72,6 –
73,0
Liczebn
ość
15
45
70
50
20
Rozwiązanie przykładu sprawdzenia
zgodności rozkładu wyników pomiaru z
rozkładem normalnym
Obliczanie średniej
Lp przedział
Środek
przedzia
łu
x
i
Liczność
w
przedzia
le
n
i
n
i
∙ x
i
1
1,0 –1,4
1,2
15
18,0
0,09
2
1,4 –1,8
1,6
45
72,0
0,36
3
1,8 –2,2
2,0
70
140,0
0,70
4
2,2 –2,6
2,4
50
120,0
0,60
5
2,6 –3,0
2,8
20
56,0
0,280
N = 200
∑ =
406,0
=
2,03
Ze względu na dokładność pomiaru rzędu
0,1 do dalszych obliczeń przyjęto średnią
= 2,0 minuty
Obliczanie odchylenia standardowego z
próbki
Lp
Środek
przedzia
łu
x
i
Liczność
w
przedzial
e
n
i
1
1,2
- 0,8
15
0,64
9,60
2
1,6
- 0,4
45
0,16
7,20
3
2,0
- 0,0
67
0,00
0,0
4
2,4
+ 0,4
50
0,16
8,00
5
2,8
+ 0,8
20
0,64
12,8
=
2,0
−
N =
200
−
37,60
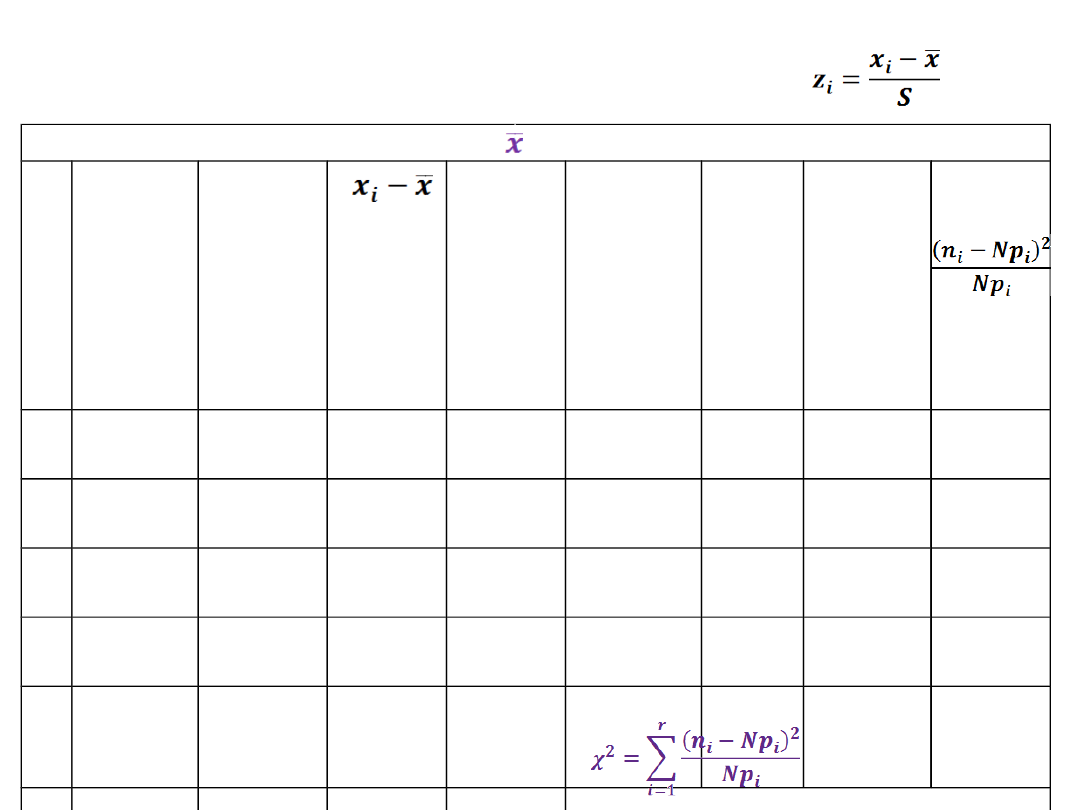
Standaryzacja rozkładu z danych
pomiarowych
Statystyki z próby:
= 2,0
oraz
S = 0,4336
L
p
przedz
iał
Liczno
ść
danyc
h z
pomiar
u
n
i
dla
prawe
go
krańc
a klas
z
i
dla
prawe
go
krańc
a klas
F(z
i
)
z tablic
dla
praweg
o
krańca
klas
p
i
=
F(z
i
)
minu
s
F(z
i-
1
)
Liczno
ść
teoret.
n
teor
=
N
i
∙p
i
1
1,0 –
1,4
15
- 0,6
- 1,38
0,084
0,08
4
16,8
0,19
2
1,4 –
1,8
45
- 0,2
- 0,46
0,323
0,23
9
47,8
0,16
3
1,8 –
2,2
70
+ 0,2
+
0,46
0,677
0,35
4
70,8
0,01
4
2,2 –
2,6
50
+ 0,6
+
1,38
0,916
0,23
9
47,8
0,10
5
2,6 –
3,0
20
+ 1,0
nie
trzeb
a
0,08
4
16,8
0,61
∑ =
200
= 1,07
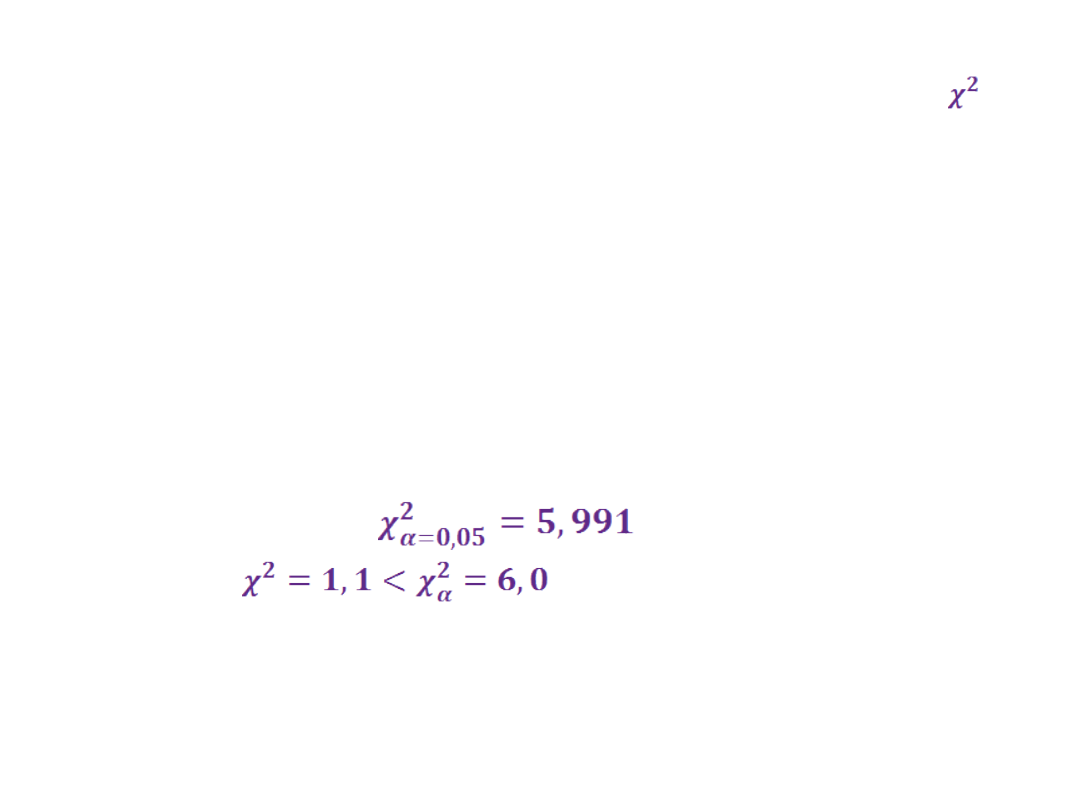
Wartość krytyczną odczytujemy z
tablic rozkładu przy poziomie
istotności
α = 0,05
dla stopni
swobody równej (r-k-1)=(5-2-1)=
2
,
gdzie r – liczba klas, k – liczba
szacowanych parametrów rozkładu
(w omawianej analizie k = 2 bo
rozkład normalny opisany jest przez
dwa parametry - średnią oraz
odchylenie standardowe).
Z tablic mamy: co
oznacza, że
wobec nie ma
podstaw do odrzucenia hipotezy
zerowej, zatem rozkład badanej
cechy jest rozkładem normalnym
(Gaussa).
KONIEC