Statystyka

- Opisowa analiza zjawisk
masowych

Opracowanie na podstawie :
„Statystyka” Mieczysław Sobczyk”

Magdalena Kaźmierczak
Anna Dobras
Aneta Kaptur
Magda Przybył
Ewa Szulc
Andrzej Wowk

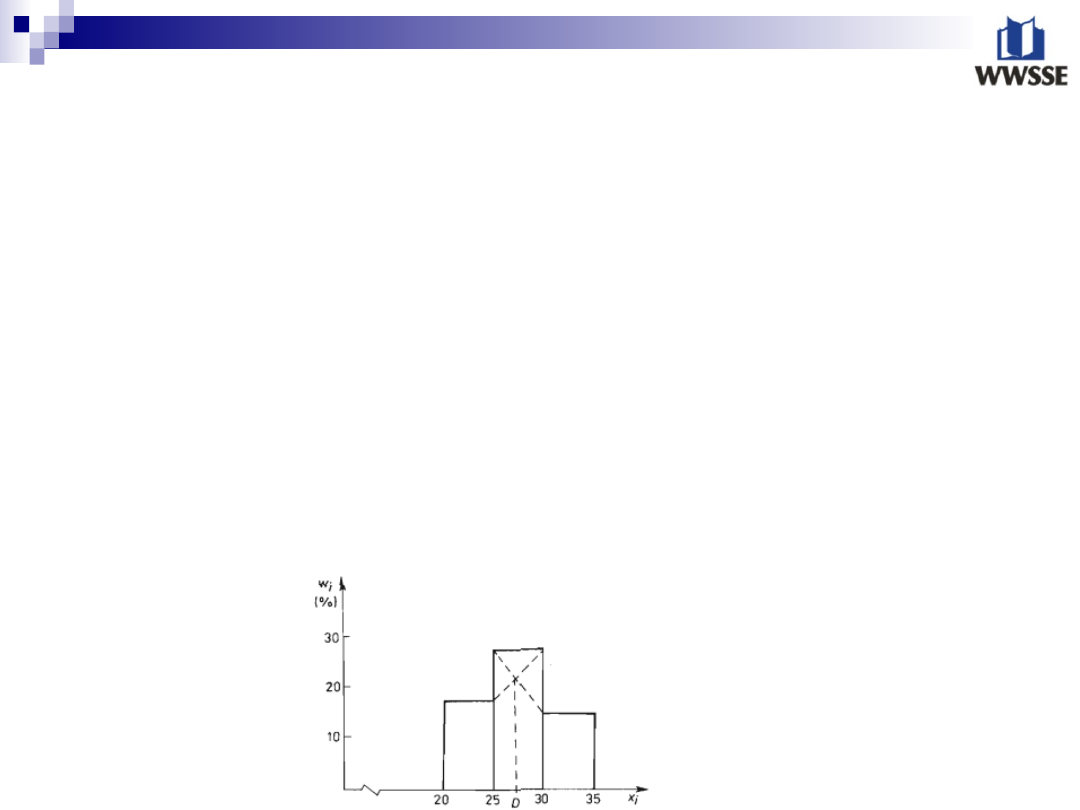
Graficzna metoda wyznaczania
dominanty

Sprowadza się do wyznaczania histogramu liczebności z
trzech przedziałów klasowych: przedziału w którym
znajduje się dominanta, oraz dwóch sąsiednich. Z górnej
podstawy najwyższego prostokąta wykreślamy dwie
przekątne łączące najbliżej położone punkty górnych
podstaw sąsiednich prostokątów, a następnie z punktu
przecięcia się przekątnych wykreślamy prostopadłą do osi
odciętych, która wyznacza wartość dominanty. Jeżeli
liczebność przedziałów przed i za przedziałem dominanty są
jednakowe, to dominanta jest równa środkowi klasy
dominującej.

2

Kwantyle



Definiuje

się je jako wartości cechy

badanej w zbiorowości, które dzielą ją na
określone części pod względem liczby
jednostek. Szeregi z których wyznacza się
kwantyle muszą być uporządkowane wg
rosnących lub malejących wartości cechy
statystycznej. Do najczęściej używanych
kwantyli zaliczamy:
- kwartyle
- decyle i centyle (percentyle)

3

Kwartyle dzielą zbiorowość
na dwie cz. w następujący
sposób:



Kwartyl pierwszy dzieli zbiorowość
uporządkowaną na dwie cz. w taki sposób, że
25 % jednostek ma wartości cechy niższe, a
75% wyższe od kwartyla pierwszego



Mediana dzieli zbiorowość uporządkowaną na
dwie równe cz. w taki sposób że 50 %
jednostek ma wartości cechy niższe, a 50%
wyższe od mediany



Kwartyl trzeci dzieli zbiorowość
uporządkowaną na dwie cz. w taki sposób, że
75 % jednostek ma wartości cechy niższe, a
25% wyższe od kwartyla trzeciego

4

W śród kwartyli wyróżniamy



Kwartyl pierwszy ( zwany dolnym)



Kwartyl drugi (określany mianem
mediany lud wartości środkowej)



Kwartyl trzeci ( zwany górnym)

5

6



W przypadku
szeregów
wyliczających
medianę, oblicza
się najczęściej
na podstawie
wzoru

gdzie Me jest symbolem mediany

Kumulacja



Kumulacja polega na kolejnym,
narastającym sumowaniu
liczebności, dotyczących
poszczególnych wariantów cechy.

7

Metody wyznaczania
kwartyli



W przypadku szeregów

rozdzielczych przedziałowych
kwartyle wyznaczamy metodą:

-graficzna
-rachunkową

8

9

Rachunkowa metoda
wyznaczania kwartyli /
wzory:

Technika obliczania kwartyli z
szeregów rozdzielczych
przedziałowych /metoda
rachunkowa/



Pierwszą czynnością związaną z
wyznaczaniem kwartyli jest
kumulacja liczebności. Następnie
wyznaczamy pozycje poszczególnych
kwartyli w szeregu, tzn.
Wykorzystując skumulowane
częstości względne, otrzymujemy:

10

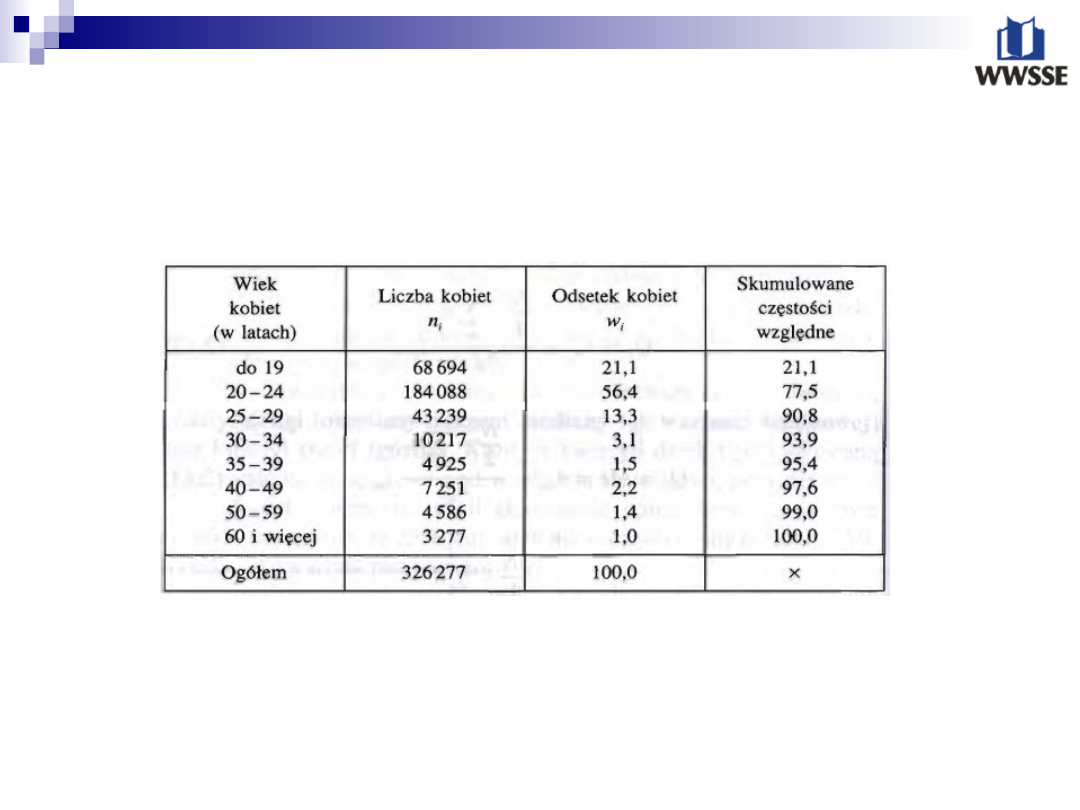
11



Wiek kobiet zawierających związek
małżeński w 1977r.

Wartość kwartyla pierwszego jest
równa:

c.d.



.

Oznacza to, że 25% kobiet zawierających związek
małżeński w 1977r. Miało mniej niż 20.35 lat, a 75% miało
więcej lat



.

Oznacza to, że 50% kobiet zawierających związek
małżeński w 1977r. Miało mniej niż 22.6 lat, a 50% miało
więcej lat



.
Oznacza to, że 75% kobiet zawierających związek
małżeński w 1977r. Miało mniej niż 24.8 lat, a 75% miało
więcej lat

12

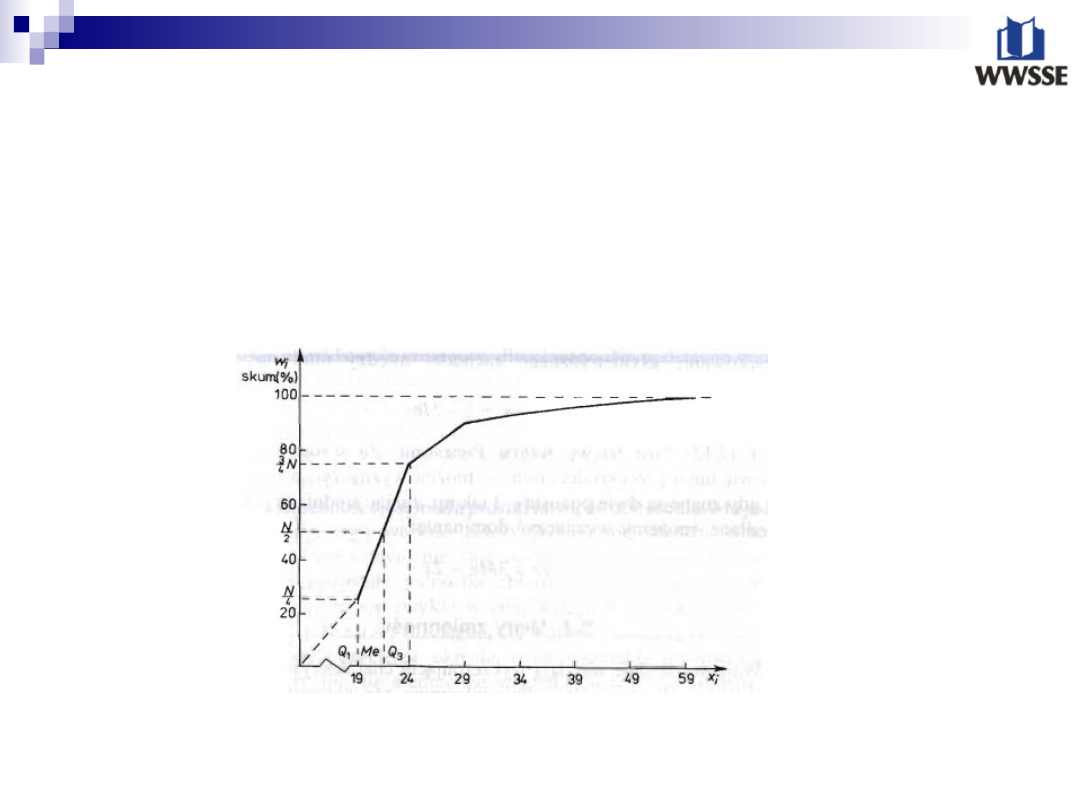
Graficzna metoda
wyznaczania kwartyli



W tym celu w układzie współrzędnych wykreślamy krzywą
częstości skumulowanej ( jest to łamana łącząca punkty o
współrzędnych: górne granice klas i odpowiadające im
skumulowane odsetki)

Kwartyle są dogodnymi parametrami w analizie struktury, mogą być wykorzystywane w tych wszystkich przypadkach w
których niemożliwe jest obliczenia z danego szeregu średniej arytmetycznej, a także dominanty.

13

Decyle i centyle
(percentyle)

wyznacza się podobnie jak kwartyle



Decyle dzielą zbiorowość
uporządkowana na 10
części pod względem
liczebności. Decyl trzeci
np. to taka wartość cechy,
że 0.3 wszystkich
jednostek badanej
zbiorowości ma wartości
od niej niższe, a 0.7
wartości wyższe. Decyli
jest 9, a 5 decyl jest
medianą.



Centyle(percentyle) dzielą
zbiorowość uporządkowaną
na 100 części pod
względem liczebności.
Centyli jest 99, a 50-siąty
centyl jest równy
medianie. Np. 39 centyl
jest taka wartością, że 0.39
wszystkich jednostek
badanej zbiorowości ma
wartości od niej niższe, a
0.61 jednostek wartości -
wyższe

14

Wartości te…



Średnia arytmetyczna, dominanta i
mediana jako miary tendencji
centralnej są powiązane ze sobą
odpowiednimi zależnościami, które
można wyrazić równościami i
nierównościami (decyduje o tym typ
rozkładu empirycznego).

15

16

Miary

zmienności

Miary zmienności



Wartości średnie nie dają wyczerpującej
charakterystyki struktury zbiorowości, nie
informują one o stopniu zmienności badanej
cechy (dyspersji). Siłę dyspersji oceniamy za
pomocą pozycyjnych i klasycznych miar
zmienności. Do miar pozycyjnych należą:
empiryczny obszar zmienności (zwany
rozstępem lub amplituda wahań) oraz
odchylenie ćwiartkowe. Grupę miar
klasycznych tworzą: odchylenie
standardowe, wariancja oraz odchylenie
przeciętne.

17

Miary zmienności



Można również podzielić na :
bezwzględne i względne.

- do bezwzględnych miar

zróżnicowania zalicza się obszar
zmienności, wariancje, odchylenie
standardowe, przeciętne i
ćwiartkowe.
- względne, miarą dyspersji
jest współczynnik zmienności
wyrażany w procentach.

18

Empiryczny obszar
zmienności



Jest różnica między największą i najmniejszą
wartością zmiennej w badanej zbiorowości:

R = x

max

- x

min

Jak wynika ze wzoru obszar zmienności możemy
określić tylko na podstawie szeregu
wyliczającego. Obszar zmienności jest miarą
prostą i łatwą do obliczenia, ma jednak poważną
wadę: jego wartość zależy jedynie od dwóch
jednostek zbiorowości, nie daje informacji jak
dalece różnią się między sobą pozostałe jednostki
zbiorowości. Dlatego też obszar zmiennej oblicza
się zwykle w celu orientacji

.

19

Odchylenie przeciętne



Określa, o ile wszystkie jednostki danej
zbiorowości różnią się średnio ze względu na
wartość zmiennej od średniej arytmetycznej tej
zmiennej. Odchylenie przeciętne jest średnią
arytmetyczną bezwzględnych wartości (modułów)
odchyleń wartości cechy od tej średniej
arytmetycznej. Oblicza się w sposób:
dla szeregu wyliczającego:

dla szeregu rozdzielczego punktowego:

dla szeregu rozdzielczego przedziałowego:

20

Obliczanie odchylenia
przeciętnego na podst.
tabeli



Wykorzystujemy wzór dla szeregu
rozdzielczego przedziałowego,
odliczamy najpierw średni czas
pracy:

21

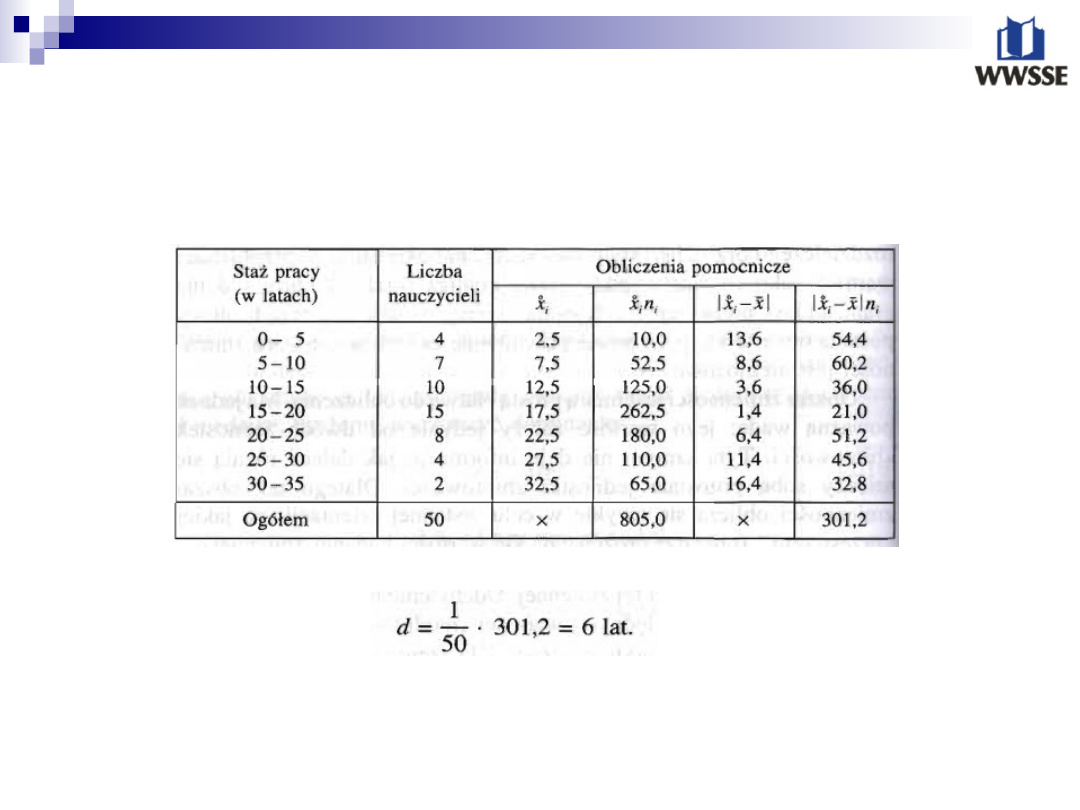
c.d.



Nauczyciele szkół średnich z miejscowości Z według stażu
pracy

Po wykonaniu odpowiednich obliczeń otrzymujemy

Otrzymany wynik oznacza, że przeciętne zróżnicowanie
badanej zbiorowości nauczycieli ze względu na staż pracy
wynosi +/- 6 lat.

22

Odchylenie ćwiartkowe



Odchylenie ćwiartkowe (Q) opiera się na
wartościach kwartyla pierwszego (Q

1

) i trzeciego

(Q

3

). Oblicza się je następująco:

Odchylenie ćwiartkowe mierzy poziom
zróżnicowania tylko części jednostek badanej
zbiorowości (pozostałej po odrzuceniu 25%
jednostek o wartościach najniższych oraz 25%
jednostek o wartościach najwyższych).
Odchylenie ćwiartkowe mierzy więc średnią
rozpiętość w połowie obszaru zmienności.

23

c.d.



Jeżeli do opisu tendencji centralnej w
danym szeregu użyto mediany, a do opisu
zmienności – odchylenia ćwiartkowego, to
można określić typowy obszar zmienności
x

typ

w następujący sposób:

Nietypowe w danej zbiorowości są te
jednostki, których wartości są niższe od Me
– Q i wyższe od Me + Q

24

Wariancja



To średnia arytmetyczna z kwadratów odchyleń
poszczególnych wartości cechy od średniej
arytmetycznej całej zbiorowości. Oblicza się w
sposób:

dla szeregu wyliczającego:

dla szeregu rozdzielczego punktowego:

dla szeregu rozdzielczego przedziałowego:

25