WOJSKOWA AKADEMIA TECHNICZNA
LABORATORIUM FIZYCZNE
Grupa szkoleniowa: E5D9 Podgrupa: 1 Prowadzący: dr inż. Wiśniewski
Łukasz Madej Ocena z przygotowania Ocena końcowa:
Dawid Kruk do ćwiczeń:..................... ...........................
Sprawozdanie z Pracy Laboratoryjnej nr 18
Temat pracy: Wyznaczanie przerwy energetycznej germanu
I. Wstęp teoretyczny
Ciała stałe ze względu na ich właściwości elektryczne dzielimy na trzy grupy :
przewodniki w których stany zapełnione sąsiadują bezpośrednio ze stanami pustymi (np. metale);
izolatory, w których najmniejsza energetyczna odległość między stanami zapełnionymi elektronami i pustymi zwana przerwę energetyczną (Eg ) jest duża tzn. większa niż 2eV (np. dla diamentu wynosi ona 5,4eV);
półprzewodniki w których przerwa energetyczna jest mniejsza niż 2 eV ( np. dla krzemu wynosi 1,1eV);
Aby elektron uczestniczył w przewodnictwie prądu elektrycznego musi pobierać energię od przyłożonego z zewnątrz pola elektrycznego , a to jest możliwe tylko wówczas gdy znajdują się one w paśmie przewodnictwa . Elektrony takie nazywamy swobodnymi , gdyż mogą poruszać się po całym krysztale . Wydajność opisanego termicznego procesu wzbudzania elektronów do pasma przewodnictwa bardzo silnie zależy od wartości przerwy energetycznej :
przy jej praktycznym braku (przewodniki) już w temperaturze kilkudziesięciu Kelwinów wszystkie elektrony biorą udział w przewodnictwie;
gdy jest ona bardzo duża (w izolatorach ) nawet w temperaturach rzędu kilkuset stopni Celsjusza elektronów swobodnych w ciele stałym jest tak mało , że praktycznie nie przewodzi on prądu;
natomiast w półprzewodnikach gdzie przerwa energetyczna jest mniejsza , już w temperaturze pokojowej część elektronów jest przeniesiona do pasma przewodnictwa co umożliwia przepływ prądu .
Ogrzewanie półprzewodnika wymusza generacją elektronów swobodnych co powoduje silny wzrost przewodnictwa.
Wielkością elektryczną określającą ilość nośników ładunku jest ich koncentracja .Koncentracją swobodnych elektronów (n) nazywamy liczbę elektronów w paśmie przewodnictwa przypadającą na jednostkę objętości ciała , koncentracją dziur (p) nazywamy liczbę dziur w paśmie walencyjnym w jednostce objętości ciała . Koncentracje nośników rosną wykładniczo z temperaturą (T).
p = n = 2(2π kT / h2)3/2 (mn mp)3/4 exp -(Eg/2kT)
k - stala Boltzmanna
h - stala Planka
mn , mp - masy efektywne dla elektronu i dziury w danym półprzewodniku
W praktyce stosuje się wzór:
p = n = n0 exp -(Eg/2kT) gdzie n0 traktuje się jako stałą niezależną od temperatury
Gęstość prądu w półprzewodnikach dana jest wzorem:
j = e (n vn + p vp)
j - gęstość prądu ;
e - ładunek elektronu;
vp , vn - średnie prędkości elektronów i dziur
Wprowadzając pojęcie ruchliwości nośników zdefiniowanej wzorami:
μn = vn/E μp = vp/E
j = e(n μn + p μp)E gdzie E - natężenie przyłożonego pola elektrycznego
Porównując ostatni wzór z prawem Ohma:
j = σE
otrzymujemy wzór na przewodnictwo elektryczne półprzewodników :
σ = e(n μn + p μp)
dla półprzewodników samoistnych słuszna więc jest zależność
σ = σ0 exp-(Eg/2kT)
Cel ćwiczenia:
W ćwiczeniu wyznaczać będziemy przerwę energetyczną germanu z pomiarów zależności rezystancji półprzewodnika samoistnego od temperatury.
R = R0 exp(Eg/2kT)
gdzie R0 - jest dobrym przybliżeniem stałą rezystancją zależną od rodzaju półprzewodnika i jego wymiarów geometrycznych.
Logarytmując te wyrażenie otrzymujemy:
log R = log R0 +0,4343 (Eg/2k) (1/T)
a więc zależność log R = f ( 1/T ) jest prostą, a jej nachylenie wynosi 0,4343 (Eg/2k)
II. Opracowanie wyników pomiarów
Tabela pomiarowa:
Lp. |
Zakres pomiarowy |
Natężenie prądu |
||
|
T [ºC] |
T [K] |
R [kΩ] |
|
1. |
20 |
293 |
0,861 |
0,5A |
2. |
25 |
298 |
0,848 |
|
3. |
30 |
303 |
0,812 |
|
4. |
35 |
308 |
0,716 |
|
5. |
40 |
313 |
0,692 |
|
6. |
45 |
318 |
0,618 |
|
7. |
50 |
323 |
0,536 |
0,7A |
8. |
55 |
328 |
0,460 |
|
9. |
60 |
333 |
0,389 |
|
10. |
65 |
338 |
0,330 |
|
11. |
70 |
343 |
0,280 |
0,9A |
12. |
75 |
348 |
0,235 |
|
13. |
80 |
353 |
0,197 |
|
14. |
85 |
358 |
0,166 |
|
15. |
90 |
363 |
0,139 |
|
16. |
95 |
368 |
0,118 |
|
17. |
100 |
373 |
0,102 |
1,1A |
18. |
105 |
378 |
0,087 |
|
19. |
110 |
383 |
0,075 |
|
20. |
115 |
388 |
0,064 |
|
21. |
120 |
393 |
0,054 |
|
1. Obliczenia
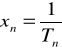
1.1 Wartości pomiarów naniesione na wykres ( Załącznik nr 1)
![]()
![]()
![]()
1.2 Wartości średnie
1.3 Odchylenia od wartości średniej
![]()
![]()
![]()
1.4 Parametry prostej dopasowanej do danej metodą Gaussa (Załącznik nr 2)
![]()
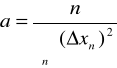
![]()
![]()
1.5 Odchylenie standardowe współczynnika kierunkowego prostej
![]()
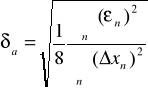
![]()
1.6 Wartość przerwy energetycznej germanu
![]()
![]()
![]()
1.7 Odchylenie standardowe przerwy energetycznej
![]()
![]()
1.8 Przedział ufności przerwy energetycznej
![]()
![]()
2. Załączniki
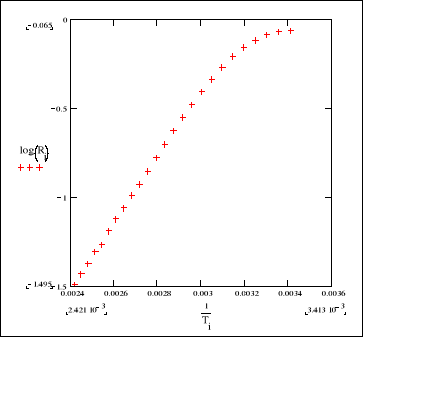
załącznik nr 1
załącznik nr 2
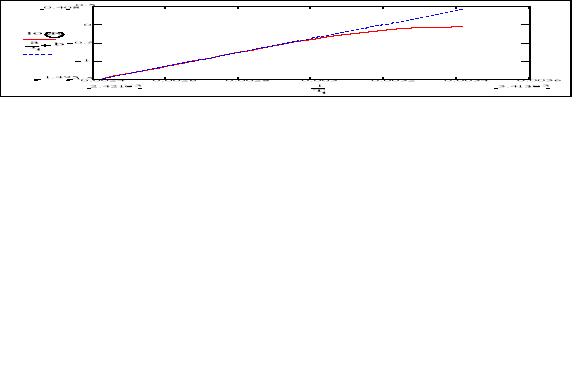
III. Wnioski
Wartość przerwy energetycznej germanu wyznaczonej przez nas wynosi:
Eg = 0,76 eV
Porównując otrzymany wynik z wartością tablicową (Eg = 0,67 eV) możemy dojść do wniosku, że jest ona nieco inna. Błąd nie mieści się nawet przedziale ufności. Najprawdopodobniej różnica wartości wynika z użycia do doświadczenia nieczystego germanu. Oprócz tego na błąd mogły wpłynąć także błędy pomiarów, niedokładność odczytu jak również niedokładność przyrządów pomiarowych.
Doświadczenie było proste i łatwe do zrealizowania, jednak bardzo rozciągłe w czasie ze względu na długi czas nagrzewania się germanu.
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
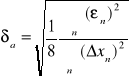
![]()
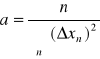
![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Wyszukiwarka
Podobne podstrony:
ÆWICZENIE NR 18 , ĆWICZENIE NR 18
Ćwiczenie nr 18, studia, Budownctwo, Semestr II, fizyka, Fizyka laborki, Fizyka - Labolatoria, Ćwicz
instrukcja do ćwiczeń nr 11 doc
Cwiczenie nr 18 Edycja 3D id 99894
Ćwiczenia nr 15 doc
Ćwiczenie nr 2 Grzesiu doc
Ćwiczenie nr 3 obliczenia doc
Sprawozdanie do ćwiczenia nr 210 doc
Ćwiczenie nr 18
Sprawozdanie do ćwiczenia nr 401 doc
Ćwiczenie nr 46 doc
Ćwiczenia nr 13 doc
ćwiczenie nr 7 ICH doc
Ćwiczenie nr 5 grzesiu doc
Ćwiczenie nr 9 (zak) doc
Ćwiczenie nr 18
Ćwiczenie nr 8 (zak) doc
więcej podobnych podstron