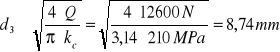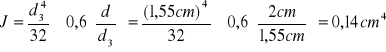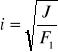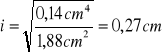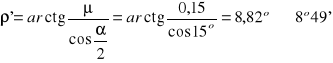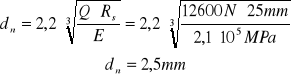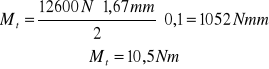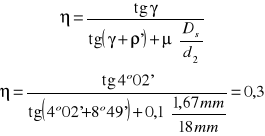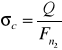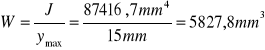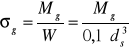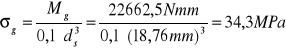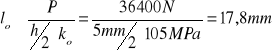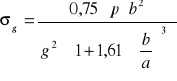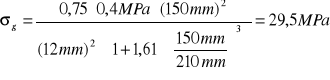POLITECHNIKA RADOMSKA

im. Kazimierza Pułaskiego

w Radomiu

Wydział Mechaniczny

Kierunek: Mechanika i Budowa Maszyn

Rok akademicki 2004/2005

Semestr piąty

Dwusłupowa biurowa prasa śrubowa

Wykonał: Prowadzący:

Paweł Musiałek dr inż. Adam Wilczek

Grupa B3

Radom 2005

[1]	[2]	[3]
DANE	OBLICZENIA I SZKICE	WYNIKI
	Założenia i wstępny szkic prasy Założenia do wstępnych obliczeń Zaprojektować biurową prasę śrubową o maksymalnym wzniosie H = 0,13 [m], czynnej powierzchni F = 0,21 x 0,15 =0,0315 [m^2], oraz nacisku powierzchniowym p = 0,4 [MPa] . Jako materiał śruby przyjmuję stal 45 ulepszaną cieplnie oraz materiał nakrętki brąz BA 1032 . Wstępny schemat prasy Obliczenia śruby Obliczenia średnicy rdzenia śruby gdzie: Q - siła nacisku obliczana ze wzoru : ,
[1]	[2]	[3]
	F1 - pole powierzchni przekroju poprzecznego śruby obliczane ze wzoru: d3 - średnica rdzenia śruby kc - dopuszczalne naprężenia ściskające wyznaczane z zależności : Re - granica plastyczności xe - współczynnik bezpieczeństwa
Re= 420 MPa; xe= 2; F= 0,0315 m^2		kc=210 MPa; Q= 12600N
kc=210 MPa; Q= 12600N	Mając wszystkie elementy możemy obliczyć średnicę rdzenia śruby z przekształconego wzoru na naprężenia ściskające:	d3=8,74 mm
d3 = 15,5 mm	Przyjmuję średnicę d3 = 15,5 mm , oraz gwint trapezowy symetryczny Tr 20 x 4 . Obliczenie pola powierzchni przekroju poprzecznego śruby Pole przekroju poprzecznego śruby F1 obliczamy z podanej wyżej zależności:	Gwint Tr 20x4; d = 20 mm; d2= 18 mm; d3 = 15,5 mm; α = 30^o F1= 1,88cm^2
[1]	[2]	[3]
d3 = 1,55 cm; d = 2 cm	Obliczenie momentu bezwładności Moment bezwładności obliczamy ze wzoru :	J= 0,14 cm^4
J= 0,14 cm^4 F1= 1,88cm^2	Obliczenie ramienia bezwładności Ramię bezwładności obliczamy ze wzoru : gdzie: J - moment bezwładności , Po podstawieniu danych otrzymujemy :	i = 0,27 cm
λgr=100 α =1; lw=20cm: imin=0,27cm.	Obliczenie smukłości pręta gdzie: α - współczynnik swobodnej długości pręta w zależności od rodzaju zamocowania lw - długość wyboczeniowa pręta i - promień bezwładności przekroju	λ = 74,07 λgr=100
Q = 12600N F1 = 188 mm^2	Obliczenie naprężeń ściskających w rdzeniu śruby	σc= 67 MPa
[1]	[2]	[3]
a=420; b=0,62 λ = 74,07	Obliczenie naprężeń krytycznych w śrubie: Ponieważ λ < λgr sprawdzamy warunek wytrzymałościowy na wyboczenie niesprężyste stosując wzór Tetmajera : gdzie : a,bo - współczynniki dobierane z tablic, uzależnione od własności materiału (Re, RH, E)	σkr=374MPa
σkr=374MPa; σc= 67 MPa	Obliczenie rzeczywistego współczynnika bezpieczeństwa na wyboczenie Współczynnik xwyb obliczamy z niżej podanego wzoru:	xwyb=5,58
d2= 18 mm; P = 4mm Dla materiału śruby i nakrętki przyjmuję współczynnik tarcia μ = 0,15 α =30^o	Sprawdzenie samohamowności gwintu gdzie : P - skok gwintu Warunek samohamowności jest spełniony ponieważ : ρ' > γ	γ=4^o02'; ρ' = 8^o49'
[1]	[2]	[3]
Q=12600N; d2=18mm; γ=4^o02'; ρ' = 8^o49'.	Obliczenie momentu skręcającego śrubę Moment skręcający śrubę obliczam korzystając z następującego wzoru : gdzie : Q - siła działająca na śrubę; d2 - średnica podziałowa gwintu śruby; γ, ρ' - kąt wzniosu linii śrubowej gwintu i pozorny kąt tarcia	Ms=25,9Nm
Q = 12600N; Rs= 25mm; E= 2,1* 10^5MPa	Moment tarcia na kulistym końcu śruby Moment ten obliczamy stosując wzór Hertza : gdzie : Ds - średnica działania siły tarcia przy założeniu równomiernego nacisku na powierzchni μ - współczynnik tarcia powierzchni kulistej śruby o podkładkę gdzie : dn - średnica pola powierzchni docisku Rs - promień na kulistym końcu śruby	dn=2,5mm ;
[1]	[2]	[3]
dn = 2,5mm Q= 12600N; Ds = 1,67mm; Przyjmujmy współczynnik tarcia μ = 0,1 (stal - stal) Ms=25,9Nm Mt=10,5Nm	Mając wszystkie dane i podstawiając je do wzoru Hertza możemy obliczyć: Całkowity moment tarcia	Ds = 1,67mm. Mt=10,5Nm; Mc = 36,4 Nm
γ=4^o02'; ρ' = 8^o49'; μ =0,1; Ds = 1,67 mm; d2 = 18 mm.	Obliczenie sprawności mechanizmu śrubowego Sprawność η obliczamy ze wzoru :	η = 0,3
d = 20 mm; d3 = 15,5 mm;	Obliczenia nakrętki Obliczenia czynnej powierzchni jednego zwoju oraz ilość zwojów nakrętki Znając powierzchnię jednego zwoju możemy obliczyć ilość zwojów nakrętki n, korzystając ze wzoru:	Fn=125,5mm^2
[1]	[2]	[3]
Q = 12600N; pdop = 12 MPa; Fn =125,5 mm^2	gdzie : pdop - naciski dopuszczalne dla nakrętki	n = 8,4
d3 =15,5 mm H = 46,5 mm; P = 4 mm.	Obliczenia wysokości nakrętki Chcąc uzyskać dobre prowadzenie śruby w nakrętce obliczam wysokość nakrętki z zależności : Znając wysokość nakrętki H oraz skok gwintu P ilość zwojów nakrętki możemy obliczyć również z zależności :	H = 46,5 mm Przyjmuję ilość zwojów nakrętki n = 12
	Przyjęcie zewnętrznej średnicy nakrętki Przyjmuje zewnętrzną średnicę nakrętki równą 32 mm.
	Obliczenia naprężeń ściskających w nakrętce Naprężenia ściskające w nakrętce obliczam stosując wzór : gdzie : Fn2 - powierzchnia nakrętki gdzie : Dn - średnica zewnętrzna nakrętki D - średnica wewnętrzna nakrętki
[1]	[2]	[3]
Dn= 32 mm; D = 20 mm ; Q = 12600N; Fn2 = 490 mm^2	stąd : Mając wszystkie dane możemy obliczyć naprężenia ściskające :	Fn2 = 490 mm^2 σc = 25,7 MPa
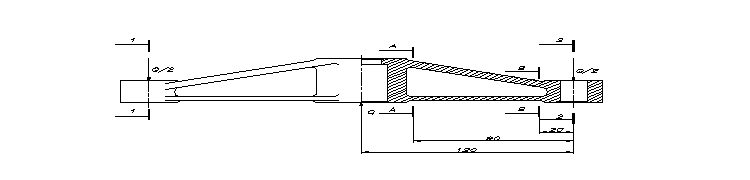
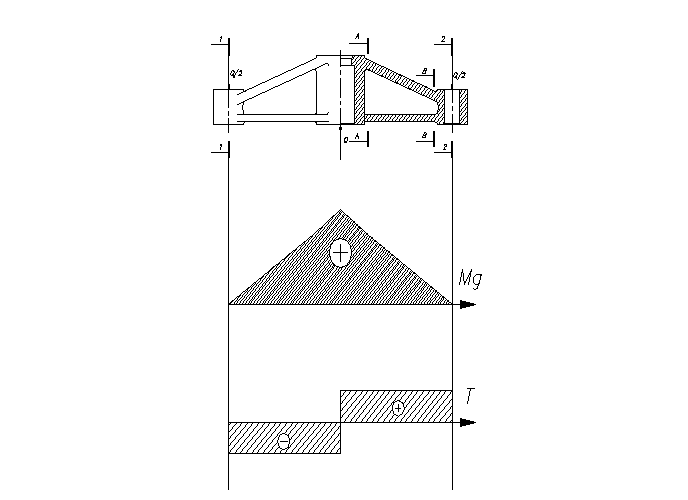
	Obliczenia belki górnej Szkic belki górnej Wobec dużej sztywności belki w porównaniu do słupków obliczamy ją jako swobodnie podpartą . Belkę obliczamy z warunku na zginanie gdzie: l - długość belki Naprężenia zginające belkę obliczamy korzystając z następującego wzoru : gdzie : W - wskaźnik wytrzymałości przekroju na zginanie
[1]	[2]	[3]
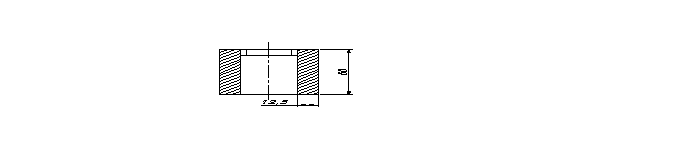
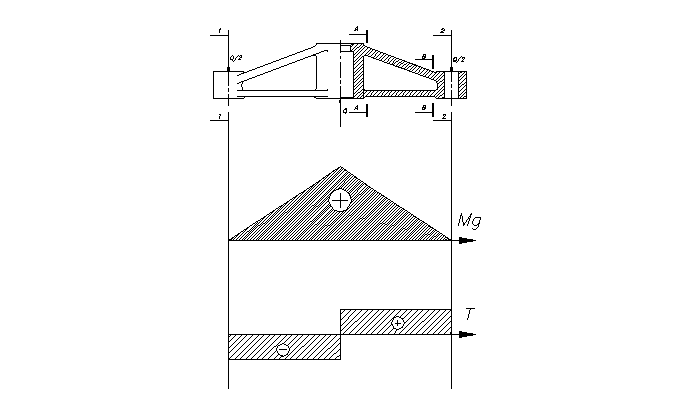
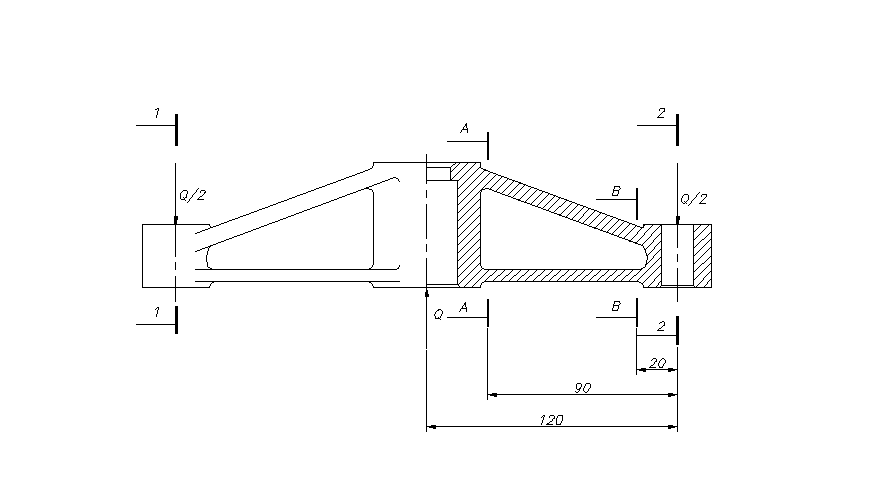
l = 240 mm; Q = 12600 N. b = 25 mm; h = 60 mm . Mg = 756000Nmm; W = 15000mm^3. Q = 12600 N; lA = 90 mm.	Obliczenia belki w przekroju środkowym gdzie: b - szerokość belki w przekroju h - wysokość belki w przekroju Obliczenia belki w przekroju A - A gdzie: lA - długość belki do przekroju A - A	Mg = 756000Nmm W = 15000mm^3 σg = 50,4 MPa Mg= 567000Nmm
[1]	[2]	[3]
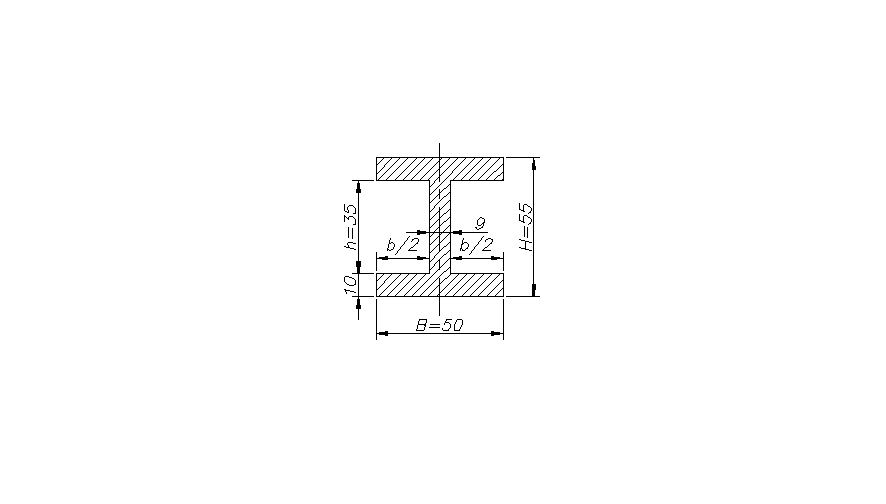
B = 55mm; H = 50mm; b = 41 mm; h = 35 mm. J = 426427,1mm^4; ymax = 25 mm . Mg= 567000Nmm; W= 17057,1mm^3. Q = 12600 N; lB = 20 mm.	gdzie: J - moment bezwładności ymax - najdalej oddalone włókna od osi przekroju poprzecznego belki Obliczenia belki w przekroju B - B gdzie: lB - długość próbki do przekroju B - B	J=426427,1mm^4 W= 17057,1mm^3 σg = 33,25 MPa Mg= 126000Nmm
[1]	[2]	[3]
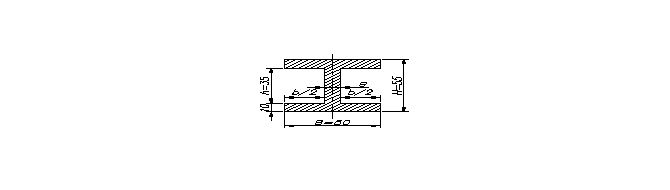
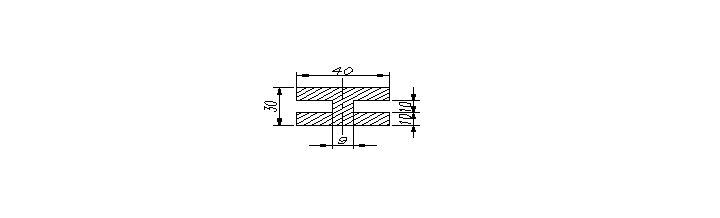
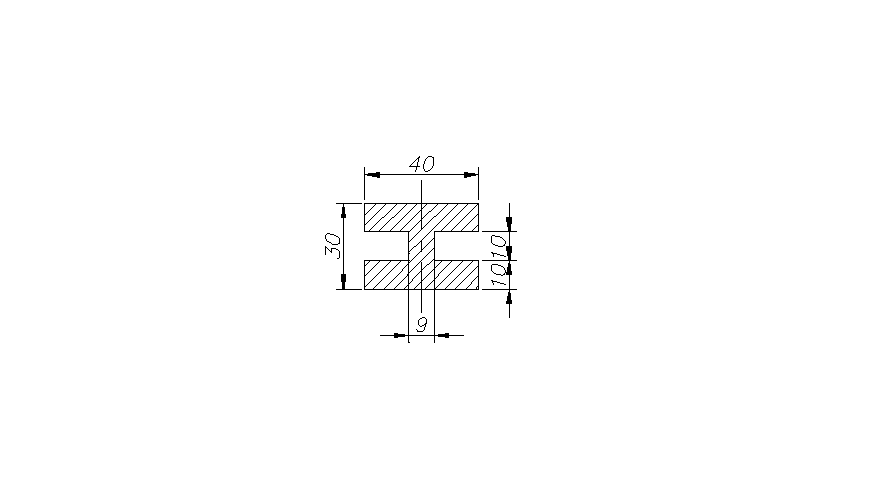
B = 40mm; H = 30mm; b = 31mm; h = 10 mm. J = 87416,7mm^4; ymax = 15 mm . Mg= 126000Nmm; W= 5827,8mm^3.		J = 87416,7mm^4 W = 5827,8mm^3 σg = 21,6 MPa
Q = 12600N Q = 12600N Q = 12600N	Obliczenie sił tnących: w przekroju środkowym w przekroju 1 - 1 w przekroju 2 - 2 Przedstawienie momentów gnących i sił tnących na wykresie Mgs = 756 Nm Ts = 12600N Mg1 = 0 T1 = - 6300N Mg2 = 0 T2 = 6300N MgA = 567 Nm MgB = 126Nm	Ts = 12600N Ts = - 6300N Ts = 6300N
[1]	[2]	[3]
A1 = 144mm^2; Q = 12600N.	Obliczenia słupków Obliczanie naprężeń rozciągających w gwincie śruby M16 gdzie: A1 - pole powierzchni przekroju poprzecznego śruby	σr = 43,75 MPa
[1]	[2]	[3]
Ms=25900Nmm; L = 240 mm.	Obliczenie siły poziomej H w gwincie nakrętki Na słupek działa także siła pozioma H od momentu skręcającego w gwincie nakrętki i można ją obliczyć z następującego wzoru: gdzie: L - odległość między słupkami	H = 107,9 N
H = 107,9 N; h = 210mm.	Obliczenie momentu zginającego słupek gdzie: h - długość słupka	Mg=22662,5Nmm
Mg=22662,5Nmm; ds = 18,76 mm.	Obliczenie naprężeń gnących Do obliczeń naprężeń przyjmujemy jako średnicę obliczeniową średnią średnicę geometryczną słupka i naprężenia obliczamy z zależności: gdzie: ds - średnia średnica geometryczna słupka	ds = 18,76 mm σg = 34,3 MPa
[1]	[2]	[3]
Q = 12600N; d = 16mm.	Obliczenie naprężeń rozciągających słupek gdzie: A2 - pole przekroju poprzecznego słupka na średnicy 16 mm	σr = 31,33 MPa
σg = 34,3 MPa; σr = 31,33 MPa.	Suma naprężeń działających na słupek	σc=65,6 MPa
Mc=36400Nmm; L = 380 mm.	Obliczenie pokrętła Obliczenie siły na jednym ręku przy dwustronnym uchwyceniu pokrętła gdzie: L - długość pokrętła	P = 95,78 N
P = 95,78 N; l = 170 mm. Mg=32565,2Nmm ; d = 22 mm	Obliczenie momentu zginającego i naprężeń gnących pokrętło gdzie: l - ramię działania siły	Mg=32565,2Nmm σg = 34,3 MPa
[1]	[2]	[3]
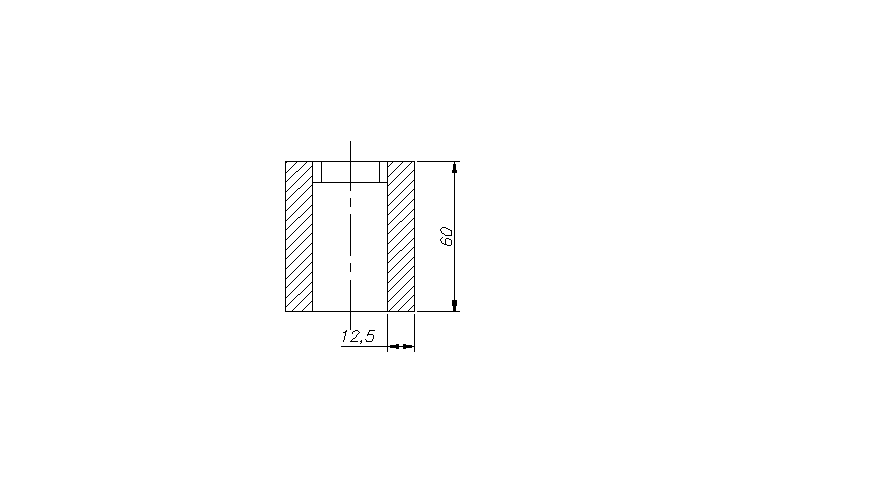
z = 0,6; kc = 175MPa. Mc = 36400Nmm d = 15,5 mm P=4690N; h =5 ; ko = 105MPa . lo = 17,8 mm ; b = 5 mm.	Obliczenie połączenia wpustowego śruby z pokrętłem Wg normy PN - 70/M - 85005 dobieram wymiary poprzeczne wpustu bxh = 5x5 mm . Przyjmujemy, że wpust będzie wykonany ze stali St7, dla której kc = 175 MPa . Obliczam wartość dopuszczalnych nacisków powierzchniowych wg wzoru : gdzie: z - współczynnik określający warunki pracy połączenia Obliczenie siły P działającej na wpust korzystając ze wzoru: gdzie: d - średnica czopa śruby Znając wartość siły działającej na wpust oraz wymiary poprzeczne wpustu i wartość dopuszczalnych nacisków powierzchniowych możemy obliczyć czynną długość wpustu lo wg niżej podanego wzoru: Obliczam całkowitą długość wpustu l wynoszącą : Przyjmuję wpust pryzmatyczny 5x5x24.	bxh=5x5mm ko = 105MPa P = 4690N lo = 17,8mm Przyjmuję l = 24mm
[1]	[2]	[3]
p = 0,4 MPa; b = 1150 mm; a = 210 mm; g = 12 mm.	Obliczanie podstawy Podstawę obliczamy jako płytę prostokątną opartą na krawędzi i równomiernie obciążoną na powierzchni (w obliczeniach uproszczonych nie uwzględniamy żeber wzmacniających). Obliczenie naprężeń gnących Obliczeń dokonujemy wg zależności : gdzie: p - naciski powierzchniowe b, a, g - wymiary podstawy	σg = 29,5 MPa

1

- 2 -

---