Laboratorium Miernictwa Elektronicznego Czwartek/P 9:20 - 12:20

	Ćwiczenie nr 2 Temat: Pomiar parametrów prawidłowego wyznaczania elementarnych parametrów amplitudowych sygnału metodą cyfrowego przetwarzania Data:
Prowadzący zajęcia:		Ocena:

Badania parametrów sygnałów przeprowadzone zostały w trybie symulacji. W trybie tym amplituda każdego z sygnałów wynosiła 5V, zatem obliczona wartość skuteczna wynosi:

• dla sygnału sinusoidalnego:
  

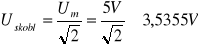
• dla sygnału trójkątnego:
  

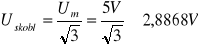
• dla sygnału prostokątnego: U_skobl=U_m=5,0000V.

1. Wyniki uzyskane podczas ćwiczeń:

1) Badanie wpływu liczby próbek na wyznaczanie wartości skutecznej.

Częstotliwość badanych sygnałów wynosiła f_s=1Hz. Zastosowano przetwornik o nieskończonej ilości bitów.

fp [Hz]	N	sygnał sinusoidalny		sygnał trójkątny		sygnał prostokątny
				Uskobl [V]	Uskzm [V]	Uskobl [V]	Uskzm [V]	Uskobl [V]	Uskzm [V]
32	32	3,5355	3,5355	2,8868	2,8980	5,0000	5,0000
64	64				3,5355			2,8895		5,0000
128	128				3,5355			2,8874		5,0000
256	256				3,5355			2,8869		5,0000
512	512				3,5355			2,8867		5,0000
1024	1024				3,5355			2,8867		5,0000
2048	2048				3,5355			2,8867		5,0000

Zgodnie z twierdzeniem Kotielnikowa - Shannona częstotliwość próbkowania powinna być co najmniej dwa razy większa od szerokości widma tego sygnału, aby można go było jednoznacznie określić. Im większa częstotliwość próbkowania, tym jest ono dokładniejsze, a zatem błąd próbkowania - mniejszy. Analizując dane zawarte w powyższej tabeli można zauważyć, że błąd próbkowania ma największą wartość w przypadku sygnału trójkątnego. Jego wartość maleje wraz ze wzrostem częstotliwości próbkowania, czyli ilości próbek w jednym okresie trwania badanego sygnału. Dla ilości próbek powyżej 512 jest on już nieznaczny (zmierzone wartości skuteczne są zbliżone do wartości rzeczywistych). Jest tak, ponieważ sygnał ten składa się z wielu harmonicznych, dlatego w celu uzyskania odpowiedniej dokładności pomiaru amplitudy należy użyć wyższej częstotliwości próbkowania niż w przypadku pozostałych sygnałów. Szerokość widma sygnału sinusoidalnego jest równa jego częstotliwości, dlatego wszystkie zastosowanie przez nas częstotliwości próbkowania były wystarczające i wyniki są poprawne. W przypadku sygnału prostokątnego, ze względu na jego kształt, wartość każdej próbki podniesiona do kwadratu będzie taka sama, więc zwiększenie ilości próbek nie wpływa na wynik pomiaru.

2) Badanie wpływu rozdzielczości użytego przetwornika na wyznaczanie wartości skutecznej.

Częstotliwość badanych sygnałów wynosiła f_s=1Hz.

Sygnał sinusoidalny

fp [Hz]	N	Uskobl [V]	Uskzm [V]
						14bit	10bit	6bit
32	32		3,5355	3,5355	3,5360	3,5379
64	64			3,5355	3,5360	3,5434
128	128			3,5354	3,5359	3,5347
256	256			3,5355	3,5360	3,5365
512	512			3,5355	3,5357	3,5343
1024	1024			3,5355	3,5357	3,5348
2048	2048			3,5355	3,5356	3,5341

Sygnał trójkątny

fp [Hz]	N	Uskobl [V]	Uskzm [V]
						14bit	10bit	6bit
32	32		2,8868	2,8980	2,8974	2,8946
64	64			2,8895	2,8894	2,8804
128	128			2,8874	2,8872	2,8811
256	256			2,8869	2,8868	2,8839
512	512			2,8867	2,8866	2,8887
1024	1024			2,8867	2,8866	2,8876
2048	2048			2,8867	2,8866	2,8872

Sygnał prostokątny

fp [Hz]	N	Uskobl [V]	Uskzm [V]
						14bit	10bit	6bit
32	32		5,0000	5,0000	5,0000	4,9600
64	64			5,0000	5,0000	4,9600
128	128			5,0000	5,0000	4,9600
256	256			5,0000	5,0000	4,9600
512	512			5,0000	5,0000	4,9600
1024	1024			5,0000	5,0000	4,9600
2048	2048			5,0000	5,0000	4,9600

Podczas badania sygnałów okresowych oprócz błędu próbkowania występuje także błąd kwantowania. Związany jest on z tym, iż wartości pobranych próbek muszą zostać przetworzone w przetworniku A/C, na wyjściu którego może pojawić się tylko skończony zbiór wartości zależny od rozdzielczości przetwornika. Dla przetwornika idealnego graniczny błąd kwantowania wynosi 0,5 kwantu. Im wyższa rozdzielczość przetwornika (im ma on więcej bitów), tym wartość jednego kwantu jest mniejsza, a zatem również błąd kwantyzacji jest mniejszy.

Analizując dane zawarte w tabelach widać, że zarówno dla sygnału sinusoidalnego, jak i trójkątnego wartości zmierzone coraz bardziej odbiegają od wartości rzeczywistych napięć skutecznych badanych sygnałów wraz z zastosowaniem przetwornika A/C o mniejszej ilości bitów. Dla przetwornika 14-sto oraz 10-cio bitowego można jeszcze zauważyć wzrost dokładności (zmniejszenie błędu) pomiaru wraz ze wzrostem częstotliwości próbkowania (błąd kwantowania nie jest duży). Dla przetwornika 6-cio bitowego wartości błędów są większe i zupełnie przypadkowo rozmieszczone. W przypadku sygnału prostokątnego błąd kwantyzacji zauważalny jest tylko przy zastosowaniu przetwornika 6-cio bitowego. Wielkości błędu nie zmieniają się (tak jak to było w przypadku sygnału sinusoidalnego i trójkątnego), ponieważ sygnał prostokątny przyjmuje jedynie dwie wartości różniące się tylko znakiem, zatem błąd kwantowania dla każdej próbki jest taki sam.

3) Badanie wpływu zwiększania okna czasowego na błąd wyznaczania wartości skutecznej.

Częstotliwość badanych sygnałów wynosiła f_s=1Hz. Zastosowano przetwornik o nieskończonej ilości bitów.

fp [Hz}	N	Uskzm [V]
				sygnał sinusoidalny	sygnał trójkątny	sygnał prostokątny
	32	64	3,5355	2,8980	5,0000
		128	3,5355	2,8980	5,0000
		256	3,5355	2,8980	5,0000

Wyniki pomiarów zamieszczone w powyższej tabeli pokazują, że zwiększenie okna czasowego nie ma wpływu na wyznaczanie wartości skutecznej pod warunkiem, iż okno czasowe jest wielokrotnością okresu badanego sygnału, ponieważ przy stałej częstotliwości próbkowania na każdy okres przypada taka sama ilość równomiernie rozmieszczonych próbek.

4) Badanie jak, na błąd wyznaczania wartości skutecznej sygnału, wpływa zbieranie próbek przez czas nie będący wielokrotnością okresu sygnału T_s.

Częstotliwość badanych sygnałów wynosiła f_s=150Hz. Zastosowano przetwornik o nieskończonej ilości bitów. Okno czasowe: T_w=a∙T_s+T_s/8

a	fp [Hz]	N	sygnał sinusoidalny		sygnał trójkątny		sygnał prostokątny
						Uskobl [V]	Uskzm [V]	Uskobl [V]	Uskzm [V]	Uskobl [V]	Uskzm [V]
1	61440		512	3,5355	3,5320	2,8868	2,8825	5,0000	5,0000
2	36141						3,4669			2,8212		5,0000
4	18618						3,4995			2,8527		5,0000
8	9452						3,5164			2,8686		5,0000
16	4762						3,5251			2,8774		5,0000
32	2390						3,5294			2,8832		5,0000

Wartość skuteczna sygnału z definicji obliczana jest za okres trwania tego sygnału lub jego wielokrotność. Ustawienie okna czasowego na czas nie będący wielokrotnością okresu powoduje powstanie błędu, ponieważ wartość skuteczną sygnału obliczamy wówczas na podstawie prawidłowych próbek zebranych w czasie będącym wielokrotnością okresu oraz dodatkowych, nieprawidłowych próbek zebranych w pozostałym czasie. Te dodatkowe próbki, w zależności od ich wartości, zawyżają lub zaniżają końcowy wynik (w szczególnych przypadkach wynik nie zmienia się).

Wraz ze zwiększeniem okna czasowego (wielokrotności okresu - a∙T_s) względny błąd maleje, a wartość zmierzona dąży do wartości poprawnej, co można również zauważyć analizując dane zawarte w tabeli dla sygnału sinusoidalnego oraz trójkątnego. Dla sygnału prostokątnego wartość skuteczna nie zależy od czasu trwania okna czasowego, ponieważ wartość każdej próbki podniesiona do kwadratu będzie taka sama.

5) Badanie jak, na błąd wyznaczania wartości skutecznej i średniej, wpływa usytuowanie okna czasowego względem mierzonego sygnału.

Okno czasowe nie jest wielokrotnością okresu sygnału próbkowanego.

Częstotliwość badanych sygnałów wynosiła f_s=200Hz. Zastosowano przetwornik o nieskończonej ilości bitów. Okna czasowe:

T_w1=2∙T_s+x∙T_s,

T_w2=16∙ T_s+x∙T_s.

	x	pozycja okna Tw (zakres próbek)	fp [Hz]	N	sygnał sinusoidalny		sygnał trójkątny		sygnał prostokątny
										Uskobl [V]	Uskzm [V]	Uskobl [V]	Uskzm [V]	Uskobl [V]	Uskzm [V]
		Tw1			1/8	0-511	48188	512	3,5355	3,4780	2,8868	2,8360	5,0000	5,0000
						127-638						3,4863			2,8406		5,0000
		Tw2			1/4	0-511	6301					3,5322			2,8825		5,0000
						127-638						3,5389			2,8909		5,0000

Jeżeli okno czasowe nie jest wielokrotnością okresu sygnału próbkowanego, to przesuwanie tego okna zauważalnie wpływa na wynik pomiaru. Jest tak dlatego, ponieważ w zależności od usytuowania okna, zmienia się zbiór wartości pobranych próbek. Efekt ten można zauważyć przeglądając dane umieszczone w powyższej tabeli. Jak widać wyniki pomiarów różnią się w zależności od położenia okna czasowego (0 - 511∙T_s lub 127∙T_s - 638∙T_s) dla T_w1 oraz T_w2 zarówno dla sygnału sinusoidalnego jak i trójkątnego. W przypadku sygnału prostokątnego, podobnie jak poprzednio wartość skuteczna nie zależy ani od czasu trwania okna czasowego ani od jego usytuowania. Dla okna T_w2 wyniki pomiarów są bardziej zbliżone do wartości rzeczywistych (obliczonych), ponieważ błąd względny spowodowany tym, że okno czasowe nie jest wielokrotnością okresu sygnału jest mniejszy niż w przypadku okna T_w2.

Należy dodać, iż jeżeli okno czasowe jest wielokrotnością okresu, to wówczas jego pozycja względem badanego sygnału nie wpływa na wynik pomiaru.

2. Wnioski

Na podstawie danych otrzymanych podczas tego ćwiczenia można stwierdzić, że dokładność wyników pomiaru wartości skutecznej sygnałów: sinusoidalnego i trójkątnego zależy od ilości próbek zebranych w czasie trwania okna czasowego (czyli od częstotliwości próbkowania) - im więcej próbek (im wyższa częstotliwość próbkowania), tym błąd próbkowania mniejszy. Liczba zebranych próbek nie wpływa na dokładność pomiaru sygnału prostokątnego.

Rozdzielczość użytego przetwornika A/C wpływa na dokładność wyników pomiarów wszystkich sygnałów - im większa rozdzielczość, tym błąd kwantowania mniejszy.

Na wyznaczanie wartości skutecznej sygnału nie wpływa za to zwiększanie okna czasowego, jeżeli jest ono wielokrotnością okresu tego sygnału. Dowodzą tego wyniki pomiarów zamieszczone w punkcie 3).

O dokładności końcowego wyniku decyduje także czas trwania okna czasowego, jeżeli nie jest on wielokrotnością okresu badanego sygnału, co można zapisać następująco:

T_w=a∙T_s+x∙T_s,

W takim przypadku otrzymany wynik nie jest poprawny. Powstały w ten sposób błąd jest tym mniejszy, im współczynnik a większy oraz x mniejszy, czyli gdy czas trwania okna dąży do okresu sygnału.

Jeżeli zmienimy usytuowanie takiego okna czasowego to wartości skuteczne sygnału sinusoidalnego oraz trójkątnego również ulegną zmianie. Dla okna będącego wielokrotnością okresu badanego sygnału oraz dla sygnału prostokątnego czas trwania okna oraz jego pozycja nie mają wpływu na końcowy wynik.

Jak widać na dokładność określenia wartości skutecznej napięcia okresowo zmiennego wpływ ma wiele czynników. W celu jak najdokładniejszego zmierzenia tej wartości należy użyć najwyższej możliwej częstotliwości próbkowania oraz przetwornika A/C o najwyższej rozdzielczości, a czas trwania okna czasowego powinien być jak najbardziej zbliżony do wartości okresu mierzonego przebiegu zmiennego.

Politechnika Wrocławska

---