Cel:
Celem ćwiczenia jest wykonanie pomiarów pojemności dla kilku kondensatorów radiowych oraz różnych ich połączeń (równolegle i szeregowe).
Wykonanie pomiarów pojemności powietrznego kondensatora cylindrycznego w zależności od długości okładek oraz wyznaczenie na podstawie tych pomiarów stałej dielektrycznej próżni.
Część doświadczalna i obliczenia:
Pojemność kondensatora płaskiego:
![]()
gdzie:
S - powierzchnia okładek
d - wzajemna odległość
Pojemność kondensatora płaskiego cylindrycznego o długości L, promieniach R1i R2:
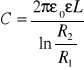
Opracowanie wyników dla kondensatorów radiowych:
1 |
2 |
3 |
4 |
5 |
|
C [F] pomiar |
C [F] obliczone |
L [m] |
Ck [F/m] |
C1 |
0,00252 |
|
Brak kabla |
Brak kabla |
C2 |
0,00988 |
|
|
|
C3 |
13,3 |
|
|
|
Cszer. |
2,46 |
2,01 |
|
|
Crów. |
13,2 |
13,3124 |
|
|
Ck |
Brak kabla |
Brak kabla |
|
|
Obliczam błąd:
dla połączenia równoległego:
![]()
dla połączenia szeregowego:
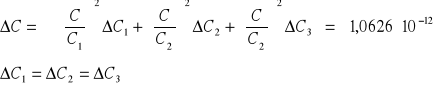
Korzystając z metody najmniejszych kwadratów obliczam współczynnik kierunkowy a prostej danej wyrażeniem y = ax + b, gdzie:
y = C,
x = L,
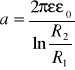
a = 0,60371517
Tabela pomiarów
L [mm] |
85 |
80 |
75 |
70 |
65 |
60 |
55 |
50 |
45 |
40 |
35 |
30 |
25 |
20 |
15 |
10 |
5 |
0 |
C1 [pF] |
114 |
108 |
105 |
102 |
99 |
96 |
93 |
91 |
88 |
85 |
82 |
79 |
76 |
73 |
70 |
67 |
65 |
62 |
C2 [pF] |
114 |
111 |
108 |
103 |
100 |
97 |
94 |
90 |
88 |
85 |
82 |
79 |
75 |
73 |
70 |
67 |
64 |
61 |
C [pF] |
114 |
109,5 |
106,5 |
102,5 |
99,5 |
96,5 |
93,5 |
90,5 |
88 |
85 |
82 |
79 |
75,5 |
73 |
70 |
67 |
64,5 |
61,5 |
Opracowanie wyników dla kondensatora cylindrycznego:
|
Xi |
Yi |
Xi2 |
Xi Yi |
Yi |
Xi+ Yi |
(Yi + Xi) 2 |
(Yi-aXi-b)2 |
1 |
0 |
61,5 |
0 |
0 |
3782,25 |
61,5 |
0 |
0,36281249 |
2 |
5 |
64,5 |
25 |
322,5 |
4160,25 |
69,5 |
4830,25 |
0,34077963 |
3 |
10 |
67 |
100 |
670 |
4489 |
77 |
5929 |
0,00424941 |
4 |
15 |
70 |
225 |
1050 |
4900 |
85 |
7225 |
0,00217264 |
5 |
20 |
73 |
400 |
1460 |
5329 |
93 |
8649 |
0,000786 |
6 |
25 |
75,5 |
625 |
1887,5 |
5700,25 |
100,5 |
10100,25 |
0,24062957 |
7 |
30 |
79 |
900 |
2370 |
6241 |
109 |
11881 |
8,31E-05 |
8 |
35 |
82 |
1225 |
2870 |
6724 |
117 |
13689 |
0,00076683 |
9 |
40 |
85 |
1600 |
3400 |
7225 |
125 |
15625 |
0,00214069 |
10 |
45 |
88 |
2025 |
3960 |
7744 |
133 |
17689 |
0,00420468 |
11 |
50 |
90,5 |
2500 |
4525 |
8190,25 |
140,5 |
19740,25 |
0,34037812 |
12 |
55 |
93,5 |
3025 |
5142,5 |
8742,25 |
148,5 |
22052,25 |
0,3623982 |
13 |
60 |
96,5 |
3600 |
5790 |
9312,25 |
156,5 |
24492,25 |
0,38510841 |
14 |
65 |
99,5 |
4225 |
6467,5 |
9900,25 |
164,5 |
27060,25 |
0,40850874 |
15 |
70 |
102,5 |
4900 |
7175 |
10506,25 |
172,5 |
29756,25 |
0,4325992 |
16 |
75 |
106,5 |
5625 |
7987,5 |
11342,25 |
181,5 |
32942,25 |
0,1047826 |
17 |
80 |
109,5 |
6400 |
8760 |
11990,25 |
189,5 |
35910,25 |
0,09310161 |
18 |
85 |
114 |
7225 |
9690 |
12996 |
199 |
39601 |
3,19175986 |
|
765 |
1558 |
44625 |
73527,5 |
139274,5 |
2323 |
327172,3 |
6,27726178 |
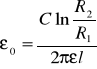
![]()
współczynnik korelacji wynosi: 0,999289802.
Wnioski:
Z przeprowadzonego doświadczenia wynika:
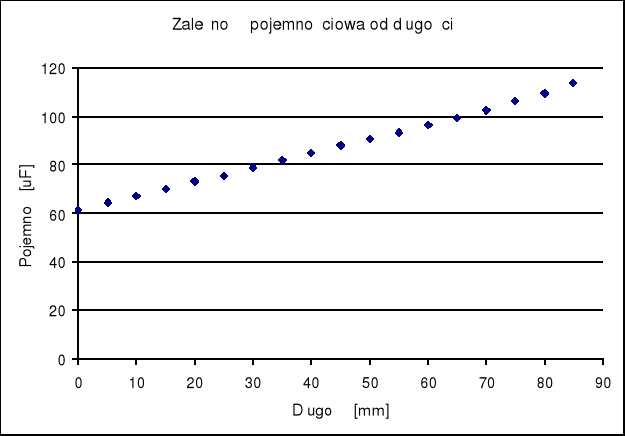
Im większe jest pokrywanie się okładek kondensatora cylindrycznego tym pojemność kondensatora jest większa.
Zależność kondensatora cylindrycznego wzrasta liniowo na co wskazuje wykres i współczynnik korelacji.
Pojemność zastępcza jest zawsze większa od największej pojemności łączonych kondensatorów.
Dla kondensatorów radiowych połączonych szeregowych
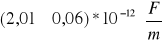
(z obliczeń)Dla kondensatorów radiowych połączonych równolegle
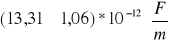
(z obliczeń)Przenikalność dielektryczna dla próżni wynosi: 8.85 * 10 -12
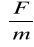
z tablic.Średnia przenikalność dielektryczna dla kondensatora cylindrycznego (z obliczeń) wynosi: (9.0

0.1) * 10 -12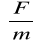
. Obliczona przenikalność nie mieści się w granicach błędu.
Ponieważ błąd w wyznaczaniu stałej dielektrycznej. Obliczeń kondensatorów radiowych mógł mieć wiele przyczyn:
błąd paralaksy przy ustawianiu śruby kondensatora cylindrycznego,
niedoskonałości urządzeń mierniczych.
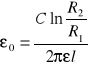
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron