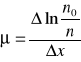Teoria do ćwiczenia:

Promieniowanie gamma jest promieniowaniem elektromagnetycznym o takim zakresie długości fali jak promieniowanie rendgenowskie, tj. od 1∗10^-10m do 1∗10^-8m. Nie powoduje ono zatem ani zmiany ładunku ani zmiany masy atomowej pierwiastka, który jest jego źródłem. Promieniowanie gamma nie stanowi niezależnego zjawiska promieniotwórczości naturalnej, a jedynie towarzyszy rozpadom α, lub β. Emisja promieniowania gamma towarzysz rozpadowi α, lub β tylko wtedy, gdy jądro nowo powstającego pierwiastka znajduje się w stanie energetycznie wyższym niż jego stan podstawowy. Atom którego jądro wysyła kwanty γ powinien w rezultacie konwersji wewnętrznej wysłać jednocześnie charakterystyczne promieniowania rentgenowskie.

Energię jaką niesie kwant γmożna określić wyrażeniem:

hv_i,j=E_i-E_j

gdzie:

E_i- energia stanu początkowego jądra

E_j- energia stanu końcowego jądra

h - stała Plancka

ν - częstotliwość fali odpowiadającej kwantowi gamma

Gamma kwant, (kwant γ) wysokoenergetyczny foton pochodzący z przemian zachodzących w jądrze atomowym lub z reakcji z udziałem cząstek elementarnych, w ogólności (przy nieznanym w szczegółach mechanizmie pochodzenia, np. w promieniowanie kosmicznym) każdy foton o długości fali mniejszej niż 1 angstrem (fale elektromagnetyczne).

Natężenie promieniowania gamma ulega osłabieniu przy przechodzeniu przez materię. Pochłanianie promieniowania gamma w danej substancji podlega (w przybliżeniu) prawu wykładniczemu:

I_o , I- natężenie wiązki przed i po absorpcji,

μ- współczynnik pochłaniania,

d- grubość warstwy pochłaniającej

Pochłanianie kwantów gamma przez ośrodki materialne zachodzi na drodze trzech elementarnych procesów:

1. zjawiska fotoelektrycznego;

2. zjawiska rozpraszania Comptona;

3. tworzenia się par elektron-pozyton;

Prawdopodobieństwo zajścia jednego z tych procesów zależne jest od energii kwantu gamma .Jeżeli energia nie przekracza 0,5MeV przeważa proces 1. , a w przedziale od 0,5 do 2,0 MeV proces 2. , powyżej 2MeV istnieje możliwość zaistnienia procesu 3.

Podczas przechodzenia przez materię równoległej wiązki promieniowania gamma następuje jej pochłanianie i rozpraszanie. Następnie wiązki promieniowania po przejściu przez materię o grubości x opisuje prawo Lamberta-Bougera.

I=I₀exp(-μx)

gdzie:

I₀- natężenie wiązki padającej

μ - Liniowy współczynnik osłabienia [cm^-1]

Liniowy współczynnik μ równa się względnemu zmniejszeniu natężenia wiązki promieniowania γ na drodze o jednostkowej długości :

Liniowy współczynnik osłabienia jest równy sumie liniowych współczynników pochłaniania rzeczywistego τ i rozproszenia σ

μ = τ + σ

Ponieważ współczynnik σ i τ są proporcjonalne do masy ciała pochłaniającego, w praktyce jest stosowany masowy współczynnik osłabienia:

μ_m = μ/ρ = τ_m + σ_m

Masowy współczynnik pochłaniania τ_m jest zależny od liczby atomowej absorbęta, jego masy atomowej oraz długości fali padającego promieniowania w następujący sposób:

gdzie:

C- stała

N₀-liczba Avogadro

A-masa atomowa pierwiastka pochłaniającego

Wzory:

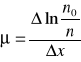
Tabele z wynkami:

1	2	3	4	5	6
x (m)	n		(1/m)	(1/m)	(m^2/kg)
x=0	n0=

Olsztyn 3.11.2005r

Temat: Promieniotwórczość, wyznaczanie masowego współczynnika pochłaniania promieniowania gamma dla różnych ciał

Kowalski Marcin

Sznitko Adam

Grupa II

TRiL

---