EKONOMIA MENEDŻERSKA (STUDIA NIESTACJONARNE)
WYKŁAD 4.
DECYZJE PRODUCENTA (PRODUKCJA I KOSZTY)
Mianem produkcji określa się proces przekształcania nakładów (czynników produkcji) w produkty i usługi.
Czynniki wytwórcze są to:
Zasoby kapitału ludzkiego (zasoby pracy)
Zasoby kapitału produkcyjnego
Zasoby materiałów
Do zasobów pracy zalicza się ludzi, ich kwalifikacje, doświadczenie i umiejętności.
Kapitał produkcyjny obejmuje niezbędne w procesie produkcji maszyny i urządzenia, hale produkcyjne, biura i inne budynki oraz zapasy.
Zasoby materiałów obejmują surowce, źródła energii, dobra pośrednie (półprodukty).
Funkcja produkcji całkowitej TP (total product) przedstawia maksymalną wielkość produkcji, jaką może osiągnąć przedsiębiorstwo, angażując daną ilość nakładów. Maksymalna wielkość produkcji oznacza, że wszystkie nakłady użyte w procesie produkcji były użyte efektywnie (nie wystąpiło zjawisko marnotrawstwa) oraz, że technologia wykorzystana w procesie produkcji była najlepszą dostępną technologią.
Funkcję produkcji można zapisać w postaci:
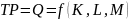 ,
,
Gdzie:
TP, Q – wielkość produkcji całkowitej
K – nakład kapitału produkcyjnego,
L – nakład pracy,
M – nakład materiałów,
Dla uproszczenia będziemy zakładać, że producent wykorzystuje tylko jeden rodzaj pracy i jeden rodzaj maszyn (nie wykorzystuje nakładu materiałów). Funkcja produkcji ma wówczas postać:
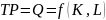 ,
,
Zwiększenie nakładów pozwala na wzrost produkcji, zatem funkcja TC jest funkcją rosnącą.
Całkowity koszt produkcji TC wyraża się wzorem:
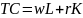 ,
,
Gdzie:
w (wage) - to stawka płac za jedną roboczogodzinę,
r (rental rate, interest rate) – to jednostkowy koszt kapitału (stawka wynagrodzenia kapitału).
Na
podstawie funkcji produkcji można wyznaczyć produkt krańcowy
danego czynnika produkcji. Jest przyrost produkcji całkowitej
spowodowany zwiększeniem nakładów tego czynnika o jednostkę, np.
produkt krańcowy pracy
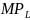 (marginal product of labour) informuje, o ile sztuk wzrośnie łączna
ilość (liczba) wytworzonego dobra po przepracowaniu kolejnej
roboczogodziny, zaś produkt krańcowy kapitału
(marginal product of labour) informuje, o ile sztuk wzrośnie łączna
ilość (liczba) wytworzonego dobra po przepracowaniu kolejnej
roboczogodziny, zaś produkt krańcowy kapitału
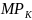 (marginal product of capital) informuje, o ile sztuk zwiększy się
produkcja po zaangażowaniu do procesu produkcji kolejnej maszyny lub
zwiększenia czasu pracy maszyny o kolejną godzinę.
(marginal product of capital) informuje, o ile sztuk zwiększy się
produkcja po zaangażowaniu do procesu produkcji kolejnej maszyny lub
zwiększenia czasu pracy maszyny o kolejną godzinę.
Produkty krańcowe nakładów oblicza się ze wzorów:
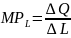 oraz
oraz
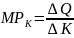 ,
,
Gdzie:
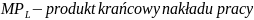 ,
,
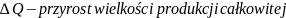 ,
,
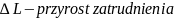 .
.
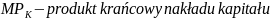 ,
,
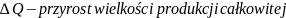 ,
,
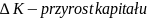 .
.
Przy nieskończenie małych zmianach (jeżeli mamy do czynienia ze zmiennymi o charakterze ciągłym) równanie przyjmuje postać:
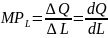 ,
stąd
,
stąd
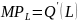 .
.
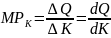 ,
stąd
,
stąd
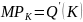 .
.
W zależności od zmian w nakładach użytych w procesie produkcji wyróżnia się krótki i długi okres produkcji. Okresem krótkim nazywana jest sytuacja, w której wielkość nakładów jednego lub więcej czynników produkcji jest stała. Czynniki te nazywane są czynnikami stałymi. Ze względu na to, że najłatwiej zmienić jest liczbę zatrudnianych pracowników, w większości teoretycznych przypadków nakład kapitału produkcyjnego traktowany jest jako czynnik stały, a funkcja produkcji w krótkim okresie przybierze postać:
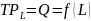 ,
,
Jednakże, w sytuacji, gdy w przedsiębiorstwie związki zawodowe sprzeciwiają się zmianie zatrudnienia, a kapitał można swobodnie wynajmować na wolnym rynku (maszyny w leasing), to praca jest czynnikiem stałym, a nakład kapitału jest zmienny.
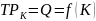 ,
,
Dopiero w długim okresie (np. wybudowanie nowego zakładu, zakończenie negocjacji ze związkami zawodowymi) przedsiębiorca (producent) może zmienić wielkość nakładów wszystkich wykorzystywanych czynników produkcji. W długim okresie nie ma zatem żadnych czynników o charakterze stałym (wszystkie są zmienne).
W krótkim okresie, w zależności od technologii stosowanej w danym przedsiębiorstwie, wielkość produkcji może szybciej lub wolniej osiągnąć pewne wartości. Jednakże zawsze przebieg zmienności funkcji jest podobny (taki sam). Występujący początkowo szybki wzrost produkcji całkowitej ustępuje przyrostom malejącym, po czym produkcja zaczyna się zmniejszać.
Innymi słowy występuje prawo malejących przychodów (prawo malejącego produktu krańcowego), zgodnie z którym zwiększanie nakładów zmiennego czynnika produkcji (pracy lub kapitału) powoduje coraz wolniejszy przyrost produkcji całkowitej.
W krótkim okresie producent podejmuje decyzję dotyczącą optymalnego poziomu zatrudnienia zmiennego czynnika wytwórczego. Po jego obliczeniu i podstawieniu do funkcji produkcji otrzymujemy wielkość produkcji całkowitej, która zapewni maksymalne zyski.
Przyjmijmy, że to praca stanowi czynnik zmienny, a kapitał ma charakter stały (jego wielkość jest dana). Wówczas, optymalny poziom ilości pracy wyznaczamy, korzystając z zasad analizy krańcowej, według której należy zrównać ze sobą korzyści krańcowe i koszty krańcowe.
Korzyść całkowitą, jaka płynie dla producenta z tytułu zatrudnienia pracowników, stanowią wpływy ze sprzedaży produktu wytworzonego przez pracowników. Korzyść krańcowa to przyrost utargu, jaki producent osiąga po sprzedaniu produktu krańcowego uzyskanego dzięki zwiększeniu liczby roboczogodzin o jednostkę. Przyrost utargu spowodowany zwiększeniem ilości pracy nazywa się KRAŃCOWYM PRZYCHODEM Z PRACY (marginal revenue product of labour).
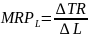 (dla zmiennych dyskretnych)
(dla zmiennych dyskretnych)
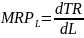 (dla
zmiennych ciągłych)
(dla
zmiennych ciągłych)
Krańcowy przychód z pracy jest iloczynem utargu krańcowego ze sprzedaży i produktu krańcowego pracy, gdyż:
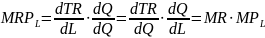 .
.
Jeżeli producent działa w warunkach konkurencji doskonałej i nie ma żadnego wpływu na cenę, to każda jednostka wytwarzanego dobra jest sprzedawana po tej samej cenie. W związku z tym, MR =P.
W takim przypadku krańcowy przychód z pracy jest iloczynem ceny dobra i produktu krańcowego pracy.
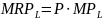 .
.
Kosztem pracy, jaki ponosi producent są wydatki na wynagrodzenia pracowników. Marginalny koszt pracy (marginal cost of labour) to przyrost kosztu całkowitego TC spowodowany zwiększeniem ilości pracy o jednostkę.
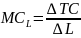 ,
a dla zmiennych ciągłych
,
a dla zmiennych ciągłych
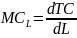 .
.
Jeśli
stawka płacy jest stała, to
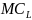 jest
także stały i równy jest w
(ang. wage):
jest
także stały i równy jest w
(ang. wage):
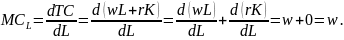
Optymalny poziom zatrudnienia w krótkim okresie wyznaczamy przyrównując:
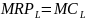 ,
,
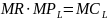
Co w przypadku stałej ceny dobra i stawki wynagrodzenia pracownika jest równoważne z:
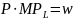 .
.
Analogicznie przedstawia się sytuacja, kiedy to kapitał jest czynnikiem zmiennym, a praca stałym.
Krańcowy
przychód z kapitału -
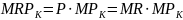 ;
;
Krańcowy
koszt kapitału -
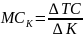 ,
a dla zmiennych ciągłych
,
a dla zmiennych ciągłych
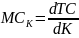 ;
;
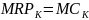 ,
,
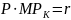 .
.
Do identycznych wniosków można dojść, szukając maksimum funkcji zysku (π).
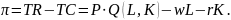
W krótkim okresie, załóżmy, że praca jest czynnikiem zmiennym, a ilość kapitału K, cena produkowanego dobra P i stawka płac są stałe. W punkcie maksimum, pochodna cząstkowa funkcji zysku musi być równa zero.
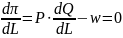
Stąd,
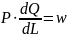 ,
,
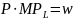 .
.
Warunek wystarczający maksymalizacji zysku – druga pochodna cząstkowa mniejsza od zera!
Ten warunek jest spełniony, gdyż działa prawa malejących przychodów.
Załóżmy teraz, że to nakłady kapitału K są czynnikiem zmiennym, a nakłady pracy L, cena produkowanego dobra P i stawka płac są stałe. Wówczas:
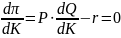 ;
;
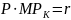 .
.
ZADANIE 1. DLA CHĘTNYCH DO DOMU
Funkcja
produkcji w fabryce środków chemicznych to:
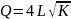 .
Nakład kapitału jest stały i wynosi 36. Produkt jest sprzedawany
po cenie równej 5 zł, a godzinowa stawka wynagrodzenia pracowników
wynosi 12 zł. Znajdź optymalny nakład pracy (w roboczogodzinach),
który zmaksymalizuje zysk przedsiębiorstwa. (Uwaga: oczywiście
mówimy w tym zadaniu o krótkim okresie).
.
Nakład kapitału jest stały i wynosi 36. Produkt jest sprzedawany
po cenie równej 5 zł, a godzinowa stawka wynagrodzenia pracowników
wynosi 12 zł. Znajdź optymalny nakład pracy (w roboczogodzinach),
który zmaksymalizuje zysk przedsiębiorstwa. (Uwaga: oczywiście
mówimy w tym zadaniu o krótkim okresie).
DŁUGI OKRES
W długim okresie producent podejmuje decyzję co do pożądanego poziomu nakładów, zarówno pracy, jak i kapitału. Producent maksymalizuje wówczas funkcję zysku względem L i K. Optymalną kombinację czynników wytwórczych wylicza się, rozwiązując układ równań:
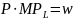
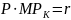
Wyliczając z obu równań P, a następnie przyrównując je do siebie otrzymamy:
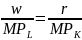 ;
;
Interpretując ten warunek, zapiszemy w postaci odwrotnej:
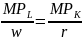 ,
,
Z czego wynika, że:
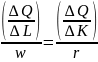 ,
,
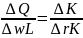 .
.
Lewa strona powyższego równania wskazuje, o ile sztuk wzrośnie produkcja, gdy producent zwiększy wydatki na pracę o 1 jednostkę pieniężną (np. PLN).
Prawa strona równania wskazuje, o ile wzrośnie produkcja, gdy producent zwiększy wydatki na kapitał o jednostkę (PLN)
Interpretacja!
Gdyby lewa strona równania była większa od prawej, przeznaczenie kolejnej jednostki pieniężnej na zakup jednostek pracy powodowałby większy przyrost produkcji niż przeznaczenie dodatkowej jednostki pieniężnej na zakup dodatkowej jednostki kapitału. Producent powinien zmniejszyć nakłady kapitału, pożytkując zaoszczędzone pieniądze na zakup nakładu pracy (roboczogodzin). Wówczas zachowa się racjonalnie w sensie ekonomicznym. Produkcja powinna być bardziej pracochłonna a mniej kapitałochłonna.
I odwrotnie, kiedy lewa strona równania byłaby mniejsza od prawej!
Jedynie w sytuacji, gdy obie strony równania są sobie równe, producent nie ma motywacji do zmiany podziału posiadanych środków na oba czynniki wytwórcze (produkcji), ponieważ osiąga ich optymalną kombinację.
Zadanie2. DLA CHĘTNYCH DO DOMU
Funkcja
produkcji w zakładzie wytwórczym ma postać:
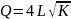 . Stawka płac wynosi 50 zł, a jednostkowa stawka wynajmu kapitału
100 zł. Jaka najtańsza kombinacja czynników wytwórczych pozwoli
wytworzyć 16000 sztuk produktu?
. Stawka płac wynosi 50 zł, a jednostkowa stawka wynajmu kapitału
100 zł. Jaka najtańsza kombinacja czynników wytwórczych pozwoli
wytworzyć 16000 sztuk produktu?
ANALIZA KOSZTÓW
Podejmując decyzje optymalizacyjne, trzeba porównać ze sobą możliwe do osiągnięcia korzyści wynikające z jakiegoś działania i koszty. Istotne jest właściwe zidentyfikowanie KOSZTÓW.
Rachunkowość rejestruje tylko KOSZTY KSIĘGOWE (historyczne, jawne, explicite), które odzwierciedlają faktycznie poniesione wydatki.
Jednakże, przy podejmowaniu decyzji przez menedżerów, liczą się nie tylko koszty księgowe, ale pełne KOSZTY EKONOMICZNE (koszty księgowe + alternatywne, utraconych możliwości). Koszt alternatywny równy jest wartości najlepszej spośród odrzuconych opcji.
Zwróćmy uwagę, że koszt ekonomiczny ponoszony jest przez każdą osobę w sytuacji wyboru!
Jeżeli istnieje rynek danego zasobu (np. pracy, pieniądza, nieruchomości, kapitału), to koszt ekonomiczny jest równy cenie, jaką ten zasób osiąga na rynku. Gdy przedsiębiorca musi wynająć na rynku dany zasób, płaci jego właścicielowi opłatę, która jest jego kosztem jawnym (explicite). Jednakże, w sytuacji, gdy sam jest właścicielem zasobu, to decyduje się na wykorzystanie go w określony sposób. Traci tym samym możliwość uzyskania dochodu z tytułu udostępnienia go na rynku innym osobom. To właśnie te utracone dochody stanowią KOSZT NIEJAWNY (implicite).
Łączne koszty ekonomiczne ponoszone przez przedsiębiorcę (jak i każdego innego decydenta) stanowią sumę kosztów jawnych i niejawnych.
Różnica między utargami całkowitymi a kosztami ekonomicznymi to zysk ekonomiczny, który jest przykładem korzyści netto.
Gdy ten zysk jest DODATNI, nazywa się ZYSKIEM NADZWYCZAJNYM. Osiągnięcie zysku nadzwyczajnego oznacza, że wygenerowane utargi pokrywają z nadwyżką sumę kosztów jawnych i utraconych dochodów. Oznacza to, że wybrana opcja jest najlepszą z możliwych.
Zysk ekonomiczny równy zero nazywa się ZYSKIEM NORMALNYM. Występuje on, gdy utarg jest równy sumie kosztów jawnych i niejawnych. W tym przypadku opłacalność danego przedsięwzięcia zrównuje się z opłacalnością najlepszej odrzuconej alternatywy.
Bodźcem do prowadzenia działalności gospodarczej jest występowanie ZYSKU NADZWYCZAJNEGO.
Dokonując analizy opłacalności danego przedsięwzięcia, trzeba wziąć pod uwagę wyłącznie KOSZTY ISTOTNE (przyrostowe, zmienne), które różnią się dla poszczególnych wariantów działań. Należy pominąć KOSZTY STAŁE, których wysokość nie zależy od tego, która opcja ostatecznie zostanie wybrana.
Nie należy również brać pod uwagę KOSZTÓW UTOPIONYCH, czyli wydatków poniesionych w przeszłości, które nie mogą ulec zmianie wskutek bieżących ani przyszłych decyzji.
Funkcje kosztów przedstawiają zależność między wielkością produkcji a najniższym poziomem kosztów, jaki trzeba ponieść na jej wytworzenie.
W krótkim okresie, wydatki na utrzymanie niektórych nakładów są stałe i nie zależą od poziomu produkcji. Nazywa się je KOSZTAMI STAŁYMI (fixed costs).
Koszty, których wysokość bezpośrednio zależy od wielkości produkcji stanowią KOSZTY ZMIENNE (variable costs).
Ich suma tworzy KOSZTY CAŁKOWITE (total costs).
TC+FC+VC
KOSZT PRZECIĘTNY (average cost) to średni koszt wytworzenia jednostki produktu. Stanowi on iloraz TC i ilości wyprodukowanego dobra.
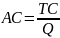 .
.
Większość kosztówstałych, przypadających średnio na jednostkę produktu to przeciętny koszt stały AFC (average fixed cost).
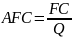 .
.
Średni koszt zmienny przypadający na jednostkę produktu nazywany jest przeciętnym kosztem stałem AVC (average variable cost):
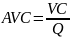 .
.
Koszty przeciętne całkowite są sumą przeciętnych kosztów stałych i zmiennych:
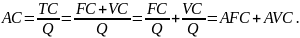
W długim okresie przedsiębiorstwo jest w stanie dostosować liczbę wszystkich czynników produkcji do zmienionych warunków: zatrudnić więcej pracowników, kupić lub wynająć kolejne maszyny, rozbudować zakład itp. Nie występują więc żadne koszty stałe.
Producent, który wypracował zysk normalny ze swojej działalności, osiąga PRÓG RENTOWNOŚCI (BEP, break-even point): zysk ekonomiczny jest zerowy, co oznacza, że utarg jest równy kosztom ekonomicznym.
TR=TC
Po podzieleniu obu stron powyższego równania przez Q otrzymujemy cenę PBEP, przy której osiągany jest próg rentowności. Jest to cena równa kosztom przeciętnym produkcji:
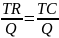 ,
,
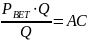 ,
,
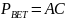 .
.
Producent maksymalizujący zysk, po zrównaniu MR i MC i wyznaczaniu optymalnego poziomu produkcji Q* powinien sprawdzić, czy zysk π (w tym punkcie) jest dodatni.
Jeśli tak, jest on największy z możliwych i producent powinien kontynuować działalność; w przeciwnym wypadku, gdy π jest mniejszy równy zero, należy sprawdzić, czy sytuacja przedsiębiorcy nie byłaby lepsza po zaprzestaniu produkcji.
W krótkim okresie po zamknięciu zakładu, firma nie osiąga utargu i nie ponosi kosztów zmiennych, ale ponosi koszty stałe.
Π(0) = - FC
Należy kontynuować produkcję mimo strat, jeżeli sytuacja producenta jest lepsza przy produkcji Q* niż przy Q=0, czyli gdy:
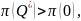
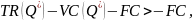
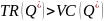
Po podzieleniu obu stron przez Q otrzymujemy:
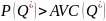 .
.
Producent powinien więc wytwarzać optymalną wielkość produkcji w krótkim okresie, jeżeli cena przekracza przeciętny koszt zmienny. Jeżeli ten warunek nie jest spełniony, należy wstrzymać produkcję, gdyż straty są zbyt duże; firma poniesie mniejsze straty przy zaprzestaniu produkcji.
W długim okresie jest możliwa likwidacja zakładu; wówczas producent nie osiąga utargu, nie ponosi żadnych kosztów, a zysk jest równy zero.
Należy kontynuować produkcję, gdy:
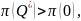
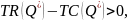
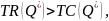
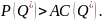
Zatem w długim okresie producent powinien prowadzić działalność wyłącznie wtedy, gdy osiąga zysk.
Cena, poniżej której należy zaprzestać produkcji w krótkim okresie, nazywa si CENĄ ZAMKNIĘCIA i jest równa AVC. Cena, poniżej której producent powinien w długim okresie zamknąć zakład i wyjść za gałęzi, to CENA WYJŚCIA, a kształtuje się na poziomie AC.
ZADANIE CLA CHĘTNYCH (DO DOMU)
Funkcja kosztu całkowitego w firmie ma postać TC=20Q2 + 2400Q + 45000. Natomiast funkcja popytu na jej produkt: P=-100Q + 6000. Jak jest optymalna wielkość produkcji? Czy wytwarzając tę ilość, firma osiągnie zysk? Jeśli nie, to czy powinna kontynuować produkcję?
Wyszukiwarka
Podobne podstrony:
EKONOMIA MENADŻERSKA notatki z wykładów, ekonomia menedżerska
wykłady EKONOMIA MENEDŻERSKA
Wykład 3 ekonomia menedżerska
wykłady EKONOMIA MENEDŻERSKA
4. konspekt - Ekonomia menedżerska, Decyzje produkcyjne w przedsiębiorstwie
EKONOMIA MENEDŻERSKA wykłady Sylabus 1202 2013 r WSM
Wykład Mikroekonomia Jasiński, Zarządzanie i Inżynieria Produkcji - studia, Ekonomia
EKONOMIA MENEDŻERSKA, Ekonomia menedżerska wykłady
6. konspekt - Ekonomia menedżerska, Struktury rynku a decyzje w przedsiębiorstwie
EKONOMIA MENEDŻERSKA wykłady Sylabus 1202 2013 r WSM
20 (poprawka) Wykład - Prawo Handlowe, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), prawo handlowe
Dystrybucja- wyklady, ekonomia up lublin, dystrybucja produktów
Opracowanie wykładu Mikroekonomia II, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), mikroekonomia
Decyzje inwestycyjne wykłady, Różne Dokumenty, MARKETING EKONOMIA ZARZĄDZANIE
decyzje inwestycyjne 28-01-10 - wyklady, Ekonomicznie, Decyzje inwestycyjne
III. Decyzje przedsiębiorstwa, ● STUDIA EKONOMICZNO-MENEDŻERSKIE (SGH i UW), ekonomia matematyczna
Prognozowanie i Symulacje - Wyklady - Jankiewicz-Siwek - 2003 (25), ● STUDIA EKONOMICZNO-MENEDŻERSKI
8. konspekt - Ekonomia menedżerska, Podejmowanie decyzji w warunkach niepewności
Ekonomia menedzerska wyklady dodatkowe id 155947
więcej podobnych podstron