Student: Łukasz Rychter Warszawa, 06.12.2009
Nr indeksu: 218882
Grupa studencka: 3M2
Data lab. 27.11.2009 14.15-16.15
Laboratorium AISDE
Sprawozdanie z ćwiczenia 3:
Drzewa, kopce, wyszukiwanie wzorca informacji, kodowanie
1) Zadanie i cel ćwiczenia
Do moich zadań należało wykonanie poleceń 1,3,4,11,12 z instrukcji do laboratorium.
Należało przeanalizować i zbadać podanym programem (modyfikowanym do własnych potrzeb i zadań) pod względem złożoności obliczeniowej i zapotrzebowania na zasoby różne algorytmy przechodzenia przez drzewa oraz algorytm obliczania wyrażeń w notacji postfiksowej, a także zamiany notacji infiksowej na postfiksową.
2) Sposób wykonania zadania
Zgodnie z poleceniem 3 program uzupełniłem o 2 dodatkowe procedury nierekurencyjnego przechodzenia drzewa w porządku pre-order – jedną wykorzystującą stos, oraz drugą nie korzystającą z żadnej dodatkowej struktury danych, a jedynie opierającą się na podstawowych zależnościach między węzłami w badanym drzewie. dokładne opisy procedur zawarte są w dalszej części sprawozdania.
Ważnym spostrzeżeniem jest, że badane drzewa są uformowane w strukturę kopca oraz węzły mają zawsze co najwyżej 2 potomków. W dodatku jednego, a nie dwóch potomków może(lecz nie musi) mieć tylko najbardziej skrajny z węzłów drzewa. Przykładowe zaimplementowane procedury przechodzenia drzewa opierają się na tych właściwościach i nie uwzględniają możliwości, iż na przykład któryś z wewnętrznych węzłów ma tylko 1 potomka. Dlatego też pisząc własne algorytmy poszedłem za tym przykładem i wykorzystałem cechy badanego drzewa pomijając niektóre z możliwych sytuacji podczas przechodzenia drzew w bardziej ogólnym przypadku.
Podczas badania wydajności algorytmów uwzględniłem fakt, że różne zadane procedury w sposób niespójny raportują o wykonywanych czynnościach – w szczególności w niektórych przypadkach operacje przypisania są dodawane do statystyk jako operacje kopiowania, w innych przypadkach nie. Z tego też względu podczas badania złożoności algorytmów nie brałem pod uwagę liczby kopiowań danych, zwłaszcza że w algorytmach tych nie odbywają się nigdy kopiowania danych samych węzłów, a co najwyżej zwykłe przypisania do zmiennych.
Badania przeprowadzałem na domowym komputerze z systemem Windows XP. W porównaniu z Macintoshem domyśla rozdzielczość mierzenia czasu jest dużo niższa – wyrażana w milisekundach co jest niewystarczające. Dlatego też zmodyfikowałem do swoich potrzeb funkcję pobierającą czas tak aby operowała ona na czasach mikrosekundowych:
#include
<windows.h> template
<class
OBJ> long
AISD<OBJ>::PobierzCzas() {
static
LARGE_INTEGER c_zero={0};
if
(c_zero.QuadPart == 0) QueryPerformanceCounter(&c_zero);
LARGE_INTEGER
c, f; QueryPerformanceCounter(&c); QueryPerformanceFrequency(&f); return
(long)((c.QuadPart-c_zero.QuadPart)/(double)f.QuadPart*1000000); //return
clock(); }
3) Wykonanie poleceń
Zad 1. „Przeanalizować sposób działania NIEREKURENCYJNYCH metod przechodzenia przez drzewo w porządku pre-order”
W dostarczonym programie jest zaimplementowana tylko 1 tego typu metoda:
template
<class
OBJ> void
Drzewa<OBJ>::PreOrderNRekurSTOS(int
Node) {
STOS<int,Drzewa<OBJ>
>s;
int
h;
this->ZA.LiPor++;
if(Node<=this->LicznoscZbioru)
{
s.push(Node,this);
while(!s.empty())
{
Visit(h=s.pop(this));
this->ZA.LiPor++;
if(NodeR(h)<=this->LicznoscZbioru)
s.push(NodeR(h),this);
this->ZA.LiPor++;
if(NodeL(h)<=this->LicznoscZbioru)
s.push(NodeL(h),this);
}
} }
Jej implementacja oparta jest na stosie. Na początek na stos odkładany jest pierwszy element, od którego zaczynamy przechodzenie drzewa. Opróżnienie stosu oznacza zakończenie algorytmu – w przypadku odwiedzenia wszystkich węzłów.
W każdym obiegu pętli ze stosu zdejmowany jest jeden element – węzeł. Przechodzimy do niego, odwiedzamy, a następnie na stos odkładani są jego potomkowie(jeśli istnieją) – najpierw prawy, następnie lewy - ponieważ zdejmowanie ze stosu odwraca kolejność działania – najpierw zdjęty ze stosu zostanie lewy potomek, a następnie prawy, co jest zgodne z naszym zamierzeniem.
W rezultacie zawsze najpierw odwiedzany jest rodzic, następnie lewy potomek i całe jego poddrzewo, po czym poprzez zdejmowanie elementów ze stosu powracamy do prawego potomka i jego poddrzewa, a w końcu do prawego potomka z któregoś z wyższych poziomów drzewa.
W danej chwili na stosie pozostają 1 lub 2 węzły z poziomu aktualnie przetwarzanego i po 1 węźle z każdego z poziomów wyższych oprócz poziomu korzenia (korzeń zdejmowany jest ze stosu już na początku 1 obiegu pętli). Maksymalna głębokość stosu jest więc równa wysokości drzewa.
Implementacja algorytmu nie jest optymalna, ponieważ często występującą sytuacją jest gdy na stos odkładamy lewego potomka, a następnie zaraz w następnym przebiegu zdejmujemy ten element ze stosu. Operacje na stosie są stosunkowo wymagające obliczeniowo, a w tym przypadku nie są one konieczne.
W dodatku przy badaniu złożoności obliczeniowej nie jest brana pod uwagę operacja
h=s.pop(this)
Po poprawieniu tej linii zawierającej ten kod w ten sposób:
Visit(h=s.pop(this)); this->ZA.LiKop++;
Uzyskujemy dla liczności=100 przykładowe wyniki:
Czas wykonania: 950
Liczba kopiowan danych: 50
Liczba porownan danych: 101
Liczba wejsc do komorki: 50
Max glebokosc stosu programu: 0
Max glebokosc stosu danych: 6
Liczba odlozen na stos danych: 50
Po modyfikacjach w kodzie i doprowadzeniu funkcji do postaci:
template
<class
OBJ> void
Drzewa<OBJ>::PreOrderNRekurSTOS(int
Node){ STOS<int,Drzewa<OBJ>
>s; int
h; this->ZA.LiPor++; if(Node<=this->LicznoscZbioru) { Visit(h=Node); this->ZA.LiKop++; do { this->ZA.LiPor++; if(NodeR(h)<=this->LicznoscZbioru)
s.push(NodeR(h),this); this->ZA.LiPor++; if(NodeL(h)<=this->LicznoscZbioru) { Visit(h=NodeL(h)); this->ZA.LiKop++; } else
{ if
(s.empty()) break; Visit(h=s.pop(this)); this->ZA.LiKop++; } }
while(1); } }
Uzyskujemy wyniki:
Czas wykonania: 788
Liczba kopiowan danych: 50
Liczba porownan danych: 101
Liczba wejsc do komorki: 50
Max glebokosc stosu programu: 0
Max glebokosc stosu danych: 5
Liczba odlozen na stos danych: 24
Poprawiona funkcja działa prawidłowo i jest bardziej wydajna, zwłaszcza pod względem liczby odłożeń na stos. Analizę kodu i szczegółowe porównania wydajnościowe pomijam, jako iż nie są one przedmiotem mojego zadania i za wystarczające uważam wykazanie możliwości udoskonaleń i przykładowe porównanie.
Zad 3. „Zaproponować, zaimplementować i przetestować własne wersje NIEREKURENCYJNYCH metod przechodzenia przez drzewo w porządku post-order”
P
template
<class
OBJ> void
Drzewa<OBJ>::PostOrderNRekurSTOS(int
Node) { STOS<int,Drzewa<OBJ>
>s; int
h, hprev; h
= Node; this->ZA.LiPor++; if(Node<=this->LicznoscZbioru)
{ s.push(Node,this);
//odłóż
pierwszy element na stos while(1)
{ //jeśli
istnieje, odłóż na stos prawego potomka
this->ZA.LiPor++; if(NodeR(h)<=this->LicznoscZbioru)
s.push(NodeR(h),this);
//jeśli
istnieje, odłóż na stos lewego potomka i przejdź do niego
this->ZA.LiPor++; if(NodeL(h)<=this->LicznoscZbioru)
s.push(h=NodeL(h),this); else
{
//jeśli
lewy potomek nie istnieje, to nie istnieje też prawy, więc
jesteśmy w liściu i należy zacząć sie cofać w górę drzewa s.pop(this);
//zdejmuje
ze stosu liść do
{ Visit(h);
//jeśli
dotarliśmy do punktu startowego kończymy this->ZA.LiPor++;
if
(h == Node) return; hprev
= h; h=s.pop(this); this->ZA.LiPor++; }
while
(hprev > h); //dopóki
cofamy się w górę drzewa
//odkłada
z powrotem na stos prawego potomka, którego potomkowie (poddrzewo)
nie byli jeszcze odwiedzeni s.push(h,
this);
} } } }
Ogólny zamysł algorytmu polega na tym, iż podróżujemy w dół drzewa, odkładając kolejno prawego i lewego potomka z każdego przechodzonego węzła, aż do dotarcia do liścia, w którym to zaczynamy wędrówkę wstecz zgodnie z uszeregowaniem elementów na stosie, jednocześnie odwiedzając elementy, aż natrafimy na węzeł, którego prawego potomka i jego poddrzewa jeszcze nie zwiedziliśmy(dzieje się tak wtedy, gdy do węzła przechodzimy z jego lewego brata). Wtedy ponownie podróżujemy w dół aż do liści i procedura się powtarza, aż powrócimy na sam szczyt drzewa (dokładnie w tej implementacji – do węzła od którego zaczęliśmy, co jest równoważne z przechodzeniem dowolnego poddrzewa zaczynającego się od podanego jako parametr wywołania funkcji węzła).
Dodatkowe informacje zawarte są w komentarzach do kodu. Algorytm został przetestowany i daje poprawne wyniki (zgodne zarówno z porządkiem post-order jak i identyczne z wynikami działania procedury rekurencyjnej post-order). Wyniki testów pomijam w sprawozdaniu.
Druga z zaimplementowanych metod nie wykorzystuje żadnego z kontenerów, a jedynie opiera się na tym iż drzewo ma formę kopca, oprócz skrajnego węzła wszystkie węzły maja 2 potomków oraz dla kopca indeks lewego potomka jest parzysty, a prawego nieparzysty.
template
<class
OBJ> void
Drzewa<OBJ>::PostOrderNRekur(int
Node) { int
h, hprev; h
= Node; this->ZA.LiPor++; if(Node<=this->LicznoscZbioru)
{ while(1) { this->ZA.LiPor++; //przechodzenie
w dół stosu po lewych potomkach aż do liścia if(NodeL(h)<=this->LicznoscZbioru)
h=NodeL(h);
else
{ do
{ Visit(h);
//jeśli
dotarliśmy do punktu startowego kończymy this->ZA.LiPor++; if
(h == Node) return; //jeśli
węzeł jest prawym potomkiem przejdź do rodzica if
(h%2) h = h/2;
else
{
//jeśli
węzeł jest lewym potomkiem przejdź do prawego potomka jeśli
istnieje, jeśli nie do rodzica
//jeśli
przeszliśmy do prawego potomka to musimy odwiedzić jego potomków,
więc przerywamy pętlę
this->ZA.LiPor++; if
( h+1<=this->LicznoscZbioru
) { ++h; break;
} else
h = h/2; } }
while
(1); } } } }
Zamysł działania tego algorytmu jest taki sam jak poprzedniego, z tą jedynie różnicą, iż przy powrocie w górę drzewa nie jest używany stos do pamiętania kolejności elementów, do których należy powrócić, a używane są odpowiednie zależności – zależnie od tego czy jesteśmy w prawym czy lewym potomku oraz czy poprzednio odwiedzaliśmy lewego brata czy też potomków danego węzła możemy jednoznacznie zdecydować do którego węzła należy się udać i czy w danym momencie go odwiedzać, czy też podróżować w dół jego poddrzewa.
Dodatkowe informacje zawarte są w komentarzach. Algorytm był oczywiście testowany i daje prawidłowe wyniki.
Zad 4. „Przeprowadzić analizę zapotrzebowania na zasoby dla poszczególnych metod przechodzenia przez drzewo (przykładowych i samodzielnie zaimplementowanych).”
Analizowanymi algorytmami są:
A) zwiedzanie rekurencyjne „in-order”
B) zwiedzanie rekurencyjne „pre-order”
C) zwiedzanie rekurencyjne „post-order”
D) zwiedzanie nierekurencyjne ze stosem „pre-order”
E) zwiedzanie nierekurencyjne ze stosem „post-order” (procedura własna 1)
F) zwiedzanie nierekurencyjne bez stosu „post-order” (procedura własna 2)
G)zwiedzanie nierekurencyjne z kolejką, horyzontalne
Przy badaniu algorytmów pominięto analizę liczby kopiowań (zgodnie z założeniami opisanymi na wstępie). Maksymalny rozmiar stosu programu i stosu danych przyjęto jako jedną zmienną dla porównań.
Tak samo ujednolicona została liczba odłożeń na stos i do kolejki.
Badano funkcje rekurencyjną „pre-order” bez poprawek proponowanych we wcześniejszej części tekstu.
Badanie zapotrzebowania algorytmu na zasoby można podzieli na 2 części:
Zasadniczą - zapotrzebowanie na zasoby pamięci – badane na podstawie rozmiarów stosu/kolejki
Dodatkową - złożoność obliczeniowa(można dyskutować, czy jest to zasób w pełnym tego słowa znaczeniu) – badana na podstawie liczby porównań, odłożeń danych na stos oraz czasu wykonywania algorytmu.
Zapotrzebowanie na pamięć – rozmiary stosu/kolejki
Algorytmy F i G nie używają stosu ani kolejki, a więc ich złożoność pamięciowa jest stała, klasy O(1)
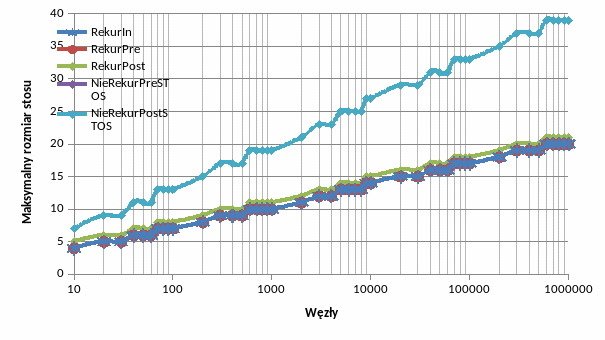
Złożoność pamięciowa – ze względu na rozmiary stosu danych/programu jest w przybliżeniu logarytmiczna (klasy O(log10n)). Dokładniej złożoność można wyrazić jako K*log10n , gdzie K jest współczynnikiem kierunkowym. Dla alg. A, B, C, D współczynnik K wynosi około. 3.2, dla algorytmu własnego E – 6.4, czyli 2 razy więcej. Jest to związane z tym, że w przypadku przechodzenia drzewa „post-order” na stosie muszą być zapamiętane po 2 węzły z wyższych poziomów drzewa niż poziom węzła aktualnie przetwarzanego. W wersji „pre-order” wystarczy pamiętać 1 węzeł. Wersja rekurencyjna przechodzenia przez drzewo „post-order” cechuje się niższym zapotrzebowaniem na pamięć, zawsze jedynie 1 element większym niż alg. A, B, D (które posiadają identyczne zapotrzebowanie), ponieważ działanie stosu wywołań funkcji programu jest odmienne niż stosu danych. Tam dodatkowo pamiętany jest punkt w kodzie z którego nastąpił skok do następnego wywołania rekurencyjnego, dzięki czemu działa logika programowa, która pozwala na pamiętanie mniejszej liczby danych na stosie (podobnie jak w wersji 2 algorytmu pisanego samodzielnie logika pozwoliła całkowicie wyeliminować stos).
Dla każdego z tych algorytmów praktyczne rozważania na temat zajętości pamięciowej stosu są jednak mało istotne, gdyż rozmiary stosu dla dużych ilości węzłów, rzędu milionów, nie przekraczają kilkudziesięciu (co nie powinno także spowodować przepełnienia stosu wywołań programu).
Zupełnie inną złożonością pamięciową charakteryzuje się algorytm przechodzenia horyzontalnego przez drzewo, z kolejką. Kolejka jest alokowana na rozmiar równy ilości węzłów, a więc złożoność pamięciowa jest liniowa, O(n). Jest to wynik dużo gorszy od poprzednich algorytmów.
W praktyce przy lepszej implementacji algorytmu wystarczyłby rozmiar kolejki równy połowie liczby węzłów (zaokrąglanej w górę).
Złożoność obliczeniowa
Liczba operacji elementarnych na stosie/kolejce danych:

Jak widać liczba operacji na stosie/kolejce rośnie liniowo wraz ze wzrostem liczby węzłów (O(n)). Dokładniej jest to K*n, gdzie n to liczba węzłów, a K współczynnik. Liczba operacji jest identyczna dla algorytmów NieRekurPreSTOS i NieRekurHoryzont – K=1. Dla algorytmu NieRekurPostSTOS K=1.5.
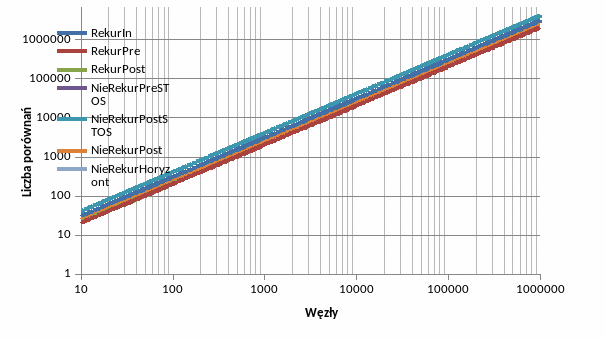
Liczba porównań choć nie jest czynnikiem tak miarodajnym dla złożoności algorytmu jako operacja elementarna jak liczba operacji na stosie/kolejce, jednak jak widać także wskazuje na złożoność liniową algorytmów postaci K*n. Współczynniki K dla kolejnych algorytmów (jak wypunktowano A-G) są równe kolejno: 3, 2, 2, 2, 4, 2.5, 2.
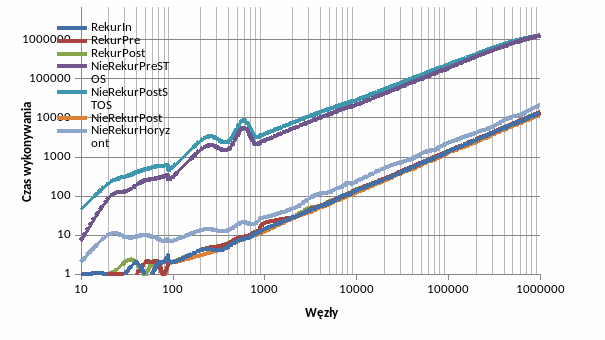
Wahania wartości dla małej ilości węzłów należy uznać za błąd pomiarowy i wiązać z pasożytniczym obciążeniem procesora przez inne procesy w systemie (co sprawdzono powtarzając pomiar).
Złożoność czasowa i tym samym obliczeniowa dla wszystkich algorytmów jest w przybliżeniu liniowa - O(n). Dokładniej określana jest przez AnB, gdzie współczynniki B są bliskie jedności(nieco poniżej), natomiast współczynniki A dla kolejnych algorytmów A-G to około: 0.015, 0.015, 0.015, 5.86, 11.33, 0.012, 0.028. Oczywiście współczynniki te silnie zależą od sprzętu, na którym wykonywany jest algorytm jak i innych czynników jak stopień optymalizacji programu podczas kompilacji. Pozwalają jednak na obserwację generalnych zależności między algorytmami.
Tak więc choć algorytmy są tej samej klasy złożoności zdecydowanie najwolniejsze okazują się te z wykorzystaniem stosu danych. Operacje na stosie zajmują dużo czasu, ponieważ wewnętrznie są one złożone – w szczególności wiążą się z przydzielaniem i zwalnianiem pamięci dla elementów stosu.
Algorytm oparty o kolejkę, bardzo podobny do tych ze stosem jest od nich znacznie szybszy (prawie tak szybki jak procedury rekurencyjne i alg.2 napisany przeze mnie) ze względu na krótki czas wykonywania elementarnych operacji na kolejce – okupione jest to niestety dużą zajętością pamięciową.
W tym miejscu należy zauważyć, że dla struktury drzewa takiej jak w badanym programie – w postaci kopca o reprezentacji w jednowymiarowej tablicy danych – kolejność przechodzenia po węzłach taką jak w algorytmie z kolejką można uzyskać bez użycia kolejki, po prostu przechodząc po kolejnych elementach z tablicy z drzewem.
Algorytmy rekurencyjne in-, pre- i post-order cechują się prawie jednakową złożonością czasową (jak również ze względu na inne czynniki). Nie jest to zaskoczeniem, gdyż algorytmy te są prawie identyczne.
Najlepszą złożonością czasową, odrobinę lepszą od algorytmów rekurencyjnych cechuje się zaimplementowany przeze mnie algorytm nierekurencyjny w wersji 2(bez stosu). Dodatkowo posiada stałe, znikome zapotrzebowanie na pamięć i nie powoduje wzrostu stosu wywołań programu jak alg. rekurencyjne.
Zad 12. „Rozszerzyć funkcjonalność metody LiczPostFix o działania ‘-‘ i ‘/’ ”
Rozszerzenie działalności metody o dodatkowe operatory sprowadzało się do rozbudowania jej o analogiczne bloki jak dla innych operacji. Dla operatorów odejmowania i dzielenia ważna jest kolejność operandów, jednak w tym przypadku jest ona prawidłowa.
double
PostFix::LiczPostFix() {
double
Wartosc=0;
if(++this->ZA.GlStoPr>this->ZA.GlStoPrMax)this->ZA.GlStoPrMax=this->ZA.GlStoPr;
while((Dane[PostFixIndex]=='
')&&(PostFixIndex<(int)strlen(Dane)))PostFixIndex++;
this->ZA.LiPor++;
if(Dane[PostFixIndex]=='+'){
PostFixIndex++;
Wartosc=LiczPostFix()+LiczPostFix();
this->ZA.GlStoPr--;
return
Wartosc;
}else
if(Dane[PostFixIndex]=='*'){
PostFixIndex++;
Wartosc=LiczPostFix()*LiczPostFix();
this->ZA.GlStoPr--;
return
Wartosc;
}
else
if(Dane[PostFixIndex]=='-'){
PostFixIndex++;
Wartosc=LiczPostFix()-LiczPostFix();
this->ZA.GlStoPr--;
return
Wartosc;
}
else
if(Dane[PostFixIndex]=='/'){
PostFixIndex++;
Wartosc=LiczPostFix()/LiczPostFix();
this->ZA.GlStoPr--;
return
Wartosc;
}
while((Dane[PostFixIndex]>='0')&&(Dane[PostFixIndex]<='9')){
Wartosc=10*Wartosc+(Dane[PostFixIndex++]-'0');
}
this->ZA.GlStoPr--;
return
Wartosc; };
Zad 11. „Przeprowadzić analizę działania i wydajności działania algorytmów analizy składniowej (klasa PostFix) i dopisać opcję konwersji postaci infixowej na postfixową (implementacja metody InFix2PostFix klasy)”
Analiza działania funkcji LiczPostFix:
Na wstępie należy zauważyć, że dana w programie testowym funkcja LiczPostFix w rzeczywistości oblicza wyrażenia w notacji prefixowej(notacji polskiej), jej nazwa jest więc myląca, a wręcz nieprawidłowa.
Funkcja zbudowana jest rekurencyjnie. Wszystkie rekurencyjne wywołania funkcji operują jednak na wspólnym globalnym indeksie PostFixIndex, który wskazuje na aktualnie przetwarzany znak z obliczanego wyrażenia. Wyrażenie odczytywane jest od lewej do prawej – zmienna PostFixIndex jest zawsze zwiększana.
Każde z wewnętrznych wywołań funkcji przetwarza 1 działanie lub odczytuje liczbę(ostatnia pętla while), która może być złożona z kilku znaków w tekście wejściowym i zwraca ją jako liczbę typu double. Odstępy w tekście wejściowym są pomijane poprzez pierwszą pętlę while.
Gdy funkcja natrafi na znak operatora wykonuje przypisane mu działanie biorąc za argumenty wartości zwrócone przez kolejne wywołania rekurencyjne funkcji. Każde z wywołań rekurencyjnych odczytuje liczbę i zwraca ją lub samo także wykonuje działania odczytując dalszą część wyrażenia i zwraca obliczoną wartość będącą argumentem dla bardziej zewnętrznego wywołania. Po wyznaczeniu lewego argumentu dla operatora wyznaczany jest prawy – cały czas przesuwając się w prawą stronę przetwarzanego tekstu.
Jeśli wyrażenie jest zapisane prawidłowo wszystkie wywołania rekurencyjne kończą się po przetworzeniu ostatniego znaku i najbardziej zewnętrzne wywołanie funkcji zwraca ostateczny wynik.
Dodatkowo warto zauważyć, że w zapisie obliczanego wyrażenia nie są wymagane odstępy między znakami, z wyjątkiem sytuacji, gdy występują kolejno 2 liczby.
Funkcja dla przykładowego wyrażenia wejściowego "/ - * + 7 * * 4 6 + 8 9 5 75 2" , które można przekształcić na naturalną dla człowieka postać infiksową ((7 + 4*6*(8+9))*5 - 75)/2 zwraca prawidłową wartość 1000.
Implementacja i opis działania funkcji InFix2PostFix:
void
PostFix::InFix2PostFix(char*
infix) { char
c, o; if(++this->ZA.GlStoPr>this->ZA.GlStoPrMax)this->ZA.GlStoPrMax=this->ZA.GlStoPr; while((infix[PostFixIndex]=='
')&&(PostFixIndex<(int)strlen(infix)))
PostFixIndex++; c
= infix[PostFixIndex]; ++PostFixIndex; if
(c == '(')
{ InFix2PostFix(infix);
//oblicza
i wypisuje lewy argument while((infix[PostFixIndex]=='
')&&(PostFixIndex<(int)strlen(infix)))
PostFixIndex++; o
= infix[PostFixIndex]; ++PostFixIndex; //odczytuje
operator InFix2PostFix(infix);//oblicza
i wypisuje prawy argument ++PostFixIndex;
//pomija
prawy nawias printf("%c
",
o); //wypisuje
operator } else
//wypisuje
liczbę { while(1) { printf("%c",
c); //wypisujemy
cyfrę c
= infix[PostFixIndex]; //odczytujemy
następny znak //jeśli
znak jest cyfrą kontynuujemy pętlę if
( c >= '0'
&& c<='9'
) ++PostFixIndex; else
break; } printf("
"); } this->ZA.GlStoPr--; }
Funkcja konwertuje zapis infiksowy – gdzie operator znajduje się między operandami - do postfiksowego, Odwrotnej Notacji Polskiej.
Ta implementacja działa prawidłowo tylko dla w pełni onawiasowanych wyrażeń typu infiks – gdzie każdy operator posiada odpowiadającą mu parę nawiasów ograniczającą jego argumenty. Pozwala to na jednoznaczne określenie kolejności działań.
Możliwe jest również skonstruowanie nieco bardziej złożonego algorytmu nie wymagającego kompletu nawiasów, w razie ich braku wykonującego działania według ustalonego priorytetu operatorów. Ogranicza to jednak zastosowanie do zestawu operatorów i przypisanych im priorytetów w danej implementacji funkcji.
Ponieważ w poleceniu nie było sprecyzowane jak dokładnie ma się zachowywać ta funkcja, wybrałem opcję pierwszą.
Funkcja w sposób rekurencyjny przetwarza ciąg wejściowy znak po znaku od lewej do prawej – podobnie jak funkcja LiczPostFix korzysta z globalnego indeksu PostFixIndex.
Wynik działania na bieżąco wypisuje na standardowym wyjściu (możliwa jest także implementacja zapisująca do bufora, jednak nie było to sprecyzowane w zadaniu).
Wywołana funkcja znajdując się na danej pozycji w wyrażeniu pomija odstępy – spacje i jeśli odczytany znak jest inny niż lewy nawias – po prostu wypisuje go na wyjście (powinna być to zawsze liczba, pętla while pozwala na odczytywanie liczb więcej niż jednocyfrowych) . Jeśli znakiem tym jest prawy nawias funkcja odczytuje całe wyrażenie aż do prawego nawiasu. Za pomocą rekurencji odczytuje i wypisuje najpierw lewy argument, potem prawy, a na końcu wypisywany jest operator odczytywany między argumentami. Działanie dobrze opisują też komentarze w kodzie.
Funkcja dla przykładowego ciągu wejściowego "((7 + ((4 * 6) * (8 + 9))) * 10)" daje prawidłowy wynik 7 4 6 * 8 9 + * + 10 *
Analiza wydajności działania funkcji LiczPostFix:
Ponieważ liczba różnych operacji elementarnych jest dość duża, a porównania czy też kopiowania(przypisania) nie są czynnikiem dominującym, decydującym o wydajności algorytmu toteż badanie wydajności będę opierał jedynie na pomiarach czasu działania funkcji.
Do badania podaję coraz więcej sklejanych ze sobą wyrażeń postaci: (((18-10)/(5+3))*1), (zapisanych w programie w formie prefiksowej „* / - 18 10 + 5 3 1”), którego to wynikiem jest 1. Wyrażenia te łącze kolejno operatorami + - * / + - * / itd. .
W rezultacie otrzymujemy coraz dłuższe wyrażenie o zwiększającym się stopniu złożoności pod względem poziomów działań i o zrównoważonej liczbie różnych operatorów.
Szczegóły implementacyjne prowadzące do spreparowania takich wyrażeń i zmierzenia dla nich czasu działania algorytmu pomijam jako nie będące przedmiotem zainteresowania.
Liczba działań = 5*liczba sklejeń. Maksymalna głębokość stosu = liczba sklejeń + 4 (w tym przypadku max głębokość stosu rośnie liniowo, jednak zależy to silnie od postaci obliczanego wyrażenia).
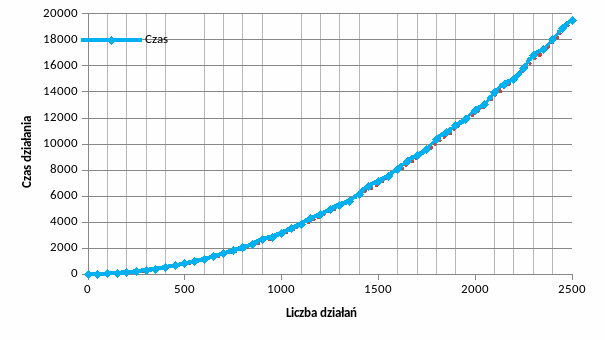
Krzywa aproksymacyjna ma postać 0.0031*n2. Algorytm ten ma więc złożoność kwadratową O(n2) w zależności od liczby działań.
Analiza wydajności funkcji Infix2PostFix:
Analiza została przeprowadzona analogicznie do powyższej. Kolejnymi operatorami w coraz dłuższe i bardziej złożone wyrażenie sklejane były wyrażenia: (((18-10)/(5+3))*1)
Dla celów pomiarów czasu w funkcji wykomentowane zostały instrukcje printf.
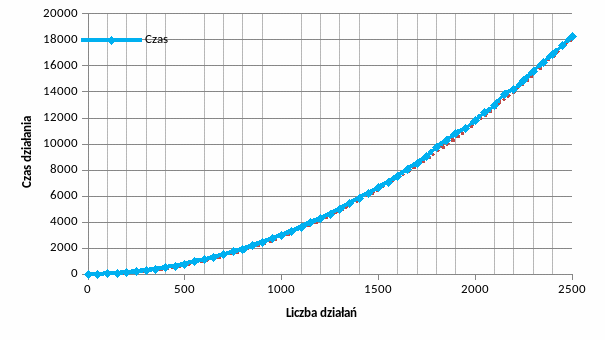
Krzywa aproksymacyjna ma postać 0.0029*n2. Algorytm ten ma więc złożoność kwadratową O(n2) w zależności od liczby działań.
4) Zebrane wyniki
|
|
|
RekurIn |
|
RekurPre |
|
RekurPost |
|||||||||
|
Liczność |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
|
10 |
|
2 |
30 |
4 |
0 |
|
2 |
20 |
4 |
0 |
|
3 |
21 |
5 |
0 |
|
20 |
|
4 |
60 |
5 |
0 |
|
4 |
40 |
5 |
0 |
|
5 |
41 |
6 |
0 |
|
30 |
|
6 |
90 |
5 |
0 |
|
5 |
60 |
5 |
0 |
|
6 |
61 |
6 |
0 |
|
40 |
|
7 |
120 |
6 |
0 |
|
7 |
80 |
6 |
0 |
|
7 |
81 |
7 |
0 |
|
50 |
|
8 |
150 |
6 |
0 |
|
7 |
100 |
6 |
0 |
|
9 |
101 |
7 |
0 |
|
60 |
|
9 |
180 |
6 |
0 |
|
10 |
120 |
6 |
0 |
|
10 |
121 |
7 |
0 |
|
70 |
|
11 |
210 |
7 |
0 |
|
11 |
140 |
7 |
0 |
|
11 |
141 |
8 |
0 |
|
80 |
|
13 |
240 |
7 |
0 |
|
12 |
160 |
7 |
0 |
|
12 |
161 |
8 |
0 |
|
90 |
|
15 |
270 |
7 |
0 |
|
14 |
180 |
7 |
0 |
|
14 |
181 |
8 |
0 |
|
100 |
|
16 |
300 |
7 |
0 |
|
15 |
200 |
7 |
0 |
|
15 |
201 |
8 |
0 |
|
200 |
|
30 |
600 |
8 |
0 |
|
29 |
400 |
8 |
0 |
|
30 |
401 |
9 |
0 |
|
300 |
|
44 |
900 |
9 |
0 |
|
43 |
600 |
9 |
0 |
|
44 |
601 |
10 |
0 |
|
400 |
|
59 |
1200 |
9 |
0 |
|
57 |
800 |
9 |
0 |
|
58 |
801 |
10 |
0 |
|
500 |
|
74 |
1500 |
9 |
0 |
|
70 |
1000 |
9 |
0 |
|
73 |
1001 |
10 |
0 |
|
600 |
|
87 |
1800 |
10 |
0 |
|
84 |
1200 |
10 |
0 |
|
91 |
1201 |
11 |
0 |
|
700 |
|
104 |
2100 |
10 |
0 |
|
99 |
1400 |
10 |
0 |
|
101 |
1401 |
11 |
0 |
|
800 |
|
118 |
2400 |
10 |
0 |
|
117 |
1600 |
10 |
0 |
|
115 |
1601 |
11 |
0 |
|
900 |
|
129 |
2700 |
10 |
0 |
|
127 |
1800 |
10 |
0 |
|
130 |
1801 |
11 |
0 |
|
1000 |
|
144 |
3000 |
10 |
0 |
|
146 |
2000 |
10 |
0 |
|
144 |
2001 |
11 |
0 |
|
2000 |
|
284 |
6000 |
11 |
0 |
|
280 |
4000 |
11 |
0 |
|
292 |
4001 |
12 |
0 |
|
3000 |
|
430 |
9000 |
12 |
0 |
|
420 |
6000 |
12 |
0 |
|
437 |
6001 |
13 |
0 |
|
4000 |
|
574 |
12000 |
12 |
0 |
|
567 |
8000 |
12 |
0 |
|
578 |
8001 |
13 |
0 |
|
5000 |
|
718 |
15000 |
13 |
0 |
|
705 |
10000 |
13 |
0 |
|
728 |
10001 |
14 |
0 |
|
6000 |
|
862 |
18000 |
13 |
0 |
|
850 |
12000 |
13 |
0 |
|
867 |
12001 |
14 |
0 |
|
7000 |
|
1004 |
21000 |
13 |
0 |
|
988 |
14000 |
13 |
0 |
|
1014 |
14001 |
14 |
0 |
|
8000 |
|
1138 |
24000 |
13 |
0 |
|
1125 |
16000 |
13 |
0 |
|
1171 |
16001 |
14 |
0 |
|
9000 |
|
1305 |
27000 |
14 |
0 |
|
1290 |
18000 |
14 |
0 |
|
1315 |
18001 |
15 |
0 |
|
10000 |
|
1433 |
30000 |
14 |
0 |
|
1409 |
20000 |
14 |
0 |
|
1438 |
20001 |
15 |
0 |
|
20000 |
|
2859 |
60000 |
15 |
0 |
|
2816 |
40000 |
15 |
0 |
|
2870 |
40001 |
16 |
0 |
|
30000 |
|
4283 |
90000 |
15 |
0 |
|
4212 |
60000 |
15 |
0 |
|
4355 |
60001 |
16 |
0 |
|
40000 |
|
5696 |
120000 |
16 |
0 |
|
5618 |
80000 |
16 |
0 |
|
5752 |
80001 |
17 |
0 |
|
50000 |
|
7122 |
150000 |
16 |
0 |
|
7032 |
100000 |
16 |
0 |
|
7268 |
100001 |
17 |
0 |
|
60000 |
|
8623 |
180000 |
16 |
0 |
|
8423 |
120000 |
16 |
0 |
|
8820 |
120001 |
17 |
0 |
|
70000 |
|
10029 |
210000 |
17 |
0 |
|
9853 |
140000 |
17 |
0 |
|
10002 |
140001 |
18 |
0 |
|
80000 |
|
11442 |
240000 |
17 |
0 |
|
11320 |
160000 |
17 |
0 |
|
11478 |
160001 |
18 |
0 |
|
90000 |
|
12848 |
270000 |
17 |
0 |
|
12832 |
180000 |
17 |
0 |
|
13060 |
180001 |
18 |
0 |
|
100000 |
|
14260 |
300000 |
17 |
0 |
|
14068 |
200000 |
17 |
0 |
|
14410 |
200001 |
18 |
0 |
|
200000 |
|
28475 |
600000 |
18 |
0 |
|
28093 |
400000 |
18 |
0 |
|
28793 |
400001 |
19 |
0 |
|
300000 |
|
42773 |
900000 |
19 |
0 |
|
42151 |
600000 |
19 |
0 |
|
43198 |
600001 |
20 |
0 |
|
400000 |
|
57077 |
1200000 |
19 |
0 |
|
56185 |
800000 |
19 |
0 |
|
57686 |
800001 |
20 |
0 |
|
500000 |
|
71284 |
1500000 |
19 |
0 |
|
70211 |
1000000 |
19 |
0 |
|
72013 |
1000001 |
20 |
0 |
|
600000 |
|
85800 |
1800000 |
20 |
0 |
|
84282 |
1200000 |
20 |
0 |
|
86451 |
1200001 |
21 |
0 |
|
700000 |
|
99806 |
2100000 |
20 |
0 |
|
98409 |
1400000 |
20 |
0 |
|
100968 |
1400001 |
21 |
0 |
|
800000 |
|
113665 |
2400000 |
20 |
0 |
|
112764 |
1600000 |
20 |
0 |
|
115263 |
1600001 |
21 |
0 |
|
900000 |
|
128549 |
2700000 |
20 |
0 |
|
126659 |
1800000 |
20 |
0 |
|
130204 |
1800001 |
21 |
0 |
|
1000000 |
|
143110 |
3000000 |
20 |
0 |
|
141016 |
2000000 |
20 |
0 |
|
144019 |
2000001 |
21 |
0 |
|
|
|
NieRekurPreSTOS |
|
NieRekurPostSTOS |
|
NieRekurPost |
|||||||||||||
|
Liczność |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
||||
|
10 |
|
89 |
21 |
4 |
10 |
|
121 |
40 |
7 |
14 |
|
2 |
26 |
0 |
0 |
||||
|
20 |
|
175 |
41 |
5 |
20 |
|
235 |
80 |
9 |
29 |
|
3 |
51 |
0 |
0 |
||||
|
30 |
|
244 |
61 |
5 |
30 |
|
338 |
120 |
9 |
44 |
|
3 |
76 |
0 |
0 |
||||
|
40 |
|
299 |
81 |
6 |
40 |
|
424 |
160 |
11 |
59 |
|
4 |
101 |
0 |
0 |
||||
|
50 |
|
347 |
101 |
6 |
50 |
|
496 |
200 |
11 |
74 |
|
5 |
126 |
0 |
0 |
||||
|
60 |
|
384 |
121 |
6 |
60 |
|
548 |
240 |
11 |
89 |
|
6 |
151 |
0 |
0 |
||||
|
70 |
|
404 |
141 |
7 |
70 |
|
574 |
280 |
13 |
104 |
|
6 |
176 |
0 |
0 |
||||
|
80 |
|
413 |
161 |
7 |
80 |
|
566 |
320 |
13 |
119 |
|
7 |
201 |
0 |
0 |
||||
|
90 |
|
400 |
181 |
7 |
90 |
|
548 |
360 |
13 |
134 |
|
8 |
226 |
0 |
0 |
||||
|
100 |
|
979 |
201 |
7 |
100 |
|
1405 |
400 |
13 |
149 |
|
8 |
251 |
0 |
0 |
||||
|
200 |
|
1677 |
401 |
8 |
200 |
|
2394 |
800 |
15 |
299 |
|
16 |
501 |
0 |
0 |
||||
|
300 |
|
1881 |
601 |
9 |
300 |
|
2655 |
1200 |
17 |
449 |
|
25 |
751 |
0 |
0 |
||||
|
400 |
|
5190 |
801 |
9 |
400 |
|
7585 |
1600 |
17 |
599 |
|
32 |
1001 |
0 |
0 |
||||
|
500 |
|
4873 |
1001 |
9 |
500 |
|
7046 |
2000 |
17 |
749 |
|
40 |
1251 |
0 |
0 |
||||
|
600 |
|
3560 |
1201 |
10 |
600 |
|
4942 |
2400 |
19 |
899 |
|
49 |
1501 |
0 |
0 |
||||
|
700 |
|
1065 |
1401 |
10 |
700 |
|
6141 |
2800 |
19 |
1049 |
|
61 |
1751 |
0 |
0 |
||||
|
800 |
|
1137 |
1601 |
10 |
800 |
|
5299 |
3200 |
19 |
1199 |
|
64 |
2001 |
0 |
0 |
||||
|
900 |
|
1201 |
1801 |
10 |
900 |
|
10869 |
3600 |
19 |
1349 |
|
72 |
2251 |
0 |
0 |
||||
|
1000 |
|
1684 |
2001 |
10 |
1000 |
|
12829 |
4000 |
19 |
1499 |
|
80 |
2501 |
0 |
0 |
||||
|
2000 |
|
10694 |
4001 |
11 |
2000 |
|
26594 |
8000 |
21 |
2999 |
|
160 |
5001 |
0 |
0 |
||||
|
3000 |
|
23768 |
6001 |
12 |
3000 |
|
41026 |
12000 |
23 |
4499 |
|
240 |
7501 |
0 |
0 |
||||
|
4000 |
|
27201 |
8001 |
12 |
4000 |
|
38110 |
16000 |
23 |
5999 |
|
329 |
10001 |
0 |
0 |
||||
|
5000 |
|
21642 |
10001 |
13 |
5000 |
|
27883 |
20000 |
25 |
7499 |
|
398 |
12501 |
0 |
0 |
||||
|
6000 |
|
48471 |
12001 |
13 |
6000 |
|
67360 |
24000 |
25 |
8999 |
|
481 |
15001 |
0 |
0 |
||||
|
7000 |
|
40723 |
14001 |
13 |
7000 |
|
59170 |
28000 |
25 |
10499 |
|
563 |
17501 |
0 |
0 |
||||
|
8000 |
|
79364 |
16001 |
13 |
8000 |
|
111086 |
32000 |
25 |
11999 |
|
631 |
20001 |
0 |
0 |
||||
|
9000 |
|
71327 |
18001 |
14 |
9000 |
|
98127 |
36000 |
27 |
13499 |
|
718 |
22501 |
0 |
0 |
||||
|
10000 |
|
60706 |
20001 |
14 |
10000 |
|
81120 |
40000 |
27 |
14999 |
|
802 |
25001 |
0 |
0 |
||||
|
20000 |
|
842606 |
40001 |
15 |
20000 |
|
1239496 |
80000 |
29 |
29999 |
|
1582 |
50001 |
0 |
0 |
||||
|
30000 |
|
202481 |
60001 |
15 |
30000 |
|
269580 |
120000 |
29 |
44999 |
|
2384 |
75001 |
0 |
0 |
||||
|
40000 |
|
255525 |
80001 |
16 |
40000 |
|
336854 |
160000 |
31 |
59999 |
|
3152 |
100001 |
0 |
0 |
||||
|
50000 |
|
219240 |
100001 |
16 |
50000 |
|
268255 |
200000 |
31 |
74999 |
|
3972 |
125001 |
0 |
0 |
||||
|
60000 |
|
215626 |
120001 |
16 |
60000 |
|
251121 |
240000 |
31 |
89999 |
|
4743 |
150001 |
0 |
0 |
||||
|
70000 |
|
446667 |
140001 |
17 |
70000 |
|
583208 |
280000 |
33 |
104999 |
|
5517 |
175001 |
0 |
0 |
||||
|
80000 |
|
298515 |
160001 |
17 |
80000 |
|
350027 |
320000 |
33 |
119999 |
|
6283 |
200001 |
0 |
0 |
||||
|
90000 |
|
336898 |
180001 |
17 |
90000 |
|
391707 |
360000 |
33 |
134999 |
|
7126 |
225001 |
0 |
0 |
||||
|
100000 |
|
364647 |
200001 |
17 |
100000 |
|
419702 |
400000 |
33 |
149999 |
|
7935 |
250001 |
0 |
0 |
||||
|
200000 |
|
515030 |
400001 |
18 |
200000 |
|
506943 |
800000 |
35 |
299999 |
|
15805 |
500001 |
0 |
0 |
||||
|
300000 |
|
741948 |
600001 |
19 |
300000 |
|
697041 |
1200000 |
37 |
449999 |
|
23588 |
750001 |
0 |
0 |
||||
|
400000 |
|
947372 |
800001 |
19 |
400000 |
|
865438 |
1600000 |
37 |
599999 |
|
31487 |
1000001 |
0 |
0 |
||||
|
500000 |
|
1142335 |
1000001 |
19 |
500000 |
|
1119490 |
2000000 |
37 |
749999 |
|
39707 |
1250001 |
0 |
0 |
||||
|
600000 |
|
1308331 |
1200001 |
20 |
600000 |
|
1620976 |
2400000 |
39 |
899999 |
|
47383 |
1500001 |
0 |
0 |
||||
|
700000 |
|
1446581 |
1400001 |
20 |
700000 |
|
2706125 |
2800000 |
39 |
1049999 |
|
55651 |
1750001 |
0 |
0 |
||||
|
800000 |
|
1584267 |
1600001 |
20 |
800000 |
|
3879711 |
3200000 |
39 |
1199999 |
|
62966 |
2000001 |
0 |
0 |
||||
|
900000 |
|
1696239 |
1800001 |
20 |
900000 |
|
4641289 |
3600000 |
39 |
1349999 |
|
71217 |
2250001 |
0 |
0 |
||||
|
1000000 |
|
1796865 |
2000001 |
20 |
1000000 |
|
5381087 |
4000000 |
39 |
1499999 |
|
78939 |
2500001 |
0 |
0 |
||||
|
|
|
NieRekurHoryzont |
|||
|
Liczność |
|
Czas |
Porównania |
MaxStos |
Odłożeń |
|
10 |
|
13 |
20 |
0 |
10 |
|
20 |
|
15 |
40 |
0 |
20 |
|
30 |
|
17 |
60 |
0 |
30 |
|
40 |
|
19 |
80 |
0 |
40 |
|
50 |
|
20 |
100 |
0 |
50 |
|
60 |
|
22 |
120 |
0 |
60 |
|
70 |
|
23 |
140 |
0 |
70 |
|
80 |
|
25 |
160 |
0 |
80 |
|
90 |
|
27 |
180 |
0 |
90 |
|
100 |
|
35 |
200 |
0 |
100 |
|
200 |
|
56 |
400 |
0 |
200 |
|
300 |
|
75 |
600 |
0 |
300 |
|
400 |
|
106 |
800 |
0 |
400 |
|
500 |
|
126 |
1000 |
0 |
500 |
|
600 |
|
155 |
1200 |
0 |
600 |
|
700 |
|
170 |
1400 |
0 |
700 |
|
800 |
|
195 |
1600 |
0 |
800 |
|
900 |
|
222 |
1800 |
0 |
900 |
|
1000 |
|
240 |
2000 |
0 |
1000 |
|
2000 |
|
467 |
4000 |
0 |
2000 |
|
3000 |
|
711 |
6000 |
0 |
3000 |
|
4000 |
|
954 |
8000 |
0 |
4000 |
|
5000 |
|
1160 |
10000 |
0 |
5000 |
|
6000 |
|
1410 |
12000 |
0 |
6000 |
|
7000 |
|
1653 |
14000 |
0 |
7000 |
|
8000 |
|
1904 |
16000 |
0 |
8000 |
|
9000 |
|
2080 |
18000 |
0 |
9000 |
|
10000 |
|
2335 |
20000 |
0 |
10000 |
|
20000 |
|
4694 |
40000 |
0 |
20000 |
|
30000 |
|
7013 |
60000 |
0 |
30000 |
|
40000 |
|
9228 |
80000 |
0 |
40000 |
|
50000 |
|
11571 |
100000 |
0 |
50000 |
|
60000 |
|
14022 |
120000 |
0 |
60000 |
|
70000 |
|
16069 |
140000 |
0 |
70000 |
|
80000 |
|
18471 |
160000 |
0 |
80000 |
|
90000 |
|
20837 |
180000 |
0 |
90000 |
|
100000 |
|
23236 |
200000 |
0 |
100000 |
|
200000 |
|
46097 |
400000 |
0 |
200000 |
|
300000 |
|
68603 |
600000 |
0 |
300000 |
|
400000 |
|
92146 |
800000 |
0 |
400000 |
|
500000 |
|
116287 |
1000000 |
0 |
500000 |
|
600000 |
|
136890 |
1200000 |
0 |
600000 |
|
700000 |
|
160897 |
1400000 |
0 |
700000 |
|
800000 |
|
184873 |
1600000 |
0 |
800000 |
|
900000 |
|
209289 |
1800000 |
0 |
900000 |
|
1000000 |
|
232677 |
2000000 |
0 |
1000000 |
|
Działania |
Czas LiczPostFix |
Czas InFix2PostFix |
|
0 |
1 |
2 |
|
50 |
12 |
15 |
|
100 |
38 |
44 |
|
150 |
77 |
87 |
|
200 |
136 |
144 |
|
250 |
208 |
221 |
|
300 |
303 |
301 |
|
350 |
394 |
400 |
|
400 |
522 |
519 |
|
450 |
652 |
643 |
|
500 |
803 |
784 |
|
550 |
975 |
986 |
|
600 |
1147 |
1115 |
|
650 |
1352 |
1313 |
|
700 |
1576 |
1496 |
|
750 |
1807 |
1721 |
|
800 |
2042 |
1943 |
|
850 |
2298 |
2187 |
|
900 |
2672 |
2459 |
|
950 |
2864 |
2723 |
|
1000 |
3163 |
3010 |
|
1050 |
3492 |
3299 |
|
1100 |
3855 |
3615 |
|
1150 |
4265 |
3976 |
|
1200 |
4589 |
4280 |
|
1250 |
4957 |
4634 |
|
1300 |
5320 |
5019 |
|
1350 |
5628 |
5450 |
|
1400 |
6167 |
5842 |
|
1450 |
6772 |
6242 |
|
1500 |
7123 |
6637 |
|
1550 |
7541 |
7076 |
|
1600 |
8064 |
7551 |
|
1650 |
8690 |
8046 |
|
1700 |
9104 |
8546 |
|
1750 |
9597 |
9086 |
|
1800 |
10349 |
9719 |
|
1850 |
10870 |
10250 |
|
1900 |
11391 |
10822 |
|
1950 |
11889 |
11193 |
|
2000 |
12579 |
11820 |
|
2050 |
13067 |
12389 |
|
2100 |
13932 |
12952 |
|
2150 |
14603 |
13793 |
|
2200 |
14988 |
14192 |
|
2250 |
15779 |
14863 |
|
2300 |
16775 |
15586 |
|
2350 |
17250 |
16246 |
|
2400 |
18003 |
16891 |
|
2450 |
18840 |
17545 |
|
2500 |
19516 |
18291 |
Wyszukiwarka
Podobne podstrony:
więcej podobnych podstron